| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
§ 1. Прямоугольные координаты.
Укажем теперь способ, позволяющий определять положение любой точки пространства числами.
Через некоторую точку О пространства проведем три взаимно перпендикулярные оси Ох, Оу, Oz — оси координат, относительно которых мы будем определять положение точек пространства. Оси координат обычно располагают так, как это указано на рис. 82; оси Ох и Оу — горизонтально, а ось Oz — вертикально; при этом ось Ох направляют вперед (в сторону читателя), ось  — слева направо, ось Oz — снизу вверх. Ось Ох называется осью абсцисс, Оу — осью ординат, Oz — осью аппликат. Точка пересечения координатных осей называется началом координат. Наконец, выберем единицу масштаба.
— слева направо, ось Oz — снизу вверх. Ось Ох называется осью абсцисс, Оу — осью ординат, Oz — осью аппликат. Точка пересечения координатных осей называется началом координат. Наконец, выберем единицу масштаба.

Рис. 82
Теперь положение всякой точки пространства можно определить тремя действительными числами — координатами этой точки.
В самом деле, всякой точке  соответствует три точки Р, Q, R на осях координат, являющиеся ее проекциями на эти оси. Обратно, зная точки Р, Q и R на осях, можно построить единственную точку М в пространстве, для которой Р, Q и R являются проекциями на координатные оси. Таким образом, определение положения точки М сводится к определению положений ее проекций
соответствует три точки Р, Q, R на осях координат, являющиеся ее проекциями на эти оси. Обратно, зная точки Р, Q и R на осях, можно построить единственную точку М в пространстве, для которой Р, Q и R являются проекциями на координатные оси. Таким образом, определение положения точки М сводится к определению положений ее проекций  и R, лежащих соответственно на осях Ох, Оу и Oz. Мы уже знаем, что положение точки Р оси Ох вполне определяется числом х, представляющим собой величину направленного отрезка ОР. Это число х, координата точки Р—проекции точки М на ось Ох, — принимается
и R, лежащих соответственно на осях Ох, Оу и Oz. Мы уже знаем, что положение точки Р оси Ох вполне определяется числом х, представляющим собой величину направленного отрезка ОР. Это число х, координата точки Р—проекции точки М на ось Ох, — принимается
за первую координату точки М и называется ее абсциссой. Совершенно так же положение точек Q и R вполне определяется числами у и z, представляющими собой величины направленных отрезкой OQ и OR. Числа у и z, координаты точек Q и R, — проекций точки М на оси  принимаются соответственно за вторую и третью координаты точки
принимаются соответственно за вторую и третью координаты точки  Вторая координата у называется ординатой и третья z — аппликатой.
Вторая координата у называется ординатой и третья z — аппликатой.

Рис. 83.
Таким образом, положение любой точки  пространства вполне определяется тройкой чисел
пространства вполне определяется тройкой чисел  z, первое из которых является абсциссой точки, второе — ординатой и третье — аппликатой.
z, первое из которых является абсциссой точки, второе — ординатой и третье — аппликатой.
Координаты точки условимся записывать в скобках рядом с буквой, обозначающей ее, ставя на первом месте абсциссу, на втором — ординату и на третьем — аппликату  .
.
Оси координат  взятые попарно, определяют три взаимно перпендикулярные плоскости
взятые попарно, определяют три взаимно перпендикулярные плоскости  называемые плоскостями координат. Эти три плоскости делят все пространство на восемь частей, называемых октантами, причем точкам каждого октанта соответствует определенная комбинация знаков координат (рис. 83):
называемые плоскостями координат. Эти три плоскости делят все пространство на восемь частей, называемых октантами, причем точкам каждого октанта соответствует определенная комбинация знаков координат (рис. 83):

Если точка М лежит в плоскости координат  то
то  аналогично для точек плоскости
аналогично для точек плоскости  координата
координата  для точек плоскости
для точек плоскости  координата
координата  Если точка М лежит на оси Ох, то
Если точка М лежит на оси Ох, то  аналогично для точек оси Оу коордииаты z и
аналогично для точек оси Оу коордииаты z и  равны нулю, для точек оси Oz координаты х и у равны нулю. Наконец, в начале координат
равны нулю, для точек оси Oz координаты х и у равны нулю. Наконец, в начале координат 
Координаты, которые принимаются в описанном способе для определения положения точки, называются прямоугольными., так как точка М определяется пересечением трех плоскостей, пересекающихся
под прямыми углами (см. задачу II), и по имени Декарта — также декартовыми. Из описанного метода координат вытекает решение двух основных задач.
Задача I. По данной точке М определить ее координаты.
Через данную точку М проводим три плоскости параллельно плоскостям координат; три точки Р, Q и R, получающиеся в пересечении этих плоскостей с осями координат Ох, Оу и Oz и являющиеся проекциями точки М на эти оси, определяют три координаты:

Проведенные через точку М три плоскости вместе с тремя координатными плоскостями образуют прямоугольный параллелепипед, ребра которого OP, OQ и OR называются координатными отрезками точки  .
.
Задача II. Зная координаты х, у и z точки М, построить эту точку.
По трем данным числам х, у и z строим три точки Р, Q и R на осях координат, откладывая соответственно по осям отрезки OP, OQ и OR, величины которых равны соответственно х, у и z. Проводя через точки Р, Q и R три плоскости, параллельные плоскостям координат, в пересечении их получим единственную точку М, для которой  z будут координатами.
z будут координатами.
Замечание 1. Если мы условимся рассматривать направленные отрезки PS и  (рис. 82) как отрезки осей, направления которых совпадают с направлениями параллельных им координатных осей, то ордината точки
(рис. 82) как отрезки осей, направления которых совпадают с направлениями параллельных им координатных осей, то ордината точки  будет выражаться не только величиной отрезка OQ, но и равной ей величиной отрезка
будет выражаться не только величиной отрезка OQ, но и равной ей величиной отрезка 
Аналогично аппликата точки  выразится как величиной отрезка OR, так и величиной отрезка
выразится как величиной отрезка OR, так и величиной отрезка 
Тогда при решении этих основных задач не является необходимым проводить плоскости, параллельные плоскостям координат. Так, в задаче I опускаем из данной точки М перпендикуляр на плоскость координат  Его основание 5 (рис. 82) определит проекцию точки М на плоскость
Его основание 5 (рис. 82) определит проекцию точки М на плоскость  Из точки 5 опускаем перпепдикуляр на ось
Из точки 5 опускаем перпепдикуляр на ось  его основание Р определит проекцию точки М на ось
его основание Р определит проекцию точки М на ось 
Следовательно, три звена направленной ломаной линии OPSM определяют три координаты точки М:

Так же при решеиии задачи II откладываем по оси Ох от точки О отрезок длиною  единиц (вперед или назад — смотря по знаку
единиц (вперед или назад — смотря по знаку  ); через конец Р этого отрезка проводим в плоскости хОу прямую параллельно оси Оу и откладываем на ней от точки Р отрезок длиною
); через конец Р этого отрезка проводим в плоскости хОу прямую параллельно оси Оу и откладываем на ней от точки Р отрезок длиною 
(вправо или влево — смотря по знаку  получим точку S, через которую проводим прямую параллельно оси Oz и откладываем на ней от точки S отрезок длиною
получим точку S, через которую проводим прямую параллельно оси Oz и откладываем на ней от точки S отрезок длиною  (вверх или вниз — смотря по знаку z). Конец этого отрезка и является искомой точкой М.
(вверх или вниз — смотря по знаку z). Конец этого отрезка и является искомой точкой М.
Направленные отрезки PS и SM (так же как и отрезки ОР,  и OR) мы будем называть координатными отрезками точки
и OR) мы будем называть координатными отрезками точки 
Направленную ломаную линию OPSM, началом которой является начало координат, а концом — точка М, и три звена которой являются координатными отрезками точки М, будем называть координатной ломаной линией точки М.

Рис. 84.
Из всего изложенного следует, что каждой точке пространства в выбранной системе координат соответствует тройка чисел  — координат точки — и, обратно, всякая тройка действительных чисел х, у, z определяет в пространстве единственную точку, для которой указанные три числа являются соответственно абсциссой, ординатой и аппликатой. Поэтому задать точку — это значит задать ее координаты; найти точку — значит найти ее координаты.
— координат точки — и, обратно, всякая тройка действительных чисел х, у, z определяет в пространстве единственную точку, для которой указанные три числа являются соответственно абсциссой, ординатой и аппликатой. Поэтому задать точку — это значит задать ее координаты; найти точку — значит найти ее координаты.

Рис. 85.
Замечание 2. Возможны два тина взаимного расположения осей прямоугольной декартовой системы координат в пространстве. Если ми будем смотреть из какой-либо точки положительной полуоси Oz на положительную полуось Оу, то ось Ох может быть направлена вправо или влево. В первом случае система координат называется правой системой (рис. 84), а во втором — левой (рис. 85). Для правой системы поворот от оси Ох к оси Оу на прямой угол будет нам казаться происходящим против часовой стрелки (если смотреть на плоскость хОу из какой-либо точки положительной полуоси Oz), а для левой — по часовой. Можно пользоваться как правой, так и левой системами. В дальнейшем мы будем применять только правую систему координат.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- ГЛАВА I. МЕТОД КООРДИНАТ
- § 2. Координаты на прямой линии.
- § 3. Расстояние между двумя точками на прямой линии.
- § 4. Прямоугольные координаты на плоскости.
- § 5. Расстояние между двумя точками на плоскости.
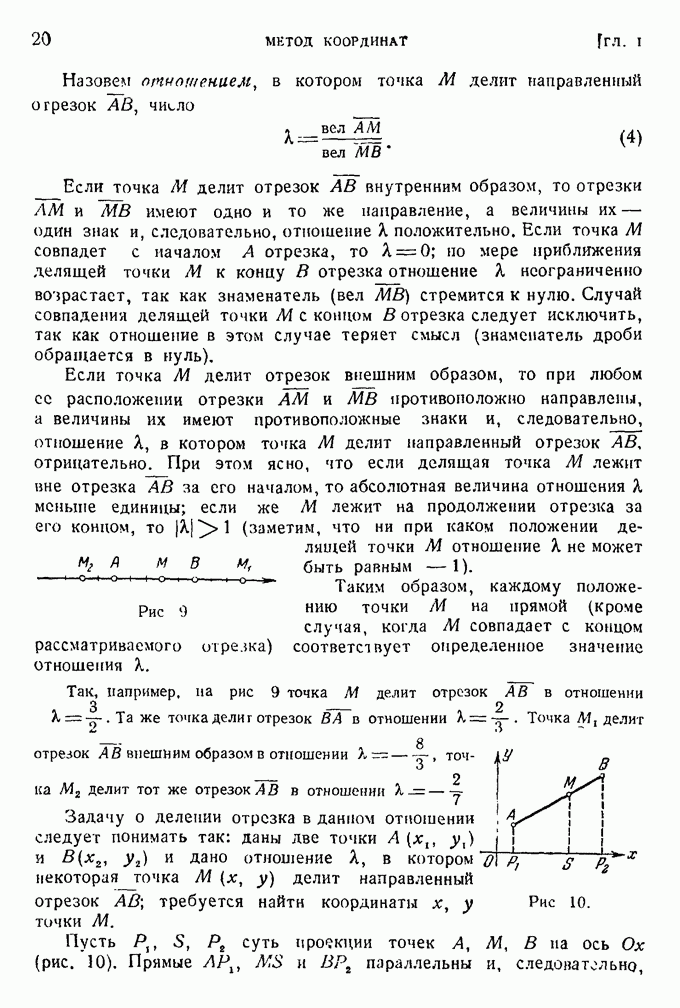
- § 6. Деление отрезка в данном отношении.
- § 7. Угол между двумя осями.
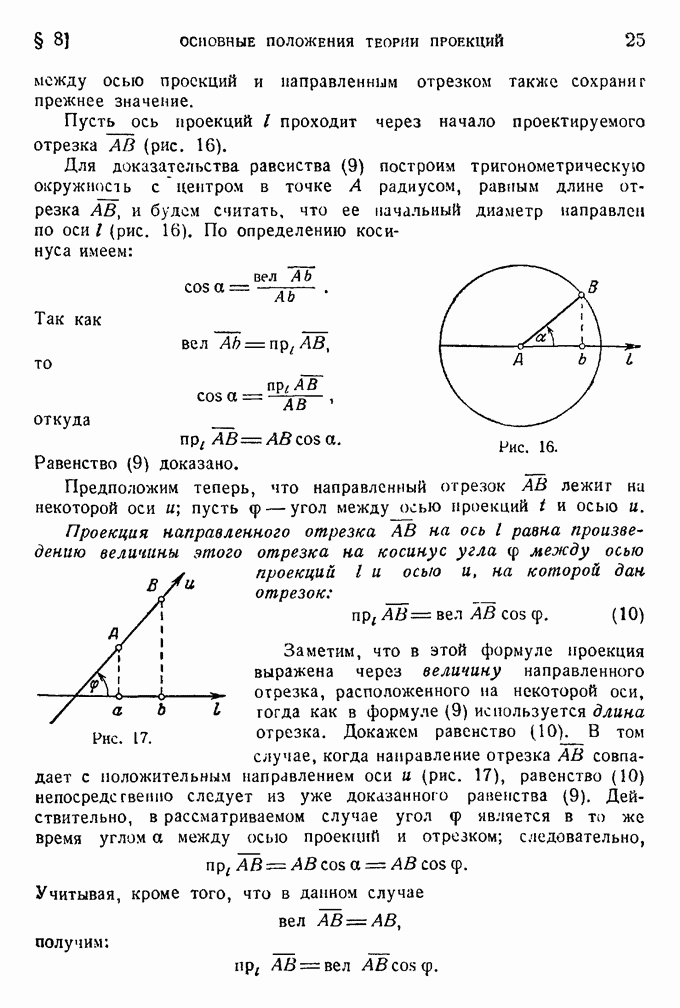
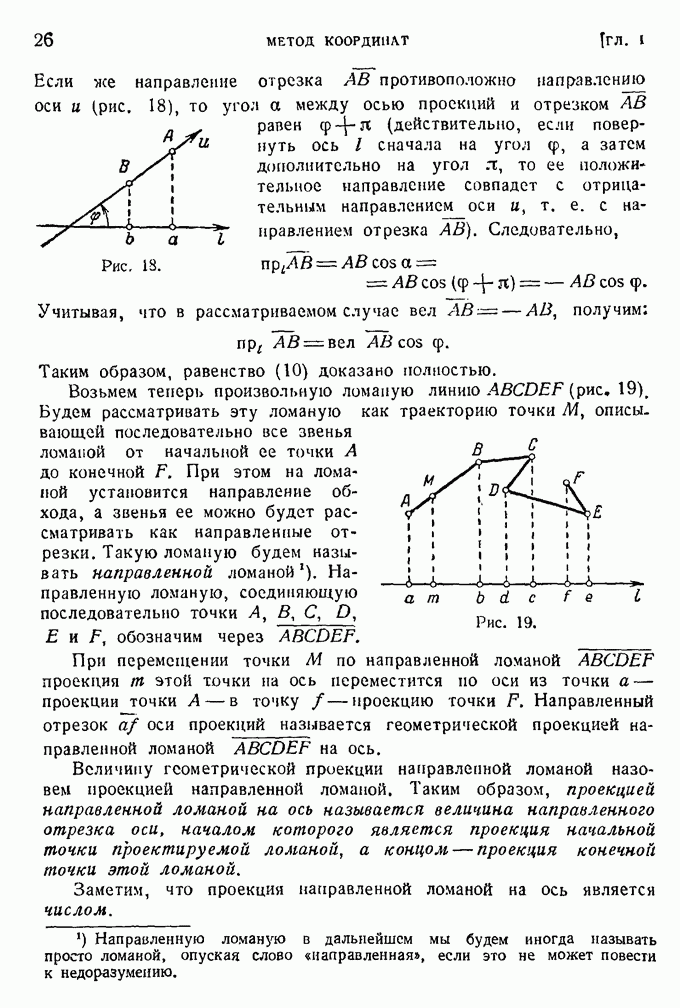
- § 8. Основные положения теории проекций.
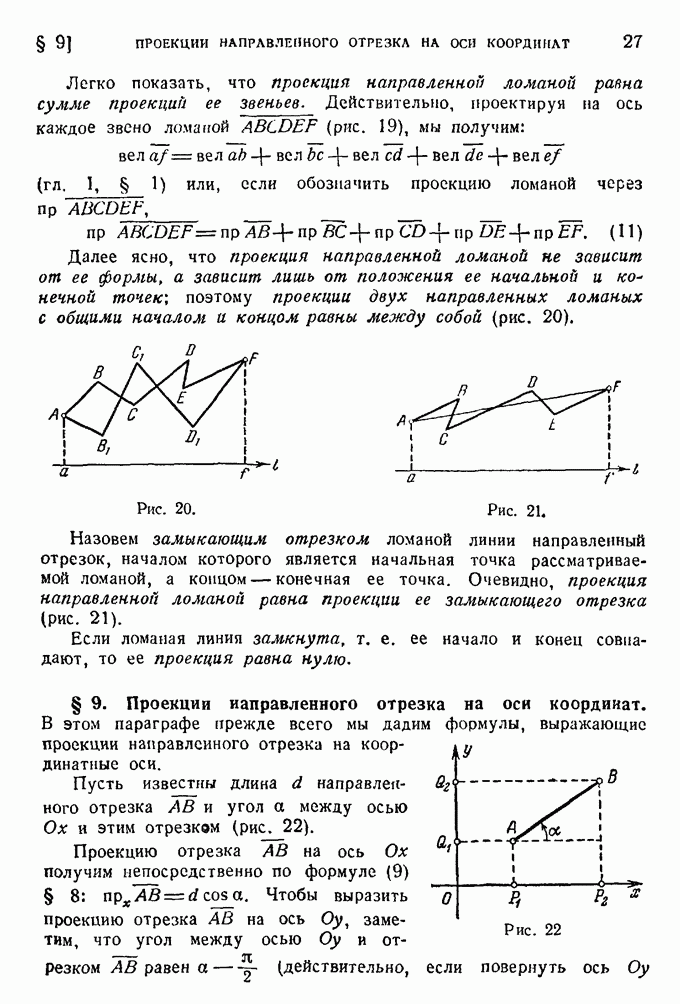
- § 9. Проекции направленного отрезка на оси координат.
- § 10. Площадь треугольника.
- § 11. Полярные координаты.
- Упражнения
- ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ
- § 1. Составление уравнений заданных линий.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Пересечение двух линий.
- § 5. Параметрические уравнения линий.
- § 6. Уравнения линий в полярных координатах.
- ГЛАВА III. ПРЯМАЯ ЛИНИЯ
- § 1. Угловой коэффициент прямой.
- § 2. Уравнение прямой линии с угловым коэффициентом.
- § 3. Геометрический смысл уравнения первой степени между двумя переменными.
- § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0.
- § 5. Уравнение прямой линии в отрезках.
- § 6. Построение прямой линии по ее уравнению.
- § 7. Угол между двумя прямыми.
- § 8. Условия параллельности и перпендикулярности двух прямых.
- § 9. Уравнение прямой, проходящей через данную точку в данном направлении.
- § 10. Взаимное расположение двух прямых на плоскости.
- § 11. Уравнение пучка прямых.
- § 12. Уравнение прямой, проходящей через две данные точки.
- § 13. Условие, при котором три данные точки лежат на одной прямой.
- § 14. Нормальное уравнение прямой линии.
- § 15. Приведение общего уравнения первой степени к нормальному виду.
- § 16. Расстояние от дайной точки до данной прямой.
- § 17. Уравнение прямой в полярной системе координат.
- Упражнения
- ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ
- § 2. Окружность.
- § 3. Эллипс.
- § 4. Гипербола и ее асимптоты.
- § 5. Парабола.
- § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки.
- § 7. Эллипс, гипербола и парабола как конические сечения.
- § 8. Эксцентриситет и директрисы эллипса.
- § 9. Эксцентриситет и директрисы гиперболы.
- § 10. Эксцентриситет и директриса параболы.
- § 11. Уравнение конического сечения в полярных координатах.
- § 12. Диаметры зллипса. Сопряженные диаметры.
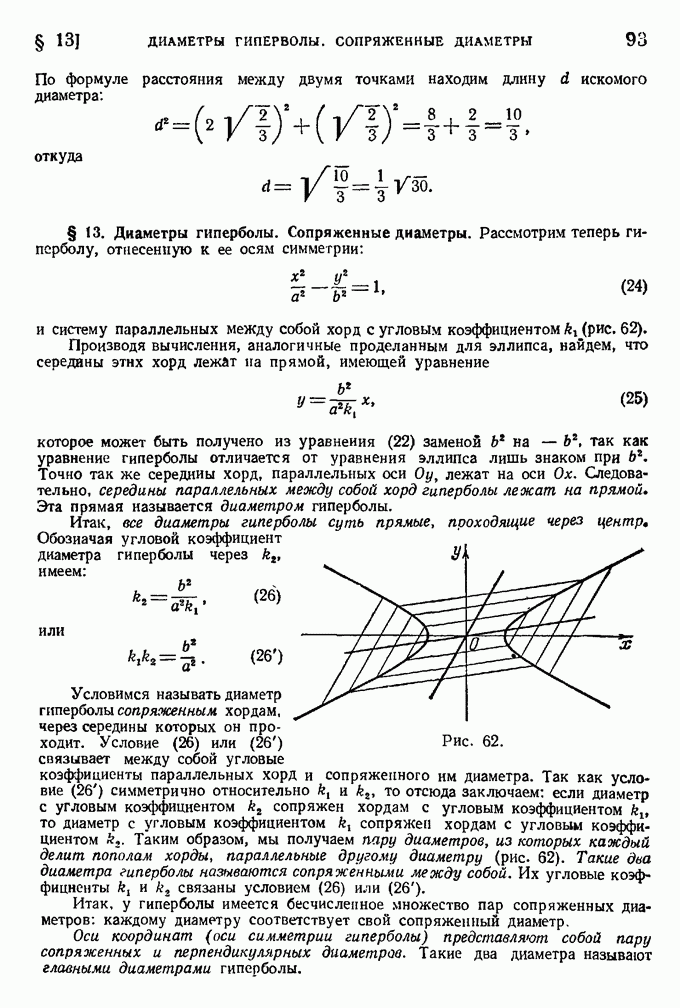
- § 13. Диаметры гиперболы. Сопряженные диаметры.
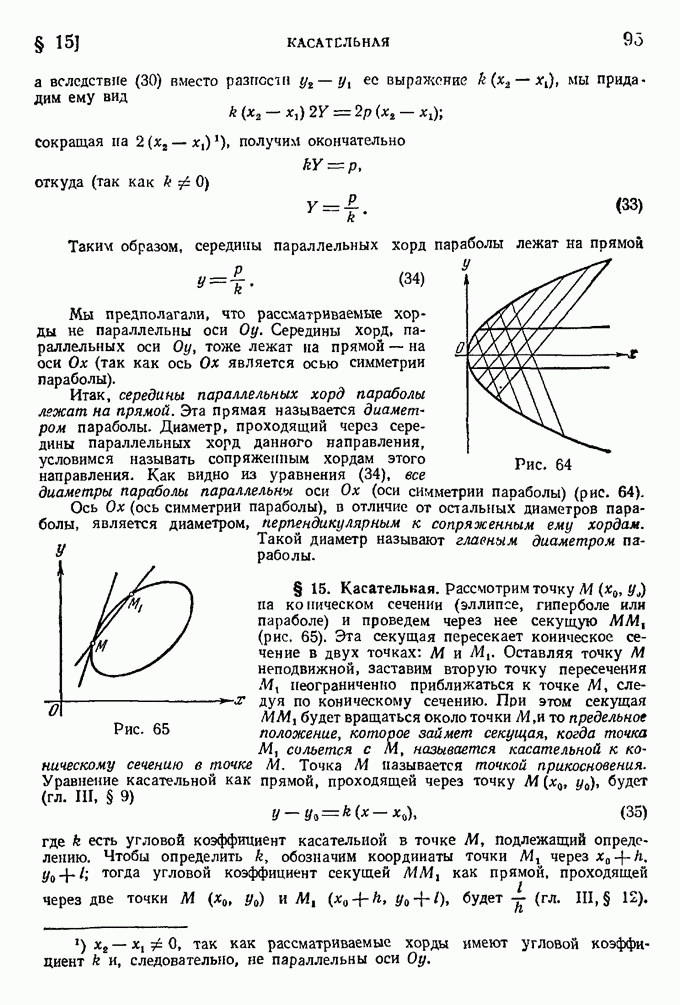
- § 14. Диаметры параболы.
- § 15. Касательная.
- § 16. Эллипс как проекция окружности.
- § 17. Параметрические уравнения эллипса.
- Упражнения
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ
- § 2. Перенос начала координат.
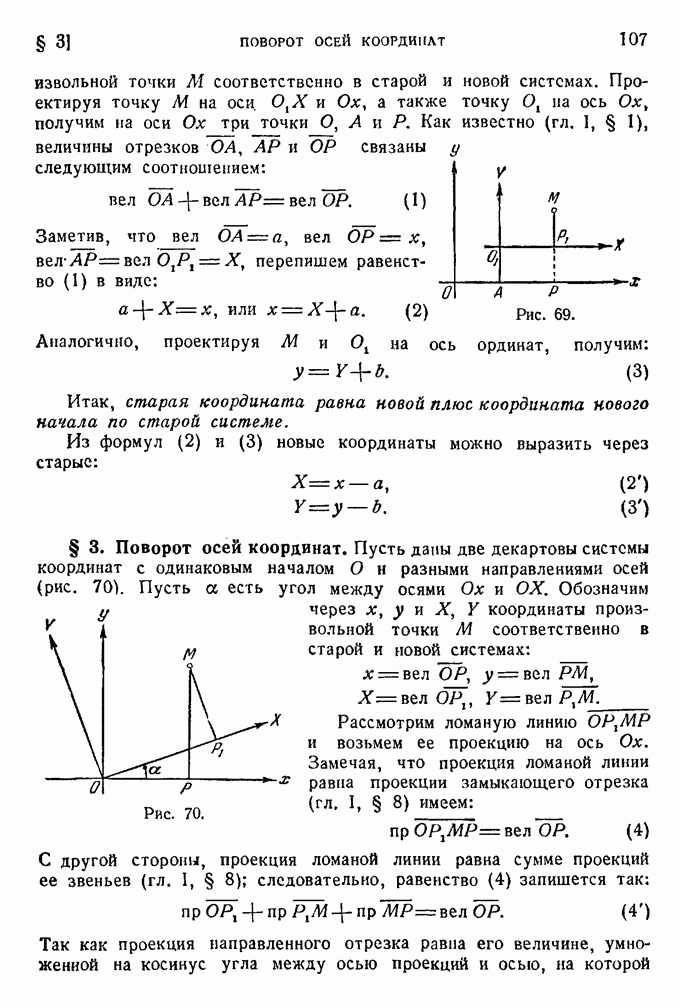
- § 3. Поворот осей координат.
- § 4. Общий случай.
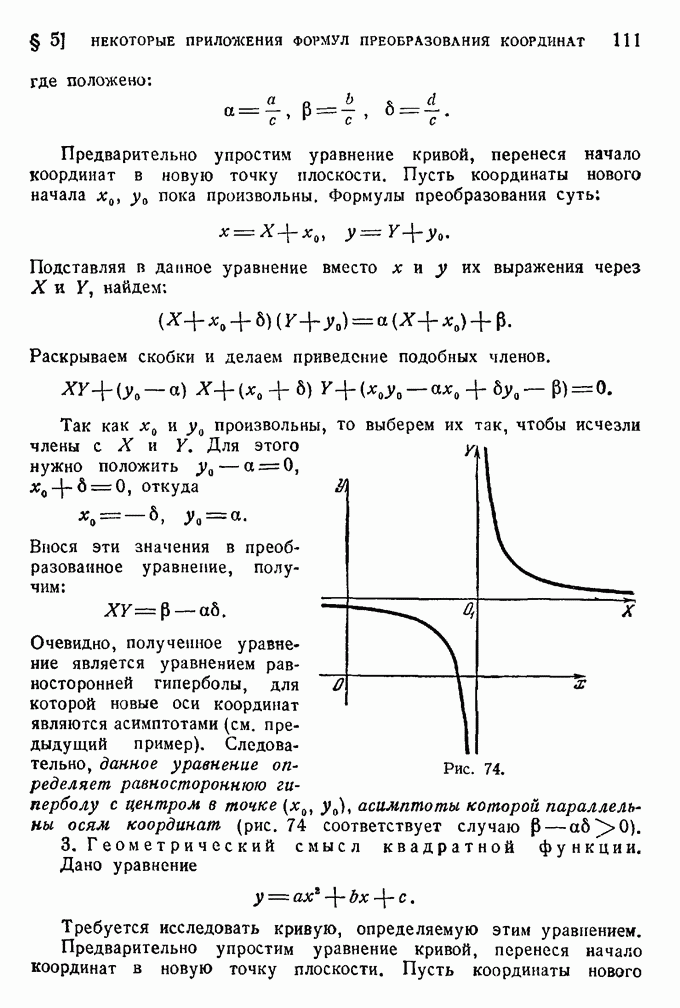
- § 5. Некоторые приложения формул преобразования координат.
- § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных.
- § 7. Преобразование общего уравнения второй степени.
- § 8. Классификация линий.
- Упражнения
- ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА
- § 2. Однородная система двух уравнений с тремя неизвестными.
- § 3. Определители 3-го порядка.
- § 4. Основные свойства определителей 3-го порядка.
- § 5. Система трех уравнений первой степени с тремя неизвестными.
- § 6. Однородная система.
- § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными.
- § 8. Некоторые приложения определителей к аналитической геометрии.
- Упражнения
- ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
- § 2. Основные задачи.
- § 3. Основные положения теории проекций в пространстве.
- § 4. Вычисление угла между двумя осями в пространстве.
- Упражнения
- ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. Сложение векторов.
- § 3. Вычитание векторов.
- § 4. Умножение вектора на число.
- § 5. Проекции вектора.
- § 6. Действия над векторами, заданными своими проекциями.
- § 7. Скалярное произведение векторов.
- § 8. Основные свойства скалярного произведения.
- § 9. Скалярное произведение векторов, заданных проекциями.
- § 10. Направление вектора.
- § 11. Векторное произведение.
- § 12. Основные свойства векторного произведения.
- § 13. Векторное произведение векторов, заданных проекциями.
- § 14. Векторно-скалярное произведение.
- § 15. Векторно-скалярное произведение в проекциях.
- § 16. Двойное векторное произведение.
- Упражнения
- ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
- § 1. Уравнение поверхности.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Сфера.
- § 5. Цилиндрические поверхности.
- § 6. Уравнения линии в пространстве.
- § 7. Пересечение трех поверхностей.
- Упражнения
- ГЛАВА IV. ПЛОСКОСТЬ
- § 1. Нормальное уравнение плоскости.
- § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду.
- § 3. Исследование общего уравнения плоскости.
- § 4. Уравнение плоскости в отрезках.
- § 5. Уравнение плоскости, проходящей через данную точку.
- § 6. Уравнение плоскости, проходящей через три данные точки.
- § 7. Угол между двумя плоскостями.
- § 8. Условия параллельности и перпендикулярности двух плоскостей.
- § 9. Точка пересечения трех плоскостей.
- § 10. Расстояние от точки до плоскости.
- Упражнения
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Уравнения прямой линии.
- § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой.
- § 3. Угол между двумя прямыми линиями.
- § 4. Условия параллельности и перпендикулярности двух прямых.
- § 5. Уравнения прямой, проходящей через две данные точки.
- § 6. Угол между прямой и плоскостью.
- § 7. Условия параллельности и перпендикулярности прямой и плоскости.
- § 8. Уравнение пучка плоскостей.
- § 9. Пересечение прямой с плоскостью.
- § 10. Условие, при котором две прямые лежат в одной плоскости.
- Упражнения
- ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА
- § 1. Классификация поверхностей.
- § 2. Цилиндрические поверхности (общий случай).
- § 3. Конические поверхности.
- § 4. Поверхности вращения.
- § 5. Эллипсоид.
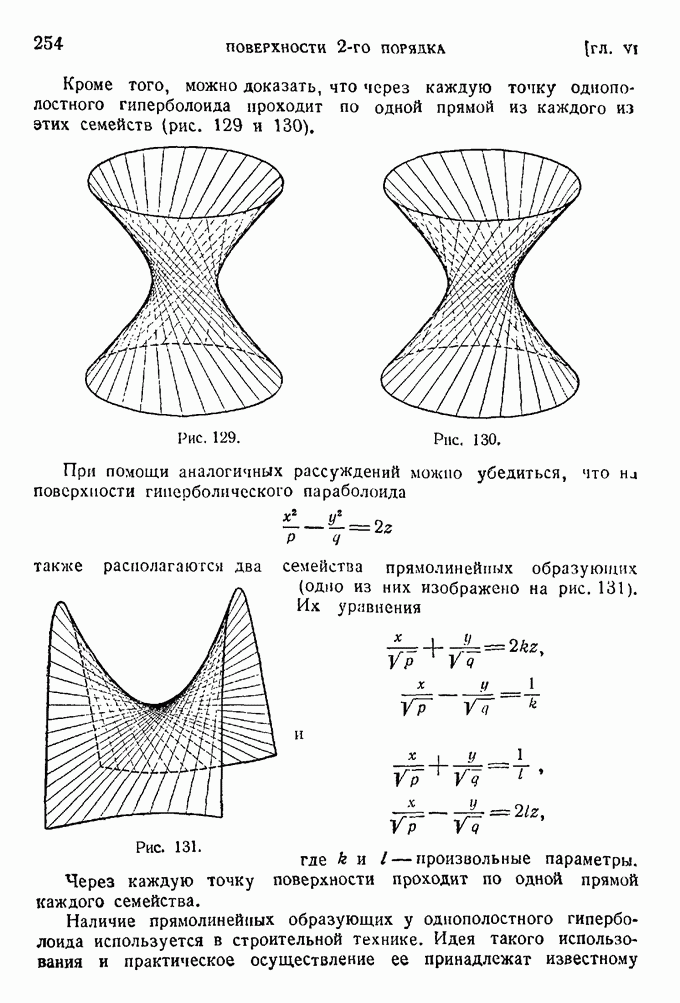
- § 6. Однополостный гиперболоид.
- § 7. Двуполостный гиперболоид.
- § 8. Эллиптический параболоид.
- § 9. Гиперболический параболоид.
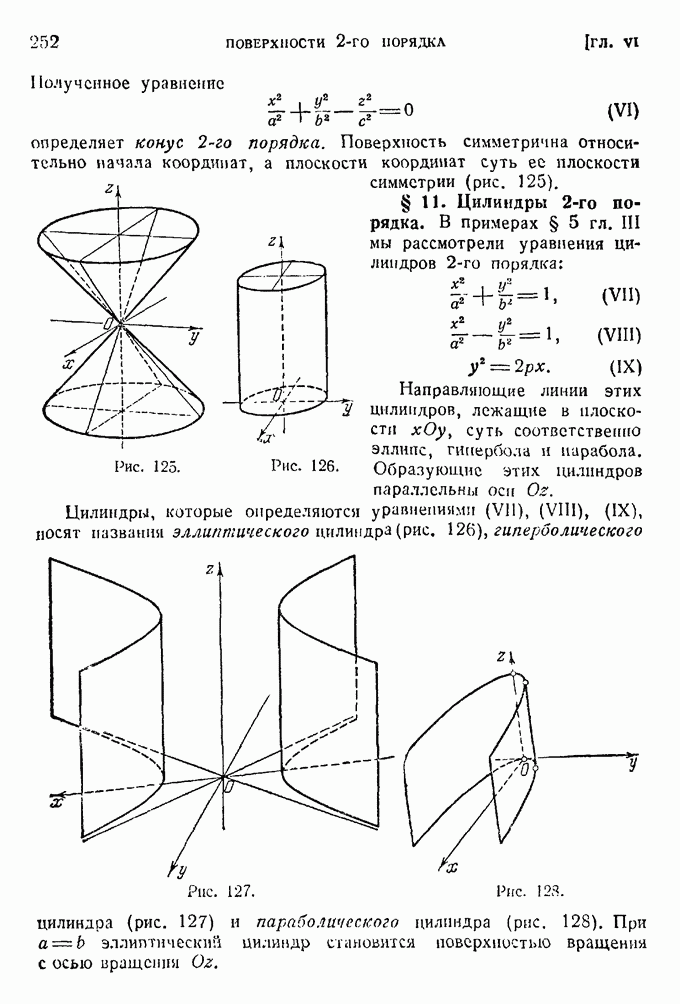
- § 10. Конус 2-го порядка.
- § 11. Цилиндры 2-го порядка.
- § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова.
- Упражнения
- Ответы