| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЗАДАЧИ К § 18
Дополняем теорию
5.1. Даны две точки:  Найдите координаты середины отрезка АВ. б) Найдите координаты точки К, которая делит отрезок АВ в заданном отношении
Найдите координаты середины отрезка АВ. б) Найдите координаты точки К, которая делит отрезок АВ в заданном отношении  Найдите координаты точки L прямой такой, что
Найдите координаты точки L прямой такой, что 
Рисуем
5.2. Нарисуйте систему координат, а в ней точку  Нарисуйте прямую а, проходящую через точку А и параллельную оси z. На прямой а отметьте точку В, у которой координата z равна 3. Запишите координаты точки В. Нарисуйте проекции точки В на оси координат. Каковы координаты
Нарисуйте прямую а, проходящую через точку А и параллельную оси z. На прямой а отметьте точку В, у которой координата z равна 3. Запишите координаты точки В. Нарисуйте проекции точки В на оси координат. Каковы координаты
этих проекций? Нарисуйте проекции точки В на плоскости координат. Каковы координаты этих проекций?
5.3. Нарисуйте систему координат, а в ней точку  Нарисуйте прямую а, проходящую через А и параллельную оси z. На прямой а отметьте точку В, у которой координата z равна 3. Решите для нее те же задачи, что и в задаче 5.1.
Нарисуйте прямую а, проходящую через А и параллельную оси z. На прямой а отметьте точку В, у которой координата z равна 3. Решите для нее те же задачи, что и в задаче 5.1.
5.4. Нарисуйте систему координат. Нарисуйте точки

Нарисуйте отрезок АВ. Пересекает ли он плоскость  Пересекает ли он другие координатные плоскости? Какой из отрезков с концами в данных точках пересекает А плоскость yz? А плоскость zx? А плоскость ху? Есть ли среди отрезков с концами в данных точках такой, который пересекает хотя бы одну ось координат?
Пересекает ли он другие координатные плоскости? Какой из отрезков с концами в данных точках пересекает А плоскость yz? А плоскость zx? А плоскость ху? Есть ли среди отрезков с концами в данных точках такой, который пересекает хотя бы одну ось координат?
Планируем
5.5. Пусть даны точки  Как найти координаты: а) середины отрезка АВ; б) точки пересечения медиан треугольника ABC; в) точки D такой, что она вместе с точками А, В, С является вершиной параллелограмма ABDC?
Как найти координаты: а) середины отрезка АВ; б) точки пересечения медиан треугольника ABC; в) точки D такой, что она вместе с точками А, В, С является вершиной параллелограмма ABDC?
5.6. Как найти расстояние АВ, если:

5.7. Как установить вид треугольника ABC по сторонам и углам, если:

5.8. Даны точки  . Требуется выяснить, какая из них ближе: а) к началу координат; б) к плоскости yz; в) к оси х? Как это сделать? г) Как найти ту из них, которая ближе всех к какой-либо координатной оси? д) Как найти ту из них, которая ближе к какой-либо координатной плоскости?
. Требуется выяснить, какая из них ближе: а) к началу координат; б) к плоскости yz; в) к оси х? Как это сделать? г) Как найти ту из них, которая ближе всех к какой-либо координатной оси? д) Как найти ту из них, которая ближе к какой-либо координатной плоскости?
5.9. Нарисуйте куб. Пусть его ребро равно 2. Выберите начало координат в одной из его вершин, положительные направления осей координат вдоль его ребер. Как найти координаты:
а) всех его вершин; б) середин ребер, выходящих из точки, которая является концом той же диагонали куба, что и начало координат; в) центров всех его граней; г) центра симметрии; д) центра правильного треугольника, вершины которого находятся в вершинах куба? Как вычислить расстояния между: е) серединами ребер, не лежащих в одной грани; ж) серединами двух скрещивающихся ребер; з) центром куба и серединой какого-либо его ребра; и) центрами двух непараллельных сечений, проходящих через вершины куба и являющихся треугольниками?
5.10. Дан куб  с ребром 2. Пусть точка К — середина AD, точка L — середина
с ребром 2. Пусть точка К — середина AD, точка L — середина  точка М — центр грани
точка М — центр грани  Как вычислить расстояния
Как вычислить расстояния  Как найти координаты точки пересечения медиан треугольника
Как найти координаты точки пересечения медиан треугольника  Как доказать, что точки пересечения медиан треугольников
Как доказать, что точки пересечения медиан треугольников  и середина диагонали
и середина диагонали  лежат на одной прямой?
лежат на одной прямой?
Представляем
5.11. Нарисуйте систему координат. Какие координаты равны нулю у точки, лежащей: а) в плоскости  на оси
на оси  на оси
на оси 
5.12. Как расположена в системе координат точка, если у нее: а) 
Оцениваем
5.13. Дан куб  , с ребром 2. В каких границах лежит расстояние
, с ребром 2. В каких границах лежит расстояние  если точка К лежит на
если точка К лежит на  точка L лежит на
точка L лежит на  причем
причем 
Сделаем
5.14. а) Пусть известны координаты трех вершин параллелограмма. Как найти координаты четвертой его вершины? б) Решите аналогичную задачу для параллелепипеда.
5.15. Точки  являются вершинами правильного тетраэдра, основание которого лежит в плоскости
являются вершинами правильного тетраэдра, основание которого лежит в плоскости  Как узнать, каковы координаты других его вершин?
Как узнать, каковы координаты других его вершин?
5.16. Пусть точка удалена от начала координат на 1. а) Запишите зависимость между ее координатами, б) Докажите, что модуль любой ее координаты не больше 1. Что это значит, если говорить о геометрических величинах? в) Докажите, что сумма квадратов любых двух ее координат не больше 1. Что это значит, если говорить о геометрических величинах? г) Пусть у
этой точки две координаты равны. Какая теперь зависимость существует между ее координатами? д) Пусть в зависимости, полученной в пункте г), одна из координат стала увеличиваться. Что будет с другой? Что это означает с геометрической точки зрения?
5.17. Дайте геометрическое истолкование таким соотношениям:

5.18. Сколько решений имеет уравнение:

ЗАДАЧИ К § 19
Рисуем
5.19. а)В системе координат нарисуйте плоскость, перпендикулярную оси  и проходящую через точку (1;0;0). Возьмите любую точку этой плоскости и объясните, почему координата равна 1. б) Нарисуйте точку
и проходящую через точку (1;0;0). Возьмите любую точку этой плоскости и объясните, почему координата равна 1. б) Нарисуйте точку  и плоскость, проходящую через точку А и перпендикулярную оси
и плоскость, проходящую через точку А и перпендикулярную оси  Каким характерным свойством обладают точки этой плоскости?
Каким характерным свойством обладают точки этой плоскости?
5.20. Нарисуйте плоскости, перпендикулярные осям координат и проходящие через точки: 
5.21. а) На плоскости  нарисуйте прямую
нарисуйте прямую  Нарисуйте плоскость, перпендикулярную плоскости
Нарисуйте плоскость, перпендикулярную плоскости  проходящую через эту прямую. Возьмите любую точку на этой плоскости. Объясните, почему для ее координат х и у верно равенство
проходящую через эту прямую. Возьмите любую точку на этой плоскости. Объясните, почему для ее координат х и у верно равенство  Решите аналогичную задачу для плоскости
Решите аналогичную задачу для плоскости  и прямой
и прямой 
5.22. Нарисуйте фигуру, уравнение которой:

5.23. Нарисуйте фигуру, которая определяется условием:

5.24. Нарисуйте фигуру, заданную условием:

Планируем
5.25. Как записать уравнение сферы:
а) с центром в начале координат и радиусом 1;
б) с центром в точке (-1;-1;1) и радиусом 1;
в) с центром в точке  и радиусом а;
и радиусом а;
г) проходящей через точки 
д) касающейся плоскости  в точке
в точке  и радиусом 3;
и радиусом 3;
е) касающейся всех трех координатных плоскостей и радиусом 1?
5.26. Как записать уравнение какой-либо прямой, которая параллельна:
а) одной из координатных плоскостей;
б) двум координатным плоскостям;
в) координатной оси?
5.27. Как записать уравнение какой-либо прямой, которая перпендикулярна: а) одной из координатных плоскостей; б) оси 
5.28. Как записать уравнение прямой:
а) проходящей через точку  и перпендикулярной плоскости
и перпендикулярной плоскости 
б) проходящей через точку  перпендикулярной оси
перпендикулярной оси  и пересекающей ее;
и пересекающей ее;
в) совпадающей с осью 
г) параллельной оси у и проходящей через точку 
д) параллельной оси у и проходящей через точку 
е) параллельной плоскостям  и проходящей через точку
и проходящей через точку 
5.29. Сфера задается уравнением  Как найти координаты точки этой сферы:
Как найти координаты точки этой сферы:
а) ближайшей к точке О;
б) самой далекой от точки О;
в) ближайшей к каждой из координатных плоскостей;
г) самой далекой от каждой из координатных плоскостей;
д) ближайшей к каждой из координатных осей;
е) самой далекой от каждой из координатных осей;
ж) ближайшей к точке 
з) самой далекой от точки 
5.30. Как написать уравнение сферы: а) с центром в точке  и радиусом а; б) с центром в точке
и радиусом а; б) с центром в точке  и касающейся одной из координатных плоскостей; в) с центром в точке
и касающейся одной из координатных плоскостей; в) с центром в точке  и касающейся одной из координатных плоскостей; г) с центром в точке
и касающейся одной из координатных плоскостей; г) с центром в точке  и касающейся одной из координатных осей?
и касающейся одной из координатных осей?
5.31. Точка имеет координаты  Как написать уравнение сферы, которая: а) проходит через эту точку; б) не проходит через эту точку; в) проходит через эту точку и имеет радиус 1?
Как написать уравнение сферы, которая: а) проходит через эту точку; б) не проходит через эту точку; в) проходит через эту точку и имеет радиус 1?
5.32. Как написать уравнение сферы, проходящей через точки:

5.33. Пусть  куб с ребром 2. Точка К — середина CD, точка L — середина
куб с ребром 2. Точка К — середина CD, точка L — середина  точка М — середина
точка М — середина  Как написать уравнение сферы, проходящей через точки:
Как написать уравнение сферы, проходящей через точки:

На какой из них лежат все вершины куба?
5.34. Как вычислить расстояние от начала координат до фигуры, заданной такими условиями:

5.35. Какая фигура в пространстве задается условиями:

5.36. Прямая задается условием: а)  Как она расположена по отношению к плоскостям координат? к осям координат?
Как она расположена по отношению к плоскостям координат? к осям координат?
5.37. Как расположены между собой прямая а, задаваемая условием  и прямая b , задаваемая условием
и прямая b , задаваемая условием 
Исследуем
5.38. В треугольнике  вершина прямого угла. Как найти координаты вершин В и С, если известно, что В и С лежат на прямой MN, где
вершина прямого угла. Как найти координаты вершин В и С, если известно, что В и С лежат на прямой MN, где 
5.39. Объем прямой треугольной призмы равен 3. Координаты трех вершин одного основания таковы:  Как найти координаты вершины призмы, лежащей на одном ребре с первой из этих вершин?
Как найти координаты вершины призмы, лежащей на одном ребре с первой из этих вершин?
Поступаем в ВУЗ.
5.40. Найдите координаты точки  лежащей на оси
лежащей на оси  и одинаково удаленной от точек
и одинаково удаленной от точек 
Ответ: 
5.41. Докажите, что треугольник ABC, вершины которого расположены в точках  прямоугольный. Найдите расстояние от начала системы координат до центра окружности, описанной около этого треугольника.
прямоугольный. Найдите расстояние от начала системы координат до центра окружности, описанной около этого треугольника.
Ответ: 
5.42. Докажите, что точки  являются вершинами прямоугольника. Вычислите длину его диагоналей и координаты их точки пересечения.
являются вершинами прямоугольника. Вычислите длину его диагоналей и координаты их точки пересечения.
Ответ: 
5.43. Составьте уравнение плоскости, перпендикулярной оси  и проходящей через точку
и проходящей через точку 
Ответ: 
5.44.  - параллелепипед
- параллелепипед  . Найдите длину диагонали
. Найдите длину диагонали 
Ответ: 7.
5.45. Тетраэдр задан координатами своих вершин  Вычислите расстояние от вершины А до точки пересечения медиан противоположной грани.
Вычислите расстояние от вершины А до точки пересечения медиан противоположной грани.
Ответ: 
5.46. Точки  лежат на окружности нижнего основания цилиндра, а точка
лежат на окружности нижнего основания цилиндра, а точка  — на его верхнем основании. Найдите координаты центров оснований и объем цилиндра.
— на его верхнем основании. Найдите координаты центров оснований и объем цилиндра.
Ответ: 
5.47. Точки  лежат на окружности основания конуса, высота которого равна 3. Конус пересекает плоскость
лежат на окружности основания конуса, высота которого равна 3. Конус пересекает плоскость  Найдите координаты его вершины и площадь сечения конуса этой плоскостью.
Найдите координаты его вершины и площадь сечения конуса этой плоскостью.
Ответ. Координаты вершины —  Площадь сечения равна
Площадь сечения равна 
ЗАДАЧИ К § 21
Рисуем
5.48. Дан параллелепипед  Нарисуйте вектор, задаваемый его вершинами и равный:
Нарисуйте вектор, задаваемый его вершинами и равный:

Нарисуйте вектор, равный  с началом в точке:
с началом в точке:

Равны ли векторы: 
5.49. Пусть  — треугольная призма. Точка К — середина ребра АС. От всех точек призмы откладывается вектор АХК. Нарисуйте фигуру, которую в призме образуют их концы.
— треугольная призма. Точка К — середина ребра АС. От всех точек призмы откладывается вектор АХК. Нарисуйте фигуру, которую в призме образуют их концы.
5.50. Пусть  - куб. От всех его точек откладывается вектор
- куб. От всех его точек откладывается вектор  где точка О—центр куба. Нарисуйте фигуру, которую образуют концы таких векторов. Нарисуйте пересечение и объединение исходного куба и полученной фигуры.
где точка О—центр куба. Нарисуйте фигуру, которую образуют концы таких векторов. Нарисуйте пересечение и объединение исходного куба и полученной фигуры.
Планируем
5.51. Пусть  - куб. Как вычислить угол между векторами:
- куб. Как вычислить угол между векторами:

Представляем
5.52. Могут ли равные векторы лежать на: а) скрещивающихся прямых; б) ребрах правильного тетраэдра; в) ребрах какого-либо правильного многогранника?
5.53. Какую фигуру образуют концы X всех единичных векторов ОХ , если эти векторы отложить от каждой точки единичной сферы с центром 
5.54. Какую фигуру образуют концы равных друг другу векторов, отложенных от: а) прямой; б) отрезка; в) плоскости; г) треугольника; д) круга; е) тетраэдра; ж) шара; з) правильного многогранника?
ЗАДАЧИ К § 22
Дополняем теорию
5.55. Докажите неравенство  Обобщите его.
Обобщите его.
Дайте геометрическое истолкование этому обобщению для случая трех векторов, не лежащих в одной плоскости.
5.56. Пусть А и В — две любые точки. Докажите, что при любом выборе точек  и
и  верно равенство:
верно равенство:

5.57. Пусть точки К и L не лежат в плоскости ЛВС. Докажите, что параллельность прямой KL и плоскости ABC равносильна выполнению равенства:  .
.
5.58. Используя векторные соотношения, запишите равенства, равносильные таким утверждениям:
а) точка X лежит на прямой АВ;
б) точка X лежит на отрезке АВ;
в) точка X лежит на плоскости 
5.59. а) Дан вектор  Какие координаты имеет вектор -а! б) Даны векторы а и b. Какие координаты имеет вектор
Какие координаты имеет вектор -а! б) Даны векторы а и b. Какие координаты имеет вектор  Даны векторы
Даны векторы  Какие координаты имеет вектор а а
Какие координаты имеет вектор а а 
Рисуем
5.60. Пусть  параллелепипед. Нарисуйте вектор АХ , равный сумме векторов АА, и:
параллелепипед. Нарисуйте вектор АХ , равный сумме векторов АА, и:

5.61. Пусть  параллелепипед. Нарисуйте вектор АХ, равный:
параллелепипед. Нарисуйте вектор АХ, равный:

5.62. Пусть  куб. Нарисуйте составляющие по плоскости ABC и прямой АА, таких векторов:
куб. Нарисуйте составляющие по плоскости ABC и прямой АА, таких векторов:

где точка К — центр грани 
5.63. Пусть  — прямоугольный параллелепипед. Точка К — середина ребра
— прямоугольный параллелепипед. Точка К — середина ребра  точка L — центр грани
точка L — центр грани  Нарисуйте составляющие по прямым АВ, AD, АА, векторов: а) АС,
Нарисуйте составляющие по прямым АВ, AD, АА, векторов: а) АС, 
Планируем
5.64. Как найти координаты вектора АВ и его длину, если:

5.65. От точки А отложили вектор  . Как найти координаты точки В, если:
. Как найти координаты точки В, если:

5.66. Как найти координаты единичного вектора (длина которого равна 1), если он образует:
а) с осью  угол 60°, а с осью у угол
угол 60°, а с осью у угол 
б) с плоскостью  угол 30°, а с плоскостью
угол 30°, а с плоскостью  угол
угол 
в) с осью z угол 60°, а с плоскостью  угол
угол 
г) с осями координат углы 
5.67. Пусть  куб с ребром 1. Начало координат в точке В, положительные лучи осей координат — лучи ВА, ВС и ВВГ Как найти координаты вектора:
куб с ребром 1. Начало координат в точке В, положительные лучи осей координат — лучи ВА, ВС и ВВГ Как найти координаты вектора:

5.68. Даны векторы  . Как найти координаты векторов:
. Как найти координаты векторов:

5.69. Даны векторы  . Как вычислить:
. Как вычислить: 
5.70. Вектор а с координатами  имеет длину 1.
имеет длину 1.
а) Какая связь между его координатами?
б) Пусть две координаты его известны. Как найти третью?
5.71. Пусть известны координаты вектора. Как вычислить углы, которые он образует с осями координат? С плоскостями координат?
5.72. Пусть  параллелепипед. Докажите, что на диагонали BXD лежат середины других диагоналей параллелепипеда и точки пересечения медиан треугольников
параллелепипед. Докажите, что на диагонали BXD лежат середины других диагоналей параллелепипеда и точки пересечения медиан треугольников 
Поступаем в ВУЗ
5.73. Даны векторы  Найдите координаты вектора
Найдите координаты вектора 
Ответ: 
5.74. Даны три ненулевых вектора а, b, с, каждые два из которых неколлинеарны. Найдите их сумму, если вектор а  коллинеарен вектору с, а вектор
коллинеарен вектору с, а вектор  с коллинеарен вектору а.
с коллинеарен вектору а.
Ответ: 0.
5.75. Даны четыре точки  Проверьте коллинеарность векторов
Проверьте коллинеарность векторов 
5.76. Пирамида задана координатами своих вершин  Найдите координаты точки М, лежащей на оси z, и координаты точки N, лежащей в плоскости SBC, если известно, что координаты вектора
Найдите координаты точки М, лежащей на оси z, и координаты точки N, лежащей в плоскости SBC, если известно, что координаты вектора  таковы —
таковы — 
5.77. В призме  точка М лежит на отрезке
точка М лежит на отрезке  так, что ВХМ:
так, что ВХМ:  Разложите вектор AM по
Разложите вектор AM по  торам
торам  .
.
Ответ: Соответственные коэффициенты разложения — 
Переключаемся
5.78. К вершине А треножника ABCD подвешен груз Р. Ножки треножника АВ, AC, AD равны, укреплены на горизонтальной плоскости, образуют между собой прямые углы, а с вертикалью — равные углы. Найдите усилия в каждой из ножек треножника.
ЗАДАЧИ К § 23
Дополняем теорию
5.79. Векторы  перпендикулярны. Какой зависимостью связаны их координаты?
перпендикулярны. Какой зависимостью связаны их координаты?
Планируем
5.80. Пусть  Как вычислить:
Как вычислить:

5.81. Векторы a, b, с — единичные, угол между а и b равен  между
между  между
между  Как вычислить:
Как вычислить:

5.82.  . Как вычислить, используя скалярное умножение:
. Как вычислить, используя скалярное умножение:

5.83. Пусть  Как вычислить угол между векторами:
Как вычислить угол между векторами:

5.84. Дан правильный тетраэдр ABCD с ребром 1. Как вычислить:  , где точка К — центр грани
, где точка К — центр грани  где точка L — середина ребра АС, а точка М — середина ребра
где точка L — середина ребра АС, а точка М — середина ребра 
5.85. Пусть  - куб с ребром 1. Как вычислить скалярные произведения вектора АВ на:
- куб с ребром 1. Как вычислить скалярные произведения вектора АВ на:

5.86. Пусть  — куб. Как вычислить угол между:
— куб. Как вычислить угол между:
а)  и DC; б)
и DC; б)  ;
;

Думаем
5.87. Дан тетраэдр ABCD. Докажите, что равносильны два утверждения:  и
и 
5.88. Даны длины трех ребер параллелепипеда, выходящих из одной вершины, и углы между ними. Как найти длину диагонали параллелепипеда, выходящей из той же вершины?
5.89. В кубе соединили отрезками середины скрещивающихся ребер. Докажите, что все такие отрезки равны.
5.90. В правильном тетраэдре РАВС с ребром 1 точка X лежит на ребре АР и  точка Y лежит на ребре ВС и
точка Y лежит на ребре ВС и  Как вычислить: a) XY; б) угол между XY и РА; в) угол между
Как вычислить: a) XY; б) угол между XY и РА; в) угол между 
5.91. Как найти  при которых вектор
при которых вектор  ортогонален вектору
ортогонален вектору  если
если 
Поступаем в ВУЗ
5.92. При каком значении z векторы  перпендикулярны?
перпендикулярны?
Ответ:  .
.
5.93. Найдите косинусы углов, которые образуют с базисными векторами вектор  .
.
Ответ: 
5.94. Векторы  являются смежными сторонами параллелограмма. Определите величину угла между диагоналями
являются смежными сторонами параллелограмма. Определите величину угла между диагоналями 
Ответ: 
5.95. Найдите угол между векторами ОА и ОВ, если О — начало координат, вектор ОА составляет с осями координат  углы, соответственно равные и точка В имеет координаты
углы, соответственно равные и точка В имеет координаты 
Ответ:  .
.
5.96. Вектор с, перпендикулярный векторам  образует с осью
образует с осью  тупой угол. Найдите его координаты, если известно, что
тупой угол. Найдите его координаты, если известно, что 
Ответ: 
5.97. Вектор а, у которого первая координата больше второй, перпендикулярен вектору  и образует с осью
и образует с осью  угол, равный 135 градусов. Найдите его координаты, если известно, что
угол, равный 135 градусов. Найдите его координаты, если известно, что 
Ответ: 
5.98. Векторы а и b взаимно перпендикулярны, а вектор с образует с каждым из них угол у. Зная, что  вычислите скалярное произведение
вычислите скалярное произведение 
Ответ: -62.
5.99. Найдите вектор  образующий равные углы с векторами
образующий равные углы с векторами  если а перпендикулярен вектору
если а перпендикулярен вектору  и угол между вектором а и осью
и угол между вектором а и осью  тупой.
тупой.
Ответ: 
5.100. Вектор в, коллинеарный вектору  образует с осью
образует с осью  острый угол. Зная, что
острый угол. Зная, что  найдите его координаты.
найдите его координаты.
Ответ: 
5.101. Длина ребра правильного тетраэдра ABCD равна а. Точка Е — середина ребра CD, точка F — середина высоты BL грани ABD. Отрезок MN с концами на прямых AD и ВС пересекает прямую EF и перпендикулярен ей. Найдите длину этого отрезка.
Ответ: 
5.102. Векторы  и
и  служат сторонами треугольника ABC. Найдите длину медианы
служат сторонами треугольника ABC. Найдите длину медианы 
Ответ: 
ЗАДАЧИ К § 24
Рисуем
5.103. Нарисуйте плоскость, уравнение которой:


Планируем
5.104. Как узнать, в какой точке плоскость  пересекает каждую из осей координат?
пересекает каждую из осей координат?
5.105. Как узнать, пересекаются ли плоскости, заданные уравнениями:

5.106. Как написать уравнение плоскости, проходящей через точку  и перпендикулярной: а) одной из осей координат; б) одной из плоскостей координат; в) двум координатным плоскостям; г) плоскости, уравнение которой
и перпендикулярной: а) одной из осей координат; б) одной из плоскостей координат; в) двум координатным плоскостям; г) плоскости, уравнение которой  плоскости, уравнение которой
плоскости, уравнение которой 
5.107. Как написать уравнение плоскости, проходящей через точку (1,1,0) и параллельной: а) одной из осей координат; б) одной из плоскостей координат; в) двум координатным плоскостям; г) плоскости, уравнение которой  плоскости, уравнение которой
плоскости, уравнение которой 
5.108. Две плоскости заданы своими уравнениями. Как выяснить, будут ли они перпендикулярны? Если нет, то как найти угол между ними? А как узнать, будут ли они параллельны?
5.109. Какую фигуру задает в пространстве условие

5.110. Дан куб с ребром 1. Выберите удобную систему координат. Как в этой системе координат записать уравнения: а) его граней; б) диагональной плоскости; в) плоскости, которая пересекает его по правильному шестиугольнику; г) его диагонали?
Представляем
5.111. Как расположена плоскость относительно осей координат, если в ее уравнении будут равны нулю: а) один коэффициент; б) два коэффициента?
5.112. Могут ли быть в уравнении плоскости равными нулю: а) все коэффициенты при неизвестных; б) три коэффициента?
5.113. Как записать уравнение прямой, по которой пересекает координатные плоскости плоскость, уравнение которой 
5.114. Какая фигура задается в пространстве таким условием:

Поступаем в ВУЗ
5.115. Найдите угол между плоскостью, проходящей через точки  и плоскостью, проходящей через точки
и плоскостью, проходящей через точки 
Ответ: 
5.116. Найдите уравнение плоскости, проходящей через точки 
Ответ: 
5.117. Уравнения плоскостей  есть
есть

прямая  является их пересечением, а) Определите координаты точки пересечения прямой
является их пересечением, а) Определите координаты точки пересечения прямой  с плоскостями
с плоскостями  Определите величину угла между прямой
Определите величину угла между прямой  и плоскостью
и плоскостью 
Ответ: 
5.118. Плоскость отсекает от боковых ребер SA, SB и SC правильной четырехугольной пирамиды SABCD с вершиной  отрезки
отрезки  SC соответственно.
SC соответственно.
Длина бокового ребра пирамиды равна а Найдите длину отрезка SN, отсекаемого этой плоскостью на ребре 
Ответ:  .
.
5.119. Дана правильная треугольная призма  Пусть точка Р делит ось
Пусть точка Р делит ось  призмы в отношении
призмы в отношении  Через точку Р и середины ребер АВ и
Через точку Р и середины ребер АВ и  проведена плоскость. В каком отношении эта плоскость делит объем призмы?
проведена плоскость. В каком отношении эта плоскость делит объем призмы?
Ответ: 
Переключаемся
5.120. Из проволоки сделан каркас куба. Где находится центр масс фигуры, получающейся после удаления из каркаса: а) одного ребра; б) двух параллельных ребер; в) двух скрещивающихся ребер; г) двух пересекающихся ребер; д) трех ребер, выходящих из одной точки; е) трех попарно скрещивающихся ребер?
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧИТАТЕЛЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ
- § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 1.2. Двугранный угол. Угол между плоскостями.
- 1.3. Плоскость и прямая в пространстве.
- 1.4. Аксиомы стереометрии.
- 1.5. Взаимное расположение двух прямых в пространстве.
- 1.6. Признаки скрещивающихся прямых.
- 1.7. Параллельные прямые.
- 1.8. Параллельное проектирование.
- § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 2.2. О значении перпендикуляра.
- 2.3. Теорема о трех перпендикулярах.
- 2.4. Признак перпендикулярности прямой и плоскости.
- 2.5. Построение плоскости, перпендикулярной данной прямой.
- 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости.
- 2.7. Теорема о прямой, перпендикулярной плоскости.
- 2.8. Перпендикулярность плоскостей.
- 2.9. Ортогональное проектирование.
- § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 3.2. Параллельность и перпендикулярность.
- 3.3. Основная теорема о параллельных плоскостях.
- 3.4. Второй признак параллельности плоскостей.
- 3.5. Расстояние и параллельность.
- 3.6. Сонаправленность лучей и угол между прямыми.
- 3.7. Параллельность и углы.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ
- § 4. СФЕРА И ШАР
- 4.2. Взаимное положение шара и плоскости.
- 4.3. Сфера и многранники.
- 4.4. Вид и изображение шара и сферы.
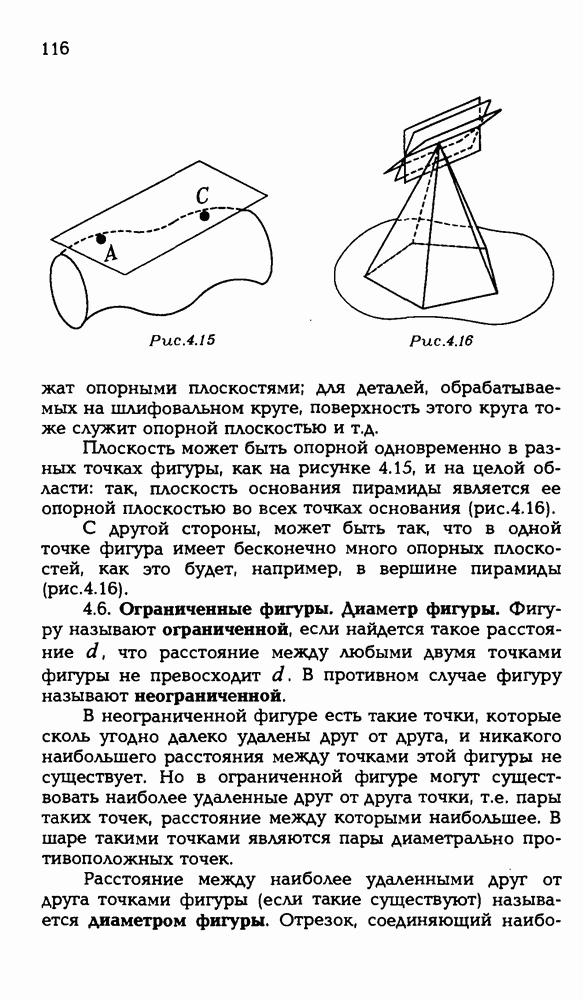
- 4.5. Опорная плоскость.
- 4.6. Ограниченные фигуры. Диаметр фигуры.
- 4.7. Опорные плоскости в концах диаметра.
- 4.8. Сфера — фигура вращения.
- 4.9. Симметрия сферы и шара.
- 4.10. Сфера — центрально симметричная фигура.
- 4.11. Сфера — зеркально симметричная фигура.
- 4.12. Отражение в плоскости и отражение в зеркале.
- § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ
- 5.2. Тригонометрия трехгранного угла.
- 5.3. Равенство трехгранных углов.
- 5.4. Сферические треугольники.
- 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников.
- § 6. ЦИЛИНДР
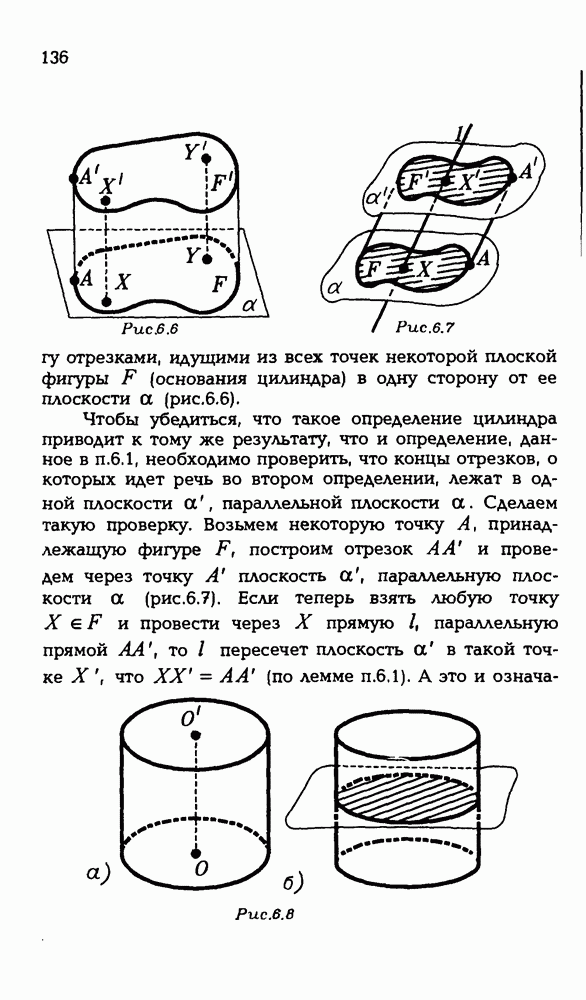
- 6.2. Другой подход к определению цилиндра.
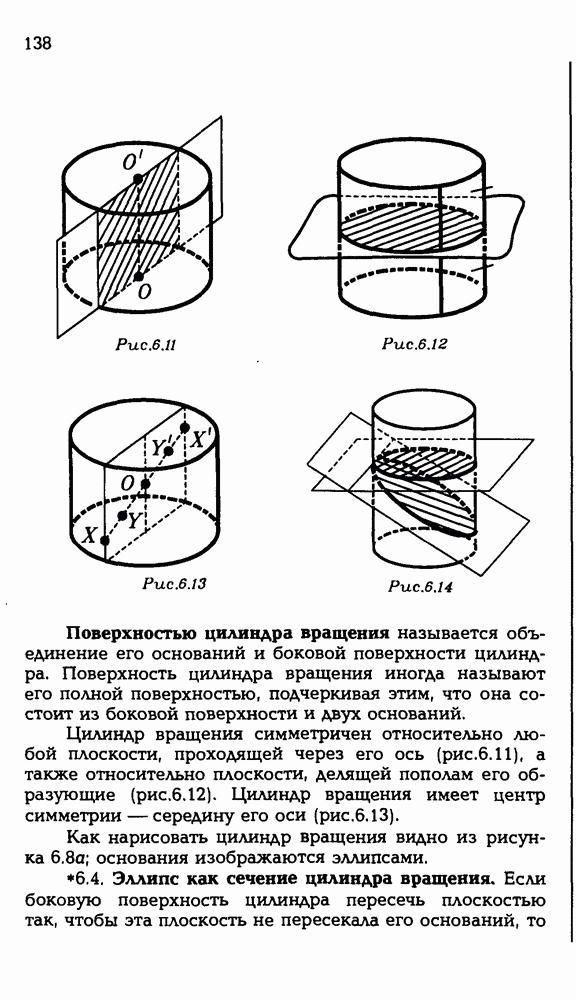
- 6.3. Цилиндр вращения.
- 6.4. Эллипс как сечение цилиндра вращения.
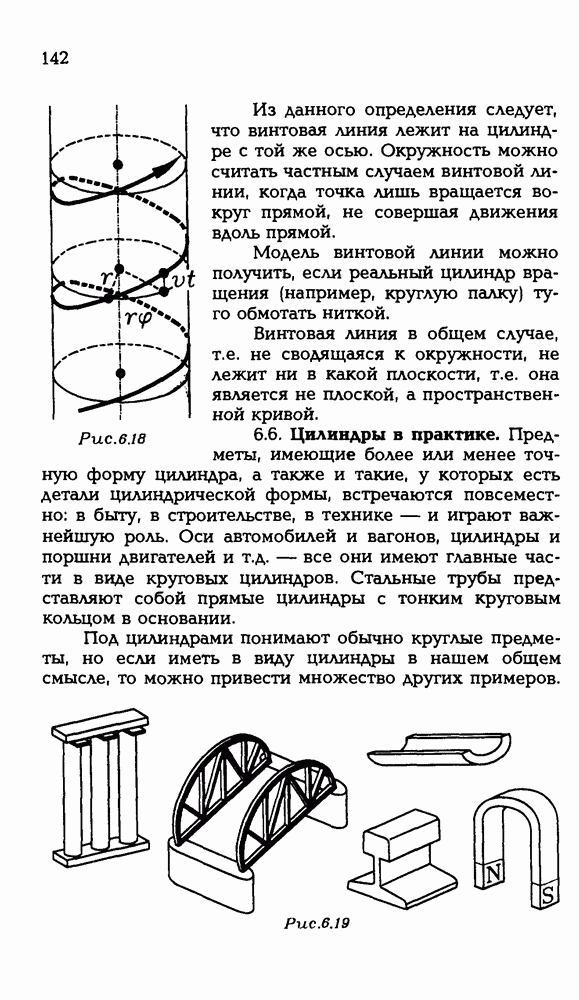
- 6.5. Винтовые линии.
- 6.6. Цилиндры в практике.
- § 7. ПРИЗМА
- 7.2. Параллелепипед.
- 7.3. Прямоугольный параллелепипед.
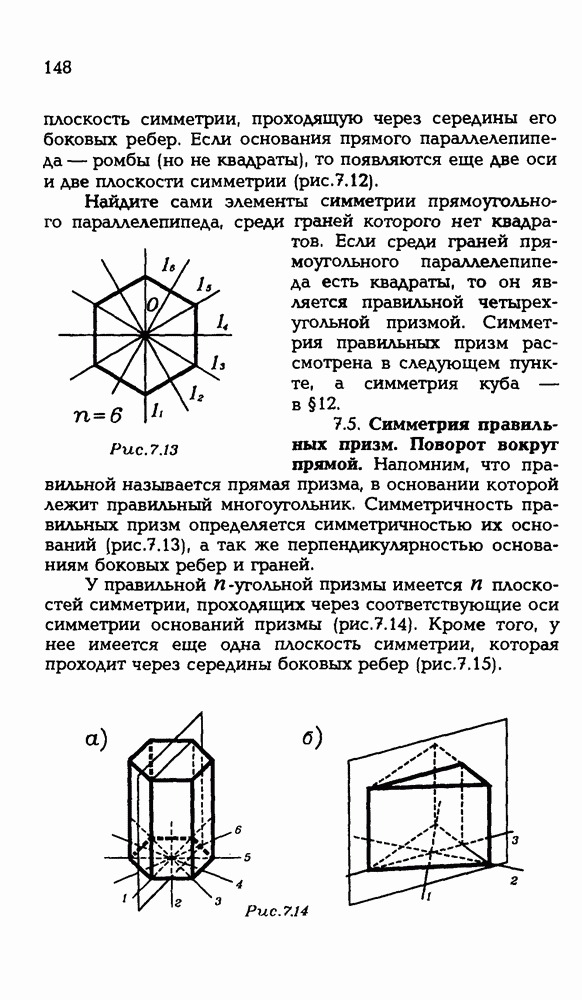
- 7.4. Симметрия параллелепипеда.
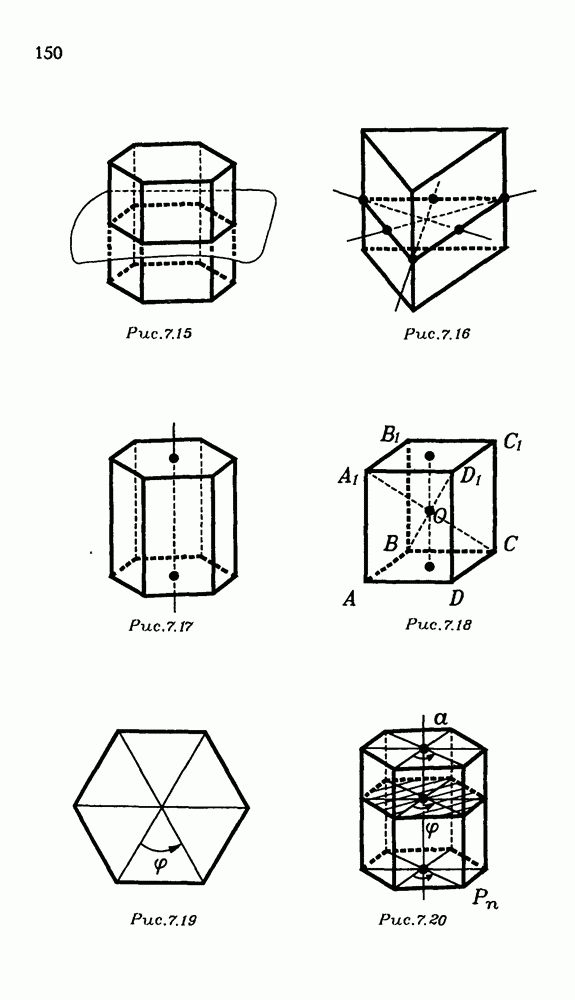
- 7.5. Симметрия правильных призм. Поворот вокруг прямой.
- § 8. КОНУС
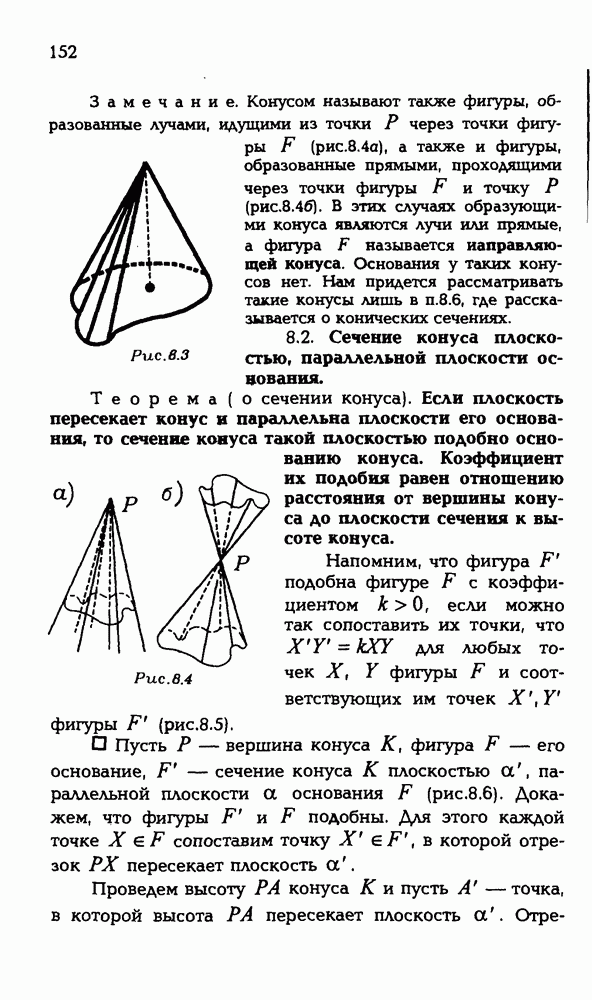
- 8.2. Сечение конуса плоскостью, параллельной плоскости основания.
- 8.3. Конус вращения.
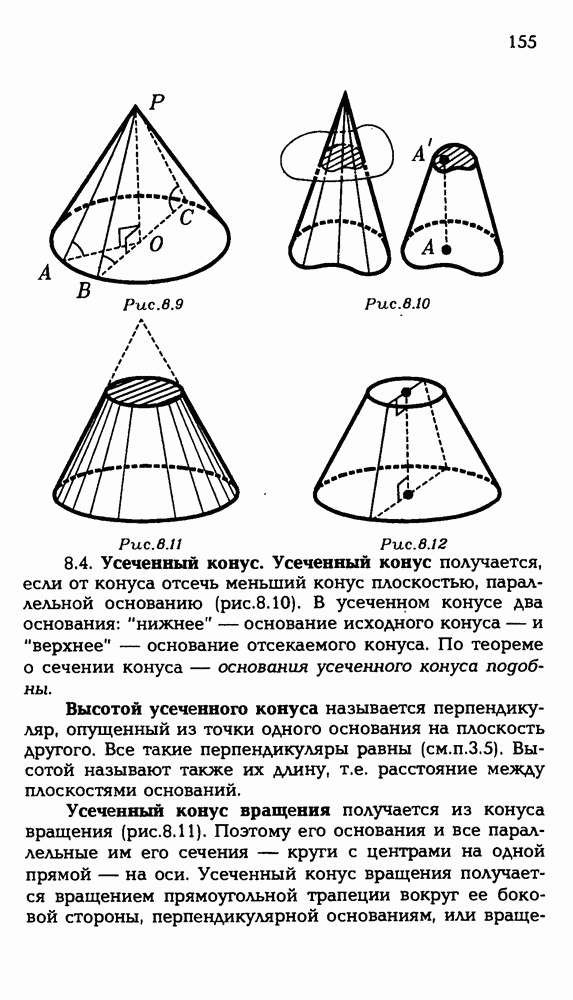
- 8.4. Усеченный конус.
- § 9. ПИРАМИДА
- 9.2. Правильная пирамида.
- 9.3. Симметрия правильной пирамиды.
- 9.4. Конусы и пирамиды в практике.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ
- § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ
- 10.2. Граница и внутренность.
- 10.3. Определение тела и замкнутой плоской области.
- 10.4. Выпуклые фигуры.
- 10.5. Выпуклые тела.
- § 11. МНОГОГРАННИКИ
- 11.2. Выпуклые многогранники.
- 11.3. Теорема Эйлера.
- 11.4. Выпуклые многогранники и выпуклые оболочки.
- 11.5. Многогранная поверхность и развертка.
- 11.6. Развертка выпуклого многогранника.
- § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
- 12.2. Классификация правильных многогранников.
- 12.3. Полуправильные многогранники.
- 12.4. Симметрия правильных многогранников.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
- § 13. ПОНЯТИЕ ОБЪЕМА
- 13.2. Определение объема.
- 13.3. Геометрические величины.
- § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА
- 14.2. Объем прямой призмы.
- § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ
- 15.2. Выражение объема через площади сечений.
- § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА
- 16.2. Объем конуса
- 16.3. Объем шара.
- 16.4. Объем тел вращения.
- 16.5. Объем шарового сегмента и шарового сектора.
- § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ
- 17.2. Площадь сферы.
- 17.3. Площадь сферических многоугольников.
- 17.4. Площадь сферического сегмента и сферического пояса.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ
- § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- 18.2. Другой способ нахождения координат точки.
- 18.3. Построение точки с данными координатами.
- 18.4. Выражение расстояния между точками.
- § 19. МЕТОД КООРДИНАТ
- 19.2. Уравнения без одной или двух координат.
- 19.3. Некоторые применения метода координат.
- § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ
- 20.2. Полярные координаты.
- 20.3. Цилиндрические координаты.
- 20.4. Сферические координаты.
- 20.5. Координатная сеть.
- § 21. ПОНЯТИЕ ВЕКТОРА
- 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов.
- 21.3. Сонаправленность и равенство векторов.
- 21.4. Признаки равенства векторов.
- 21.5. Радиус-вектор.
- § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 22.2. Разложение вектора на составляющие.
- 22.3. Умножение вектора на число.
- 22.4. Координаты вектора.
- 22.5. Равенство координат векторов и координат точек.
- 22.6. Разложение векторов по базису.
- 22.7. Ориентация базиса.
- § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ
- 23.2. Выражение скалярного произведения через координаты.
- 23.3. Свойства скалярного умножения.
- 23.4. Применения скалярного умножения.
- 23.5. Скалярное произведение и проекции.
- § 24. ВЕКТОРНЫЙ МЕТОД
- 24.2. Общее уравнение плоскости.
- 24.3. Векторное задание отрезка.
- 24.4. Некоторые теоремы о треугольниках и тетраэдрах.
- 24.5. Центр масс системы материальных точек.
- 24.6. Центры масс и выпуклые многогранники.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 6. ПРЕОБРАЗОВАНИЯ
- 25.1. Преобразования фигур.
- 25.2. Определения движения и равенства фигур.
- 25.3. Преобразования симметрии.
- 25.4. Параллельный перенос.
- 25.5. Поворот.
- § 26. СВОЙСТВА ДВИЖЕНИЙ
- 26.2. Общие свойства движений.
- 26.3. Теоремы о задании движений.
- 26.4. Неподвижные точки движений.
- 26.5. Два рода движений.
- 26.6. Теорема подвижности пространства.
- 26.7. Композиция отражений в плоскости.
- § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА
- 27.2. Движения первого рода как винтовые движения.
- 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот.
- 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения.
- § 28. ПОДОБИЕ
- 28.2. Гомотетия.
- 28.3. Свойства подобия.
- 28.4. Группы преобразований.
- § 29. ИНВЕРСИЯ
- 29.2. Аналитическое задание инверсии.
- 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии.
- 29.4. Сохранение величин углов при инверсии.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ОТВЕТЫ И УКАЗАНИЯ
- ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ