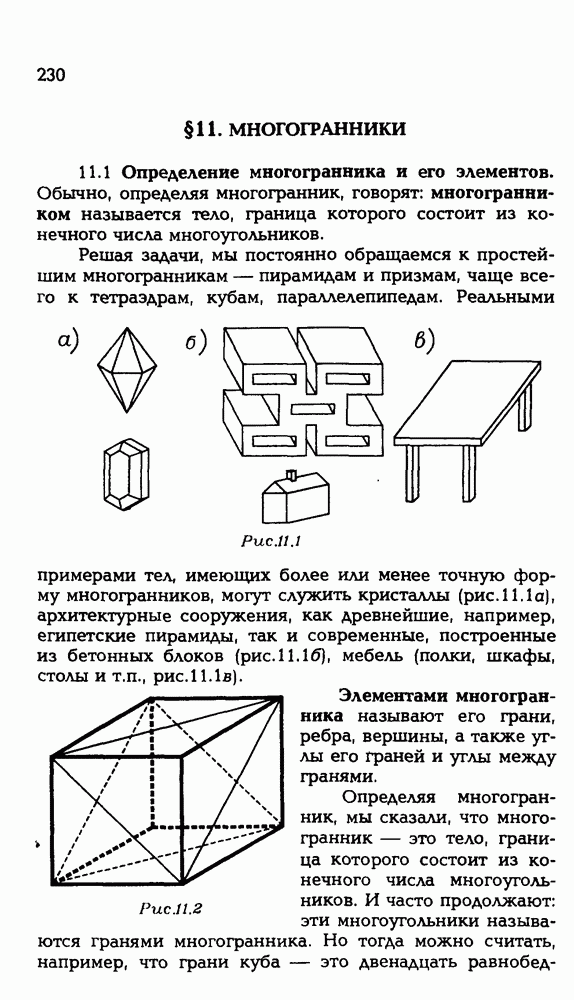
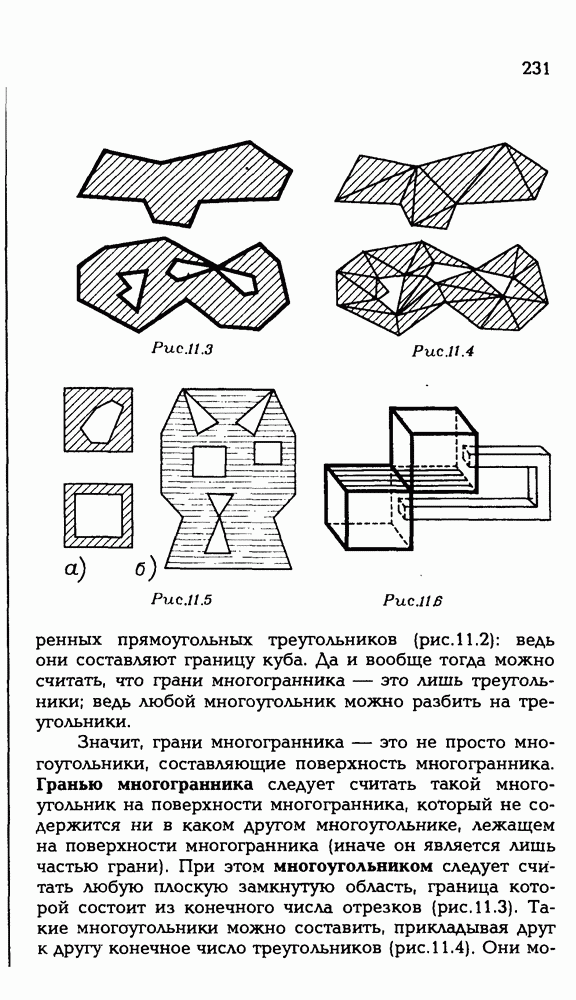
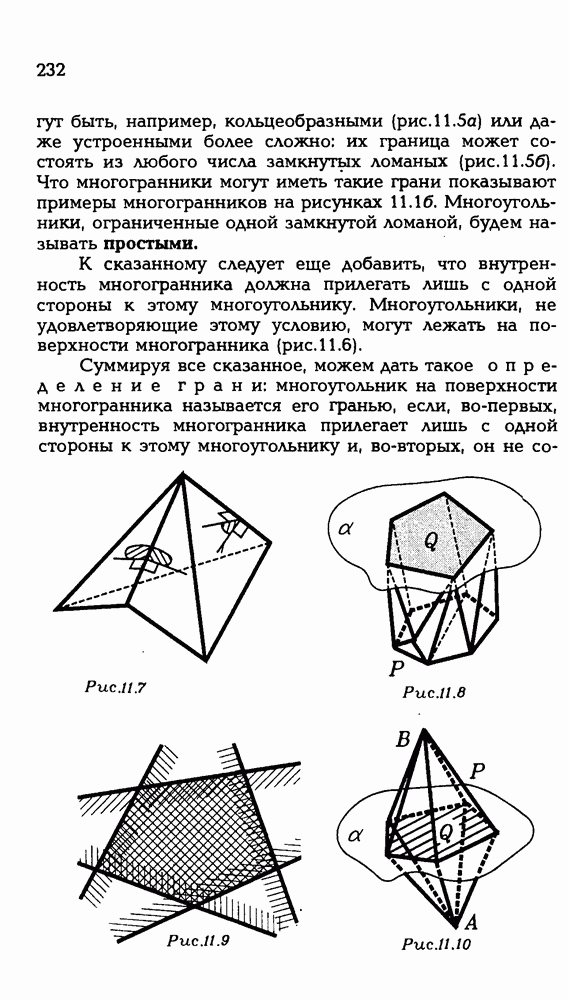
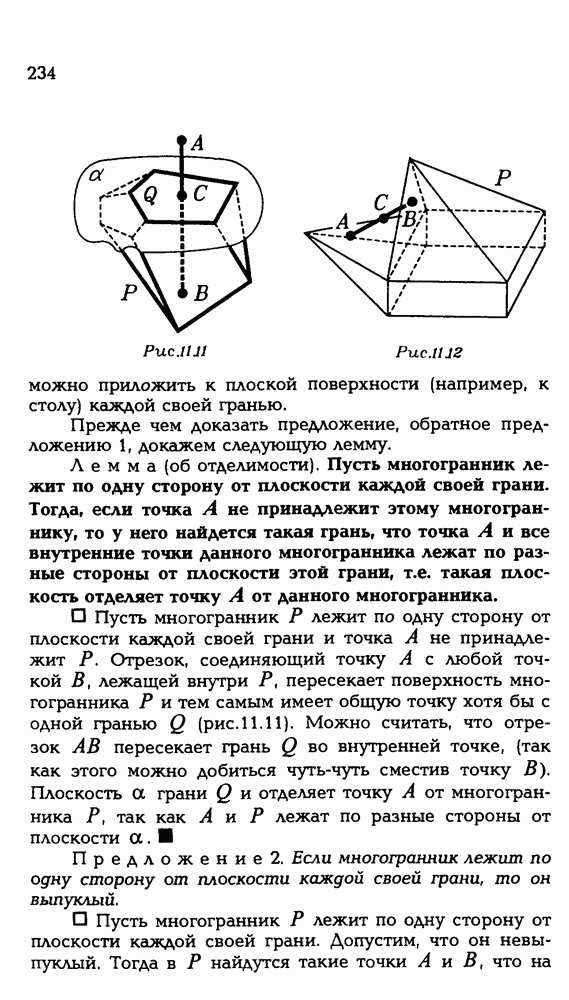
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.3. Теорема Эйлера.
Рассмотрим любой выпуклый многогранник Р. Пусть  — число его вершин,
— число его вершин,  — число его ребер,
— число его ребер,  число его граней.
число его граней.
Леонардом Эйлером была доказана удивительная теорема.
Теорема Эйлера. Для любого выпуклого многогранника 
Проверьте это равенство на примерах  -угольной пирамиды,
-угольной пирамиды,  -угольной призмы или
-угольной призмы или  -угольной усеченной пирамиды.
-угольной усеченной пирамиды.
В этих примерах выпуклость многогранников не предполагается. И действительно, теорема Эйлера справедлива не только для выпуклых многогранников, но и для таких многогранников, которые могут быть получены из выпуклых с помощью непрерывной деформации "без

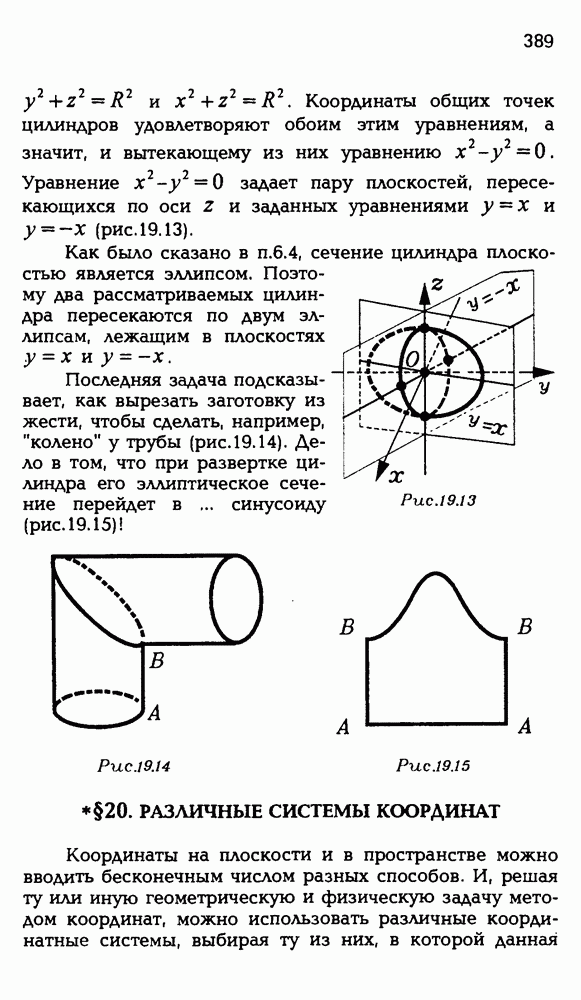
Рис. 11.13

Рис. 11.14
разрывов и склеиваний" (мы не даем точных определений таким деформациям, но интуитивно ясно, о каких деформациях идет речь). При этом ясно, что поскольку в теореме Эйлера речь идет лишь об элементах поверхности многогранника, то в ее условии, говоря "многогранник", можно иметь в виду многогранную поверхность, а не многогранное тело, и эта теорема относится именно к поверхностям, а не к телам. Более того, в формуле Эйлера величина  определяется лишь сетью вершин и ребер на поверхности выпуклого многогранника. Эта величина не изменится, если мы деформируем рассматриваемую многогранную поверхность, например, в сферу, а сеть вершин и ребер многогранника — в некоторую сеть точек и кривых на сфере. Тогда можно считать
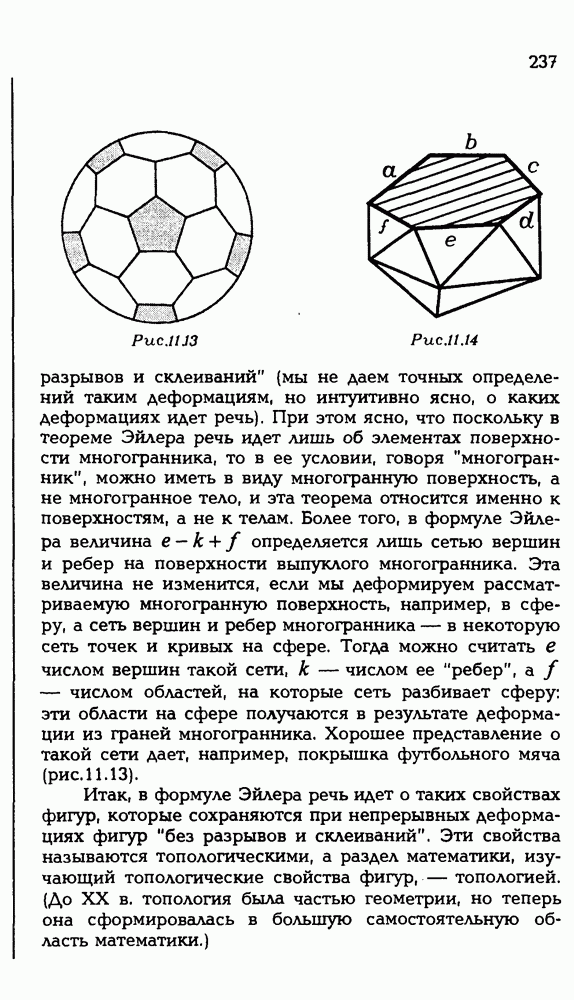
определяется лишь сетью вершин и ребер на поверхности выпуклого многогранника. Эта величина не изменится, если мы деформируем рассматриваемую многогранную поверхность, например, в сферу, а сеть вершин и ребер многогранника — в некоторую сеть точек и кривых на сфере. Тогда можно считать  числом вершин такой сети, к — числом ее "ребер", a f — числом областей, на которые сеть разбивает сферу: эти области на сфере получаются в результате деформации из граней многогранника. Хорошее представление о такой сети дает, например, покрышка футбольного мяча (рис. 11.13).
числом вершин такой сети, к — числом ее "ребер", a f — числом областей, на которые сеть разбивает сферу: эти области на сфере получаются в результате деформации из граней многогранника. Хорошее представление о такой сети дает, например, покрышка футбольного мяча (рис. 11.13).
Итак, в формуле Эйлера речь идет о таких свойствах фигур, которые сохраняются при непрерывных деформациях фигур "без разрывов и склеиваний". Эти свойства называются топологическими, а раздел математики, изучающий топологические свойства фигур, — топологией. (До XX в. топология была частью геометрии, но теперь она сформировалась в большую самостоятельную область математики.)
Возможностью таких деформаций, не изменяющих числа  , мы и воспользуемся при доказательстве теоремы Эйлера. Поступим так. Пусть Р — выпуклый многогранник,
, мы и воспользуемся при доказательстве теоремы Эйлера. Поступим так. Пусть Р — выпуклый многогранник,  — числа его вершин, ребер и граней. Удалим из Р любую его грань Q, оставив ее стороны и вершины (рис. 11.14). Оставшуюся многогранную поверхность обозначим через Р. Число вершин
— числа его вершин, ребер и граней. Удалим из Р любую его грань Q, оставив ее стороны и вершины (рис. 11.14). Оставшуюся многогранную поверхность обозначим через Р. Число вершин  одно и то же — е. Точно так же
одно и то же — е. Точно так же  одно и то же число ребер — k. А число f граней у Р на единицу меньше, чем у Р. т. е.
одно и то же число ребер — k. А число f граней у Р на единицу меньше, чем у Р. т. е.  Поэтому равенство Эйлера
Поэтому равенство Эйлера  равносильно равенству
равносильно равенству

А это равенство мы докажем с помощью следующей леммы.
Лемма. Пусть простой многоугольник Q разбит некоторой сетью, состоящей из точек (вершин сети) и соединяющих их отрезков (ребер сети), на f простых многоугольников  Ту. Если в — число вершин в этой сети, а к — число ее ребер (считая вершины и стороны самого многоугольника Q), то
Ту. Если в — число вершин в этой сети, а к — число ее ребер (считая вершины и стороны самого многоугольника Q), то 

Рис. 11.15
Среди простых многоугольников, на которые разбит многоугольник Q, всегда найдется такой многоугольник  , что, удалив
, что, удалив  из Q, мы снова получим один простой многоугольник
из Q, мы снова получим один простой многоугольник  (рис. 11.15). (Попробуйте точно обосновать существование такого многоугольника
(рис. 11.15). (Попробуйте точно обосновать существование такого многоугольника  . Вообще говоря, не каждый из многоугольников разбиения, выходящих на границу многоугольника Q, обладает таким свойством. Например, им не обладает многоугольник
. Вообще говоря, не каждый из многоугольников разбиения, выходящих на границу многоугольника Q, обладает таким свойством. Например, им не обладает многоугольник  ).
).
Удалив многоугольник  из Q, мы удалим все его внутренние точки и только те его вершины (и ребра), которые не являются вершинами (и ребрами) других многоугольников, входящих в разбиение Q. Поэтому если, удаляя многоугольник
из Q, мы удалим все его внутренние точки и только те его вершины (и ребра), которые не являются вершинами (и ребрами) других многоугольников, входящих в разбиение Q. Поэтому если, удаляя многоугольник  , мы удалим часть границы многоугольника Q, которая является ломаной, состоящей из
, мы удалим часть границы многоугольника Q, которая является ломаной, состоящей из  ребер, то мы при этом удалим
ребер, то мы при этом удалим  вершину. Итак, для разбиения многоугольника
вершину. Итак, для разбиения многоугольника  число его вершин
число его вершин  , число его ребер
, число его ребер  а число многоугольников
а число многоугольников  Следовательно,
Следовательно,

Таким образом, число  не изменяется при описанном удалении многоугольника
не изменяется при описанном удалении многоугольника  . Продолжив такие операции
. Продолжив такие операции  раз, мы придем к одному простому многоугольнику, для которого число его вершин
раз, мы придем к одному простому многоугольнику, для которого число его вершин  равно числу его ребер
равно числу его ребер  Поскольку, очевидно,
Поскольку, очевидно,  то равенство е — к
то равенство е — к  справедливо.
справедливо.
Теперь, чтобы завершить доказательство теоремы Эйлера, достаточно "растянуть" многогранную поверхность Р вместе с сетью ее вершин и ребер на плоскость в плоский многоугольник и воспользоваться доказанной леммой. То, что это можно сделать, интуитивно ясно, и можно было бы на этом закончить доказательство. Для тех же, кто хочет подкрепить это интуитивное убеждение некоторым рассуждением, укажем один из способов такого "растяжения".
Возьмем внутри грани Q любую точку О. Любой луч, идущий из О в точку  , пересекает Р лишь в точке X. Ясно, что это свойство сохранится, если точку О чуть сместить до положения О вне многогранника Р (рис. 11.16). (Попробуйте точно указать, где может находиться такая точка О.) Спроектируем теперь вершины, ребра и грани многогранника Р из Она грань Q. Получим в Q сеть, разбивающую грань Q на
, пересекает Р лишь в точке X. Ясно, что это свойство сохранится, если точку О чуть сместить до положения О вне многогранника Р (рис. 11.16). (Попробуйте точно указать, где может находиться такая точка О.) Спроектируем теперь вершины, ребра и грани многогранника Р из Она грань Q. Получим в Q сеть, разбивающую грань Q на  выпуклых
выпуклых
многоугольников  . В этой сети столько же вершин и ребер (считая вершины и ребра многоугольника Q), сколько вершин и ребер у многогранника Р. Каждый из многоугольников
. В этой сети столько же вершин и ребер (считая вершины и ребра многоугольника Q), сколько вершин и ребер у многогранника Р. Каждый из многоугольников  соответствующий некоторой грани Q многогранника Р, можно получить так: взять пирамиду с вершиной О и основанием Q) и пересечь ее многоугольником Q. К этому разбиению грани Q на многоугольники
соответствующий некоторой грани Q многогранника Р, можно получить так: взять пирамиду с вершиной О и основанием Q) и пересечь ее многоугольником Q. К этому разбиению грани Q на многоугольники  и применяется лемма.
и применяется лемма.

Рис. 11.16
Замечание. Одним из главных моментов проведенного доказательства является возможность "распрямить и положить на плоскость" поверхность многогранника после того, как у него удалена одна грань, которая является простым многоугольником. Этого нельзя сделать, например, для многогранника, изображенного на рисунке 11.17. Для него уже 

Рис. 11.17
Но для многогранников любого строения и вообще для тел выполняется обобщенная теорема Эйлера. Для всех сетей, которые могут быть "нарисованы" на поверхности данного тела или любого получаемого из него деформацией без разрывов и склеиваний, число  одно и то же при условии, что каждую "грань" (область) можно деформировать в простой многоугольник (с тем же числом сторон).
одно и то же при условии, что каждую "грань" (область) можно деформировать в простой многоугольник (с тем же числом сторон).
Л. Эйлер (1707—1783) — великий математик, физик и астроном; швейцарец по рождению, он был членом Петербургской академии наук и работал в России в 1727 —1741 и в 1766-1783 г.г,
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧИТАТЕЛЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ
- § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 1.2. Двугранный угол. Угол между плоскостями.
- 1.3. Плоскость и прямая в пространстве.
- 1.4. Аксиомы стереометрии.
- 1.5. Взаимное расположение двух прямых в пространстве.
- 1.6. Признаки скрещивающихся прямых.
- 1.7. Параллельные прямые.
- 1.8. Параллельное проектирование.
- § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 2.2. О значении перпендикуляра.
- 2.3. Теорема о трех перпендикулярах.
- 2.4. Признак перпендикулярности прямой и плоскости.
- 2.5. Построение плоскости, перпендикулярной данной прямой.
- 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости.
- 2.7. Теорема о прямой, перпендикулярной плоскости.
- 2.8. Перпендикулярность плоскостей.
- 2.9. Ортогональное проектирование.
- § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 3.2. Параллельность и перпендикулярность.
- 3.3. Основная теорема о параллельных плоскостях.
- 3.4. Второй признак параллельности плоскостей.
- 3.5. Расстояние и параллельность.
- 3.6. Сонаправленность лучей и угол между прямыми.
- 3.7. Параллельность и углы.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ
- § 4. СФЕРА И ШАР
- 4.2. Взаимное положение шара и плоскости.
- 4.3. Сфера и многранники.
- 4.4. Вид и изображение шара и сферы.
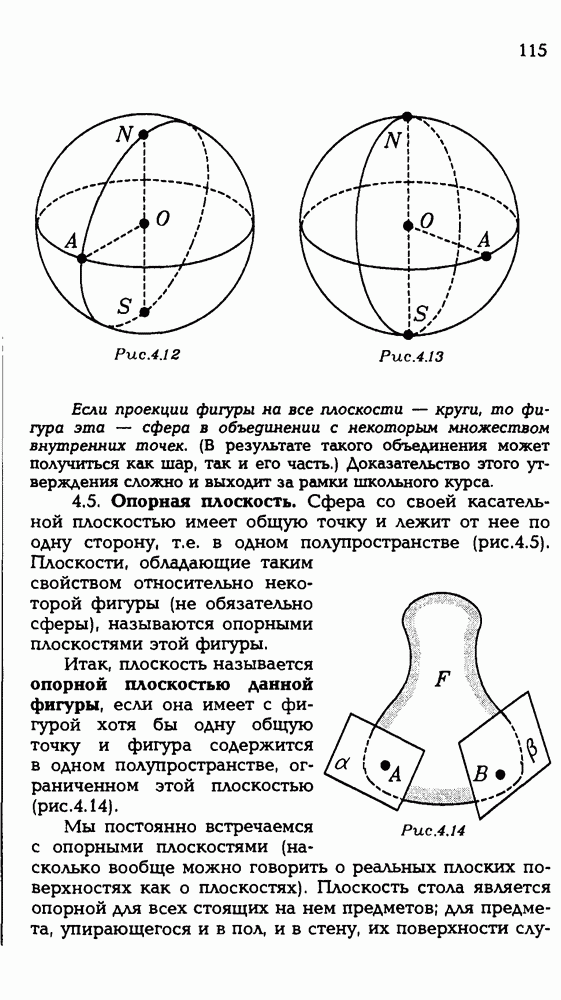
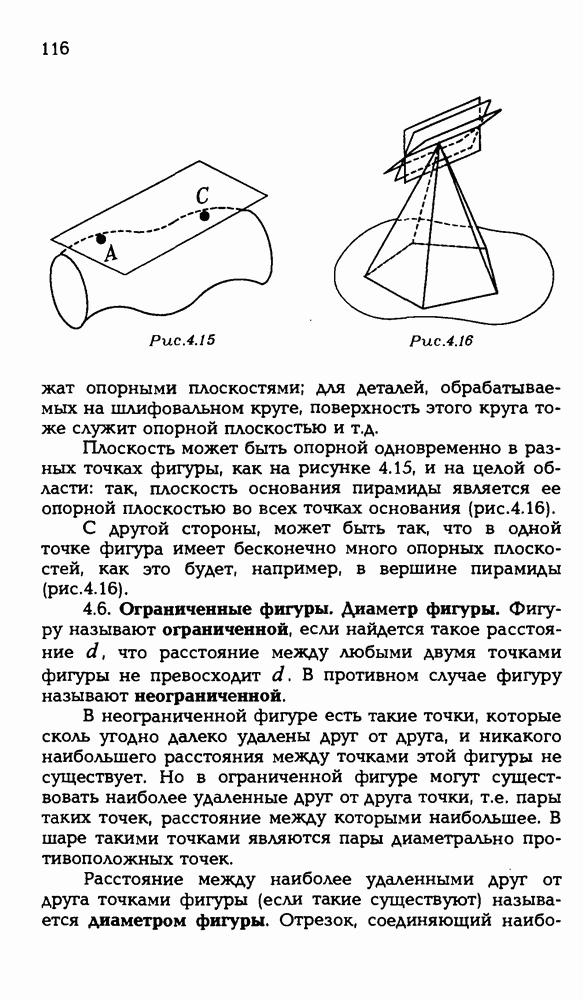
- 4.5. Опорная плоскость.
- 4.6. Ограниченные фигуры. Диаметр фигуры.
- 4.7. Опорные плоскости в концах диаметра.
- 4.8. Сфера — фигура вращения.
- 4.9. Симметрия сферы и шара.
- 4.10. Сфера — центрально симметричная фигура.
- 4.11. Сфера — зеркально симметричная фигура.
- 4.12. Отражение в плоскости и отражение в зеркале.
- § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ
- 5.2. Тригонометрия трехгранного угла.
- 5.3. Равенство трехгранных углов.
- 5.4. Сферические треугольники.
- 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников.
- § 6. ЦИЛИНДР
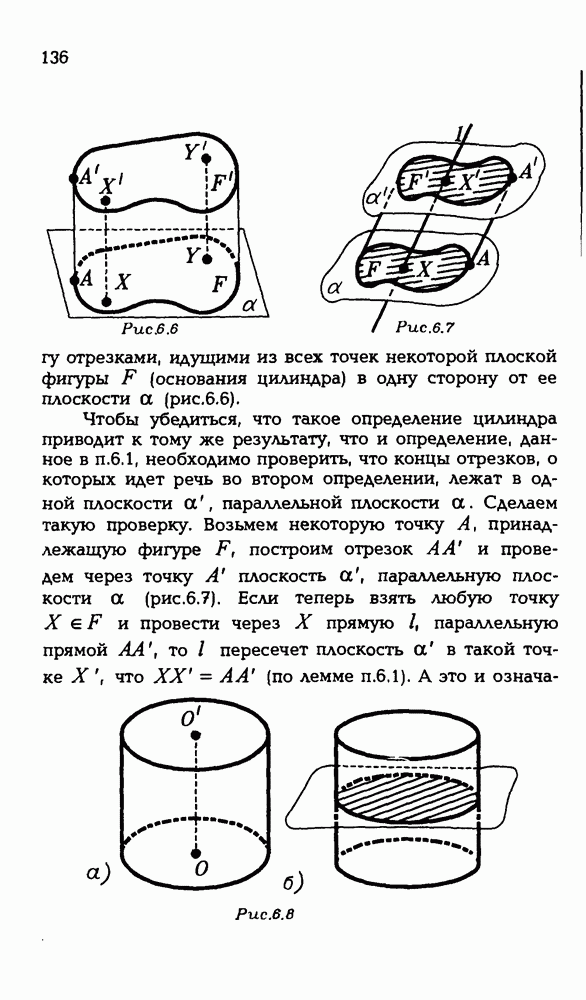
- 6.2. Другой подход к определению цилиндра.
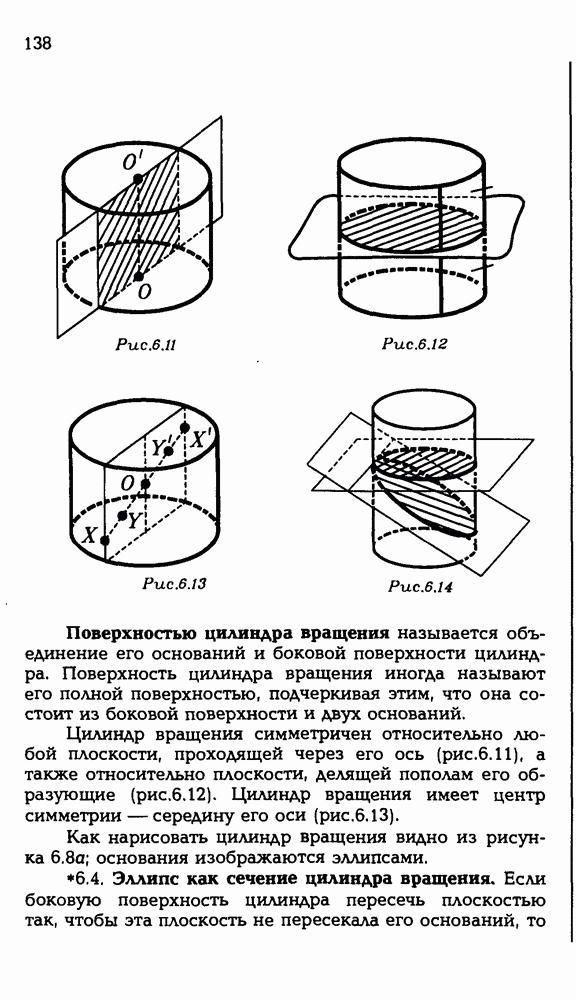
- 6.3. Цилиндр вращения.
- 6.4. Эллипс как сечение цилиндра вращения.
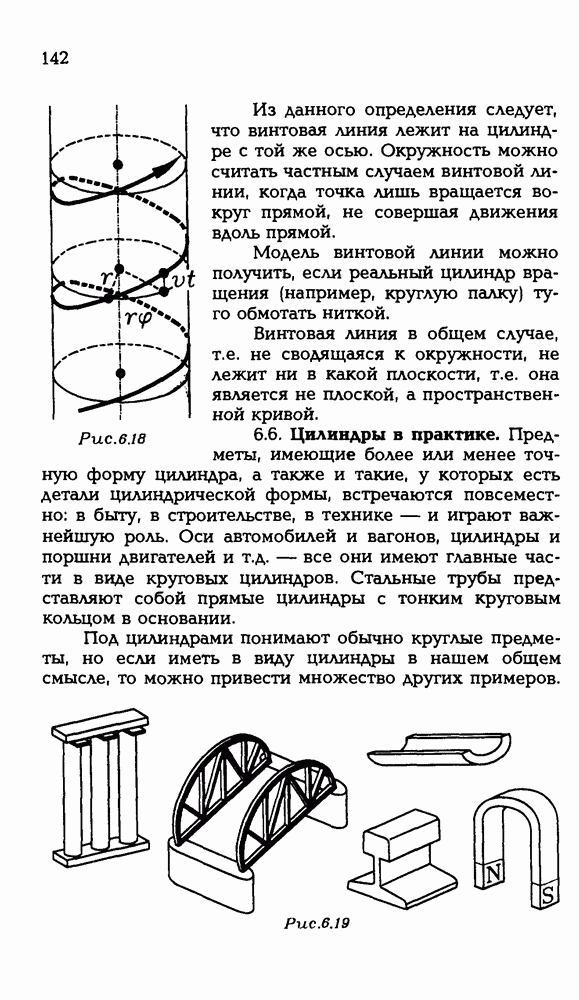
- 6.5. Винтовые линии.
- 6.6. Цилиндры в практике.
- § 7. ПРИЗМА
- 7.2. Параллелепипед.
- 7.3. Прямоугольный параллелепипед.
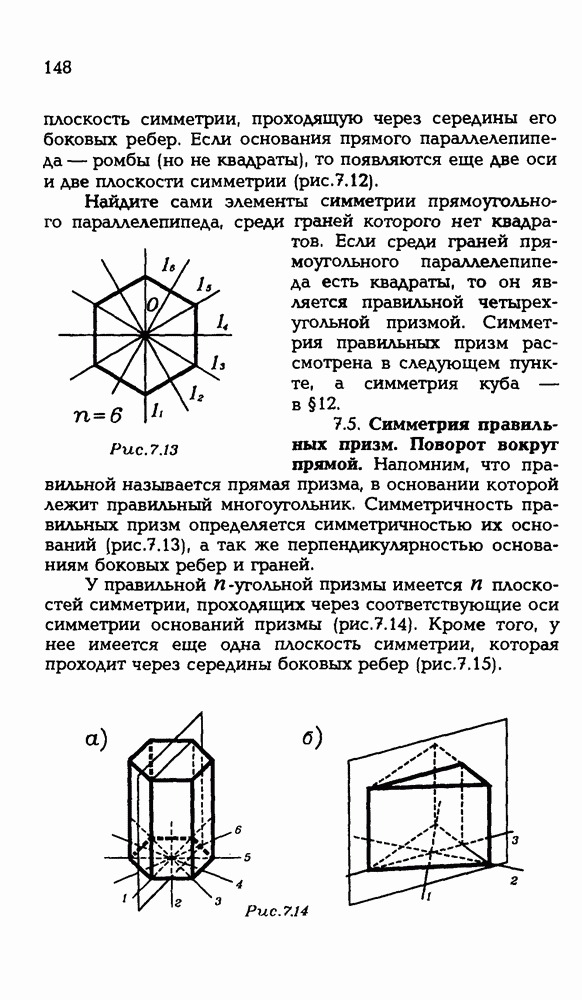
- 7.4. Симметрия параллелепипеда.
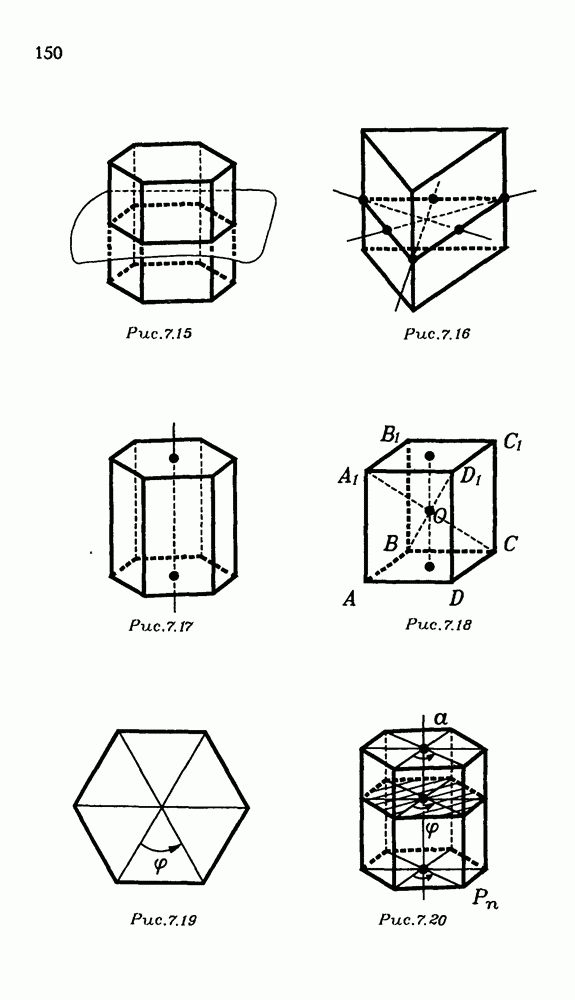
- 7.5. Симметрия правильных призм. Поворот вокруг прямой.
- § 8. КОНУС
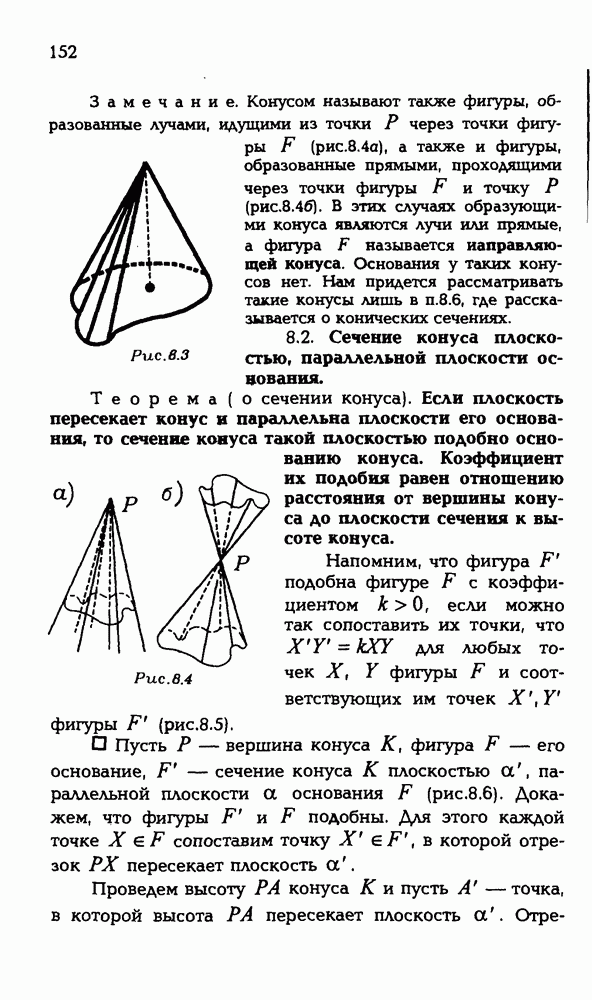
- 8.2. Сечение конуса плоскостью, параллельной плоскости основания.
- 8.3. Конус вращения.
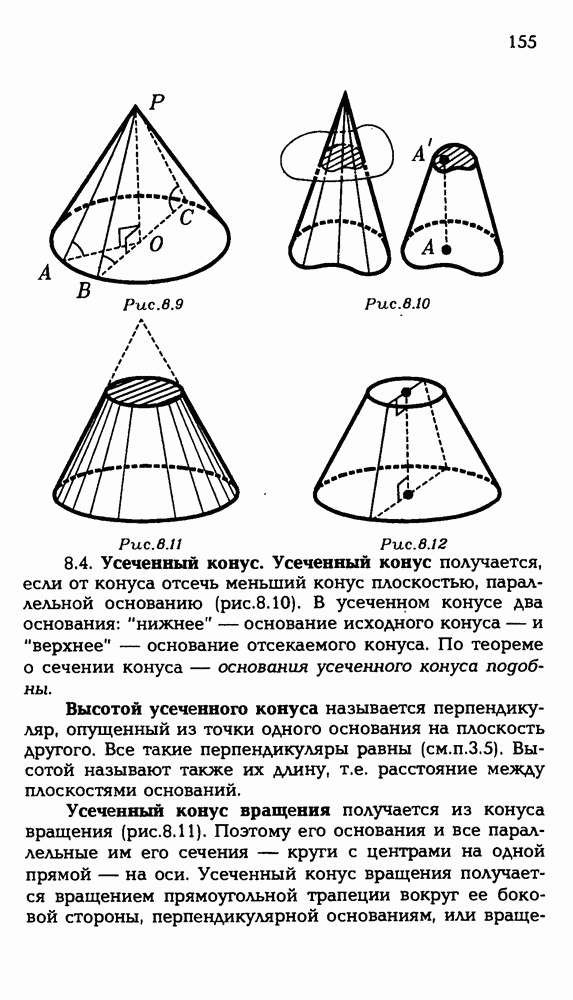
- 8.4. Усеченный конус.
- § 9. ПИРАМИДА
- 9.2. Правильная пирамида.
- 9.3. Симметрия правильной пирамиды.
- 9.4. Конусы и пирамиды в практике.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ
- § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ
- 10.2. Граница и внутренность.
- 10.3. Определение тела и замкнутой плоской области.
- 10.4. Выпуклые фигуры.
- 10.5. Выпуклые тела.
- § 11. МНОГОГРАННИКИ
- 11.2. Выпуклые многогранники.
- 11.3. Теорема Эйлера.
- 11.4. Выпуклые многогранники и выпуклые оболочки.
- 11.5. Многогранная поверхность и развертка.
- 11.6. Развертка выпуклого многогранника.
- § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
- 12.2. Классификация правильных многогранников.
- 12.3. Полуправильные многогранники.
- 12.4. Симметрия правильных многогранников.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
- § 13. ПОНЯТИЕ ОБЪЕМА
- 13.2. Определение объема.
- 13.3. Геометрические величины.
- § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА
- 14.2. Объем прямой призмы.
- § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ
- 15.2. Выражение объема через площади сечений.
- § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА
- 16.2. Объем конуса
- 16.3. Объем шара.
- 16.4. Объем тел вращения.
- 16.5. Объем шарового сегмента и шарового сектора.
- § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ
- 17.2. Площадь сферы.
- 17.3. Площадь сферических многоугольников.
- 17.4. Площадь сферического сегмента и сферического пояса.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ
- § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- 18.2. Другой способ нахождения координат точки.
- 18.3. Построение точки с данными координатами.
- 18.4. Выражение расстояния между точками.
- § 19. МЕТОД КООРДИНАТ
- 19.2. Уравнения без одной или двух координат.
- 19.3. Некоторые применения метода координат.
- § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ
- 20.2. Полярные координаты.
- 20.3. Цилиндрические координаты.
- 20.4. Сферические координаты.
- 20.5. Координатная сеть.
- § 21. ПОНЯТИЕ ВЕКТОРА
- 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов.
- 21.3. Сонаправленность и равенство векторов.
- 21.4. Признаки равенства векторов.
- 21.5. Радиус-вектор.
- § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 22.2. Разложение вектора на составляющие.
- 22.3. Умножение вектора на число.
- 22.4. Координаты вектора.
- 22.5. Равенство координат векторов и координат точек.
- 22.6. Разложение векторов по базису.
- 22.7. Ориентация базиса.
- § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ
- 23.2. Выражение скалярного произведения через координаты.
- 23.3. Свойства скалярного умножения.
- 23.4. Применения скалярного умножения.
- 23.5. Скалярное произведение и проекции.
- § 24. ВЕКТОРНЫЙ МЕТОД
- 24.2. Общее уравнение плоскости.
- 24.3. Векторное задание отрезка.
- 24.4. Некоторые теоремы о треугольниках и тетраэдрах.
- 24.5. Центр масс системы материальных точек.
- 24.6. Центры масс и выпуклые многогранники.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 6. ПРЕОБРАЗОВАНИЯ
- 25.1. Преобразования фигур.
- 25.2. Определения движения и равенства фигур.
- 25.3. Преобразования симметрии.
- 25.4. Параллельный перенос.
- 25.5. Поворот.
- § 26. СВОЙСТВА ДВИЖЕНИЙ
- 26.2. Общие свойства движений.
- 26.3. Теоремы о задании движений.
- 26.4. Неподвижные точки движений.
- 26.5. Два рода движений.
- 26.6. Теорема подвижности пространства.
- 26.7. Композиция отражений в плоскости.
- § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА
- 27.2. Движения первого рода как винтовые движения.
- 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот.
- 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения.
- § 28. ПОДОБИЕ
- 28.2. Гомотетия.
- 28.3. Свойства подобия.
- 28.4. Группы преобразований.
- § 29. ИНВЕРСИЯ
- 29.2. Аналитическое задание инверсии.
- 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии.
- 29.4. Сохранение величин углов при инверсии.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ОТВЕТЫ И УКАЗАНИЯ
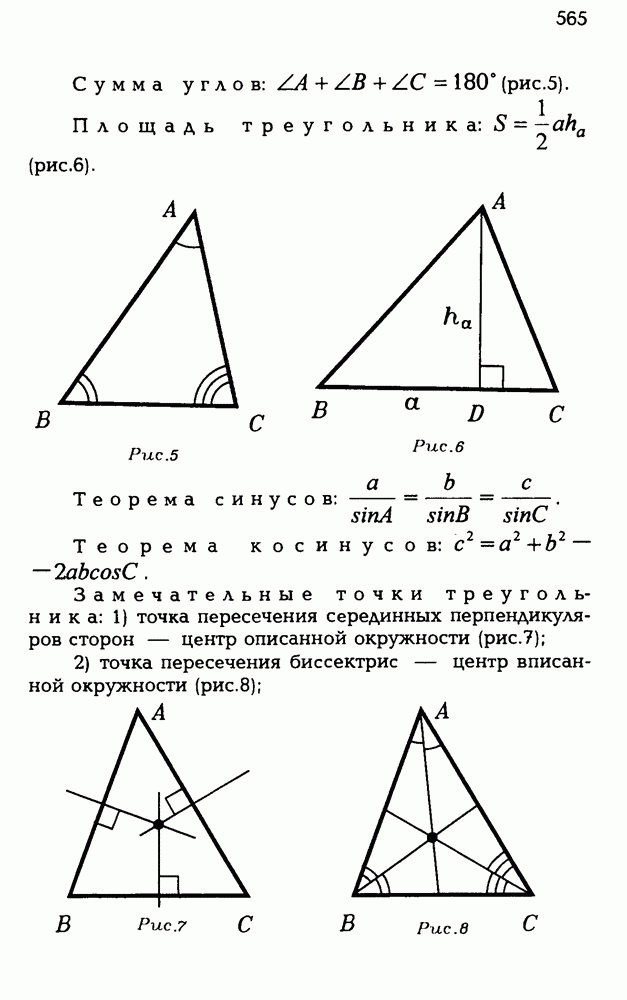
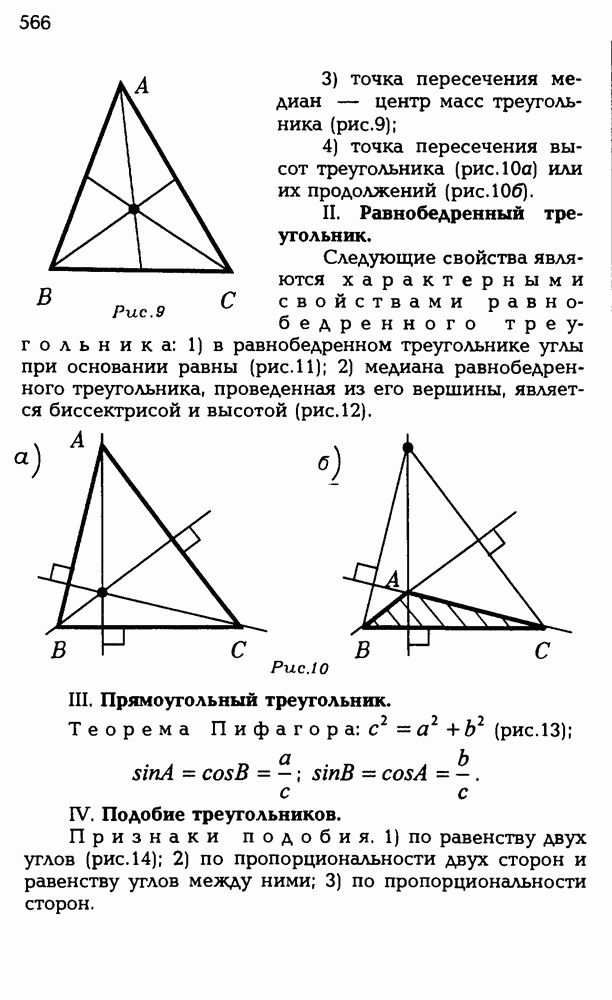
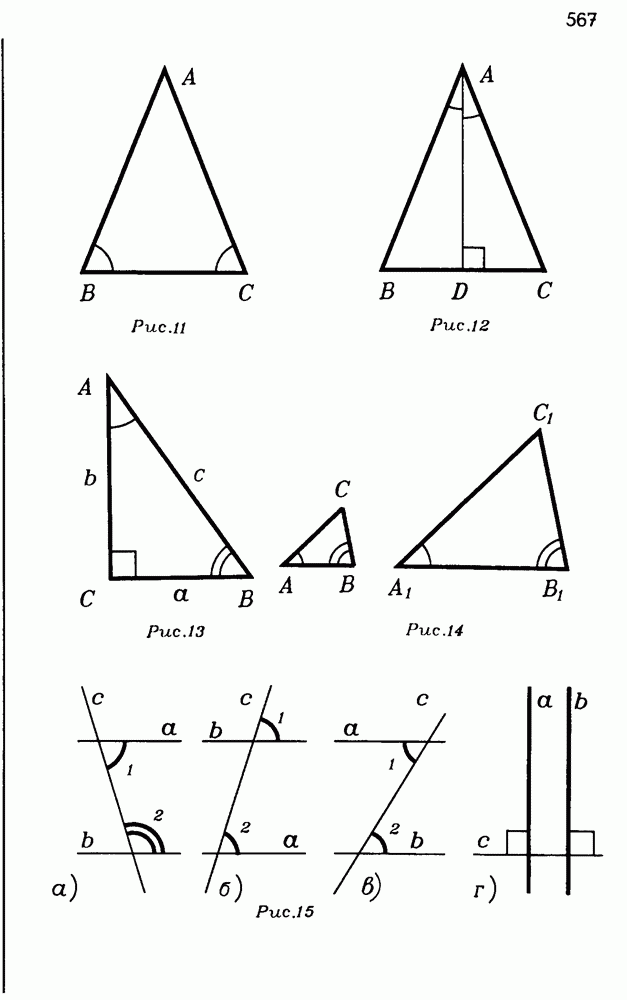
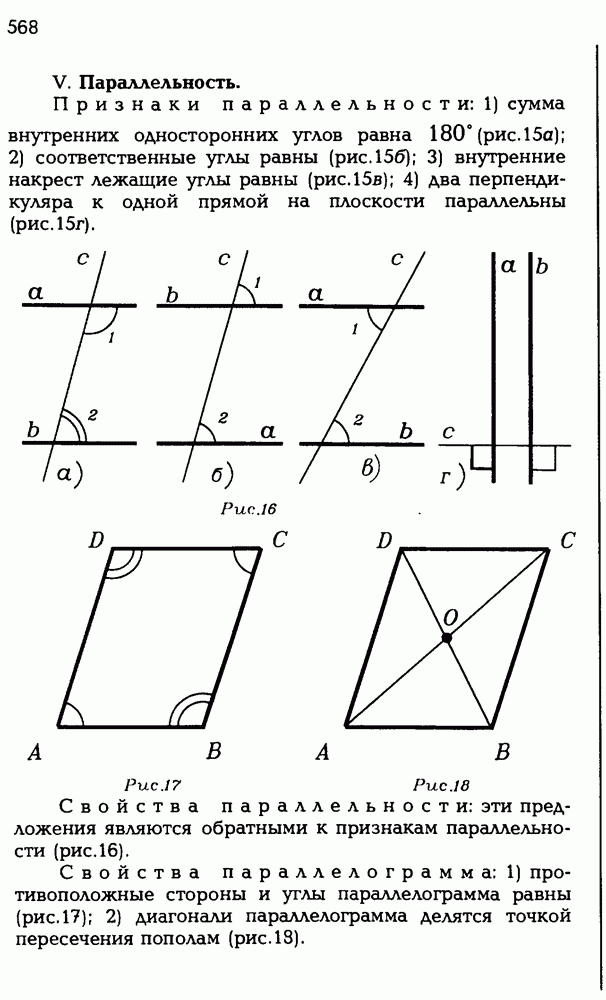
- ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ