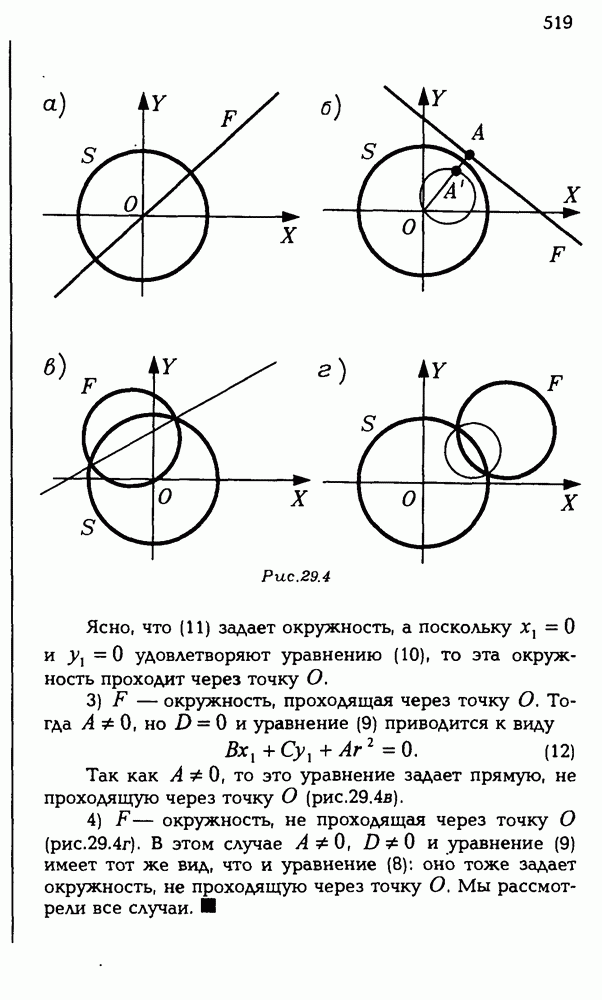| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЗАДАЧИ К § 25
Рисуем
6.1. Пусть  — правильная призма. Перенос задается вектором: а) 0,5АВ ; б) АО, где О — центр нижнего основания. Нарисуйте образ призмы при этом переносе. Нарисуйте объединение и пересечение исходной и полученной призм.
— правильная призма. Перенос задается вектором: а) 0,5АВ ; б) АО, где О — центр нижнего основания. Нарисуйте образ призмы при этом переносе. Нарисуйте объединение и пересечение исходной и полученной призм.
6.2. Дан правильный тетраэдр. Нарисуйте тетраэдр, который получается из данного в результате: а) центральной симметрии относительно середины высоты; б) зеркальной симметрии относительно плоскости, проходящей через середину высоты перпендикулярно к ней; в) поворота на 60° вокруг его высоты; г) поворота на 90" вокруг прямой, соединяющей середины его противоположных ребер. Нарисуйте объединение и пересечение исходного и полученного тетраэдров.
6.3. Дан куб. Нарисуйте куб, который получается из данного в результате: а) переноса на вектор, направленный по его диагонали, длиной в половину этой диагонали; б) центральной симметрии относительно точки, находящейся на его диагонали и делящей ее в отношении 2:1; в) зеркальной симметрии относительно плоскости, которая пересекает его по правильному шестиугольнику; г) поворота на 90" вокруг прямой, проходящей через середины двух параллельных ребер, не лежащих в одной грани. Нарисуйте объединение и пересечение исходного и полученного кубов.
6.4. Нарисуйте тела, которые можно получить, вращая круг
6.5. Нарисуйте тела, которые получаются при вращении: а) куба вокруг ребра; б) куба вокруг диагонали; в) правильного тетраэдра вокруг ребра; г) конуса вокруг прямой, параллельной оси и проходящей вне его.
Планируем
6.6. Как найти объем и площадь поверхности фигур — объединений и пересечений — из задач 6.1, 6.2?
6.7. Как найти объем и площадь поверхности фигур из задачи 6.5?
Представляем
6.8. Может ли центр симметрии тела не принадлежать ему?
6.9. Два равных отрезка: а) параллельны; б) имеют ровно одну общую точку; в) скрещиваются. Каким движением можно один из них отобразить на другом?
6.10. Два отрезка симметричны друг другу относительно двух плоскостей. Какая получится фигура, если их концы последовательно соединить отрезками?
6.11. Через некоторую прямую проведены всевозможные плоскости. Данная точка отражается от всех этих плоскостей. Какую фигуру образуют все полученные точки?
6.12. Верно ли, что: а) наклонный параллелепипед, две грани которого перпендикулярны основанию, имеет плоскость симметрии; б) среди граней параллелепипеда, имеющего плоскость симметрии, есть прямоугольники; в) параллелепипед, имеющий две плоскости симметрии, является прямоугольным?
6.13. Как разрезать куб на три равные пирамиды?
Оцениваем
6.14. Прямоугольный треугольник с гипотенузой d вращается вокруг одного из катетов. При каком условии объем тела вращения будет наибольшим?
6.15. Периметр равнобедренного треугольника равен Р. Этот треугольник вращается вокруг основания. Какой из таких треугольников дает наибольший объем тела вращения?
Думаем
6.16. Центр куба отражается в плоскости каждой его грани. Докажите, что полученные точки являются вершинами октаэдра. Можно ли таким путем получить и другие правильные многогранники?
6.17. В данный шар вписан:
а) правильный тетраэдр;
б) куб. Грани этого многогранника продлили до пересечения со сферой. На какие фигуры разделилась сфера? На какие фигуры разделился шар? Сколько среди них равных друг другу?
Исследуем
6.18. Является ли движением пространства такое его преобразование, которое точке с координатами  ставит в соответствие точку с координатами:
ставит в соответствие точку с координатами:


6.19. Многогранник имеет центр симметрии, центр описанного шара, центр вписанного шара и центр масс. Сколько из этих точек могут совпадать?
Поступаем в ВУЗ
6.20. Из конца диаметра шара проведена хорда так, что поверхность, образуемая вращением ее вокруг этого диаметра, делит объем шара на две равновеликие части. Определите угол между хордой и диаметром.
Ответ: 
6.21. Равносторонний треугольник со стороной а вращается вокруг внешней оси, параллельной стороне треугольника и отстоящей от нее на расстоянии, равном половине высоты треугольника. Найдите объем тела вращения.
Ответ: 
6.22. Треугольник  вращается вокруг биссектрисы AD. Докажите, что площади поверхностей, описанных при этом сторонами АВ и АС, относятся как объемы, полученные вращением частей ABD и
вращается вокруг биссектрисы AD. Докажите, что площади поверхностей, описанных при этом сторонами АВ и АС, относятся как объемы, полученные вращением частей ABD и 
6.23. Равнобедренный треугольник, основание которого равно а, а угол при основании а, вращается вокруг прямой, проходящей через один из концов основания перпендикулярно к нему. Найдите площадь поверхности получившегося при этом тела вращения.
Ответ: 
6.24. Часть квадрата ABCD, оставшаяся после того, как из него вырезали четверть окружности с центтюм в вершине D и радиусами, равными стороне квадрата, вращается вокруг оси, проходящей через D параллельно диагонали АС. Найдите объем полученного тела вращения, если сторона квадрата равна а.
Ответ: 
6.25. Площадь прямоугольной трапеции ABCD равна  , длина высоты АВ равна h, величина острого угла ADC трапеции
, длина высоты АВ равна h, величина острого угла ADC трапеции
равна а. На боковой стороне CD взята точка Е так, что  . Найдите объем тела, полученного вращением четырехугольника ABED вокруг прямой АВ.
. Найдите объем тела, полученного вращением четырехугольника ABED вокруг прямой АВ.
Ответ:  .
.
6.26. Найдите объем тела, полученного при вращении правильного шестиугольника вокруг его стороны, равной а
Ответ: 
6.27. На окружности полукруга радиуса R даны точки А и В. Если N — один из концов диаметра, а О — центр окружности, то  Определите площадь полной поверхности тела, образованного вращением кругового сектора АОВ вокруг диаметра.
Определите площадь полной поверхности тела, образованного вращением кругового сектора АОВ вокруг диаметра.
Ответ: 
6.28. Дан правильный тетраэдр ABCD. Каждая из его вершин симметрично отражена относительно плоскости противоположной ей грани, в результате чего получены соответственно точки KLMN. Найдите отношение объемов исходного и полученного тетраэдров.
Ответ: 
6.29. В тетраэдре проведены отрезки, соединяющие его вершины с точками пересечения медиан противоположных граней. Все они пересекаются в точке О. Второй тетраэдр симметричен первому относительно точки О. Объем исходного тетраэдра равен V. Найдите объем общей части двух тетраэдров.
Ответ: 0,5V.
6.30. Сторона основания правильной призмы  имеет длину а, а боковое ребро — длину 1,125а Точка Е — середина ребра АВ, а точка М — лежит на отрезке ЕС и ЕМ
имеет длину а, а боковое ребро — длину 1,125а Точка Е — середина ребра АВ, а точка М — лежит на отрезке ЕС и ЕМ  ЕС. Вторая призма симметрична призме
ЕС. Вторая призма симметрична призме  относительно прямой
относительно прямой  Найдите объем общей части этих призм.
Найдите объем общей части этих призм.
Ответ:  .
.
6.31. Дан правильный тетраэдр объема V. Второй тетраэдр получается из первого поворотом его на угол
а  вокруг прямой, соединяющей середины скрещивающихся ребер тетраэдра. Найдите объем общей части этих двух тетраэдров.
вокруг прямой, соединяющей середины скрещивающихся ребер тетраэдра. Найдите объем общей части этих двух тетраэдров.
Ответ: 
6.32. Куб с ребром а повернули на 90" вокруг прямой, соединяющей середины двух параллельных и не лежащих в одной грани ребер. Найдите объем общей части исходного куба и повернутого.
Ответ: 
6.33. Правильная треугольная пирамида со стороной основания а повернута вокруг оси симметрии на угол 60. Определите объем общей части исходной и повернутой пирамид, если боковые грани — прямоугольные треугольники.
Ответ: 
6.34. В шар радиуса R вписан правильный тетраэдр. Поворотом его на угол — вокруг высоты получается новый тетраэдр, вписанный в шар. Найдите объем части шара, внешней по отношению к обоим тетраэдрам.
Ответ; 
6.35. Конус вращения вокруг оси — прямой, перпендикулярной его высоте и проходящей через вершину. Найдите площадь сечения полученного тела вращения плоскостью, проходящей через ось вращения, если образующая конуса равна 5, а высота равна 4.
Ответ:  .
.
ЗАДАЧИ К § 26
Дополняем теорию
6.36. Докажите, что плоскость переходит в параллельную ей плоскость (если не в себя) в результате:
а) переноса; б) центральной симметрии.
Планируем
6.37. В кубе  точка О — центр грани ABCD. Как вычислить угол между прямой В, О и:
точка О — центр грани ABCD. Как вычислить угол между прямой В, О и:
а) прямой  прямой
прямой  плоскостью
плоскостью 
г) плоскостью 
6.38. Пусть PABCD — пирамида, в основании которой лежит ромб ABCD. РВЦАВС). Площадь грани РВС равна S. Через точку К — середину ребра AD — проводится сечение, параллельное плоскости РАВ . Как найти его площадь?
6.39. Каждая боковая грань правильного тетраэдра совершила поворот вокруг ребер основания на один и тот же угол во внешнюю сторону. При этом получился многогранник с шестью вершинами и равными ребрами. На какой угол повернулись грани?
Представляем
6.40. Найдутся ли два равных круговых сечения одной плоскостью у двух неравных конусов, если они стоят на одной плоскости по одну сторону от нее?
6.41. Две окружности центрально-симметричны и не лежат в одной плоскости. Верно ли, что они лежат на поверхности: а) одной сферы; б) одного цилиндра? А если эти окружности зеркально-симметричны?
6.42. В каком случае два равных:
а) шара; б) цилиндра; в) конуса центрально-симметричны? Зеркально симметричны?
6.43. Какими поворотами шар можно отобразить на себя?
6.44. Какими поворотами одна из данных фигур отображается на другую, если эти фигуры: а) две прямые; б) две плоскости; в) два равных шара? Найдется ли такой поворот, который при этом и вторую фигуру отобразит на первую?
6.45. Всегда ли, вращая выпуклую фигуру, мы получим выпуклое тело?
Думаем
6.46. Используя свойства переноса, докажите, что: а) два перпендикуляра к одной плоскости параллельны; б) две плоскости, перпендикулярные одной прямой, параллельны; в) если прямая параллельна прямой, перпендикулярной плоскости, то она перпендикулярна плоскости; г) линейные углы двугранного угла равны между собой.
6.47. Докажите, что объединение двух плоскостей является фигурой: а) центрально-симметричной; б) зеркально-симметричной.
6.48. Прямая, b получена из прямой а отражением в плоскости а. Эти прямые имеют общую точку. Докажите, что эта точка лежит в плоскости а.
6.49. В шаре радиусом R провели через центр две плоскости, образующие между собой угол  . Как узнать, в каком отношении они разбили объем шара?
. Как узнать, в каком отношении они разбили объем шара?
6.50. Через биссектрису угла провели плоскость. Докажите, что стороны угла образуют с ней равные углы.
Исследуем
6.51. Можно ли равными параллелепипедами заполнить все пространство? Можно ли это сделать другими равными многогранниками?
6.52. Будет ли сечение центрально-симметричного тела, проходящее через центр симметрии, центрально-симметрично?
6.53. Тело центрально-симметрично. Будет ли центральносимметрична его ортогональная проекция? Будет ли верно обратное?
6.54. Каждое из двух тел центрально-симметрично. Будет ли центрально-симметрично их: а) объединение; б) пересечение?
6.55. Центрально-симметричное тело разделили плоскостью. Одна его часть оказалась центрально-симметричной. Будет ли таковой и другая его часть?
6.56. Существует ли многогранник, имеющий любое наперед заданное число плоскостей симметрии?
ЗАДАЧИ К § 27
Дополняем теорию
6.57. Докажите, что композиция двух отражений в пересекающихся плоскостях является поворотом, а в двух параллельных плоскостях — параллельным переносом.
6.58. Нарисуйте фигуру, которая переходит в себя в результате: а) винта; б) зеркального поворота; в) скользящего отражения.
6.59. Пусть  куб. В результате некоторого движения он переходит в другой куб. Нарисуйте этот другой куб, если движение таково: а) винт с осью поворота, проходящей через центры
куб. В результате некоторого движения он переходит в другой куб. Нарисуйте этот другой куб, если движение таково: а) винт с осью поворота, проходящей через центры  граней
граней 
вектором  а угол поворота равен
а угол поворота равен  зеркальный поворот на
зеркальный поворот на  с осью поворота
с осью поворота  , и отражением в плоскости, перпендикулярной прямой
, и отражением в плоскости, перпендикулярной прямой  и проходящей через центр куба; в) скользящее отражение, где отражение происходит в плоскости, перпендикулярной диагонали куба и проходящей через центр куба, а вектор равен АС.
и проходящей через центр куба; в) скользящее отражение, где отражение происходит в плоскости, перпендикулярной диагонали куба и проходящей через центр куба, а вектор равен АС.
6.60. Пусть РАВС — правильный тетраэдр. В результате движения он переходит в другой тетраэдр. Нарисуйте этот другой тетраэдр, если движение таково:
а) винт с осью поворота  центр основания), углом поворота 60" и вектором
центр основания), углом поворота 60" и вектором 
б) зеркальный поворот с осью поворота PQ, углом поворота 60° и плоскостью отражения, перпендикулярной PQ и проходящей через середину высоты 
в) скользящее отражение с плоскостью отражения, проходящей через РВ и К — середину АС, и вектором 0,5 КВ.
Представляем
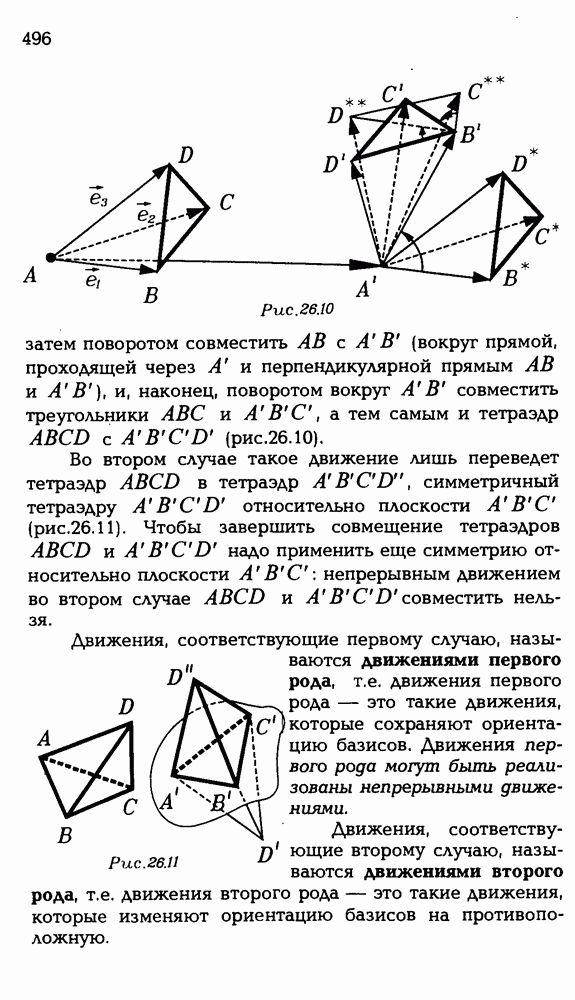
6.61. Сохраняет ли ориентацию базиса: а) перенос; б) центральная симметрия; в) зеркальная симметрия; г) поворот; д) винт; е) зеркальный поворот; ж) скользящее отражение?
6.62. Имеет ли движение неподвижные точки, если это движение: а) перенос; б) центральная симметрия; в) зеркальная симметрия; г) поворот; д) винт; е) зеркальный поворот; ж) скользящее отражение?
6.63. Даны два равных равнобедренных треугольника. Какими движениями их можно совместить, если они имеют общую: а) вершину равных сторон; б) сторону основания; в) боковую сторону; г) медиану к основанию; д) среднюю линию боковых сторон?
6.64. Пусть  — куб. Каким движением можно отобразить: а) ребро АА, на ребро
— куб. Каким движением можно отобразить: а) ребро АА, на ребро  ребро АВ на ребро
ребро АВ на ребро  диагональ на другую диагональ; г) отрезок В, С на отрезок
диагональ на другую диагональ; г) отрезок В, С на отрезок  отрезок, соединяющий середины параллельных ребер, не лежащих в одной грани, на другой такой же; е) треугольник
отрезок, соединяющий середины параллельных ребер, не лежащих в одной грани, на другой такой же; е) треугольник  на треугольник
на треугольник  треугольник С, BD на треугольник
треугольник С, BD на треугольник  треугольник С, BD на треугольник
треугольник С, BD на треугольник
угольник  треугольник
треугольник  на треугольник
на треугольник  сечение
сечение  на сечение
на сечение  Будет ли в таком движении и вторая фигура отображаться на первую?
Будет ли в таком движении и вторая фигура отображаться на первую?
6.65. Пусть ABCD — правильный тетраэдр. Каким движением можно отобразить:
а) ребро AD на ребро  ребро AD на ребро ВС;
ребро AD на ребро ВС;
в) одну из его высот на другую;
г) отрезок, соединяющий середины противоположных ребер, на другой такой же отрезок;
д) сечение одной плоскостью симметрии на другое такое же;
е) сечение, являющееся квадратом, на другое такое же? Будет ли в таком движении и вторая фигура отображаться на первую?
6.66. В результате каких движений отображается на себя:
а) отрезок; б) прямая; в) круг; г) квадрат; д) правильный многоугольник; е) ромб; ж) плоскость; з) двугранный угол?
6.67. В результате каких движений отображается на себя тетраэдр РАВС, у которого: а)  ; б)
; б) 
6.68. Тело является объединением двух шаров, но не шаром. Какими движениями оно отображается на себя?
6.69. У четырехугольной пирамиды: а) все боковые ребра равны и противоположные плоские углы при вершине равны;
б) все плоские углы при вершине равны и противоположные боковые ребра равны. Какими движениями ее можно самосовместить?
6.70. Какими движениями отображается на себя антипризма?
6.71. Как разделить куб на: а) 8 равных кубов; б) 6 равных пирамид; в) 3 равные пирамиды; г) 4 равные треугольные призмы?
6.72. Как разделить прямую треугольную призму на 3 равновеликих тетраэдра? Есть ли среди них равные?
6.73. Как разделить параллелепипед на: а) 6 равновеликих пирамид; б) три равновеликие пирамиды? Есть ли среди них равные?
6.74. В шаре радиусом 1 провели три радиуса ОА, ОВ, ОС, из которых каждые два перпендикулярны. Какая часть объема шара ограничена четвертями больших кругов шара ОАВ, ОАС, ОВС и поверхностью? А какая часть поверхности?
Думаем
6.75. Две правильные четырехугольные пирамиды  и
и  имеют общее основание ABCD. Точка К — середина ребра
имеют общее основание ABCD. Точка К — середина ребра  , точка L — середина ребра
, точка L — середина ребра  точка М — точка пересечения медиан в грани
точка М — точка пересечения медиан в грани  , точка N — точка пересечения медиан в грани
, точка N — точка пересечения медиан в грани  . Докажите, что:
. Докажите, что:

д) расстояние от точки К до плоскости  равно расстоянию от точки L до плоскости РХВС.
равно расстоянию от точки L до плоскости РХВС.
Исследуем
6.76. Возьмите композицию любых двух известных вам движений и выясните: а) меняет ли она ориентацию плоскости; б) имеет ли она неподвижные точки?
6.77. Сколько неподвижных точек может иметь каждое известное вам движение? Как они расположены? А сколько оно может иметь неподвижных прямых? Плоскостей?
6.78. Прямая b получается из прямой а некоторым движением. Установите расположение этих прямых между собой, если это движение: а) винт; б) зеркальный поворот; в) зеркальное отражение.
Переключаемся
6.79. На цилиндре радиусом R и высотой Н намотана проволока. Как вы узнаете ее длину?
6.80. Вам нужно спроектировать винтовую лестницу. Как вы будете действовать?
6.81. Можете ли вы объяснить принцип действия уголкового отражателя? Он составлен из трех попарно перпендикулярных зеркал.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧИТАТЕЛЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ
- § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 1.2. Двугранный угол. Угол между плоскостями.
- 1.3. Плоскость и прямая в пространстве.
- 1.4. Аксиомы стереометрии.
- 1.5. Взаимное расположение двух прямых в пространстве.
- 1.6. Признаки скрещивающихся прямых.
- 1.7. Параллельные прямые.
- 1.8. Параллельное проектирование.
- § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 2.2. О значении перпендикуляра.
- 2.3. Теорема о трех перпендикулярах.
- 2.4. Признак перпендикулярности прямой и плоскости.
- 2.5. Построение плоскости, перпендикулярной данной прямой.
- 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости.
- 2.7. Теорема о прямой, перпендикулярной плоскости.
- 2.8. Перпендикулярность плоскостей.
- 2.9. Ортогональное проектирование.
- § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 3.2. Параллельность и перпендикулярность.
- 3.3. Основная теорема о параллельных плоскостях.
- 3.4. Второй признак параллельности плоскостей.
- 3.5. Расстояние и параллельность.
- 3.6. Сонаправленность лучей и угол между прямыми.
- 3.7. Параллельность и углы.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ
- § 4. СФЕРА И ШАР
- 4.2. Взаимное положение шара и плоскости.
- 4.3. Сфера и многранники.
- 4.4. Вид и изображение шара и сферы.
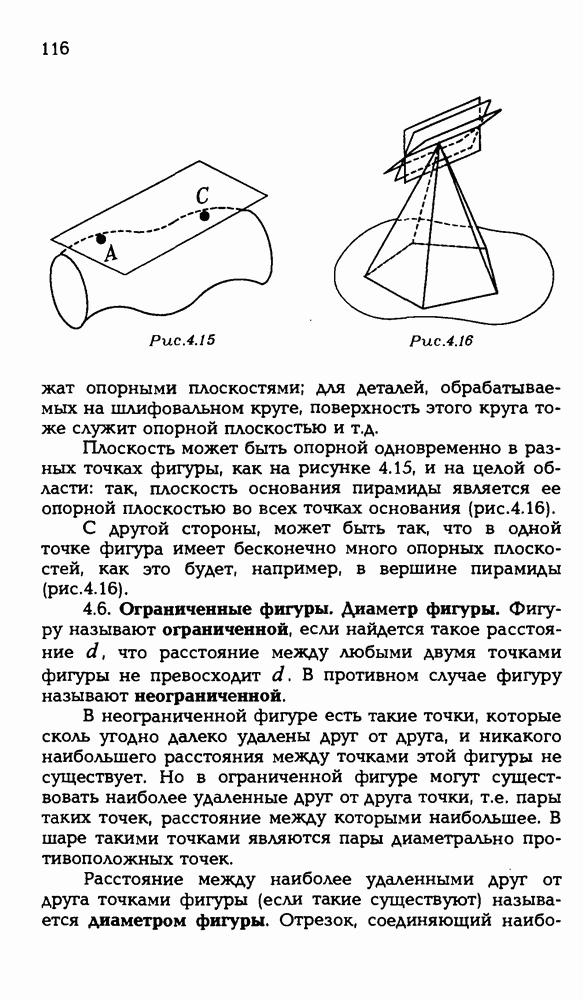
- 4.5. Опорная плоскость.
- 4.6. Ограниченные фигуры. Диаметр фигуры.
- 4.7. Опорные плоскости в концах диаметра.
- 4.8. Сфера — фигура вращения.
- 4.9. Симметрия сферы и шара.
- 4.10. Сфера — центрально симметричная фигура.
- 4.11. Сфера — зеркально симметричная фигура.
- 4.12. Отражение в плоскости и отражение в зеркале.
- § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ
- 5.2. Тригонометрия трехгранного угла.
- 5.3. Равенство трехгранных углов.
- 5.4. Сферические треугольники.
- 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников.
- § 6. ЦИЛИНДР
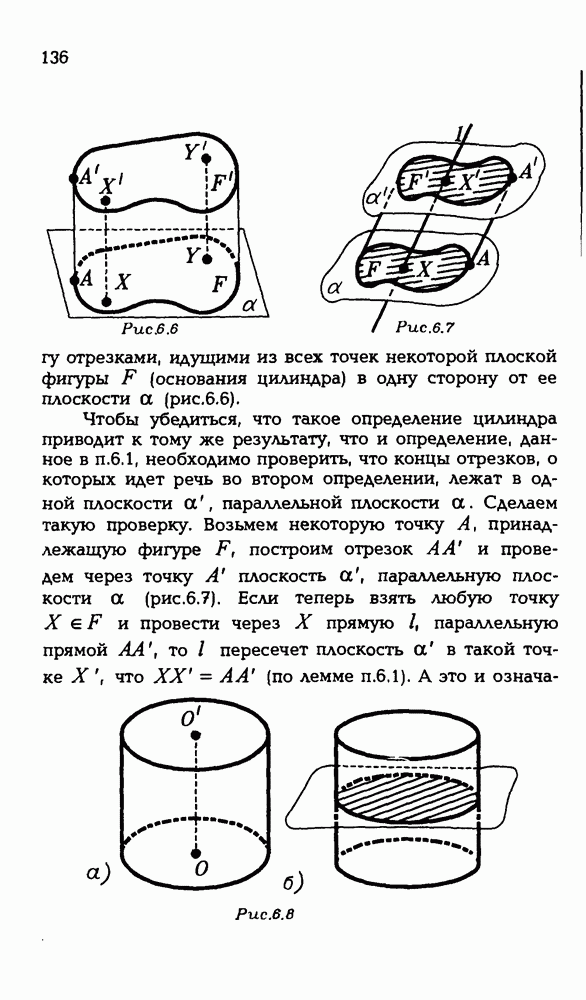
- 6.2. Другой подход к определению цилиндра.
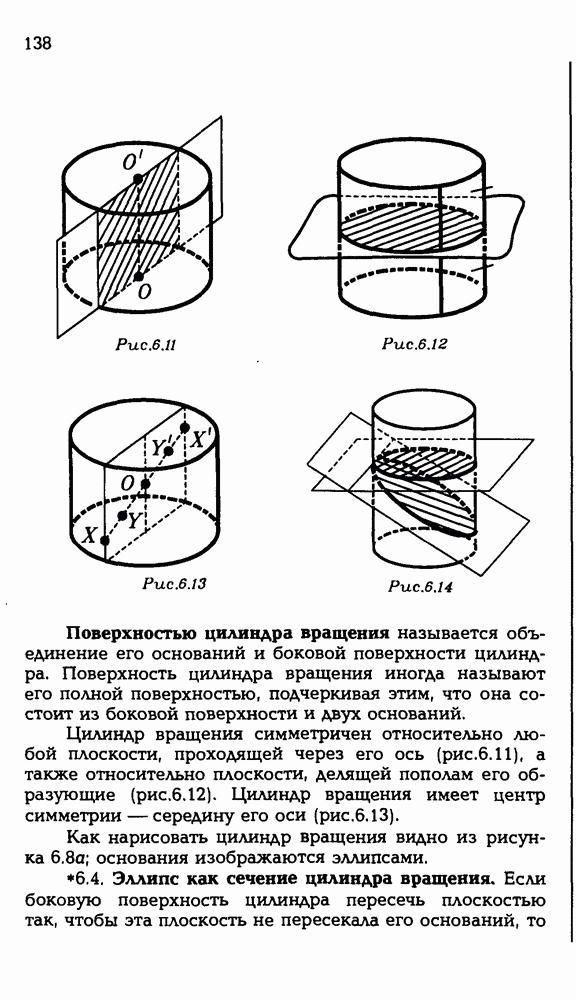
- 6.3. Цилиндр вращения.
- 6.4. Эллипс как сечение цилиндра вращения.
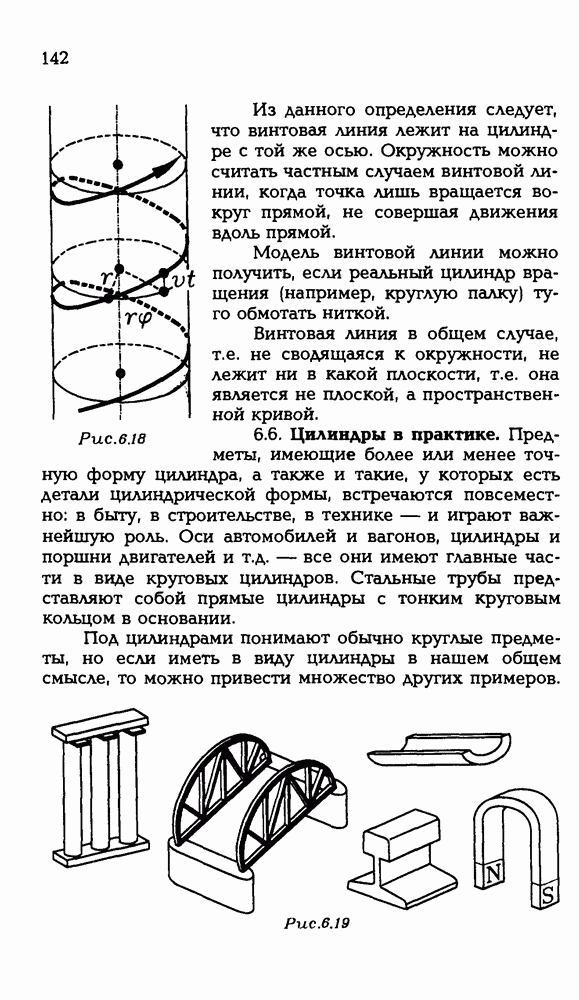
- 6.5. Винтовые линии.
- 6.6. Цилиндры в практике.
- § 7. ПРИЗМА
- 7.2. Параллелепипед.
- 7.3. Прямоугольный параллелепипед.
- 7.4. Симметрия параллелепипеда.
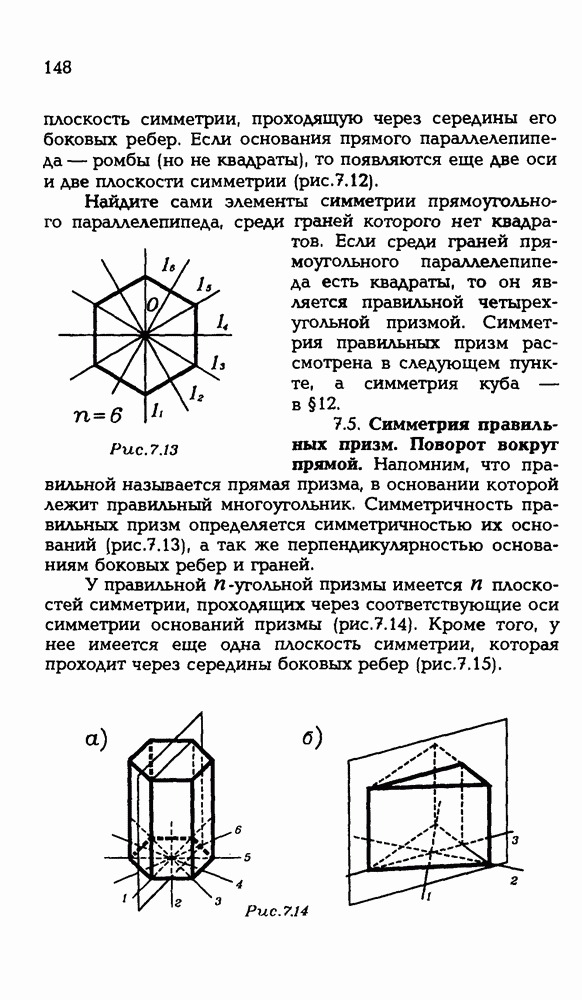
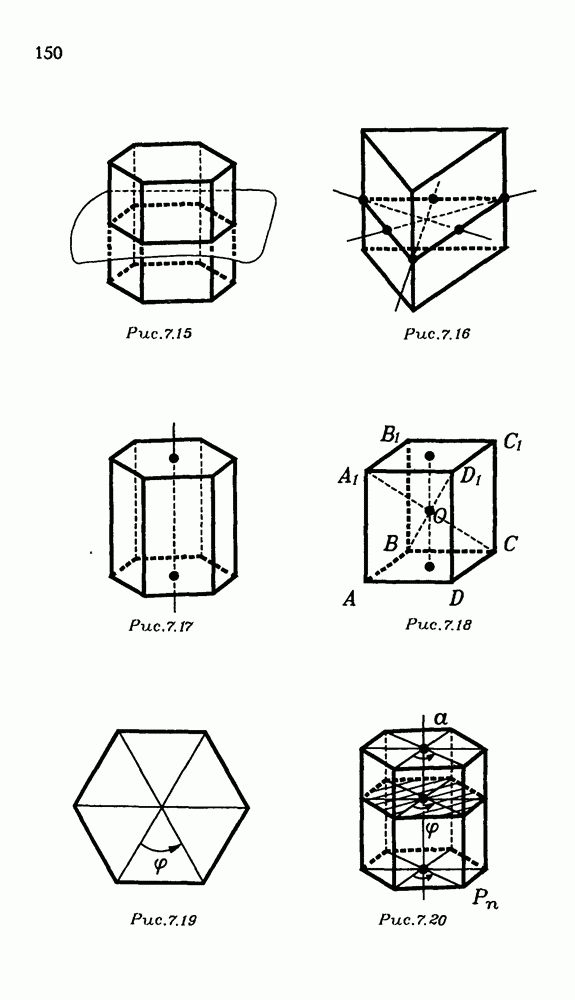
- 7.5. Симметрия правильных призм. Поворот вокруг прямой.
- § 8. КОНУС
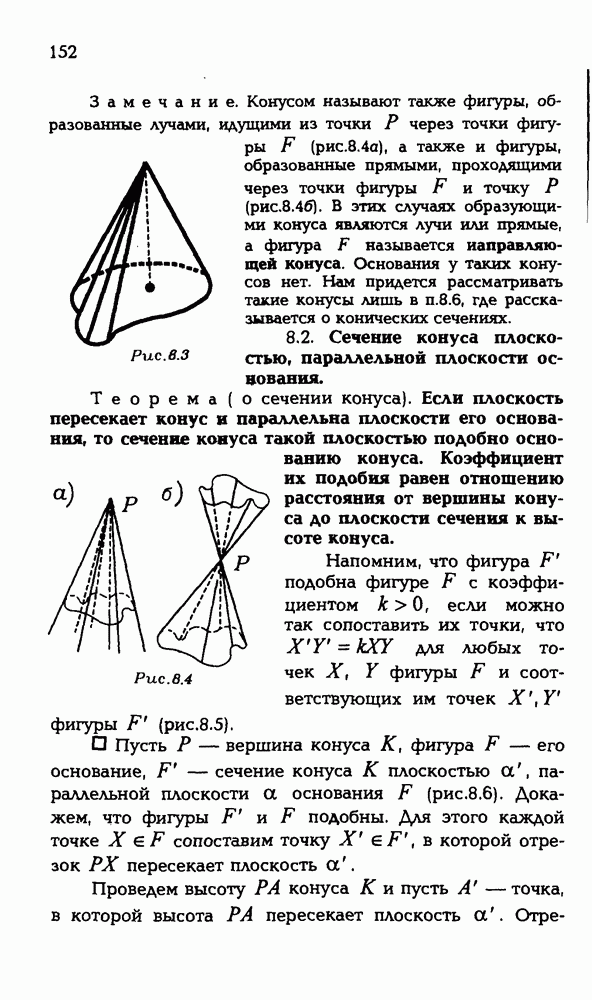
- 8.2. Сечение конуса плоскостью, параллельной плоскости основания.
- 8.3. Конус вращения.
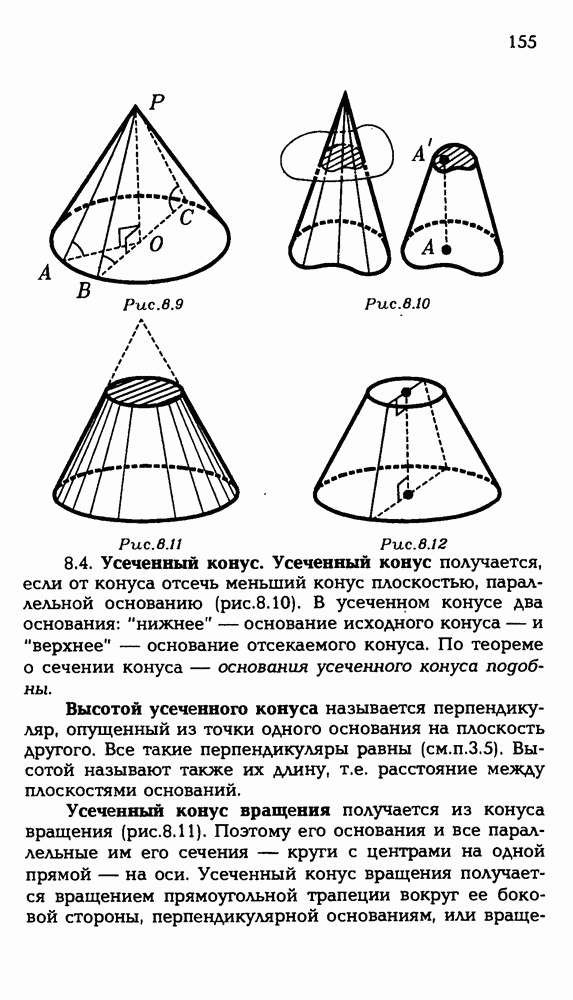
- 8.4. Усеченный конус.
- § 9. ПИРАМИДА
- 9.2. Правильная пирамида.
- 9.3. Симметрия правильной пирамиды.
- 9.4. Конусы и пирамиды в практике.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ
- § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ
- 10.2. Граница и внутренность.
- 10.3. Определение тела и замкнутой плоской области.
- 10.4. Выпуклые фигуры.
- 10.5. Выпуклые тела.
- § 11. МНОГОГРАННИКИ
- 11.2. Выпуклые многогранники.
- 11.3. Теорема Эйлера.
- 11.4. Выпуклые многогранники и выпуклые оболочки.
- 11.5. Многогранная поверхность и развертка.
- 11.6. Развертка выпуклого многогранника.
- § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
- 12.2. Классификация правильных многогранников.
- 12.3. Полуправильные многогранники.
- 12.4. Симметрия правильных многогранников.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
- § 13. ПОНЯТИЕ ОБЪЕМА
- 13.2. Определение объема.
- 13.3. Геометрические величины.
- § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА
- 14.2. Объем прямой призмы.
- § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ
- 15.2. Выражение объема через площади сечений.
- § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА
- 16.2. Объем конуса
- 16.3. Объем шара.
- 16.4. Объем тел вращения.
- 16.5. Объем шарового сегмента и шарового сектора.
- § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ
- 17.2. Площадь сферы.
- 17.3. Площадь сферических многоугольников.
- 17.4. Площадь сферического сегмента и сферического пояса.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ
- § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- 18.2. Другой способ нахождения координат точки.
- 18.3. Построение точки с данными координатами.
- 18.4. Выражение расстояния между точками.
- § 19. МЕТОД КООРДИНАТ
- 19.2. Уравнения без одной или двух координат.
- 19.3. Некоторые применения метода координат.
- § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ
- 20.2. Полярные координаты.
- 20.3. Цилиндрические координаты.
- 20.4. Сферические координаты.
- 20.5. Координатная сеть.
- § 21. ПОНЯТИЕ ВЕКТОРА
- 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов.
- 21.3. Сонаправленность и равенство векторов.
- 21.4. Признаки равенства векторов.
- 21.5. Радиус-вектор.
- § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 22.2. Разложение вектора на составляющие.
- 22.3. Умножение вектора на число.
- 22.4. Координаты вектора.
- 22.5. Равенство координат векторов и координат точек.
- 22.6. Разложение векторов по базису.
- 22.7. Ориентация базиса.
- § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ
- 23.2. Выражение скалярного произведения через координаты.
- 23.3. Свойства скалярного умножения.
- 23.4. Применения скалярного умножения.
- 23.5. Скалярное произведение и проекции.
- § 24. ВЕКТОРНЫЙ МЕТОД
- 24.2. Общее уравнение плоскости.
- 24.3. Векторное задание отрезка.
- 24.4. Некоторые теоремы о треугольниках и тетраэдрах.
- 24.5. Центр масс системы материальных точек.
- 24.6. Центры масс и выпуклые многогранники.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 6. ПРЕОБРАЗОВАНИЯ
- 25.1. Преобразования фигур.
- 25.2. Определения движения и равенства фигур.
- 25.3. Преобразования симметрии.
- 25.4. Параллельный перенос.
- 25.5. Поворот.
- § 26. СВОЙСТВА ДВИЖЕНИЙ
- 26.2. Общие свойства движений.
- 26.3. Теоремы о задании движений.
- 26.4. Неподвижные точки движений.
- 26.5. Два рода движений.
- 26.6. Теорема подвижности пространства.
- 26.7. Композиция отражений в плоскости.
- § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА
- 27.2. Движения первого рода как винтовые движения.
- 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот.
- 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения.
- § 28. ПОДОБИЕ
- 28.2. Гомотетия.
- 28.3. Свойства подобия.
- 28.4. Группы преобразований.
- § 29. ИНВЕРСИЯ
- 29.2. Аналитическое задание инверсии.
- 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии.
- 29.4. Сохранение величин углов при инверсии.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ОТВЕТЫ И УКАЗАНИЯ
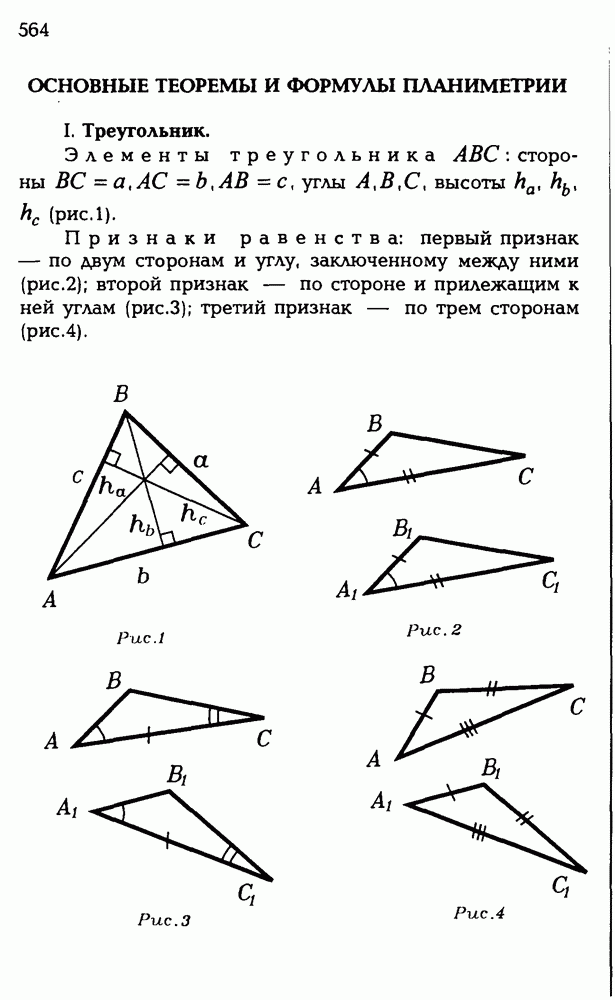
- ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ