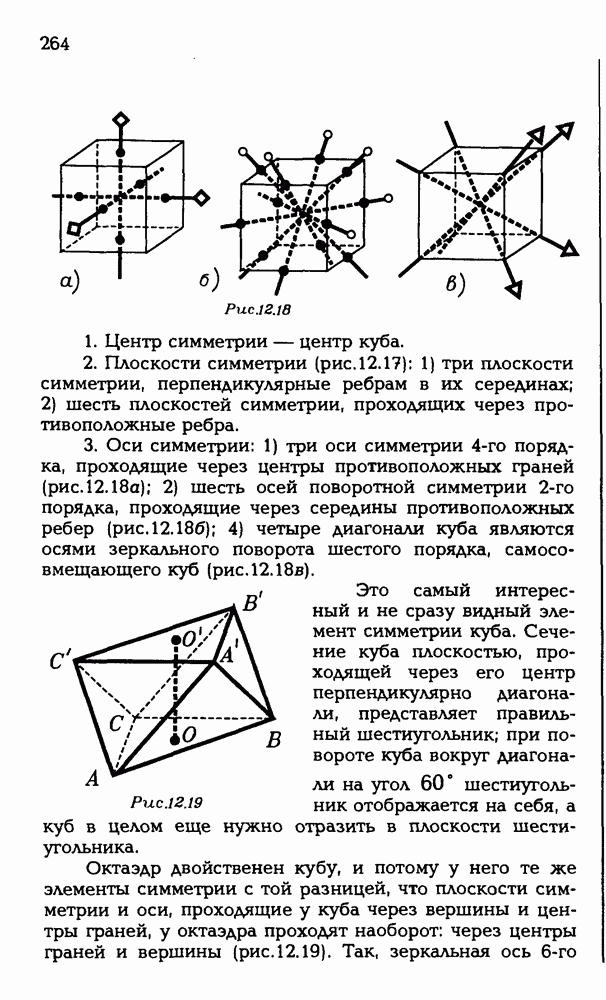
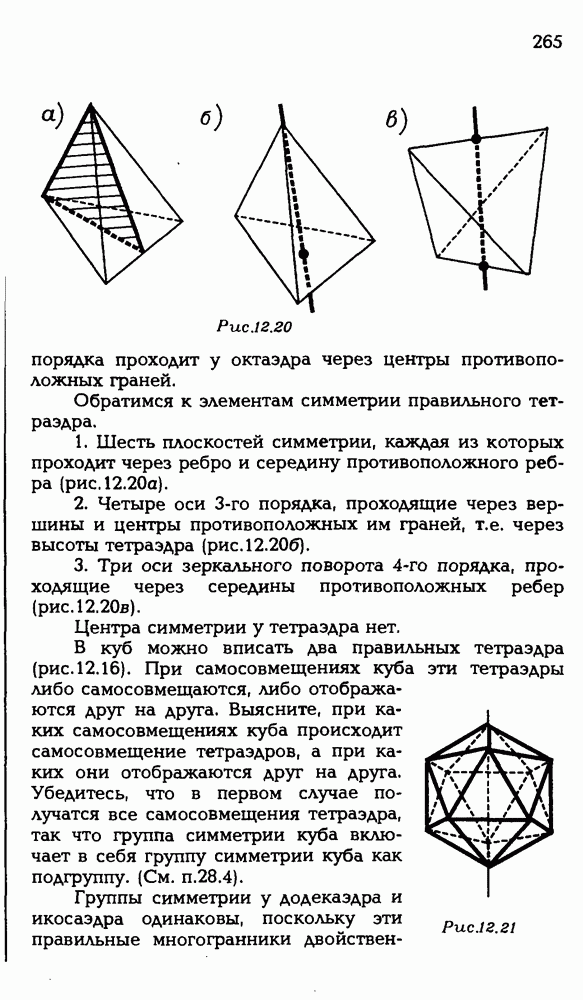
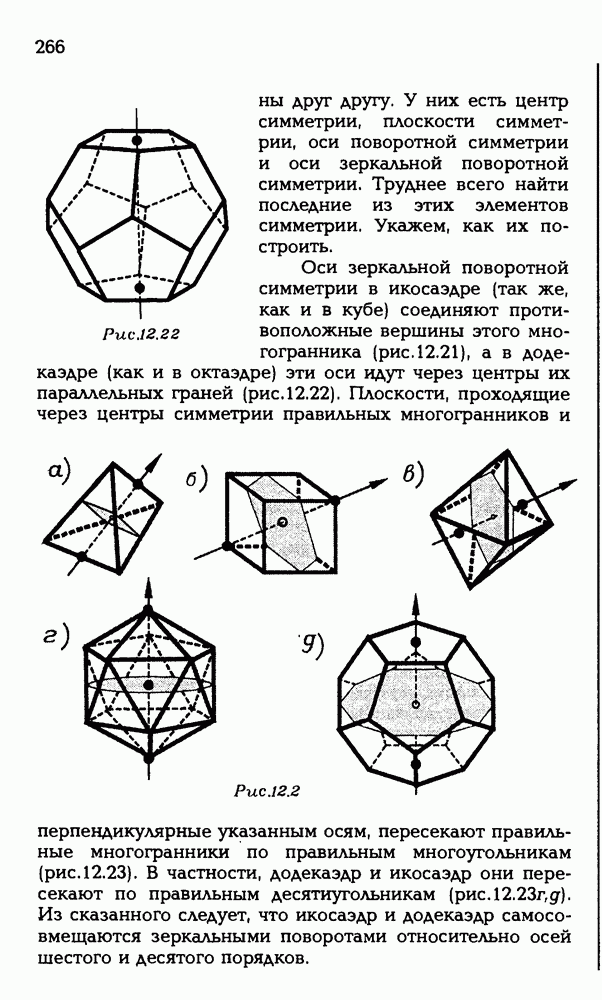
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЗАДАЧИ К § 10
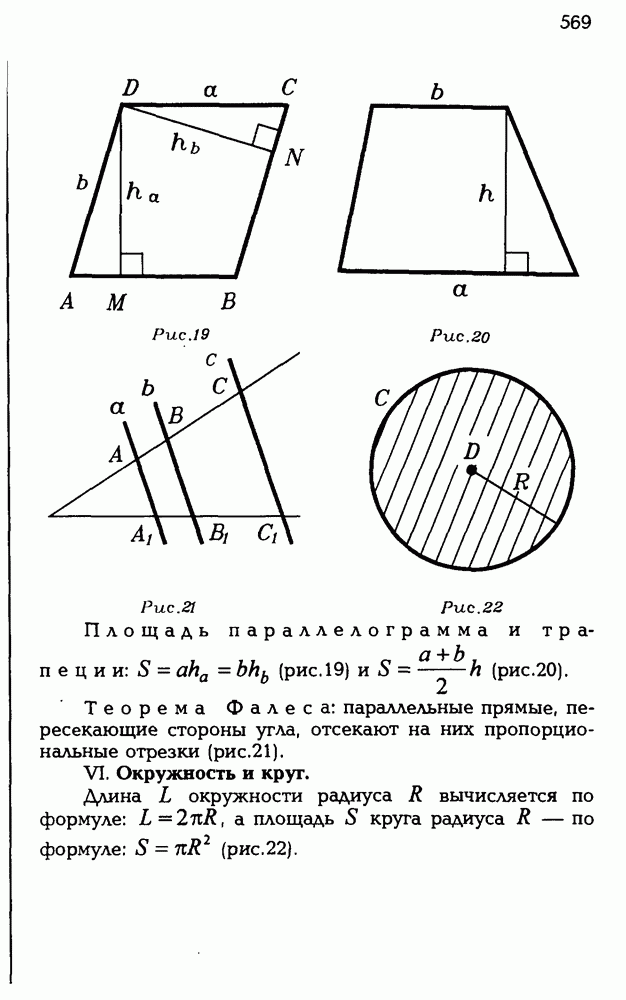
Рисуем
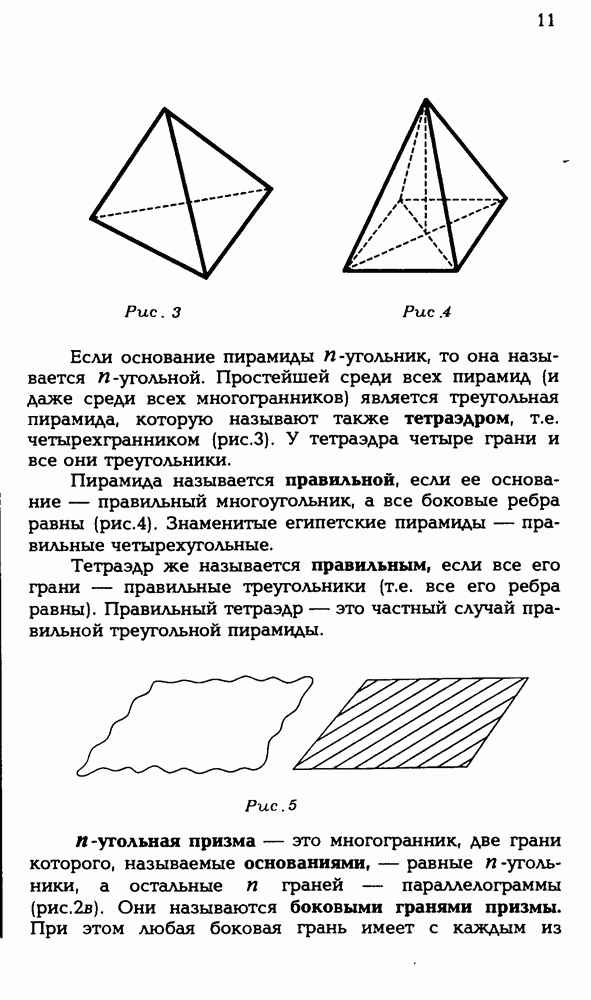
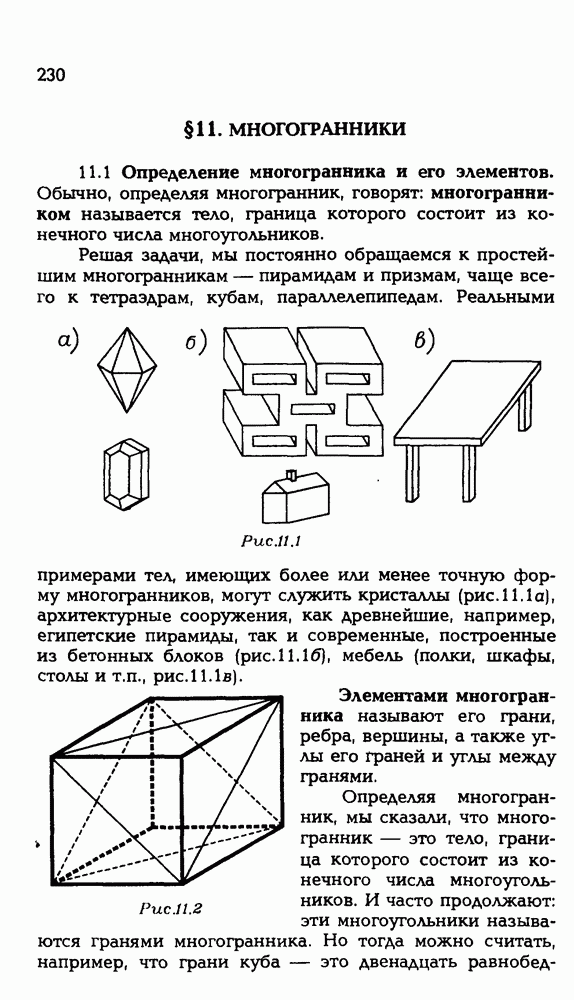
3.1. Нарисуйте неплоскую фигуру, имеющую внутренние точки, у которой границей является: а) конечное число точек;
б) конечное число треугольников: в) пять квадратов; г) объединение двух сфер.
3.2. Нарисуйте выпуклую фигуру, являющуюся объединением: а) двух тетраэдров; б) двух шаров; в) двух кубов; г) шара и куба; д) двух невыпуклых фигур.
3.3. Нарисуйте тело, которое при проектировании на три попарно перпендикулярные плоскости, дают такие фигуры: а) равные квадраты; б) равные равносторонние треугольники;
в) равные круги.
3.4. а) Нарисуйте тело, которое можно одной плоскостью разбить на два тела меньшего диаметра, б) Нарисуйте такое тело, для которого это сделать нельзя. (Диаметр — это наибольшее расстояние между двумя точками фигуры).
3.5. Нарисуйте тело, отличное от шара, каждое сечение которого плоскостью, проходящей через некоторую прямую, является кругом или точкой.
3.6. Нарисуйте фигуру, которая получается в результате вращения: а) отрезка вокруг прямой, не лежащей с ним в одной плоскости; б) круга вокруг прямой, лежащей в его плоскости; в) квадрата вокруг прямой, не лежащей с ним в одной плоскости и проходящей через его вершину; г) шара вокруг прямой, не имеющей с ним общих точек; д) куба вокруг диагонали. Какая из этих фигур будет телом? Выпуклым телом?
Планируем
Для выпуклых тел выделим такие характеристики: диаметр, ширину (наименьшее расстояние между параллельными опорными плоскостями), радиус наименьшего шара, содержащего данное тело ("габаритность") и радиус наибольшего шара, который умещается в данном теле ("пузатость").
3.7. Как найти эти характеристики для: а) цилиндра с радиусом 2 и образующей 1; б) конуса с радиусом 1 и образующей 3; в) усеченного конуса, у которого радиусы оснований равны 3 и 1, а образующая равна 4; в) объединения цилиндра и полушара, имеющих общее основание, причем радиус полуша-ра равен образующей цилиндра и равен 2.
Представляем
3.8. Приведите пример неплоской фигуры, которая: а) вся состоит только из граничных точек; б) содержит только внутренние точки.
3.9. Дан куб. Некоторая точка удалена от каждой его вершины на расстояние, меньше длины его ребра. Лежит ли она в кубе? Если нет, то сколько вершин надо оставить, чтобы точка оказалась внутри куба?
3.10. а) Останется ли фигура выпуклой, если из нее удалить точку? б) А если добавить к ней точку? в) Из выпуклого тела удалили точку. Будет ли оставшаяся фигура выпуклым телом?
3.11. Может ли невыпуклая фигура: а) иметь выпуклое сечение; б) иметь бесконечно много невыпуклых параллельных сечений; в) иметь только выпуклые сечения?
3.12. Может ли невыпуклая фигура иметь выпуклую проекцию при проектировании на: а) одну плоскость; б) три попарно перпендикулярные плоскость? в) каждую плоскость?
3.13. Всегда ли выпуклые фигуры имеют ближайшие точки?
3.14. Является ли выпуклым телом: а) пересечение двух шаров; б) объединение двух шаров; в) пересечение двух полупространств; г) объединение двух полупространств; д) пересечение шара и полупространства; е) объединение шара и полупространства?
Сделаем
3.15. Выпуклая фигура содержит три точки, не лежащие на одной прямой. Докажите, что она содержит треугольник с вершинами в этих точках.
3.16. Докажите, что окружность, имеющая три общие точки со сферой, лежит на ней.
Исследуем
3.17. Пусть  — куб. Какой по отношению к кубу является точка X такая, что:
— куб. Какой по отношению к кубу является точка X такая, что:  где точка К — середина ребра АВ; б)
где точка К — середина ребра АВ; б)  если ребро куба равно 2?
если ребро куба равно 2?
3.18. Какое положение по отношению к шару занимает точка X такая, из которой диаметр этого шара виден под: а) прямым утлом; б) острым утлом; в) тупым утлом?
Поступаем в ВУЗ
3.19. Тело состоит из двух конусов, имеющих общее основание и расположенных по разные стороны от плоскости основания. Найдите радиус шара, вписанного в тело, если радиусы оснований конусов равны 1, а высоты 1 и 2.
Ответ:  .
.
Переключаемся
3.20. Можно ли из куска сыра, делая только плоские разрезы, получить невыпуклый его кусок?
ЗАДАЧИ К § 11
Дополняем теорию
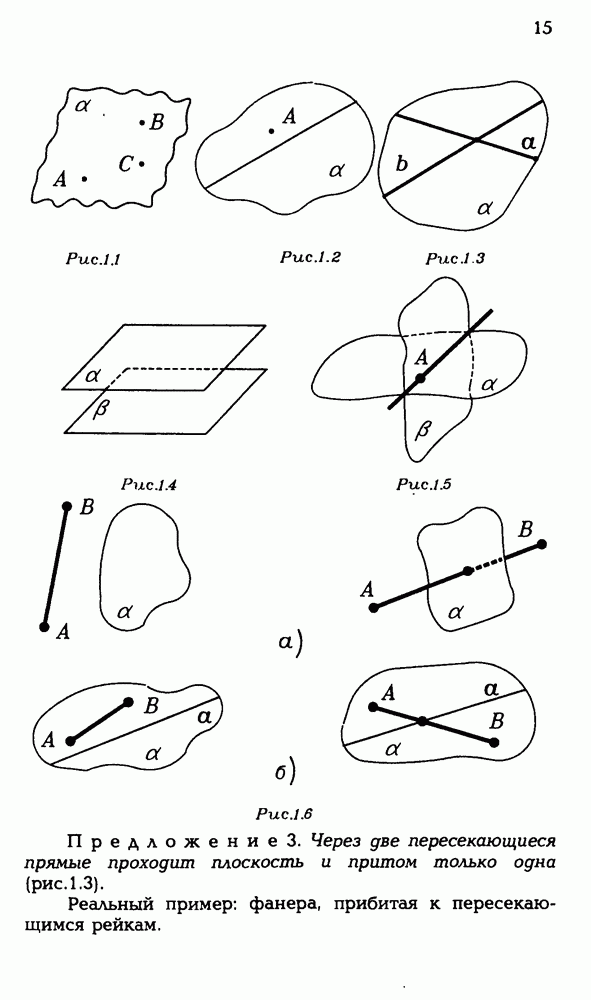
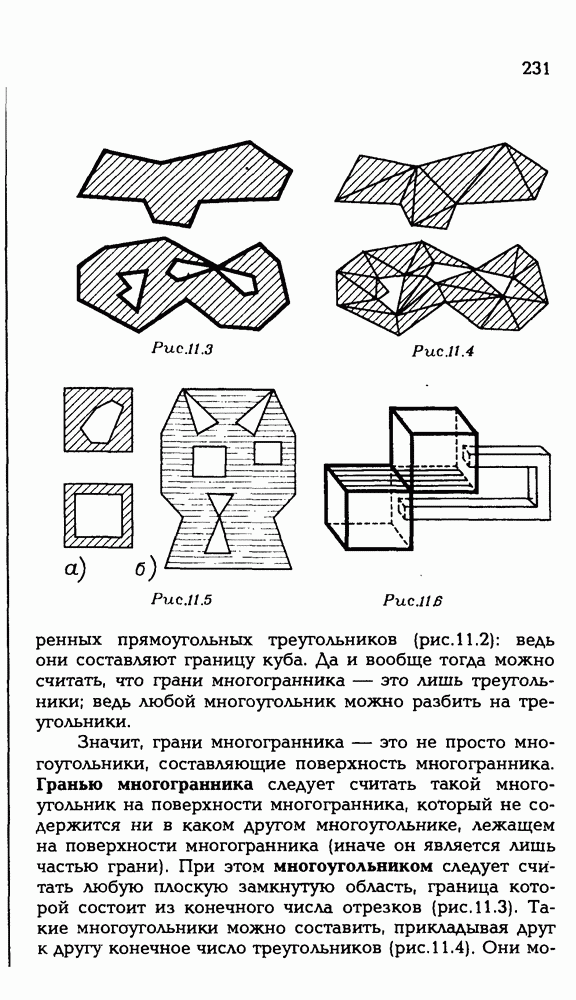
3.21. Докажите, что каждая грань многогранника, вписанного в сферу, вписывается в окружность.
Рисуем
3.22. Нарисуйте два выпуклых многогранника так, чтобы было выпуклым многогранником: а) их объединение; б) их пересечение; в) их объединение и их пересечение.
3.23. Нарисуйте многогранник, который является пересечением такого числа полупространств: а) 4; б) 5; в) 6; г) 7; д) 8.
3.24. Нарисуйте многогранник, у которого: а) 6 ребер; б) 8 ребер; в) 12 ребер и все грани — треугольники; г) 15 ребер и все грани — треугольники; д) 12 ребер и из каждой вершины выходит три ребра; е) 15 ребер и из каждой вершины выходит три ребра; ж) 12 ребер и все грани — четырехугольники; з) 15 ребер и все грани — четырехугольники.
3.25. Нарисуйте многогранник: а) все грани которого треугольники, но не тетраэдр; б) все грани которого квадраты, но не куб; в) все грани которого прямоугольники, но не прямоугольный параллелепипед; г) все грани которого неравные четырехугольники; д) все грани которого пятиугольники; е) четыре грани которого — правильные треугольники, а еще четыре — правильные шестиугольники.
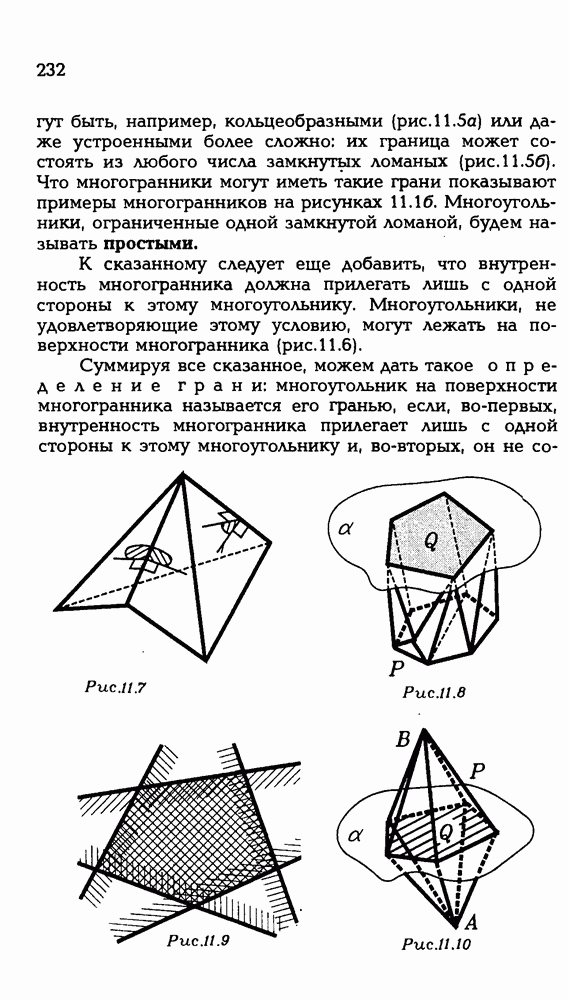
3.26. Нарисуйте выпуклый многогранник, у которого: а) вершин столько же, сколько граней; б) вершин в два раза больше, чем граней; в) вершин в два раза больше, чем ребер; г) граней столько же, сколько ребер; д) вершин столько же,
сколько ребер; е) треугольных граней столько же, сколько четырехугольных, а других граней нет.
3.27. Нарисуйте куб. Нарисуйте на его поверхности вершины: а) правильного тетраэдра; б) другого куба.
3.28. Нарисуйте тетраэдр. Нарисуйте такой многогранник, у которого: а) все вершины лежат на ребрах тетраэдра, причем на каждом ребре ровно одна вершина; б) все вершины лежат на гранях тетраэдра, причем на каждой грани ровно одна вершина; в) все вершины лежат на гранях тетраэдра, причем на каждой грани ровно две вершины.
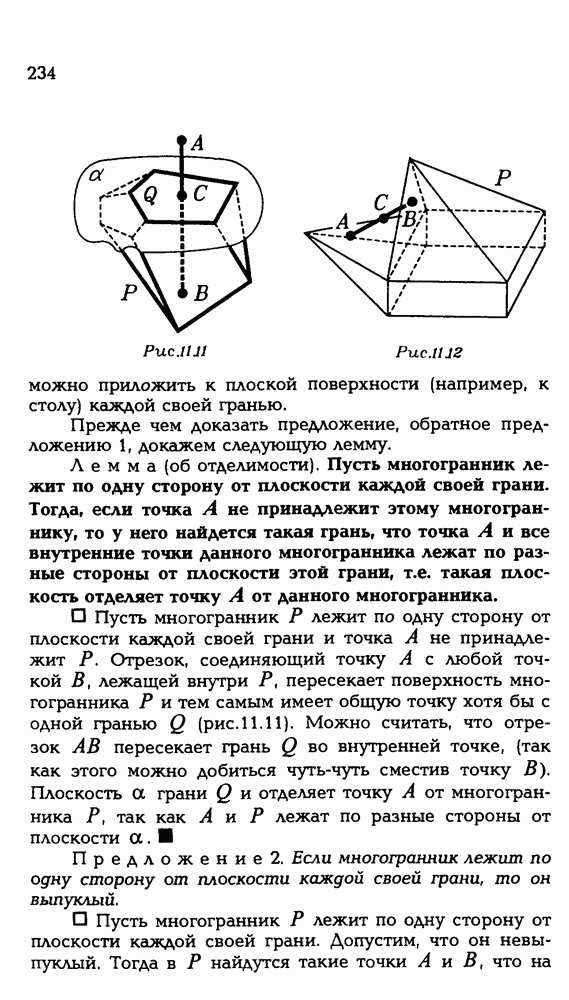
3.29. Нарисуйте многогранник, у которого могут быть такие сечения: а) квадрат, прямоугольник и правильный шестиугольник; б) равносторонний треугольник, квадрат и трапеция; в) ромб, равнобедренный треугольник и прямоугольник; г) объединение двух треугольников без общих точек.
3.30. Вращаясь вокруг одного из ребер многогранника, плоскость дает такие сечения: а) равнобедренный треугольник; б) прямоугольник; в) параллелограмм; г) равнобокую трапецию. Нарисуйте такой многогранник.
3.31. а) Нарисуйте тераэдр. Нарисуйте плоскость, проходящую через его ребро параллельно противоположному ребру. Нарисуйте все такие плоскости, б) Нарисуйте куб. Нарисуйте плоскость, проходящую через его ребро и параллельную диагональной плоскости куба, параллельной данному ребру. Нарисуйте все такие плоскости, в) Нарисуйте параллелепипед. Нарисуйте плоскость, проходящую через его вершину и параллельную плоскости, проходящей через три его вершины, соседние с взятой. Нарисуйте все такие плоскости. В каждом случае нарисуйте многогранник, ограниченный проведенными плоскостями.
3.32. Нарисуйте многогранник, который при освещении параллельным пучком света дает тень в виде: а) квадрата; б) равнобедренного треугольника; в) равностороннего треугольника; г) правильного шестиугольника; д) равнобокой трапеции; е) прямоугольника; ж) ромба. Попробуйте нарисовать такой многогранник, который дает тени нескольких указанных видов.
3.33. Нарисуйте разбиение на тетраэдры таких многогранников: а) четырехугольной пирамиды; б) усеченной треугольной пирамиды; в) треугольной призмы; г) прямоугольного параллелепипеда. При этом найдите наименьшее число плоскостей разбиения.
3.34. Нарисуйте такие многогранники: a) ABCDKL, в котором грань ABCD — квадрат со стороной 2, грани АКБ и CLD — равносторонние треугольники, ребра KL и AD параллельны между собой,  в котором ABCD
в котором ABCD
квадрат со стороной 2, грани  равнобокие трапеции, плоскости которых перпендикулярны плоскости ABC, причем
равнобокие трапеции, плоскости которых перпендикулярны плоскости ABC, причем  грань
грань  прямоугольник, плоскость которого параллельна плоскости ABC и удалена от нее на 3; в)
прямоугольник, плоскость которого параллельна плоскости ABC и удалена от нее на 3; в)  в котором грань ABCD — квадрат со стороной 2, грань
в котором грань ABCD — квадрат со стороной 2, грань  квадрат со стороной
квадрат со стороной  перпендикулярна плоскости ABC,
перпендикулярна плоскости ABC,  перпендикулярна плоскости ЛВС, плоскости ABC и АХВХСХ параллельны,
перпендикулярна плоскости ЛВС, плоскости ABC и АХВХСХ параллельны,  Каждый из этих многогранников разбейте на тетраэдры наименьшим числом плоскостей.
Каждый из этих многогранников разбейте на тетраэдры наименьшим числом плоскостей.
3.35. Нарисуйте всевозможные развертки: а) правильного тетраэдра; б) куба; в) правильной треугольной призмы.
3.36. Нарисуйте многогранник, имеющий центр симметрии и: а) одну плоскость симметрии; б) две плоскости симметрии; в) три плоскости симметрии.
Планируем
3.37. Пусть ABC — правильный треугольник со стороной 1. На этом основании построены две пирамиды: РХАВС и  причем
причем  находятся по одну сторону от основания. Рассматриваются сечения многогранника, являющегося объединением этих пирамид, плоскостью, параллельной основанию. Пусть
находятся по одну сторону от основания. Рассматриваются сечения многогранника, являющегося объединением этих пирамид, плоскостью, параллельной основанию. Пусть  — расстояние от плоскости сечения до
— расстояние от плоскости сечения до  Как найти зависимость от
Как найти зависимость от  площади сечения?
площади сечения?
3.38. В тетраэдре РАВС сумма плоских углов при каждой из вершин  равна 180°. Площадь треугольника ABC равна 1. Как узнать площади остальных граней
равна 180°. Площадь треугольника ABC равна 1. Как узнать площади остальных граней 
Представляем
3.39. Сколько вершин, ребер и граней у многогранника, который является объединением таких двух многогранников, имеющих только общую грань: а) двух прямоугольных параллелепипедов; б) четырехугольной пирамиды и куба; в) двух тетраэдров?
3.40. Многогранник разделили на части одной плоскостью, а) Сколько при этом может получиться частей? б) Является ли каждая полученная часть многогранником? в) Как изменятся полученные вами результаты, если исходный многогранник был выпуклым?
3.41. Приведите пример многогранника, около которого: а) можно описать сферу; б) нельзя описать сферу.
3.42. Пусть каждая грань многогранника может быть вписана в окружность. Значит ли это, что его можно вписать в сферу?
3.43. Приведите пример многогранника, в который: а) можно вписать сферу; б) нельзя вписать сферу.
3.44. Приведите пример многогранника, для которого существует: а) и вписанная, и описанная сфера; б) только описанная сфера; в) только вписанная сфера. Приведите пример многогранника, для которого не существует ни вписанной, ни описанной сферы.
3.45. Какие плоскости симметрии имеют многограннники, составленные из двух равных: а) кубов; б) треугольных призм с общей гранью; в) прямоугольных тетраэдров с общей гранью; г) правильных четырехугольных пирамид?
Оцениваем
3.46. Нарисуйте кратчайший путь по поверхности из центра одной грани в центр соседней грани: а) правильного тетраэдра; б) куба.
Сделаем
3.47. Докажите, что существует многогранник с любым числом ребер, большим 7.
Исследуем
3.48. Существует ли выпуклый многогранник, у которого 13 граней, а в каждой по 13 сторон? Обобщите полученный результат.
3.49. Всякий ли треугольник может быть разверткой тетраэдра?
3.50. Существует ли многогранник, имеющий любое наперед заданное число плоскостей симметрии?
Переключаемся
3.51. Пролезет ли правильный тетраэдр с высотой 1 в щель меньшей ширины?
ЗАДАЧИ К § 12
Дополняем теорию
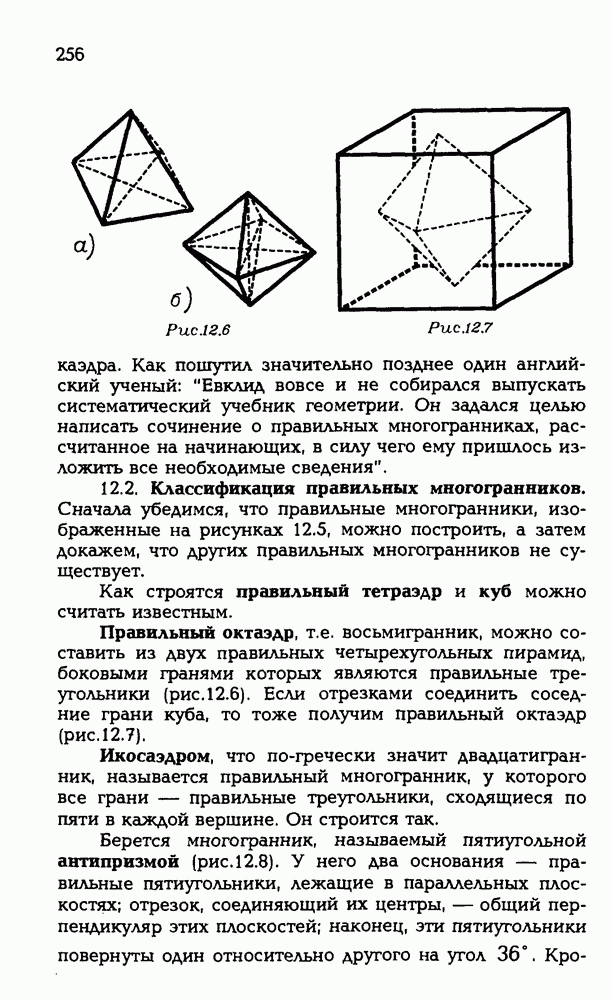
3.52. Докажите, что в любом правильном многограннике есть точка, равноудаленная от его: а) вершин; б) граней; в) ребер. Докажите, что эта точка — одна и та же. (Такую точку естественно назвать центром правильного многогранника).
Рисуем
3.53. Нарисуйте правильный тетраэдр, а) Нарисуйте тетраэдр, центрально симметричный данному относительно середины высоты. Нарисуйте объединение и пересечение исходного и полученного тетраэдров, б) Нарисуйте тетраэдр, зеркально симметричный данному относительно плоскости, проходящей через середину высоты перпендикулярно ей. Нарисуйте объединение и пересечение исходного и полученного тетраэдров, в) Пусть каждая его вершина отражается в плоскости противоположной ей грани. Нарисуйте объединение и пересечение исходного и полученного тетраэдров, г) Нарисуйте тетраэдр, полученный из данного поворотом вокруг высоты на 60°. Нарисуйте объединение и пересечение исходного и полученного тетраэдров, д) Нарисуйте тетраэдр, полученный из данного поворотом вокруг прямой, соединяющей середины противоположных ребер, на 90°. Нарисуйте объединение и пересечение исходного и полученного тетраэдров.
3.54. Нарисуйте куб. а) Нарисуйте куб, который получается из данного центральной симметрией относительно точки, делящей его диагональ в отношении 1:2, считая от вершины. Нарисуйте объединение и пересечение исходного и полученного кубов; б) Нарисуйте куб, который получается из данного зеркальной симметрией относительно плоскости, проходящей через три его вершины, являющиеся концами ребер, выходящими из одной вершины куба. Нарисуйте объединение и пересечение исходного и полученного кубов; в) Нарисуйте куб, который получается из данного поворотом на 90° относительно прямой, проходящей через середины двух его параллельных ребер, не лежащих на одной грани куба. Нарисуйте объединение и пересечение исходного и полученного кубов.
3.55. Нарисуйте вершины правильного: а) тетраэдра на поверхности куба; б) октаэдра на поверхности куба; в) октаэдра на поверхности правильного тетраэдра; г) октаэдра на поверхности икосаэдра; д) куба на поверхности додекаэдра; е) икосаэдра на поверхности куба.
Планируем
3.56. Пусть PABCDQ — октаэдр с ребром 1 (ABCD — квадрат). Как вычислить расстояния между: а) А и плоскостью  прямыми АР и
прямыми АР и  прямыми PD и AQ; г) плоскостями ADQ и ВСР
прямыми PD и AQ; г) плоскостями ADQ и ВСР
Представляем
3.57. Какие элементы симметрии имеет объединение двух правильных тетраэдров с общей гранью?
3.58. Какие элементы симметрии имеет объединение двух кубов с общей гранью?
Оцениваем
3.59. В правильном тетраэдре SABC длина каждого ребра равна а. На ребре SA взята точка Мтак, что  на
на  взята точка N, а на плоскости ABC взята точка Р. Когда имеет наименьшую величину сумма длин отрезков MN и
взята точка N, а на плоскости ABC взята точка Р. Когда имеет наименьшую величину сумма длин отрезков MN и 
Сделаем
3.60. В правильном тетраэдре РАВС на его ребрах отложены равные отрезки РК и PL (точка К на ребре РА, точка L на ребре  а также СМ и CN (точка М на ребре АС, точка N на ребре СВ). Докажите, что ML = KN.
а также СМ и CN (точка М на ребре АС, точка N на ребре СВ). Докажите, что ML = KN.
Исследуем
3.61. а) Существует ли в правильном тетраэдре точка, из которой каждое ребро основания видно под прямым углом? б) А такая, из которой каждое ребро видно под прямым углом?
Поступаем в ВУЗ
3.62. Дан правильный тетраэдр ABCD. Точка М — середина ребра AD, точка О — центр треугольника ABC, точка N — середина ребра АВ, точка К — середина ребра CD. Найдите величину угла между прямыми МО и 
Ответ:  .
.
3.63. Точки М к N — соответственно середины ребер АС и SB правильного тетраэдра SABC. Ребра тетраэдра имеют длину 1. На прямых  и CN выбраны точки Р и Q так, что прямая PQ параллельна прямой ВМ. Найдите длину отрезка
и CN выбраны точки Р и Q так, что прямая PQ параллельна прямой ВМ. Найдите длину отрезка 
Ответ: 
3.64. Длина каждого ребра треугольной пирамиды РАВС равна 1. BD — высота треугольника ABC. Равносторонний треугольник BDE лежит в плоскости, образующей угол  с ребром АС, причем точки Р и Е лежат по одну сторону от плоскости ABC. Найти расстояние между точками Р и Е.
с ребром АС, причем точки Р и Е лежат по одну сторону от плоскости ABC. Найти расстояние между точками Р и Е.
Ответ: 
3.65. В правильном тетраэдре SABC плоскость а проходит через вершины  и середину М ребра АВ, плоскость
и середину М ребра АВ, плоскость  проходит через вершину В и точки К и L — середины ребер SA и SC соответственно. Плоскости
проходит через вершину В и точки К и L — середины ребер SA и SC соответственно. Плоскости  пересекаются по прямой
пересекаются по прямой  . Найдите величину угла между прямой
. Найдите величину угла между прямой  и плоскостью грани
и плоскостью грани 
Ответ: 
3.66. В правильном тетраэдре ABCD проведены два сечения, каждое из которых параллельно ребрам АВ и CD. Площадь части грани ABC, заключенной между секущими плоскостями, на s больше площади грани ACD, заключенной между этими же плоскостями. На сколько площадь одного сечения больше площади другого?
Ответ: 
3.67. Ребро правильного тетраэдра ABCD равно а. Найти радиус сферы, вписанной в трехгранный угол, образованный гранями тетраэдра с вершиной в точке А, и касающейся плоскости, проведенной через середины ребер АВ, AD, ВС.
Ответ: 
3.68. Ребро правильного тетраэдра ABCD равно а. На ребрах АВ и CD расположены соответственно точки Е и F. Прямая EF пересекает описанную около тетраэдра сферу в точках М и N так, что  Найти
Найти 
Ответ: 
3.69. Ребро правильного тетраэдра ABCD равно а. На ребре BD расположена точка М так, что  . Прямой круговой конус расположен так, что его вершина находится на середине ребра АС, а окружность основания проходит через точку М и пересекает ребра АВ и ВС. Найдите радиус основания этого конуса.
. Прямой круговой конус расположен так, что его вершина находится на середине ребра АС, а окружность основания проходит через точку М и пересекает ребра АВ и ВС. Найдите радиус основания этого конуса.
Ответ: 
3.70. Найти площадь проекции куба со стороной а на плоскость, перпендикулярную его диагонали.
Ответ: 
3.71. В кубе  через диагональ
через диагональ  и середину ребра AD проходит плоскость. Найдите расстояние от середины ребра АВ до этой плоскости, если длина ребра куба равна 3.
и середину ребра AD проходит плоскость. Найдите расстояние от середины ребра АВ до этой плоскости, если длина ребра куба равна 3.
Ответ: 2.
3.72. В кубе  через вершину В и середины М и N ребер AD и СС, проведена плоскость. Найдите угол наклона этой плоскости к плоскости грани ABCD.
через вершину В и середины М и N ребер AD и СС, проведена плоскость. Найдите угол наклона этой плоскости к плоскости грани ABCD.
Ответ:  .
.
3.73. Ребро куба  имеет длину 12. Точка К лежит на продолжении ребра ВС на расстоянии 9 от вершины С. Точка L ребра АВ удалена от А на 5. Точка М делит отрезок
имеет длину 12. Точка К лежит на продолжении ребра ВС на расстоянии 9 от вершины С. Точка L ребра АВ удалена от А на 5. Точка М делит отрезок  в отношении
в отношении  считая от
считая от  Найдите площадь сечения куба плоскостью
Найдите площадь сечения куба плоскостью 
Ответ: 156.
3.74. Каждое ребро куба разделено на три отрезка равной длины. Докажите, что полученные 24 точки деления принадлежат одной сфере.
Переключаемся
3.75. Внутри грани реального правильного тетраэдра взяли точку. Как найти расстояние от нее до противоположной этой грани вершины, делая измерения только на его поверхности?
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧИТАТЕЛЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ
- § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 1.2. Двугранный угол. Угол между плоскостями.
- 1.3. Плоскость и прямая в пространстве.
- 1.4. Аксиомы стереометрии.
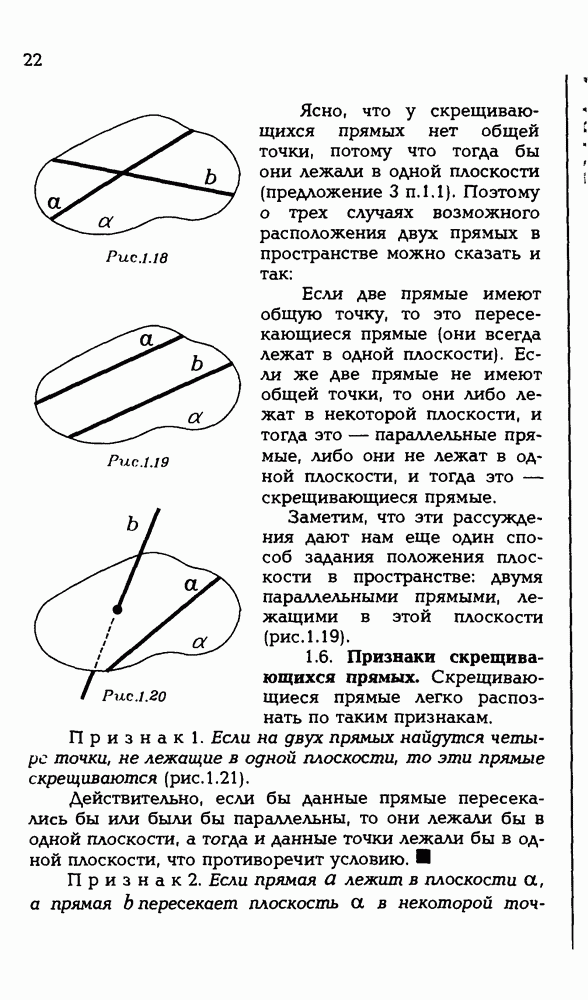
- 1.5. Взаимное расположение двух прямых в пространстве.
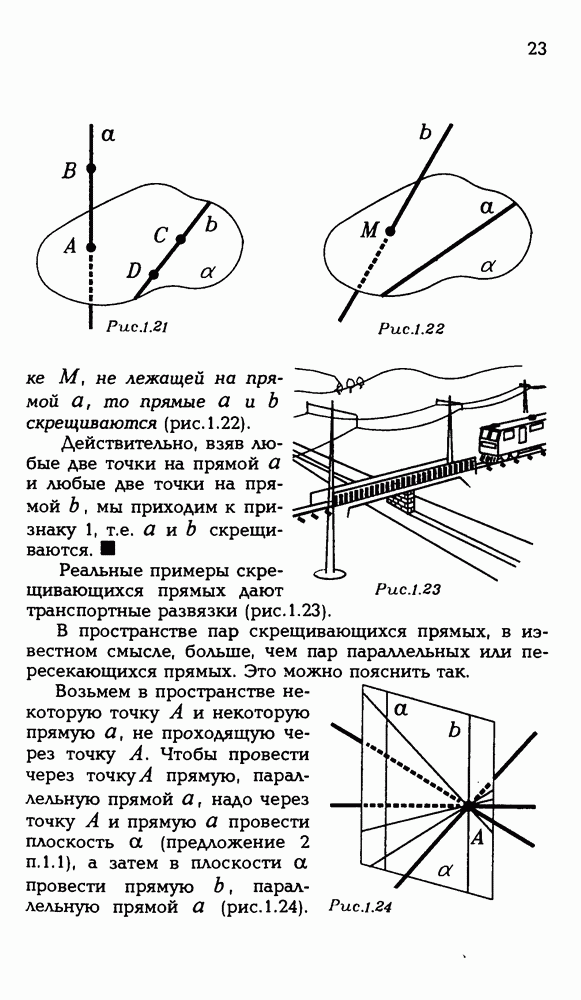
- 1.6. Признаки скрещивающихся прямых.
- 1.7. Параллельные прямые.
- 1.8. Параллельное проектирование.
- § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 2.2. О значении перпендикуляра.
- 2.3. Теорема о трех перпендикулярах.
- 2.4. Признак перпендикулярности прямой и плоскости.
- 2.5. Построение плоскости, перпендикулярной данной прямой.
- 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости.
- 2.7. Теорема о прямой, перпендикулярной плоскости.
- 2.8. Перпендикулярность плоскостей.
- 2.9. Ортогональное проектирование.
- § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 3.2. Параллельность и перпендикулярность.
- 3.3. Основная теорема о параллельных плоскостях.
- 3.4. Второй признак параллельности плоскостей.
- 3.5. Расстояние и параллельность.
- 3.6. Сонаправленность лучей и угол между прямыми.
- 3.7. Параллельность и углы.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ
- § 4. СФЕРА И ШАР
- 4.2. Взаимное положение шара и плоскости.
- 4.3. Сфера и многранники.
- 4.4. Вид и изображение шара и сферы.
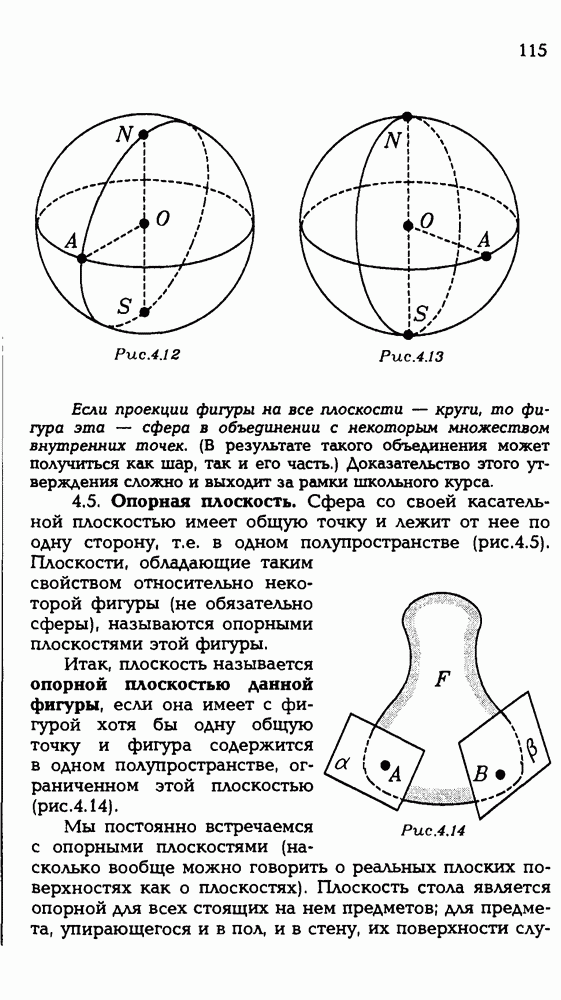
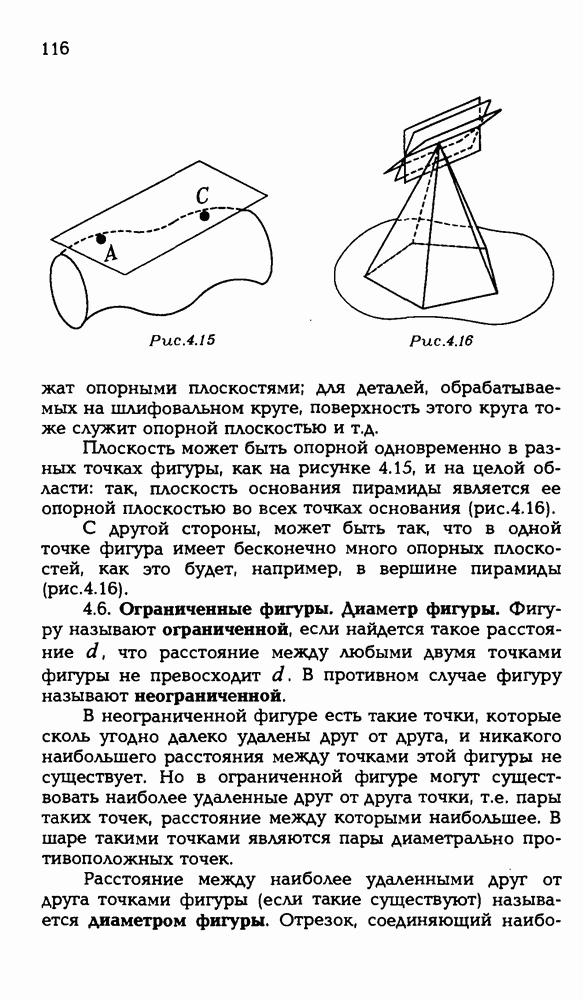
- 4.5. Опорная плоскость.
- 4.6. Ограниченные фигуры. Диаметр фигуры.
- 4.7. Опорные плоскости в концах диаметра.
- 4.8. Сфера — фигура вращения.
- 4.9. Симметрия сферы и шара.
- 4.10. Сфера — центрально симметричная фигура.
- 4.11. Сфера — зеркально симметричная фигура.
- 4.12. Отражение в плоскости и отражение в зеркале.
- § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ
- 5.2. Тригонометрия трехгранного угла.
- 5.3. Равенство трехгранных углов.
- 5.4. Сферические треугольники.
- 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников.
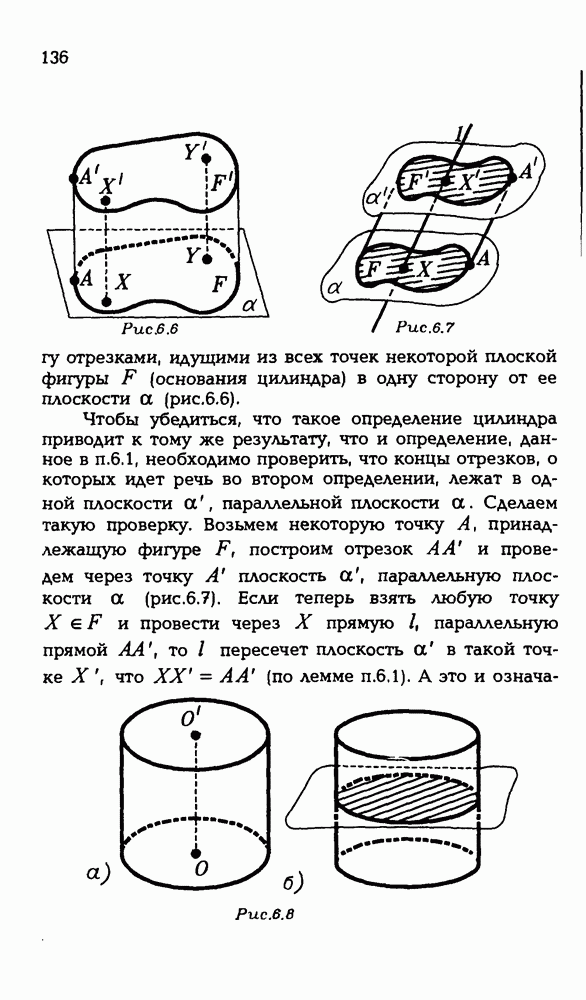
- § 6. ЦИЛИНДР
- 6.2. Другой подход к определению цилиндра.
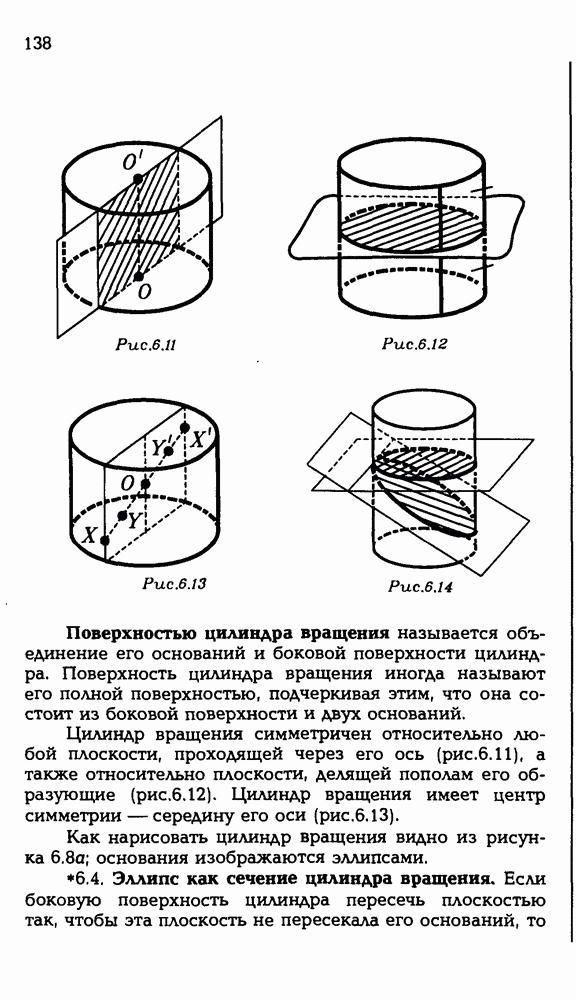
- 6.3. Цилиндр вращения.
- 6.4. Эллипс как сечение цилиндра вращения.
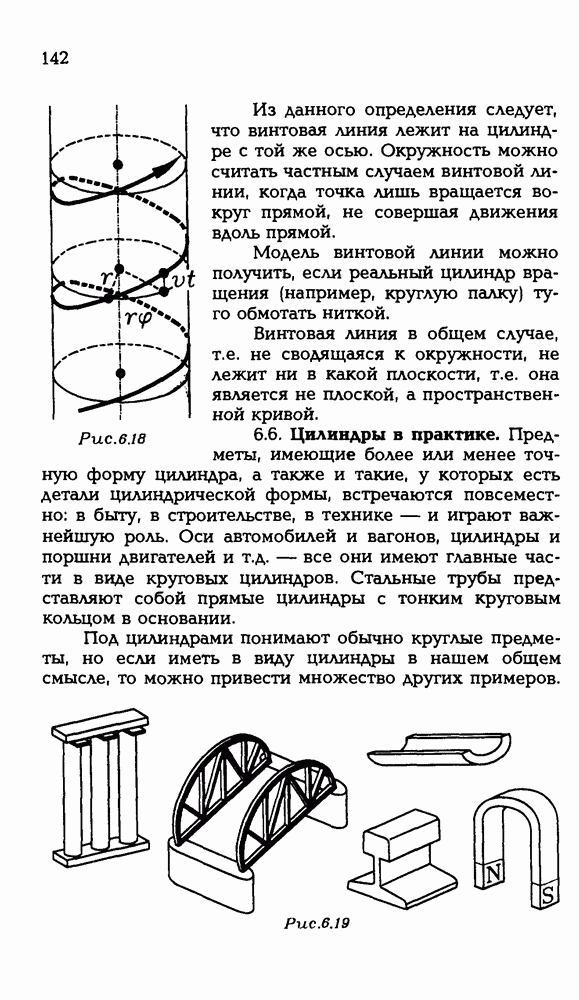
- 6.5. Винтовые линии.
- 6.6. Цилиндры в практике.
- § 7. ПРИЗМА
- 7.2. Параллелепипед.
- 7.3. Прямоугольный параллелепипед.
- 7.4. Симметрия параллелепипеда.
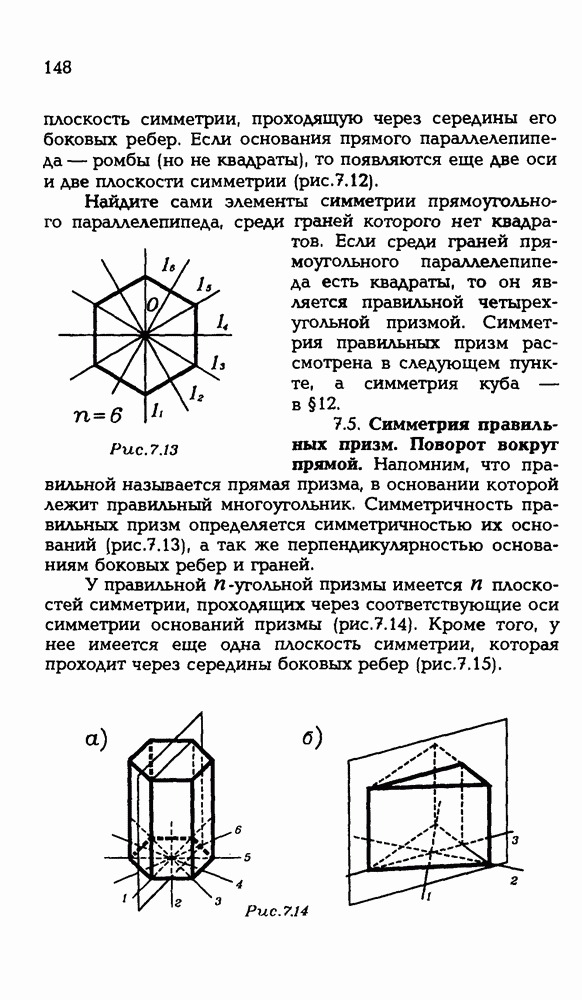
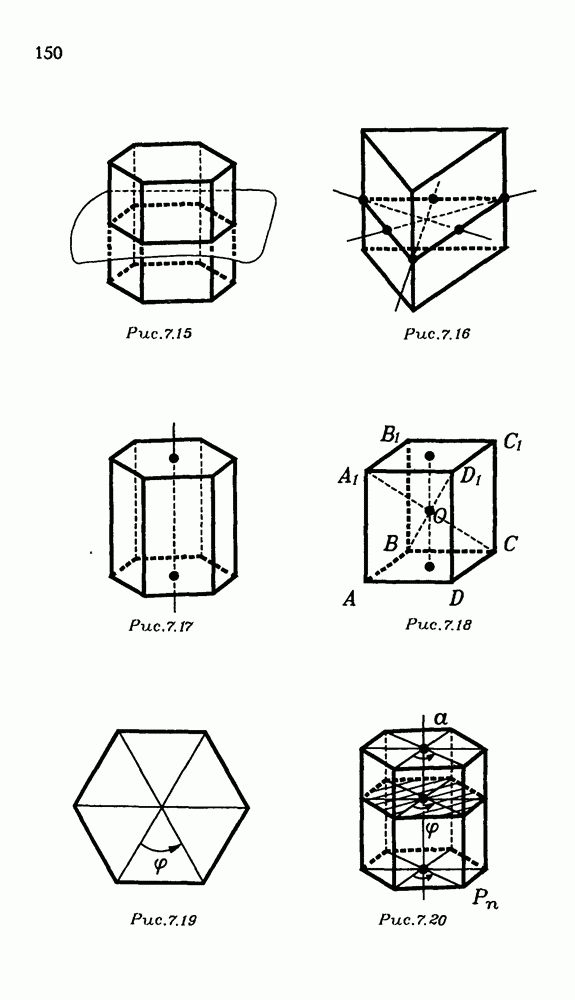
- 7.5. Симметрия правильных призм. Поворот вокруг прямой.
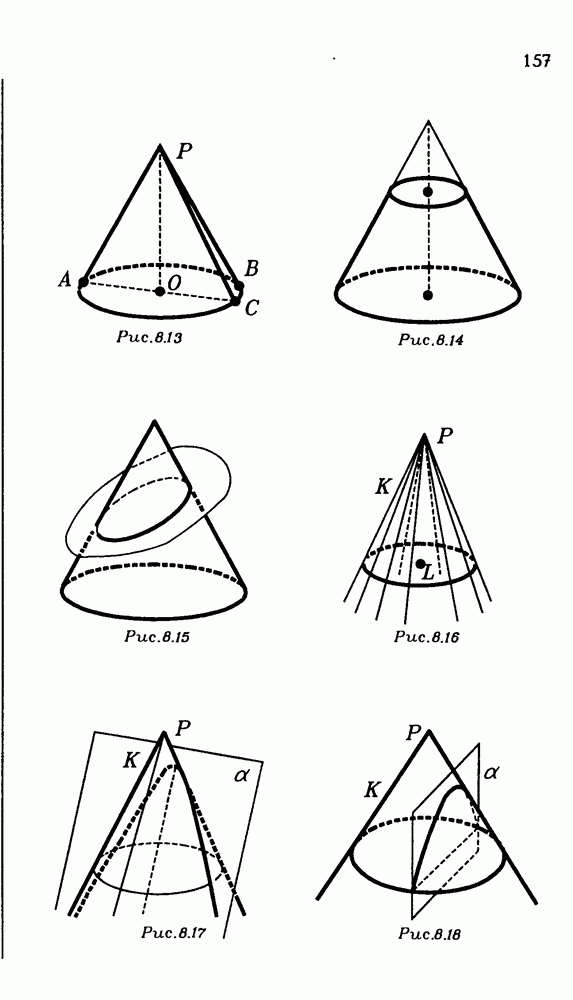
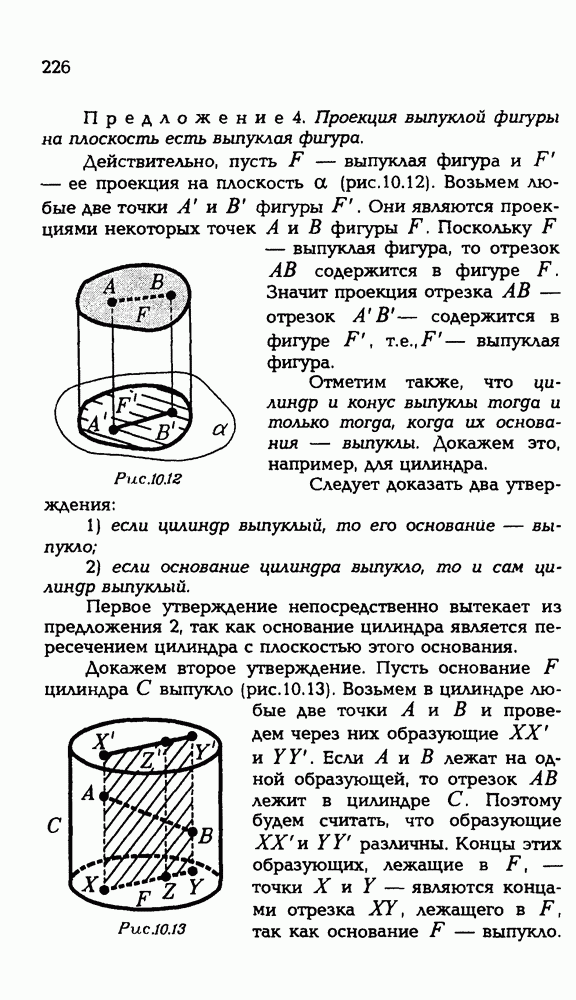
- § 8. КОНУС
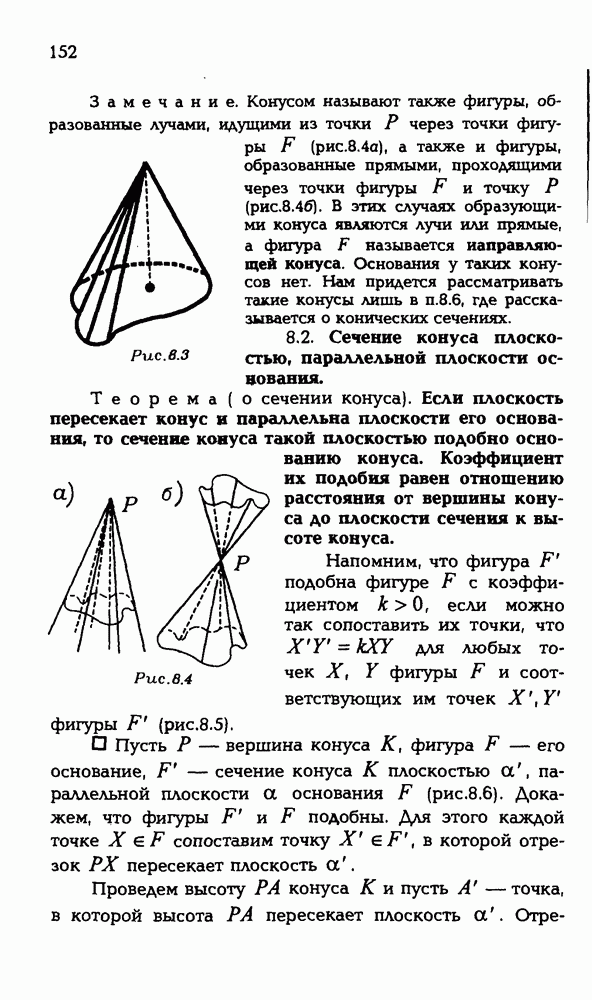
- 8.2. Сечение конуса плоскостью, параллельной плоскости основания.
- 8.3. Конус вращения.
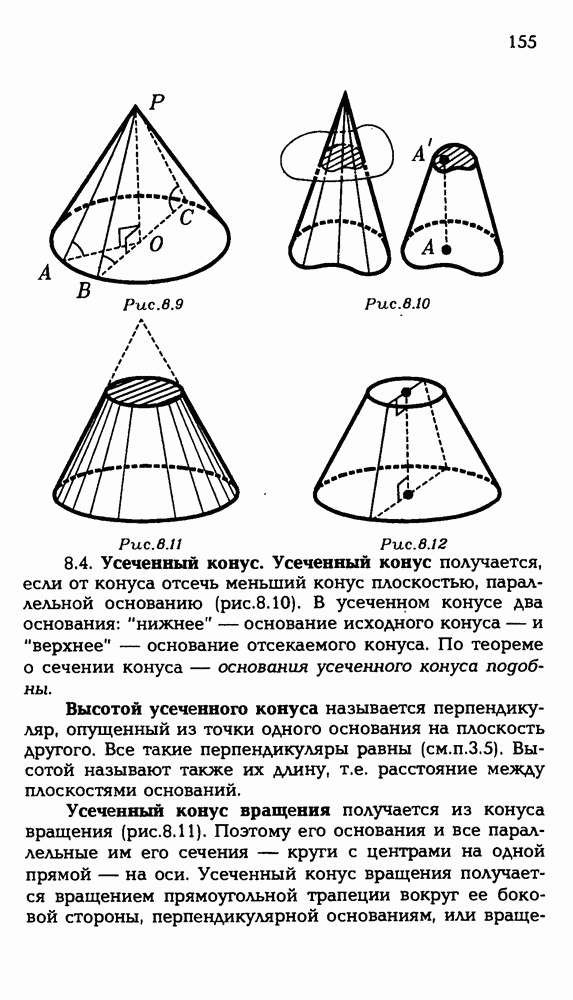
- 8.4. Усеченный конус.
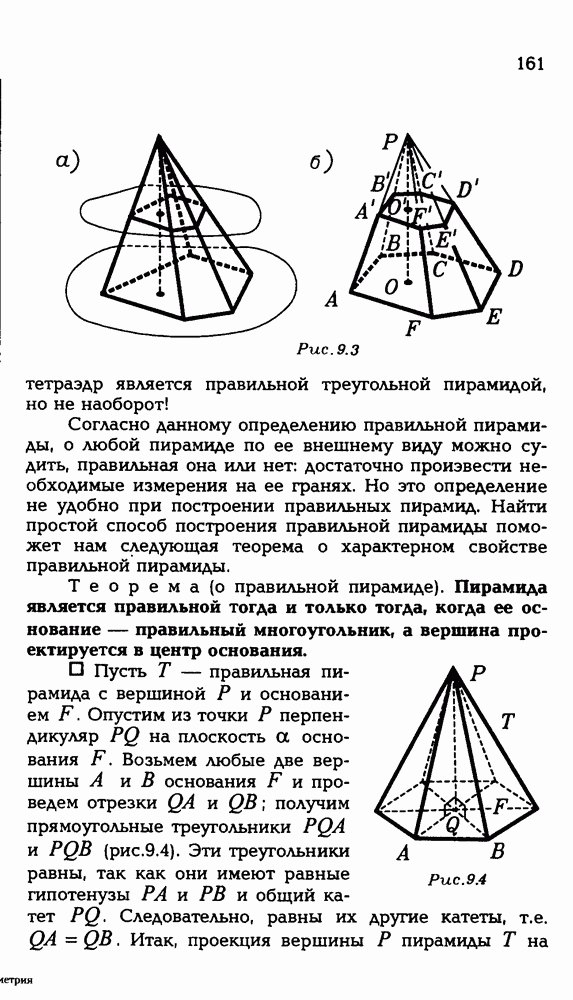
- § 9. ПИРАМИДА
- 9.2. Правильная пирамида.
- 9.3. Симметрия правильной пирамиды.
- 9.4. Конусы и пирамиды в практике.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ
- § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ
- 10.2. Граница и внутренность.
- 10.3. Определение тела и замкнутой плоской области.
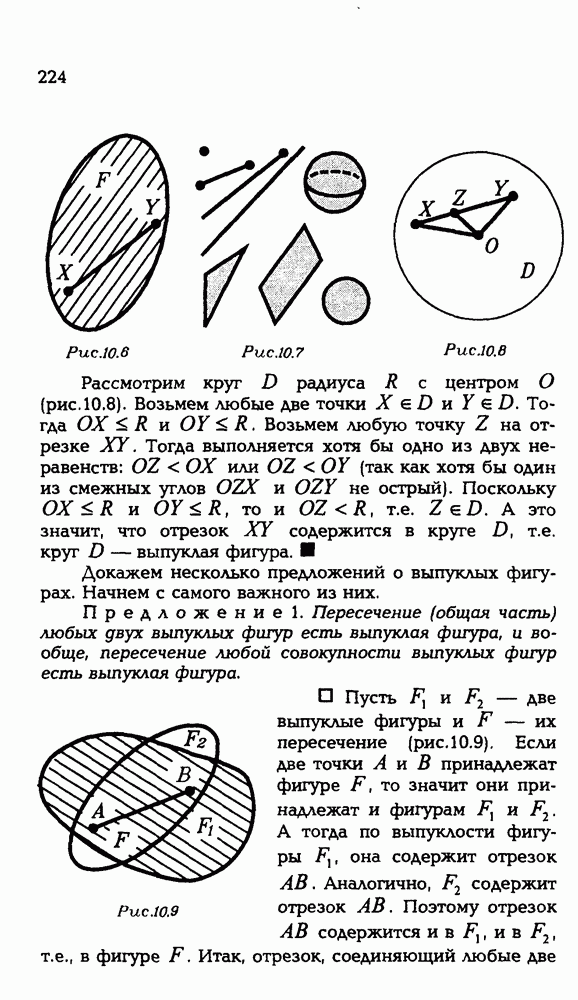
- 10.4. Выпуклые фигуры.
- 10.5. Выпуклые тела.
- § 11. МНОГОГРАННИКИ
- 11.2. Выпуклые многогранники.
- 11.3. Теорема Эйлера.
- 11.4. Выпуклые многогранники и выпуклые оболочки.
- 11.5. Многогранная поверхность и развертка.
- 11.6. Развертка выпуклого многогранника.
- § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
- 12.2. Классификация правильных многогранников.
- 12.3. Полуправильные многогранники.
- 12.4. Симметрия правильных многогранников.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
- § 13. ПОНЯТИЕ ОБЪЕМА
- 13.2. Определение объема.
- 13.3. Геометрические величины.
- § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА
- 14.2. Объем прямой призмы.
- § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ
- 15.2. Выражение объема через площади сечений.
- § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА
- 16.2. Объем конуса
- 16.3. Объем шара.
- 16.4. Объем тел вращения.
- 16.5. Объем шарового сегмента и шарового сектора.
- § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ
- 17.2. Площадь сферы.
- 17.3. Площадь сферических многоугольников.
- 17.4. Площадь сферического сегмента и сферического пояса.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ
- § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- 18.2. Другой способ нахождения координат точки.
- 18.3. Построение точки с данными координатами.
- 18.4. Выражение расстояния между точками.
- § 19. МЕТОД КООРДИНАТ
- 19.2. Уравнения без одной или двух координат.
- 19.3. Некоторые применения метода координат.
- § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ
- 20.2. Полярные координаты.
- 20.3. Цилиндрические координаты.
- 20.4. Сферические координаты.
- 20.5. Координатная сеть.
- § 21. ПОНЯТИЕ ВЕКТОРА
- 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов.
- 21.3. Сонаправленность и равенство векторов.
- 21.4. Признаки равенства векторов.
- 21.5. Радиус-вектор.
- § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 22.2. Разложение вектора на составляющие.
- 22.3. Умножение вектора на число.
- 22.4. Координаты вектора.
- 22.5. Равенство координат векторов и координат точек.
- 22.6. Разложение векторов по базису.
- 22.7. Ориентация базиса.
- § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ
- 23.2. Выражение скалярного произведения через координаты.
- 23.3. Свойства скалярного умножения.
- 23.4. Применения скалярного умножения.
- 23.5. Скалярное произведение и проекции.
- § 24. ВЕКТОРНЫЙ МЕТОД
- 24.2. Общее уравнение плоскости.
- 24.3. Векторное задание отрезка.
- 24.4. Некоторые теоремы о треугольниках и тетраэдрах.
- 24.5. Центр масс системы материальных точек.
- 24.6. Центры масс и выпуклые многогранники.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 6. ПРЕОБРАЗОВАНИЯ
- 25.1. Преобразования фигур.
- 25.2. Определения движения и равенства фигур.
- 25.3. Преобразования симметрии.
- 25.4. Параллельный перенос.
- 25.5. Поворот.
- § 26. СВОЙСТВА ДВИЖЕНИЙ
- 26.2. Общие свойства движений.
- 26.3. Теоремы о задании движений.
- 26.4. Неподвижные точки движений.
- 26.5. Два рода движений.
- 26.6. Теорема подвижности пространства.
- 26.7. Композиция отражений в плоскости.
- § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА
- 27.2. Движения первого рода как винтовые движения.
- 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот.
- 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения.
- § 28. ПОДОБИЕ
- 28.2. Гомотетия.
- 28.3. Свойства подобия.
- 28.4. Группы преобразований.
- § 29. ИНВЕРСИЯ
- 29.2. Аналитическое задание инверсии.
- 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии.
- 29.4. Сохранение величин углов при инверсии.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ОТВЕТЫ И УКАЗАНИЯ
- ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ