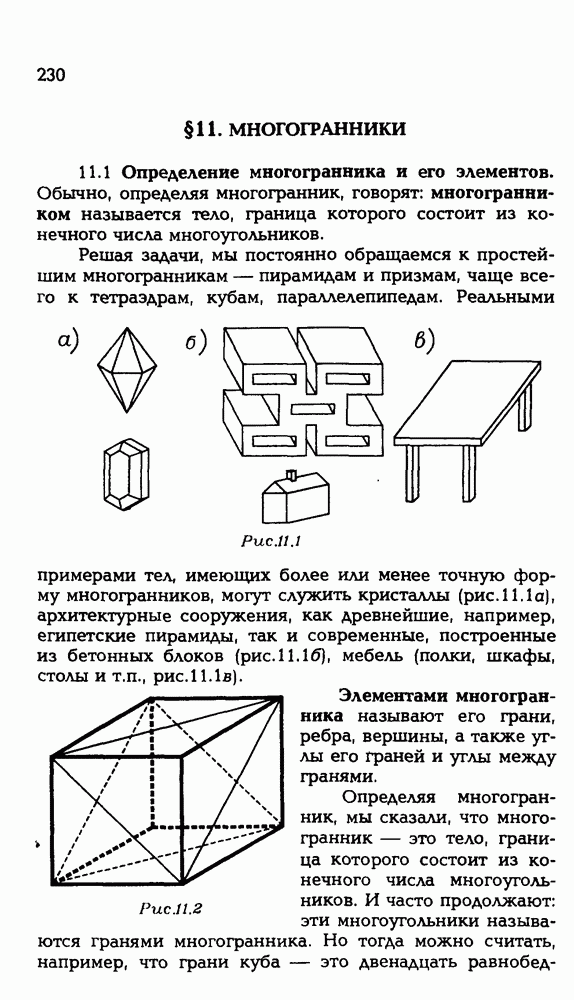
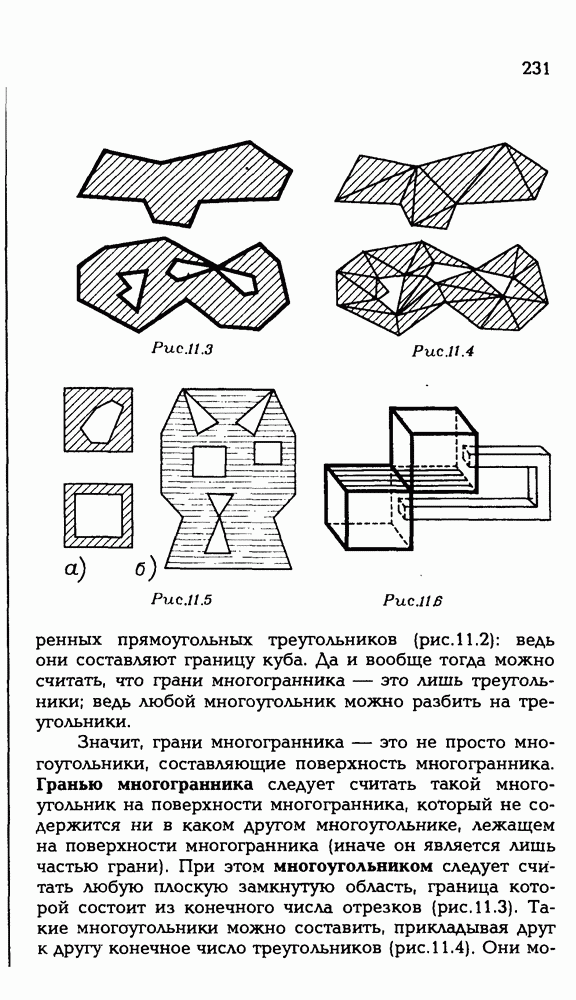
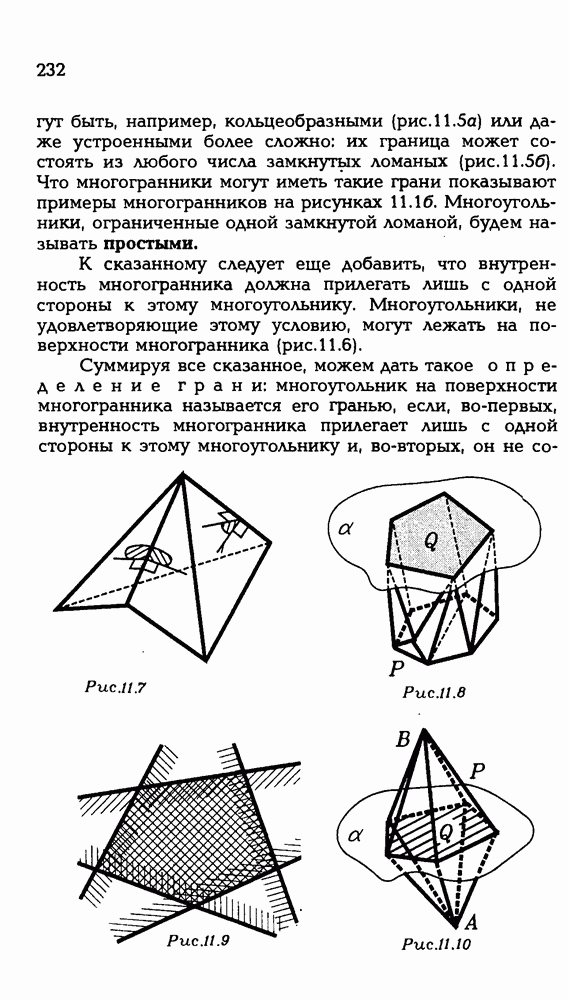
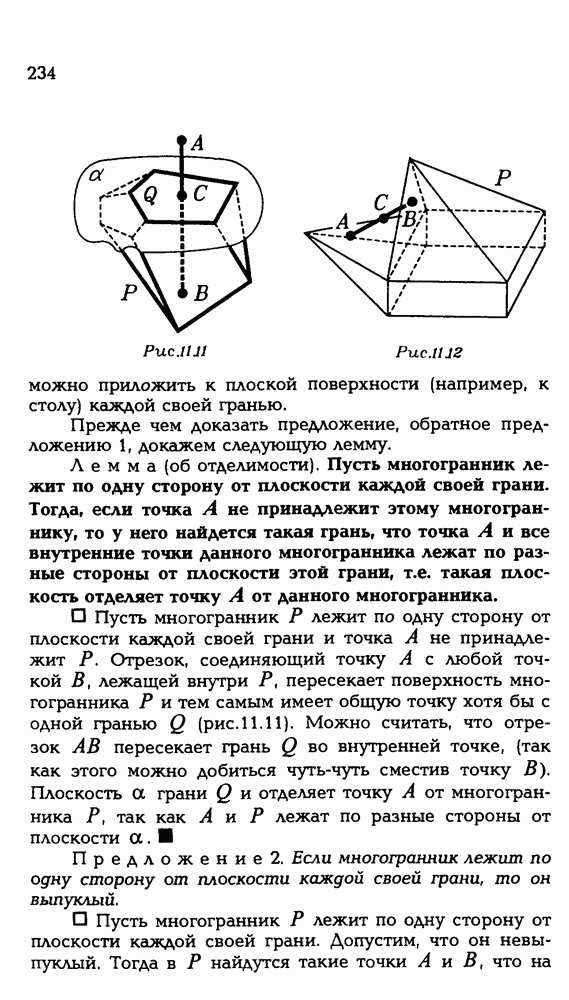
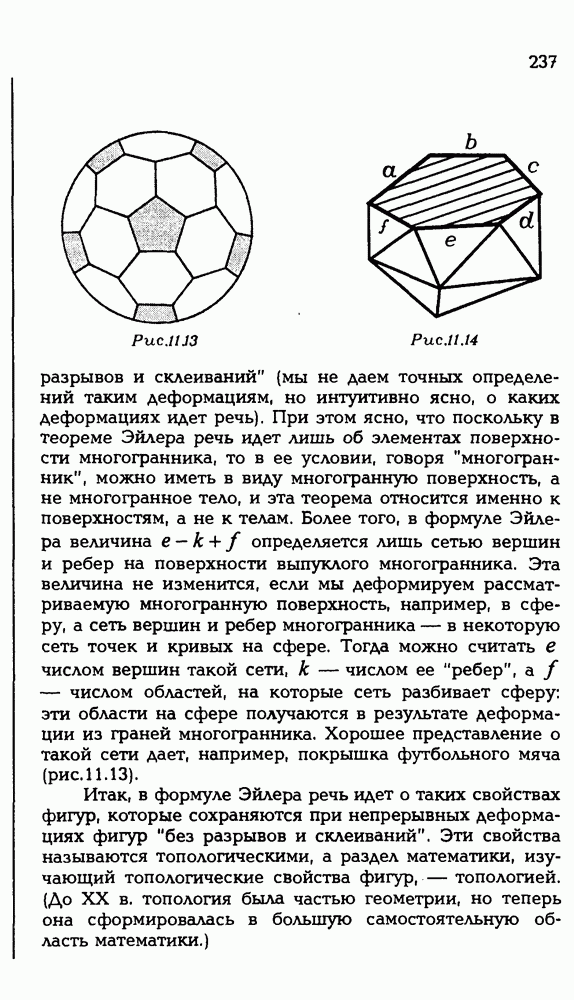
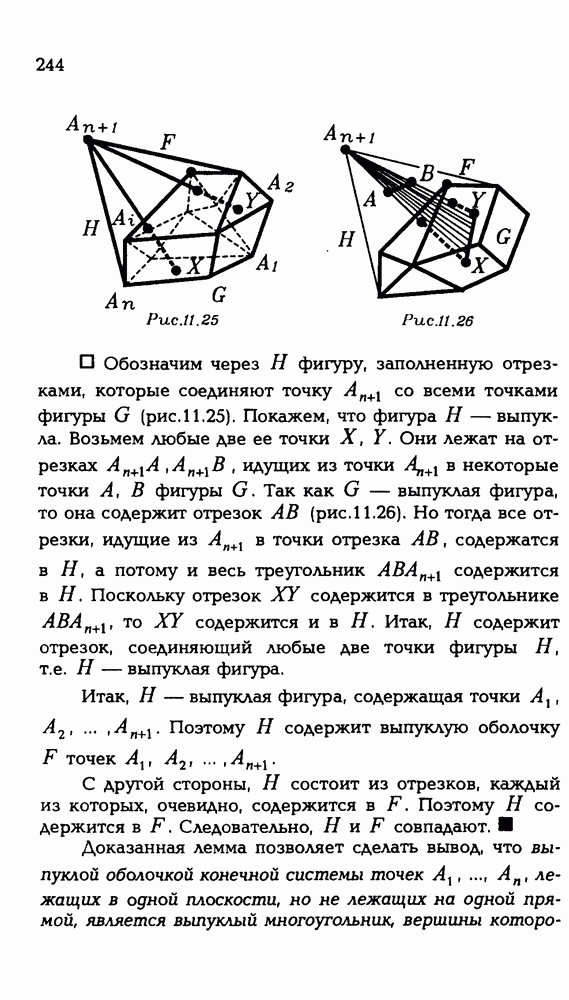
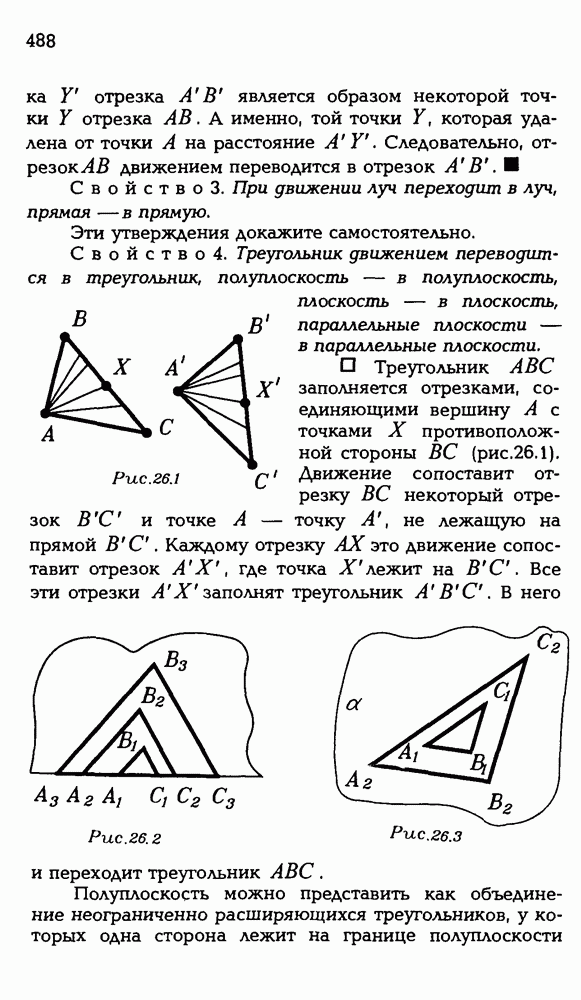
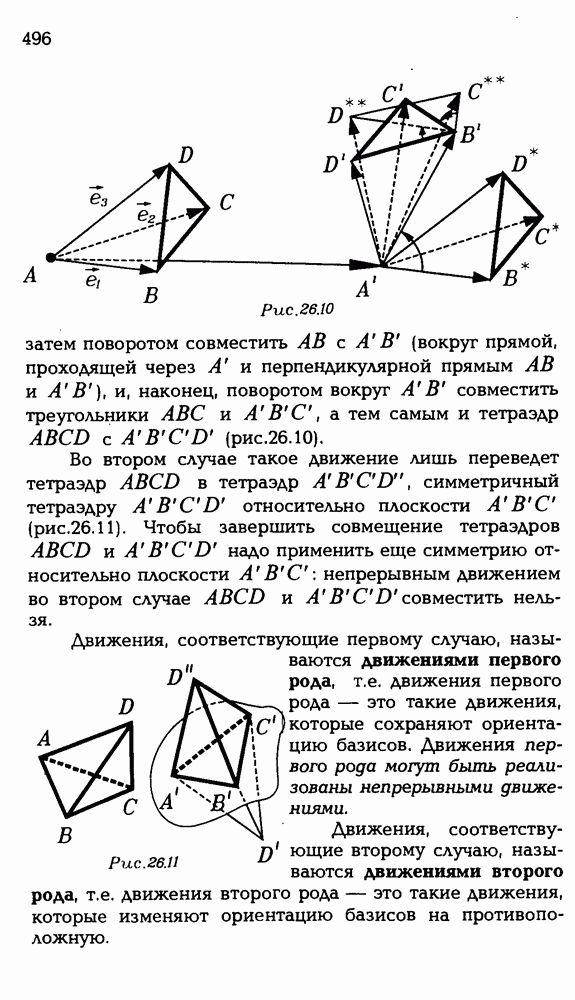
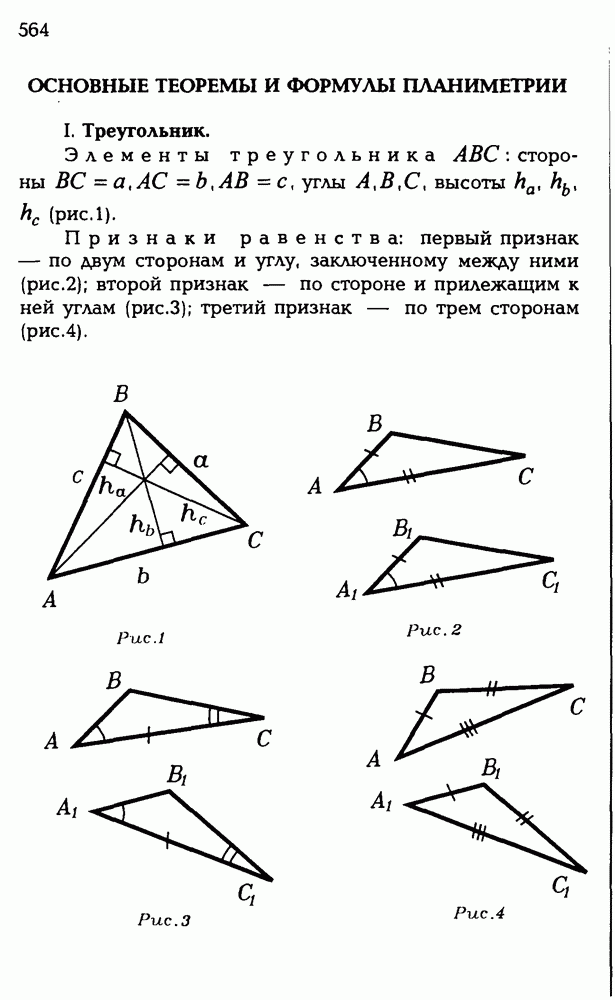
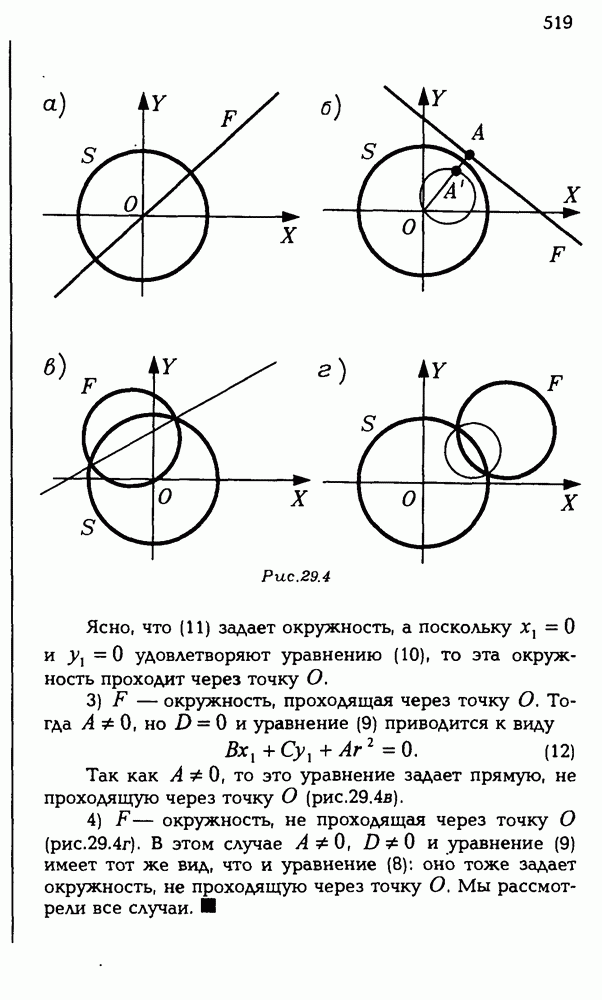| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
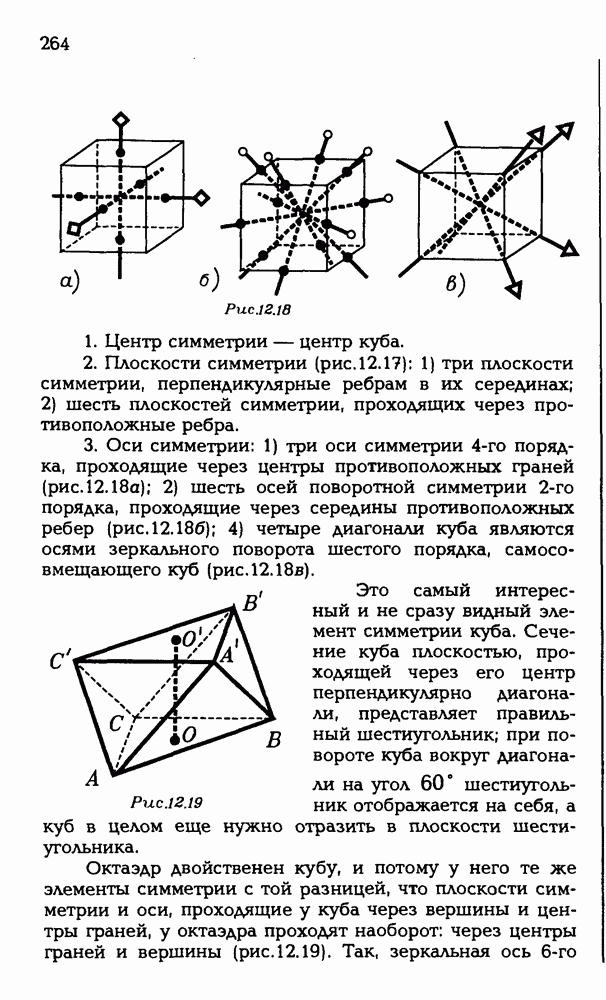
ЗАДАЧИ С РЕШЕНИЯМИ
ЗАДАЧИ К §18—20
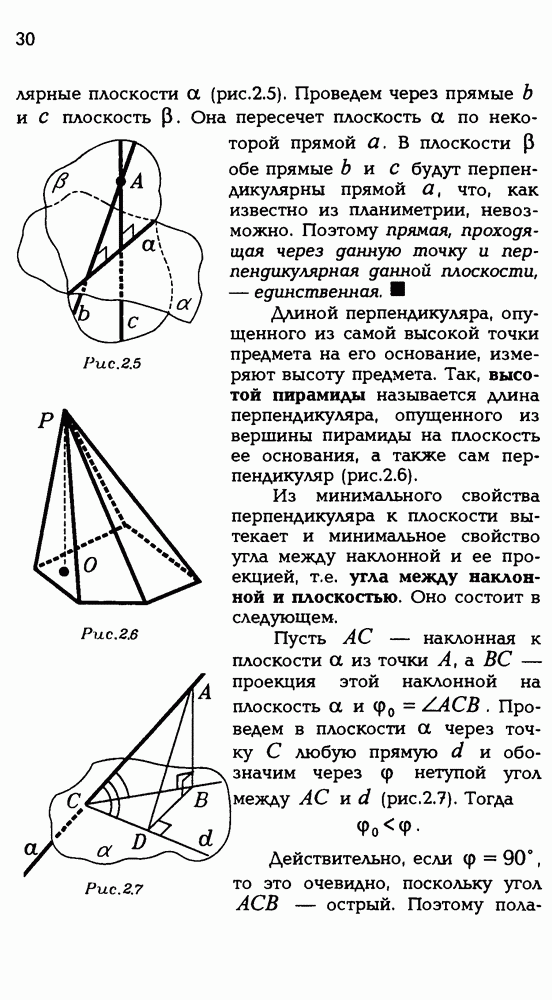
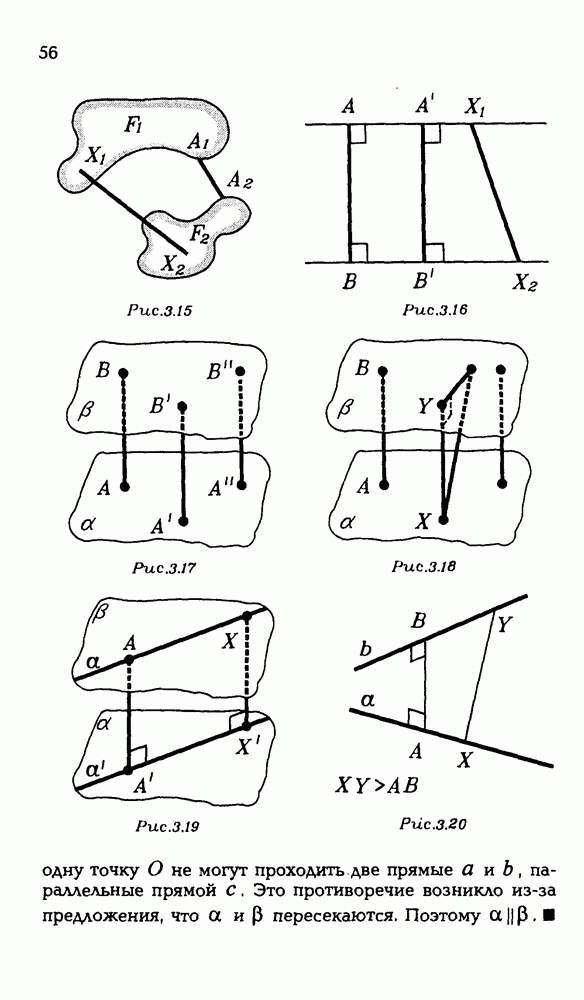
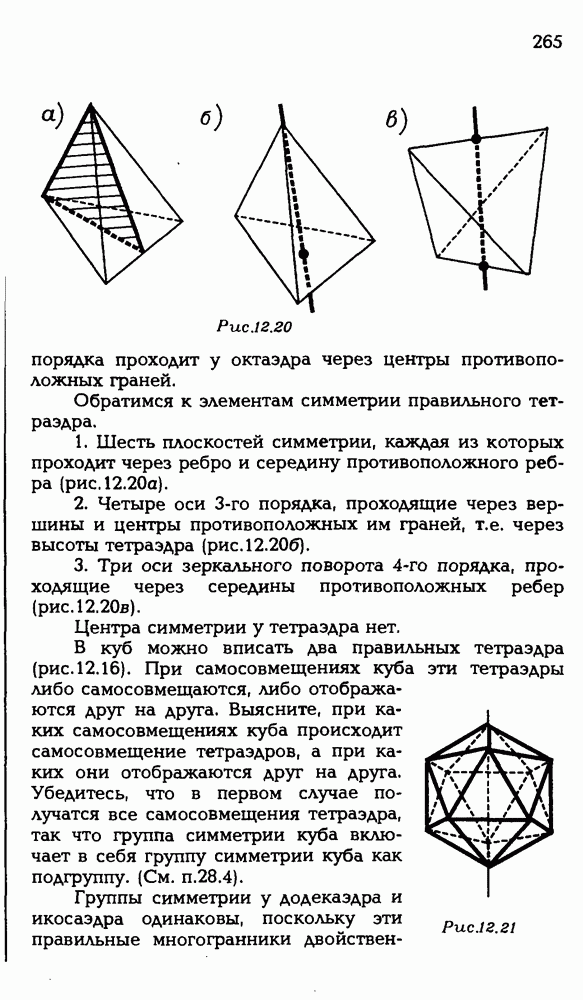
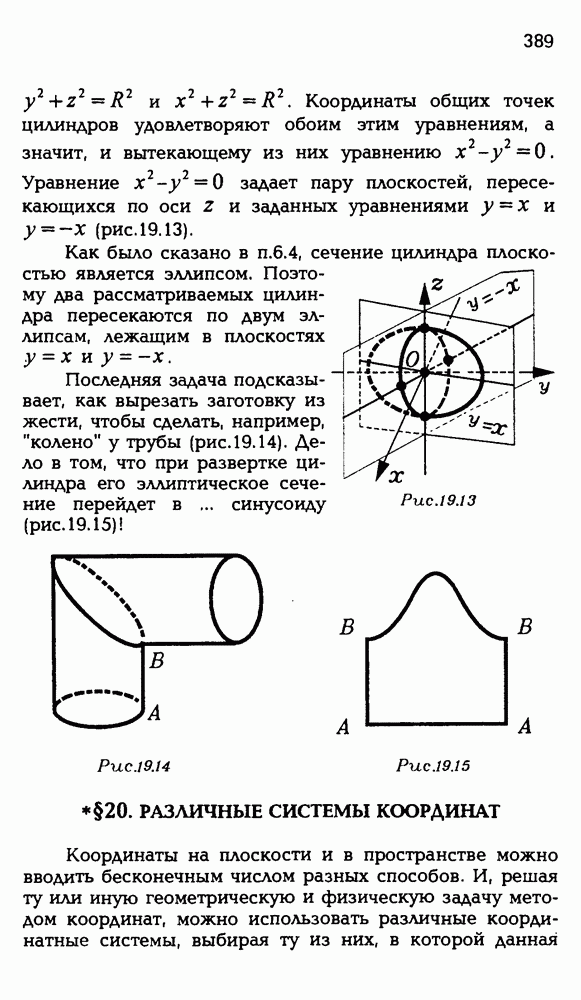
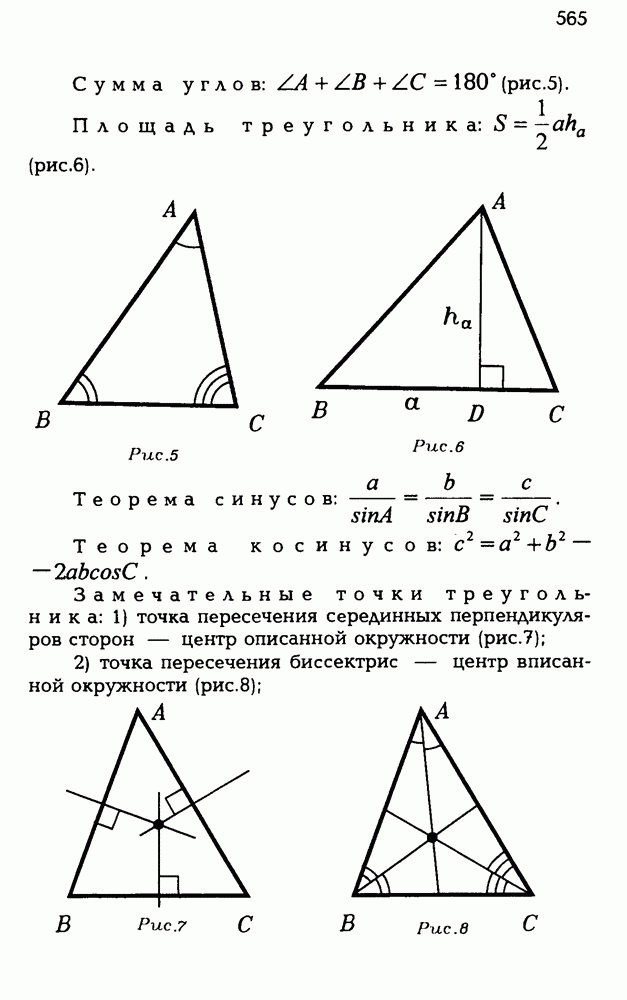
Методом координат можно решать вполне традиционные геометрические задачи, в формулировках которых вовсе отсутствует даже упоминание о координатах. Вот несложный тому пример.
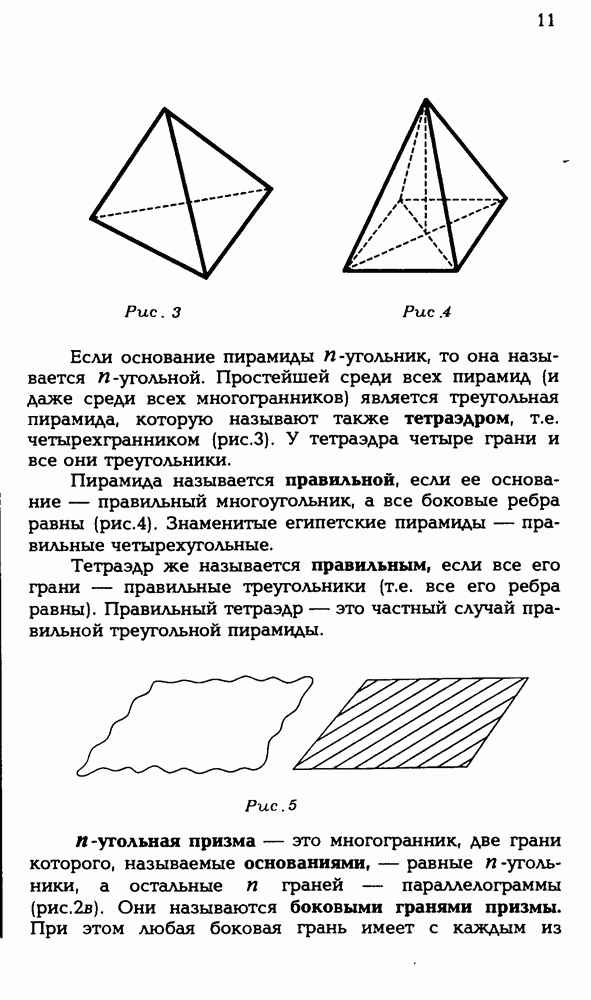
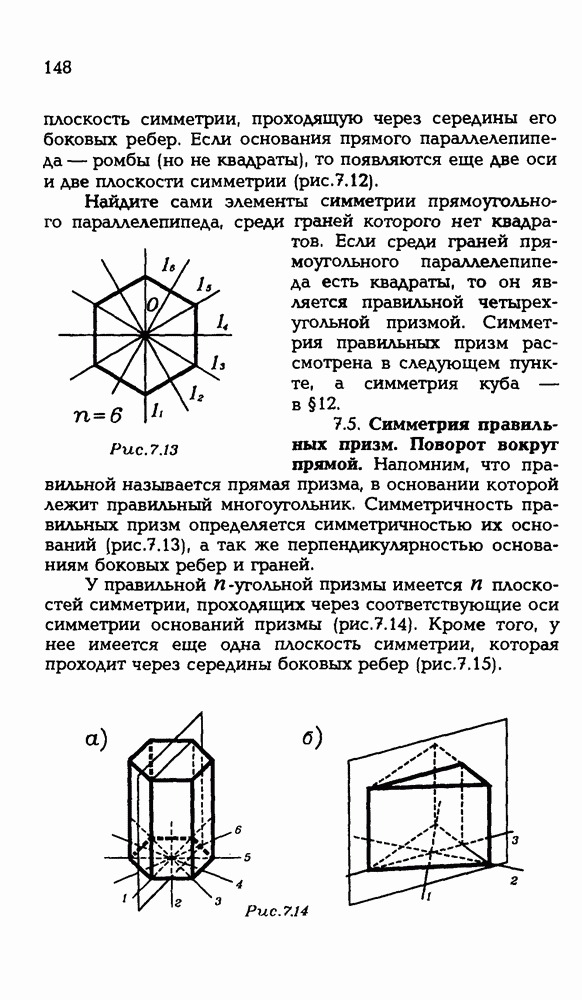
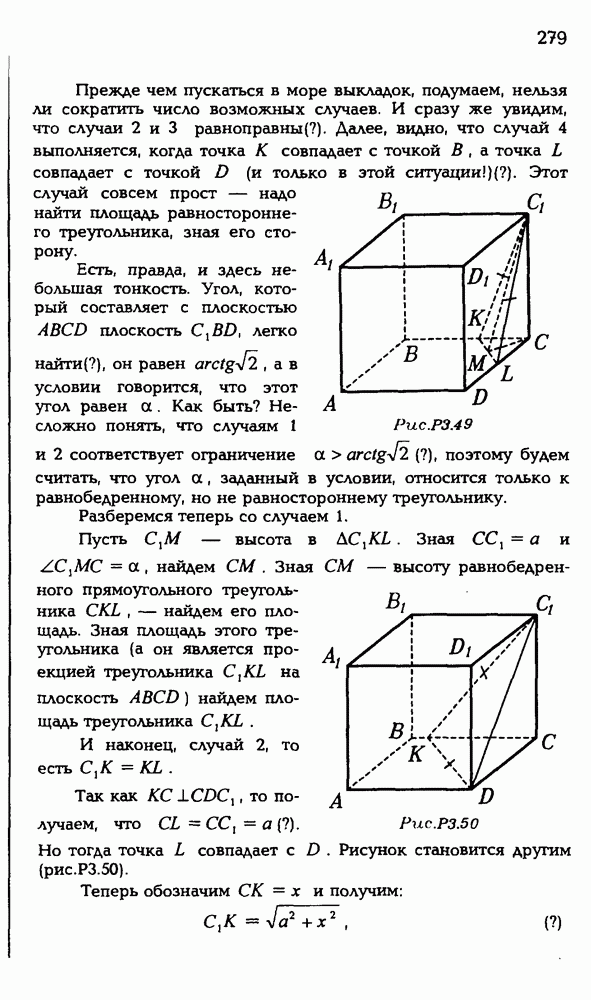
5.1. Дан куб  с ребром 2 (рис. Р 3.87). Чему равен радиус сферы, проходящей через точку К — середину
с ребром 2 (рис. Р 3.87). Чему равен радиус сферы, проходящей через точку К — середину  , точку L — середину
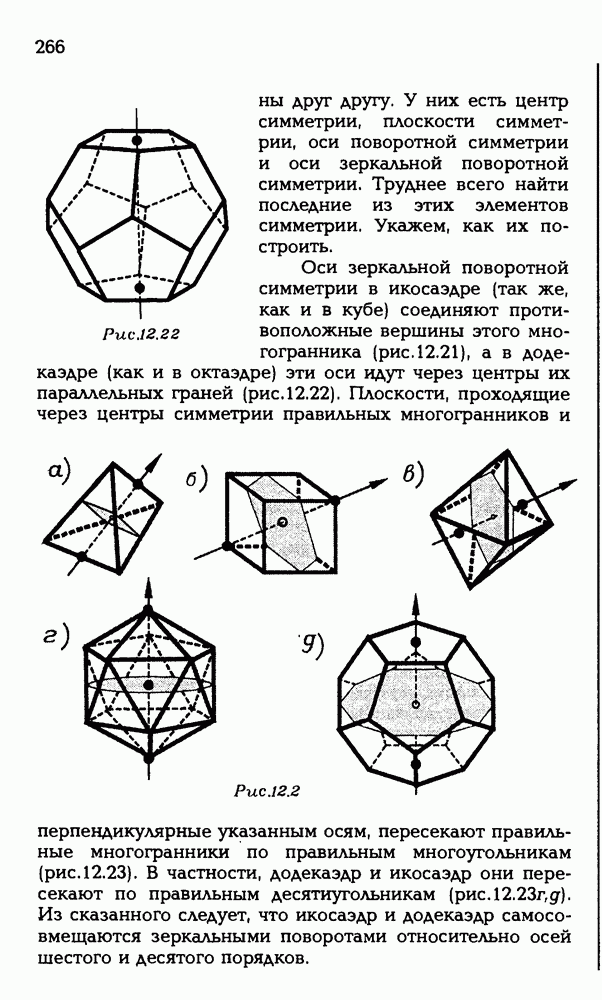
, точку L — середину  точку М — середину CD и
точку М — середину CD и 

Рис. Р 3.87
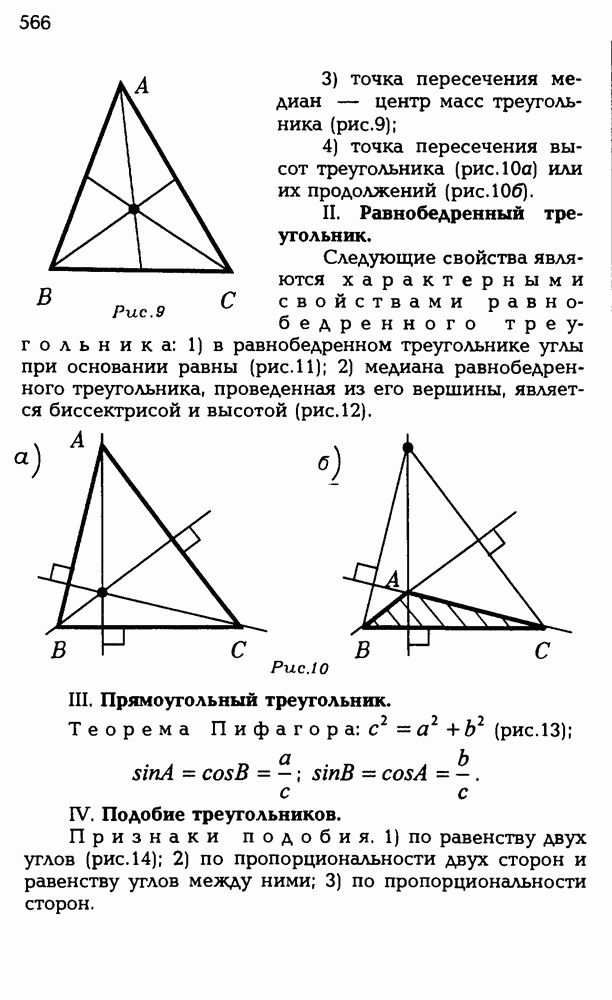
Выберем такую систему координат. Начало ее в точке А, луч AD — положительное направление оси  луч АВ — положительное направление оси у, луч
луч АВ — положительное направление оси у, луч  — положительное направление оси z. Запишем координаты данных точек в выбранной системе координат:
— положительное направление оси z. Запишем координаты данных точек в выбранной системе координат:  Пусть центр сферы О имеет координаты (x;y;z). Тогда
Пусть центр сферы О имеет координаты (x;y;z). Тогда  Запишем эти расстояния в координатном виде, причем для удобства обойдемся без радикалов. Тогда
Запишем эти расстояния в координатном виде, причем для удобства обойдемся без радикалов. Тогда

Чтобы решить систему с тремя переменными, обычно достаточно трех уравнений (?). Составим такую систему

Решив ее, получим, что 
Итак, центр находится в точке (1;1,5;1,5). Но тогда 
Конечно, такой способ может показаться скучноватым по сравнению с "чисто" геометрическим решением (кстати, а какое оно?). Но тот, кто уверен в своих умениях проводить длинные выкладки, может смело ему доверять.
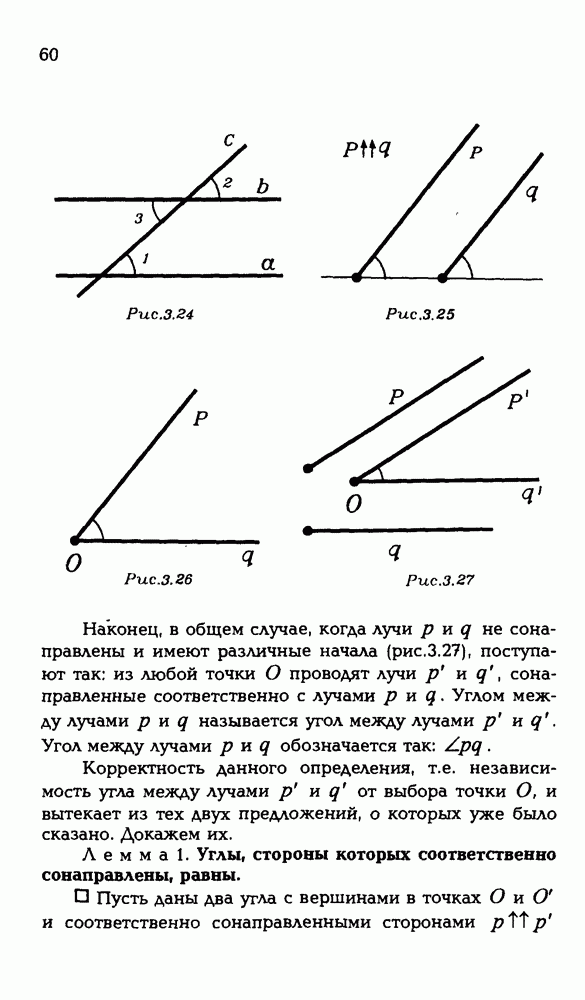
5.2. Что из себя представляет фигура, каждая точка которой равноудалена от плоскости  и от точки
и от точки 
Вопрос на первый взгляд не вполне ясен. На самом деле требуется вот что: получив уравнение этой фигуры, узнать в
нем какую-либо известную фигуру — плоскость, шар и т.д. или, если это не получилось, анализируя это уравнение, попытаться получить некоторое представление о свойствах фигуры.
Приступим. Сначала надо получить уравнение этой фигуры. Прежде всего, выразим в координатах исходные данные. Для этого выберем произвольную точку  принадлежащую данной фигуре. Расстояние от нее до плоскости
принадлежащую данной фигуре. Расстояние от нее до плоскости  равно
равно  , а
, а

Итак,

Упрощая это уравнение, придем к такому равенству:

Первое, что напрашивается сделать теперь — это избавиться от модуля. Здесь это возможно, ибо  Итак, мы пришли к уравнению
Итак, мы пришли к уравнению 
То, что за ним "скрывается" не плоскость и не сфера — понятно (?). Но что? Какая фигура? С какими свойствами?
Начинаем исследование полученного уравнения.
Прежде всего, мы обратим внимание на то, что переменные х и у находятся в четной степени (в квадрате), а потому при смене знака каждого из них на противоположный ничего в уравнении не изменится. Для фигуры, которая "скрылась" за этим уравнением, сие обстоятельство означает симметрию относительно осей х и у, а также относительно плоскостей 
Ясно, далее, что  . Это означает, что фигура ограничена снизу (если ось z направлена вверх) плоскостью
. Это означает, что фигура ограничена снизу (если ось z направлена вверх) плоскостью 
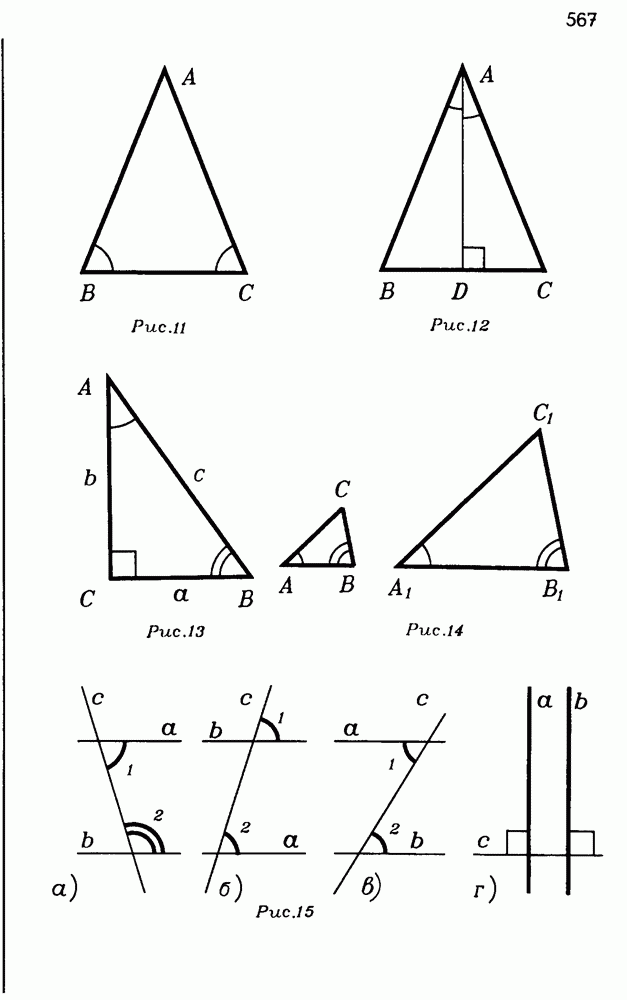
Попробуем теперь разобраться в сечениях этой фигуры, хотя бы самых простых. Возьмем сначала сечение плоскостью, параллельной плоскости  Уравнение такой плоскости
Уравнение такой плоскости  . Возьмем, к примеру,
. Возьмем, к примеру,  . И получим, что в этой плоскости выполняется равенство
. И получим, что в этой плоскости выполняется равенство  Но за ним стоит не что иное, как окружность с центром на оси z и радиусом 2. По аналогии заключаем, что так будет при любом
Но за ним стоит не что иное, как окружность с центром на оси z и радиусом 2. По аналогии заключаем, что так будет при любом  Но тогда оказывается, что вся фигура — это семейство расширяющихся окружностей с центрами на оси
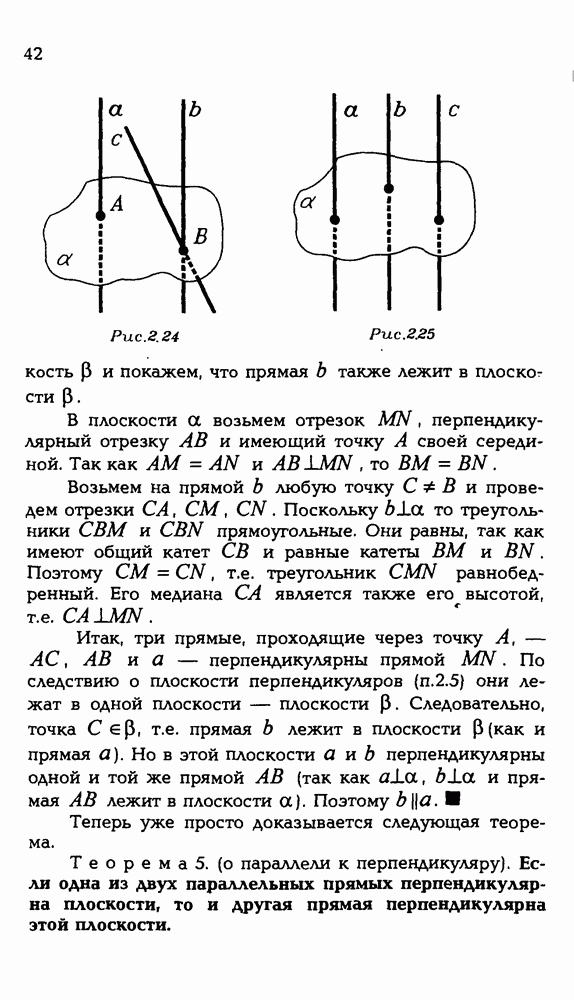
Но тогда оказывается, что вся фигура — это семейство расширяющихся окружностей с центрами на оси  Уже стало яснее (рис. Р 3.88).
Уже стало яснее (рис. Р 3.88).
Пойдем дальше и рассмотрим сечения, параллельные другим координатным плоскостям. Пусть, например,  то есть мы сечем данную фигуру плоскостью, параллельной плоскости
то есть мы сечем данную фигуру плоскостью, параллельной плоскости  Получаем:
Получаем:

Узнаете параболу в плоскости  ? И так всегда, если брать любые значения
? И так всегда, если брать любые значения  . И точно так же будет, если брать любые значения
. И точно так же будет, если брать любые значения 
Такую фигуру можно представить как результат вращения некоторой!?) параболы вокруг оси  . Такая фигура и называется соответственно — параболоид вращения.
. Такая фигура и называется соответственно — параболоид вращения.

Рис. Р 3.88
И вот еще что. Логика наших рассуждений была такой. Мы доказали, что всякая точка фигуры удовлетворяет некоему уравнению, после чего шел анализ уравнения. Но откуда мы знаем, что в это уравнение не попали "лишние" точки?
Иначе говоря, необходимо показать, что для всякой точки, координаты которой удовлетворяют уравнению, выполняется равенство, заданное условием, то есть расстояние от нее до плоскости  равно расстоянию от нее до точки А . Часто (в нашем случае также) это доказательство сводится к проверке равносильности выкладок при работе с уравнением. Проверьте эту равносильность самостоятельно. А.
равно расстоянию от нее до точки А . Часто (в нашем случае также) это доказательство сводится к проверке равносильности выкладок при работе с уравнением. Проверьте эту равносильность самостоятельно. А.
5.3. Сколько решений имеет уравнение

На первый взгляд мы имеем дело с задачей по алгебре. Метод координат, однако, позволяет "увидеть" эту задачу как геометрическую.
В самом деле, выражение  можно дополнить до вида
можно дополнить до вида  . В соответствии с формулой расстояния между точками это выражение равно расстоянию между точкой
. В соответствии с формулой расстояния между точками это выражение равно расстоянию между точкой  и точкой
и точкой 
Аналогично рассуждая, "видим", что выражение  равно расстоянию между той же точкой
равно расстоянию между той же точкой  и точкой
и точкой 
Таким образом, слева в исходном уравнении стоит сумма двух расстояний:  Посчитаем теперь расстояние ВС.
Посчитаем теперь расстояние ВС.
Оно равно  .
.
Если  (один из случаев в условии задачи), то имеем равенство
(один из случаев в условии задачи), то имеем равенство  Оно возможно тогда и только тогда, когда точка А лежит на отрезке
Оно возможно тогда и только тогда, когда точка А лежит на отрезке  Значит, при
Значит, при  уравнение имеет бесконечное множество решений.
уравнение имеет бесконечное множество решений.
Если  (другой случай в условии задачи), то имеем неравенство:
(другой случай в условии задачи), то имеем неравенство:  (так как
(так как  Но такое неравенство не может иметь место при любом положении точки
Но такое неравенство не может иметь место при любом положении точки  Значит, при
Значит, при  уравнение не имеет решений.
уравнение не имеет решений.
И, наконец, если  (последний случай из условия), то имеем неравенство
(последний случай из условия), то имеем неравенство  (так как
(так как  Такое неравенство имеет место при любом положении точки А вне отрезка ВС
Такое неравенство имеет место при любом положении точки А вне отрезка ВС  Значит, при
Значит, при  уравнение имеет бесконечное множество решений.
уравнение имеет бесконечное множество решений.
Обратите внимание на то, что сами решения нам, согласно условию, не нужны. Именно поэтому координатный метод в данной задаче оказался эффективным.
ЗАДАЧИ К §§ 21-24
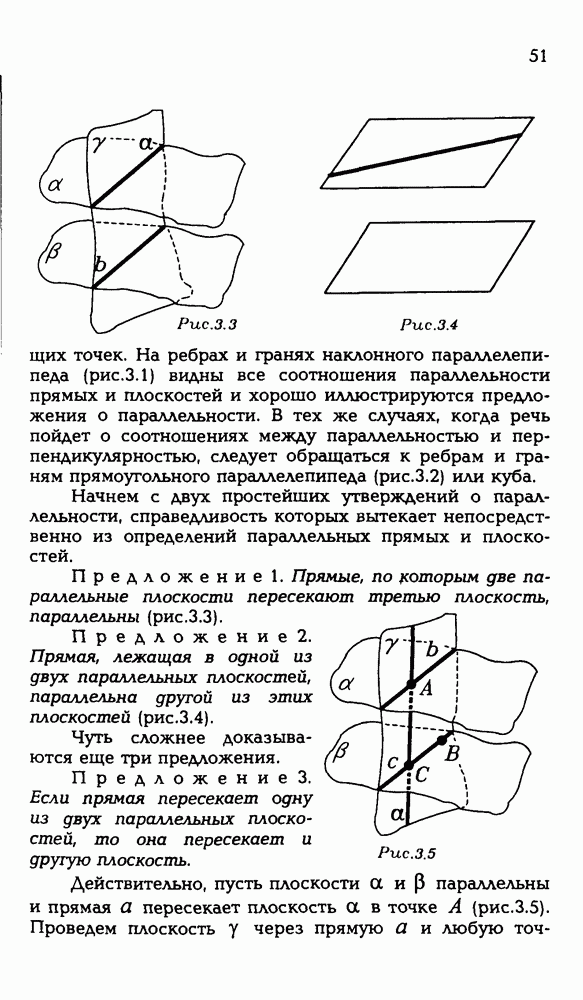
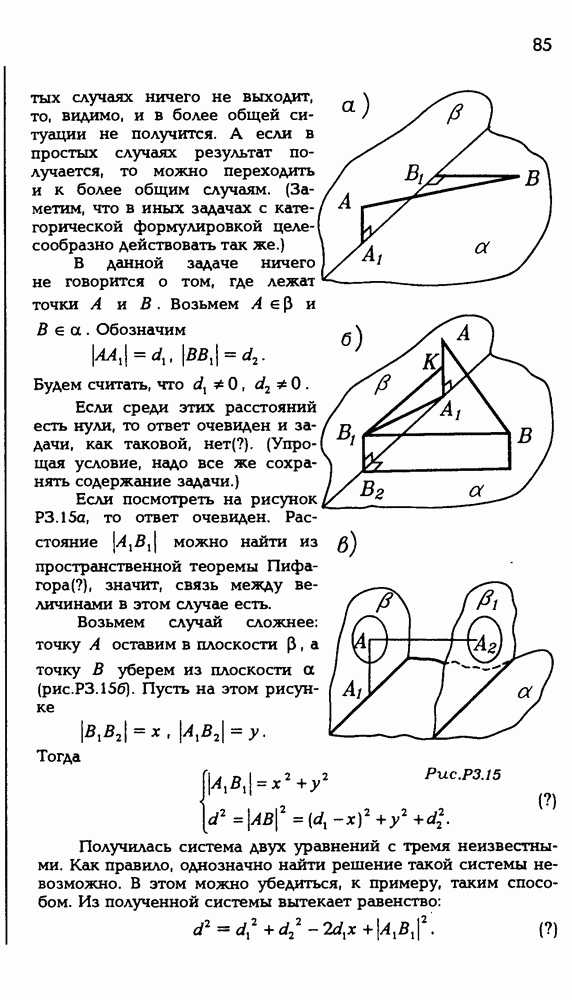
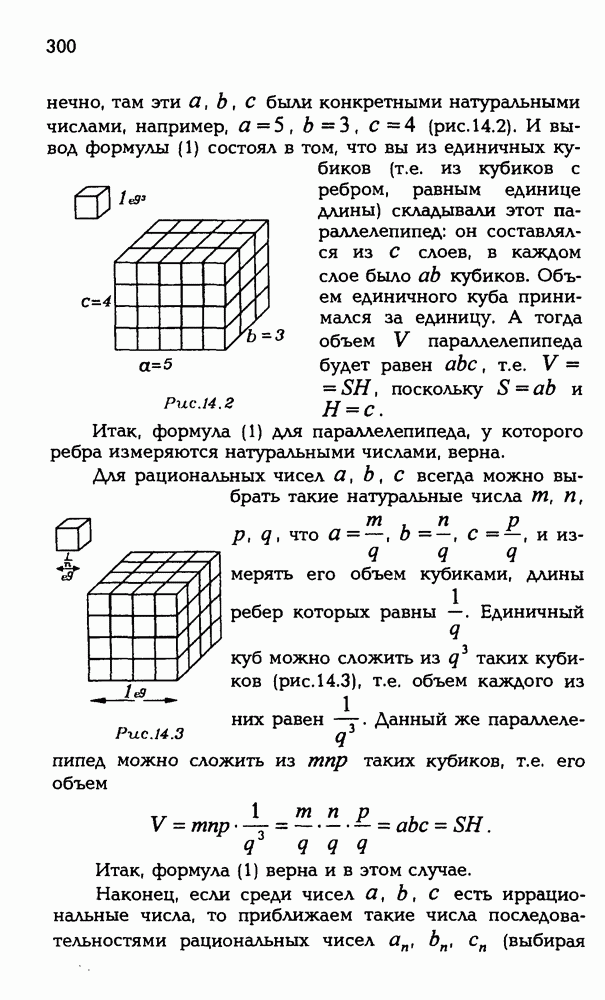
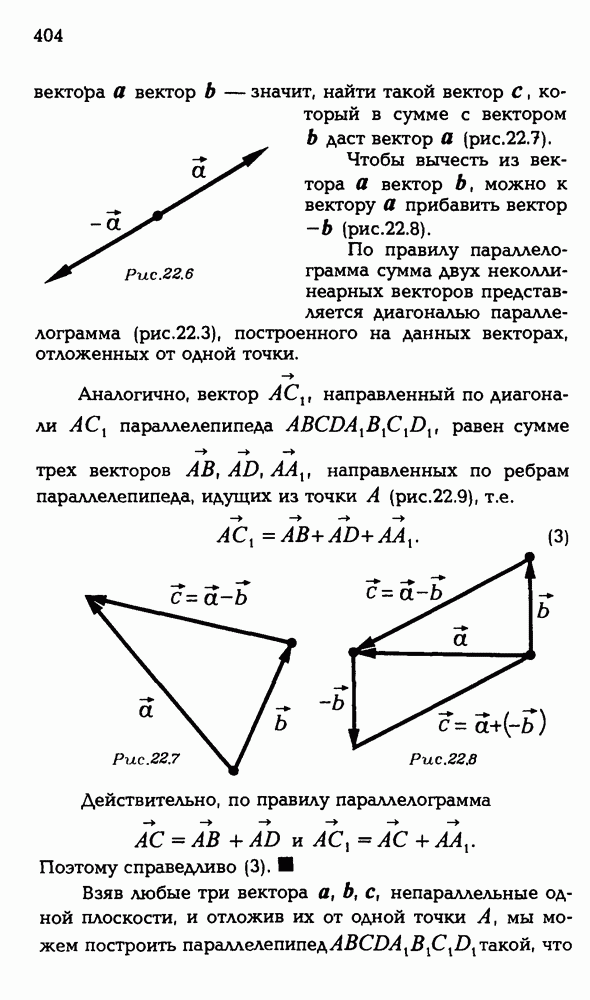
5.4.  — параллелепипед. Докажите, что для всякой точки О выполняется равенство
— параллелепипед. Докажите, что для всякой точки О выполняется равенство

Запишем первое из этих равенств:  Оно равносильно такому:
Оно равносильно такому:  , которое в свою очередь, равносильно такому
, которое в свою очередь, равносильно такому  Но последнее равенство в параллелепипеде выполняется.
Но последнее равенство в параллелепипеде выполняется.
Аналогично доказывается и второе равенство.
Что же интересного в этой простой задаче?
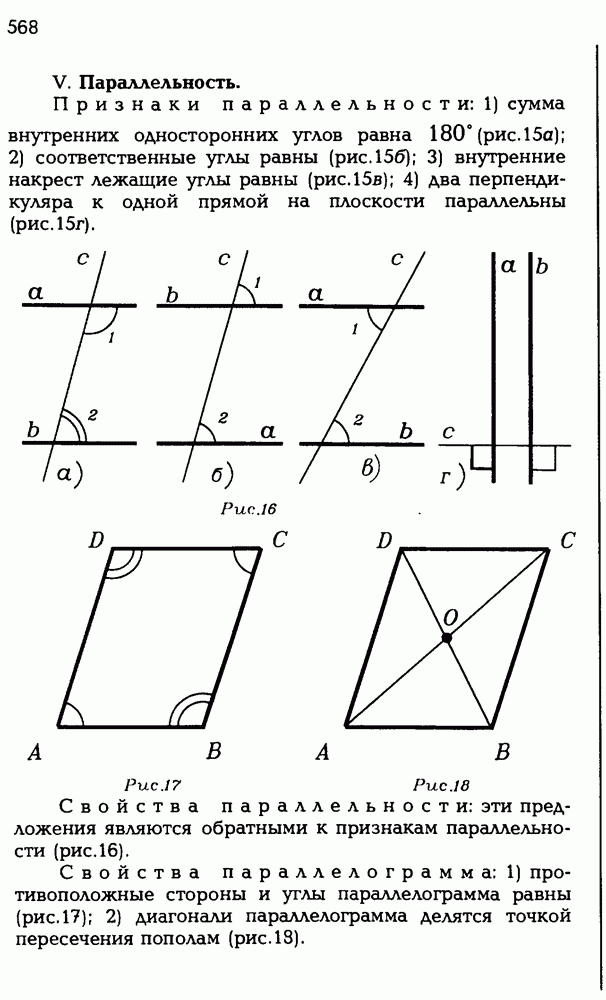
Для начала заметим, что в решении нам понадобился не весь параллелепипед, а только два его диагональных сечения. Эти диагональные сечения  являются параллелограммами (рис. Р 3.89). Так что у нас задача не про параллелепипед, а про параллелограммы, точнее, про один параллелограмм —
являются параллелограммами (рис. Р 3.89). Так что у нас задача не про параллелепипед, а про параллелограммы, точнее, про один параллелограмм —  , потому что для второго надо доказать то же, что и для первого. Выглядит эта задача так:
, потому что для второго надо доказать то же, что и для первого. Выглядит эта задача так:  параллелограмм, а точка О — произвольная точка пространства. Докажите, что
параллелограмм, а точка О — произвольная точка пространства. Докажите, что 
Кроме того, мы в решении нигде не использовали то обстоятельство, что задана неплоская фигура. Что из этого следует? А то, что данную задачу можно переформулировать как задачу планиметрии (?). Тем не менее, решение будет точно таким же.

Рис. Р 3.89
Вот это и стоит запомнить.
Именно: при решении задач векторным способом может оказаться, что решение не зависит от размерности заданных фигур.
Поэтому, решив векторным способом планиметрическую задачу, посмотрите, не проходит ли это же решение в пространстве. И наоборот.

Рис. Р 3.90
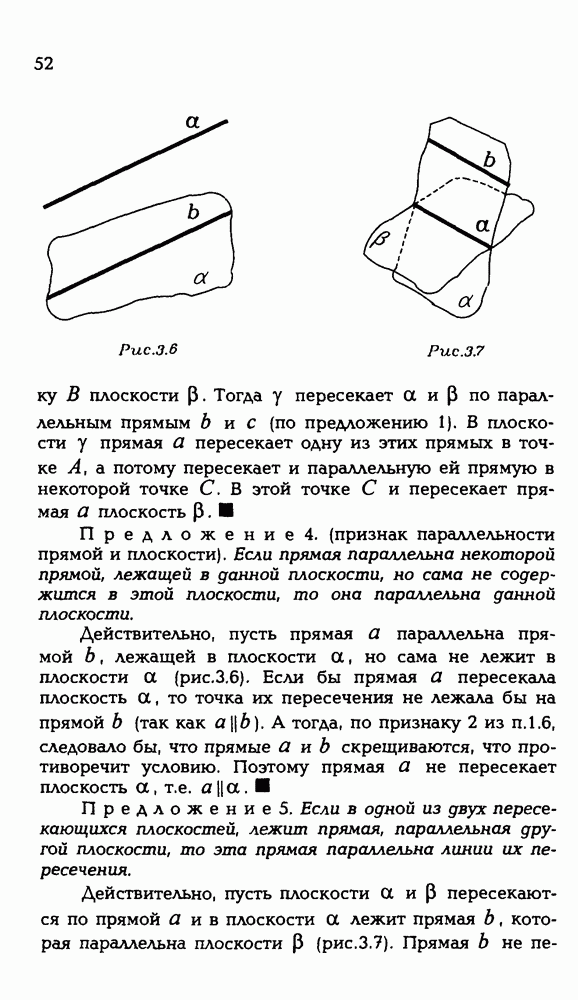
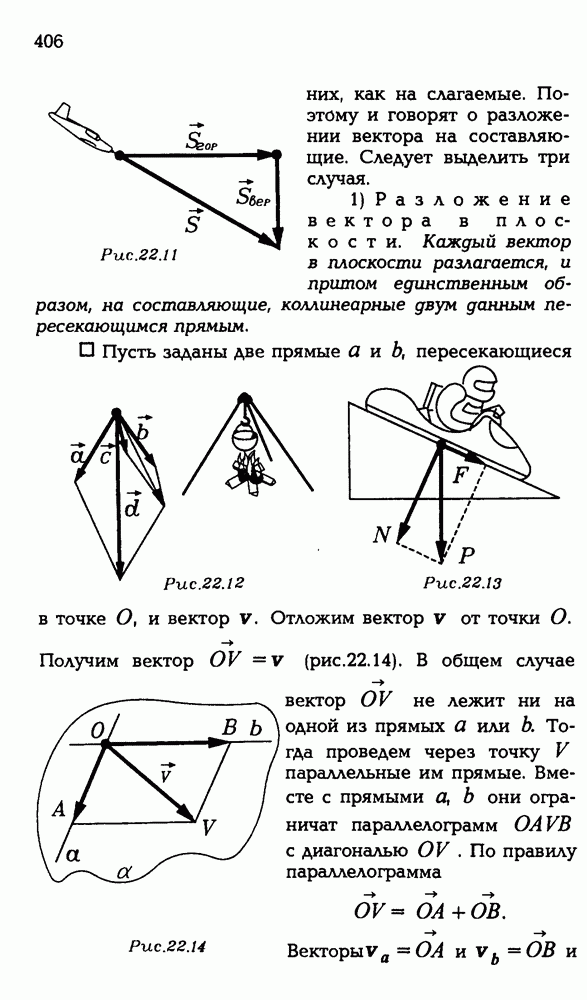
5.5. Докажите, что: а) диагонали параллелограмма пересекаются и в точке пересечения делятся пополам; б) диагонали параллелепипеда пересекаются и в точке пересечения делятся пополам.
а) Вам эта задача хорошо знакома из планиметрии; тем легче показать, как ее можно решить векторным методом.
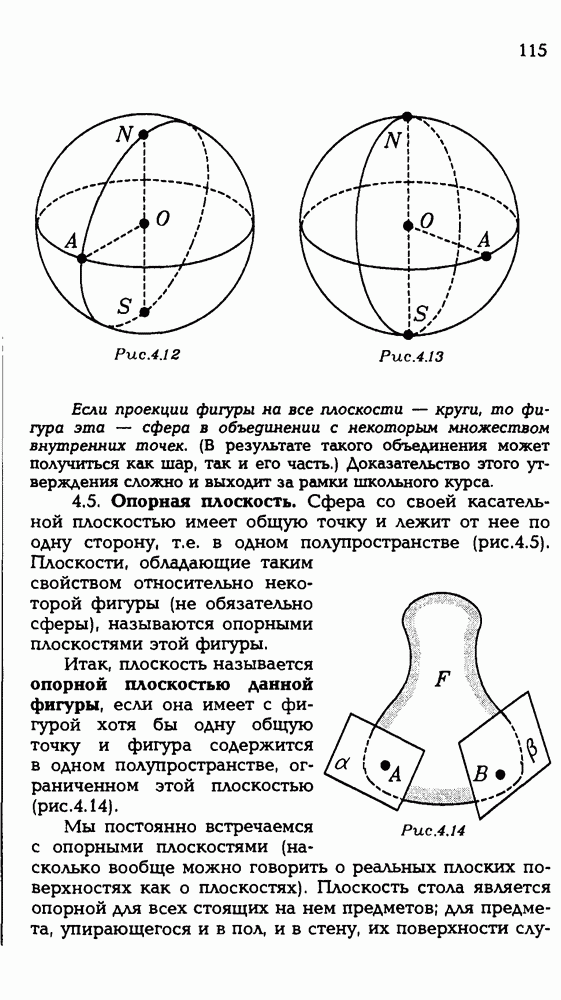
Пусть ABCD — параллелограмм (рис. Р 3.90). В плоскости ABC выберем базис из двух векторов, как-то связанных с данным параллелограммом. Можно в качестве базиса взять, например, векторы АВ и AD. Пусть X — общая точка двух диагоналей АС и BD данного параллелограмма. Ее принадлежность каждой из них запишем в векторном виде: 
 Получили векторную систему. Существование общей точки X у отрезков АС и BD равносильно существованию чисел
Получили векторную систему. Существование общей точки X у отрезков АС и BD равносильно существованию чисел  , удовлетворяющих этой системе.
, удовлетворяющих этой системе.
Для решения ее вектор АХ из каждого уравнения разложим в выбранном базисе. Во втором уравнении это уже сделано. Легко доводится до нужного вида и первое уравнение. Так как  то
то  . Получилось, что вектор АХ в одном и том же базисе АВ и AD представлен двумя разложениями:
. Получилось, что вектор АХ в одном и том же базисе АВ и AD представлен двумя разложениями: 
Но мы знаем, что разложение вектора в базисе единственно! Поэтому получаем систему:  Так как
Так как  то
то  . Отсюда
. Отсюда  .
.
Таким образом, исходная система имеет решение. Значит, общая точка диагоналей АС и BD существует. Далее, из того, что  следует, что X — середина диагонали АС , а из того, что
следует, что X — середина диагонали АС , а из того, что  следует, что X — середина диагонали
следует, что X — середина диагонали 
Задача решена.
В решении аналогичных задач (на плоскости или в пространстве) этим методом всегда присутствуют такие моменты:
1. Выбор базиса (наиболее удобного для дальнейшей работы).
2. Выбор нужного нам "ключевого" вектора, который мы будем в этом базисе раскладывать двумя способами.
3. Получение двух разложений "ключевого" вектора. Сначала можно выражать его через любые векторы, но обязательно довести разложение до векторов базиса.
4. Составление и решение системы, связывающей неизвестные коэффициенты двух разложений векторов в базисе.
5. Проверка того, что полученные числовые значения для коэффициентов удовлетворяют наложенным на них условиям.
6. Окончательное истолкование полученных результатов, т. е. в безвекторной форме.
Решите по указанной схеме задачу пункта б).
5.6. Пусть  — параллелепипед. Как найти такую точку X, для которой выполняется равенство
— параллелепипед. Как найти такую точку X, для которой выполняется равенство  Единственна ли такая точка? Решите аналогичную задачу для тетраэдра. Как обобщить полученные результаты?
Единственна ли такая точка? Решите аналогичную задачу для тетраэдра. Как обобщить полученные результаты?
Как и во многих задачах, где заданы векторы, здесь можно обойтись без рисунка. Но надо сначала хорошо понять задачу. Что значит "найти точку", если мы не "привязываем" ее к той или иной геометрической фигуре? Одно из возможных толкований таково. Зафиксируем в пространстве одну точку — где угодно — (назовем ее полюсом) и неизвестную точку будем искать как конец вектора, отложенного от точки О. Но для этого потребуется все векторы, участвующие в задаче, выразить через векторы с началом в точке О. (Такая техника работы с векторами называется радиус-векторной.)
Тогда:

и исходное равенство нуль-вектору суммы этих 8 векторов перепишется в виде 
Откуда  .
.
Так как точки  вершины данного параллелепипеда, то мы можем считать известной (нарисовать) их сумму, затем их суммы, что и приводит к тому, чтобы считать вектор ОХ найденным. Но тогда мы нашли и точку X (при желании ее можно даже нарисовать!).
вершины данного параллелепипеда, то мы можем считать известной (нарисовать) их сумму, затем их суммы, что и приводит к тому, чтобы считать вектор ОХ найденным. Но тогда мы нашли и точку X (при желании ее можно даже нарисовать!).
Перейдем к единственности такой точки X. Предположим, что их больше одной и пусть  — две такие точки. Тогда верны равенства
— две такие точки. Тогда верны равенства

Вычитая из первого равенства второе, мы запишем эту разность в таком виде

или чуть иначе

Но сумма в каждой скобке равна  Поэтому приходим к равенству
Поэтому приходим к равенству  откуда
откуда  , что и означает совпадение точек
, что и означает совпадение точек  .
.
Поэтому задача о единственности решена положительно — найденная нами точка X действительно одна.
Мы решили задачу чисто векторно, без всякого рисунка. Используя рисунок, мы могли бы ускорить дело. В самом деле, искомая точка "видна невооруженным глазом" — это точка пересечения диагоналей параллелепипеда !?).
Использование векторов для доказательства единственности, видимо, — кратчайший путь к результату.
Более того, при обобщении полученного факта, векторы незаменимы. В этом легко убедиться самим.
5.7. Даны три некомпланарных вектора а, b, с. Найдите числа  и q, при которых векторы
и q, при которых векторы  с коллинеарны.
с коллинеарны.
Здесь нужно четко понимать терминологию. Некомпланарность трех векторов означает, что ни один из них не может быть представлен в виде линейной комбинации двух других. Иначе говоря, нет таких чисел а, и  что
что 
Аналогичное требование для векторов а и b. Нет таких чисел  что
что  и нет таких чисел
и нет таких чисел  что
что  . В частности, из этого следует, что среди данных векторов нет
. В частности, из этого следует, что среди данных векторов нет  Коллинеарность двух ненулевых векторов означает, что один из них (любой) получается из другого умножением на некоторое число, не равное 0.
Коллинеарность двух ненулевых векторов означает, что один из них (любой) получается из другого умножением на некоторое число, не равное 0.
Прежде всего заметим, что вектор  , как и вектор а
, как и вектор а  отличен от 0.
отличен от 0.
Если  то
то  что противоречит некомпланарности векторов а, b, с.
что противоречит некомпланарности векторов а, b, с.
Если а  то
то  и мы приходим к тому же противоречию.
и мы приходим к тому же противоречию.
Но тогда можно записать, что существует такое  при котором
при котором

Каждый из коэффициентов при векторах а, b, с в этом равенстве равен 0 — иначе мы получили бы, что хоть один из них является линейной комбинацией двух остальных, а это противоречит их некомпланарности (?). Отсюда получаем систему  Решая ее, получим, что
Решая ее, получим, что  ,
,
5.8. Пусть  Доказать, что
Доказать, что 
Как методы алгебры и анализа помогают получать результаты в геометрии, вы, разумеется, знаете. Любопытно теперь посмотреть, как можно использовать скалярное произведение для решения задач, на первый взгляд очень далеких от геометрии.
Начало решения совершенно неожиданно. Рассмотрим вектор  и еще вектор
и еще вектор  . Тогда их скалярное произведение равно
. Тогда их скалярное произведение равно  Итак, сумму
Итак, сумму  можно рассматривать как скалярное произведение векторов а и
можно рассматривать как скалярное произведение векторов а и 

А про скалярное произведение мы знаем, что для него выполняется такое неравенство:

Но

И мы имеем, что

Отсюда

или

что и требовалось доказать.
Любопытно также, что эта задача может быть решена и координатным способом с привлечением простейших геометрических представлений. Равенство  задает нам плоскость в пространстве. Неравенство
задает нам плоскость в пространстве. Неравенство  означает, что квадрат расстояния от некоторой точки до начала координат не меньше, чем
означает, что квадрат расстояния от некоторой точки до начала координат не меньше, чем  . Наша задача теперь выглядит так: доказать, что всякая точка плоскости
. Наша задача теперь выглядит так: доказать, что всякая точка плоскости  удалена от начала координат не меньше, чем на
удалена от начала координат не меньше, чем на 
Чтобы убедиться в этом, достаточно найти расстояние от начала координат до этой  Теперь мы можем заметить, что эта плоскость "высекает" на осях координат единичные отрезки, иначе говоря — ребра единичного куба с общей его вершиной — началом координат. Известно, однако, что расстояние от вершины куба до плоскости, определяемой соседними с нею вершинами составляет от диагонали куба, которая в единичном кубе равна
Теперь мы можем заметить, что эта плоскость "высекает" на осях координат единичные отрезки, иначе говоря — ребра единичного куба с общей его вершиной — началом координат. Известно, однако, что расстояние от вершины куба до плоскости, определяемой соседними с нею вершинами составляет от диагонали куба, которая в единичном кубе равна  Итак, расстояние от начала координат до нашей плоскости как раз и равно . Но тогда квадрат расстояния от начала координат до любой точки нашей плоскости не меньше, чем
Итак, расстояние от начала координат до нашей плоскости как раз и равно . Но тогда квадрат расстояния от начала координат до любой точки нашей плоскости не меньше, чем  что и требовалось доказать.
что и требовалось доказать.
5.9. Докажите, что для любых точек А, В, С, D выполниется равенство  Какие следствия можно получить из этого равенства для тетраэдра ABCD?
Какие следствия можно получить из этого равенства для тетраэдра ABCD?
и эту задачу решим, ничего не рисуя. Выберем начало 0 и каждый вектор в левой части равенства запишем, как разность векторов с началом в точке 0. Тогда выражение

после упрощения дает 0, что и требовалось установить.
Из доказанного равенства, например, вытекает, что если у тетраэдра ABCD две пары скрещивающихся ребер ортогональны, то и третья пара ребер ортогональна.
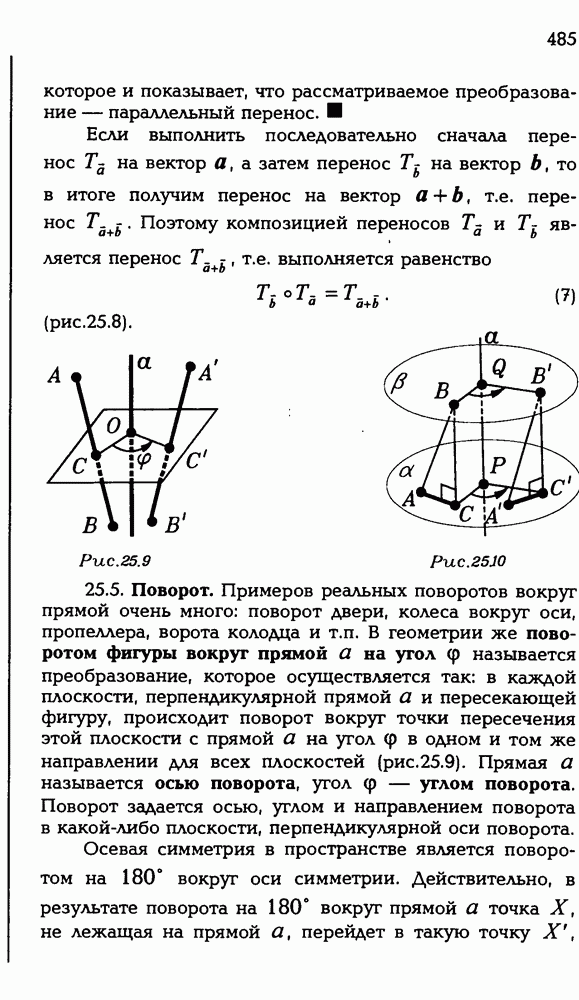
5.10. В кубе  с ребром 1 точка X лежит на диагонали
с ребром 1 точка X лежит на диагонали  причем
причем  точка Y лежит на диагонали
точка Y лежит на диагонали  причем
причем  Как вычислить
Как вычислить  угол между
угол между  угол между
угол между 
В качестве базиса выберем векторы AD, АВ, АА, (рис. Р 3.91) и все необходимые векторы будем раскладывать по этому базису.
а) Сначала формула для вычисления расстояния:


Рис. Р 3.91
Далее, разложение вектора XY по выбранному базису:

Тогда

Поэтому  Любопытно заметить, что XY оказалось равно
Любопытно заметить, что XY оказалось равно 
б) Запишем формулу для угла  между ненулевыми векторами а и
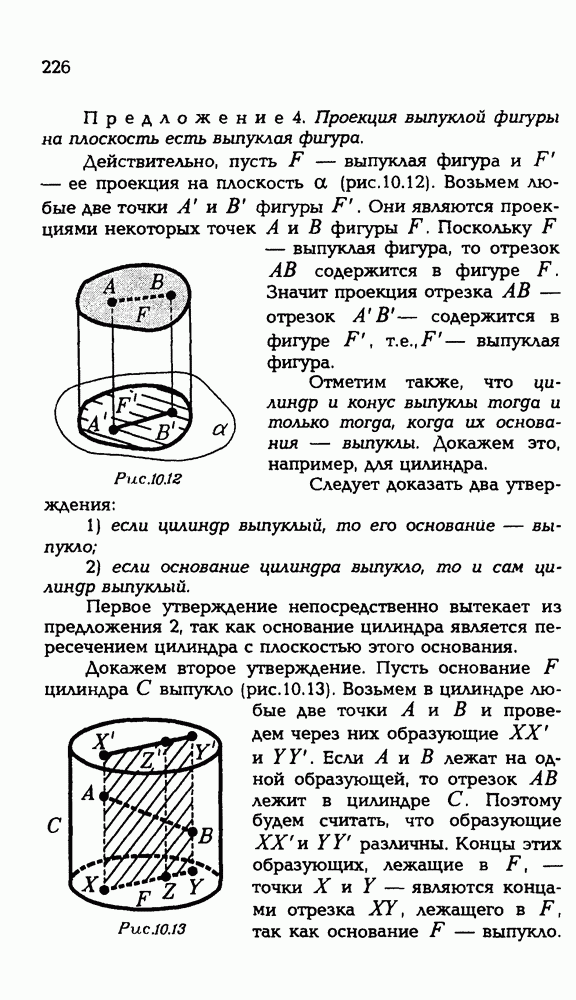
между ненулевыми векторами а и 

Про вектор XY мы знаем и разложение его по базису:

и его длину:

Для вектора  имеем:
имеем:

Поэтому угол а между XY и  определится из равенства
определится из равенства

Итак, прямые XY и  перпендикулярны.
перпендикулярны.
в) Выкладки, аналогичные предыдущим, покажут, что прямые XY и  — перпендикулярны. Сделайте их сами.
— перпендикулярны. Сделайте их сами.
Из результатов пунктов б) и в) следует, что XY — общий перпендикуляр прямых  а значит расстояние между ними равно
а значит расстояние между ними равно 
Выберите три точки с конкретными координатами. Составьте уравнение плоскости, проходящей через эти точки.
Пусть даны три точки:  Их координаты выбраны произвольно. Для составления уравнения плоскости, проходящей через эти точки, можно пойти разными путями.
Их координаты выбраны произвольно. Для составления уравнения плоскости, проходящей через эти точки, можно пойти разными путями.
Первый путь. Пишем уравнение плоскости в виде

Подставим в это уравнение координаты всех данных точек. Получим систему из трех уравнений с четырьмя неизвестными: А, В, С, D. Для ее решения один из неизвестных коэффициентов (скажем  будем считать параметром и выразим, решая систему, оставшиеся коэффициенты через этот параметр. Если эта система имеет единственное решение (т.е. существует плоскость, причем единственная, проходящая через данные точки), то коэффициенты А, В, С будут иметь вид
будем считать параметром и выразим, решая систему, оставшиеся коэффициенты через этот параметр. Если эта система имеет единственное решение (т.е. существует плоскость, причем единственная, проходящая через данные точки), то коэффициенты А, В, С будут иметь вид  Подставим эти значения А, В, С в исходное уравнение и, сократив обе его части на D (в случае D 0), придем к искомому уравнению плоскости. Самостоятельно проделайте всю эту работу в данном конкретном случае. Как вы разберетесь со случаем
Подставим эти значения А, В, С в исходное уравнение и, сократив обе его части на D (в случае D 0), придем к искомому уравнению плоскости. Самостоятельно проделайте всю эту работу в данном конкретном случае. Как вы разберетесь со случаем  ?
?
Второй путь векторный. Пусть точка  лежит в плоскости KLM. Тогда
лежит в плоскости KLM. Тогда

(Можно было выразить LT или МТ через оставшиеся векторы. Здесь надо быть аккуратным и проверить, что два вектора, через которые мы выражаем третий, действительно образуют базис плоскости. Как это сделать?)
Запишем координаты векторов. Если О — начало координат, то

значит,  аналогично
аналогично

Перепишем равенство (1) в координатном виде:

Отсюда получим 

Выразим  из каких-либо двух уравнений системы (2) — проще всего из второго и третьего уравнения. Получим:
из каких-либо двух уравнений системы (2) — проще всего из второго и третьего уравнения. Получим:

Подставим полученные значения  в первое уравнение системы (2). Окончательно, получим
в первое уравнение системы (2). Окончательно, получим 
Это и будет искомое уравнение плоскости.
5.12. Найдите расстояние между параллельными плоскостями 
Как и всякую задачу о фигурах, заданных уравнениями, ее можно решить, не прибегая к рисунку. Попробуйте отыскать такое решение — это не просто.
Мы же разберемся с этой задачей, используя рисунок (рис. Р 3.92).

Рис. Р 3.92
Обозначим первую плоскость а, отметим на осях координат точки, в которых они пересекают плоскость а , назовем их А, В, С. (Для нахождения абсциссы точки А достаточно в уравнении плоскости а положить 
Получим  . Аналогично находим координаты на осях у и
. Аналогично находим координаты на осях у и 
Обозначим вторую плоскость Р и проделаем для нее то же, что и для плоскости а — получим точки 
(Треугольники ABC и KLM называются "треугольниками следов" для плоскостей  . Отрезки АВ, ВС, АС — отрезки, по которым плоскость а пересекает координатные четверти на плоскостях
. Отрезки АВ, ВС, АС — отрезки, по которым плоскость а пересекает координатные четверти на плоскостях  — как бы "следы" плоскости а на координатных плоскостях.)
— как бы "следы" плоскости а на координатных плоскостях.)
Расстояние между параллельными плоскостями равно длине их общего перпендикуляра, причем он может быть проведен из любой точки одной их них на другую.
Здесь удобно провести перпендикуляр из точки С на плоскость KLM. Обозначим его CD (причем рисовать его не будем, рассчитывая на ваше пространственное мышление). Тогда  , где
, где  угол
угол  и осталось только найти
и осталось только найти  . Так как угол
. Так как угол  то его можно найти как угол между вектором CD и единичным вектором к оси
то его можно найти как угол между вектором CD и единичным вектором к оси 
Единичный вектор к оси z имеет координаты  , а вектор CD — это вектор нормали к каждой из данных плоскостей, а поэтому имеет координаты
, а вектор CD — это вектор нормали к каждой из данных плоскостей, а поэтому имеет координаты 
Тогда

Окончательно,

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧИТАТЕЛЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ
- § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 1.2. Двугранный угол. Угол между плоскостями.
- 1.3. Плоскость и прямая в пространстве.
- 1.4. Аксиомы стереометрии.
- 1.5. Взаимное расположение двух прямых в пространстве.
- 1.6. Признаки скрещивающихся прямых.
- 1.7. Параллельные прямые.
- 1.8. Параллельное проектирование.
- § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 2.2. О значении перпендикуляра.
- 2.3. Теорема о трех перпендикулярах.
- 2.4. Признак перпендикулярности прямой и плоскости.
- 2.5. Построение плоскости, перпендикулярной данной прямой.
- 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости.
- 2.7. Теорема о прямой, перпендикулярной плоскости.
- 2.8. Перпендикулярность плоскостей.
- 2.9. Ортогональное проектирование.
- § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 3.2. Параллельность и перпендикулярность.
- 3.3. Основная теорема о параллельных плоскостях.
- 3.4. Второй признак параллельности плоскостей.
- 3.5. Расстояние и параллельность.
- 3.6. Сонаправленность лучей и угол между прямыми.
- 3.7. Параллельность и углы.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ
- § 4. СФЕРА И ШАР
- 4.2. Взаимное положение шара и плоскости.
- 4.3. Сфера и многранники.
- 4.4. Вид и изображение шара и сферы.
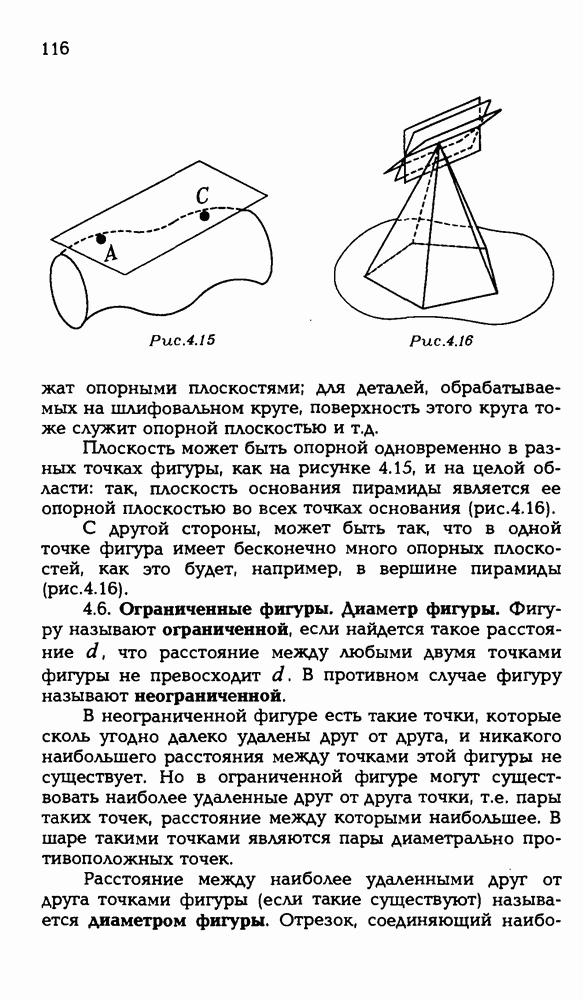
- 4.5. Опорная плоскость.
- 4.6. Ограниченные фигуры. Диаметр фигуры.
- 4.7. Опорные плоскости в концах диаметра.
- 4.8. Сфера — фигура вращения.
- 4.9. Симметрия сферы и шара.
- 4.10. Сфера — центрально симметричная фигура.
- 4.11. Сфера — зеркально симметричная фигура.
- 4.12. Отражение в плоскости и отражение в зеркале.
- § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ
- 5.2. Тригонометрия трехгранного угла.
- 5.3. Равенство трехгранных углов.
- 5.4. Сферические треугольники.
- 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников.
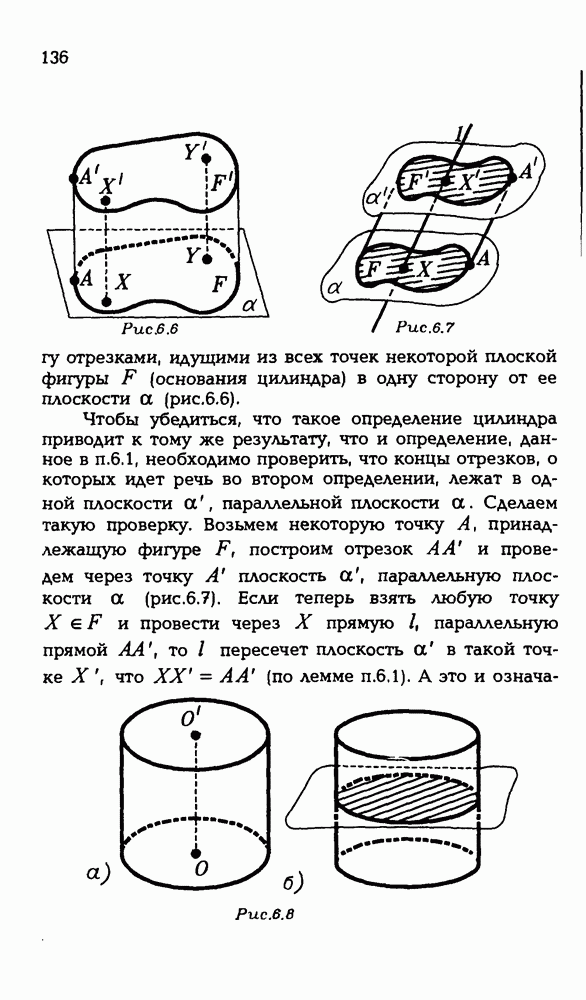
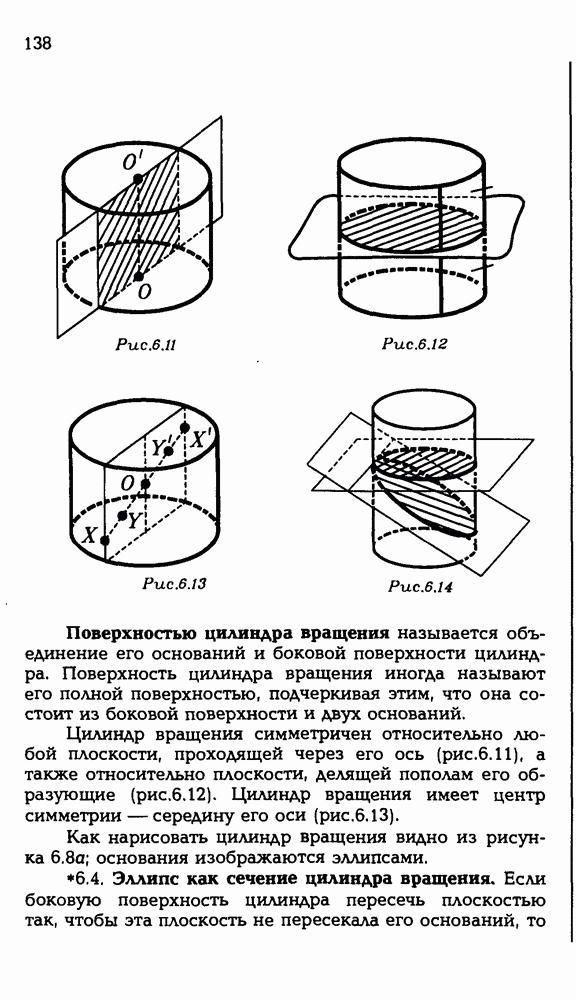
- § 6. ЦИЛИНДР
- 6.2. Другой подход к определению цилиндра.
- 6.3. Цилиндр вращения.
- 6.4. Эллипс как сечение цилиндра вращения.
- 6.5. Винтовые линии.
- 6.6. Цилиндры в практике.
- § 7. ПРИЗМА
- 7.2. Параллелепипед.
- 7.3. Прямоугольный параллелепипед.
- 7.4. Симметрия параллелепипеда.
- 7.5. Симметрия правильных призм. Поворот вокруг прямой.
- § 8. КОНУС
- 8.2. Сечение конуса плоскостью, параллельной плоскости основания.
- 8.3. Конус вращения.
- 8.4. Усеченный конус.
- § 9. ПИРАМИДА
- 9.2. Правильная пирамида.
- 9.3. Симметрия правильной пирамиды.
- 9.4. Конусы и пирамиды в практике.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ
- § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ
- 10.2. Граница и внутренность.
- 10.3. Определение тела и замкнутой плоской области.
- 10.4. Выпуклые фигуры.
- 10.5. Выпуклые тела.
- § 11. МНОГОГРАННИКИ
- 11.2. Выпуклые многогранники.
- 11.3. Теорема Эйлера.
- 11.4. Выпуклые многогранники и выпуклые оболочки.
- 11.5. Многогранная поверхность и развертка.
- 11.6. Развертка выпуклого многогранника.
- § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
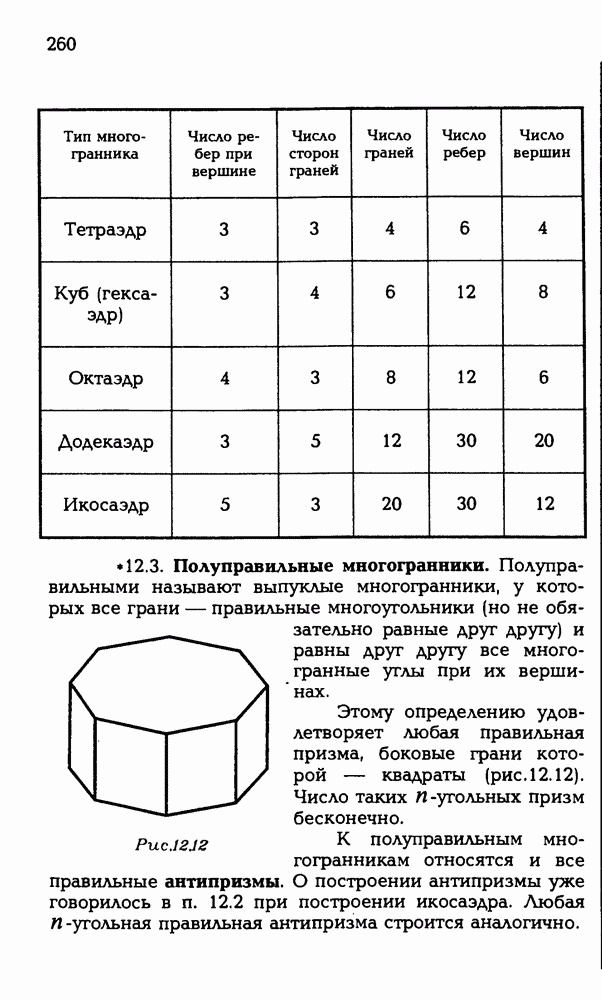
- 12.2. Классификация правильных многогранников.
- 12.3. Полуправильные многогранники.
- 12.4. Симметрия правильных многогранников.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
- § 13. ПОНЯТИЕ ОБЪЕМА
- 13.2. Определение объема.
- 13.3. Геометрические величины.
- § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА
- 14.2. Объем прямой призмы.
- § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ
- 15.2. Выражение объема через площади сечений.
- § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА
- 16.2. Объем конуса
- 16.3. Объем шара.
- 16.4. Объем тел вращения.
- 16.5. Объем шарового сегмента и шарового сектора.
- § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ
- 17.2. Площадь сферы.
- 17.3. Площадь сферических многоугольников.
- 17.4. Площадь сферического сегмента и сферического пояса.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ
- § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- 18.2. Другой способ нахождения координат точки.
- 18.3. Построение точки с данными координатами.
- 18.4. Выражение расстояния между точками.
- § 19. МЕТОД КООРДИНАТ
- 19.2. Уравнения без одной или двух координат.
- 19.3. Некоторые применения метода координат.
- § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ
- 20.2. Полярные координаты.
- 20.3. Цилиндрические координаты.
- 20.4. Сферические координаты.
- 20.5. Координатная сеть.
- § 21. ПОНЯТИЕ ВЕКТОРА
- 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов.
- 21.3. Сонаправленность и равенство векторов.
- 21.4. Признаки равенства векторов.
- 21.5. Радиус-вектор.
- § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 22.2. Разложение вектора на составляющие.
- 22.3. Умножение вектора на число.
- 22.4. Координаты вектора.
- 22.5. Равенство координат векторов и координат точек.
- 22.6. Разложение векторов по базису.
- 22.7. Ориентация базиса.
- § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ
- 23.2. Выражение скалярного произведения через координаты.
- 23.3. Свойства скалярного умножения.
- 23.4. Применения скалярного умножения.
- 23.5. Скалярное произведение и проекции.
- § 24. ВЕКТОРНЫЙ МЕТОД
- 24.2. Общее уравнение плоскости.
- 24.3. Векторное задание отрезка.
- 24.4. Некоторые теоремы о треугольниках и тетраэдрах.
- 24.5. Центр масс системы материальных точек.
- 24.6. Центры масс и выпуклые многогранники.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 6. ПРЕОБРАЗОВАНИЯ
- 25.1. Преобразования фигур.
- 25.2. Определения движения и равенства фигур.
- 25.3. Преобразования симметрии.
- 25.4. Параллельный перенос.
- 25.5. Поворот.
- § 26. СВОЙСТВА ДВИЖЕНИЙ
- 26.2. Общие свойства движений.
- 26.3. Теоремы о задании движений.
- 26.4. Неподвижные точки движений.
- 26.5. Два рода движений.
- 26.6. Теорема подвижности пространства.
- 26.7. Композиция отражений в плоскости.
- § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА
- 27.2. Движения первого рода как винтовые движения.
- 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот.
- 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения.
- § 28. ПОДОБИЕ
- 28.2. Гомотетия.
- 28.3. Свойства подобия.
- 28.4. Группы преобразований.
- § 29. ИНВЕРСИЯ
- 29.2. Аналитическое задание инверсии.
- 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии.
- 29.4. Сохранение величин углов при инверсии.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ОТВЕТЫ И УКАЗАНИЯ
- ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ