| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЗАДАЧИ С РЕШЕНИЯМИ
ЗАДАЧИ К § 1
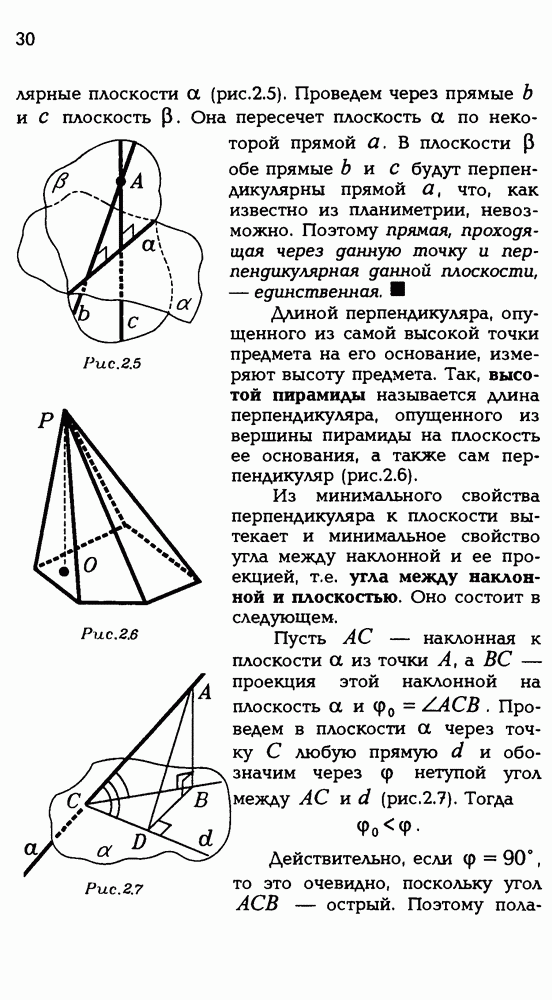
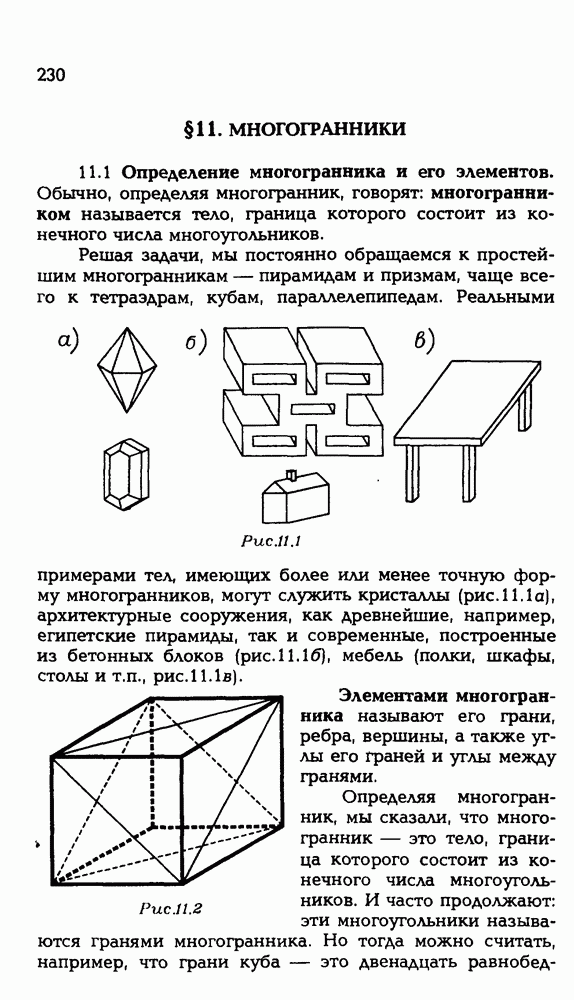
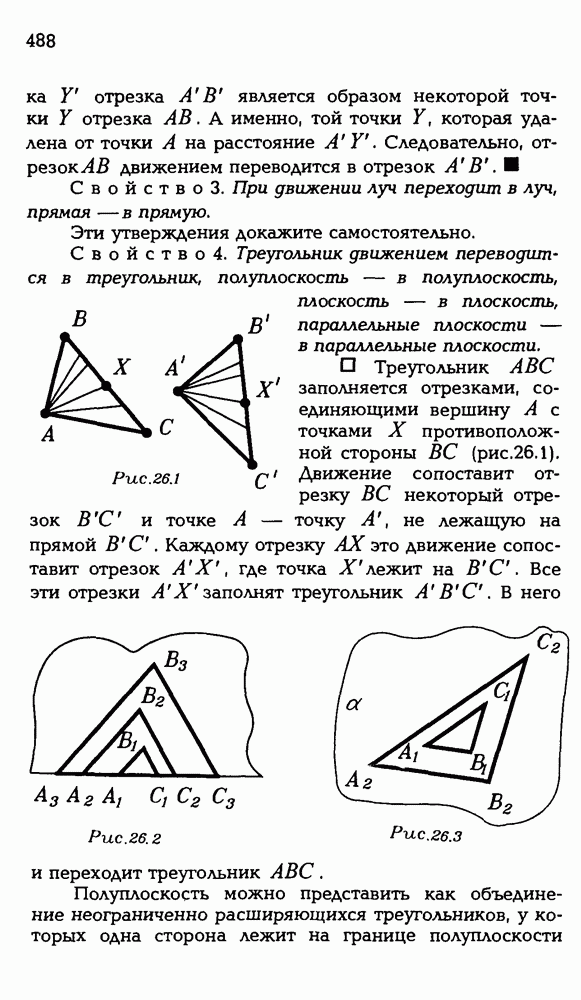
1.1. Пусть РАВС — тетраэдр. Нарисуйте его сечение плоскостью (XYZ), если точка X лежит внутри ребра РВ, точка  лежит внутри ребра АС, точка Z лежит внутри ребра АВ.
лежит внутри ребра АС, точка Z лежит внутри ребра АВ.
Сечение многогранника — многоугольник. Он определяется своими вершинами. Его вершинами являются точки, в которых плоскость сечения пересекается с ребрами многогранника. Если какие-то из этих точек пересечения лежат в одной грани многогранника, то соединив их, получим сторону

Рис. Р3.1

Рис. Р3.2
комого сечения. Естественно начинать построение сечения с проведения таких отрезков, если они есть. Поэтому проведем отрезки XZ и YZ — две стороны искомого сечения (рис. Р3.1).
Для нахождения других его сторон можно действовать по-разному. Вот один из способов. Посмотрим, где плоскость сечеиия пересекает прямые, содержащие ребра тетраэдра. В данном случае нас могут интересовать прямые ВС, PC, РА. Выберем одну из них, пусть это будет (РА). Внимание! Сейчас главный момент решения! Эта прямая будет пересекать плоскость сечения в той точке, в которой она пересекает прямую, лежащую в плоскости сечения. Найдем точку пересечения  — эти прямые лежат в плоскости РА В и, судя по рисунку (?), не являются параллельными.
— эти прямые лежат в плоскости РА В и, судя по рисунку (?), не являются параллельными.
Пусть Т — общая точка прямых РА и  а значит, точка, в которой прямая РА пересекается с плоскостью
а значит, точка, в которой прямая РА пересекается с плоскостью 
Точка Т дает нам также общую точку плоскости сечения и плоскости РАС — ведь (РА) лежит в [РАС). А одна такая точка, общая для (РАС) и плоскости сечения, уже есть — это точка . Тогда прямая YT является общей для этих плоскостей. На нашем рисунке она пересекает ребро  Обозначим точку их пересечения через
Обозначим точку их пересечения через  . Теперь, осталось только соединить точку К с точкой
. Теперь, осталось только соединить точку К с точкой  , и нужное сечение нарисовано.
, и нужное сечение нарисовано.
Можно было бы действовать несколько иначе. Например, можно сначала найти точку пересечения прямой ВС с плоскостью сечения — результат был бы один и тот же (?).
И, наконец, о том, почему у нас получилось такое построение. Ведь могло бы оказаться, что тех точек пересечения, которые мы ищем, просто нет! Прямая РА вполне может быть параллельна
(XZ) при соответствующем выборе точек. Как быть тогда?
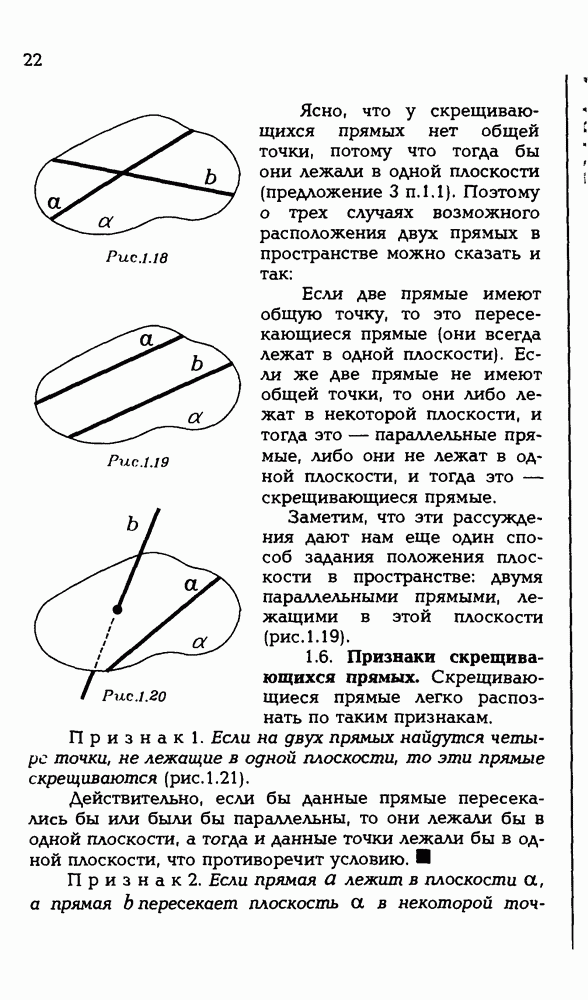
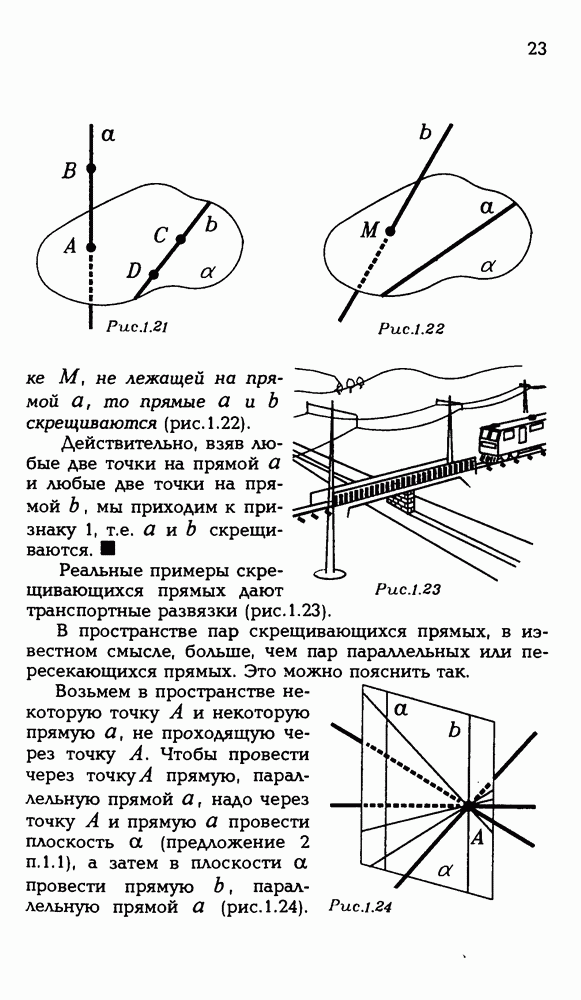
1.2. Дано к попарно скрещивающихся прямых. Докажите, что: а) существуют точки, не лежащие на этих прямых;
б) существует плоскость, которая пересекает каждую из них;
в) существует прямая, которая скрещивается с каждой из них.
а) Проведем плоскость через одну из данных прямых. Остальные прямые либо пересекают эту плоскость, либо не имеют с ней общих точек — других случаев расположения быть не может. Как бы там ни было, в проведенной плоскости найдутся точки, не принадлежащие данным прямым (?).
б) Выберем точку в пространстве и проведем через нее прямые, параллельные каждой из данных прямых. Найдется плоскость, которая пересекает все эти прямые (?). Но тогда она пересекает и все данные прямые (?).
А вот решение, основанное на наглядных соображениях. Через одну из данных прямых проведем плоскость. Если нам повезет, то она будет пересекать все остальные данные прямые. Если нет и найдутся прямые, которых она не пересекает, то будем поворачивать нашу плоскость вокруг прямой, через которую она была проведена, пока не добьемся нужного нам положения. Осталось добиться того, чтобы плоскость пересекала и первоначально взятую прямую. Но ведь таким поворотом этого не добиться! Как же быть? А мы эту плоскость “чуть-чуть пошевелим" так, чтобы она уже не содержала первую прямую, а пересекала ее — этого можно добиться также поворотом, но только вокруг другой прямой (какой?). Ясно, что при таком "малом шевелении" можно считать, что взаимное положение плоскости и каждой из этих прямых не изменилось. Значит задача решена.
в) В плоскости, построенной в пункте б), возьмем прямую, которая проходит мимо всех точек пересечения этой плоскости с данными прямыми. Такая прямая всегда найдется (?). Она и будет искомой согласно одному из признаков скрещивающихся прямых.
1.3. Пусть  — точки пространства. Известно, что расстояния
— точки пространства. Известно, что расстояния  Может ли
Может ли 
Вопрос задачи на первый взгляд выглядит странно. В самом деле, а почему расстояние  не может равняться
не может равняться 
Иначе говоря, а какие могут быть на величину  ограничения? Точки
ограничения? Точки  будем считать вершинами тетраэдра
будем считать вершинами тетраэдра
Вот и нарисуем тетраэдр, у Которого все ребра, включая BD, отвечают условию задачи. И все.
Здесь уместно остановиться и подумать...
Полезно, например, найти аналогию с планиметрией. Фигура плоскости, аналогичная тетраэдру, — треугольник. И вы помните, конечно, что стороны треугольника не могут быть любыми отрезками — сумма двух любых из них должна быть больше третьего (так называемое неравенство треугольника). Значит, существование треугольника, стороны которого равны данным отрезкам, должно быть доказано.
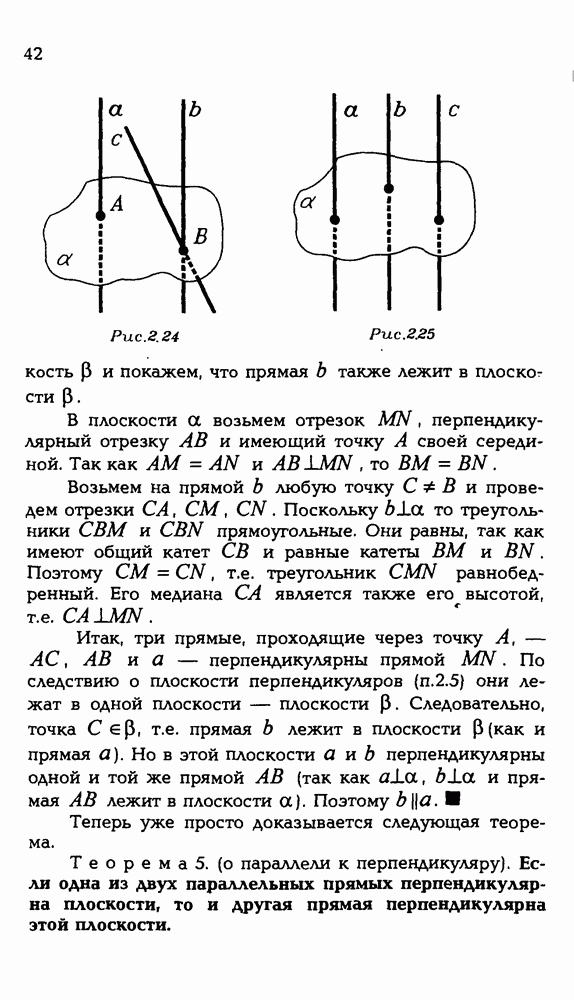
Так же обстоят дела и с тетраэдром. Откуда мы знаем, что существует тетраэдр с любыми ребрами? Между прочим, ясно, что с любыми ребрами и не существует. Ведь каждая его грань
— треугольник, а значит, для его ребер, лежащих в каждой грани, должно выполняться неравенство треугольника.
В данной задаче для ребер каждой грани неравенство треугольника выполняется. Но может быть, есть и другие условия, необходимые для существования тетраэдра с шестью произвольными ребрами? Аналогия с треугольником оказалась полезной, но все-таки тетраэдр не треугольник.
Задачу о существовании тетраэдра с шестью заданными ребрами нам пока не решить, мы сделаем это позже. Но с данной задачей все же попробуем справиться.
Прежде всего заметим, что вычислить  исходя из условий задачи, невозможно. Для того, чтобы в этом убедиться, достаточно мысленно вращать треугольник ACD вокруг
исходя из условий задачи, невозможно. Для того, чтобы в этом убедиться, достаточно мысленно вращать треугольник ACD вокруг  , а треугольник АБС оставить неподвижным. Очевидно, что все данные в задаче от этого не изменяются,
, а треугольник АБС оставить неподвижным. Очевидно, что все данные в задаче от этого не изменяются,  меняться будет.
меняться будет.
Далее заметим, что треугольники ACD и ABC прямоугольные. (По существу это обстоятельство не принципиально
— они могли бы быть и другими, от этого содержание задачи и ее решение не изменяются.)
Посмотрим теперь, какие значения может принимать 
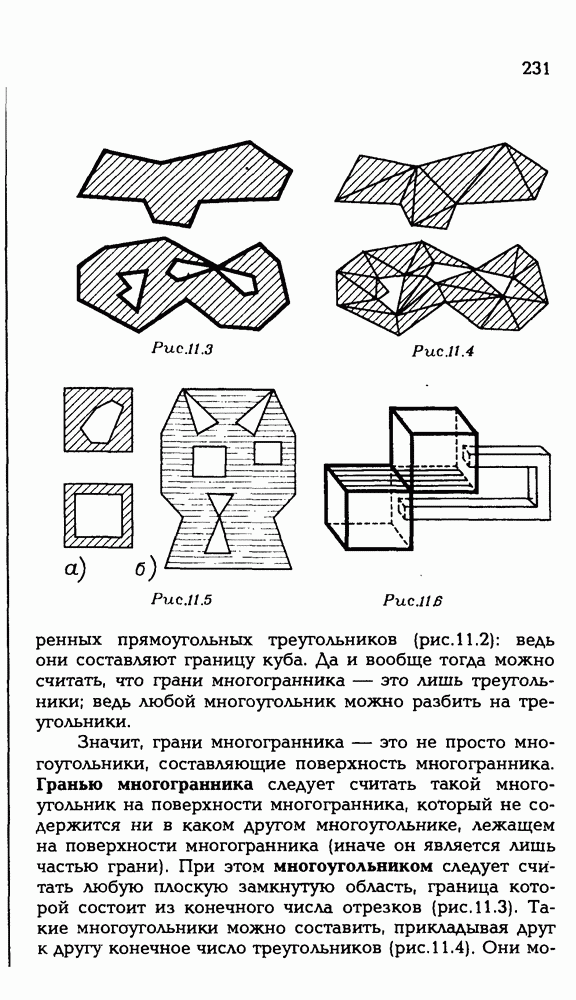
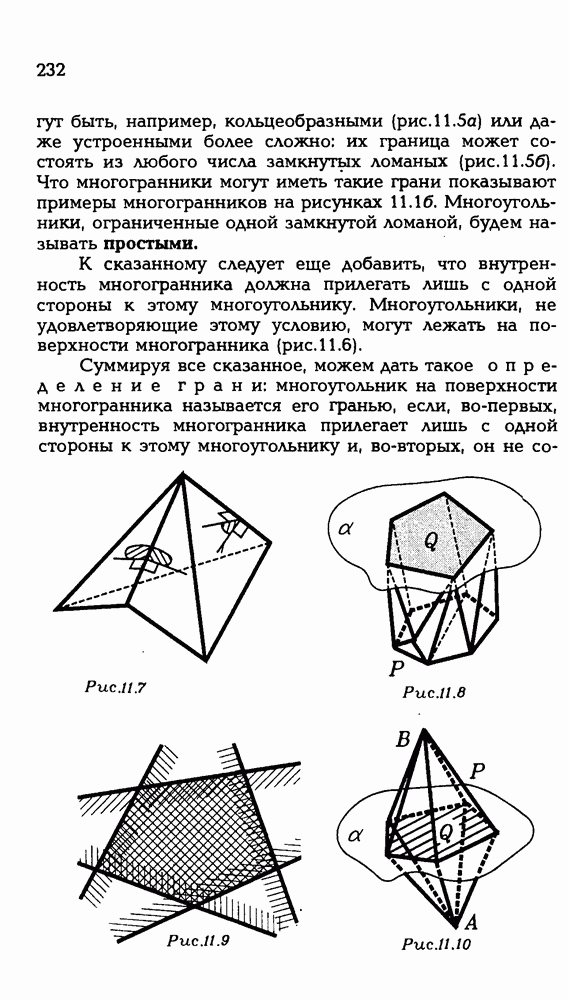
Для этого зафиксируем два положения треугольника  когда его плоскость совпадает с плоскостью ЛВС . Первое положение, когда точка D находится с той же стороны от (АС), что и точка В (рис. Р З.З). Второе положение, когда она находится с другой стороны от (АС), нежели точка В (рис. Р 3.4). В первом положении
когда его плоскость совпадает с плоскостью ЛВС . Первое положение, когда точка D находится с той же стороны от (АС), что и точка В (рис. Р З.З). Второе положение, когда она находится с другой стороны от (АС), нежели точка В (рис. Р 3.4). В первом положении  . Во втором положении
. Во втором положении  Первое число меньше
Первое число меньше  , а второе число больше 4.
, а второе число больше 4.

Рис. Р 3.3.

Рис. Р 3.4.
Значит, при каком-то положении треугольника 
Задача решена.
Обратите внимание на то, что нам неважно, как изменяется  увеличивается или уменьшается. Важным для решения оказалось то, что число 4 находится между двумя значениями
увеличивается или уменьшается. Важным для решения оказалось то, что число 4 находится между двумя значениями  Отсюда ясно, что вместо 4 мы могли бы взять любое число, которое находится в границах от 3 до
Отсюда ясно, что вместо 4 мы могли бы взять любое число, которое находится в границах от 3 до  — решение было бы таким же.
— решение было бы таким же.
1.4. В правильном тетраэдре РАВС с ребром 2 через точку К — середину ребра РА проводится сечение, параллельное (ВС). В каких границах находятся его площадь и периметр?
Мы приводим решение этой несложной задачи, ибо в ней есть некоторые "тонкости".
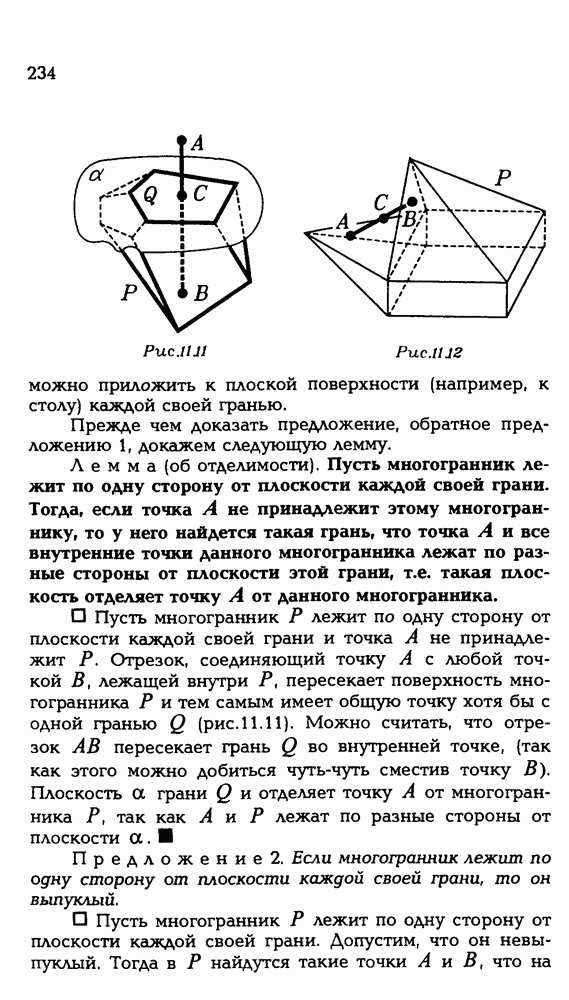
Прежде всего, какова форма сечения? Для того чтобы установить это, полезно (но не обязательно) представить себе некую переменную плоскость, удовлетворяющую условию задачи. В нашем случае такой плоскостью является, например, плоскость, проходящая через прямую  (рис.
(рис.  ). Представим себе, что такая плоскость вращается вокруг (KL). Что же мы увидим в сечении тетраэдра такой плоскостью?
). Представим себе, что такая плоскость вращается вокруг (KL). Что же мы увидим в сечении тетраэдра такой плоскостью?

Рис. Р 3.5
Мы увидим треугольник с вершиной в точке , одна из сторон которого параллельна (ВС) (?). Такая сторона может лежать в грани ABC и в грани РВС. При более внимательном
взгляде обнаруживается, что треугольник этот равнобедренный и точка К — его вершина (?).
Треугольник КВС для большей общности также будем считать одним из возможных сечений. Эта оговорка необходима, так как по определению прямая, лежащая в плоскости, не является ей параллельной. А у нас прямая ВС лежит в плоскости КВС . Эту оговорку (а также ей аналогичную для переменной плоскости, параллельной некоторой плоскости) примем на все задачи подобного рода.
Кроме того, нельзя забывать о плоскости  Сечение тетраэдра этой плоскостью — отрезок РА .
Сечение тетраэдра этой плоскостью — отрезок РА .
Итак, сечение тетраэдра в этой задаче — равнобедренный треугольник или отрезок. Можно договориться для некоторой общности результатов, что площадь отрезка принимается равной  (С периметром отрезка дело обстоит сложнее, но содержательно это уже ничего не добавляет.)
(С периметром отрезка дело обстоит сложнее, но содержательно это уже ничего не добавляет.)
Разберемся теперь с площадью треугольника сечения. Пусть MN — переменное основание сечения, КО — переменная его высота. (Здесь надо объяснить, почему точка О находится на отрезке АТ, где точка Г — середина ребра ВС 
Легко доказать, что наибольшее значение  равно
равно  а наибольшее значение
а наибольшее значение  равно
равно  Тогда наибольшее значение площади сечения равно площади треугольника КВС (?).
Тогда наибольшее значение площади сечения равно площади треугольника КВС (?).
Наименьшего значения площадь треугольного сечения не достигает, ибо основание  а значит, и площадь треугольника KMN (при ограниченности высоты КО) можно сделать сколь угодно малыми.
а значит, и площадь треугольника KMN (при ограниченности высоты КО) можно сделать сколь угодно малыми.
Перейдем к периметру сечения. Он равен 
Наибольшее значение  равно
равно  а наибольшее значение
а наибольшее значение  равно
равно  Поэтому наибольшее значение периметра сечения — периметр треугольника КВС. Вычислите его.
Поэтому наибольшее значение периметра сечения — периметр треугольника КВС. Вычислите его.
Наименьшее значение периметра сразу определить  Без выкладок тут не обойтись. Пусть
Без выкладок тут не обойтись. Пусть  Тогда
Тогда  а периметр —
а периметр — 
С использованием производной получаем, что наименьшее значение данной функции на промежутке  достигается в точке
достигается в точке  (Разумеется, вам нужно самостоятельно проделать все необходимые выкладки.)
(Разумеется, вам нужно самостоятельно проделать все необходимые выкладки.)
Но при  треугольное сечение перестает существовать, оно, как говорят, вырождается в отрезок РА (именно поэтому мы считаем, что х > 0, а не х > 0). А для нас представляет интерес, повторяем, именно треугольные сечения. Значит, нам приходится считать, что периметр сечения наименьшего значения не достигает.
треугольное сечение перестает существовать, оно, как говорят, вырождается в отрезок РА (именно поэтому мы считаем, что х > 0, а не х > 0). А для нас представляет интерес, повторяем, именно треугольные сечения. Значит, нам приходится считать, что периметр сечения наименьшего значения не достигает.
Итак, ответ: площадь треугольного сечения лежит в границах от 0 до  не включая 0; периметр треугольного сечения лежит в границах от 2 до
не включая 0; периметр треугольного сечения лежит в границах от 2 до  не включая
не включая 
ЗАДАЧИ К § 2
1.5. Какую фигуру в пространстве образуют все точки, равноудаленные от двух данных точек?
Искомой фигурой на плоскости является прямая, перпендикулярная отрезку, соединяющему данные точки, и проходящая через его середину. Эту прямую называют серединным перпендикуляром отрезка. Она является осью симметрии двух данных точек.
Перейдем к пространству. В каждой плоскости, проходящей через данные точки А и В, искомой фигурой является ось симметрии отрезка АВ . Таких плоскостей бесконечно много, поэтому искомая фигура будет состоять из бесконечного множества всех этих осей симметрии. Можно себе представить, что искомая фигура получена как бы вращением одной из этих осей вокруг (АВ).
Таким образом, из соображений наглядности можно предположить, что искомой фигурой является плоскость. Проходит она через середину отрезка АВ (точку О) и перпендикулярна отрезку  Назовем эту плоскость а.
Назовем эту плоскость а.
Теперь убедимся в этом, доказав два утверждения:
1. Каждая точка X плоскости а равноудалена от 
2. В плоскости а содержатся все точки, равноудаленные от точек А и В. Иначе говоря, если точка Y такова, что YA — YB, то она лежит в плоскости а.
Докажем утверждение 1.

Рис. Р 3.6
Если точка  то она лежит на прямой ХО , принадлежащей плоскости а (рис. Р 3.6а). Так как
то она лежит на прямой ХО , принадлежащей плоскости а (рис. Р 3.6а). Так как  , то
, то  Получилось, что прямая ХО перпендикулярна отрезку АВ и проходит через его середину, т.е. является его осью симметрии. Но тогда
Получилось, что прямая ХО перпендикулярна отрезку АВ и проходит через его середину, т.е. является его осью симметрии. Но тогда 
А теперь докажем утверждение 2.
Пусть точка Y такова, что  Рассмотрим плоскость AYB (рис. Р 3.6б). Так как
Рассмотрим плоскость AYB (рис. Р 3.6б). Так как  то Y лежит на оси симметрии отрезка АВ, находящейся в плоскости
то Y лежит на оси симметрии отрезка АВ, находящейся в плоскости  Иными словами,
Иными словами,  . Мы знаем, что все перпендикуляры, проведенные к данной прямой в данной ее точке, лежат в одной плоскости — той, которая перпендикулярна прямой в этой точке. В нашем случае такой плоскостью и является плоскость а. Значит, (YO) лежит в а . Но тогда и точка Y лежит в плоскости а.
. Мы знаем, что все перпендикуляры, проведенные к данной прямой в данной ее точке, лежат в одной плоскости — той, которая перпендикулярна прямой в этой точке. В нашем случае такой плоскостью и является плоскость а. Значит, (YO) лежит в а . Но тогда и точка Y лежит в плоскости а.
Второе утверждение можно доказать иначе, рассмотрев пересечение плоскости A YB и плоскости ОС. Попробуйте это сделать самостоятельно.
В планиметрии результат этой задачи понадобился для построения окружности, описанной около многоугольника. Стереометрический вариант этой задачи понадобится нам в дальнейшем курсе, когда мы будем описывать сферу около многогранника. А
1.6. Докажите, что существует точка, равноудаленная от всех вершин правильного тетраэдра. Обобщите это утверждение.
Пусть РАВС — правильный тетраэдр, а точка О — центр его основания.
1) Докажите, что углы  равны.
равны.
2) Возьмите любую точку X на отрезке PQ и докажите, что расстояния ХА , ХВ , ХС равны.
3) Сравните расстояния ХА и ХР при двух положениях точки X: когда она совпадает с Р и когда она совпадает с  Используйте соображения непрерывности.
Используйте соображения непрерывности.
Нужное нам положение точки X на отрезке PQ можно установить с помощью вычислений. Прежде всего обозначьте ребро тетраэдра, например, через d (можно было бы его считать равным 1 или 2). Вычислите  Теперь можно доказать, что треугольник PAQ прямоугольный. Для этого из треугольника РАК (точка К — середина ребра ВС
Теперь можно доказать, что треугольник PAQ прямоугольный. Для этого из треугольника РАК (точка К — середина ребра ВС  найдите угол РАК (вычислив его косинус). Потом из треугольника PAQ установите, что угол PQA прямой. Точка X , находясь на отрезке
найдите угол РАК (вычислив его косинус). Потом из треугольника PAQ установите, что угол PQA прямой. Точка X , находясь на отрезке  равноудалена от вершин
равноудалена от вершин  — это мы уже доказали. Считая расстояние от точки X до точки Р неизвестным, составьте и решите уравнение для его нахождения.
— это мы уже доказали. Считая расстояние от точки X до точки Р неизвестным, составьте и решите уравнение для его нахождения.
Обобщение трудностей не вызовет, но при его доказательстве вас, вероятно, будет поджидать сюрприз.
Как вы думаете, единственна ли такая точка? Как вы обоснуете свое предположение? А
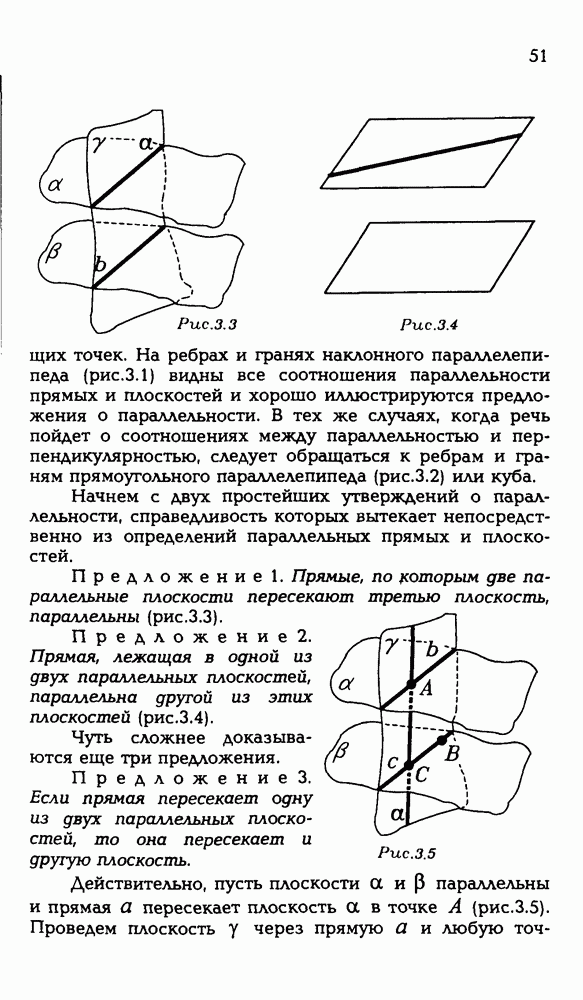
1.7. Через середины сторон треугольника проведены плоскости, перпендикулярные этим сторонам. Докажите, что общая прямая этих плоскостей перпендикулярна плоскости треугольника. Обобщите это утверждение.
Пусть ABC — данный треугольник, точка К — середина стороны АС , точка L — середина стороны ВС , точка М — середина стороны АВ . Плоскость, перпендикулярную (АС) и проходящую через К, обозначим а, плоскость, перпендикулярную (ВС) и проходящую через  а плоскость, перпендикулярную (АВ) и проходящую через М, — у (рис. Р 3.7).
а плоскость, перпендикулярную (АВ) и проходящую через М, — у (рис. Р 3.7).

Рис. Р 3.7
Прежде всего докажем, что все эти плоскости имеют общую прямую. Возьмем сначала плоскости  . Каждая из
. Каждая из
них пересекает (ABC). Прямые пересечения этих плоскостей с (ABC) являются серединными перпендикулярами к отрезкам АС и ВС (?), а потому имеют общую точку. Так как  имеют общую точку, то они имеют общую прямую — назовем ее а. (Разумеется,
имеют общую точку, то они имеют общую прямую — назовем ее а. (Разумеется,  не совпадают
не совпадают 
Докажем, что прямая а лежит в плоскости у. Так как  то все точки прямой а равноудалены от точек А и С . Так как
то все точки прямой а равноудалены от точек А и С . Так как  то все точки прямой а равноудалены от точек С и В . Отсюда следует, что все точки прямой а равноудалены от точек А и В, а потому прямая а лежит в плоскости, перпендикулярной (АВ) и проходящей через точку М — середину отрезка АВ , т.е. в плоскости у.
то все точки прямой а равноудалены от точек С и В . Отсюда следует, что все точки прямой а равноудалены от точек А и В, а потому прямая а лежит в плоскости, перпендикулярной (АВ) и проходящей через точку М — середину отрезка АВ , т.е. в плоскости у.
Теперь докажем, что  . Так как
. Так как  , то
, то  . Так как
. Так как  то
то  . Но тогда (ABC) перпендикулярна прямой пересечения плоскостей
. Но тогда (ABC) перпендикулярна прямой пересечения плоскостей  , т.е. прямой а. .
, т.е. прямой а. .
Теперь займемся обобщениями. В этой задаче естественно вместо треугольника взять многоугольник. Самостоятельно сформулируйте и докажите это общее утверждение. Обобщая, можно двинуться и в другом направлении, отбросив условие, что плоскости проходят именно через середины сторон треугольника. Как будет выглядеть это обобщение и как оно доказывается? И, наконец, можно объединить и первое, и второе обобщение. Сделайте это.
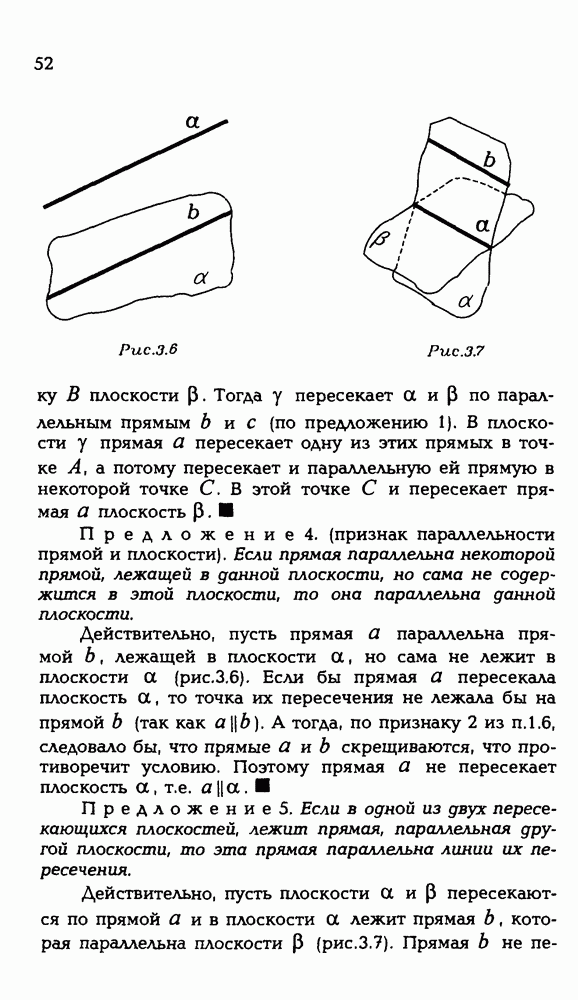
1.8. Точка А лежит в плоскости а . На этой плоскости взяли прямую а, не проходящую через А, и провели к ней перпендикуляр АВ . Через точку В , перпендикулярно к прямой а, провели другую прямую — ВС. Из точки А в плоскости ABC провели  перпендикулярно (ЛД). Докажите, что
перпендикулярно (ЛД). Докажите, что  .
.
Любопытно, что перпендикулярность (AD) и а можно доказать, используя только признак перпендикулярности прямой и плоскости, да еще понадобится теорема Пифагора.
Уже известно (по условию), что  Но
Но  Осталось найти еще одну прямую плоскости а, перпендикулярную (AD), Такой прямой является прямая, проходящая через точку А и пересекающая прямую а в любой точке X,
Осталось найти еще одну прямую плоскости а, перпендикулярную (AD), Такой прямой является прямая, проходящая через точку А и пересекающая прямую а в любой точке X,
 (рис. Р 3.8). Итак, докажем, что
(рис. Р 3.8). Итак, докажем, что  . Для этого достаточно убедиться в том, что
. Для этого достаточно убедиться в том, что

Из соответствующих прямоугольных треугольников следуют такие соотношения:

Из этих равенств можно получить и требуемое соотношение (?). Доказательство закончено, но над ним стоит поразмыслить. Мы ведь хотели найти в плоскости а еще одну, кроме (АВ), прямую, проходящую через А и перпендикулярную (AD). А фактически нашли их бесконечное множество, ведь точка X — любая на прямой а, кроме В . А так как  по условию, то получается, что (AD) перпендикулярна почти всем прямым плоскости а , проходящим через А , кроме одной — той, которая параллельна а. Если удастся доказать эту последнюю перпендикулярность, то получится, что мы доказали перпендикулярность и а без ссылки на признак.
по условию, то получается, что (AD) перпендикулярна почти всем прямым плоскости а , проходящим через А , кроме одной — той, которая параллельна а. Если удастся доказать эту последнюю перпендикулярность, то получится, что мы доказали перпендикулярность и а без ссылки на признак.

Рис. Р 3.8
Для доказательства того, что (AD) перпендикулярна этой "последней" прямой, назовем ее b, есть разные идеи. Вот одна из них.
Будем проводить прямые (АХ) так, чтобы угол между (АХ) и b делался сколь угодно малым. В этом смысле прямая АХ будет все "ближе” к прямой b. Но если сколько угодно "близкая" к b прямая образует с (AD) прямой угол, то и сама b также будет образовывать с (AD) прямой угол.
Реализуем эту идею. Для доказательства перпендикулярности (DA) и b достаточно взять любую точку Y прямой b, не совпадающую с А , и доказать, что 
Возьмем такую точку У . Затем в плоскости  не на прямой b) возьмем точку
не на прямой b) возьмем точку  такую, что
такую, что  . В силу того, что угол ZAY может быть сколь угодно мал, расстояние между точками Z и У может быть сколь угодно мало (?).
. В силу того, что угол ZAY может быть сколь угодно мал, расстояние между точками Z и У может быть сколь угодно мало (?).
Так как  , то
, то  . В треугольнике
. В треугольнике  Значит,
Значит,  . И так как
. И так как  сколь угодно мало, то
сколь угодно мало, то  , что и требовалось.
, что и требовалось.
1.9. Лучи ОА и ОВ лежат в плоскости а . Луч ОС образует с ними равные углы. Какое положение на плоскости а занимает проекция луча ОС на эту плоскость?

Рис. Р 3.9
Конфигурация лучей, заданная в условии, нам уже встречалась. Если нарисовать правильную пирамиду СОАВ с вершиной в точке С, то  . Так как точка С проектируется в центр основания Q, то луч ОС проектируется в луч OQ (рис. Р 3.9а). Луч OQ является биссектрисой угла АО В, так как пирамида правильная. Поэтому можно предположить, что проекцией луча ОС будет биссектриса угла АО В не только при угле АО В , равном
. Так как точка С проектируется в центр основания Q, то луч ОС проектируется в луч OQ (рис. Р 3.9а). Луч OQ является биссектрисой угла АО В, так как пирамида правильная. Поэтому можно предположить, что проекцией луча ОС будет биссектриса угла АО В не только при угле АО В , равном  , но и в общем случае. Если посмотреть на данную конфигурацию как бы сверху, в направлении перпендикуляра из любой точки луча ОС на плоскость АО В, то в силу равенства углов СОА и СОВ увидим луч ОС как биссектрису угла АОВ.
, но и в общем случае. Если посмотреть на данную конфигурацию как бы сверху, в направлении перпендикуляра из любой точки луча ОС на плоскость АО В, то в силу равенства углов СОА и СОВ увидим луч ОС как биссектрису угла АОВ.
Теперь, когда стало ясно, что нужно доказывать, перейдем к самому доказательству. Пусть точка С, — проекция точки С
на плоскость АОВ, тогда луч ОС, — проекция луча ОС. Мы хотим доказать, что  Равенство углов чаще всего доказывается на основании равенства треугольников, проще всего прямоугольных треугольников. Такие легко построить, проведя
Равенство углов чаще всего доказывается на основании равенства треугольников, проще всего прямоугольных треугольников. Такие легко построить, проведя  (рис. Р 3.9б). Для доказательства их равенства достаточно получить, что
(рис. Р 3.9б). Для доказательства их равенства достаточно получить, что  Эти отрезки лежат в треугольниках ОСК и OCL (рис. Р 3.9в) Треугольники ОСК и ОСЬ также прямоугольные
Эти отрезки лежат в треугольниках ОСК и OCL (рис. Р 3.9в) Треугольники ОСК и ОСЬ также прямоугольные  по теореме о трех перпендикулярах, аналогично
по теореме о трех перпендикулярах, аналогично  имеют общую гипотенузу ОС и равные углы СОК и COL (по условию). Из равенства этих треугольников следует, что
имеют общую гипотенузу ОС и равные углы СОК и COL (по условию). Из равенства этих треугольников следует, что  Теперь, перейдя к треугольникам
Теперь, перейдя к треугольникам  и
и  получим, что углы
получим, что углы  равны, что и требовалось.
равны, что и требовалось.
В этом доказательстве мы полагали, что точка С, находится внутри угла АОВ, но может быть и так, что С, совпадает с О или С, лежит вне угла АОВ. Не может быть только такого положения точки  когда она лежит внутри стороны угла или внутри ее продолжения. (Подумайте почему.) Подумайте, какое положение на плоскости АОВ будет занимать луч ОС, в этих случаях.
когда она лежит внутри стороны угла или внутри ее продолжения. (Подумайте почему.) Подумайте, какое положение на плоскости АОВ будет занимать луч ОС, в этих случаях.
Подумайте также над тем, как зависит положение точки С, на плоскости АОВ от величины данных равных углов СОА и 
1.10. Прямая b лежит в плоскости а , а прямая а пересекает а в некоторой точке прямой b. Пусть прямая а, — проекция  Тогда
Тогда

Какие следствия отсюда можно получить? Как эту формулу можно обобщить?
Пусть прямые а, а, и b проходят через точку  (рис.
(рис.  ). Построим прямоугольные треугольники с заданными углами. Для этого спроектируем любую точку
). Построим прямоугольные треугольники с заданными углами. Для этого спроектируем любую точку  на плоскость а, а затем полученную точку А, спроектируем на прямую b и получим точку В (рис.
на плоскость а, а затем полученную точку А, спроектируем на прямую b и получим точку В (рис.  ). На основании теоремы о ближайшей точке, точка В — проекция точки А на прямую b. (Все это можно было бы обосновать, сославшись на теорему о трех перпендикулярах.)
). На основании теоремы о ближайшей точке, точка В — проекция точки А на прямую b. (Все это можно было бы обосновать, сославшись на теорему о трех перпендикулярах.)

Рис. Р 3.10
Теперь

Из треугольника  имеем:
имеем:

Из треугольника  имеем:
имеем:

Из треугольника  имеем:
имеем:

Перемножив равенства (а) и (б), получим:

что и требовалось.
Получили формулу, предположив, что прямые а, и b не являются перпендикулярными. Проверьте, будет ли верна формула в случае, когда 
Перейдем к следствиям из формулы. Из нее можно выразить  или
или  Особенно важно в дальнейшем выражение для
Особенно важно в дальнейшем выражение для  так как оно даст возможность вычислить угол между прямой и плоскостью.
так как оно даст возможность вычислить угол между прямой и плоскостью.
Как обобщение этой формулы можно рассмотреть случай, когда прямые а и b скрещиваются. Тогда проведем прямую  через точку
через точку  Так как
Так как  то формула остается верной и в этом случае. Теперь по этой формуле можно вычислять угол между скрещивающимися прямыми. При удачном выборе плоскоти
то формула остается верной и в этом случае. Теперь по этой формуле можно вычислять угол между скрещивающимися прямыми. При удачном выборе плоскоти
а искомый угол вычисляется очень быстро. Пусть, например, нам нужно вычислить угол  между прямыми, проходящими через скрещивающиеся диагонали соседних граней куба (рис. Р 3.10г). Согласно полученной формуле
между прямыми, проходящими через скрещивающиеся диагонали соседних граней куба (рис. Р 3.10г). Согласно полученной формуле

(Здесь в качестве плоскости а взята плоскость грани  .)
.)
Отсюда получаем:

Наконец, эта формула может быть применена для вычисления углов не только между прямыми, но и между лучами. Напомним, что угол между лучами может быть тупым, а угол между прямыми нет. Подумайте, как обосновать применимость этой формулы для вычисления угла между лучами. А
1.11. Может ли проекция острого утла при проектировании на некоторую плоскость быть прямым углом?
Посмотрите на рисунок Р 3.11а. Пусть угол ABC — данный угол. Плоскость а мы возьмем так, что она перпендикулярна биссектрисе ВК этого угла. Она и будет у нас плоскостью проекций.
В таком положении проекцией угла ABC является угол АКС. Угол А КС развернутый, его величина — 180°.
Будем теперь поворачивать угол ABC вокруг [АС). В тот момент, когда точка В окажется на плоскости а рис. Р 3.11б), проекцией угла ABC на плоскость а будет он сам, т.е. острый угол. Изменение угла, являющегося проекцией данного, происходило непрерывно от  до острого
до острого

Рис. Р 3.11
угла. Значит, в какой-то момент он равняется 
Все это можно увидеть, наблюдая за тенью от циркуля, освещенного настольной лампой.
Любопытно заметить, что мы нигде не воспользовались тем, что проектирование ортогональное. Значит, полученный результат верен для произвольного параллельного проектирования. И это можно увидеть, наблюдая за тенью от циркуля.
Задача может быть решена и вычислением. Посмотрите на рисунок Р 3.11в. На нем угол ABC данный,  точка
точка  — проекция точки В на плоскость а. Считая известными
— проекция точки В на плоскость а. Считая известными  и величину данного угла, можно вычислить расстояние от
и величину данного угла, можно вычислить расстояние от  , до (АС), при котором
, до (АС), при котором 
Итак, задача решена. И сразу же возникает похожая задача: "А верно ли это для тупого угла?". Точнее: "Может ли проекцией тупого угла быть прямой угол?".
Решить ее можно теми же способами. Но есть третий, более изящный способ. Попробуйте найти его.
1.12. Пусть  — куб. Вычислите угол, который образуют плоскости
— куб. Вычислите угол, который образуют плоскости 

Рис. Р 3.12
Если вычислять этот угол с помощью его линейного угла, то можно встретить определенные трудности при построении линейного угла одного из получившихся двугранных углов. В самом деле, перпендикуляры из точек А и  на общую прямую этих плоскостей не попадут в одну и ту же точку этой прямой (рис. Р 3.12) (?). Значит, продолжая все же идти по этому пути, придется проделать еще какие-то построения (?). Это решение можно довести до результата, но красивым его не назовешь.
на общую прямую этих плоскостей не попадут в одну и ту же точку этой прямой (рис. Р 3.12) (?). Значит, продолжая все же идти по этому пути, придется проделать еще какие-то построения (?). Это решение можно довести до результата, но красивым его не назовешь.
Можно выбрать другой двугранный угол между этими плоскостями, и решение окажется более быстрым)?). Другой путь решения основан на том, что угол между плоскостями равен углу между прямыми, перпендикулярными этим плоскостям. Действительно, так как

то искомый угол равен углу между  . А этот угол можно найти устно (?).
. А этот угол можно найти устно (?).
Этот способ вычисления двугранных углов стоит запомнить. Но он не является универсальным, бывает так, что перпендикулярные плоскостям прямые расположены не столь удачно, как здесь (придумайте сами такой случай).
ЗАДАЧИ К § 3
1.13. Даны две параллельные плоскости  и произвольная точка А. Расстояния
и произвольная точка А. Расстояния  известны. Как вычислить расстояние
известны. Как вычислить расстояние  Приведите численные примеры.
Приведите численные примеры.
Введем обозначения:  . В задаче, зная величины d и
. В задаче, зная величины d и  надо найти
надо найти 
Прежде всего заметим, что положение точки А относительно плоскостей  может быть различным. Для удобства отметим на рисунке все возможные положения точки (рис.Р3.13а) относительно данных плоскостей на прямой
может быть различным. Для удобства отметим на рисунке все возможные положения точки (рис.Р3.13а) относительно данных плоскостей на прямой  , перпендикулярной плоскости а (а значит, и плоскости Р).
, перпендикулярной плоскости а (а значит, и плоскости Р).

Рис. Р 3.13
Случаи, когда  или
или  неинтересны, поэтому рассмотрим положения
неинтересны, поэтому рассмотрим положения 
Для положения  имеем
имеем  откуда
откуда 
Для положения  имеем
имеем  откуда
откуда 
Для положения  имеем
имеем  откуда
откуда 
Таким образом, мы видим, что искомая величина зависит от положения точки А относительно данных плоскостей и задача не имеет однозначного решения.
Заметим, что задачу можно свести к планиметрической, проведя плоскость у через прямую  . Пусть плоскость у пересекает плоскость а по прямой а, а плоскость Р — по прямой b. На рисунке Р 3.136, показано соответствующее положение точек и прямых в плоскости у .
. Пусть плоскость у пересекает плоскость а по прямой а, а плоскость Р — по прямой b. На рисунке Р 3.136, показано соответствующее положение точек и прямых в плоскости у .
В дальнейшем, при решении задач иногда сводят пространственную задачу к планиметрической: вместо пространственной фигуры рассматривают ее сечение или ее проекцию, причем, на этой плоской картине сохраняются те свойства исходной фигуры, которые позволяют решить задачу.
1.14. Какой вид имеют сечения куба, перпендикулярные его диагонали? Какое из них имеет наибольшую площадь? Чему она равна в кубе с ребром 1?

Рис. Р 3.14
Такие сечения мы уже знаем. Одно из них — плоскостью  Все остальные будут ему параллельны?
Все остальные будут ему параллельны?
Разберемся сначала с формой этих сечений. Для удобства будем считать, что переменное сечение движется параллельно себе по направлению от вершины А, к вершине С . Пусть точка  точка пересечения диагонали
точка пересечения диагонали  с плоскостью
с плоскостью  Пересекая отрезок
Пересекая отрезок  внутри его, переменное сечение будет
внутри его, переменное сечение будет  Сразу же заметим, что треугольник в сечении будет получаться и еще на одном участке диагонали — от точки
Сразу же заметим, что треугольник в сечении будет получаться и еще на одном участке диагонали — от точки  точки пересечения диагонали АХС с
точки пересечения диагонали АХС с  до С. На участке
до С. На участке  сечение можно легко нарисовать. Эта легкость обеспечивается теоремой о том, что две параллельные плоскости пересекаются третьей по параллельными
сечение можно легко нарисовать. Эта легкость обеспечивается теоремой о том, что две параллельные плоскости пересекаются третьей по параллельными
прямым. Из рисунка Р 3.14 видно, что на этом участке сечение является шестиугольником.
Любопытный получился шестиугольник! У него все углы равны(?) и стороны, идущие через одну, равны между собой (?). Изучение свойств такого шестиугольника — прекрасное упражнение в геометрии.
Однако вернемся к нашей задаче. Следующий вопрос — о наибольшей площади такого сечения. Прежде чем писать для нее формулу и вычислять ее наибольшее значение, попытаемся предсказать результат.
Представьте себе, что вы разглядываете это переменное сечение в направлении диагонали  от
от  . А еще лучше — возьмите кубик и нарисуйте на нем такие сечения. После того, как оно пройдет точку
. А еще лучше — возьмите кубик и нарисуйте на нем такие сечения. После того, как оно пройдет точку  оно станет, как мы уже знаем, шестиугольником. Некоторое время после прохождения точки
оно станет, как мы уже знаем, шестиугольником. Некоторое время после прохождения точки  , этот шестиугольник будет расширяться, и мы будем видеть, что его последующие положения содержат предыдущие. Значит, его площадь будет какое-то время увеличиваться!?). До каких же пор?
, этот шестиугольник будет расширяться, и мы будем видеть, что его последующие положения содержат предыдущие. Значит, его площадь будет какое-то время увеличиваться!?). До каких же пор?
Теперь представьте себе второго наблюдателя, который смотрит в направлении диагонали С А, на переменное сечение, движущееся от С к  . В силу симметрии ситуации он также будет видеть сечение, увеличивающееся по площади. Когда эти два расширяющиеся сечения встретятся, тогда и получится сечение с наибольшей площадью. Где же произойдет эта встреча? Из соображений симметрии заключаем, что это произойдет в середине отрезка АХС .
. В силу симметрии ситуации он также будет видеть сечение, увеличивающееся по площади. Когда эти два расширяющиеся сечения встретятся, тогда и получится сечение с наибольшей площадью. Где же произойдет эта встреча? Из соображений симметрии заключаем, что это произойдет в середине отрезка АХС .
Эти рассуждения подсказали нам ответ. Теперь перейдем к его обоснованию. Вычислить площадь шестиугольника произвольной формы непросто. Поэтому сделаем так. Три стороны этого сечения, лежащие в гранях  продолжим до пересечения с прямыми ВС,
продолжим до пересечения с прямыми ВС,  в точках К, L, М соответственно. (А почему в результате получится треугольник
в точках К, L, М соответственно. (А почему в результате получится треугольник  ). Тогда S — площадь шестиугольника можно найти как разность S, — площади треугольника KLM — и
). Тогда S — площадь шестиугольника можно найти как разность S, — площади треугольника KLM — и  где
где  площадь малого треугольника в плоскости сечения при вершинах К, L, М. (А почему эти три площади равны?) Обозначим
площадь малого треугольника в плоскости сечения при вершинах К, L, М. (А почему эти три площади равны?) Обозначим  Тогда
Тогда

и

Из свойств полученного квадратного трехчлена, учитывая, что  (?), можно получить ответы на все вопросы к задаче. Мы знаем, что кроме шестиугольного сечения, возможно и треугольное. До конца задачу доведите самостоятельно.
(?), можно получить ответы на все вопросы к задаче. Мы знаем, что кроме шестиугольного сечения, возможно и треугольное. До конца задачу доведите самостоятельно.
1.15. Плоскости  перпендикулярны.
перпендикулярны.  — перпендикуляр на а из точки
— перпендикуляр на а из точки  — перпендикуляр на
— перпендикуляр на  из точки В. Можно ли установить связь между величинами
из точки В. Можно ли установить связь между величинами 
Установить связь между величинами — значит, в конечном итоге найти формулу, в которой были бы все эти величины да еще, возможно, некоторые постоянные. Если вы нашли формулу, в которой, кроме этих величин, есть и другие, то останавливаться нельзя. Лишние величины надо постараться убрать из формулы. Если это не получается, то мы приходим к мысли о том, что связь между данными величинами однозначно установить невозможно. В самом деле, если в формуле присутствует еще хотя бы одна "лишняя" величина, то ей можно придавать различные численные значения и получать отсюда разные формулы, связывающие данные величины. Но на один вопрос еще надо постараться ответить: "Это только нам не удалось убрать из формулы "лишнюю" величину или это в принципе невозможно?" Для того, чтобы ответить на такой вопрос, требуется дополнительное исследование.
Перед тем, как перейти к непосредственному решению задачи, заметим следующее. Вопрос о связи величин между собой можно несколько видоизменить. Можно искать не формулу, связывающую данные величины между собой, а любую из них, считая, что все остальные известны.
Обратите теперь внимание на то, как поставлен вопрос к задаче. Его форма не категорическая, а предположительная: “Можно ли...?" (Бывает и так: "Можете ли вы...?". Тут есть оттенки. Какие?) Когда вас в математической задаче спрашивают: "А можно ли сделать то-то и то-то?" — лучше начинать свое решение с самых простых случаев. Если в этих, более простых

Рис. Р 3.15
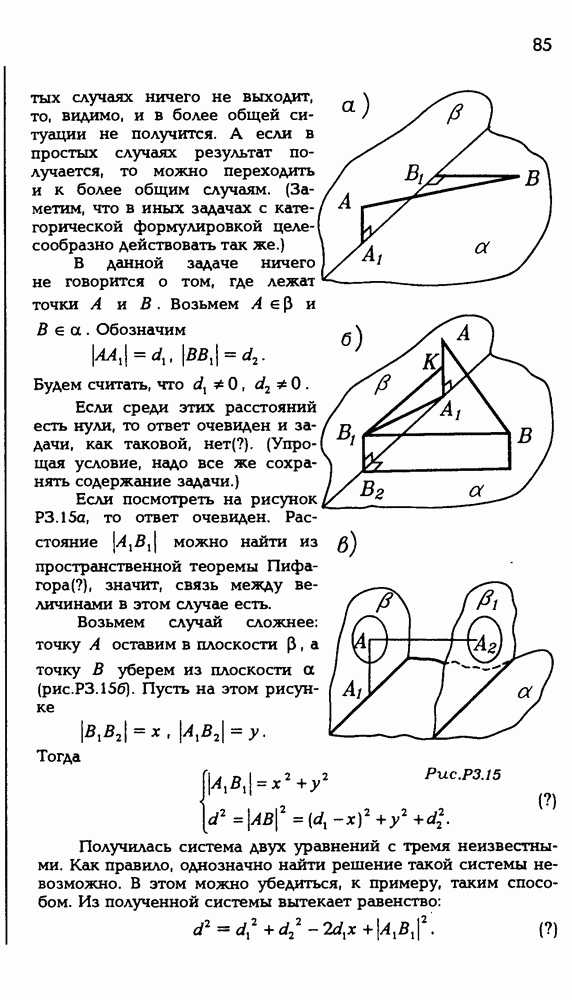
случаях ничего не выходит, то, видимо, и в более общей ситуации не получится. А если в простых случаях результат получается, то можно переходить и к более общим случаям. (Заметим, что в иных задачах с категорической формулировкой целесообразно действовать так же.) 
В данной задаче ничего не говорится о том, где лежат точки А и В. Возьмем  и
и  Обозначим
Обозначим

Будем считать, что 
Если среди этих расстояний есть нули, то ответ очевиден и задачи, как таковой,  (Упрощая условие, надо все же сохранять содержание задачи.)
(Упрощая условие, надо все же сохранять содержание задачи.)
Если посмотреть на рисунок  то ответ очевиден. Расстояние
то ответ очевиден. Расстояние  можно найти из пространственной теоремы Пифагора (?), значит, связь между величинами в этом случае есть.
можно найти из пространственной теоремы Пифагора (?), значит, связь между величинами в этом случае есть.
Возьмем случай сложнее: точку А оставим в плоскости  а точку В уберем из плоскости а (рис. Р3.15б). Пусть на этом рисунке
а точку В уберем из плоскости а (рис. Р3.15б). Пусть на этом рисунке

Тогда

Получилась система двух уравнений с тремя неизвестными. Как правило, однозначно найти решение такой системы невозможно. В этом можно убедиться, к примеру, таким способом. Из полученной системы вытекает равенство:

Замечаем, что  зависит от
зависит от  линейно, следовательно, выразить
линейно, следовательно, выразить  через данные величины невозможно.
через данные величины невозможно.
Теперь ясно, что и в более общем случае, когда A g Р, установить связь между этими величинами не удастся (?).
Попытаемся разобраться в заданной ситуации подробнее: а почему такой связи нет? Какова геометрическая природа этого явления? (К отысканию геометрической сути задачи нас побуждает и чисто алгебраическое решение. Мы пришли к ответу, составив некую систему и проанализировав ее решение. А нельзя ли к тому же ответу прийти чисто геометрическим методом, т. е. рассматривая фигуры в пространстве?) Вернемся к рисунку Р 3.15а. Зафиксируем точку А в плоскости Р и поставим такой вопрос: "А где может находиться, исходя из условий задачи, точка  как
как  , то В находится на плоскости, параллельной плоскости Р, удаленной от Р на расстояние
, то В находится на плоскости, параллельной плоскости Р, удаленной от Р на расстояние  Таких плоскостей две, возьмем одну из них Р, (рис. Р 3.15в). Так как точка В находится на фиксированном расстоянии от А , то она будет находиться на фиксированном расстоянии и от точки
Таких плоскостей две, возьмем одну из них Р, (рис. Р 3.15в). Так как точка В находится на фиксированном расстоянии от А , то она будет находиться на фиксированном расстоянии и от точки  проекции точки А На плоскость
проекции точки А На плоскость  Но это означает, что она находится на некоторой окружности в плоскости Р с центром в точке
Но это означает, что она находится на некоторой окружности в плоскости Р с центром в точке  Но тогда точка В, — проекция точки В на плоскость Р — будет находиться на окружности с центром в точке А (?). А теперь видно, что
Но тогда точка В, — проекция точки В на плоскость Р — будет находиться на окружности с центром в точке А (?). А теперь видно, что  не определяется однозначно.
не определяется однозначно.  кстати, хорошо видно, в каких границах находится
кстати, хорошо видно, в каких границах находится 
Теперь, когда задача решена, стоит задуматься: а почему же нам не удалось найти  в ситуации, изображенной на рисунке? И еще: найти
в ситуации, изображенной на рисунке? И еще: найти  , т. е. установить связь между данными величинами, оказалось невозможно. Можно ли ввести в рассмотрение другие величины, такие, что для нового набора величин (данных и вновь введенных) можно установить связь между ними?
, т. е. установить связь между данными величинами, оказалось невозможно. Можно ли ввести в рассмотрение другие величины, такие, что для нового набора величин (данных и вновь введенных) можно установить связь между ними?

Рис. Р 3.16

Рис. Р 3.17
1.16. В наклонной треугольной призме  каждое ребро основания равно 1. Ребро
каждое ребро основания равно 1. Ребро  , равное
, равное  образует равные углы с ребрами ВА и ВС. Расстояние от
образует равные углы с ребрами ВА и ВС. Расстояние от  до (ABC) равно 1. Вычислите расстояние между основаниями призмы.
до (ABC) равно 1. Вычислите расстояние между основаниями призмы.
Прежде всего обратим внимание на то, что надо найти расстояние между основаниями призмы, т. е. между фигурами, лежащими в параллельных плоскостях, а не между самими параллельными плоскостями. Для такого случая естественно вычислить расстояние между параллельными плоскостями и расстояние между одним основанием призмы — возьмем ABC — и проекцией основания  на
на  Но расстояние между плоскостями дано, значит, осталось вычислить второе расстояние, и задача будет решена.
Но расстояние между плоскостями дано, значит, осталось вычислить второе расстояние, и задача будет решена.
Для нахождения второго расстояния необходимо спроектировать верхнее основание на плоскость нижнего. Для этого спроектируем вершины треугольника  Начнем с вершины
Начнем с вершины  — это удобнее всего. Так как
— это удобнее всего. Так как  , она проектируется на прямую, проходящую через биссектрису ВК угла ABC (?). Но нам этого мало(?). Точка Н — проекция точки
, она проектируется на прямую, проходящую через биссектрису ВК угла ABC (?). Но нам этого мало(?). Точка Н — проекция точки  — лежит на прямой ВК, а точнее? На луче ВК
— лежит на прямой ВК, а точнее? На луче ВК  На его продолжении? На отрезке ВК
На его продолжении? На отрезке ВК  Одно ясно сразу — она лежит не в точке
Одно ясно сразу — она лежит не в точке  Однозначно ответить на вопрос, где находится точка Н — на луче ВК или на его продолжении, исходя из условий задачи, невозможно!?). Может быть случай, показанный на рисунке
Однозначно ответить на вопрос, где находится точка Н — на луче ВК или на его продолжении, исходя из условий задачи, невозможно!?). Может быть случай, показанный на рисунке  а может быть случай, показанный на рисунке
а может быть случай, показанный на рисунке  Все зависит от вида призмы.
Все зависит от вида призмы.

Рис. Р 3.18
Решим сначала задачу, когда точка Н лежит на луче ВК . Выясним, лежит ли она на отрезке ВК . Вычисляем  а затем сравниваем их между собой:
а затем сравниваем их между собой:

поэтому точка Н лежит вне треугольника ABC. Теперь проекции точек А, и С, легко построить (?). Расстояние между треугольником ABC и проекцией треугольника  равно (?). Тогда искомое расстояние равно —
равно (?). Тогда искомое расстояние равно — 
Перейдем теперь к ситуации, изображенной на рисунке. Пусть Н — проекция точки В, — находится на продолжении луча ВК , причем, как и в предыдущем случае,  Теперь самое важное — установить положение проекций точек
Теперь самое важное — установить положение проекций точек  и С, по отношению к треугольнику, а еще точнее — выяснить, как расположена по отношению к этому треугольнику прямая
и С, по отношению к треугольнику, а еще точнее — выяснить, как расположена по отношению к этому треугольнику прямая  являющаяся проекцией прямой
являющаяся проекцией прямой  на (ABC) (точка Q — проекция точки
на (ABC) (точка Q — проекция точки  а точка Т — проекция точки
а точка Т — проекция точки  ). Ясно (рис. Р 3.18), что
). Ясно (рис. Р 3.18), что  (?).
(?).
Поэтому найдем 

(точка  — середина ребра
— середина ребра  точка S — точка пересечения
точка S — точка пересечения  Обоснуйте приведенные выкладки. Подставим числовые данные и получим:
Обоснуйте приведенные выкладки. Подставим числовые данные и получим:

Расстояние оказалось отрицательным! Но это невозможно! Почему же у нас так получилось?
Все дело в рисунке Р3.18. Этот рисунок неверен! На нем  пересекает треугольник
пересекает треугольник  Но именно это нам и нужно выяснить!
Но именно это нам и нужно выяснить!
Теперь мы знаем, что такого рисунка быть не может, а значит, (QT) проходит вне треугольника  (Если быть совсем точным, то надо еще объяснить, почему (QT) не проходит через вершину
(Если быть совсем точным, то надо еще объяснить, почему (QT) не проходит через вершину  Значит, на самом деле верен рисунок
Значит, на самом деле верен рисунок  . Но тогда расстояние между треугольниками ABC и HQT равно
. Но тогда расстояние между треугольниками ABC и HQT равно  . Тогда искомое расстояние равно —
. Тогда искомое расстояние равно — 
Любопытно, что в обоих случаях расстояние оказалось одним и тем же.
Итак, ответ: расстояние между основаниями призмы равно  .
.

Рис. Р 3.19
Ответ получен, но есть еще над чем подумать. Почему в двух разных случаях ответ оказался одинаковым? Может быть, это совпадение обусловлено числовыми данными, а может быть, дело в другом? И еще, вычислив  во втором случае и получив, что
во втором случае и получив, что  мы оставили и выкладки, и рисунок. Однако, если бы мы их продолжили и вычислили
мы оставили и выкладки, и рисунок. Однако, если бы мы их продолжили и вычислили  то увидели бы, что результат получился тот же, что и на новом рисунке. Как вы это объясните?
то увидели бы, что результат получился тот же, что и на новом рисунке. Как вы это объясните?
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧИТАТЕЛЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ
- § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 1.2. Двугранный угол. Угол между плоскостями.
- 1.3. Плоскость и прямая в пространстве.
- 1.4. Аксиомы стереометрии.
- 1.5. Взаимное расположение двух прямых в пространстве.
- 1.6. Признаки скрещивающихся прямых.
- 1.7. Параллельные прямые.
- 1.8. Параллельное проектирование.
- § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 2.2. О значении перпендикуляра.
- 2.3. Теорема о трех перпендикулярах.
- 2.4. Признак перпендикулярности прямой и плоскости.
- 2.5. Построение плоскости, перпендикулярной данной прямой.
- 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости.
- 2.7. Теорема о прямой, перпендикулярной плоскости.
- 2.8. Перпендикулярность плоскостей.
- 2.9. Ортогональное проектирование.
- § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 3.2. Параллельность и перпендикулярность.
- 3.3. Основная теорема о параллельных плоскостях.
- 3.4. Второй признак параллельности плоскостей.
- 3.5. Расстояние и параллельность.
- 3.6. Сонаправленность лучей и угол между прямыми.
- 3.7. Параллельность и углы.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ
- § 4. СФЕРА И ШАР
- 4.2. Взаимное положение шара и плоскости.
- 4.3. Сфера и многранники.
- 4.4. Вид и изображение шара и сферы.
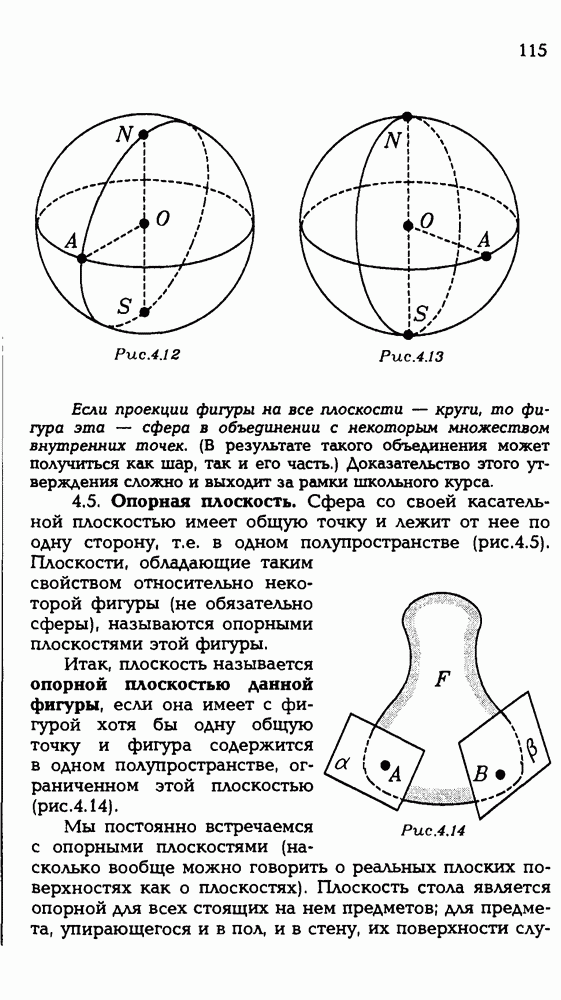
- 4.5. Опорная плоскость.
- 4.6. Ограниченные фигуры. Диаметр фигуры.
- 4.7. Опорные плоскости в концах диаметра.
- 4.8. Сфера — фигура вращения.
- 4.9. Симметрия сферы и шара.
- 4.10. Сфера — центрально симметричная фигура.
- 4.11. Сфера — зеркально симметричная фигура.
- 4.12. Отражение в плоскости и отражение в зеркале.
- § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ
- 5.2. Тригонометрия трехгранного угла.
- 5.3. Равенство трехгранных углов.
- 5.4. Сферические треугольники.
- 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников.
- § 6. ЦИЛИНДР
- 6.2. Другой подход к определению цилиндра.
- 6.3. Цилиндр вращения.
- 6.4. Эллипс как сечение цилиндра вращения.
- 6.5. Винтовые линии.
- 6.6. Цилиндры в практике.
- § 7. ПРИЗМА
- 7.2. Параллелепипед.
- 7.3. Прямоугольный параллелепипед.
- 7.4. Симметрия параллелепипеда.
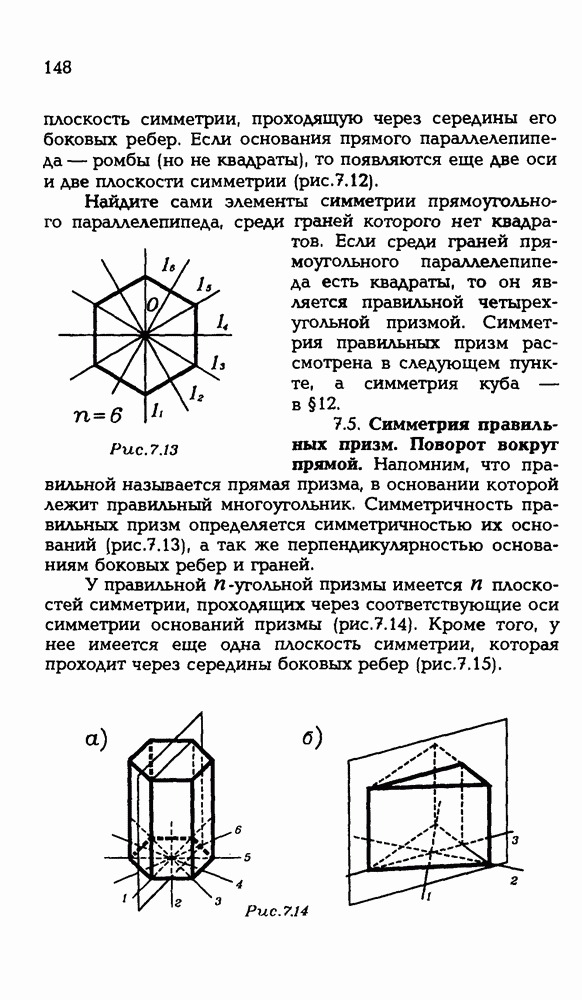
- 7.5. Симметрия правильных призм. Поворот вокруг прямой.
- § 8. КОНУС
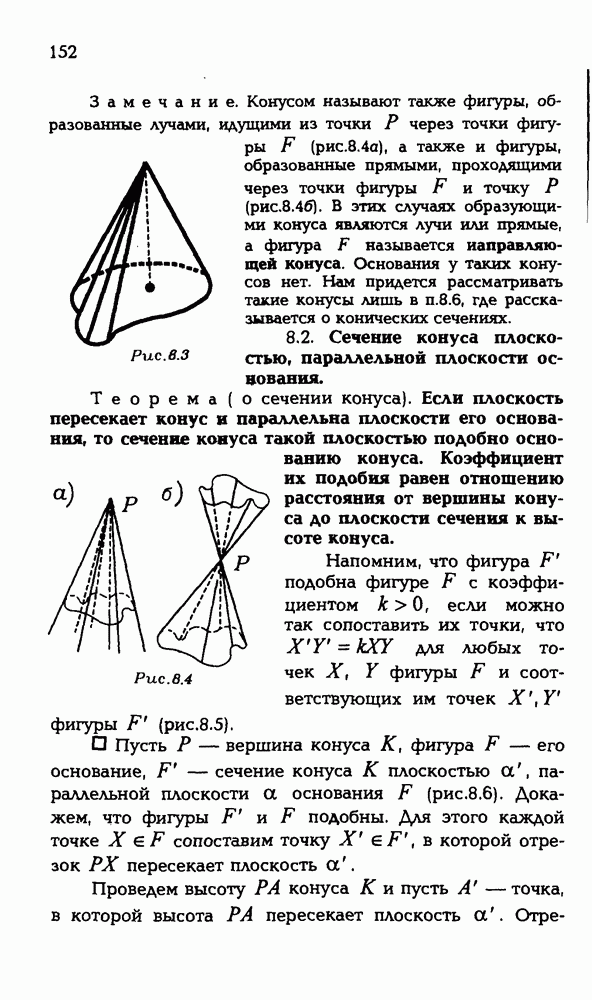
- 8.2. Сечение конуса плоскостью, параллельной плоскости основания.
- 8.3. Конус вращения.
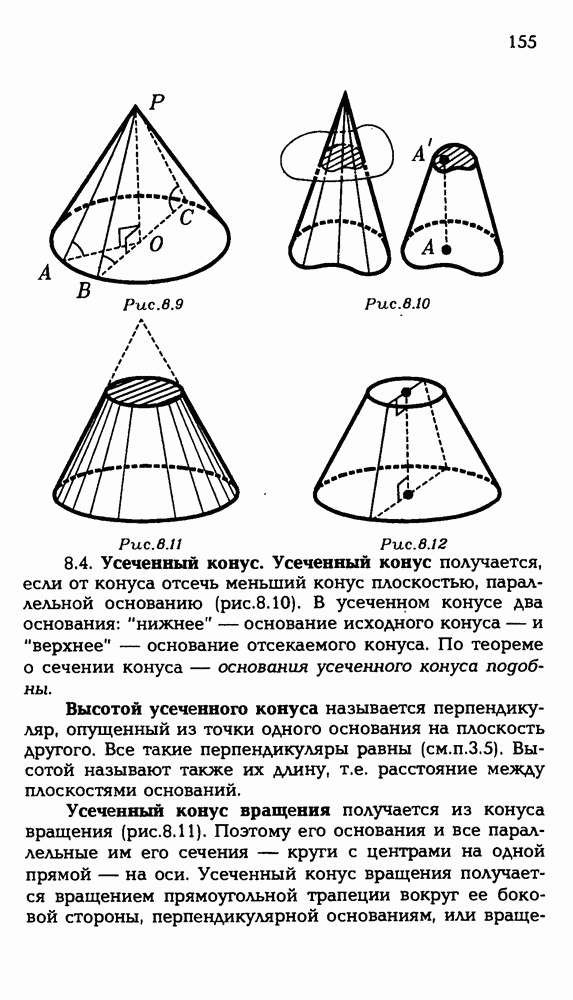
- 8.4. Усеченный конус.
- § 9. ПИРАМИДА
- 9.2. Правильная пирамида.
- 9.3. Симметрия правильной пирамиды.
- 9.4. Конусы и пирамиды в практике.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ
- § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ
- 10.2. Граница и внутренность.
- 10.3. Определение тела и замкнутой плоской области.
- 10.4. Выпуклые фигуры.
- 10.5. Выпуклые тела.
- § 11. МНОГОГРАННИКИ
- 11.2. Выпуклые многогранники.
- 11.3. Теорема Эйлера.
- 11.4. Выпуклые многогранники и выпуклые оболочки.
- 11.5. Многогранная поверхность и развертка.
- 11.6. Развертка выпуклого многогранника.
- § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
- 12.2. Классификация правильных многогранников.
- 12.3. Полуправильные многогранники.
- 12.4. Симметрия правильных многогранников.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
- § 13. ПОНЯТИЕ ОБЪЕМА
- 13.2. Определение объема.
- 13.3. Геометрические величины.
- § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА
- 14.2. Объем прямой призмы.
- § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ
- 15.2. Выражение объема через площади сечений.
- § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА
- 16.2. Объем конуса
- 16.3. Объем шара.
- 16.4. Объем тел вращения.
- 16.5. Объем шарового сегмента и шарового сектора.
- § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ
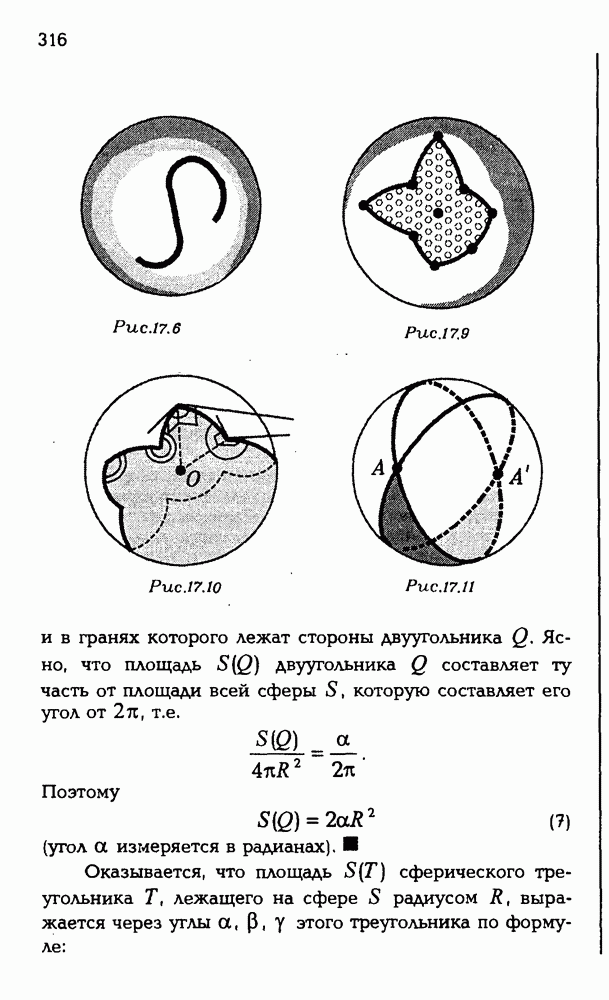
- 17.2. Площадь сферы.
- 17.3. Площадь сферических многоугольников.
- 17.4. Площадь сферического сегмента и сферического пояса.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ
- § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- 18.2. Другой способ нахождения координат точки.
- 18.3. Построение точки с данными координатами.
- 18.4. Выражение расстояния между точками.
- § 19. МЕТОД КООРДИНАТ
- 19.2. Уравнения без одной или двух координат.
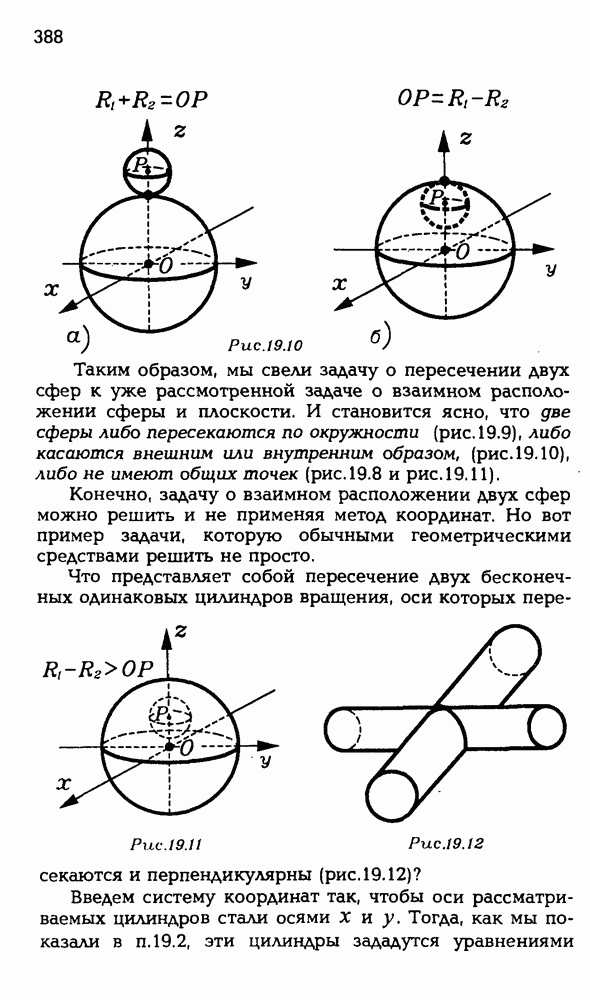
- 19.3. Некоторые применения метода координат.
- § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ
- 20.2. Полярные координаты.
- 20.3. Цилиндрические координаты.
- 20.4. Сферические координаты.
- 20.5. Координатная сеть.
- § 21. ПОНЯТИЕ ВЕКТОРА
- 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов.
- 21.3. Сонаправленность и равенство векторов.
- 21.4. Признаки равенства векторов.
- 21.5. Радиус-вектор.
- § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 22.2. Разложение вектора на составляющие.
- 22.3. Умножение вектора на число.
- 22.4. Координаты вектора.
- 22.5. Равенство координат векторов и координат точек.
- 22.6. Разложение векторов по базису.
- 22.7. Ориентация базиса.
- § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ
- 23.2. Выражение скалярного произведения через координаты.
- 23.3. Свойства скалярного умножения.
- 23.4. Применения скалярного умножения.
- 23.5. Скалярное произведение и проекции.
- § 24. ВЕКТОРНЫЙ МЕТОД
- 24.2. Общее уравнение плоскости.
- 24.3. Векторное задание отрезка.
- 24.4. Некоторые теоремы о треугольниках и тетраэдрах.
- 24.5. Центр масс системы материальных точек.
- 24.6. Центры масс и выпуклые многогранники.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 6. ПРЕОБРАЗОВАНИЯ
- 25.1. Преобразования фигур.
- 25.2. Определения движения и равенства фигур.
- 25.3. Преобразования симметрии.
- 25.4. Параллельный перенос.
- 25.5. Поворот.
- § 26. СВОЙСТВА ДВИЖЕНИЙ
- 26.2. Общие свойства движений.
- 26.3. Теоремы о задании движений.
- 26.4. Неподвижные точки движений.
- 26.5. Два рода движений.
- 26.6. Теорема подвижности пространства.
- 26.7. Композиция отражений в плоскости.
- § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА
- 27.2. Движения первого рода как винтовые движения.
- 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот.
- 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения.
- § 28. ПОДОБИЕ
- 28.2. Гомотетия.
- 28.3. Свойства подобия.
- 28.4. Группы преобразований.
- § 29. ИНВЕРСИЯ
- 29.2. Аналитическое задание инверсии.
- 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии.
- 29.4. Сохранение величин углов при инверсии.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ОТВЕТЫ И УКАЗАНИЯ
- ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ