| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЗАДАЧИ С РЕШЕНИЯМИ
ЗАДАЧИ К § 4
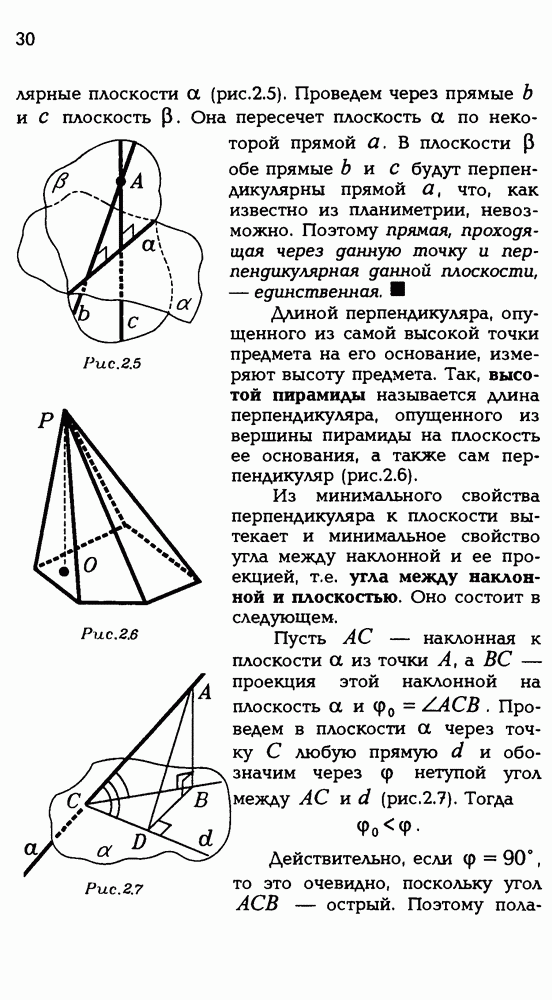
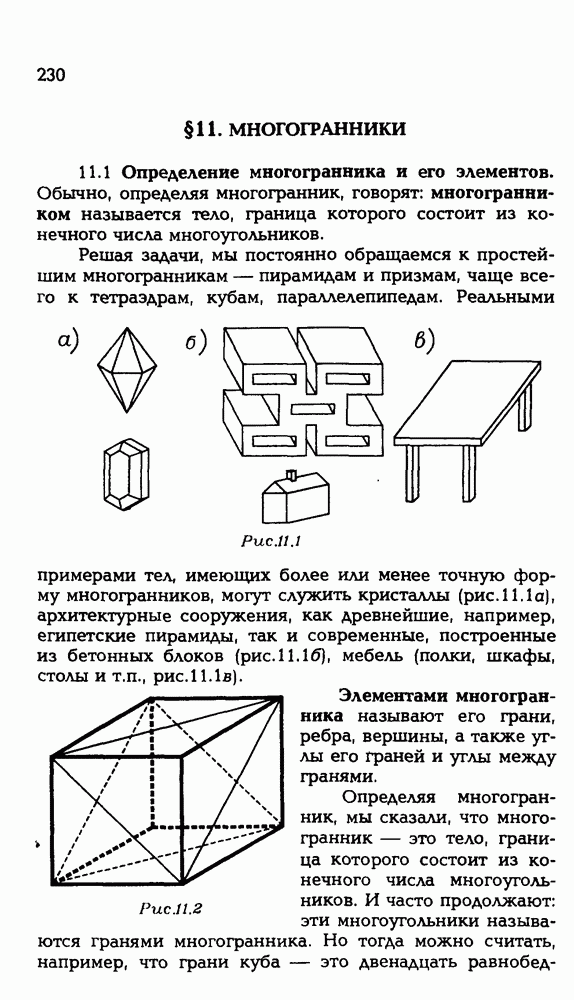
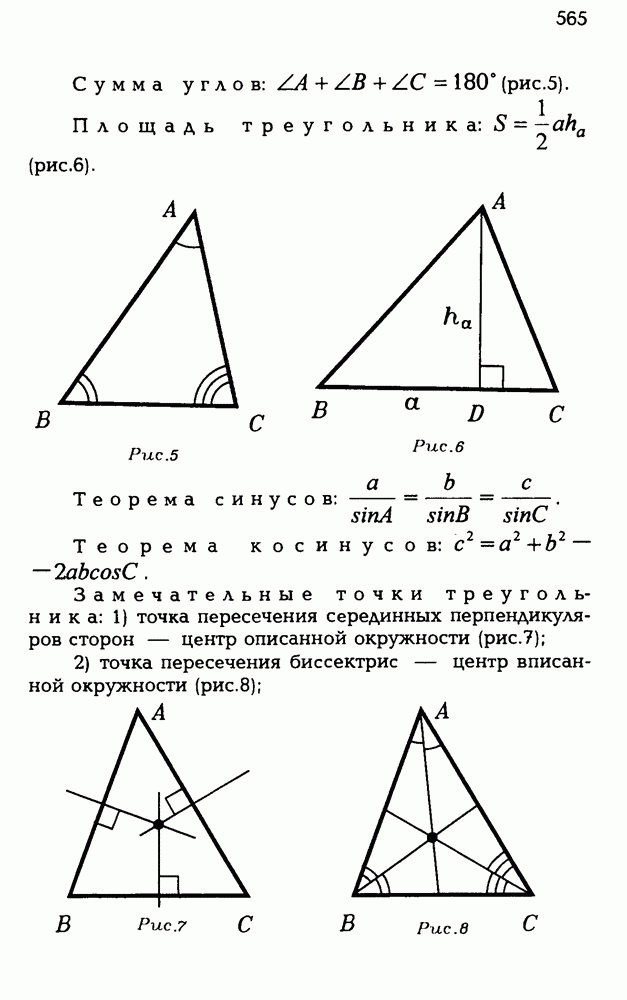
2.1. Даны два круга одного шара, окружности которых лежат на сфере и имеют единственную общую точку. Докажите, что прямая пересечения плоскостей, в которых лежат эти круги, имеет с шаром единственную общую точку.

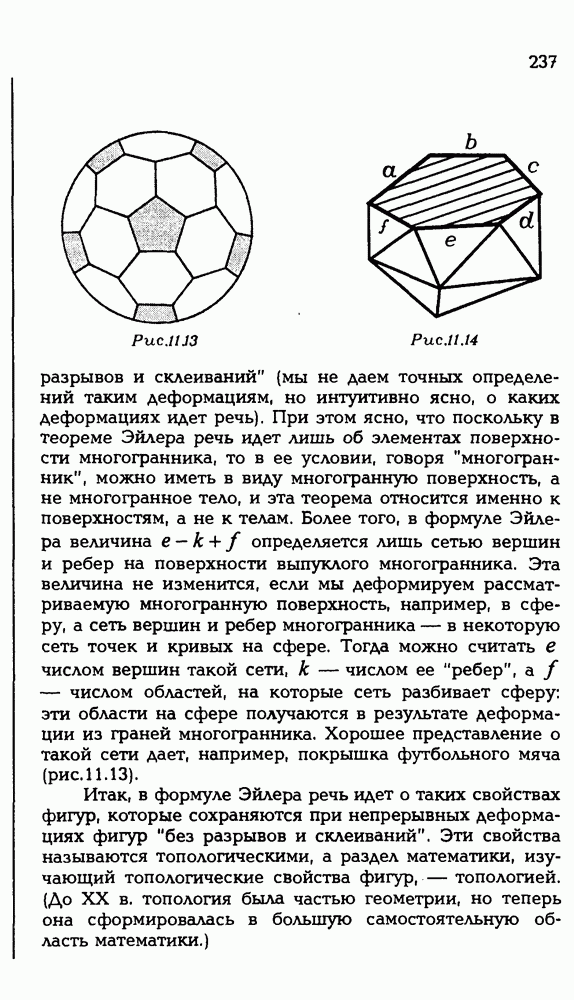
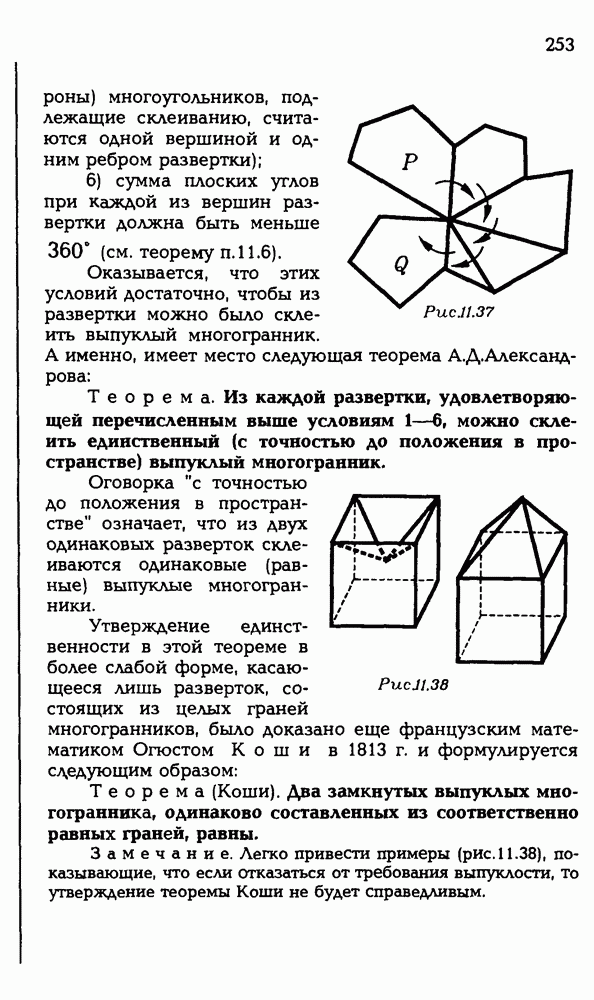
Рис. Р 3.20
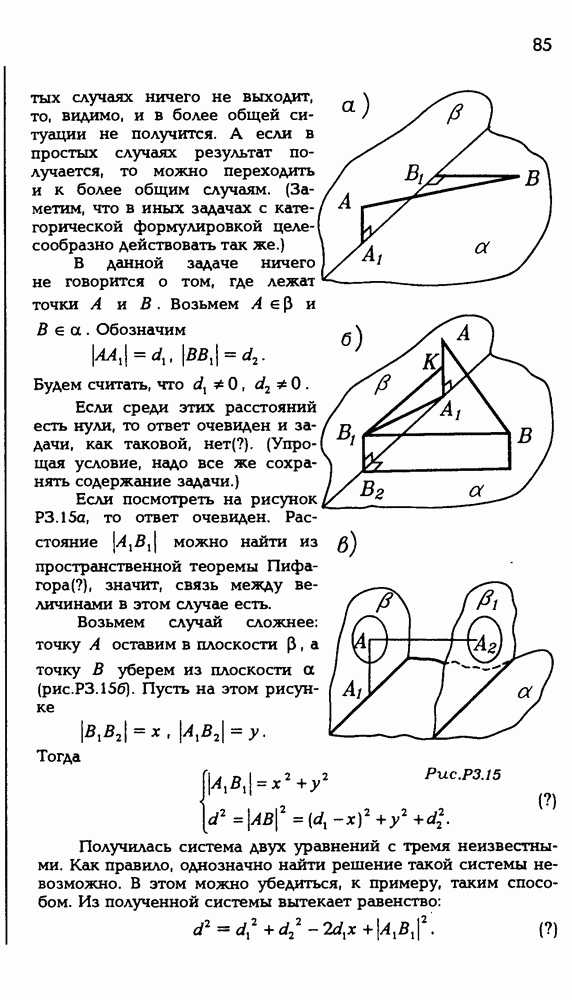
Пусть (рис. Р3.20) точка О — центр шара, точки О, и  — центры данных кругов,
— центры данных кругов,  — плоскости, в которых они лежат, А — общая точка этих кругов, а — общая прямая плоскостей
— плоскости, в которых они лежат, А — общая точка этих кругов, а — общая прямая плоскостей 
Для доказательства достаточно установить, что а является касательной хотя бы к одной из данных окружностей. В самом деле, пусть а — касательная к окружности с центром  Проведем (ОА) и
Проведем (ОА) и  Что же мы видим? Если а — касательная, то а
Что же мы видим? Если а — касательная, то а  Но тогда (?). Отсюда следует, что а — касательная к большей окружности, которая получается в сечении шара плоскостью, проходящей через О и а Но тогда а имеет с шаром единственную общую точку (?).
Но тогда (?). Отсюда следует, что а — касательная к большей окружности, которая получается в сечении шара плоскостью, проходящей через О и а Но тогда а имеет с шаром единственную общую точку (?).

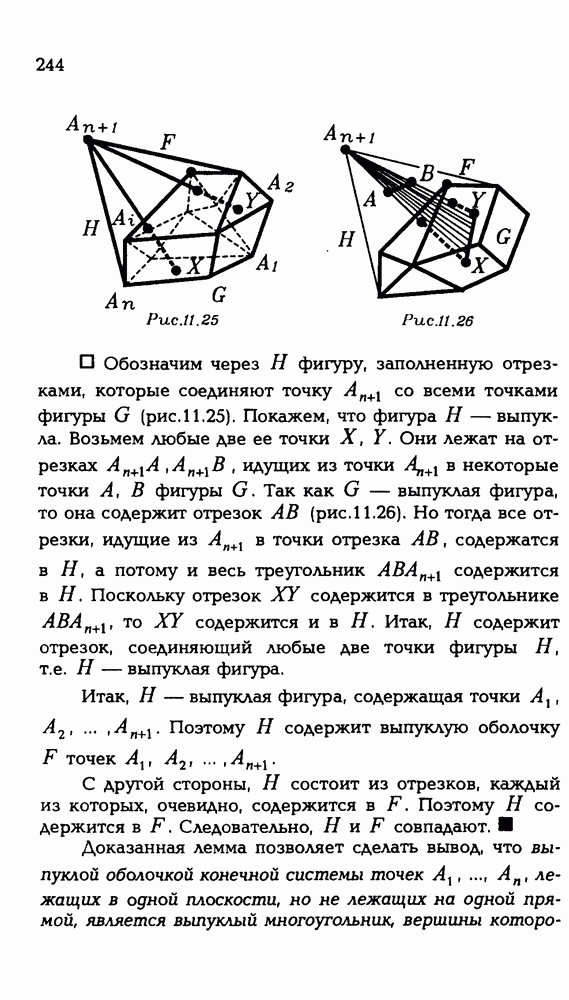
Рис. Р 3.21
Осталось доказать, что а действительно касательная хотя бы к одной из данных окружностей. Пусть это не так, т.е. а не является касательной ни к одной из них. Тогда рисунок будет такой (?) (см. рис. Р3.21). Центр шара О лежит, как мы уже знаем, на перпендикуляре к а, проходящем через точку  и на перпендикуляре к
и на перпендикуляре к  , проходящем через
, проходящем через  Однако непохоже, чтобы эти перпендикуляры пересекались
Однако непохоже, чтобы эти перпендикуляры пересекались 
И в самом деле, если бы это произошло, то точка О была бы равноудалена от трех точек  прямой а, что невозможно.
прямой а, что невозможно.
Итак, а — касательная хотя бы к одной из данных окружностей, а тогда, как мы уже показали, она имеет с шаром единственную общую точку.
Заметим к этому доказательству, что нам хватило того обстоятельства, что а — касательная хоть к одной из данных окружностей. На самом деле, а — касательная к каждой окружности (?), но в процессе доказательства это не понадобилось.
Доказательство получилось не слишком коротким, да еще с элементами "от противного". Нельзя ли короче? (Этот вопрос всегда уместен!) Оказывается можно. Вот более короткое рассуждение.
Пусть а имеет с шаром еще одну общую точку, назовем ее В. Так как  , то
, то  Кроме того, В принадлежит шару. Значит, В принадлежит сечению шара плоскостью а, т. е. кругу с центром
Кроме того, В принадлежит шару. Значит, В принадлежит сечению шара плоскостью а, т. е. кругу с центром  . Аналогично В принадлежит кругу с центром
. Аналогично В принадлежит кругу с центром  . Получилось, что данные круги имеют еще одну общую точку, что противоречит условию.
. Получилось, что данные круги имеют еще одну общую точку, что противоречит условию.
Ясно, что получилось короче, но осталось "от противного". А нельзя ли напрямую? Можно! Обозначим данные круги К, и  , а шар
, а шар  . Тогда
. Тогда

Всего одна строчка! Причем любопытно, что в этом рассуждении не использовалось то условие, что даны именно шар и круги. Да, но что же тогда использовалось и что мы на самом деле доказали? Тут есть над чем подумать...

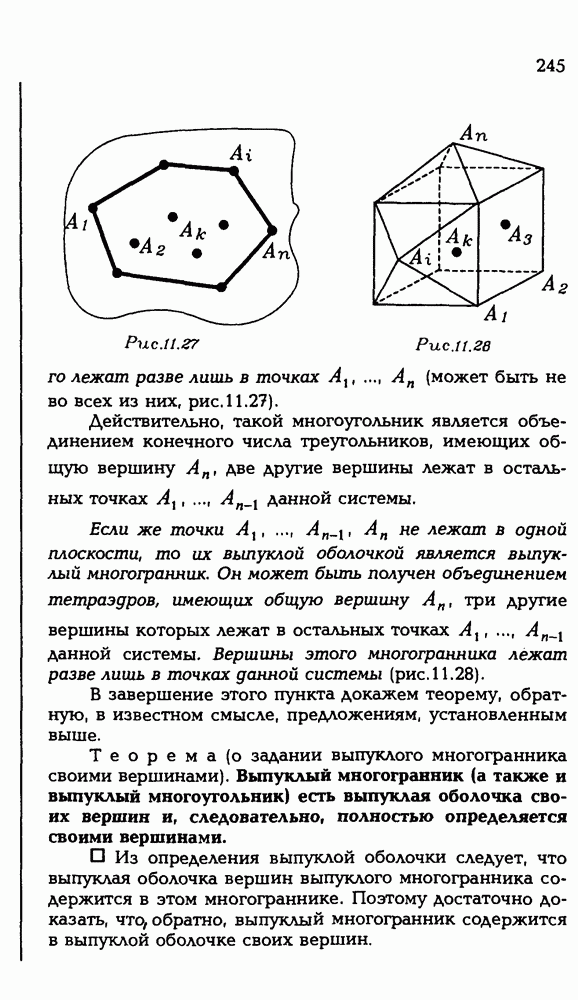
Рис. Р 3.22
Что касается самой задачи, то интересно вот что. Уже зная, что а имеет с шаром единственную общую точку, мы легко получаем, что а — касательная к каждой из данных окружностей (?). Если же эти два круга не лежат в одном шаре, то, как легко видеть, а может и не быть их общей касательной). Таким образом, принадлежность двух кругов одному шару и наличие у них общей касательной равносильны (если круги не лежат в одной плоскости).
2.2. Докажите, что пересечение двух сфер, отличное от точки, является окружностью.
“На пальцах" это делается так. Рассмотрим рисунок Р 3.22.
Здесь нарисованы две полуокружности с центрами в точках  и
и  пересекающиеся в точке
пересекающиеся в точке  Будем вращать
Будем вращать
эту конфигурацию вокруг  . Полуокружности при вращении дадут сферы, а точка М — окружность.
. Полуокружности при вращении дадут сферы, а точка М — окружность.
Идею можно довести до конца, надо только понять, что стоит за словами "будем вращать". Увы, быстро не получится.
Поэтому выберем другой путь. Через точку М проведем плоскость, перпендикулярную прямой  Она пересечет первую сферу по окружности. И вторую тоже. Эти две окружности лежат в проведенной нами плоскости, имеют общий центр — точку пересечения проведенной плоскости и прямой
Она пересечет первую сферу по окружности. И вторую тоже. Эти две окружности лежат в проведенной нами плоскости, имеют общий центр — точку пересечения проведенной плоскости и прямой  . И радиус каждой из них равен расстоянию от М до
. И радиус каждой из них равен расстоянию от М до  Значит, получается не две разных окружности, а две совпадающие, то есть одна.
Значит, получается не две разных окружности, а две совпадающие, то есть одна.
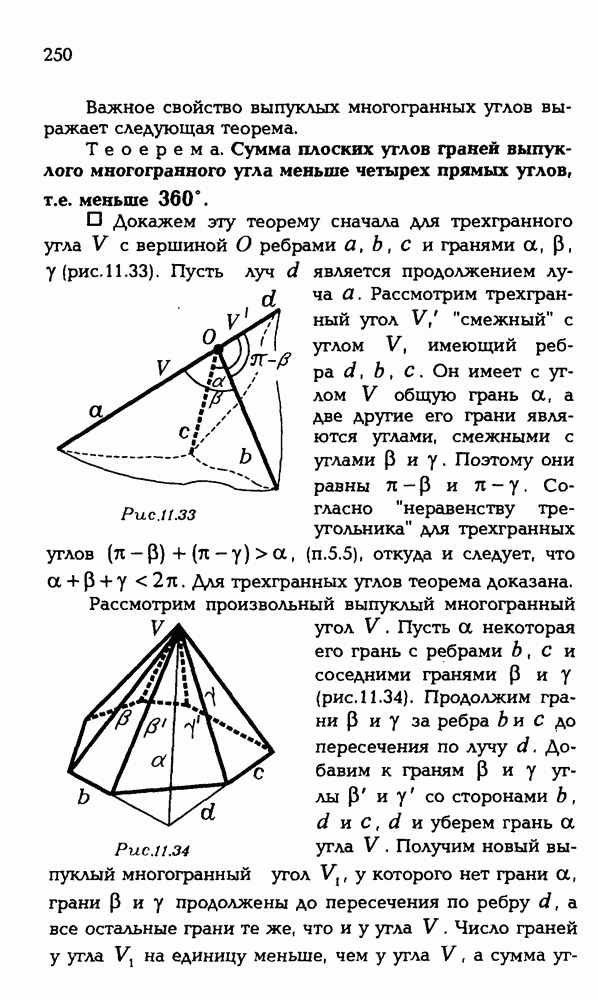
Итак, общая линия двух сфер является окружностью (рис. Р 3.23), тот же результат получается и при другом расположении сфер (?).

Рис. Р 3.23
2.3. На плоскости лежат два шара радиусами  Они имеют единственную общую точку.
Они имеют единственную общую точку.
а) На каком расстоянии от плоскости находится эта точка, б) На каком расстоянии между собой находятся точки касания шаров и плоскости, в) Чему равен радиус наименьшей сферы, касающейся данных шаров и плоскости? А наибольшей?
Стоит запомнить, что сведение стереометрической задачи к планиметрической, как правило, облегчает ее решение. Покажем это.
Обозначим данную плоскость а, центры данных шаров О, и  точки касания шаров с плоскостью
точки касания шаров с плоскостью  общую точку шаров —
общую точку шаров — 
Проведем плоскость через прямые  . В результате приходим к такому рисунку (рис. Р 3.24) (?). На нем нет окружностей сечения, считается, что
. В результате приходим к такому рисунку (рис. Р 3.24) (?). На нем нет окружностей сечения, считается, что  перпендикуляр из М на а,
перпендикуляр из М на а,  точка пересечения
точка пересечения 
а) Обозначим  через а, тогда
через а, тогда  Из подобия треугольников
Из подобия треугольников  находим а:
находим а:

Тогда

 подобен
подобен  . Отсюда находим
. Отсюда находим


Рис. Р 3.24
б) Проведем  Из треугольника
Из треугольника  получим
получим

в) Наименьшая сфера, отвечающая условию, имеет центр в проведенной нами  Обозначим его
Обозначим его  (рис. Р 3.25). Так как
(рис. Р 3.25). Так как  то, используя результат задачи б), получим
то, используя результат задачи б), получим

откуда

А наибольшей сферы, удовлетворяющей условию задачи, нет(?).

Рис. P 3.25
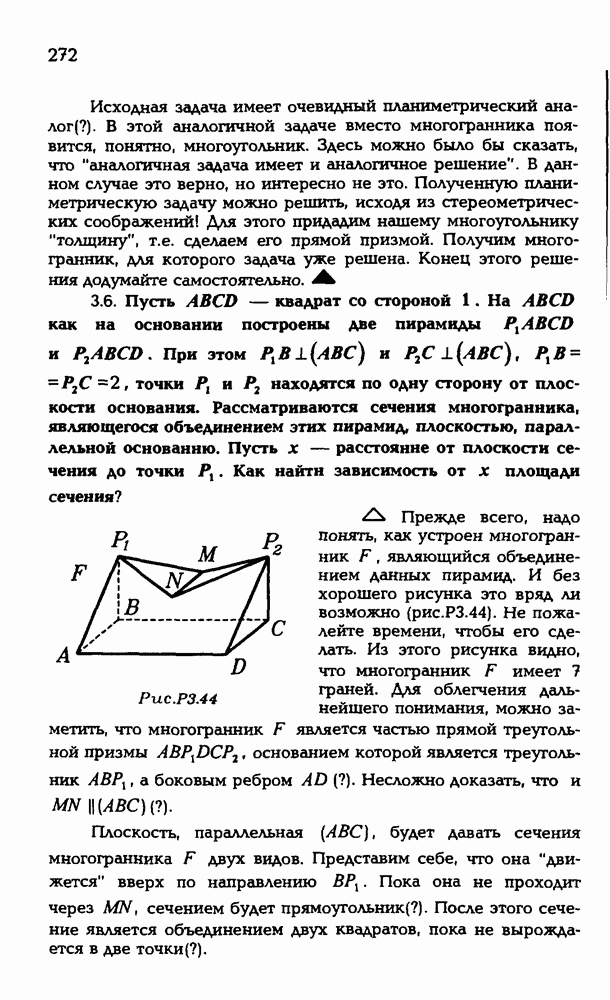
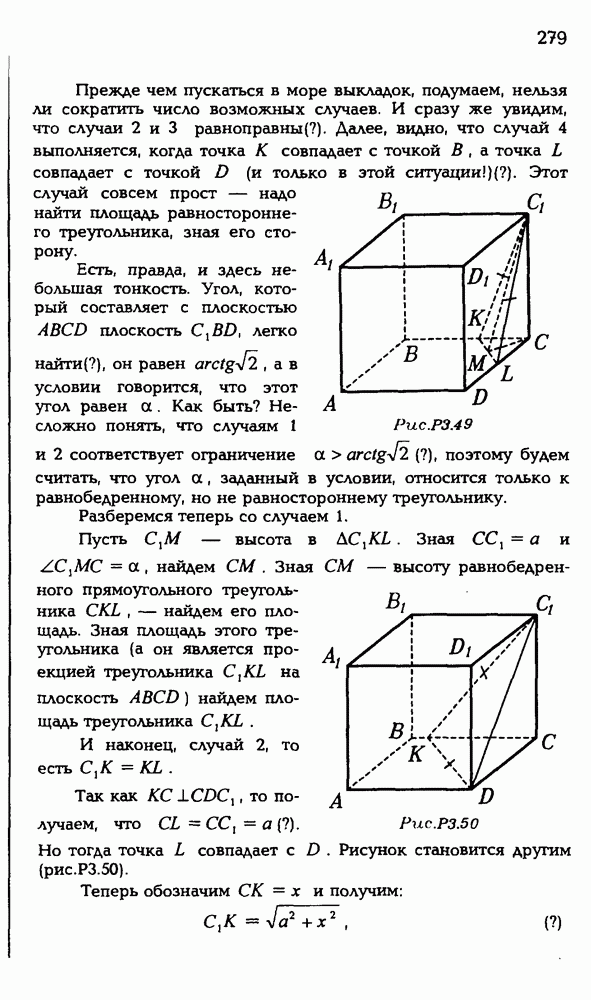
2.4. В правильной треугольной пирамиде известен двугранный угол при основании. Как найти двугранный угол при боковом ребре?
Обычный путь решения таков. Выбираем пару ребер пирамиды, которые являются ребрами двух двугранных углов, о которых идет речь в задаче. Чтобы рисунок был понагляднее, выберем скрещивающиеся ребра пирамиды. Итак, пусть в пирамиде РАВС выбраны ребра  Рисуем далее линейные углы двугранных углов при основании (ZPKC) и при боковом ребре [ZALB)
Рисуем далее линейные углы двугранных углов при основании (ZPKC) и при боковом ребре [ZALB)

Рис. Р 3.26
(рис. Р 3.26). Тут уже возможны "неприятности”, точка L может оказаться за пределами пирамиды — не на ребре  а на его продолжении). Примем величину угла при основании за а, а величину угла при боковом ребре за (3. Нам требуется выразить величину (3 через величину а. Для этого, обычно, вводят линейный параметр, то есть считают известным некий полезный для решения задачи отрезок. Примем, к примеру, длину отрезка АВ за а или за 1, или еще лучше за 2, чтобы удобнее делить на 2. Затем находим цепочку треугольников, пройдя по которой, мы сможем найти угол Р, имея угол а и отрезок
а на его продолжении). Примем величину угла при основании за а, а величину угла при боковом ребре за (3. Нам требуется выразить величину (3 через величину а. Для этого, обычно, вводят линейный параметр, то есть считают известным некий полезный для решения задачи отрезок. Примем, к примеру, длину отрезка АВ за а или за 1, или еще лучше за 2, чтобы удобнее делить на 2. Затем находим цепочку треугольников, пройдя по которой, мы сможем найти угол Р, имея угол а и отрезок  (Разумеется, найти угол — все равно что найти какую-либо его тригонометрическую функцию.) Все это несложно и полезно проделать самому.
(Разумеется, найти угол — все равно что найти какую-либо его тригонометрическую функцию.) Все это несложно и полезно проделать самому.
Используя соотношения в трехгранном угле — главным образом теорому косинусов — мы можем решить задачу быстрее и при этом избежать “неприятностей”, связанных с расположением точек на рисунке.
Рассмотрим трехгранный угол с вершиной А и ребрами АВ, АС, АР. По теореме косинусов запишем такое равенство

Обозначим  запишем его покрасивее:
запишем его покрасивее:

Отсюда получаем

В том же трехгранном угле запишем теорему косинусов для двугранного угла при ребре 

Перепишем эту формулу покрасивее:

В принципе, если говорить о геометрии — задача решена. Из формулы (1) надо выразить  через известный по условию
через известный по условию  , затем выразить
, затем выразить  через
через  , после чего получим косинус нужного нам угла
, после чего получим косинус нужного нам угла  . После выкладок
. После выкладок  получается
получается  . Задача решена.
. Задача решена.
ЗАДАЧИ К § 6
2.5. Как вычислить расстояние между двумя точками на поверхности цилиндра, если измерения можно проводить только на его поверхности?
Могут представиться разные ситуации: 1) обе точки лежат на боковой поверхности цилиндра; 2) одна точка лежит на боковой поверхности цилиндра, а другая — на его основании; 3) обе точки лежат на основаниях цилиндра и при этом: а) на одном и том же основании и б) на разных основаниях. Ситуация а) относится к планиметрии и в данном случае тривиальна.
Наиболее принципиальный случай в ситуации 1). Пусть две точки лежат на боковой поверхности цилиндра, расстояние между ними надо найти, не забираясь внутрь цилиндра — это легко себе представить, если цилиндр сделан, к примеру, из металла. (Обратите внимание, что надо найти расстояние между двумя точками в пространстве, а не по поверхности цилиндра.)

Рис. Р 3.27
Для вычисления расстояния между двумя точками можно воспользоваться соотношениями в треугольнике, где лежит соответствующий отрезок, или пространственной теоремой Пифагора. В данном случае нужный нам треугольник лежит внутри цилиндра, и потому к нему не подобраться. Пойдем вторым путем.
Для применения пространственной теоремы Пифагора проведем три взаимно перпендикулярные прямые, естественно, связанные с цилиндром. Пусть одна из них проходит через ось цилиндра, а две другие взаимно перпендикулярные прямые проходят через диаметры нижнего основания (рис. Р 3.27). Пусть А и В — данные точки,  — проекции
— проекции
отрезка АВ на эти прямые. Тогда согласно пространственной теореме Пифагора  Можно заметить, что
Можно заметить, что  равно квадрату длины проекции отрезка АВ на плоскость нижнего основания цилиндра).
равно квадрату длины проекции отрезка АВ на плоскость нижнего основания цилиндра).  — разность расстояний точек А и В до плоскости нижнего основания цилиндра. Теперь действуем так: через точки А и В проводим образующие цилиндра до пересечения с нижним основанием в точках
— разность расстояний точек А и В до плоскости нижнего основания цилиндра. Теперь действуем так: через точки А и В проводим образующие цилиндра до пересечения с нижним основанием в точках  соответственно. Измерим
соответственно. Измерим  Находим:
Находим:

В остальных случаях задача принципиально решается так же. В случае 3,6) надо преодолеть небольшую техническую трудность — найти проекцию одной из точек на плоскость основания, в которой лежит другая из них (?).
Условие этой реальной задачи можно усложнить (самим!). Можно, например, сделать естественное предположение о том, что к основаниям цилиндра не подобраться. Скажем, данный цилиндр — это достаточно длинная труба или этих оснований вообще нет — отломаны. Как решить задачу в этом случае?
Как и во всякой задаче с реальными объектами, при решении могут появиться чисто практические вопросы. Например, здесь: а какие измерительные приборы имеются? А что можно делать на поверхности цилиндра?
Сначала получите хоть какое-либо решение задачи, и для этого можете считать, что у вас есть любые средства и возможности. Затем постарайтесь свести эти средства и возможности до минимума, буквально до подручных средств. В данной задаче практически можно обойтись только линейкой с делениями (если цилиндр не слишком большой для этой линейки). А.
ЗАДАЧИ К § 7
2.6. Дана прямая треугольная призма достаточной высоты. Докажите, что ее можно пересечь плоскостью так, чтобы в сечении получился равносторонний треугольник.
Пусть треугольник ABC является перпендикулярным сечением призмы. Пусть  или
или  Если в сечении призмы можно получить равносторонний треугольник, то любой треугольник, плоскость которого будет параллельна плоскости этого треугольника, также будет
Если в сечении призмы можно получить равносторонний треугольник, то любой треугольник, плоскость которого будет параллельна плоскости этого треугольника, также будет
равносторонним!?). Поэтому без ограничения общности мы можем считать, что одна из вершин равностороннего треугольника, находится в точке С . Пусть  искомый треугольник (рис. Р 3.28). Обозначим
искомый треугольник (рис. Р 3.28). Обозначим  Если удастся найти такие х и у, что
Если удастся найти такие х и у, что  то задача будет решена. (Теперь ясно, почему одну из вершин искомого треугольника взяли в точке С . Если бы не это, то пришлось бы вводить еще одно неизвестное расстояние
то задача будет решена. (Теперь ясно, почему одну из вершин искомого треугольника взяли в точке С . Если бы не это, то пришлось бы вводить еще одно неизвестное расстояние  и решение получилось бы длиннее.)
и решение получилось бы длиннее.)

Рис. Р 3.28
Для нахождения х и у легко составить такую систему:

Эту систему решите самостоятельно.
Кроме того, заметим, что данный рисунок не является единственно возможным. Искомый треугольник может располагаться так, что его вершины  , будут находиться по разные стороны от (ABC). Тогда система примет несколько другой
, будут находиться по разные стороны от (ABC). Тогда система примет несколько другой  . Решение ее будет таким же. Впрочем, без рассмотрения второй системы можно обойтись, сведя второй случай к первому (?).
. Решение ее будет таким же. Впрочем, без рассмотрения второй системы можно обойтись, сведя второй случай к первому (?).
Технические трудности существенно возрастут, если вы захотите по этой же идее решить задачу б). Поэтому перейдем к более геометричному решению этой задачи.
Прежде всего заметим, что хотя бы один из двугранных углов данной призмы меньше  Выберем на ребре этого двугранного угла призмы точку А и будем строить равносторонний треугольник с вершиной в точке А, стороны которого лежат на гранях призмы.
Выберем на ребре этого двугранного угла призмы точку А и будем строить равносторонний треугольник с вершиной в точке А, стороны которого лежат на гранях призмы.
Мы тем самым несколько ослабляем требование задачи, а значит, несколько упрощаем ее.
Пусть АК и AL — два равных отрезка в гранях призмы  Тогда ясно, что треугольник AKL равносторонний (рис. Р З.29.). Если мы продлим его стороны АК и AL до пересечения с ребрами призмы, то получим треугольник
Тогда ясно, что треугольник AKL равносторонний (рис. Р З.29.). Если мы продлим его стороны АК и AL до пересечения с ребрами призмы, то получим треугольник  Очевидно, что он будет равносторонним, а значит, искомым, если
Очевидно, что он будет равносторонним, а значит, искомым, если  . Основная идея решения задачи
. Основная идея решения задачи

Рис. Р 3.29
будет основана на том, что "ключевой" треугольник AKL такой, что  всегда можно построить.
всегда можно построить.
Самый трудный момент решения — понять, при каком условии будут параллельны  Для этого мы проведем перпендикулярное сечение призмы ABC. Пусть
Для этого мы проведем перпендикулярное сечение призмы ABC. Пусть  проекция отрезка KL на плоскость
проекция отрезка KL на плоскость  Оказывается,
Оказывается,  тогда и только тогда, когда
тогда и только тогда, когда  Значит, чтобы добиться параллельности
Значит, чтобы добиться параллельности  и (KL), достаточно добиться параллельности
и (KL), достаточно добиться параллельности  и [ВС). А это сделать можно.
и [ВС). А это сделать можно.
Точку К можно получить сколь угодно близкой к точке А (?), но из этого следует, что

Теперь поменяем ролями точки К и L. Но тогда

Из соображений непрерывности найдется такое положение точек К и  что
что  Но тогда
Но тогда  , т.е.
, т.е.  и "ключевой" треугольник существует.
и "ключевой" треугольник существует.
Для окончательной отделки решения необходимо обосновать расположение треугольника AKL выше плоскости  Но это вы сделайте самостоятельно
Но это вы сделайте самостоятельно 
2.7. В наклонной треугольной призме  основанием является равнобедренный прямоугольный треугольник
основанием является равнобедренный прямоугольный треугольник  грань
грань  — квадрат. Боковое ребро призмы равно а, высота призмы равна
— квадрат. Боковое ребро призмы равно а, высота призмы равна  . Найти угол между: а) боковым ребром и скрещивающимся с ним ребром основания; б) боковым ребром и плоскостью основания; в) плоскостью боковой грани, являющейся квадратом и плоскостью основания; г) плоскостями боковых граней.
. Найти угол между: а) боковым ребром и скрещивающимся с ним ребром основания; б) боковым ребром и плоскостью основания; в) плоскостью боковой грани, являющейся квадратом и плоскостью основания; г) плоскостями боковых граней.
Прежде всего сделаем хороший рисунок (рис. Р 3.30).

Для нахождения угла между СС, и ВС (обозначим его через  применим формулу, полученную в задаче 10 к главе 1. Для этого спроектируем вершину С, на плоскость
применим формулу, полученную в задаче 10 к главе 1. Для этого спроектируем вершину С, на плоскость 
— проекция точки  и проведем отрезок
и проведем отрезок  Теперь по этой формуле
Теперь по этой формуле

Угол DCC, обозначим (для удобства записей) через 
Исходя из условия задачи  поэтому
поэтому

Поэтому


Рис. Р 3.30
Найдя тригонометрическую функцию угла, мы можем считать, что нашли сам угол (эта договоренность действует во всех подобных задачах).
б) А этот угол мы нашли при решении задачи из пункта а). Вы это замечаете?
в) И этот угол фактически уже найден при решении задачи а). Если вы пока не видите в чем дело, проведите среднюю линию квадрата АВАХВХ, параллельную боковому ребру призмы и продлите CD до пересечения с АВ .
г) Довольно просто искать двугранные углы по теореме косинусов для трехгранного угла.
В нашем случае

по условию  поэтому
поэтому

но

И так как мы обозначили  через х , то
через х , то

Найти  , зная
, зная  (найденный в пункте а)), — дело техники, причем тригонометрической.
(найденный в пункте а)), — дело техники, причем тригонометрической.
Попробуйте сами тем же методом найти угол (то есть его тригонометрическую функцию) между плоскостями граней 
Стоит еще заметить, что угол между плоскостями не может быть тупым. Поэтому, если в результате вычислений мы получаем отрицательный косинус, то это значит,  мы нашли не сам угол между плоскостями, а смежный к нему.
мы нашли не сам угол между плоскостями, а смежный к нему.
ЗАДАЧИ К § 8
2.8. Через середину высоты усеченного конуса провели сечение, параллельное основанию. Были высказаны два предположения: 1) площадь сечения равна среднему арифметическому площадей оснований и 2) площадь сечения равна среднему геометрическому площадей оснований. Верно ли какое-либо из этих предположений?
Прежде всего заметим, что первое предположение выглядит похожим на истину. В планиметрии есть нечто подобное — теорема о средней линии трапеции.
Ответ на вопрос задачи можно получить непосредственным вычислением площади такого сечения(?). Но мы будем действовать иначе.
При решении достаточно сложной задачи обычно возникают разные предположения. Прежде чем их начать доказывать, полезно убедиться в том, что это стоит делать. Для этого можно привести примеры, в которых это предположение верно, но можно поискать и контрпримеры, в которых оно неверно, тогда и доказывать нет смысла.
Примером или контрпримером часто бывают предельные случаи для ситуации, описанной в задаче.
В нашей задаче возьмем в качестве такого предельного случая конус, который получается из данного усеченного конуса, когда площадь одного основания равна нулю. Тогда согласно предположению площадь сечения равна половине площади другого основания. Но это неверно(?). Значит, для нашего предположения найден контрпример и доказывать его нет смысла.
В заключении подумайте, что еще стоит добавить для окончания решения.
2.9. Пусть R — радиус основания конуса, L — длина его образующей, Н — его высота,  — диаметр описанной около конуса сферы. Найдите зависимость между этими величинами.
— диаметр описанной около конуса сферы. Найдите зависимость между этими величинами.
Задача эта простая, но есть в ней несколько особенностей, которые стоит запомнить. Во-первых, и конус, и сфера, описанная около него, — фигуры вращения. Поэтому лучше рисовать комбинацию не пространственных фигур, а тех, которые при вращении дают данную нам пространственную комбинацию. В нашем случае рисунок таков (рис. Р 3.31).

Рис. Р 3.31
Здесь нарисована полуокружность с диаметром  , а в ней расположен прямоугольный треугольник, один из катетов которого лежит на диаметре полуокружности.
, а в ней расположен прямоугольный треугольник, один из катетов которого лежит на диаметре полуокружности.
Если эту плоскую конфигурацию вращать вокруг диаметра, то мы и получим сферу, описанную вокруг конуса.
Во-вторых, с самого начала не ясно, где расположен центр сферы относительно конуса: в нем, вне его или на его основании. При обычном способе решения с помощью треугольников приходится разбирать все эти три случая.
Мы сделаем иначе. Проведем отрезок ВР и рассмотрим теперь новый рисунок (рис. Р 3.32).

Рис. Р 3.32
На этом рисунке треугольник АВР — прямоугольный, ибо угол В опирается на диаметр окружности АР . Но тогда можно использовать известные соотношения в прямоугольном треугольнике:

К этим двум зависимостям добавим еще ту, что получается по теореме Пифагора из треугольника 

Теперь вы можете сами поупражняться в решении задач такого типа: даны две из этих четырех величин и требуется найти остальные.
ЗАДАЧИ К § 9
2.10. В правильной четырехугольной пирамиде известны сторона основания и высота. Как вычислить площадь сечения, проходящего через сторону основания перпендикулярно противоположной боковой грани? Выберите сами числовые данные и получите результат.
Пусть  — искомое сечение (рис. Р 3.33). Прежде всего определим вид этого четырехугольника. Так как
— искомое сечение (рис. Р 3.33). Прежде всего определим вид этого четырехугольника. Так как  то
то  Но тогда
Но тогда  (Почему?)
(Почему?)

Рис. Р 3.33
Предположим, что  , тогда четырехугольник
, тогда четырехугольник  — параллелограмм. Учитывая, что
— параллелограмм. Учитывая, что  , получим (по признаку параллельности плоскостей), что плоскости ADD, и SCC, параллельны, — но они имеют общую точку Р. Значит, наше предположение неверно и на самом деле
, получим (по признаку параллельности плоскостей), что плоскости ADD, и SCC, параллельны, — но они имеют общую точку Р. Значит, наше предположение неверно и на самом деле  — трапеция. (К тому же результату могли бы прийти иначе:
— трапеция. (К тому же результату могли бы прийти иначе:  ),
),  следовательно,
следовательно,  не параллелограмм.)
не параллелограмм.)
Нам известны сторона основания пирамиды и высота PQ. Запишем формулу площади трапеции 

В ней неизвестны  и А — расстояние между прямыми CD и
и А — расстояние между прямыми CD и  . Рассмотрим сечение пирамиды
. Рассмотрим сечение пирамиды  где точка К — середина АВ, точка L — середина
где точка К — середина АВ, точка L — середина  Обозначим буквой М точку пересечения КР и
Обозначим буквой М точку пересечения КР и  Так как
Так как  то
то  Значит, LM — высота трапеции и ее длина есть неизвестная величина
Значит, LM — высота трапеции и ее длина есть неизвестная величина  . Кроме того,
. Кроме того,  (Обоснуйте это.)
(Обоснуйте это.)
Для удобства дальнейших вычислений рассмотрим отдельно треугольник PKL (рис. Р 3.34). Он равнобедренный  . В нем известно KL (равное AD). РК находим из
. В нем известно KL (равное AD). РК находим из
треугольника PKQ по теореме Пифагора. Так как в треугольнике PKL известны три стороны, то можно найти его площадь, а уже затем и высоту LM на боковую сторону РК .
Перейдем к вычислению  . Так как
. Так как  , то
, то  подобен ЫРАВ , а коэффициентом подобия является отношение
подобен ЫРАВ , а коэффициентом подобия является отношение 
Этот коэффициент равен также отношению  , которое можно вычислить из треугольника
, которое можно вычислить из треугольника 
Пусть, к примеру,  (чтобы легче было делить пополам).
(чтобы легче было делить пополам).  Теперь проведите все вычисления.
Теперь проведите все вычисления.

Рис. Р 3.34
Решая эту задачу, предположили, что искомое сечение является четырехугольником, и доказали, что оно является трапецией Но оно необязательно будет четырехугольником. Рассмотрим треугольник PKL. В нем LM — высота из вершины основания на боковую сторону. Однако хорошо известно, что такая высота необязательно пересекает именно сторону треугольника — она может проходить и через Р, если треугольник PKL прямоугольный, и проходить за стороной РК , если треугольник PKL тупоугольный. Соответственно, площадь искомого сечения будет получаться другой. (Объясните.)
В связи с этим надо подумать: а какое именно сечение получается при выбранных нами числовых данных — трапеция, треугольник или отрезок? Для этого определим вид треугольника 

Так как  то треугольник PKL остроугольный, значит, высота LM падает именно на сторону РК , а тогда сечение является трапецией, как мы и предполагали.
то треугольник PKL остроугольный, значит, высота LM падает именно на сторону РК , а тогда сечение является трапецией, как мы и предполагали.
2.11. Известны длины ребер тетраэдра. Как найти его высоту?
Пусть РАВС — данный тетраэдр, PQ — искомая высота.
Длину отрезка PQ найдем из какого-либо треугольника, в котором он находится. Таким треугольником может быть треугольник  где
где  перпендикуляр из Q на (ВС) (рис. Р 3.35).
перпендикуляр из Q на (ВС) (рис. Р 3.35).  находим из треугольника РВС
находим из треугольника РВС  линейный угол двугранного угла при ребре ВС . Его можно найти по теореме косинусов для трехгранного угла с вершиной В (или
линейный угол двугранного угла при ребре ВС . Его можно найти по теореме косинусов для трехгранного угла с вершиной В (или  ). После этого находим
). После этого находим 
В этом несложном решении осталось обосновать его независимость от рисунка. Положение точки  для решения несущественно(?). Впрочем, если точка Q находится внутри треугольника ABC, то хотя бы одна проекция точки Q на прямые, проходящие через стороны треугольника, будет лежать внутри стороны треугольника ABC (?), ее можно назвать точкой
для решения несущественно(?). Впрочем, если точка Q находится внутри треугольника ABC, то хотя бы одна проекция точки Q на прямые, проходящие через стороны треугольника, будет лежать внутри стороны треугольника ABC (?), ее можно назвать точкой  . А что если точка Q находится вне треугольника
. А что если точка Q находится вне треугольника  Есть два варианта ответа. Первый — убедиться в том, что для любого положения точки Q по отношению к треугольнику ABC решение принципиально не меняется (?). Второй — доказать, что в любом тетраэдре проекция хоть одной вершины лежит внутри противоположной ее грани, и тем самым свести задачу к уже рассмотренному случаю(?).
Есть два варианта ответа. Первый — убедиться в том, что для любого положения точки Q по отношению к треугольнику ABC решение принципиально не меняется (?). Второй — доказать, что в любом тетраэдре проекция хоть одной вершины лежит внутри противоположной ее грани, и тем самым свести задачу к уже рассмотренному случаю(?).

Рис. Р 3.35
Вычислительная часть этой задачи довольно длинная. Тем любопытнее то обстоятельство, что ответ может быть получен без всяких вычислений. Отрезок, равный высоте тетраэдра, может быть построен циркулем и линейкой 
Эту задачу мы решали в предположении, что тетраэдр дан. Но на нее можно посмотреть несколько иначе.
Поставить вопрос: "Можно ли построить тетраэдр, ребра которого равны шести данным отрезкам?" (Аналогичная задача на плоскости хорошо известна.) К решению этой задачи можно подойти разными путями. Один из них идет от задачи, рассмотренной нами только 
2.12. Найдите радиус шара, вписанного в правильную  -угольную пирамиду, зная сторону основания а и плоский угол при вершине
-угольную пирамиду, зная сторону основания а и плоский угол при вершине 

Рис. Р 3.36
Для решения достаточно рассмотреть часть такой пирамиды, являющейся тетраэдром. Основанием этого тетраэдра является треугольник, у которого две вершины — это две соседние вершины правильного  -угольника, лежащего в основании пирамиды, а третья вершина — центр основания этого правильного многоугольника. Вершина этого тетраэдра — это вершина данной пирамиды (рис. Р 3.36).
-угольника, лежащего в основании пирамиды, а третья вершина — центр основания этого правильного многоугольника. Вершина этого тетраэдра — это вершина данной пирамиды (рис. Р 3.36).
На этом рисунке PQ — высота данной пирамиды и ребро тетраэдра, QAB — основание тетраэдра.
Центр О вписанной сферы лежит на PQ — в той точке, где PQ пересекается с биссектором двугранного угла при ребре АВ или, что все равно, с биссектрисой СО линейного угла PCQ этого двугранного угла, начало которой в середине 

Рис. Р 3.37
Треугольник PCQ рассмотрим отдельно  Проведем в нем еще
Проведем в нем еще  Что есть на этом рисунке?
Что есть на этом рисунке?  где
где  — радиус вписанного шара(?). PQ - высота данной пирамиды, PC — ее апофема,
— радиус вписанного шара(?). PQ - высота данной пирамиды, PC — ее апофема,  — радиус окружности, вписанной в основание пирамиды.
— радиус окружности, вписанной в основание пирамиды.
Перейдем к самим вычислениям.
Из подобия треугольников POD и  имеем:
имеем:

 где
где  — высота данной пирамиды.
— высота данной пирамиды.

Тогда

откуда

Высоту Я находим из APQC по теореме Пифагора. Получаем

И, окончательно,

Можно еще попытаться упростить полученное выражение, но это уже неважно.
И еще. Когда вы будете знать формулы для объемов, вернитесь к этой задаче. Тогда ее можно будет сделать короче.
2.13. В данную правильную треугольную усеченную пирамиду с боковым ребром а можно поместить сферу, касающуюся всех граней, и сферу, касающуюся всех ребер. Найти стороны оснований пирамиды.

Рис. Р 3.38
Усеченную пирамиду сначала надо нарисовать. Удобно сделать так — сперва нарисовать исходную "полную" пирамиду, а потом отсечь от нее "макушку".
В нашем случае рисунок будет такой (рис. Р 3.38).
Данная нам пирамида —  — высота "полной" пирамиды,
— высота "полной" пирамиды,  — ее часть до верхнего основания усеченной пирамиды.
— ее часть до верхнего основания усеченной пирамиды.
Эта задача сводится к планиметрической, при этом не надо рисовать ни одной из данных сфер.
Так как в усеченную пирамиду можно вписать сферу, касающуюся всех ребер, то в ее боковую грань можно вписать окружность (?). Обозначим  будет удобнее делить эти отрезки пополам) и для описанного четырехугольника
будет удобнее делить эти отрезки пополам) и для описанного четырехугольника  получим, что
получим, что  откуда
откуда


Рис. Р 3.39
Из существования вписанного шара следует, что существует полуокружность, расположенная в трапеции  — апофема "полной" пирамиды) так, что ее центр лежит в середине
— апофема "полной" пирамиды) так, что ее центр лежит в середине  а сама она касается остальных трех сторон трапеции(?).
а сама она касается остальных трех сторон трапеции(?).
Сделаем отдельный рисунок (рис. Р 3.39). О - центр шара,  — точки касания. Но тогда
— точки касания. Но тогда

Осталось выразить эти величины через х и у. Из AABC

Из 

Из трапеции 

получаем уравнение

Решив систему уравнений (1) и (2), получим, что стороны оснований равны 
2.14. В правильной четырехугольиой пирамиде центры вписанного и описанного шаров совпадают. Найдите косииус двугранного угла при основании.
Пусть PABCD — правильная четырехугольная пирамида, PQ — ее высота, О — центр вписанного и описанного шара,

Рис.
РК — апофема пирамиды, OS — перпендикуляр на грань PCD (рис. Р 3.40). Тогда ОР — радиус описанного шара, OS  — радиус вписанного шара. Обозначим QK через
— радиус вписанного шара. Обозначим QK через  РК — через у, радиус описанного шара —
РК — через у, радиус описанного шара —  а радиус вписанного —
а радиус вписанного —  . Искомый косинус выражаем из
. Искомый косинус выражаем из 

Так как  то из
то из  запишем
запишем

Получили первое уравнение

Из  по теореме Пифагора
по теореме Пифагора

значит,

И, наконец, из  в котором
в котором  по теореме Пифагора имеем
по теореме Пифагора имеем  значит,
значит,

Запишем полученные уравнения как систему

В этой системе четыре неизвестных, а уравнений всего три. Как же ее решать? А ее и не надо решать, ибо нужны не х и у, а их отношение.
Из (3) получаем  подставив это значение
подставив это значение  в (2), получаем
в (2), получаем

отсюда

Из (1) получаем

Приравняем правые части

Левую часть можно упростить, ибо знаменатель раскладывается на множители)?). Получаем

Числитель и знаменатель левой части поделим на  Получим
Получим

Но  . Тогда
. Тогда 
Решая это тригонометрическое уравнение, получим три корня, причем два из них не подходят по условию задачи. Остается один, именно

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧИТАТЕЛЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ
- § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 1.2. Двугранный угол. Угол между плоскостями.
- 1.3. Плоскость и прямая в пространстве.
- 1.4. Аксиомы стереометрии.
- 1.5. Взаимное расположение двух прямых в пространстве.
- 1.6. Признаки скрещивающихся прямых.
- 1.7. Параллельные прямые.
- 1.8. Параллельное проектирование.
- § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 2.2. О значении перпендикуляра.
- 2.3. Теорема о трех перпендикулярах.
- 2.4. Признак перпендикулярности прямой и плоскости.
- 2.5. Построение плоскости, перпендикулярной данной прямой.
- 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости.
- 2.7. Теорема о прямой, перпендикулярной плоскости.
- 2.8. Перпендикулярность плоскостей.
- 2.9. Ортогональное проектирование.
- § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 3.2. Параллельность и перпендикулярность.
- 3.3. Основная теорема о параллельных плоскостях.
- 3.4. Второй признак параллельности плоскостей.
- 3.5. Расстояние и параллельность.
- 3.6. Сонаправленность лучей и угол между прямыми.
- 3.7. Параллельность и углы.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ
- § 4. СФЕРА И ШАР
- 4.2. Взаимное положение шара и плоскости.
- 4.3. Сфера и многранники.
- 4.4. Вид и изображение шара и сферы.
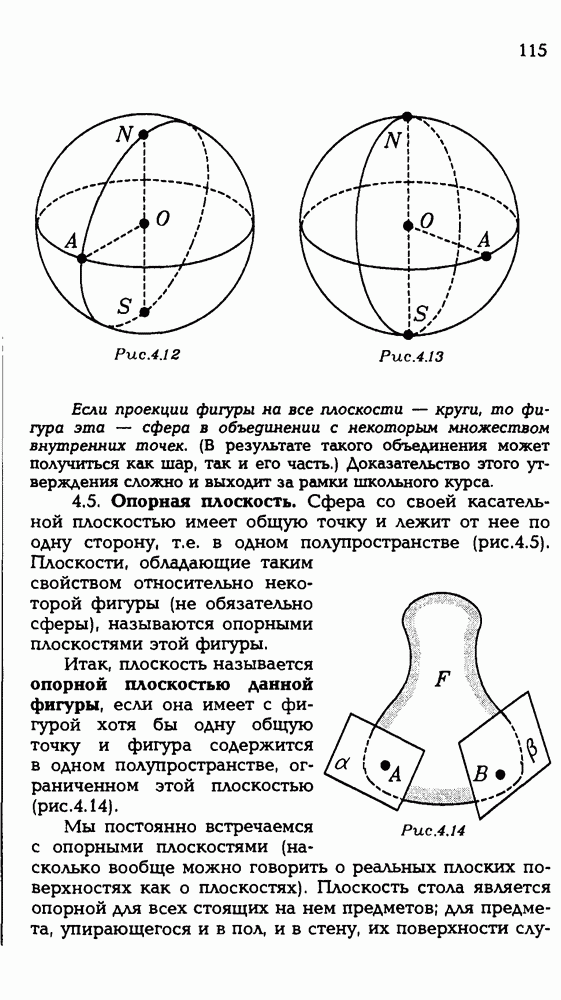
- 4.5. Опорная плоскость.
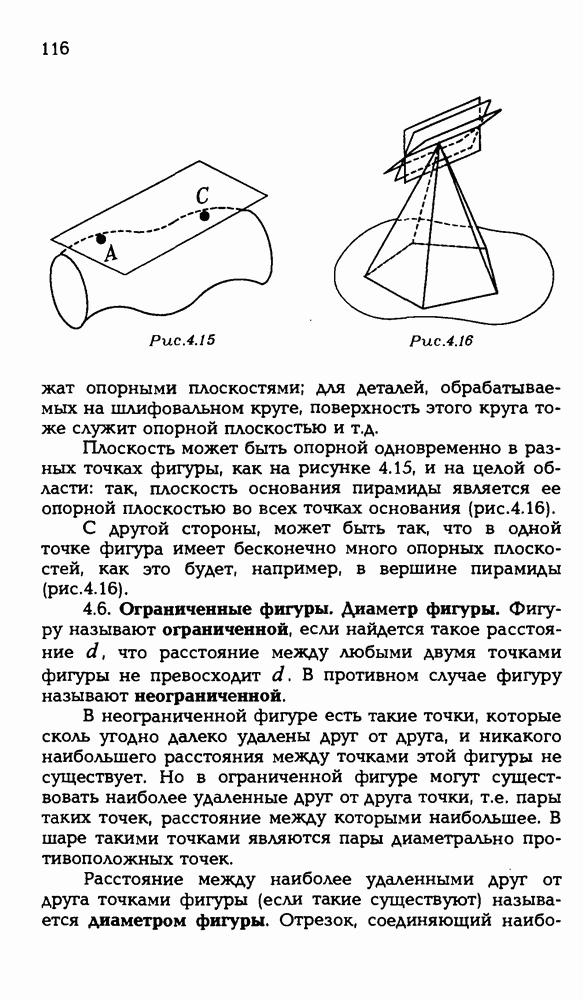
- 4.6. Ограниченные фигуры. Диаметр фигуры.
- 4.7. Опорные плоскости в концах диаметра.
- 4.8. Сфера — фигура вращения.
- 4.9. Симметрия сферы и шара.
- 4.10. Сфера — центрально симметричная фигура.
- 4.11. Сфера — зеркально симметричная фигура.
- 4.12. Отражение в плоскости и отражение в зеркале.
- § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ
- 5.2. Тригонометрия трехгранного угла.
- 5.3. Равенство трехгранных углов.
- 5.4. Сферические треугольники.
- 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников.
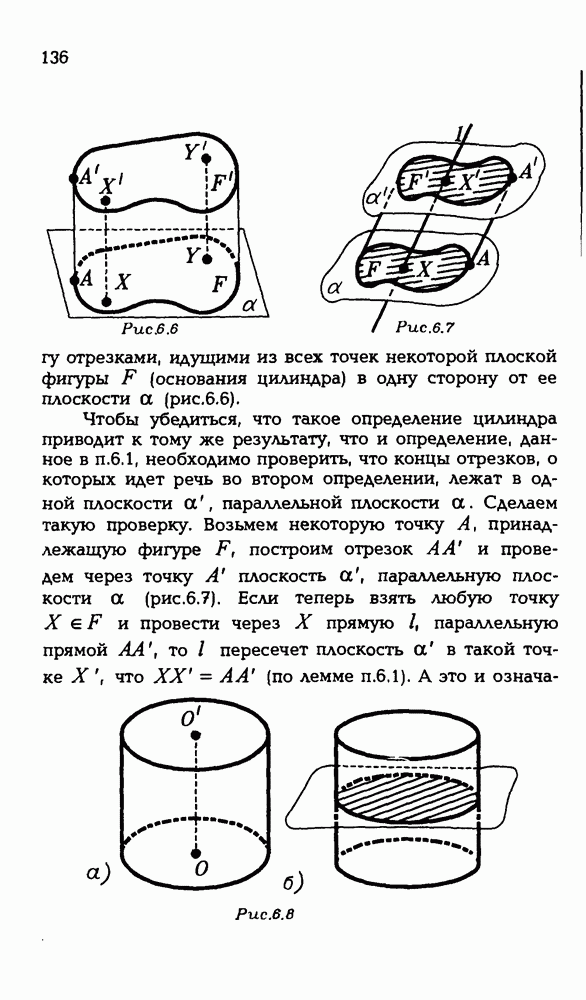
- § 6. ЦИЛИНДР
- 6.2. Другой подход к определению цилиндра.
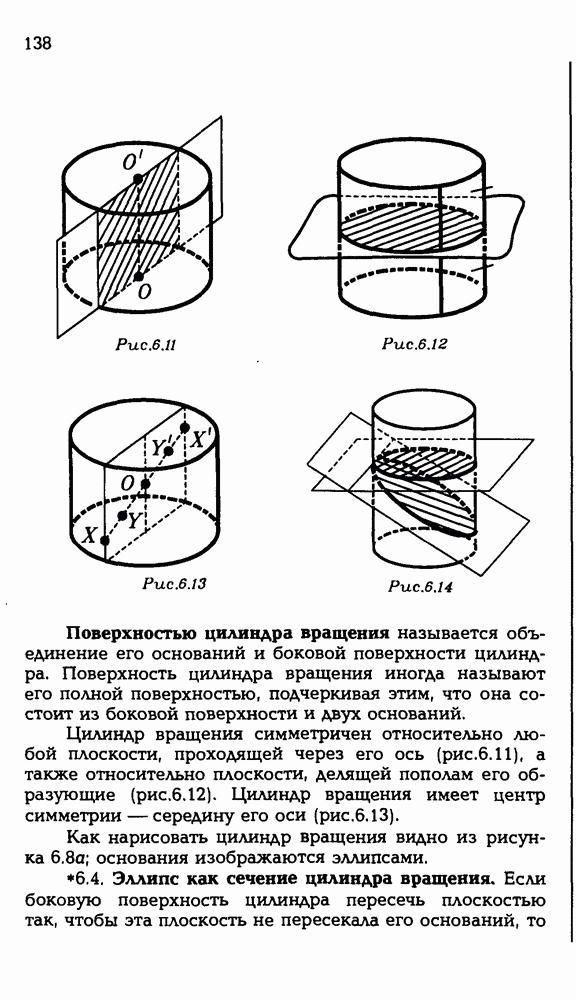
- 6.3. Цилиндр вращения.
- 6.4. Эллипс как сечение цилиндра вращения.
- 6.5. Винтовые линии.
- 6.6. Цилиндры в практике.
- § 7. ПРИЗМА
- 7.2. Параллелепипед.
- 7.3. Прямоугольный параллелепипед.
- 7.4. Симметрия параллелепипеда.
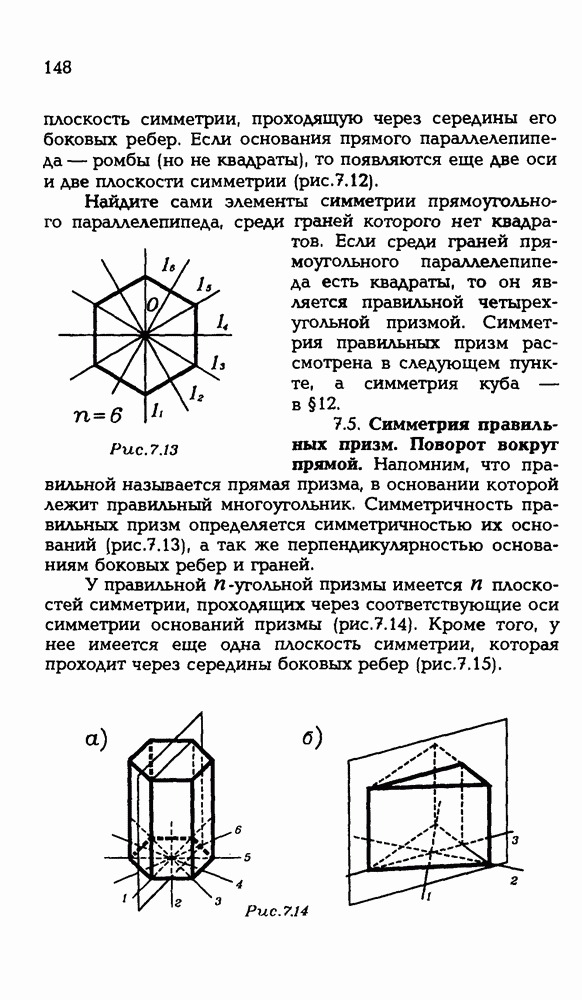
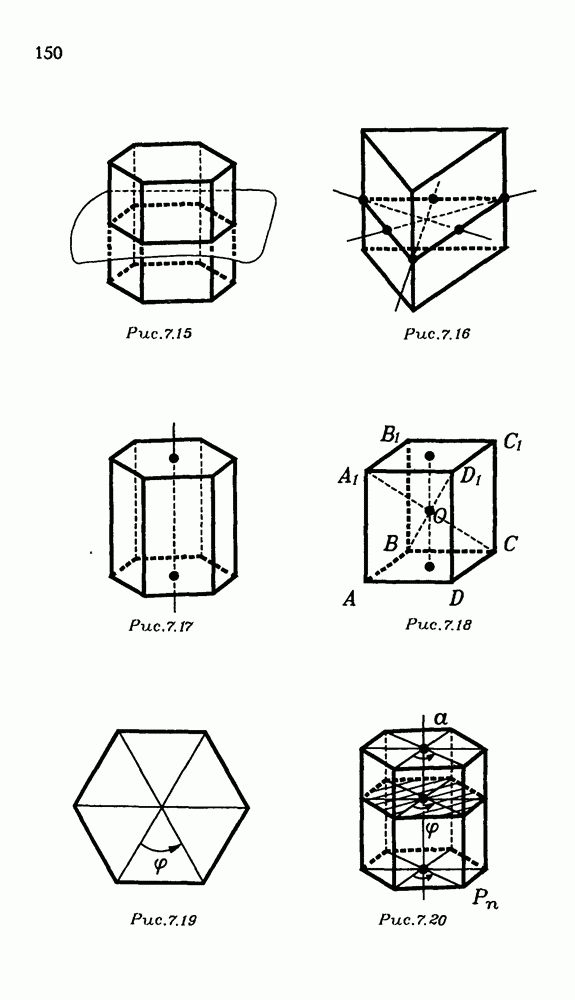
- 7.5. Симметрия правильных призм. Поворот вокруг прямой.
- § 8. КОНУС
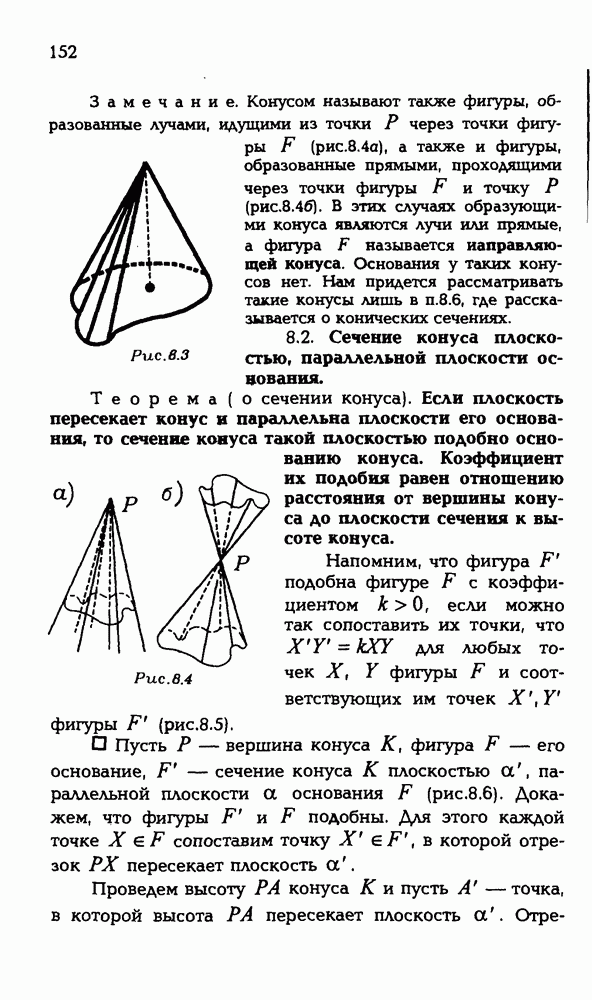
- 8.2. Сечение конуса плоскостью, параллельной плоскости основания.
- 8.3. Конус вращения.
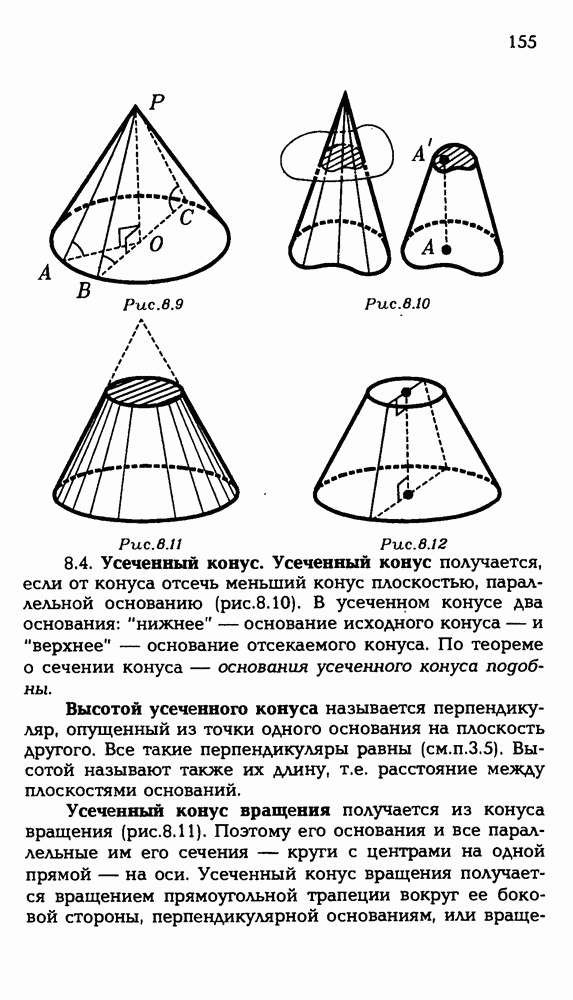
- 8.4. Усеченный конус.
- § 9. ПИРАМИДА
- 9.2. Правильная пирамида.
- 9.3. Симметрия правильной пирамиды.
- 9.4. Конусы и пирамиды в практике.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ
- § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ
- 10.2. Граница и внутренность.
- 10.3. Определение тела и замкнутой плоской области.
- 10.4. Выпуклые фигуры.
- 10.5. Выпуклые тела.
- § 11. МНОГОГРАННИКИ
- 11.2. Выпуклые многогранники.
- 11.3. Теорема Эйлера.
- 11.4. Выпуклые многогранники и выпуклые оболочки.
- 11.5. Многогранная поверхность и развертка.
- 11.6. Развертка выпуклого многогранника.
- § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
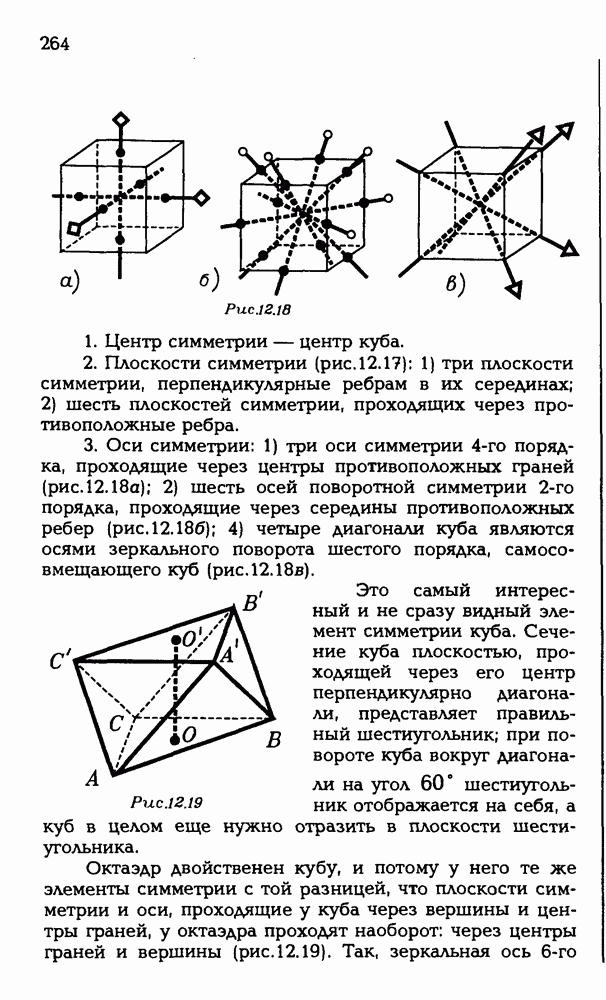
- 12.2. Классификация правильных многогранников.
- 12.3. Полуправильные многогранники.
- 12.4. Симметрия правильных многогранников.
- ЗАДАЧИ С РЕШЕНИЯМИ
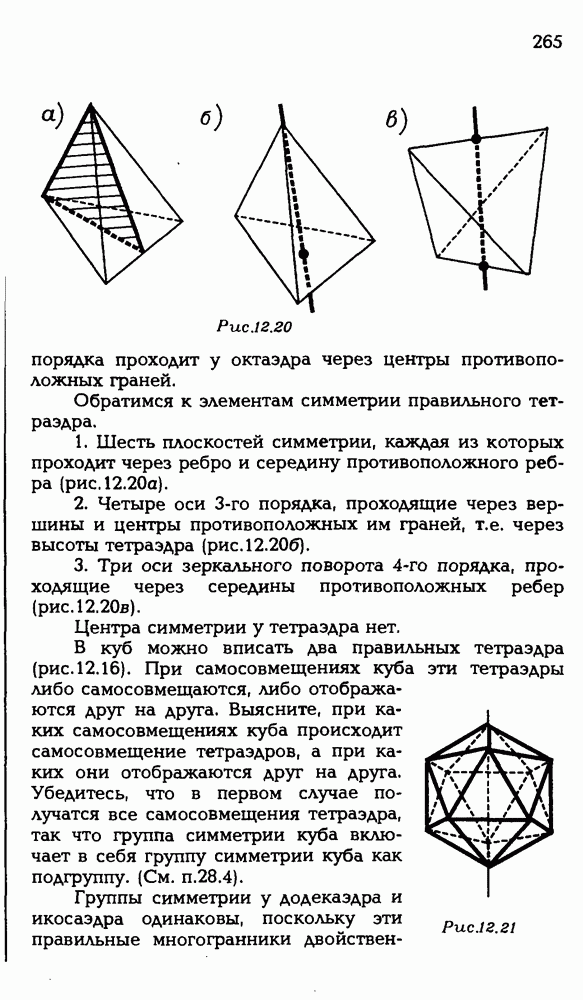
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
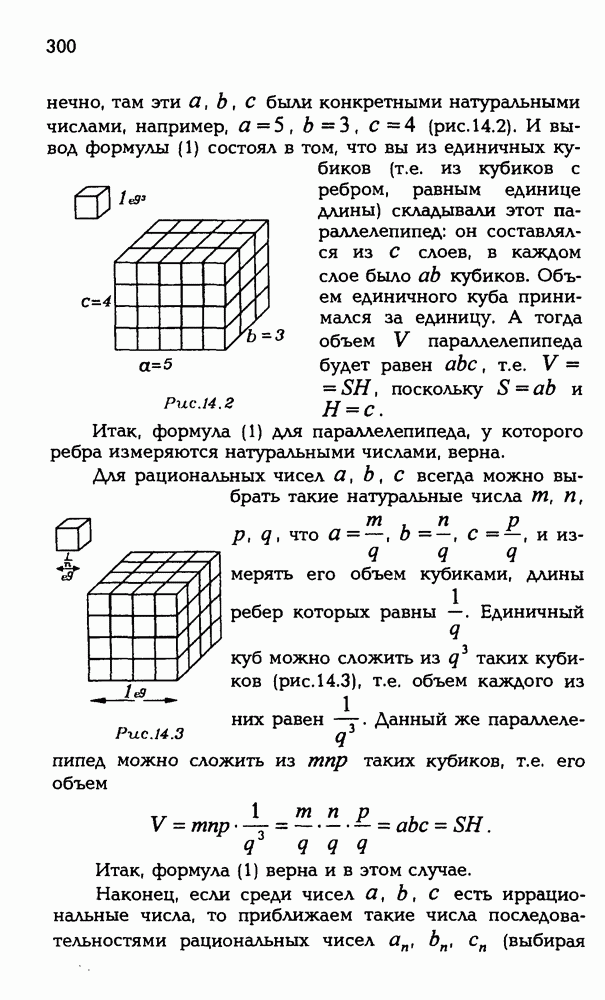
- ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
- § 13. ПОНЯТИЕ ОБЪЕМА
- 13.2. Определение объема.
- 13.3. Геометрические величины.
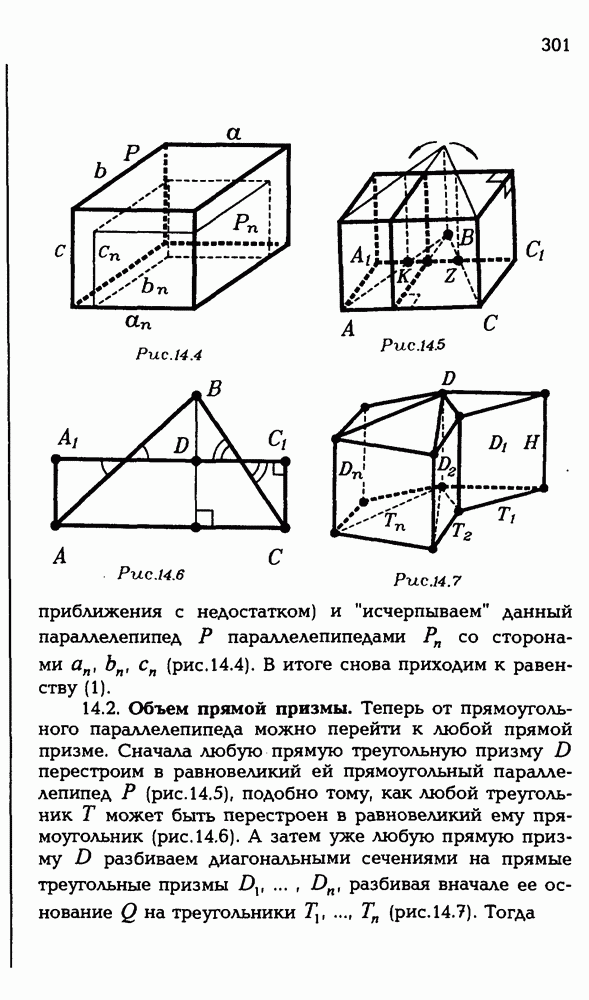
- § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА
- 14.2. Объем прямой призмы.
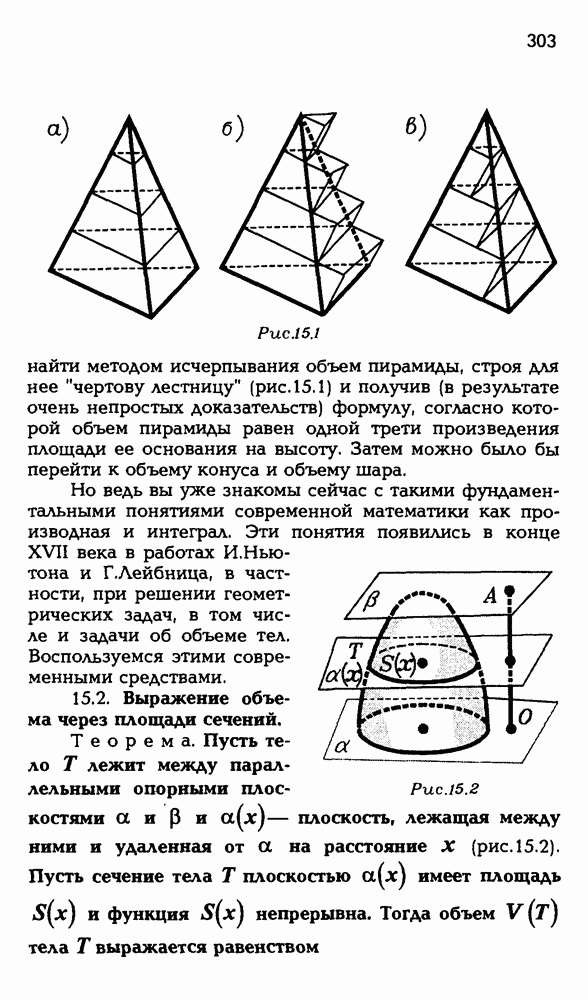
- § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ
- 15.2. Выражение объема через площади сечений.
- § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА
- 16.2. Объем конуса
- 16.3. Объем шара.
- 16.4. Объем тел вращения.
- 16.5. Объем шарового сегмента и шарового сектора.
- § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ
- 17.2. Площадь сферы.
- 17.3. Площадь сферических многоугольников.
- 17.4. Площадь сферического сегмента и сферического пояса.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
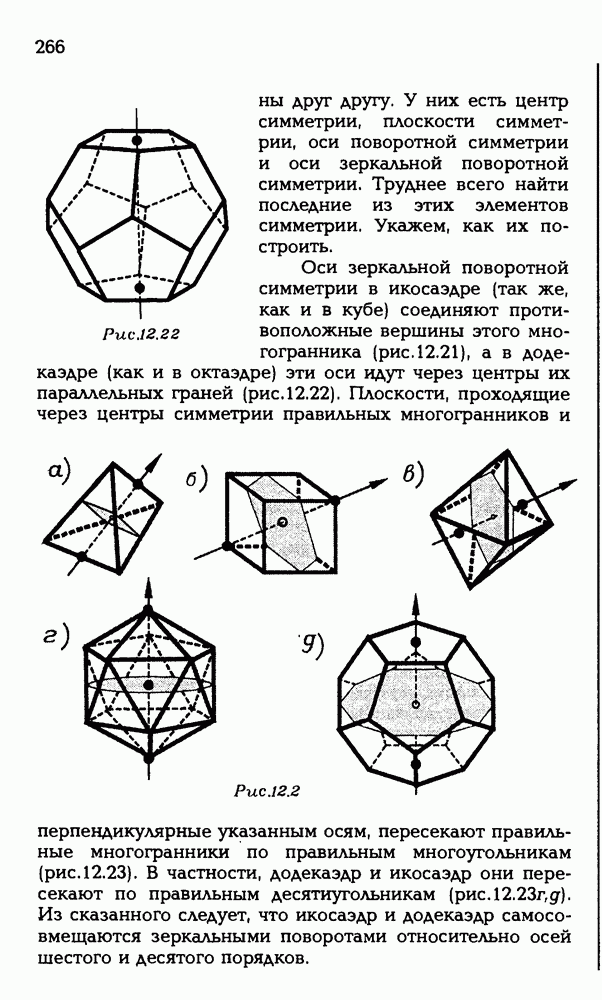
- ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ
- § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- 18.2. Другой способ нахождения координат точки.
- 18.3. Построение точки с данными координатами.
- 18.4. Выражение расстояния между точками.
- § 19. МЕТОД КООРДИНАТ
- 19.2. Уравнения без одной или двух координат.
- 19.3. Некоторые применения метода координат.
- § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ
- 20.2. Полярные координаты.
- 20.3. Цилиндрические координаты.
- 20.4. Сферические координаты.
- 20.5. Координатная сеть.
- § 21. ПОНЯТИЕ ВЕКТОРА
- 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов.
- 21.3. Сонаправленность и равенство векторов.
- 21.4. Признаки равенства векторов.
- 21.5. Радиус-вектор.
- § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 22.2. Разложение вектора на составляющие.
- 22.3. Умножение вектора на число.
- 22.4. Координаты вектора.
- 22.5. Равенство координат векторов и координат точек.
- 22.6. Разложение векторов по базису.
- 22.7. Ориентация базиса.
- § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ
- 23.2. Выражение скалярного произведения через координаты.
- 23.3. Свойства скалярного умножения.
- 23.4. Применения скалярного умножения.
- 23.5. Скалярное произведение и проекции.
- § 24. ВЕКТОРНЫЙ МЕТОД
- 24.2. Общее уравнение плоскости.
- 24.3. Векторное задание отрезка.
- 24.4. Некоторые теоремы о треугольниках и тетраэдрах.
- 24.5. Центр масс системы материальных точек.
- 24.6. Центры масс и выпуклые многогранники.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 6. ПРЕОБРАЗОВАНИЯ
- 25.1. Преобразования фигур.
- 25.2. Определения движения и равенства фигур.
- 25.3. Преобразования симметрии.
- 25.4. Параллельный перенос.
- 25.5. Поворот.
- § 26. СВОЙСТВА ДВИЖЕНИЙ
- 26.2. Общие свойства движений.
- 26.3. Теоремы о задании движений.
- 26.4. Неподвижные точки движений.
- 26.5. Два рода движений.
- 26.6. Теорема подвижности пространства.
- 26.7. Композиция отражений в плоскости.
- § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА
- 27.2. Движения первого рода как винтовые движения.
- 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот.
- 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения.
- § 28. ПОДОБИЕ
- 28.2. Гомотетия.
- 28.3. Свойства подобия.
- 28.4. Группы преобразований.
- § 29. ИНВЕРСИЯ
- 29.2. Аналитическое задание инверсии.
- 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии.
- 29.4. Сохранение величин углов при инверсии.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ОТВЕТЫ И УКАЗАНИЯ
- ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ