| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЗАДАЧИ К § 14
Рисуем
4.1. Нарисуйте цилиндр. Нарисуйте такое его сечение, которое делит его на: а) два равновеликих цилиндра вращения; б) два равновеликих произвольных цилиндра; в) две равновеликие части, не являющиеся цилиндрами.
4.2. Нарисуйте цилиндр. Нарисуйте такое его сечение, которое отсекает от него треть объема.
4.3. Нарисуйте цилиндр. Нарисуйте цилиндр, объем которого в два раза больше объема данного цилиндра.
Планируем
4.4. На плоскости стоит цилиндрический сосуд известных размеров. В сосуд доверху налита вода. Как узнать, на какой высоте над плоскостью будет находиться ее верхний край, если сосуд укрепить на плоскости так, что диагональ его осевого сечения будет перпендикулярна плоскости?
4.5. Прямоугольник со сторонами а и b вращают вокруг: а) каждой из неравных сторон; б) осей его симметрии; в) прямых, параллельных сторонам и удаленных от него на расстояние
h. Как найти отношение объемов полученных тел в каждом случае?
4.6. В единичном кубе через ребро основания проводится сечение. Как вычислить объемы полученных частей куба, если плоскость сечения составляет с плоскостью основания угол 
Представляем
4.7. Как разделить на две равновеликие части: а) куб; б) прямоугольный параллелепипед: в) правильную треугольную призму?
4.8. Как разделить куб на равновеликие части, если их: а) три; б) четыре; в) пять? Постарайтесь предложить как можно больше разных способов.
Решите аналогичную задачу для правильной треугольной призмы.
Оцениваем
4.9. При каком условии достигает граничных значений объем цилиндра, вписанного в: а) сферу радиуса R; б) конус с радиусом R и образующей 
4.10. Как из усеченного конуса сделать цилиндр наибольшего объема?
4.11. Из куска картона квадратной формы делают правильную четырехугольную призму без верхней крышки. Для этого по углам куска отрезают равные квадратики и оставшуюся фигуру склеивают по линиям разрезов. Как при этой операции добиться наибольшего объема у призмы?
4.12. Основанием прямой призмы является квадрат. Призма вписана в полушар радиуса R так, что ее нижнее основание лежит в плоскости большого круга полушара, а вершины верхнего основания лежат на шаровой поверхности. При каком положении призмы ее объем является наибольшим?
4.13. Диагональ прямоугольного параллелепипеда имеет длину d и образует с двумя смежными боковыми гранями равные углы, величина которых равна а. При каком условии объем параллелепипеда будет максимальным?
4.14. При каком условии достигает граничных значений объем: а) правильной четырехугольной призмы с диагональю, равной 1; б) прямоугольного параллелепипеда, у которого одно ребро в два раза больше другого, а диагональ равна 1; в) прямоугольного параллелепипеда, у которого сумма трех измерений равна 1?
4.15. Как из шара радиусом R вырезать правильную призму с наибольшим объемом, если эта призма: а) треугольная; б) четырехугольная?
4.16. Дан полушар. В каком положении находятся в нем имеющие наибольший объем: а) прямоугольный параллелепипед; б) правильная треугольная призма; в) цилиндр?
4.17. Дан конус. В каком положении находятся в нем имеющие наибольший объем; а) прямоугольный параллелепипед; б) правильная треугольная призма; в) цилиндр?
Сделаем
4.18. Через каждое ребро куба проведена плоскость, составляющая одинаковые углы с плоскостями граней, содержащих это ребро. При этом она не проходит через его внутренние точки. Во сколько раз объем полученного многогранника больше объема куба?
Составьте аналогичную задачу для плоскостей, проходящих через вершины куба.
Исследуем
4.19. Можно ли найти объем прямоугольного параллелепипеда, зная площади: а) двух его неравных граней; б) трех его граней?
Поступаем в ВУЗ
4.20. Сфера, касающаяся нижнего основания цилиндра, имеет единственную общую точку с окружностью его верхнего основания и делит ось цилиндра в отношении  считая от центра одного из оснований. Найдите объем цилиндра, если известно, что сфера касается двух его образующих, находящихся на расстоянии 8 друг от друга.
считая от центра одного из оснований. Найдите объем цилиндра, если известно, что сфера касается двух его образующих, находящихся на расстоянии 8 друг от друга.
Ответ:  .
.
4.21. Дана прямая призма  , стороны основания которой
, стороны основания которой  . В каком отношении объем вписанного в призму цилиндра делится плоскостью
. В каком отношении объем вписанного в призму цилиндра делится плоскостью 
Ответ: 
4.22. Правильная треугольная призма  описана около шара радиусом
описана около шара радиусом  . Точка М — середина бокового ребра
. Точка М — середина бокового ребра  , точка N — середина бокового ребра
, точка N — середина бокового ребра  . В шар вписан прямой круговой цилиндр так, что его основание лежит в плоскости AMN. Найдите объем этого цилиндра.
. В шар вписан прямой круговой цилиндр так, что его основание лежит в плоскости AMN. Найдите объем этого цилиндра.
Ответ: 
4.23. Дана прямая треугольная призма  , у которой
, у которой  Через вершину А проведена плоскость,
Через вершину А проведена плоскость,
пересекающая ребра ВВ, и СС, соответственно в точках М и N. Найдите, в каком отношении делит эта плоскость объем призмы, если известно, что  биссектриса угла
биссектриса угла  .
.
Ответ: 
4.24. Основание прямой треугольной призмы — равнобедренный треугольник, у которого стороны, равные а, образуют угол а. Диагональ грани, противолежащей этому углу, образует с другой боковой гранью угол  Найдите объем призмы.
Найдите объем призмы.
Ответ: 
4.25. Шар вписан в прямую призму, в основании которой лежит прямоугольный треугольник. В этом треугольнике перпендикуляр, опущенный из вершины прямого угла на гипотенузу, имеет длину  и составляет с одним из катетов угол а. Найдите объем призмы.
и составляет с одним из катетов угол а. Найдите объем призмы.
Ответ: 
4.26. Объем прямоугольного параллелепипеда равен V. Если все его ребра увеличить на а, то его объем станет  , а если их укоротить на а, то объем будет равен V2. Найти длину диагонали параллелепипеда.
, а если их укоротить на а, то объем будет равен V2. Найти длину диагонали параллелепипеда.
Ответ: 
4.27. В прямоугольном параллелепипеде точка пересечения диагоналей нижнего основания соединена с серединой бокового ребра отрезком длины  . Этот отрезок образует с основанием параллелепипеда угол a, а с боковой гранью — угол
. Этот отрезок образует с основанием параллелепипеда угол a, а с боковой гранью — угол  Найдите объем параллелепипеда.
Найдите объем параллелепипеда.
Ответ: 
4.28. Объем бруска, имеющего форму прямоугольного параллелепипеда равен  площадь полной поверхности равна 280 с
площадь полной поверхности равна 280 с  периметр основания равен 40 см. Найдите размеры бруска.
периметр основания равен 40 см. Найдите размеры бруска.
Ответ: 
4.29. В куб с ребром а вписана правильная шестиугольная призма так, что диагональ куба проходит через центры оснований призмы и на каждой грани куба лежат по две вершины призмы. Найдите объем призмы, если сторона ее основания в 3 раза меньше ребра куба.
Ответ: 
Переключаемся
4.30. Одно полено в два раза длинее другого, но зато в два раза тоньше его. Какое из этих поленьев имеет больший объем?
4.31. а) В цилиндрическом сосуде находится жидкость. Предложите различные способы узнать, больше или меньше половины объема налито, б) В цилиндрическом сосуде была налита доверху вода. Сосуд наклонили на некоторый угол. Как узнать, какая часть воды вылилась?
4.32. В цилиндрической бочке с водой есть сливной кран. Вода из него уже не выливается. Как узнать, какая часть воды осталась в бочке?
4.33. Как узнать длину намотанной в рулон бумаги?
4.34. В стеклянный кубический сосуд надо влить воды так, чтобы ее объем составлял — объема сосуда. Как это сделать, ничего не измеряя?
ЗАДАЧИ К § 16
Дополняем теорию
4.35. Для наклонной призмы рассмотрим такие величины: V — объем,  — площадь перпендикулярного сечения, L — боковое ребро. Докажите, что
— площадь перпендикулярного сечения, L — боковое ребро. Докажите, что 
Рисуем
4.36. Нарисуйте наклонную призму, имеющую плоскость симметрии. Нарисуйте ее сечение, которое делит ее на две равновеликие части и проходит: а) через боковое ребро; б) параллельно основанию; в) как-то иначе.
4.37. Нарисуйте параллелепипед. Нарисуйте такое его сечение, которое делит его на две равновеликие части и проходит: а) через боковое ребро; б) через ребро основания; в) через диагональ грани; г) через диагональ; д) как-то иначе.
4.38. а) Нарисуйте правильный тетраэдр. Нарисуйте сечение, которое делит его на две равновеликие части, б) Решите аналогичную задачу для правильной треугольной пирамиды;
в) Решите аналогичную задачу для произвольного тетраэдра.
4.39. Нарисуйте правильную четырехугольную пирамиду. Нарисуйте ее сечение, которое делит ее на две равновеликие части.
Планируем
4.40. Как найти объем призмы  с ребром основания 2 и боковым ребром 1, если: а) боковое ребро составляет с основанием угол
с ребром основания 2 и боковым ребром 1, если: а) боковое ребро составляет с основанием угол  грань
грань  — прямоугольник, плоскость которого наклонена к плоскости основания под углом
— прямоугольник, плоскость которого наклонена к плоскости основания под углом  две ее боковые грани перпендикулярны основанию; д) две ее боковые грани одинаково наклонены к основанию и составляют с ним угол 60; е) две ее боковые грани одинаково наклонены к основанию и составляют между собой угол
две ее боковые грани перпендикулярны основанию; д) две ее боковые грани одинаково наклонены к основанию и составляют с ним угол 60; е) две ее боковые грани одинаково наклонены к основанию и составляют между собой угол 
4.41. В параллелепипеде  все грани ромбы с острым углом 60 и стороной 1. Как вычислить его объем, если в вершине сходятся: а) острые углы трех ромбов; б) острый угол одного ромба и тупые углы других ромбов?
все грани ромбы с острым углом 60 и стороной 1. Как вычислить его объем, если в вершине сходятся: а) острые углы трех ромбов; б) острый угол одного ромба и тупые углы других ромбов?
4.42. Как вычислить объем конуса, у которого: а) образующая равна 1 и составляет с основанием угол  образующая равна 2, а высота равна 1; в) образующая равна диаметру основания и равна а?
образующая равна 2, а высота равна 1; в) образующая равна диаметру основания и равна а?
4.43. Как найти объем усеченного конуса, у которого известны: а) радиусы обоих оснований и образующая; б) радиусы обоих оснований и угол наклона образующей к плоскости основания?
4.44. Как вычислить объем тела, полученного при вращении: а) равностороннего треугольника со стороной 2 вокруг его оси симметрии; б) равностороннего треугольника со стороной 1 вокруг прямой, параллельной его оси симметрии и проходящей через его вершину; в) равнобокой трапеции с основаниями 4 и 2, углом при основании  вокруг ее симметрии; г) ромба со стороной 1 и острым углом 60° вокруг меньшей
вокруг ее симметрии; г) ромба со стороной 1 и острым углом 60° вокруг меньшей
диагонали; д) ромба со стороной 1 и острым углом 60 вокруг прямой, параллельной меньшей диагонали и проходящей через его вершину?
4.45. Как найти объем правильной треугольной (четырехугольной) пирамиды, у которой известны: а) сторона основания и высота; б) сторона основания и боковое ребро; в) сторона основания и двугранный угол при основании; г) боковое ребро и его угол с основанием; д) боковое ребро и двугранный угол между соседними боковыми гранями; е) высота и плоский угол при вершине?
4.46. Как вычислить объем правильной четырехугольной пирамиды PABCD, у которой основанием является квадрат ABCD со стороной 1, РА — 2 и: а) вершина Р проектируется в точку В; б) вершина Р проектируется в точку; в) угол между РА и плоскостью  д) плоскость основания перпендикулярна граням PAD и РАВ
д) плоскость основания перпендикулярна граням PAD и РАВ
4.47. Как найти объем правильной усеченной треугольной (четырехугольной) пирамиды, у которой известны: а) сторона оснований и высота; б) стороны оснований и боковое ребро;
в) стороны оснований и угол бокового ребра с основанием;
г) стороны оснований и угол между боковой гранью и основанием?
4.48. Как найти объем тетраэдра РАВС, у которого  и: а) вершина Р проектируется в точку В;
и: а) вершина Р проектируется в точку В;
б) вершина Р проектируется в середину ребра  вершина Р проектируется в центр основания; г) угол между РА и плоскостью ABC равен 45; д)
вершина Р проектируется в центр основания; г) угол между РА и плоскостью ABC равен 45; д) 
4.49. Как найти объем тетраэдра, если известно, что: а) его основанием является равнобедренный прямоугольный треугольник с катетом d, боковые ребра у него равны, а угол между боковыми гранями, проходящими через катеты, равен  стороны его основания равны 1, а все боковые ребра наклонены к основанию под углом
стороны его основания равны 1, а все боковые ребра наклонены к основанию под углом  известны его боковые ребра и углы между ними?
известны его боковые ребра и углы между ними?
4.50. Как найти объем четырехугольной пирамиды, основанием которой является квадрат со стороной 1 и у которой: а) боковые ребра равны 2; б) одна боковая грань перпендикулярна основанию и является равносторонним треугольником;
в) две боковые грани перпендикулярны основанию, а наибольшее боковое ребро равно 2; г) три боковые ребра равны 1?
Представляем
4.51. Может ли наклонная призма с очень длинными боковыми ребрами иметь весьма малый объем?
4.52. Как одной плоскостью разбить на две равновеликие части: а) правильный тетраэдр; б) правильную четырехугольную пирамиду?
4.53. Пусть РАВС — правильный тетраэдр. Точка К — середина АС, точка L — середина АР, точка М — середина ВР, точка N — середина ВС. В каком отношении делит объем тетраэдра его сечение, проходящее через: а) РВ и точку К; б) АС и точку М; в) CL и точку  г) LM и точку N; д) KN и LM; е) АВ под углом
г) LM и точку N; д) KN и LM; е) АВ под углом  к основанию?
к основанию?
4.54. Как разбить параллелепипед на: а) 6 равновеликих пирамид; б) 3 равновеликие пирамиды?
4.55. Как разбить одной плоскостью на равновеликие части: а) цилиндр; б) конус; в) усеченный конус; г) шар; д) шаровой сегмент; е) шаровой сектор; ж) шаровой пояс?
4.56. На какие по объему части разбивается шар единичного радиуса, если в нем провести: а) два больших круга, плоскости которых перпендикулярны; б) два больших круга, плоскости которых образуют угол  три больших круга, плоскости которых попарно перпендикулярны?
три больших круга, плоскости которых попарно перпендикулярны?
Оцениваем
4.57. Образующая конуса равна 1. а) Какой из таких конусов имеет наибольший объем? б) В каких границах находится объем такого конуса, если его высота лежит в промежутке  . В каких границах находится объем такого конуса, если его высота лежит в промежутке
. В каких границах находится объем такого конуса, если его высота лежит в промежутке 
4.58. Какой из конусов имеет наибольший объем среди конусов: а) имеющих данную площадь осевого сечения; б) имеющих данный периметр осевого сечения?
4.59. Из данного конуса с радиусом основания 1 и высотой 1 делают конус. Вершина этого конуса находится в центре основания данного, оси этих конусов лежат на одной прямой. В каком положении этот конус имеет наибольший объем?
4.60. Объем какого конуса является наибольшим и наименьшим среди конусов: а) вписанных в сферу радиуса  описанных около сферы радиуса R; в) описанных около цилиндра с радиусом R и высотой Н?
описанных около сферы радиуса R; в) описанных около цилиндра с радиусом R и высотой Н?
4.61. Боковое ребро правильной треугольной пирамиды наклонено к плоскости ее основания под углом  Одно основание правильной треугольной призмы принадлежит основанию пирамиды, а вершины другого лежат на боковых ребрах пирамиды. Все ребра призмы равны а. Когда такая пирамида имеет наименьший объем?
Одно основание правильной треугольной призмы принадлежит основанию пирамиды, а вершины другого лежат на боковых ребрах пирамиды. Все ребра призмы равны а. Когда такая пирамида имеет наименьший объем?
4.62. В конус заданного объема вписан тетраэдр, в основании которого лежит равнобедренный треугольник. В каком положении этот тетраэдр имеет наибольший объем?
4.63. Какая из четырехугольных пирамид имеет наибольший объем среди: а) правильных пирамид, у которых боковое ребро равно 1; б) пирамид, у которых основанием является прямоугольник, одна сторона которого в два раза больше другой стороны, а боковое ребро равно 1; в) пирамид, у которых основанием является прямоугольник, а все боковые ребра равны одной из сторон этого прямоугольника и равны 1; г) правильных пирамид, разверткой которых является квадрат со стороной 2, причем всем вершинам квадрата соответствует в развертке вершина пирамиды?
4.64. В основании пирамиды квадрат со стороной 2, ее высота равна 1. Какая из следующих пирамид содержит наибольший по объему шар: а) правильная четырехугольная; б) пирамида, у которой вершина проектируется в середину ребра основания; в) пирамида, у которой вершина проектируется в вершину основания?
4.65. В правильную четырехугольную пирамиду, боковые грани которой наклонены к плоскости основания под углом  вписан цилиндр (одно основание цилиндра лежит в плоскости основания пирамиды, а окружность второго его основания имеет по одной общей точке с каждой боковой гранью пирамиды). Радиус основания цилиндра и его высота равны г. В каком положении пирамида имеет наименьший объем?
вписан цилиндр (одно основание цилиндра лежит в плоскости основания пирамиды, а окружность второго его основания имеет по одной общей точке с каждой боковой гранью пирамиды). Радиус основания цилиндра и его высота равны г. В каком положении пирамида имеет наименьший объем?
4.66. В конусе расположены два шара единичного радиуса, касающиеся основания конуса в точках, симметричных относительно центра основания. Каждый из шаров касается боковой поверхности конуса и другого шара. При каком условии объем конуса будет наименьшим?
4.67. В шар радиуса R вписываются тела. В каждом случае найдите в каком положении имеют наибольший объем: а) параллелепипед; б) правильная треугольная пирамида; в) правильная четырехугольная пирамида; г) правильная треугольная призма; д) цилиндр; е) усеченный конус .
Сделаем
4.68. Два прямых двугранных угла, ребра которых перпендикулярны, пересекаются так, что ребро каждого из них образует равные углы с гранями другого двугранного угла. Расстояние между ребрами двугранных углов равно а. Как найти объем многогранника, являющегося их пересечением?
4.69. Найдите внутри тетраэдра ABCD точку Р такую, что объемы тетраэдров РАВС, PACD, PBCD, PBAD равны.
4.70. Дан выпуклый многогранник, у которого все грани равновелики. Внутри его берется точка. Докажите, что при любом положении точки сумма расстояний от нее до плоскостей его граней одна и та же.
Исследуем
4.71. Боковые ребра треугольной пирамиды имеют одинаковую длину а . Два плоских угла при вершине пирамиды равны а, а третий плоский угол равен (3. Как найти объем пирамиды?
4.72. а) Правильный тетраэдр с объемом V срезан по углам плоскостями так, что на каждой грани образовался правильный многоугольник. Как найти объем оставшегося многогранника? б) Решите аналогичную задачу для куба.
4.73. Отрезок CD длиной 1 движется по прямой, перпендикулярной прямой АВ.  Расстояние между прямыми АВ и CD равно 1. а) Меняется ли при этом движении объем тетраэдра ABCD? б) Ответьте на тот же вопрос, если отрезок CD вращается вокруг общего перпендикуляра АС к прямым АВ и
Расстояние между прямыми АВ и CD равно 1. а) Меняется ли при этом движении объем тетраэдра ABCD? б) Ответьте на тот же вопрос, если отрезок CD вращается вокруг общего перпендикуляра АС к прямым АВ и 
Поступаем в ВУЗ
4.74. Дана треугольная призма  Плоскость пересекает ребра АХВХ,
Плоскость пересекает ребра АХВХ,  и ВС соответственно в точках М, N и Р. Найдите, в каком отношении делит эта плоскость объем призмы, если известно, что
и ВС соответственно в точках М, N и Р. Найдите, в каком отношении делит эта плоскость объем призмы, если известно, что 
Ответ: 
4.75. В параллелепипеде длины трех ребер, выходящих из общей вершины, равны соответственно 2, 4 и 6. Углы между ребрами, взятыми попарно, равны . Найдите объем параллелепипеда.
Ответ: 
4.76. В основание прямого кругового конуса вписан квадрат, сторона которого равна а. Плоскость, проходящая через вершину конуса и одну из сторон этого квадрата, дает в сечении с поверхностью конуса треугольник, угол при вершине которого равен а . Определите объем конуса.
Ответ: 
4.77. В шар радиуса R вписан конус, образующая которого составляет с плоскостью основания угол а. Вычислите объем конуса.
Ответ:  .
.
4.78. В прямой круговой конус вписан шар. Радиус круга касания поверхности шара и боковой поверхности конуса равен  . Прямая, соединяющая центр шара с произвольной точкой окружности основания конуса, составляет с высотой конуса острый угол а. Найдите объем конуса.
. Прямая, соединяющая центр шара с произвольной точкой окружности основания конуса, составляет с высотой конуса острый угол а. Найдите объем конуса.
Ответ: 
4.79. Найдите объем конуса, описанного около правильной четырехугольной пирамиды, сторона основания которой равна а, а двугранный угол при основании равен 
Ответ: 
4.80. Высота конуса равна h. Плоские углы при вершине правильной четырехугольной пирамиды, вписанной в этот конус, равны а. Определите объем конуса.
Ответ: 
4.81. Вершина А правильной призмы  совпадает с вершиной конуса, вершины В и С лежат на боковой поверхности этого конуса, а вершины В, и С, — на окружности его основания. Найдите отношение объемов конуса и призмы, если
совпадает с вершиной конуса, вершины В и С лежат на боковой поверхности этого конуса, а вершины В, и С, — на окружности его основания. Найдите отношение объемов конуса и призмы, если 
Ответ:  .
.
4.82. Сторона основания правильной треугольной пирамиды равна а, боковые грани наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
Ответ: 
4.83. В правильной треугольной пирамиде плоский угол при вершине равен а, а кратчайшее расстояние между боковым ребром и противолежащей стороной основания равно а. Найдите объем пирамиды.
Ответ:  .
.
4.84. В правильной треугольной призме  точка D — середина ребра
точка D — середина ребра  . Правильная треугольная пирамида расположена так, что плоскость ее основания совпадает с плоскостью ABC, одно боковое ребро проходит через вершину В, другое — через точку D, а третье ребро пересекает ребро
. Правильная треугольная пирамида расположена так, что плоскость ее основания совпадает с плоскостью ABC, одно боковое ребро проходит через вершину В, другое — через точку D, а третье ребро пересекает ребро  Найдите отношение объема пирамиды к объему призмы.
Найдите отношение объема пирамиды к объему призмы.
Ответ: 
4.85. В цилиндр вписана правильная треугольная пирамида так, что одно из ее боковых ребер есть образующая цилиндра. Найдите объем пирамиды по радиусу R основания цилиндра и по величине двугранного угла а при боковом ребре пирамиды.
Ответ: 
4.86. В основании пирамиды лежит равнобедренный треугольник с периметром  и углом а при основании. Определите объем пирамиды, если боковые грани ее наклонены к плоскости основания под углом
и углом а при основании. Определите объем пирамиды, если боковые грани ее наклонены к плоскости основания под углом 
Ответ: 
4.87. В основании пирамиды лежит прямоугольный треугольник с гипотенузой с и острым углом а, боковые ребра пирамиды наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
Ответ:  .
.
4.88. Прямоугольный треугольник с гипотенузой с и острым углом а служит основанием пирамиды. Ее боковая грань, проходящая через гипотенузу, перпендикулярна основанию, а две другие боковые грани наклонены к нему под углом Р. Найдите объем пирамиды.
Ответ: 
4.89. В треугольной пирамиде РАВС все плоские углы трехгранных углов с вершинами в точках А и В равны а  Определите объем пирамиды.
Определите объем пирамиды.
Ответ: 
4.90. Объем тетраэдра ABCD равен 5. Через середины ребер AD и ВС проведена плоскость, пересекающая ребро CD в точке М. При этом отношение длины отрезка DM к длине отрезка МС равно  Вычислите площадь сечения тетраэдра указанной плоскостью, если расстояние от нее до вершины А равно 1.
Вычислите площадь сечения тетраэдра указанной плоскостью, если расстояние от нее до вершины А равно 1.
Ответ: 3.
4.91. В тетраэдре SABC площадь основания ABC равна 7. Углы ABC, ASB и двугранный угол при ребре АВ являются прямыми. Рассматриваются проекции тетраэдра на всевозможные плоскости, проходящие через прямую АВ . Наибольшая из площадей таких проекций равна 14, а наименьшая —  Найдите объем тетраэдра.
Найдите объем тетраэдра.
Ответ: 
4.92. Объем конуса равен V. В конус вписана пирамида, в основании которой лежит равнобедренный треугольник с углом между боковыми сторонами, равным а. Найдите объем пирамиды.
Ответ: 
4.93. В треугольной пирамиде РАВС все ребра равны друг другу. На ребре РА взята точка М такая, что  на ребре РВ — точка N такая, что
на ребре РВ — точка N такая, что  РВ. Через точки
РВ. Через точки  проведена плоскость, параллельная медиане AD основания ABC. Найдите отношение объема треугольной пирамиды, отсекаемой от исходной проведенной плоскостью, к объему пирамиды РАВС.
проведена плоскость, параллельная медиане AD основания ABC. Найдите отношение объема треугольной пирамиды, отсекаемой от исходной проведенной плоскостью, к объему пирамиды РАВС.
Ответ: 1:6.
4.94. Найдите объем параллелепипеда  , если известно, что объем пирамиды АМКР равен V , где М — точка пересечения диагоналей параллелепипеда, К — точка пересечения диагоналей грани
, если известно, что объем пирамиды АМКР равен V , где М — точка пересечения диагоналей параллелепипеда, К — точка пересечения диагоналей грани  , и Р — точка пересечения медиан треугольника
, и Р — точка пересечения медиан треугольника 
Ответ:  .
.
4.95. Шар радиуса R касается всех боковых граней треугольной пирамиды в серединах сторон ее основания. Отрезок, соединяющий вершину пирамиды с центром шара, делится пополам точкой пересечения с основанием пирамиды. Найдите объем пирамиды.
Ответ: 
4.96. Найдите объем правильной усеченной треугольной пирамиды, если сторона ее большего основания равна а, двугранный угол, образованный боковой гранью и плоскостью основания, равен  , а высота пирамиды равна
, а высота пирамиды равна 
Ответ: 
4.97. Двугранный угол при боковом ребре правильной четырехугольной пирамиды равен утроенному двугранному углу
при ее основании. Найдите объем пирамиды, если ее высота равна Н.
Ответ:  .
.
4.98. Куб с ребром а расположен в правильной четырехугольной пирамиде так, что четыре его вершины лежат на боковых ребрах, а другие четыре лежат на основании пирамиды. Боковая грань пирамиды образует с основанием угол а. Найдите объем пирамиды.
Ответ:  .
.
4.99. Основанием пирамиды служит равнобокая трапеция, у которой острый угол равен а, а площадь равна S. Все боковые грани пирамиды составляют с плоскостью основания пирамиды один и тот же угол, равный  Найдите объем пирамиды.
Найдите объем пирамиды.
Ответ: 
4.100. В шар радиуса R вписана четырехугольная пирамида, все боковые ребра которой наклонены к плоскости основания под углом а . В основании пирамиды лежит прямоугольник с углом Р между диагоналями. Найдите объем пирамиды.
Ответ: — 
4.101. В пирамиду, основанием которой служит ромб с острым углом а , вписан шар радиуса R. Боковые грани пирамиды наклонены к плоскости основания под углом Р. Найдите объем пирамиды.
Ответ: 
4.102. Длина образующей конуса равна  угол образующей с плоскостью основания равен а. Найдите объем описанной около конуса пирамиды, основанием которой служит ромб с острым углом
угол образующей с плоскостью основания равен а. Найдите объем описанной около конуса пирамиды, основанием которой служит ромб с острым углом 
Ответ:  .
.
4.103. В правильной шестиугольной пирамиде  (
( — вершина) точки К и L выбраны на ребрах ES и AF соответственно так, что
— вершина) точки К и L выбраны на ребрах ES и AF соответственно так, что  . Точки R и Т расположены на прямых DK и SL так, что прямая RT перпендикулярна плоскости SAD. Высота пирамиды равна
. Точки R и Т расположены на прямых DK и SL так, что прямая RT перпендикулярна плоскости SAD. Высота пирамиды равна  Найдите объем пирамиды.
Найдите объем пирамиды.
Ответ: 
4.104. Через вершину правильной треугольной пирамиды и середины двух сторон основания проведена плоскость. Определите площадь сечения и объемы частей пирамиды, на которые она разделена сечением, зная сторону основания а и угол а , образованный плоскостью сечения с основанием.
Ответ: Площадь сечения  , один из объемов
, один из объемов  .
.
4.105. Дана правильная треугольная пирамида РАВС. Ребро PC этой пирамиды совпадает с боковым ребром правильной треугольной призмы  и CP — боковые ребра;
и CP — боковые ребра;  одно из оснований). Вершины призмы
одно из оснований). Вершины призмы  , лежат в плоскости грани РАВ пирамиды. Какую долю от объема всей пирамиды составляет объем ее части, лежащей внутри призмы, если отношение длины бокового ребра пирамиды к длине стороны основания пирамиды равно
, лежат в плоскости грани РАВ пирамиды. Какую долю от объема всей пирамиды составляет объем ее части, лежащей внутри призмы, если отношение длины бокового ребра пирамиды к длине стороны основания пирамиды равно 
Ответ: 
4.106. Многогранник имеет 6 граней: АВСК, ЕМРН, АВМЕ, ВСРМ, СКНР, АКНЕ. Все его вершины лежат на сфере радиуса  Грани АВСК и ЕМРН лежат в параллельных плоскостях, расстояние между которыми 2. Известно, что
Грани АВСК и ЕМРН лежат в параллельных плоскостях, расстояние между которыми 2. Известно, что  площадь грани ЕМРН равна 5, а объем многогранника равен
площадь грани ЕМРН равна 5, а объем многогранника равен  Найдите длину ребра ВМ.
Найдите длину ребра ВМ.
Ответ: 
4.107. Наклонная призма  имеет своими основаниями трапеции ABCD и
имеет своими основаниями трапеции ABCD и  Сумма площадей параллельных боковых граней призмы равна S, а расстояние между
Сумма площадей параллельных боковых граней призмы равна S, а расстояние между
этими гранями равно d. Найдите объем многогранника  .
.
Ответ: 
4.108. Около правильной треугольной пирамиды со стороной основания а и углом наклона бокового ребра к плоскости основания, равным а, описан шар. Найдите его объем.
Ответ: 
4.109. В шар вписана правильная четырехугольная пирамида, у которой боковое ребро составляет с плоскостью основания угол а. Объем пирамиды равен V. Найдите объем шара.
Ответ:  .
.
Переключаемся
4.110. Предложите какой-нибудь способ, чтобы узнать, сколько воды налито в коническом сосуде: больше или меньше половины?
4.111. Как вычислить радиус металлического шарика, используя линейку и цилиндрическую пробирку?
4.112. В ящике, имеющем форму прямоугольного параллелепипеда, находятся металлические шарики. Ящик заполнен ими доверху, его размеры во много раз больше размеров шарика. Предложите способ для приближенного подсчета числа шариков
4.113. Известно, что спелый арбуз не тонет в воде. Какие вам понадобятся данные, если вы хотите выбрать хороший арбуз, не делая в нем выреза?
4.114. Из одной и той же массы мыльной жидкости можно делать пузыри разных размеров. Как меняется их толщина при увеличении их радиуса? Попробуйте произвести некие расчеты.
4.115. Попробуйте прикинуть, какую часть от объема шара — в процентах — составляет объем его части, заключенной между его сферой и сферой, радиус которой составляет 0,9 от радиуса шара. А потом проверьте предсказанный результат вычислением.
ЗАДАЧИ К § 17
Дополняем теорию
4.116. Докажите, что: а) площадь боковой поверхности прямой призмы равна произведению периметра основания на образующую; б) площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на образующую; в) площадь боковой поверхности правильной пирамиды равна произведению периметра основания на половину апофемы.
4.117. Докажите, что площадь боковой поверхности правильной усеченной пирамиды равна среднему арифметическому периметров оснований, умноженному на апофему.
4.118. Докажите, что площадь боковой поверхности усеченного конуса равна произведению среднего арифметического периметров оснований на образующую.
Рисуем
4.119. Нарисуйте сечение, которое делит на две равновеликие части поверхность: а) куба; б) прямоугольного параллелепипеда; в) произвольного параллелепипеда; г) правильной треугольной пирамиды.
4.120. Нарисуйте сечение, которое делит на две равновеликие части поверхность: а) правильного тетраэдра; б) правильной треугольной пирамиды; в) правильной четырехутольной пирамиды.
4.121. Нарисуйте сечение, которое делит на две равновеликие части поверхность: а) цилиндра; б) цилиндра без верхнего основания; в) конуса; г) усеченного конуса; д) усеченного конуса без одного из оснований.
4.122. Нарисуйте сечение, которое делит на две равновеликие части поверхность: а) сферы; б) полусферы; в) сферического сегмента; г) сферического пояса.
Планируем
4.123. В призме  основанием является правильный треугольник со стороной 1, а боковое ребро равно 2. Как вычислить площадь ее поверхности, если: а) грань
основанием является правильный треугольник со стороной 1, а боковое ребро равно 2. Как вычислить площадь ее поверхности, если: а) грань  — прямоугольник, плоскость которого составляет с основанием угол
— прямоугольник, плоскость которого составляет с основанием угол  вершина В, проектируется в центр нижнего основания?
вершина В, проектируется в центр нижнего основания?
4.124. Как вычислить площадь поверхности правильной треугольной (четырехугольной) пирамиды, у которой: а) сторона основания равна 2, а высота равна 1; б) боковое ребро равно 3, а высота равна 2; в) боковое ребро равно 1, а угол бокового
ребра с основанием равен  ребро основания равно 2, а угол боковой грани с основанием равен
ребро основания равно 2, а угол боковой грани с основанием равен 
4.125. Как вычислить площадь боковой поверхности правильной треугольной (четырехугольной) усеченной пирамиды, у которой известны стороны оснований и: а) боковое ребро; б) угол бокового ребра с основанием; в) угол между боковой гранью и основанием; г) высота; д) угол между соседними боковыми гранями?
4.126. Как вычислить площадь поверхности цилиндра, у которого: а) осевым сечением является квадрат со стороной 2; б) разверткой боковой поверхности является прямоугольник со сторонами 1 и 2?
4.127. Как вычислить площадь поверхности конуса, у которого: а) осевое сечение является равносторонним треугольником со стороной 2; б) разверткой боковой поверхности является четверть круга радиусом 1; в) образующая равна 1 и составляет с основанием угол (р 
4.128. Как вычислить площадь поверхности, полученной при вращении равностороннего треугольника со стороной 1 вокруг: а) высоты; б) стороны; в) прямой, проходящей через вершину и параллельной его высоте; г) прямой, параллельной его стороне и удаленной от нее на расстояние 1; д) прямой, параллельной его высоте и удаленной от нее на расстояние 
4.129. Как вычислить площадь поверхности, полученной при вращении квадрата со стороной 1 вокруг: а) диагонали; б) прямой, проходящей через его вершину и параллельной диагонали; в) прямой, параллельной диагонали и удаленной от центра квадрата на 1?
4.130. Как вычислить площадь поверхности, полученной при вращении: а) ромба со стороной 1 и углом в  вокруг меньшей диагонали; б) прямоугольника со сторонами 1 и 2 вокруг диагонали; в) прямоугольной трапеции с основаниями 1 и 2 и короткой боковой стороной, равной 1, вокруг длинной боковой стороны?
вокруг меньшей диагонали; б) прямоугольника со сторонами 1 и 2 вокруг диагонали; в) прямоугольной трапеции с основаниями 1 и 2 и короткой боковой стороной, равной 1, вокруг длинной боковой стороны?
4.131. Как вычислить радиус сферы, вписанной в: а) правильный тетраэдр с ребром 1; б) правильный октаэдр с ребром 1; в) правильную  -угольную призму с известными ребрами; д) треугольную пирамиду, основанием которой является равнобедренный треугольник, две стороны которого равны 1, угол между ними равен
-угольную призму с известными ребрами; д) треугольную пирамиду, основанием которой является равнобедренный треугольник, две стороны которого равны 1, угол между ними равен  высота равна 1, а вершина проектируется в середину основания равнобедренного треугольника;
высота равна 1, а вершина проектируется в середину основания равнобедренного треугольника;
е) параллелепипед, все грани которого ромбы со стороной 1 и острым углом  при одной из вершин?
при одной из вершин?
Представляем
4.132. Куб с ребром 1 разрезали на 1000 равных между собой кубиков. Попробуйте оценить "на глаз", во сколько раз общая поверхность полученных кубиков больше поверхности исходного куба.
4.133. Поверхность тела разделили плоскостью на две равновеликие части. Значит ли это, что при этом разделили пополам и объем тела, если исходным телом является: а) куб; б) прямоугольный параллелепипед; в) правильная треугольная призма; г) правильный тетраэдр; д) правильная четырехугольная пирамида с равными ребрами; е) цилиндр; ж) конус; з) усеченный конус; и) шар; к) полушар? В каком случае верны обратные утверждения?
Оцениваем
4.134. Какой из прямоугольных параллелепипедов с квадратным основанием имеет наибольший объем, если: а) площадь его поверхности равна 1; б) площадь его поверхности без одного из оснований равна 
4.135. В основании прямоугольного параллелепипеда лежит квадрат. Объем параллелепипеда равен V. При каком условии поверхность параллелепипеда будет наименьшей?
4.136. Диагональ правильной четырехугольной призмы равна 1. Какая из таких призм имеет наибольшую площадь: а) боковой поверхности; б) поверхности?
4.137. Какая из правильных треугольных призм объемом 1 имеет наибольшую и наименьшую площадь поверхности?
4.138. Объем правильной треугольной пирамиды равен 1. Какая из таких пирамид имеет наибольшую и наименьшую:
а) площадь боковой поверхности; б) площадь поверхности?
4.139. а) Объем цилиндра равен V. Какой из таких цилиндров имеет наибольшую и наименьшую площадь поверхности?
б) Площадь поверхности цилиндра равна S. Какой из таких цилиндров нмеет наибольший и наименьший объем? в) Объем цилиндра равен V. Какой из таких цилиндров имеет наибольшую и наименьшую площадь боковой поверхности? г) Площадь боковой поверхности цилиндра равна S. Какой из таких цилиндров имеет наибольший и наименьший объем?
4.140. Образующая конуса равна 1. Какой из таких конусов имеет наибольшую площадь: а) поверхности; б) боковой поверхности?
4.141. Периметр осевого сечения конуса равен 2. Какой из таких конусов имеет наибольшую площадь: а) поверхности; б) боковой поверхности?
4.142. Объем конуса равен V. Какой из таких конусов имеет наибольшую площадь: а) поверхности; б) боковой поверхности?
4.143. Конус лежит на горизонтальной плоскости, касаясь ее боковой поверхностью. Площадь основания конуса равна  , площадь боковой поверхности
, площадь боковой поверхности  На какой высоте над плоскостью находится наивысшая точка конуса?
На какой высоте над плоскостью находится наивысшая точка конуса?
Сделаем
4.144. В правильной  -угольной пирамиде все грани, включая основание, равновелики. Ее высота равна h. Как найти ее площадь поверхности и объем?
-угольной пирамиде все грани, включая основание, равновелики. Ее высота равна h. Как найти ее площадь поверхности и объем?
4.145. Сфера касается всех ребер правильного тетраэдра. Как узнать, какая часть площади сферы находится внутри него?
Исследуем
4.146. Как найти площадь поверхности конуса, вписанного в сферу радиуса 2, если его основание удалено от центра сферы на 1?
Поступаем в ВУЗ
4.147. Основанием наклонной призмы  является равносторонний треугольник ABC со стороной а. Вершина А проектируется в точку пересечения медиан треугольника ABC и боковое ребро составляет с плоскостью основания угол 45°. Найдите площадь боковой поверхности призмы.
является равносторонний треугольник ABC со стороной а. Вершина А проектируется в точку пересечения медиан треугольника ABC и боковое ребро составляет с плоскостью основания угол 45°. Найдите площадь боковой поверхности призмы.
Ответ: 
4.148. В правильной треугольной пирамиде задан F — угол между высотой и боковым ребром пирамиды. Найдите отношение квадрата высоты боковой грани к боковой поверхности пирамиды.
Ответ:  .
.
4.149. Полная поверхность правильной четырехугольной пирамиды равна S, а плоский угол при вершине равен а . Найдите объем пирамиды.
Ответ: 
4.150. Основанием пирамиды служит квадрат, две боковые грани пирамиды перпендикулярны к ее основанию, две другие образуют с основанием угол a. В эту пирамиду вписан куб так, что четыре его вершины лежат на боковых ребрах пирамиды, а четыре другие — на основании пирамиды. Зная, что боковое ребро куба равно а, найдите боковую поверхность пирамиды.
Ответ: 
4.151. В шар радиуса R вписана пирамида с квадратным основанием. Одно из боковых ребер пирамиды перпендикулярно плоскости основания, а наибольшее боковое ребро образует с ней угол a. Определите полную поверхность пирамиды.
Ответ: 
4.152. Боковые грани четырехугольной пирамиды — равные равнобедренные треугольники, а в основании пирамиды лежит ромб, одна диагональ которого в два раза длиннее другой. Найдите объем пирамиды, если известно, что площадь боковой поверхности равна 6, а среди боковых ребер есть два ребра, составляющих тупой угол.
Ответ: 
4.153. Квадрат ABCD, сторона которого равна 1, служит основанием пирамиды с вершиной S. Двугранные углы, образуемые гранями ASB, BSC, CSD и DSA с основанием, относятся как числа 1, 2, 7, 2. Найдите боковую поверхность пирамиды.
Ответ: 
4.154. Плоскость, параллельная основанию пирамиды, делит ее на две части равного объема. Найдите отношение площадей боковых поверхностей этих частей.
Ответ: 
4.155. В цилиндр вписан прямоугольный параллелепипед. Одна из сторон его основания равна b. Диагональ параллелепипеда образует с плоскостью основания угол а, а с боковой гранью, проходящей через данную сторону, — угол Р. Найдите боковую поверхность цилиндра.
Ответ: 
4.156. Поверхность шара, вписанного в конус, боковая поверхность конуса и полная поверхность конуса образуют геометрическую прогрессию. Найдите объем конуса, если радиус вписанного в него шара равен 
Ответ: 
4.157. Угол при вершине осевого сечения конуса равен 2а, а высота конуса равна Я. Найдите объем вписанного в этот конус шара, а также площадь полной поверхности конуса.
Ответ: 
4.158. В правильную треугольную усеченную пирамиду с двугранным углом а при основании вписан усеченный конус. Определите боковую поверхность конуса, если апофема боковой грани пирамиды равна сумме радиусов оснований конуса, а радиус меньшего основания конуса равен  .
.
Ответ: 
4.159. Боковая поверхность конуса с образующей а развернута в сектор, центральный угол которого равен  Найдите объем конуса.
Найдите объем конуса.
Ответ: 
4.160. Высота цилиндра равна высоте конуса. Боковая поверхность цилиндра относится к боковой поверхности конуса как 3:2. Кроме того, угол, составленный образующей конуса с плоскостью основания, равен a. Найдите отношение объема цилиндра к объему конуса.
Ответ: 
4.161. В усеченный конус можно вписать шар. Докажите, что объем этого конуса равен произведению площади его поверхности на  высоты.
высоты.
4.162. Усеченный конус и правильная шестиугольная призма расположены так, что верхнее основание усеченного конуса вписано в верхнее основание призмы, а нижнее основание усеченного конуса описано около нижнего основания призмы. Известно, что высота усеченного конуса равна сумме радиусов его оснований. Найдите отношение площадей боковых поверхностей этих тел.
Ответ: 3:1.
4.163. Сфера касается всех боковых ребер правильной четырехугольной призмы и ее оснований. Найдите отношение площади поверхности сферы, лежащей вне призмы, к площади полной поверхности призмы.
Ответ: 
4.164. Докажите, что  , где
, где  — объем и поверхность треугольной пирамиды;
— объем и поверхность треугольной пирамиды;  — объем и поверхность вписанного в эту пирамиду шара.
— объем и поверхность вписанного в эту пирамиду шара.
4.165. Даны правильный тетраэдр и шар, площади поверхностей которых относятся как  Можно ли шар поместить в тетраэдр, если: а)
Можно ли шар поместить в тетраэдр, если: а) 
Ответ: а) да; б) нет.
4.166. В усеченный конус вписан полушар, объем которого составляет — объема усеченного конуса. Найдите отношение боковой поверхности конуса к сферической поверхности полушара.
Ответ:  или
или  .
.
Переключаемся
4.167. Как вы думаете, почему иные лекарства делают в виде порошка? А другие почему-то нет.
4.168. Вам требуется выяснить, какую часть солнечной энергии принимает на себя Земля. Какие данные вам для этого потребуются 
4.169. Два полных сферических чайника, один большой, а другой маленький, одновременно закипели, а потом стали остывать. В каком из них вода быстрее остынет?
4.170. Два мыльных пузыря площадью S слиплись в сферический пузырь. Что вы можете сказать о площади поверхности нового сферического пузыря?
4.171. а) На высоте Я над Землей висит спутник. Какая часть Земли видна с него? б) На какой высоте над Землей и сколько спутников достаточно иметь, чтобы с них можно было видеть всю Землю?
4.172. Известно, что если растают все льды Гренландии, то произойдет мировая катастрофа. Не можете ли вы оценить ее масштабы?
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧИТАТЕЛЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ
- § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 1.2. Двугранный угол. Угол между плоскостями.
- 1.3. Плоскость и прямая в пространстве.
- 1.4. Аксиомы стереометрии.
- 1.5. Взаимное расположение двух прямых в пространстве.
- 1.6. Признаки скрещивающихся прямых.
- 1.7. Параллельные прямые.
- 1.8. Параллельное проектирование.
- § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 2.2. О значении перпендикуляра.
- 2.3. Теорема о трех перпендикулярах.
- 2.4. Признак перпендикулярности прямой и плоскости.
- 2.5. Построение плоскости, перпендикулярной данной прямой.
- 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости.
- 2.7. Теорема о прямой, перпендикулярной плоскости.
- 2.8. Перпендикулярность плоскостей.
- 2.9. Ортогональное проектирование.
- § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 3.2. Параллельность и перпендикулярность.
- 3.3. Основная теорема о параллельных плоскостях.
- 3.4. Второй признак параллельности плоскостей.
- 3.5. Расстояние и параллельность.
- 3.6. Сонаправленность лучей и угол между прямыми.
- 3.7. Параллельность и углы.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ
- § 4. СФЕРА И ШАР
- 4.2. Взаимное положение шара и плоскости.
- 4.3. Сфера и многранники.
- 4.4. Вид и изображение шара и сферы.
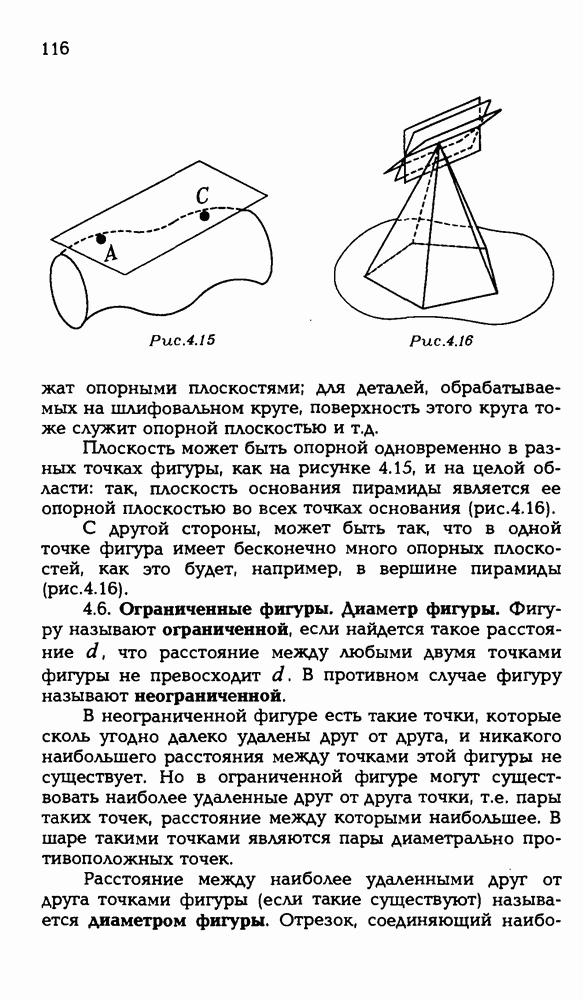
- 4.5. Опорная плоскость.
- 4.6. Ограниченные фигуры. Диаметр фигуры.
- 4.7. Опорные плоскости в концах диаметра.
- 4.8. Сфера — фигура вращения.
- 4.9. Симметрия сферы и шара.
- 4.10. Сфера — центрально симметричная фигура.
- 4.11. Сфера — зеркально симметричная фигура.
- 4.12. Отражение в плоскости и отражение в зеркале.
- § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ
- 5.2. Тригонометрия трехгранного угла.
- 5.3. Равенство трехгранных углов.
- 5.4. Сферические треугольники.
- 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников.
- § 6. ЦИЛИНДР
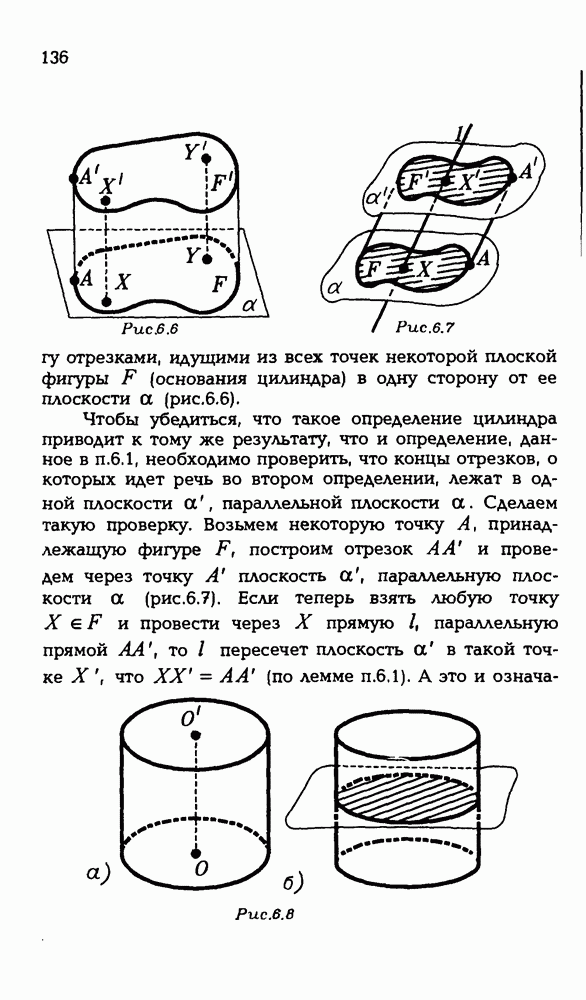
- 6.2. Другой подход к определению цилиндра.
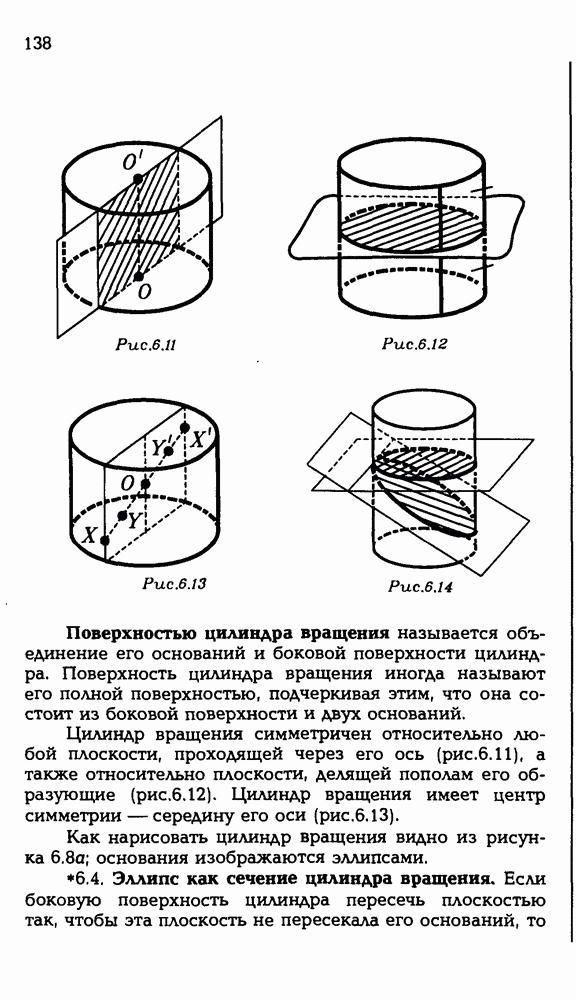
- 6.3. Цилиндр вращения.
- 6.4. Эллипс как сечение цилиндра вращения.
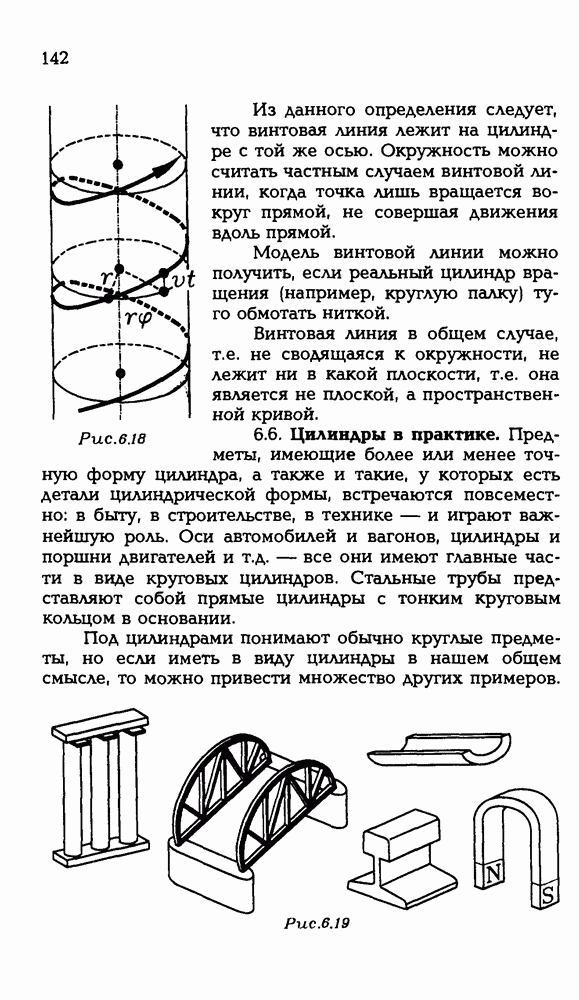
- 6.5. Винтовые линии.
- 6.6. Цилиндры в практике.
- § 7. ПРИЗМА
- 7.2. Параллелепипед.
- 7.3. Прямоугольный параллелепипед.
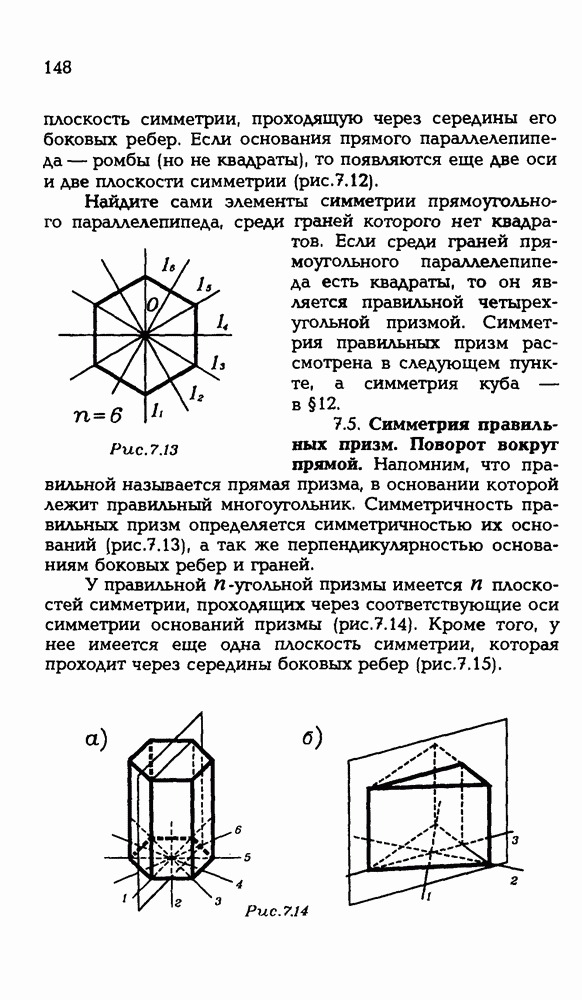
- 7.4. Симметрия параллелепипеда.
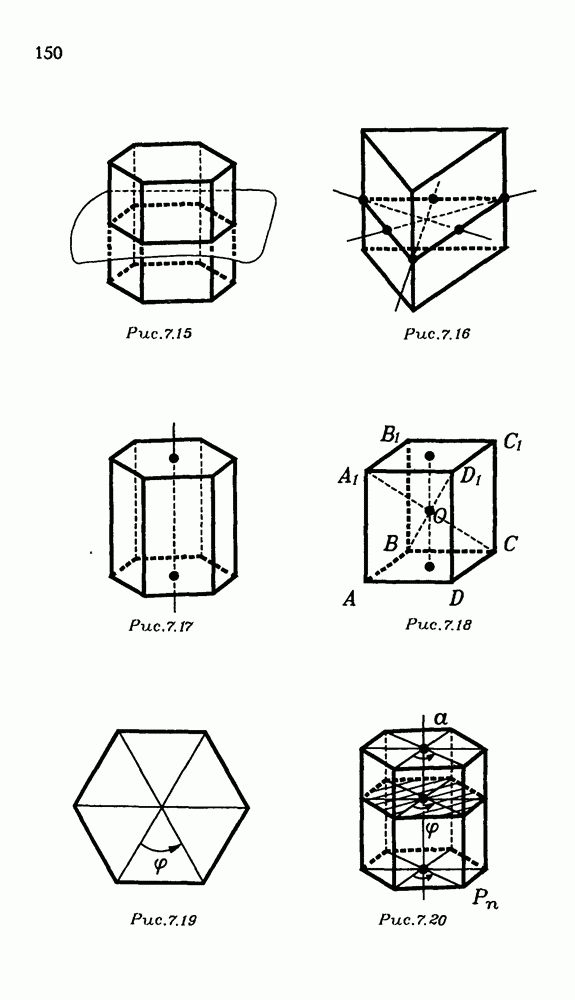
- 7.5. Симметрия правильных призм. Поворот вокруг прямой.
- § 8. КОНУС
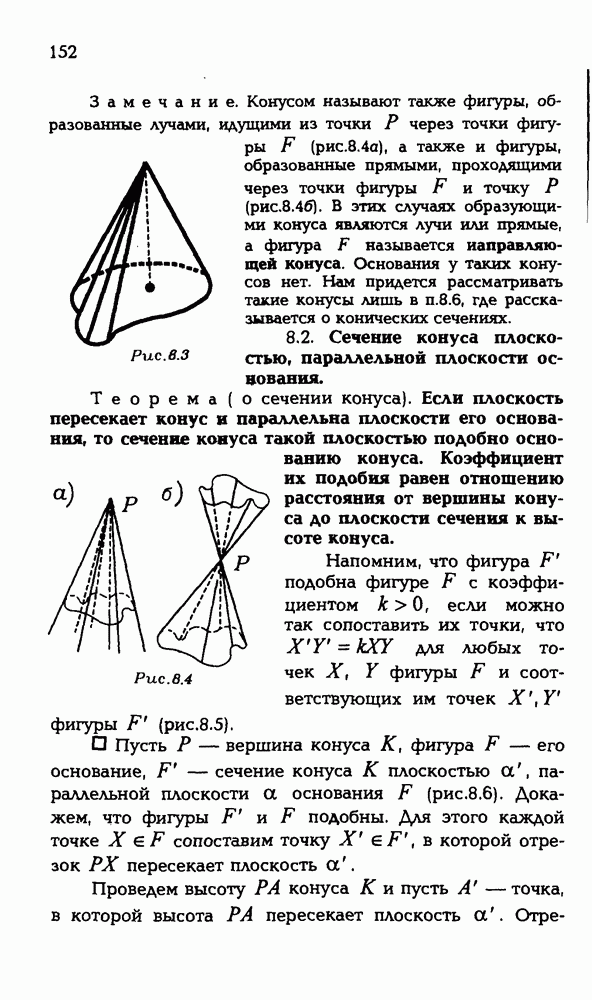
- 8.2. Сечение конуса плоскостью, параллельной плоскости основания.
- 8.3. Конус вращения.
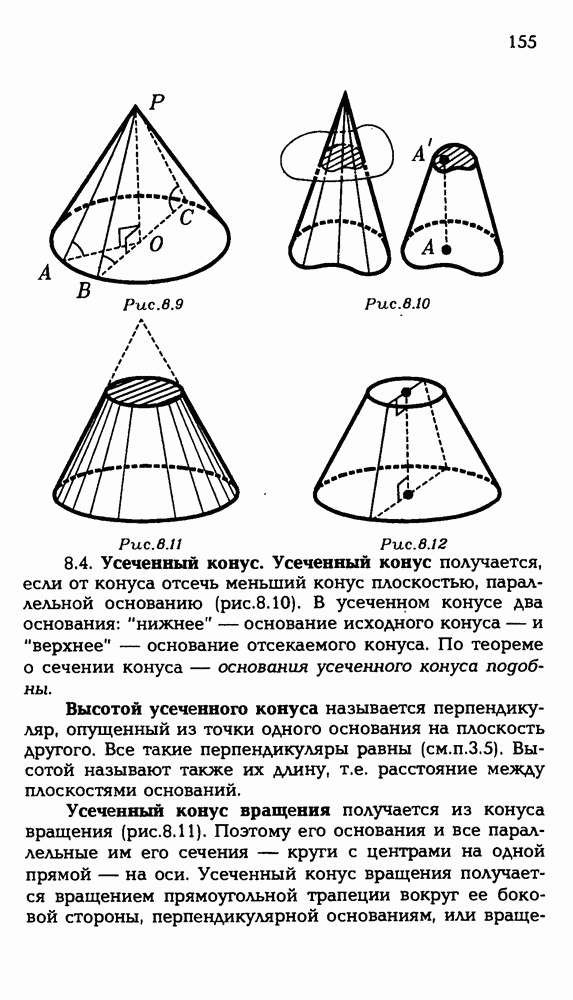
- 8.4. Усеченный конус.
- § 9. ПИРАМИДА
- 9.2. Правильная пирамида.
- 9.3. Симметрия правильной пирамиды.
- 9.4. Конусы и пирамиды в практике.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ
- § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ
- 10.2. Граница и внутренность.
- 10.3. Определение тела и замкнутой плоской области.
- 10.4. Выпуклые фигуры.
- 10.5. Выпуклые тела.
- § 11. МНОГОГРАННИКИ
- 11.2. Выпуклые многогранники.
- 11.3. Теорема Эйлера.
- 11.4. Выпуклые многогранники и выпуклые оболочки.
- 11.5. Многогранная поверхность и развертка.
- 11.6. Развертка выпуклого многогранника.
- § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ
- 12.2. Классификация правильных многогранников.
- 12.3. Полуправильные многогранники.
- 12.4. Симметрия правильных многогранников.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
- § 13. ПОНЯТИЕ ОБЪЕМА
- 13.2. Определение объема.
- 13.3. Геометрические величины.
- § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА
- 14.2. Объем прямой призмы.
- § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ
- 15.2. Выражение объема через площади сечений.
- § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА
- 16.2. Объем конуса
- 16.3. Объем шара.
- 16.4. Объем тел вращения.
- 16.5. Объем шарового сегмента и шарового сектора.
- § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ
- 17.2. Площадь сферы.
- 17.3. Площадь сферических многоугольников.
- 17.4. Площадь сферического сегмента и сферического пояса.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ
- § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- 18.2. Другой способ нахождения координат точки.
- 18.3. Построение точки с данными координатами.
- 18.4. Выражение расстояния между точками.
- § 19. МЕТОД КООРДИНАТ
- 19.2. Уравнения без одной или двух координат.
- 19.3. Некоторые применения метода координат.
- § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ
- 20.2. Полярные координаты.
- 20.3. Цилиндрические координаты.
- 20.4. Сферические координаты.
- 20.5. Координатная сеть.
- § 21. ПОНЯТИЕ ВЕКТОРА
- 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов.
- 21.3. Сонаправленность и равенство векторов.
- 21.4. Признаки равенства векторов.
- 21.5. Радиус-вектор.
- § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 22.2. Разложение вектора на составляющие.
- 22.3. Умножение вектора на число.
- 22.4. Координаты вектора.
- 22.5. Равенство координат векторов и координат точек.
- 22.6. Разложение векторов по базису.
- 22.7. Ориентация базиса.
- § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ
- 23.2. Выражение скалярного произведения через координаты.
- 23.3. Свойства скалярного умножения.
- 23.4. Применения скалярного умножения.
- 23.5. Скалярное произведение и проекции.
- § 24. ВЕКТОРНЫЙ МЕТОД
- 24.2. Общее уравнение плоскости.
- 24.3. Векторное задание отрезка.
- 24.4. Некоторые теоремы о треугольниках и тетраэдрах.
- 24.5. Центр масс системы материальных точек.
- 24.6. Центры масс и выпуклые многогранники.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ГЛАВА 6. ПРЕОБРАЗОВАНИЯ
- 25.1. Преобразования фигур.
- 25.2. Определения движения и равенства фигур.
- 25.3. Преобразования симметрии.
- 25.4. Параллельный перенос.
- 25.5. Поворот.
- § 26. СВОЙСТВА ДВИЖЕНИЙ
- 26.2. Общие свойства движений.
- 26.3. Теоремы о задании движений.
- 26.4. Неподвижные точки движений.
- 26.5. Два рода движений.
- 26.6. Теорема подвижности пространства.
- 26.7. Композиция отражений в плоскости.
- § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА
- 27.2. Движения первого рода как винтовые движения.
- 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот.
- 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения.
- § 28. ПОДОБИЕ
- 28.2. Гомотетия.
- 28.3. Свойства подобия.
- 28.4. Группы преобразований.
- § 29. ИНВЕРСИЯ
- 29.2. Аналитическое задание инверсии.
- 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии.
- 29.4. Сохранение величин углов при инверсии.
- ЗАДАЧИ С РЕШЕНИЯМИ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ОТВЕТЫ И УКАЗАНИЯ
- ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ