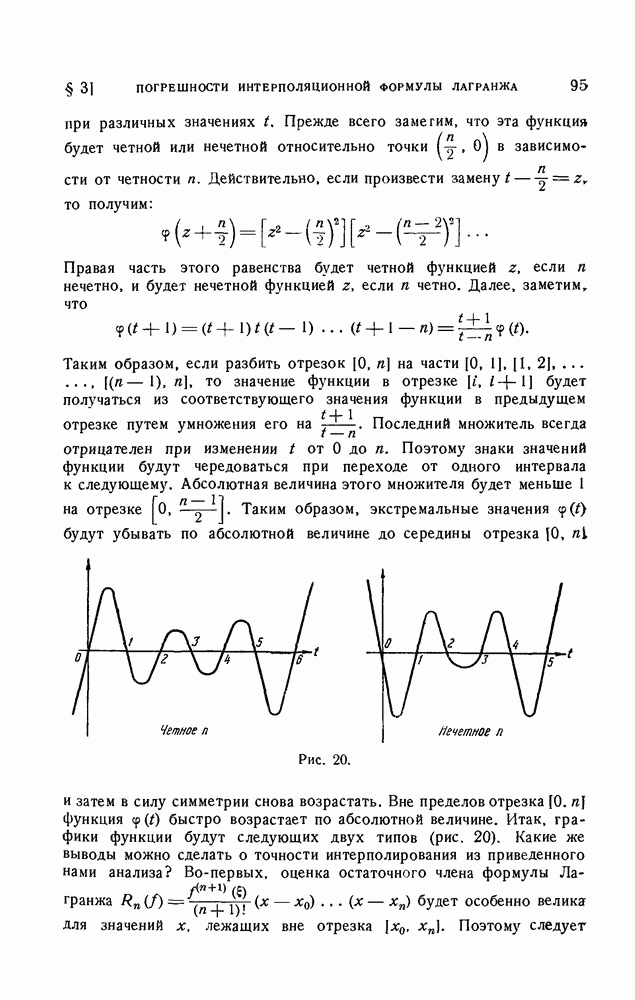
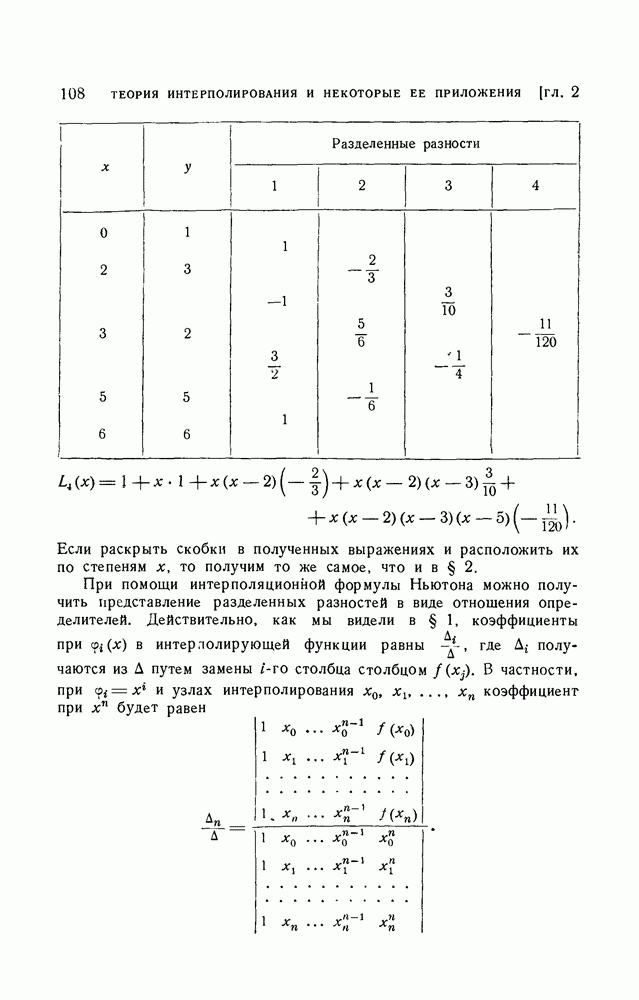
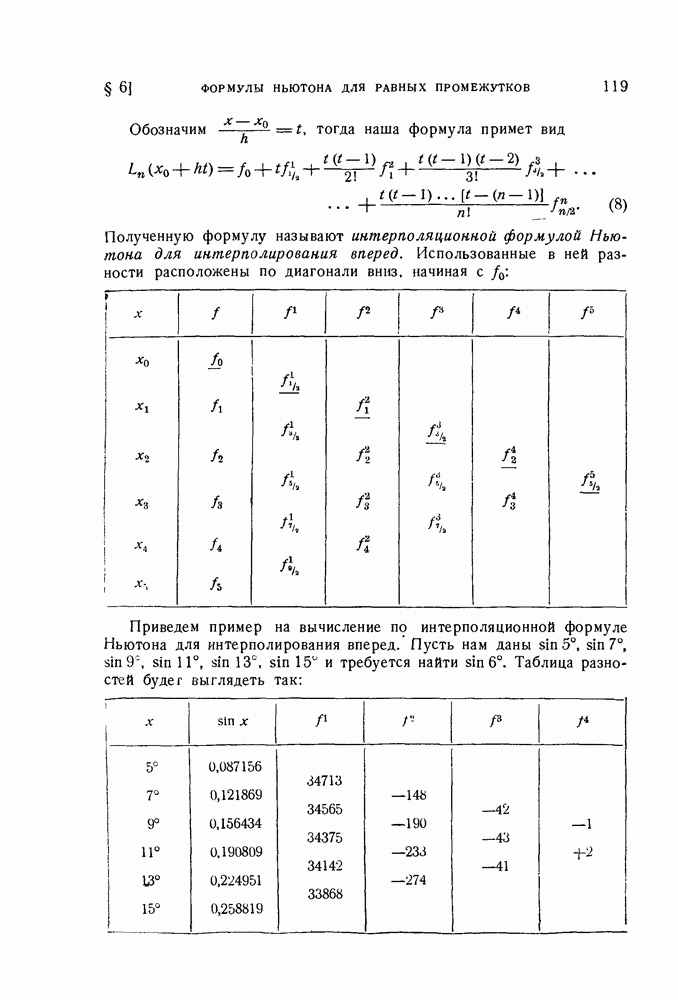
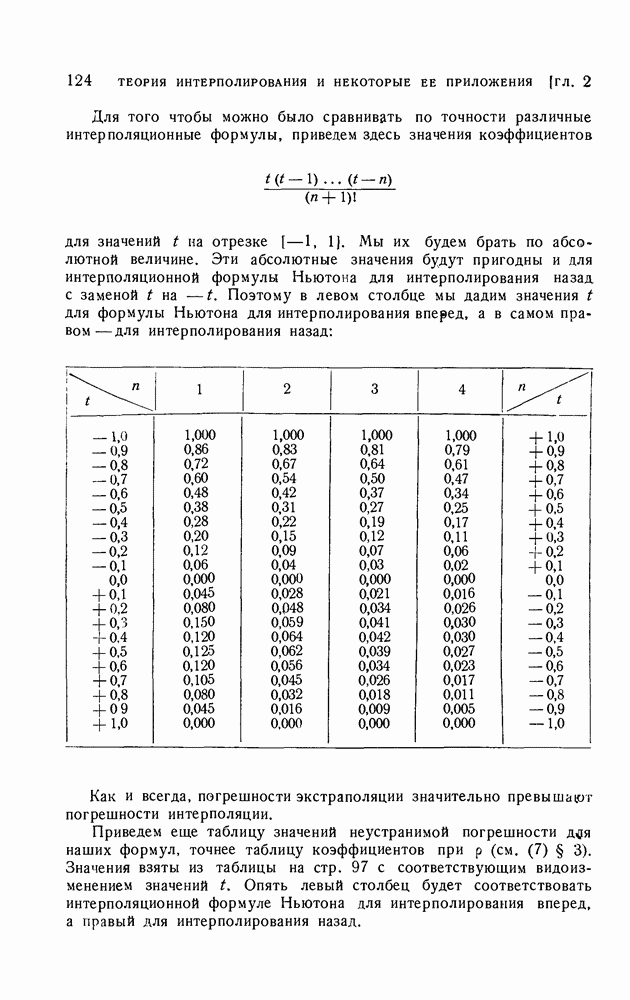
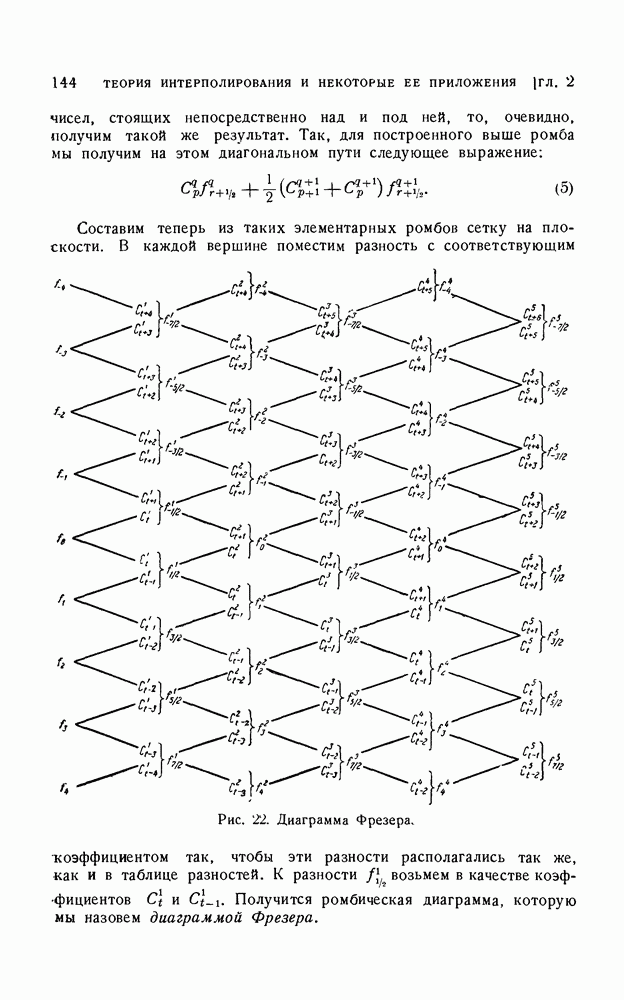
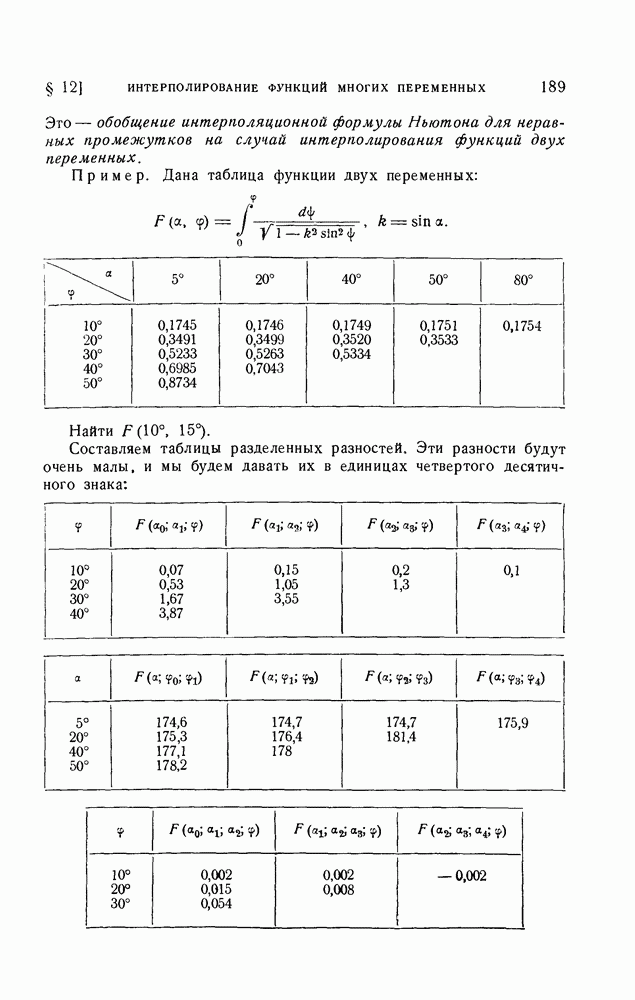
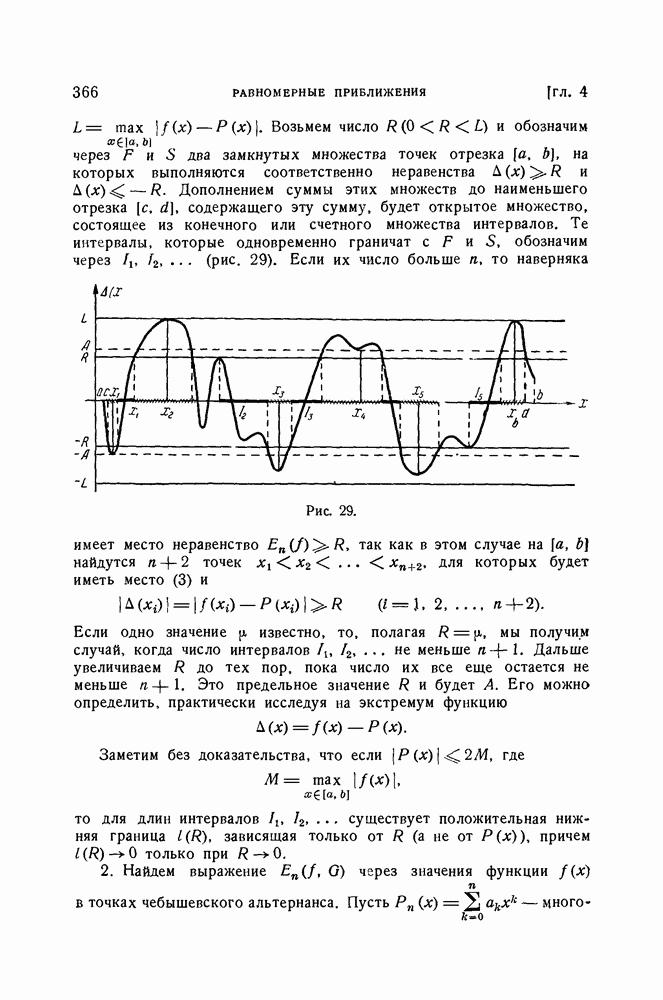
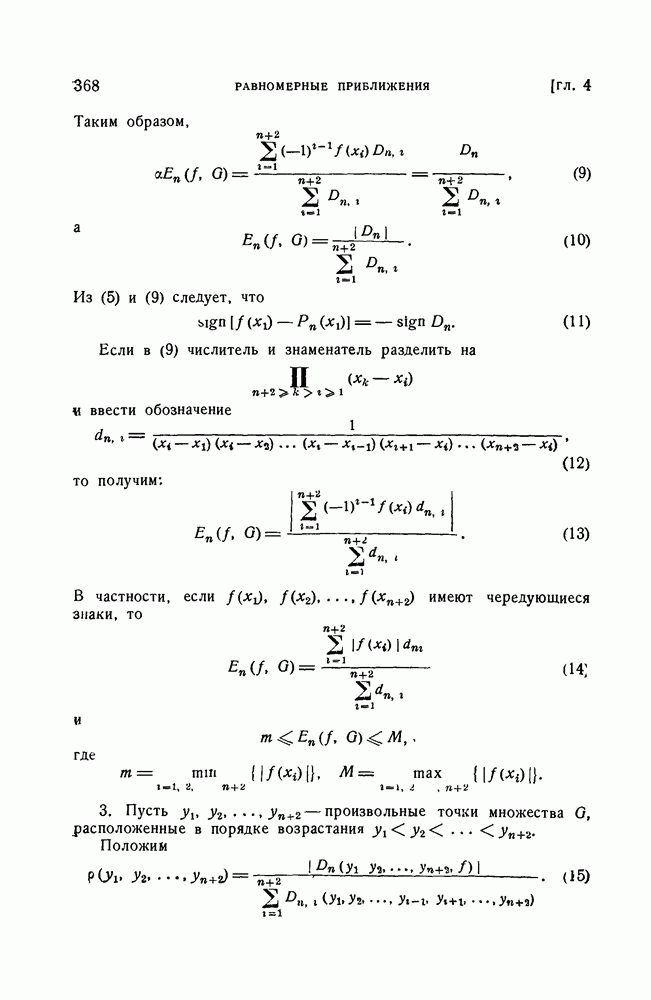
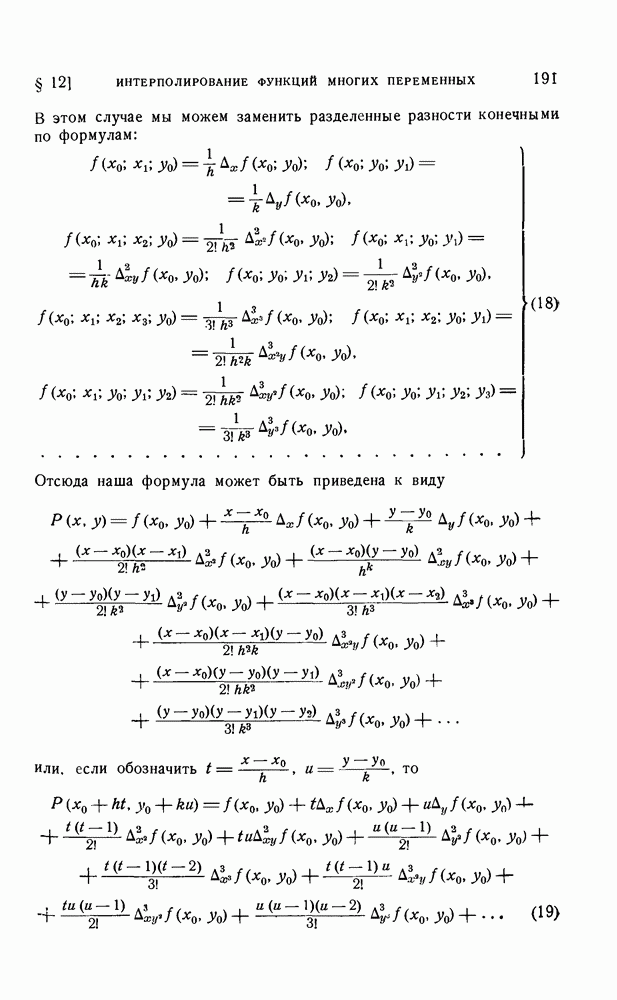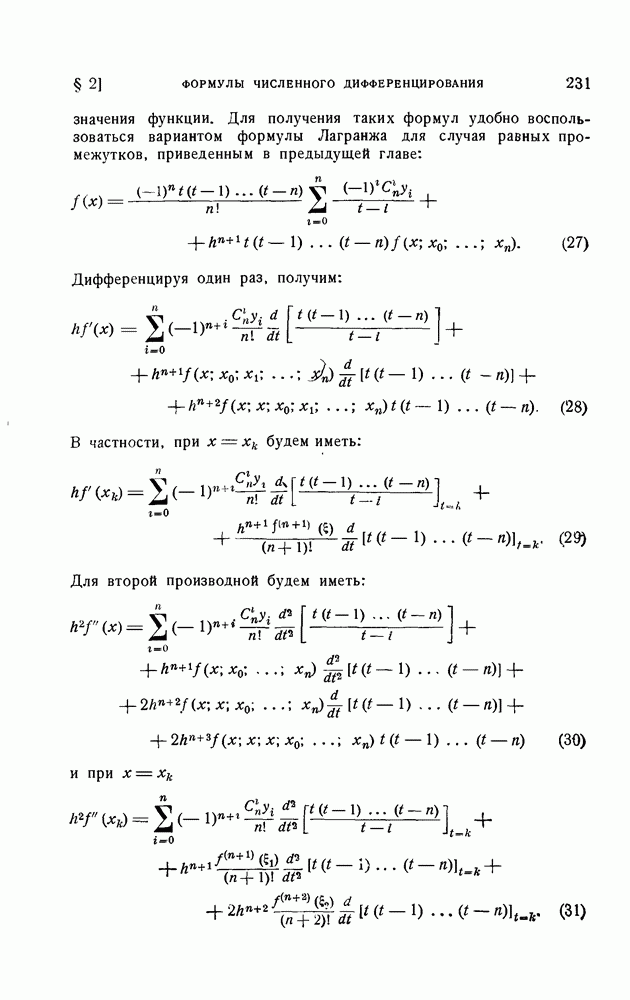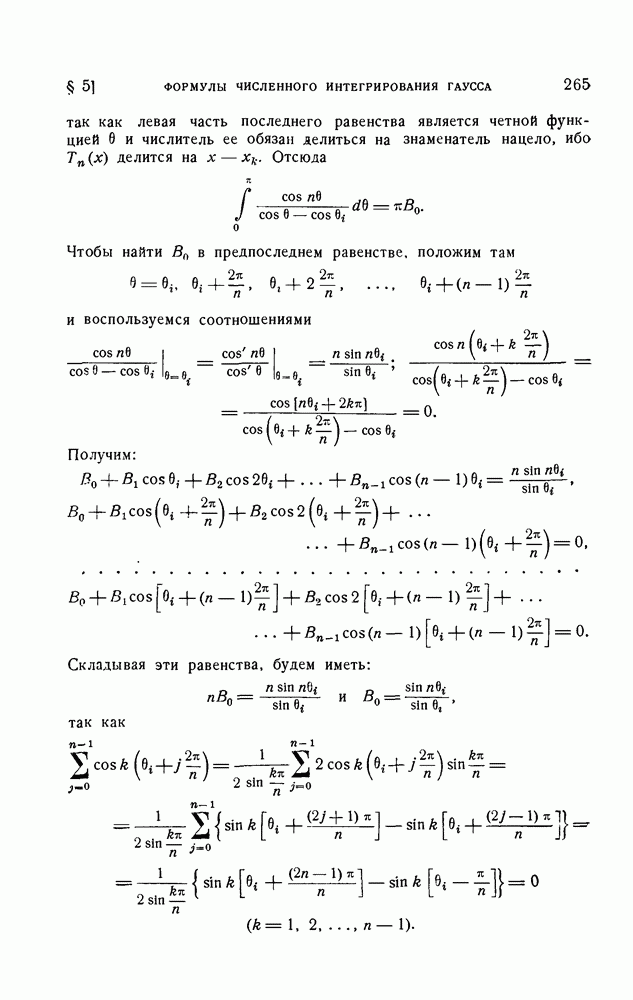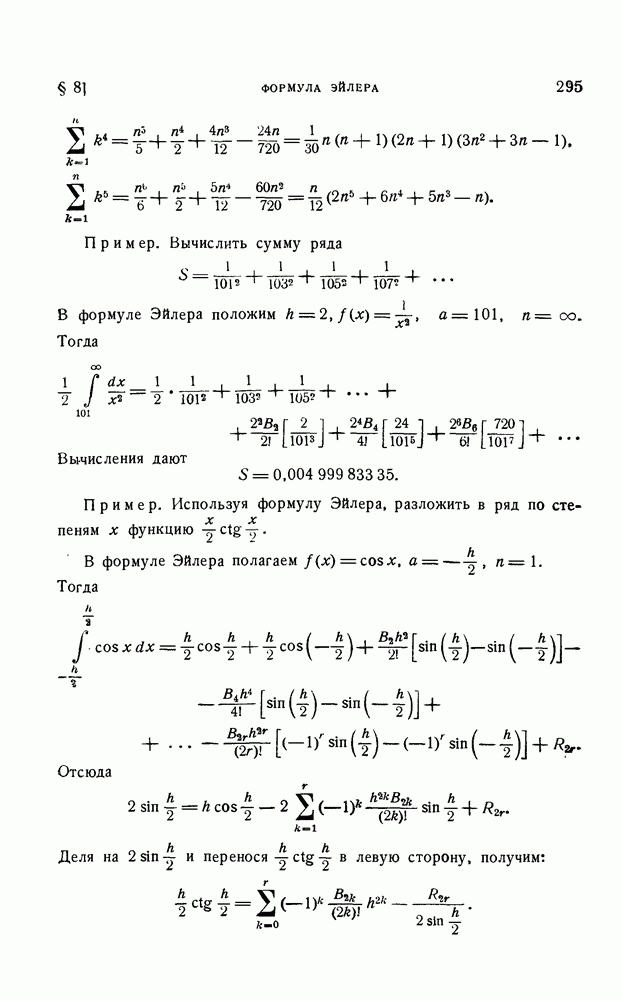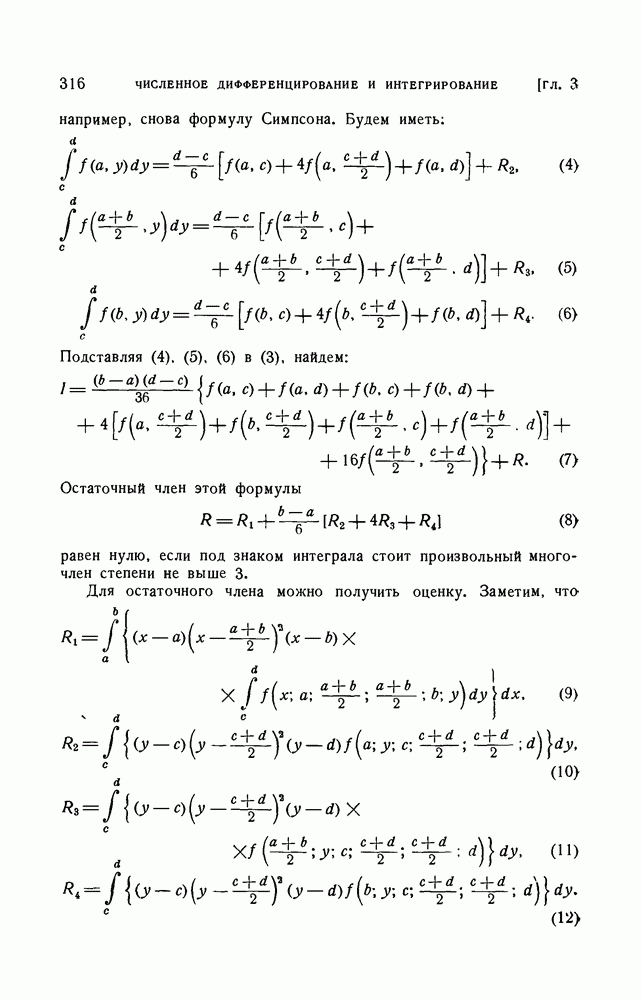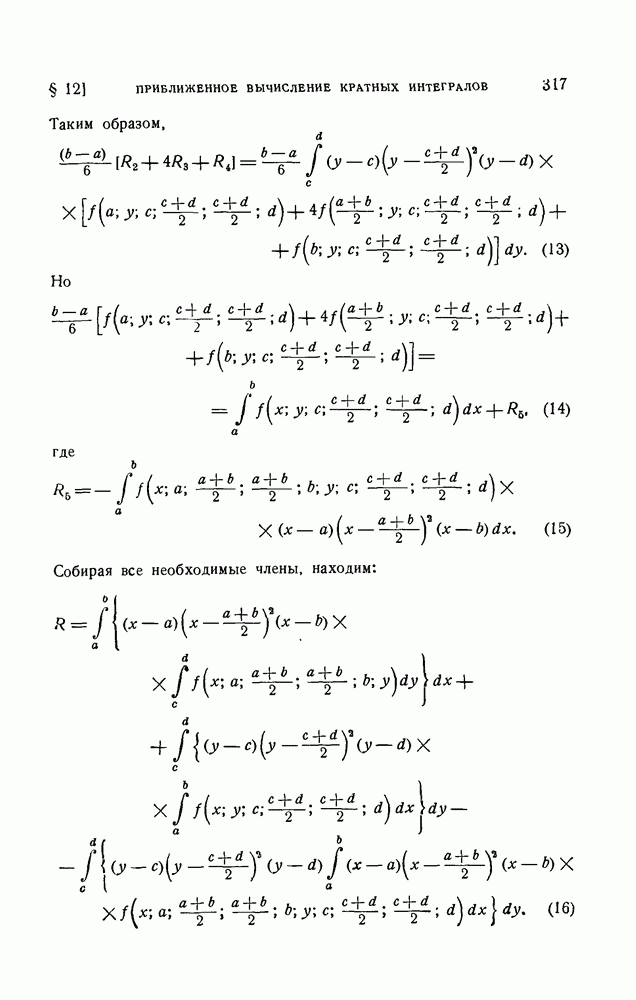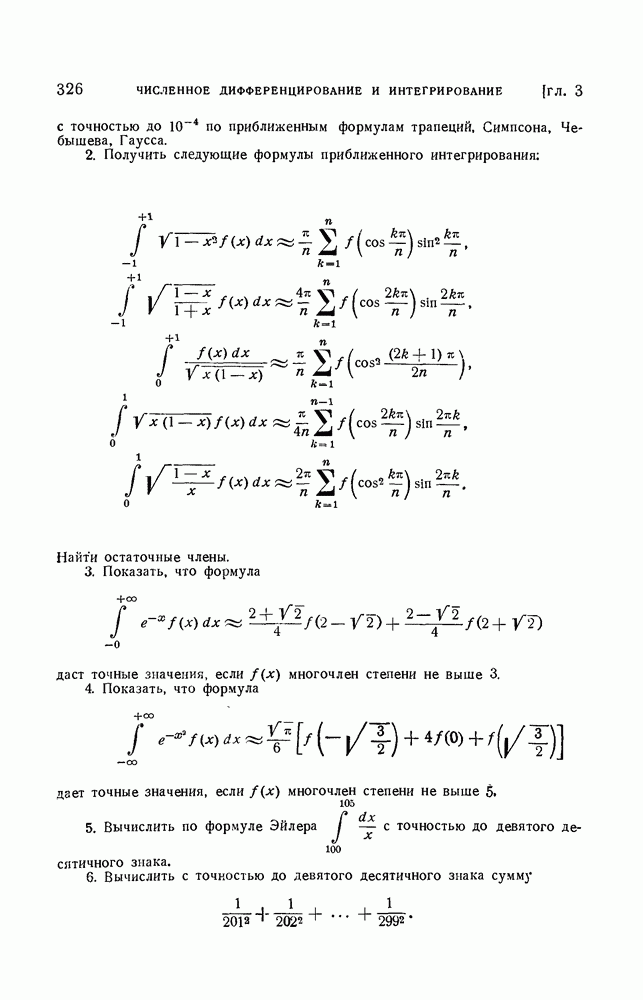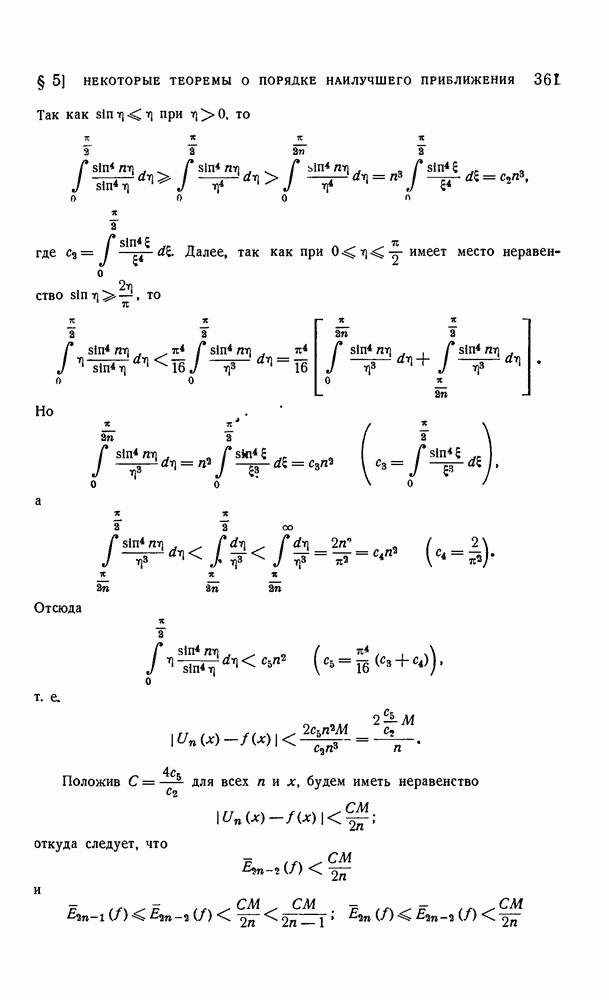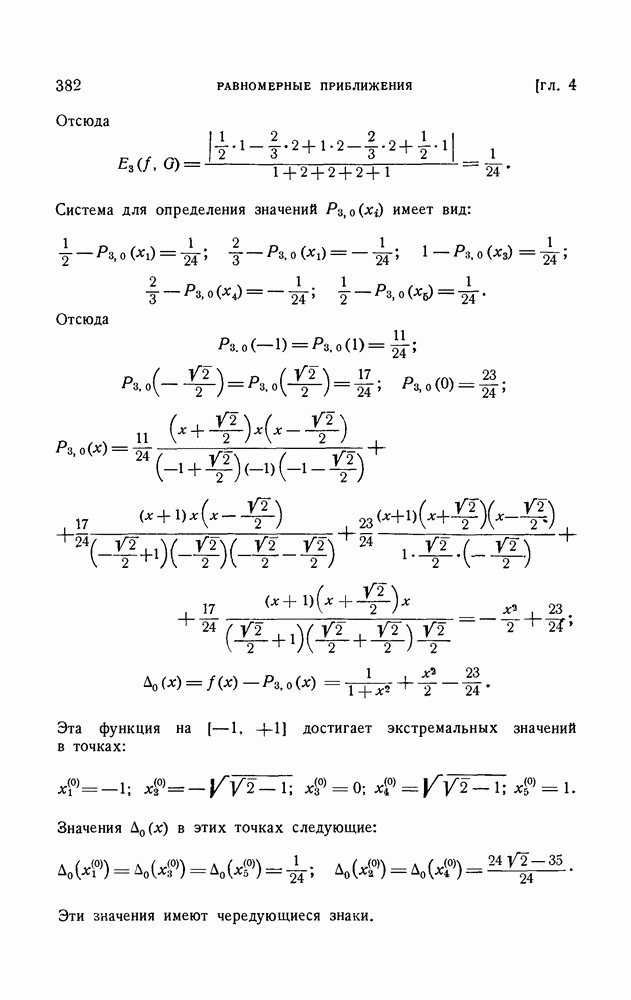| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
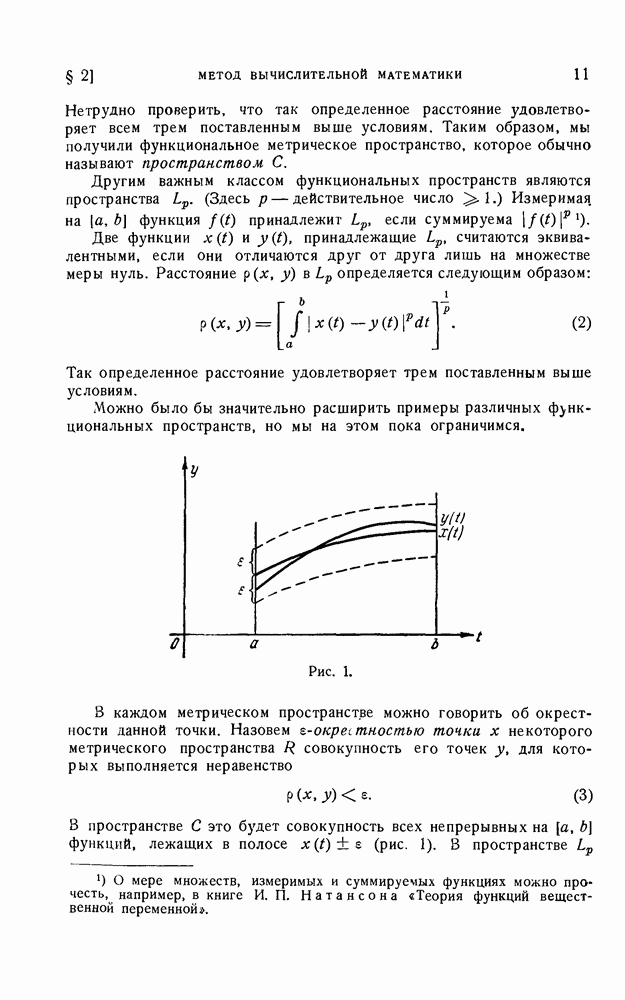
§ 6. Сходимость рядов по ортогональным системам многочленов
Как мы видели, для сходимости ряда Фурье для некоторого элемента гильбертова пространства к этому элементу в смысле нормы пространства требуются полнота пространства и полнота ортогональной системы, по которой строится ряд Фурье.
Для доказательства того, что это имеет место в рассматриваемом нами случае, нам будут нужны некоторые сведения из теории функций действительного переменного.
Приведем пока две теоремы:
Теорема Леви. Если на  дан ряд неотрицательных измеримых функций
дан ряд неотрицательных измеримых функций

и если

то почти везде на  сходится ряд
сходится ряд  (Почти везде на
(Почти везде на  означает, что всюду за исключением, быть может, множества меры нуль.)
означает, что всюду за исключением, быть может, множества меры нуль.)
Теорема Фату. Если  последовательность неотрицательных измеримых функций, заданных на
последовательность неотрицательных измеримых функций, заданных на  почти везде сходящаяся к функции
почти везде сходящаяся к функции  если при всех
если при всех 

то и

Доказательств этих теорем здесь приводить не будем и отсылаем читателя к любому более или менее полному курсу теории функций действительного переменного.
Относительно веса  будем предполагать, что
будем предполагать, что  почти всюду на
почти всюду на  и суммируем на этом промежутке.
и суммируем на этом промежутке.
Докажем следующую теорему, показывающую полноту пространства 
Если последовательность  сходится в себе, то она имеет предел, также принадлежащий
сходится в себе, то она имеет предел, также принадлежащий 
Пусть последовательность функций  сходится в себе в пространстве
сходится в себе в пространстве  Тогда можно найти такую последовательность натуральных чисел
Тогда можно найти такую последовательность натуральных чисел

что

при любых  больших
больших  Здесь
Здесь  В частности,
В частности,

и ряд

будет сходиться. Применим неравенство Буняковского к функциям  и Получим:
и Получим:

Следовательно, сходится ряд

По теореме Леви почти везде сходится ряд

а следовательно, и ряд

Таким образом, последовательность  имеет предел почти всюду на
имеет предел почти всюду на  Обозначим его через
Обозначим его через 
Покажем, что  принадлежит к
принадлежит к  и что она является пределом последовательности
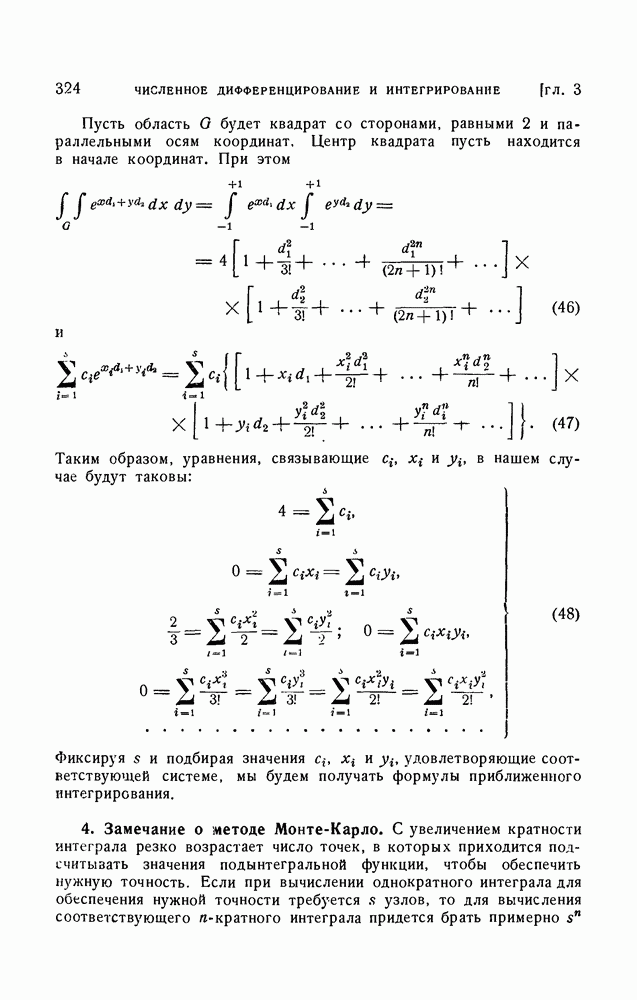
и что она является пределом последовательности  в смысле метрики
в смысле метрики  Для заданного
Для заданного  найдем такое
найдем такое  что при
что при  будет:
будет:

Последнее неравенство будет выполнено, если мы закрепим  и будем произвольным образом увеличивать
и будем произвольным образом увеличивать 
Применим теорему Фату, взяв в качестве  функции
функции

и в качестве функции  функции
функции

Тогда получим:

Следовательно, функция  а поэтому и
а поэтому и  принадлежат к
принадлежат к  Более того, мы доказали, что последовательность
Более того, мы доказали, что последовательность  сходится в среднем с весом
сходится в среднем с весом  Докажем теперь теорему:
Докажем теперь теорему:
Множество  всех измеримых ограниченных функций на
всех измеримых ограниченных функций на  множество С непрерывных на
множество С непрерывных на  функций и множество
функций и множество  всех многочленов всюду плотные множества в
всех многочленов всюду плотные множества в 
Пусть  На основании свойств интеграла Лебега для произвольного
На основании свойств интеграла Лебега для произвольного  можно подобрать такое
можно подобрать такое  что как только мера произвольного множества
что как только мера произвольного множества  будет меньше
будет меньше  , то
, то

(это свойство называют абсолютной непрерывностью).
Функция  почти всюду конечна. Поэтому можно указать такое
почти всюду конечна. Поэтому можно указать такое  что мера множества, на котором
что мера множества, на котором  будет меньше 8. Закрепив это
будет меньше 8. Закрепив это  положим
положим

Очевидно,  и
и

Первая часть теоремы доказана.
Для доказательства второй части теоремы находим  такую, что
такую, что  Пусть
Пусть  . Лузиным была доказана теорема, утверждающая, что для любого
. Лузиным была доказана теорема, утверждающая, что для любого  существует такая непрерывная функция
существует такая непрерывная функция  которая отличается от
которая отличается от  лишь на множестве меры, не превышающей 8, и удовлетворяющая неравенству При этом получим:
лишь на множестве меры, не превышающей 8, и удовлетворяющая неравенству При этом получим:

В силу абсолютной непрерывности интеграла Лебега последний интеграл может быть сделан меньше чем  Таким образом,
Таким образом,

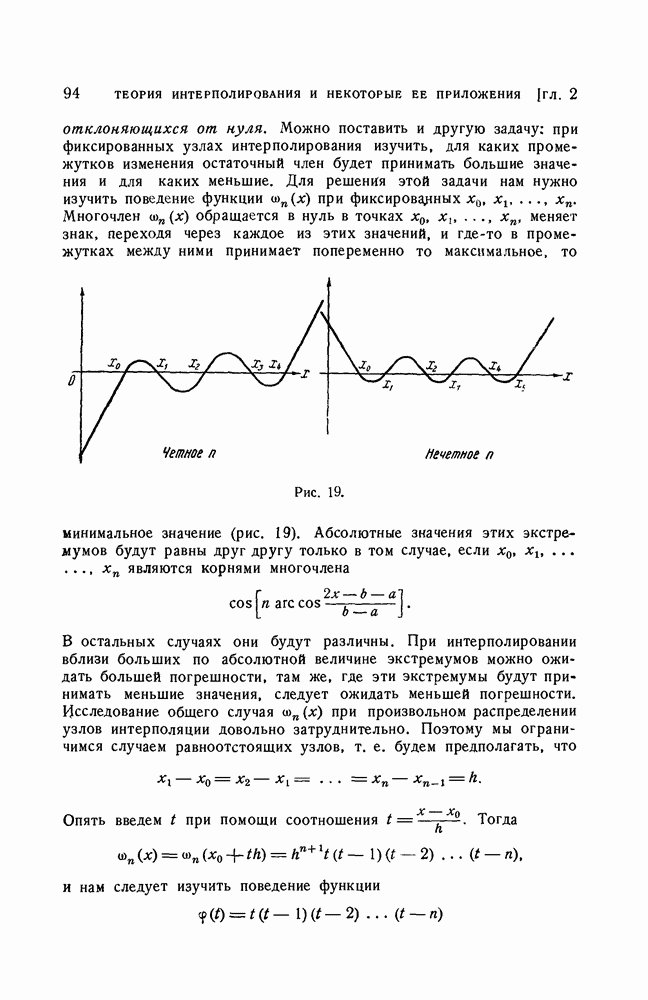
Перейдем к третьей части. Найдем непрерывную функцию  удовлетворяющую условию
удовлетворяющую условию  В силу теоремы
В силу теоремы
Вейерштрасса можно найти такой многочлен  что
что

Тогда

и если  то
то  Теорема доказана полностью.
Теорема доказана полностью.
Из теоремы следует, что в  многочлены с рациональными коэффициентами также образуют всюду плотное множество. Это множество счетно. Следовательно,
многочлены с рациональными коэффициентами также образуют всюду плотное множество. Это множество счетно. Следовательно,  сепарабельное пространство. Кроме того, отсюда следует, что построенные на степенях
сепарабельное пространство. Кроме того, отсюда следует, что построенные на степенях  ортогональные многочлены образуют полную систему.
ортогональные многочлены образуют полную систему.
В результате наших рассуждений мы можем утверждать, что образованные нами ряды по ортогональным многочленам будут сходиться к разлагаемой в ряд функции в смысле метрики т. е. если  частичная сумма соответствующего ряда, то
частичная сумма соответствующего ряда, то 

Во многих случаях, встречающихся на практике, полученная нами сходимость в среднем бывает недостаточна. Нужна либо обычная сходимость, либо даже равномерная сходимость.
Пусть  - ортонормированная на
- ортонормированная на  система многочленов с весом
система многочленов с весом  Тогда функции
Тогда функции  будет соответствовать ряд Фурье по этой ортонормированной системе
будет соответствовать ряд Фурье по этой ортонормированной системе

где

Следовательно,

Обозначим

На основании тождества Кристофеля — Дарбу

Таким образом,

В частности, если  то при любом
то при любом 

и, следовательно,

Умножая обе части последнего равенства на  и пользуясь тем, что интегрирование ведется по
и пользуясь тем, что интегрирование ведется по  мы можем записать:
мы можем записать:

Отсюда

Оценим величину

Если предполагать, что коэффициенты при старших членах  положительны, то
положительны, то  Далее,
Далее,

где через С обозначено наибольшее из чисел  По неравенству Буняковского
По неравенству Буняковского

Обозначим

При этом  и получаем:
и получаем:

Пусть функция

принадлежит  Обозначим коэффициенты Фурье этой функции по ортогональной системе
Обозначим коэффициенты Фурье этой функции по ортогональной системе  через
через  Очевидно,
Очевидно,  при
при  Поэтому если
Поэтому если  равномерно ограничены в точке х, то
равномерно ограничены в точке х, то

и

Если многочлены  равномерно ограничены на всем отрезке
равномерно ограничены на всем отрезке  то наше утверждение будет справедливо для любой точки
то наше утверждение будет справедливо для любой точки  при меньших предположениях о
при меньших предположениях о  а именно достаточно потребовать, чтобы существовал интеграл
а именно достаточно потребовать, чтобы существовал интеграл

Выражение

называют функцией Лебега ортонормированной системы  Справедлива теорема:
Справедлива теорема:
Если  непрерывная функция, удовлетворяющая условию
непрерывная функция, удовлетворяющая условию

то ее ряд Фурье по ортогональной системе  сходится в точке х.
сходится в точке х.
Действительно, если  является многочленом наилучшего равномерного приближения для
является многочленом наилучшего равномерного приближения для  то
то

Следовательно,

Но тогда

и правая часть стремится к нулю при  . Будем называть
. Будем называть  числами Лебега. Если 6]
числами Лебега. Если 6]

то, как следует из последней оценки, ряд Фурье функции  по ортогональной системе
по ортогональной системе  будет равномерно сходиться к
будет равномерно сходиться к 
При различных весах  мы получим различные условия, которые нужно наложить на функцию
мы получим различные условия, которые нужно наложить на функцию  для того, чтобы ее ряд Фурье по соответствующей ортогональной системе сходился к
для того, чтобы ее ряд Фурье по соответствующей ортогональной системе сходился к  Но при любом весе свойство непрерывности
Но при любом весе свойство непрерывности  не обеспечивает такой сходимости в каждой точке отрезка
не обеспечивает такой сходимости в каждой точке отрезка  Это было показано В.
Это было показано В.  Николаевым. Исследование сходимости рядов по ортогональным многочленам очень сложно, и мы не имеем возможности излагать здесь все тонкости вопроса. Ограничимся перечислением некоторых фактов, связанных с теми ортогональными системами, которые были приведены ранее.
Николаевым. Исследование сходимости рядов по ортогональным многочленам очень сложно, и мы не имеем возможности излагать здесь все тонкости вопроса. Ограничимся перечислением некоторых фактов, связанных с теми ортогональными системами, которые были приведены ранее.
Для многочленов Якоби справедлива следующая теорема: Если  имеет на
имеет на  непрерывную производную порядка
непрерывную производную порядка  где
где  наименьшее целое число, большее или равное
наименьшее целое число, большее или равное  , то ее ряд Фурье по многочленам Якоби равномерно сходится к
, то ее ряд Фурье по многочленам Якоби равномерно сходится к 
В частности, для многочленов Лежандра  Для многочленов Чебышева первого рода
Для многочленов Чебышева первого рода  Можно показать, что равномерная сходимость в этом случае будет иметь место, если потребовать лишь ограниченность первой производной. Для многочленов Чебышева второго рода
Можно показать, что равномерная сходимость в этом случае будет иметь место, если потребовать лишь ограниченность первой производной. Для многочленов Чебышева второго рода  Здесь также возможно уточнение теоремы, а именно достаточно потребовать выполнения для функции
Здесь также возможно уточнение теоремы, а именно достаточно потребовать выполнения для функции  условия Дини — Липшица:
условия Дини — Липшица:

 модуль непрерывности
модуль непрерывности  , т. e.
, т. e.  для того чтобы обеспечить сходимость ряда по многочленам Чебышева второго рода на отрезке
для того чтобы обеспечить сходимость ряда по многочленам Чебышева второго рода на отрезке  и равномерную сходимость на всяком отрезке
и равномерную сходимость на всяком отрезке 
Для сходимости рядов по многочленам Лагерра достаточно потребовать, чтобы функция  была кусочно-гладкой на
была кусочно-гладкой на  и сходимости интеграла
и сходимости интеграла

При этом в точках непрерывности  ряд сходится к
ряд сходится к  а в точках разрыва к
а в точках разрыва к 
Аналогичные условия достаточны для сходимости рядов по многочленам Эрмита. Первое требование здесь сохраняется, а вместо предыдущего интеграла требуется ограниченность

Равномерная сходимость рядов по ортогональным многочленам к заданной функции имеет практический интерес, так как если нам необходимо достаточно хорошее равномерное приближение функции с помощью многочленов, то в случае равномерной сходимости ряда за приближающий многочлен можно принять частную сумму ряда, построение которого во многих случаях достаточно просто.
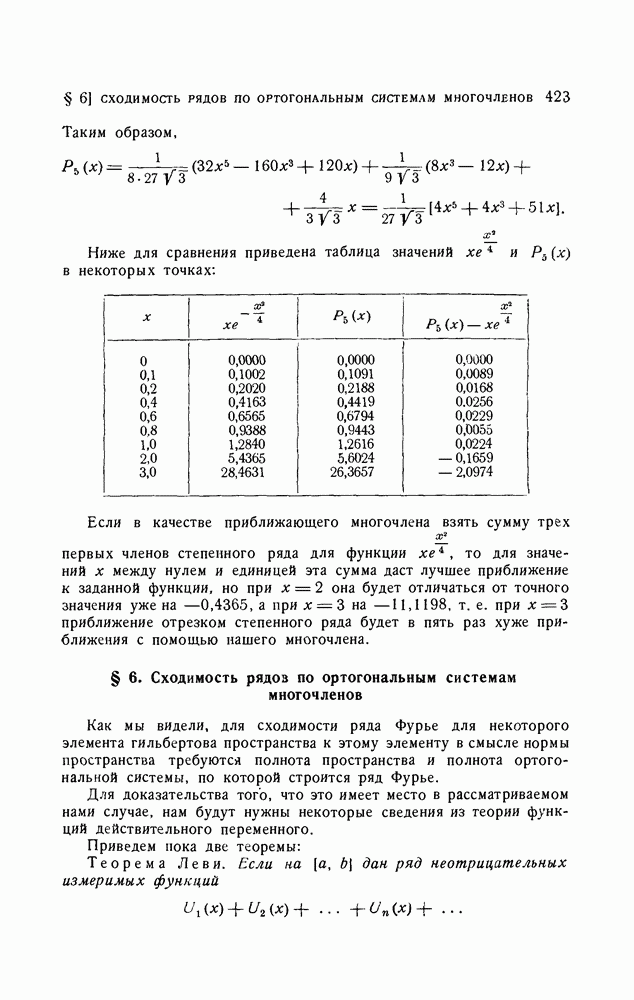
Пример. Построить многочлен, равномерно приближающий функцию

на отрезке  с точностью 0,0005.
с точностью 0,0005.
Функция  непрерывна вместе с производной
непрерывна вместе с производной  на отрезке
на отрезке  Следовательно, ряд Фурье этой функции по многочленам Чебышева первого рода сходится к ней равномерно. Поэтому будем искать многочлен, равномерно приближающий функцию
Следовательно, ряд Фурье этой функции по многочленам Чебышева первого рода сходится к ней равномерно. Поэтому будем искать многочлен, равномерно приближающий функцию  как частную сумму ряда Фурье по многочленам Чебышева. Разложение
как частную сумму ряда Фурье по многочленам Чебышева. Разложение  по многочленам Чебышева легко получить следующим образом. Известно разложение
по многочленам Чебышева легко получить следующим образом. Известно разложение

Положив здесь  получим:
получим:

Если за приближение функции будем принимать сумму первых  членов этого разложения, то погрешность не будет превосходить величины
членов этого разложения, то погрешность не будет превосходить величины

Нам необходимо взять  таким, чтобы
таким, чтобы

Для этого достаточно потребовать, чтобы имело место неравенство

Наименьшее целое значение  удовлетворяющее этому условию, будет
удовлетворяющее этому условию, будет  Таким образом, за многочлен, приближающий
Таким образом, за многочлен, приближающий  с точностью до 0,0005, можно взять
с точностью до 0,0005, можно взять

Используя то же самое разложение по многочленам Чебышева, можно получить многочлен пятой степени, дающий на отрезке  приближение функции
приближение функции  с точностью до 0,0001. Для этого нужно поступить следующим образом. За приближающий многочлен возьмем
с точностью до 0,0001. Для этого нужно поступить следующим образом. За приближающий многочлен возьмем  Многочлен
Многочлен  уклоняется от
уклоняется от  на отрезке
на отрезке  не более чем на
не более чем на

В  многочлен
многочлен  войдет с коэффициентом
войдет с коэффициентом  с коэффициентом
с коэффициентом  Из теории наилучших приближений
Из теории наилучших приближений
мы знаем, что на отрезке  наименее уклоняется от нуля многочлен
наименее уклоняется от нуля многочлен

причем величина этого уклонения равна Таким образом, если мы заменим  многочленом
многочленом

являющимся многочленом наилучшего приближения к  на отрезке
на отрезке  в совокупности многочленов степени не выше пятой, то мы совершим погрешность не более
в совокупности многочленов степени не выше пятой, то мы совершим погрешность не более  Заменяя в
Заменяя в  член
член  многочленом
многочленом  мы совершим погрешность не более чем
мы совершим погрешность не более чем

После подстановки и приведения подобных членов получим многочлен пятой степени, уклоняющийся от  на отрезке
на отрезке  не более чем на
не более чем на

т. е. мы получим в пять раз лучшую точность приближения с помощью многочлена той же пятой степени.
Аналогично можно показать, что многочлен уклонение которого от  на отрезке
на отрезке  меньше 0,0005, можно тем же приемом преобразовать в многочлен четвертой степени, уклонение которого от
меньше 0,0005, можно тем же приемом преобразовать в многочлен четвертой степени, уклонение которого от  также не превосходит 0,0005.
также не превосходит 0,0005.
На этом пути часто удается построить многочлены, дающие очень хорошие приближения к заданной функции 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
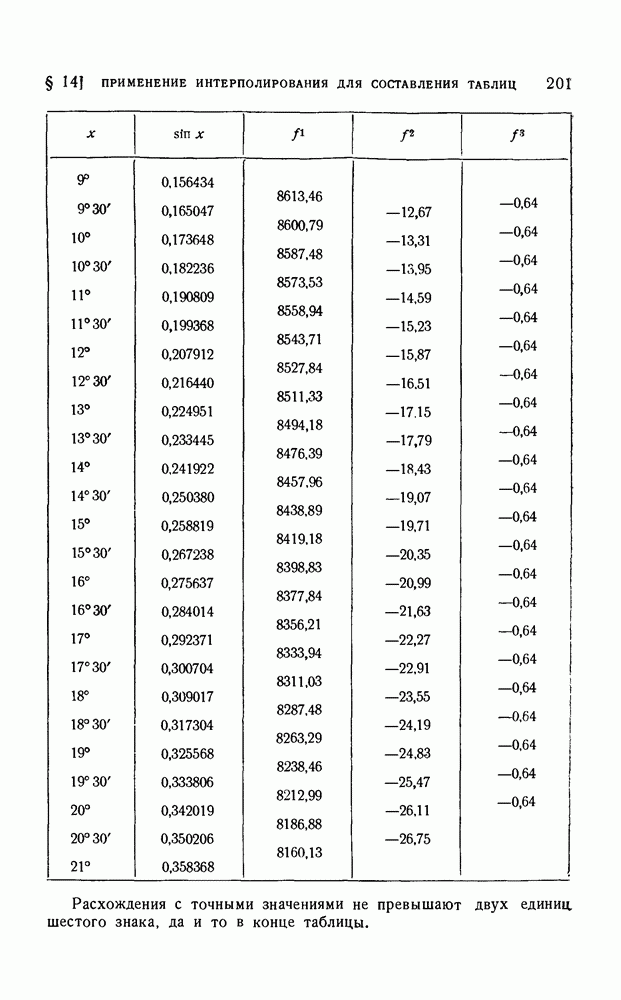
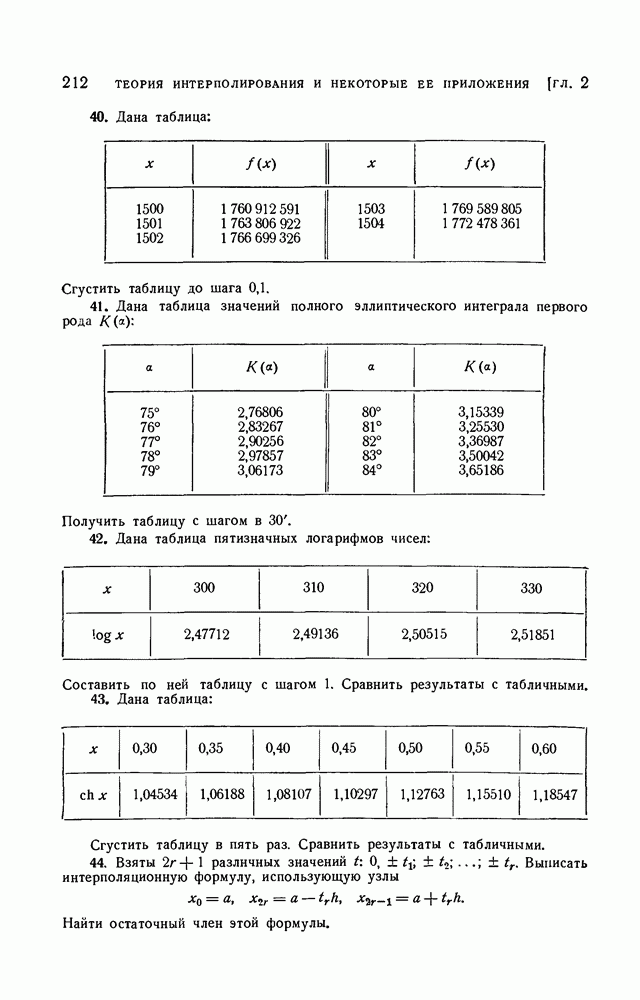
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
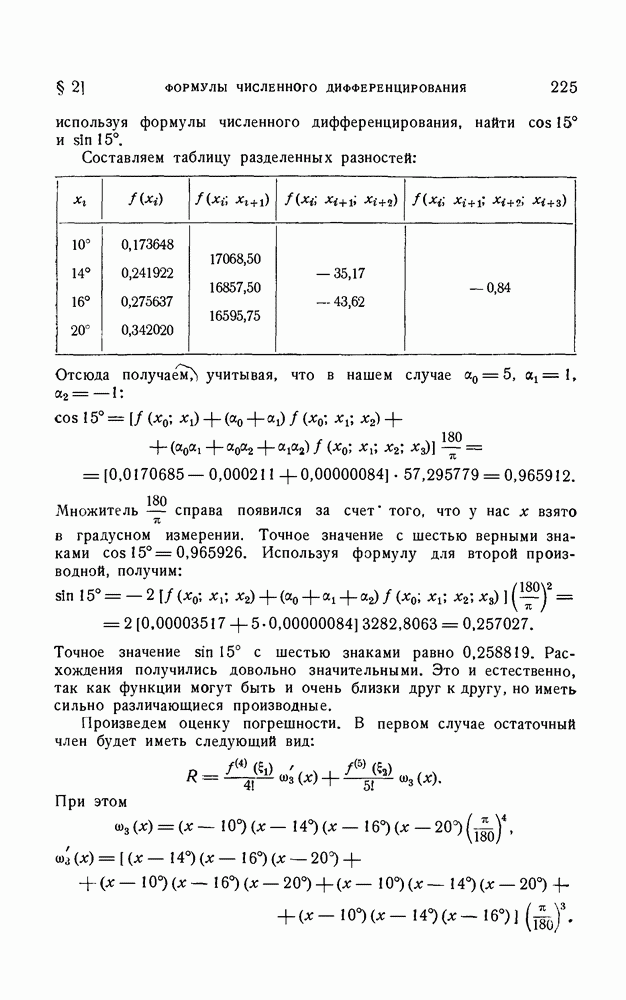
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
- § 3. Задача численного интегрирования
- § 4. Формулы Ньютона — Котеса
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
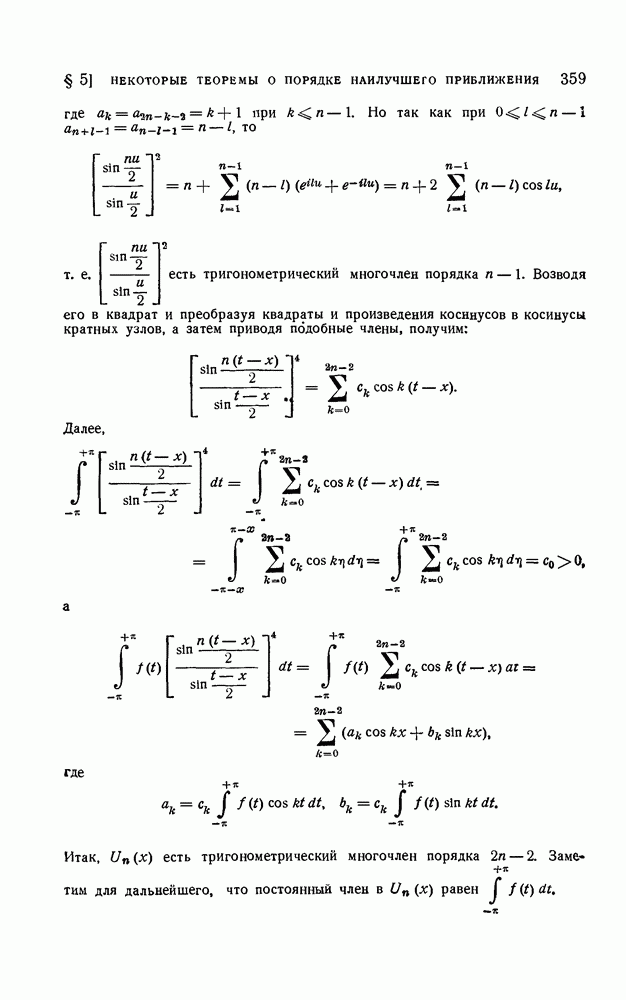
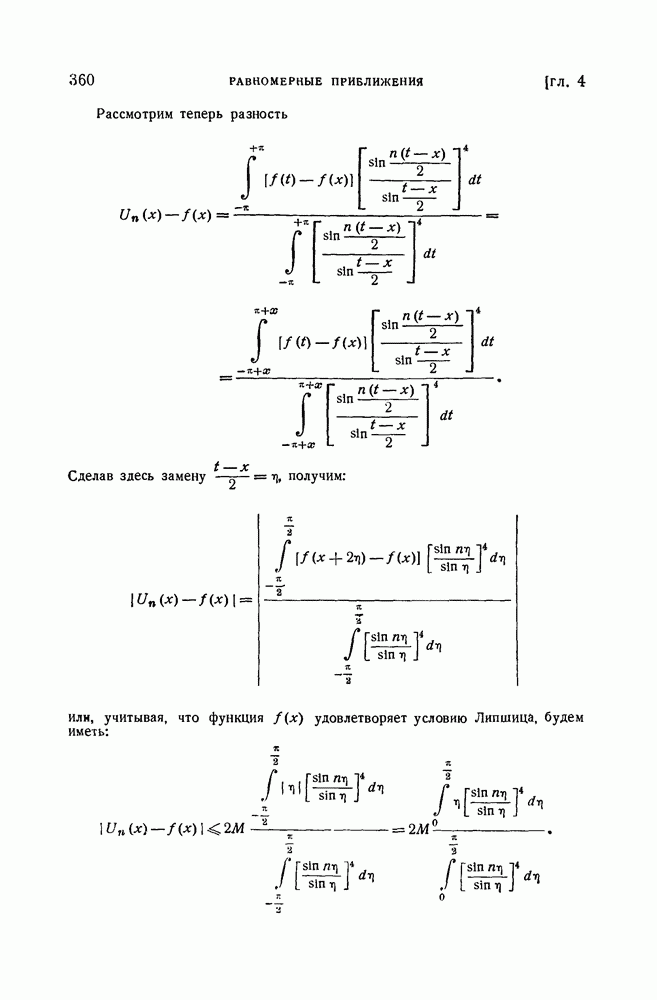
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
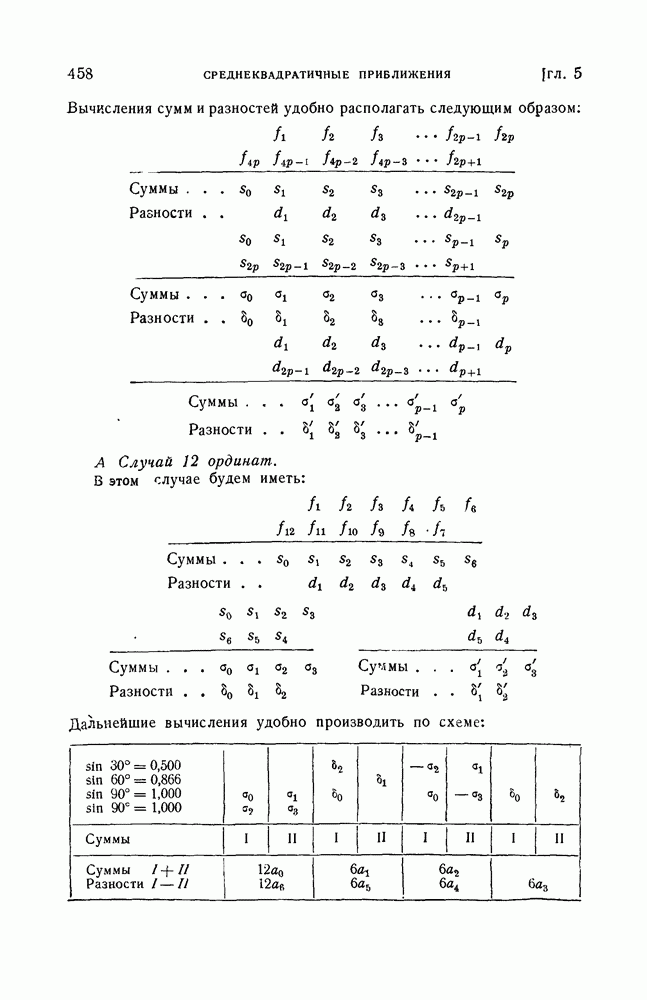
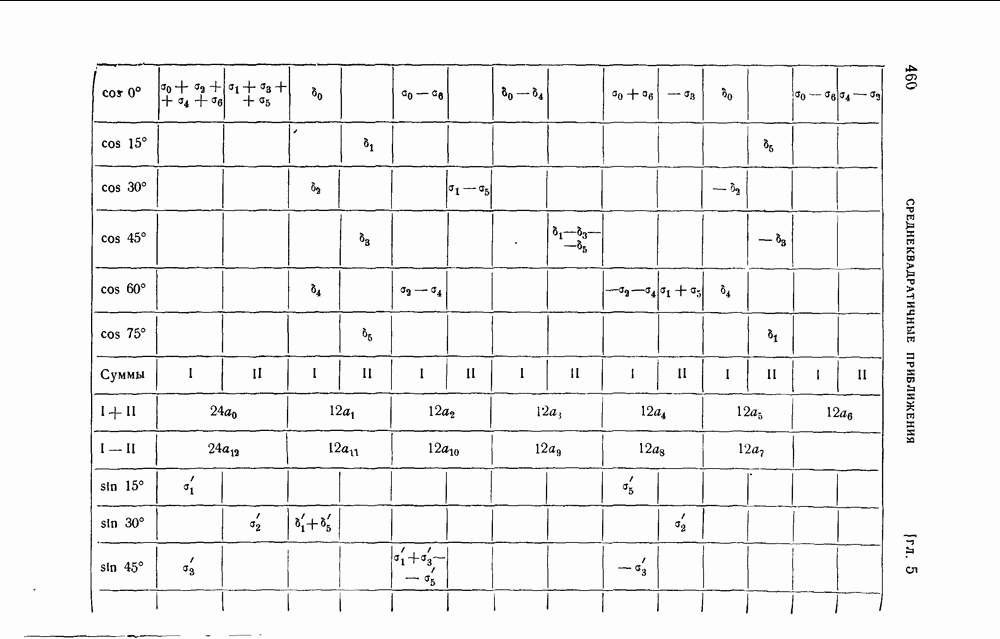
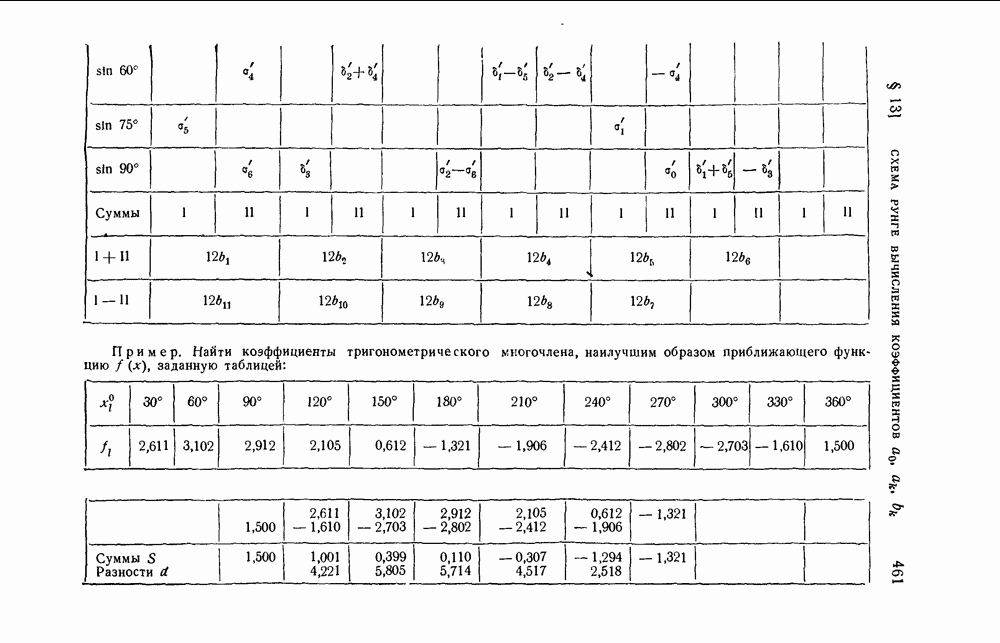
- § 13. Схема Рунге вычисления коэффициентов … в случае …