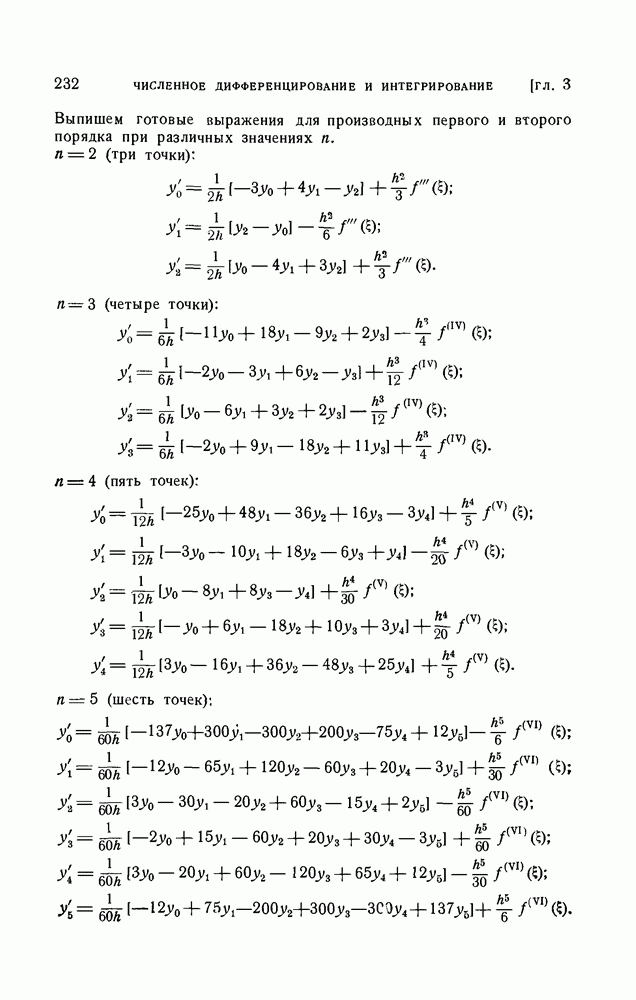| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 14. Применение интерполирования для составления таблиц
Теория интерполирования имеет большие приложения при составлении таблиц функций. Получив задание на составление таблиц тех или иных функций, математик должен решить перед началом вычислений ряд вопросов. Должна быть выбрана формула, по которой будут производиться вычисления. Эта формула может изменятся от участка к участку. Обычно формулы для вычисления значений функции, использующие способ задания функции, бывают громоздкими и поэтому их используют для получения некоторых опорных значений и затем путем субтабулирования сгущают таблицу. Формула, дающая опорные значения функции, должна обеспечивать нужную точность таблиц с учетом последующего субтабулирования. Если предполагается составить таблицы с постоянным шагом, то должен быть определен шаг таблицы. Шаг таблицы связан с двумя факторами: объемом таблиц и интерполяционной формулой, по которой будут вычисляться промежуточные значения уже в готовой таблице. Чем больше будет шаг, тем больше членов интерполяционной формулы придется использовать при пользовании этой таблицей на практике. Это создает некоторые неудобства при использовании таблицы. С другой стороны, чем меньше шаг, тем больше объем таблиц, что также не очень удобно. Математик должен как-то согласовать действие этих противоположных факторов с учетом средств вычислений, имеющихся в распоряжении потребителя. Если таблица должна быть введена в быстродействующую машину, то особенно важно уменьшить ее объем. При этом можно отказаться от постоянства шага и использовать, например, узлы Чебышева на отдельных участках, для которых, как мы видели, получается наилучшая оценка остаточного члена интерполяционной формулы. При определении шага таблицы будут иметь значение и такие факторы, как наличие вычислительных средств и время, отведенное на вычисления.
Мы не можем здесь входить в детали каждого из поставленных вопросов и остановимся лишь на выборе шага и субтабулировании,
Чаще всего таблицы функций составляются так, чтобы была допустима линейная интерполяция (т. е. интерполяция с использованием первых двух членов формулы). В этом случае остаточный член будет иметь вид

Здесь 5 принадлежит интервалу между двумя соседними табличными значениями аргумента, в котором лежит  заключено между 0 и 1. Произведение
заключено между 0 и 1. Произведение  принимает наибольшее по модулю значение при
принимает наибольшее по модулю значение при  Это значение равно
Это значение равно  Следовательно,
Следовательно,

Чтобы ошибка интерполирования не превышала по абсолютной величине а, необходимо выбирать  удовлетворяющим условию
удовлетворяющим условию

Нужно помнить, что наряду с этой ошибкой — ошибкой метода, при практическом вычислении промежуточных значений будут возникать еще неустранимая погрешность и погрешность округлений. Как мы видели ранее, неустранимая погрешность при линейной интерполяции будет равна погрешности табулированных значений функций. Погрешность округления будет зависеть от вычислительных средств и от программы вычислений. Поэтому здесь мы ее касаться не будем.
Совершенно аналогично можно исследовать квадратичную интерполяцию и интерполяцию более высоких порядков. Если, например, используется интерполяционная формула Эверетта, то остаточный член будет иметь вид

и в этом случае наибольшее значение для  на [0,1]
на [0,1]

будет достигаться при  Это значение равно
Это значение равно  Таким образом,
Таким образом,

и для того чтобы ошибка квадратичной интерполяции не превышала а, нужно, чтобы шаг  удовлетворял условию
удовлетворял условию
И здесь, кроме этой ошибки метода, возникают неустранимая ошибка и ошибка округления. Неустранимая ошибка будет такова же, как
и для формулы Гаусса, взятой до третьих разностей. Как видно из приведенной ранее таблицы, неустранимая погрешность не может больше чем в 1,4 раза превысить абсолютные погрешности табулированных значений.
Аналогично можно исследовать и другие формулы. Рассмотрим теперь вопрос о субтабулировании. Как применяется формула Эверетта для субтабулирования, мы уже знаем. Приведем здесь еще один способ субтабулирования.
Пусть  данные последовательные значения функции, соответствующие шагу аргумента, равному
данные последовательные значения функции, соответствующие шагу аргумента, равному  их разности. Предположим, что нам нужно сгустить таблицу в
их разности. Предположим, что нам нужно сгустить таблицу в  раз, т. е. новый шаг будет
раз, т. е. новый шаг будет  . Обозначим новые значения функции соответственно
. Обозначим новые значения функции соответственно 
Здесь  последовательные значения функции между
последовательные значения функции между  Будем для определенности считать, что разности пятого порядка исходных значений функции постоянны. Найдем выражения для разностей значений функции с новым шагом через разности с прежним шагом. Для этого используем операторное исчисление, примененное нами ранее для вывода интерполяционных формул. По формуле Ньютона для интерполирования вперед будем иметь:
Будем для определенности считать, что разности пятого порядка исходных значений функции постоянны. Найдем выражения для разностей значений функции с новым шагом через разности с прежним шагом. Для этого используем операторное исчисление, примененное нами ранее для вывода интерполяционных формул. По формуле Ньютона для интерполирования вперед будем иметь:

Обозначим через  разность с шагом
разность с шагом  Тогда
Тогда

Таким образом, операторы  связаны следующим соотношением:
связаны следующим соотношением:

Следовательно, степени их будут связаны таким соотношением:

Отсюда последовательно получаем:

После того как получены разности, нетрудно, используя постоянство разностей пятого порядка, произвести субтабулирование. Сначала заполняем столбец пятых разностей, затем четвертых и т. д., пока не придем к значениям функции. Эти формулы, связывающие  можно получить и без операторного исчисления. Рассмотрим, как это делается на примере. Возьмем те же значения
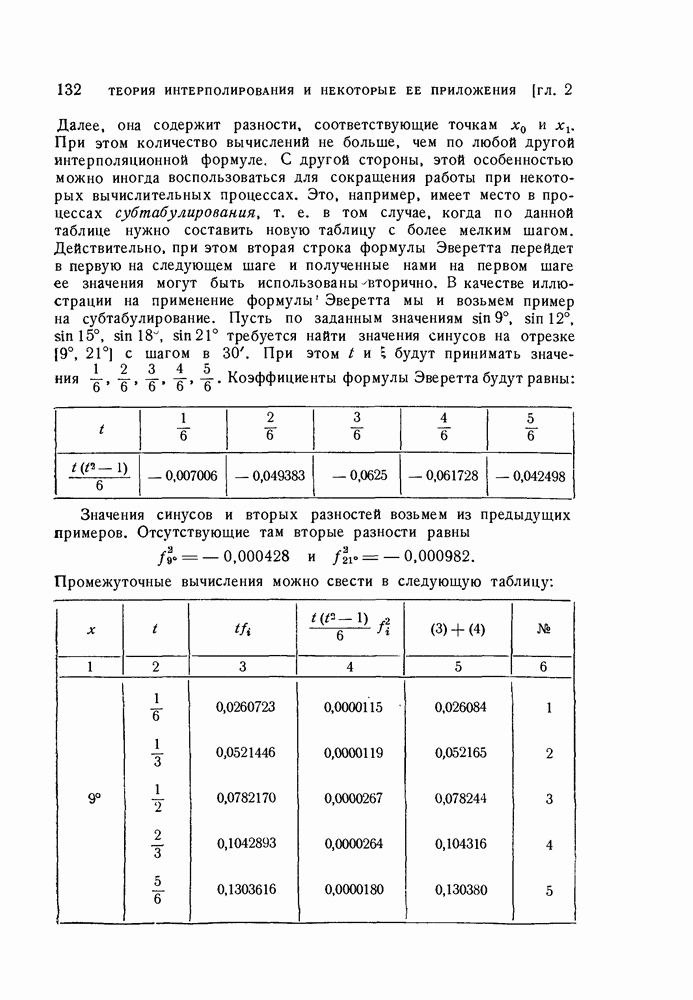
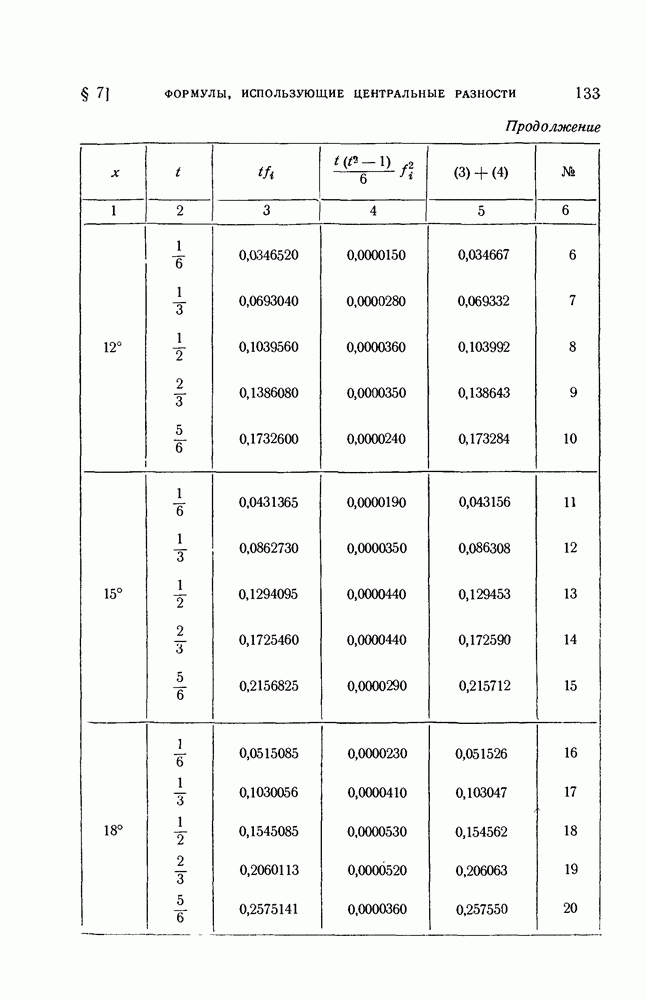
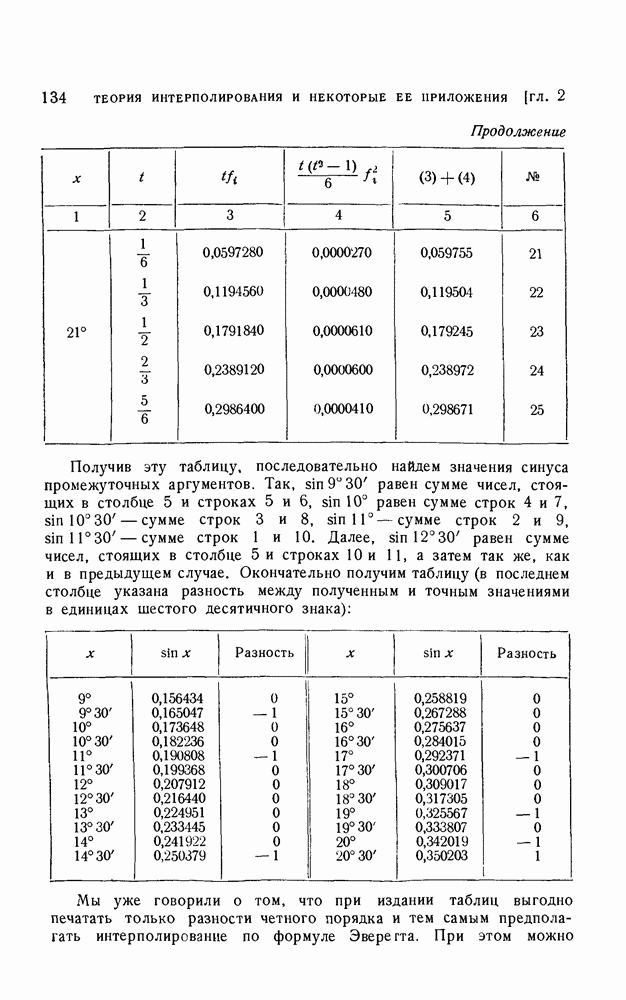
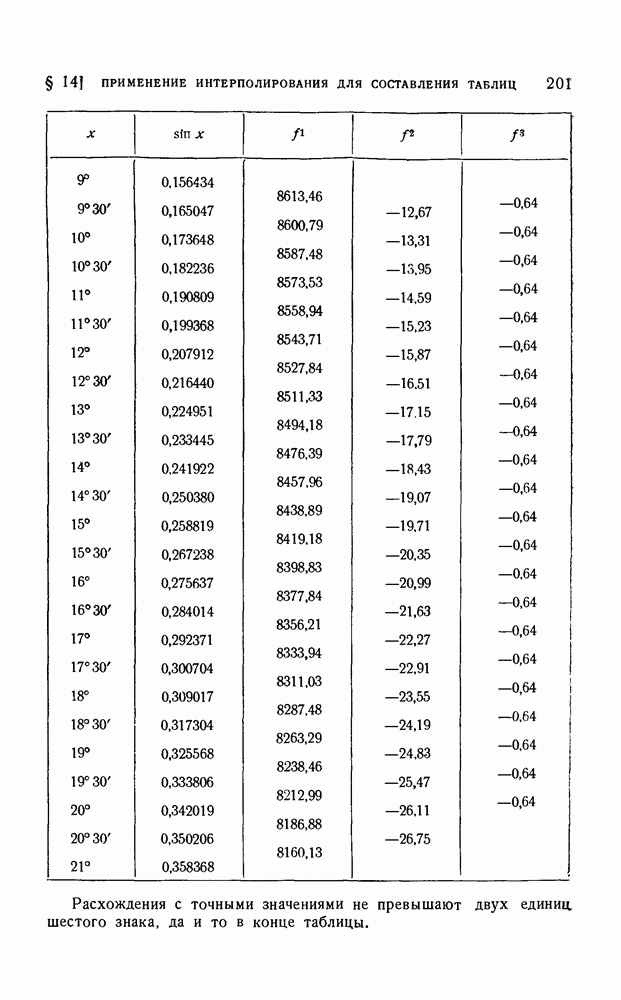
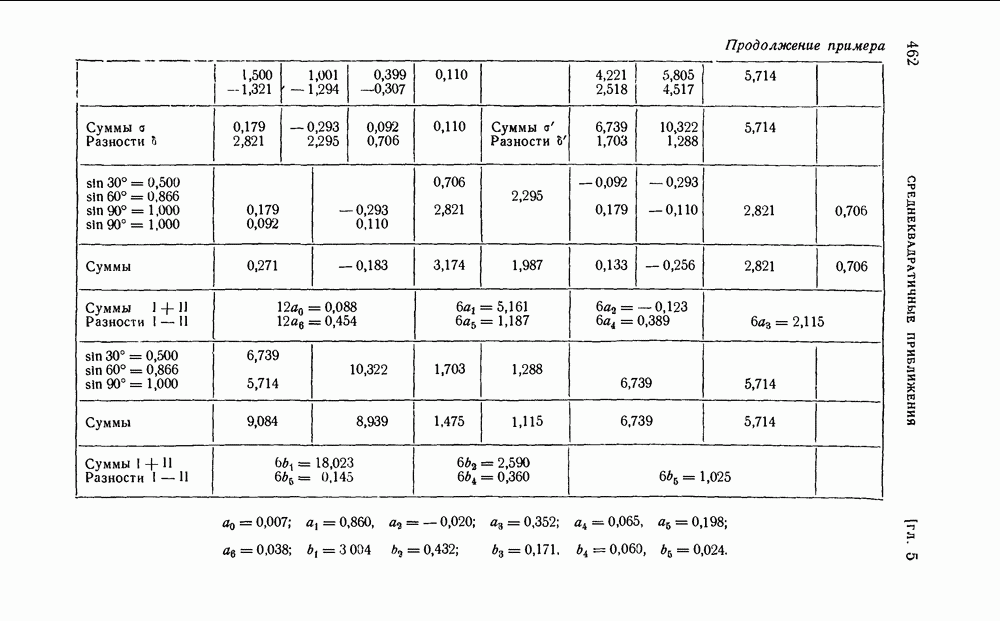
можно получить и без операторного исчисления. Рассмотрим, как это делается на примере. Возьмем те же значения  которые мы использовали ранее в § 7, и получим таблицу с шагом в 30. Таблица исходных значений функции и их разностей выглядит следующим образом:
которые мы использовали ранее в § 7, и получим таблицу с шагом в 30. Таблица исходных значений функции и их разностей выглядит следующим образом:
(см. скан)
В нашем случае  Последовательно получаем:
Последовательно получаем:


Будем обозначать разности с новым шагом чертой сверху. Первые разности будут выражаться так через предыдущие разности:

Вторые разности будут иметь вид:

Третьи разности будут равны:

Подставляя сюда числовые значения, получим:

Далее вычисления проводим так же, как в § 6, где мы продолжали таблицу многочлена. Сначала заполняем столбец третьих разностей, затем вторых, первых и, наконец, столбец значений функции. В узловых точках записываем данные нам значения. Расхождения могут произойти за счет округлений. Таблица выглядит так
(см. скан)
Расхождения с точными значениями не превышают двух единиц, шестого знака, да и то в конце таблицы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
- § 3. Задача численного интегрирования
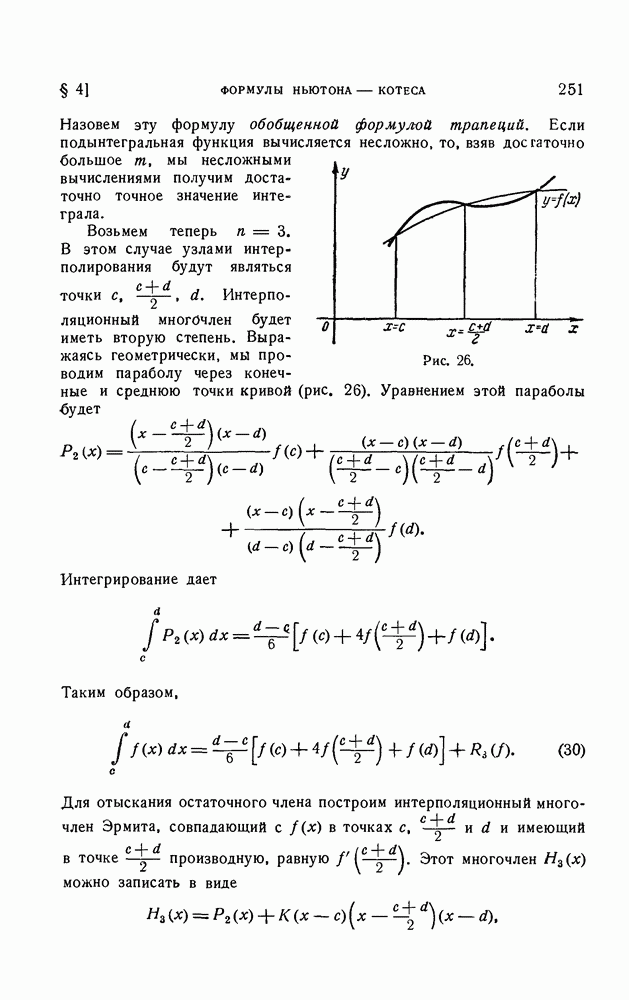
- § 4. Формулы Ньютона — Котеса
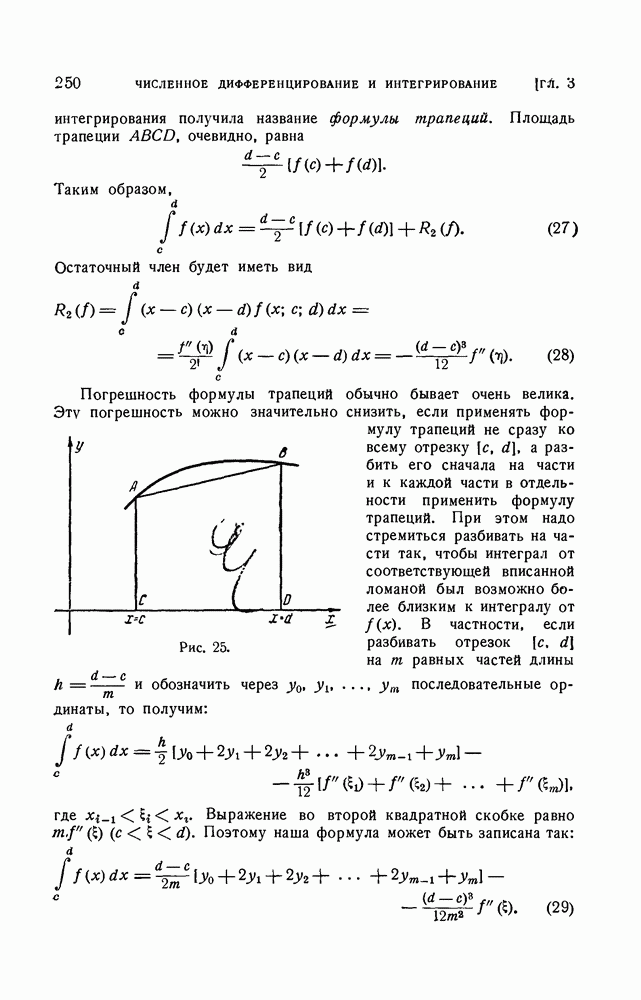
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
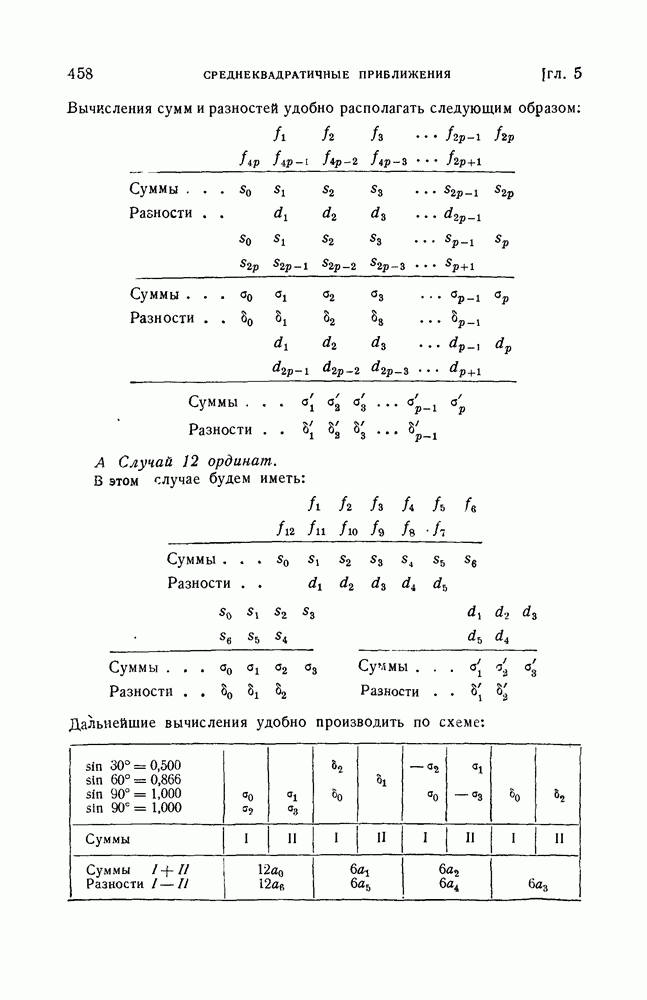
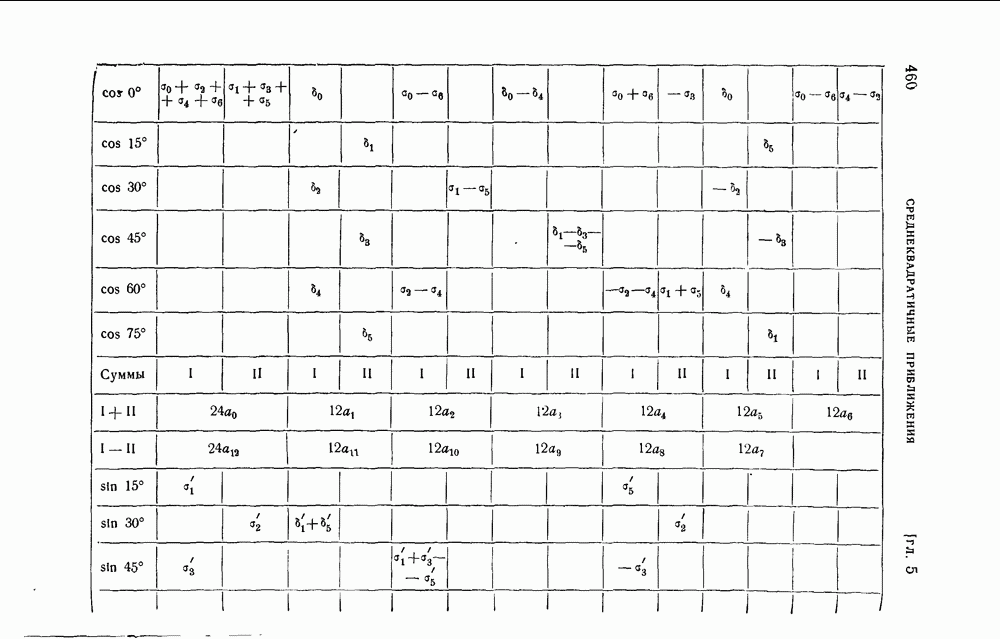
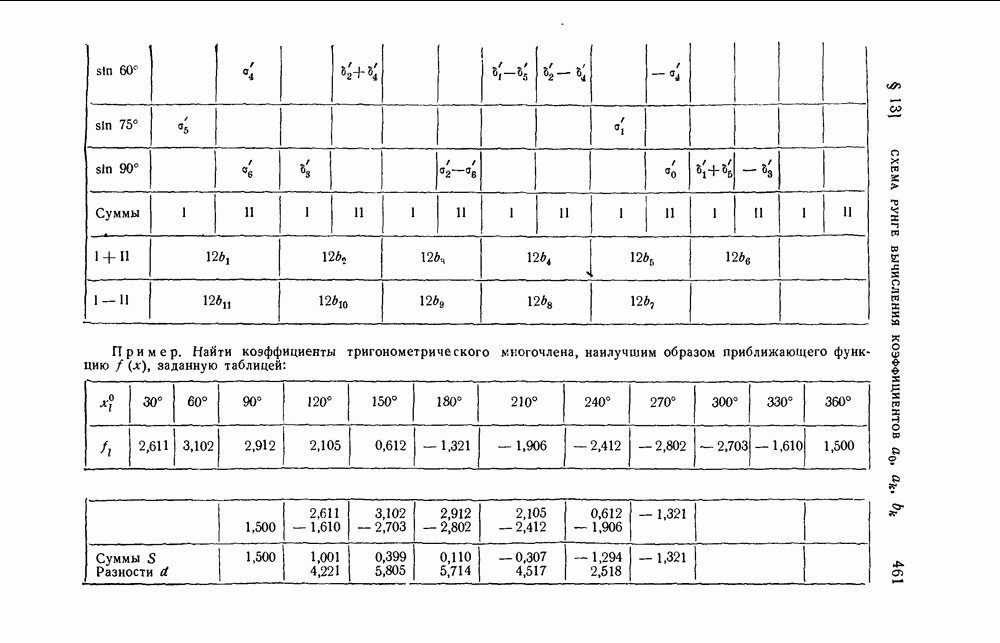
- § 13. Схема Рунге вычисления коэффициентов … в случае …