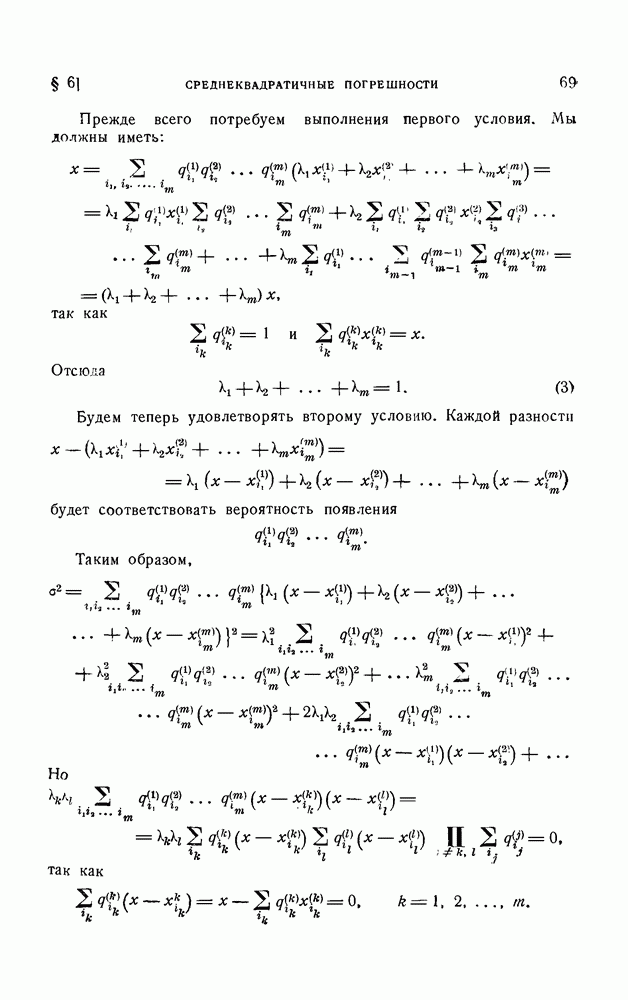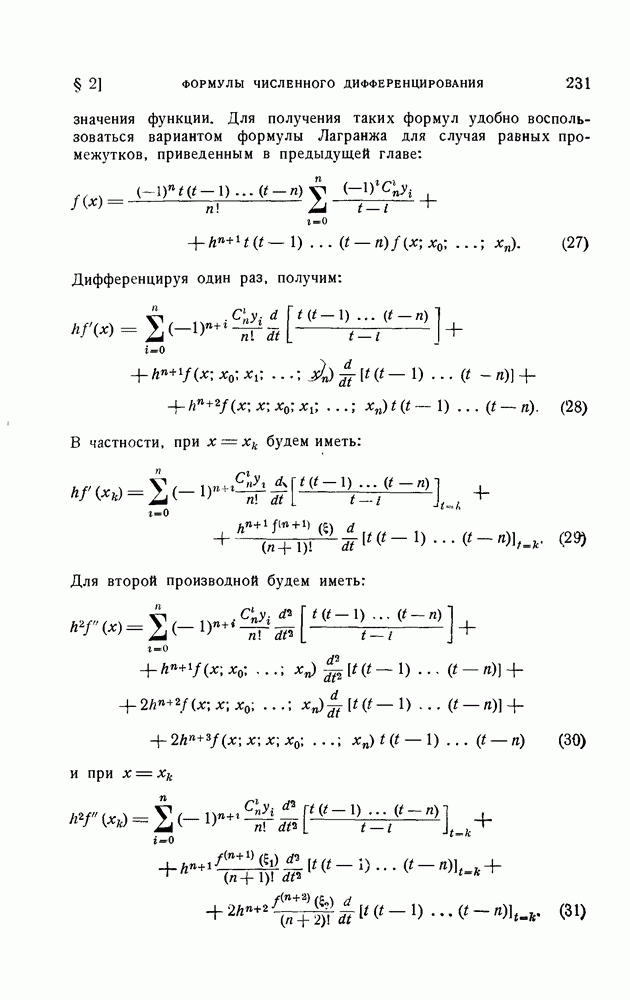| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. Интерполирование периодических функций
В тех случаях, когда интерполируемая функция  обладает свойством
обладает свойством  то естественно на базисные функции
то естественно на базисные функции  накладывать такое же ограничение
накладывать такое же ограничение  Такие функции можно рассматривать как периодические с периодом
Такие функции можно рассматривать как периодические с периодом  Для периодических функций можно также ввести понятие систем Чебышева на отрезке
Для периодических функций можно также ввести понятие систем Чебышева на отрезке  Совокупность функций
Совокупность функций  удовлетворяющих условию
удовлетворяющих условию  будем называть периодической системой Чебышева на отрезке
будем называть периодической системой Чебышева на отрезке  если любая линейная комбинация
если любая линейная комбинация

 не все коэффициенты которой нули, имеет на
не все коэффициенты которой нули, имеет на  не более
не более  корней при условии, что
корней при условии, что  считаются за один корень.
считаются за один корень.
Докажем, что порядок  периодических систем Чебышева должен быть четным. Для доказательства рассмотрим определитель
периодических систем Чебышева должен быть четным. Для доказательства рассмотрим определитель

где  некоторые точки отрезка
некоторые точки отрезка  при
при  уменьшая общности, мы можем предполагать, что ни одна из точек
уменьшая общности, мы можем предполагать, что ни одна из точек  не совпадает ни с а, ни с
не совпадает ни с а, ни с  В противном случае мы воспользовались бы периодичностью функций и сдвинули бы наш отрезок
В противном случае мы воспользовались бы периодичностью функций и сдвинули бы наш отрезок  на некоторую величину вправо или влево.
на некоторую величину вправо или влево.
Если функции  составляют систему Чебышева, то
составляют систему Чебышева, то  не может обращаться в нуль ни в одной точке
не может обращаться в нуль ни в одной точке  за исключением
за исключением  в которых, конечно, он равен нулю. Докажем, что в этом случае
в которых, конечно, он равен нулю. Докажем, что в этом случае  меняет знак при переходе через каждое из
меняет знак при переходе через каждое из  Предположим, что это не так и
Предположим, что это не так и  точка, при переходе через которую
точка, при переходе через которую  не меняет знака. Тогда рассмотрим определитель
не меняет знака. Тогда рассмотрим определитель  построенный так же,
построенный так же,  за исключением
за исключением  столбца, в котором
столбца, в котором  заменены на
заменены на  где
где  произвольная точка
произвольная точка  отличная от всех
отличная от всех  также является линейной комбинацией
также является линейной комбинацией  Она отлична от нуля в точке
Она отлична от нуля в точке  а в силу непрерывности функций
а в силу непрерывности функций  и в некоторой окрестности
и в некоторой окрестности  Рассмотрим функцию
Рассмотрим функцию

где X — некоторое действительное число, имеющее такой знак, что  в некоторой окрестности
в некоторой окрестности  имеют одинаковые знаки. Обозначим через
имеют одинаковые знаки. Обозначим через  наименьшее расстояние между точками
наименьшее расстояние между точками  Выберем X настолько малым по абсолютной величине, что
Выберем X настолько малым по абсолютной величине, что  имеет такой же знак, как и
имеет такой же знак, как и  . Тогда
. Тогда  имеет в точках
имеет в точках  чередующиеся знаки и, следовательно, имеет по крайней мере два корня на интервале
чередующиеся знаки и, следовательно, имеет по крайней мере два корня на интервале  того,
того,  обращается в нуль в точках
обращается в нуль в точках  Таким образом, эта функция имеет на отрезке
Таким образом, эта функция имеет на отрезке  корней. Но она является линейной комбинацией
корней. Но она является линейной комбинацией  не равной тождественно нулю. Следовательно, она не может обращаться в нуль на отрезке
не равной тождественно нулю. Следовательно, она не может обращаться в нуль на отрезке  более чем в
более чем в  точках. Мы пришли к противоречию. Таким образом, мы доказали, что
точках. Мы пришли к противоречию. Таким образом, мы доказали, что  при переходе через каждую из точек
при переходе через каждую из точек  меняет знак.
меняет знак.
В силу периодичности  Итак, при возрастании х от а до
Итак, при возрастании х от а до  определитель
определитель  раз меняет знак и приходит
раз меняет знак и приходит
к прежнему значению. Это может быть только в том случае, когда  четное число.
четное число.
Простейшей периодической системой Чебышева является система

Период этой системы равен Мы можем ее использовать и для интерполирования функций, имеющих другой период. Для этого нужно только предварительно линейной заменой независимого переменного сделать длину периода равной  В силу предыдущих рассуждений мы должны рассматривать систему
В силу предыдущих рассуждений мы должны рассматривать систему

Покажем, что такая система функций при любом  образует периодическую систему Чебышева. Для этого рассмотрим произвольный тригонометрический многочлен
образует периодическую систему Чебышева. Для этого рассмотрим произвольный тригонометрический многочлен

коэффициенты которого комплексные или действительные числа. Будем говорить, что этот тригонометрический многочлен имеет порядок  если по крайней мере один из коэффициентов
если по крайней мере один из коэффициентов  или
или  отличен от нуля. Если
отличен от нуля. Если  то
то  имеет ровно
имеет ровно  корней в полосе
корней в полосе  Действительно, производя замену независимого переменного
Действительно, производя замену независимого переменного  мы получим:
мы получим:

где  при
при  при
при  является алгебраическим многочленом степени
является алгебраическим многочленом степени  относительно z. В силу наших предположений относительно коэффициентов
относительно z. В силу наших предположений относительно коэффициентов  коэффициенты при
коэффициенты при  этого многочлена отличны от нуля. Следовательно, он имеет ровно
этого многочлена отличны от нуля. Следовательно, он имеет ровно  корней и ни один из корней не равен нулю. Каждому из этих корней в силу определения
корней и ни один из корней не равен нулю. Каждому из этих корней в силу определения  будет соответствовать одно и только одно значение х, принадлежащее полосе
будет соответствовать одно и только одно значение х, принадлежащее полосе  Это и будут корни
Это и будут корни  Других корней
Других корней  иметь не может. Если условия, которые мы накладывали на
иметь не может. Если условия, которые мы накладывали на  не выполнены, то
не выполнены, то  может иметь в нашей полосе менее
может иметь в нашей полосе менее  нулей.
нулей.
Как следствие предыдущих рассуждений получаем: если два тригонометрических многочлена совпадают в  точках
точках  при
при  то они совпадают тождественно.
то они совпадают тождественно.
Перейдем теперь к фактическому отысканию тригонометрических интерполяционных многочленов. Пусть нам заданы  узлов
узлов 
 принадлежащих полуотрезку [0, Определитель
принадлежащих полуотрезку [0, Определитель  в нашем случае примет вид
в нашем случае примет вид

Найдем величину этого определителя. Для этого представим каждую из тригонометрических функций в показательной форме. При этом получим:

Преобразуем этот определитель, вынося из столбцов общие множители или  и
и  прибавляя к каждому столбцу с четным номером столбец с нечетным номером, на единицу большим. В результате будем иметь:
прибавляя к каждому столбцу с четным номером столбец с нечетным номером, на единицу большим. В результате будем иметь:

Вынесем двойки за знак определителя из столбцов с четными номерами и вычтем эти столбцы из столбцов с нечетными номерами, на единицу большими. В полученном определителе

вынесем из каждой строки  В результате этого найдем:
В результате этого найдем:

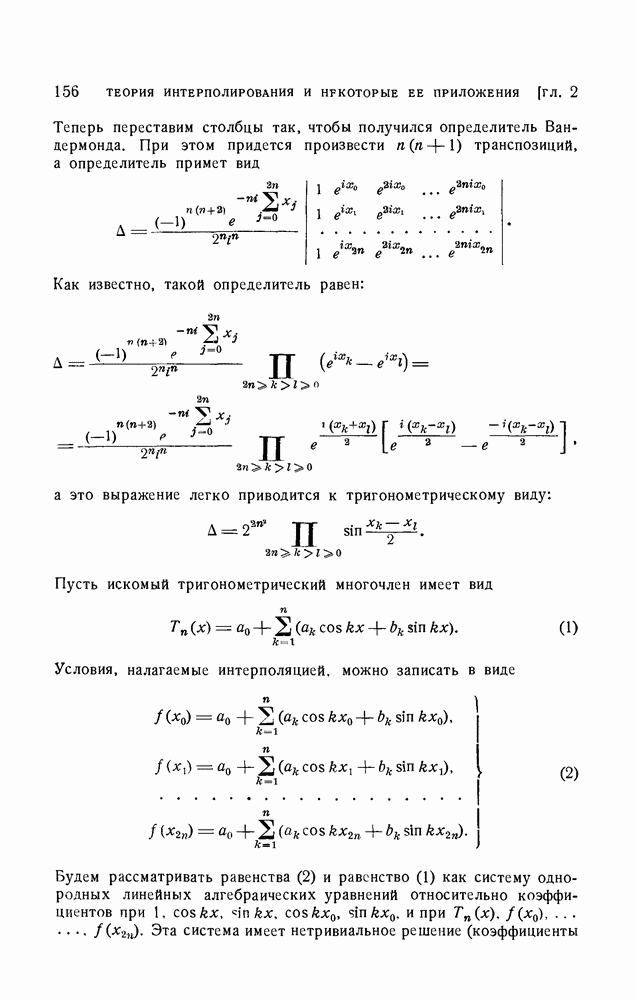
Теперь переставим столбцы так, чтобы получился определитель Вандермонда. При этом придется произвести  транспозиций, а определитель примет вид
транспозиций, а определитель примет вид

Как известно, такой определитель равен:

а это выражение легко приводится к тригонометрическому виду:

Пусть искомый тригонометрический многочлен имеет вид

Условия, налагаемые интерполяцией, можно записать в виде

Будем рассматривать равенства (2) и равенство (1) как систему однородных линейных алгебраических уравнений относительно коэффициентов при  и при
и при  Эта система имеет нетривиальное решение (коэффициенты
Эта система имеет нетривиальное решение (коэффициенты
при  равны —1). Следовательно, определитель системы равен нулю:
равны —1). Следовательно, определитель системы равен нулю:

Раскрывая этот определитель по элементам первого столбца, получим:

Здесь  означает определитель
означает определитель  в котором 1-я строка заменена первой строкой из написанного выше определителя. Так как эти определители имеют такое же строение, как и определитель
в котором 1-я строка заменена первой строкой из написанного выше определителя. Так как эти определители имеют такое же строение, как и определитель  то мы получим после очевидных сокращений:
то мы получим после очевидных сокращений:

Что это действительно тригонометрический многочлен, обнаруживается простыми тригонометрическими преобразованиями. В числителе каждого слагаемого мы имеем произведение  множителей вида
множителей вида  Произведение двух таких множителей дает
Произведение двух таких множителей дает

т. е. тригонометрический многочлен первого порядка. Теперь докажем, что произведение двух тригонометрических многочленов  соответственно порядков тип даст тригонометрический многочлен порядка
соответственно порядков тип даст тригонометрический многочлен порядка  Действительно, в это произведение войдут члены вида
Действительно, в это произведение войдут члены вида  Но
Но

Если коэффициенты многочлена  обозначить через
обозначить через  и а коэффициенты многочлена
и а коэффициенты многочлена  буквами и то коэффициент
буквами и то коэффициент
при  в произведении
в произведении  будет равен
будет равен  а коэффициент при
а коэффициент при  По крайней мере один из этих коэффициентов отличен от нуля. Это и доказывает утверждение. Таким образом, каждое слагаемое написанной интерполяционной формулы является тригонометрическим многочленом порядка и и, следовательно, вся сумма также является тригонометрическим многочленом порядка не выше
По крайней мере один из этих коэффициентов отличен от нуля. Это и доказывает утверждение. Таким образом, каждое слагаемое написанной интерполяционной формулы является тригонометрическим многочленом порядка и и, следовательно, вся сумма также является тригонометрическим многочленом порядка не выше 
Выполнение интерполяционных условий проверяется непосредственно. Таким образом,  решает поставленную задачу. Можно было бы не производить выкладок с определителями, а сразу написать выражение для
решает поставленную задачу. Можно было бы не производить выкладок с определителями, а сразу написать выражение для  и проверить, что все условия будут выполнены.
и проверить, что все условия будут выполнены.
Приведем пример на применение полученной интерполяционной формулы.
Построить тригонометрический многочлен второго порядка, который бы в точках  принимал соответственно значения
принимал соответственно значения  . В этом случае получим:
. В этом случае получим:

Числитель первой дроби будет равен

Знаменатель ее равен

Итак, первая дробь равна

Числитель второго слагаемого даст

а знаменатель

а второе слагаемое равно

Числитель третьего слагаемого равен

а знаменатель

и третье слагаемое равно

Складывая найденные выражения для каждого из слагаемых, получим:

Проверкой убеждаемся, что действительно этот многочлен удовлетворяет всем условиям.
Если интерполируемая функция четная, то естественно искать четный интерполирующий многочлен. Точно так же для нечетных интерполируемых функций естественно разыскивать нечетный интерполирующий многочлен.
Рассмотрим сначала случай четных функций  Пусть
Пусть  задана на отрезке
задана на отрезке  В качестве базисной системы интерполирующих функций возьмем
В качестве базисной системы интерполирующих функций возьмем

Каждая из функций этой системы также четная. Поэтому мы можем задавать узлы интерполирования на какой-нибудь из половин рассматриваемого отрезка. Выберем полуотрезок  Пусть на нем заданы узлы
Пусть на нем заданы узлы  соответствующие им значения функции
соответствующие им значения функции  Если среди узлов имеется точка 0, то будем считать, что она соответствует
Если среди узлов имеется точка 0, то будем считать, что она соответствует  Построим
Построим
тригонометрический интерполяционный многочлен порядка  принимающий в точках
принимающий в точках  соответственно значения
соответственно значения  Мы можем применить предыдущие рассуждения, так как длина отрезка равна
Мы можем применить предыдущие рассуждения, так как длина отрезка равна  . При этом получим:
. При этом получим:
(см. скан)
Используем формулы

и

Дробь, стоящая в первом слагаемом, примет вид

Объединим члены с одинаковыми  в первой и второй суммах. Они будут иметь общий множитель
в первой и второй суммах. Они будут иметь общий множитель

Члены, стоящие при этом общем множителе, дадут

Таким образом,  в этом случае будет иметь вид
в этом случае будет иметь вид

Это будет четный многочлен, принимающий при  значения
значения
Приведем следующий числовой пример.
Построить четный тригонометрический многочлен, который при  принимает соответственно значения 2, 1, 0.
принимает соответственно значения 2, 1, 0.
В этом случае будем иметь:

Совершенно аналогично можно построить нечетный многочлен, который при  принимает значения
принимает значения 
 Для этого будем строить тригонометрический многочлен
Для этого будем строить тригонометрический многочлен  порядка
порядка  который в точках
который в точках  принимает соответственно значения
принимает соответственно значения  в этом случае
в этом случае

Как и прежде, обнаружим, что если объединить члены с одинаковыми  то можно будет вынести общие множители:
то можно будет вынести общие множители:

Коэффициентами при этих общих множителях будут

Итак, окончательное выражение для  будет иметь вид
будет иметь вид

Это будет нечетный тригонометрический многочлен, принимающий при  значения
значения  Приведем и для этого случая числовой примео.
Приведем и для этого случая числовой примео.
Построить нечетный тригонометрический многочлен, который при  принимает значения
принимает значения  По общей форме будем иметь:
По общей форме будем иметь:

Проверкой убеждаемся, что этот многочлен удовлетворяет поставленным условиям.
Как мы видели, практическое построение тригонометрических интерполяционных многочленов чрезвычайно громоздко. Естественно ожидать, что если узлы равноотстоящие, то задача упростится. Построение тригонометрических многочленов для случая равноотстоящих узлов составляет задачу гармонического анализа. К этому вопросу мы еще вернемся в разделе среднеквадратичных приближений.
Так как последние две задачи имеют всегда единственное решение, то системы функций  первая на
первая на  а вторая на
а вторая на  образуют системы Чебышева.
образуют системы Чебышева.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
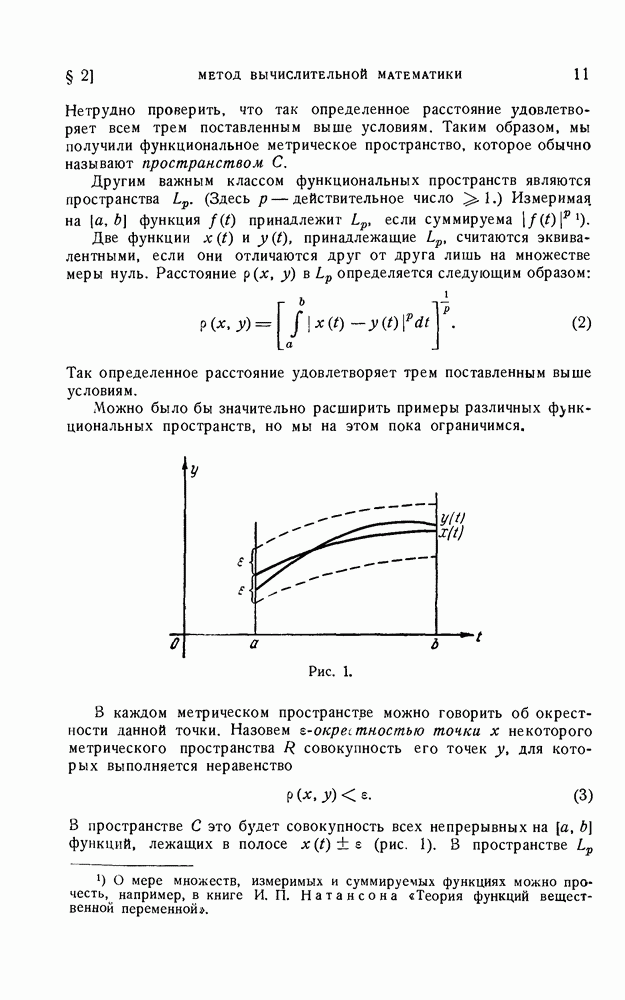
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
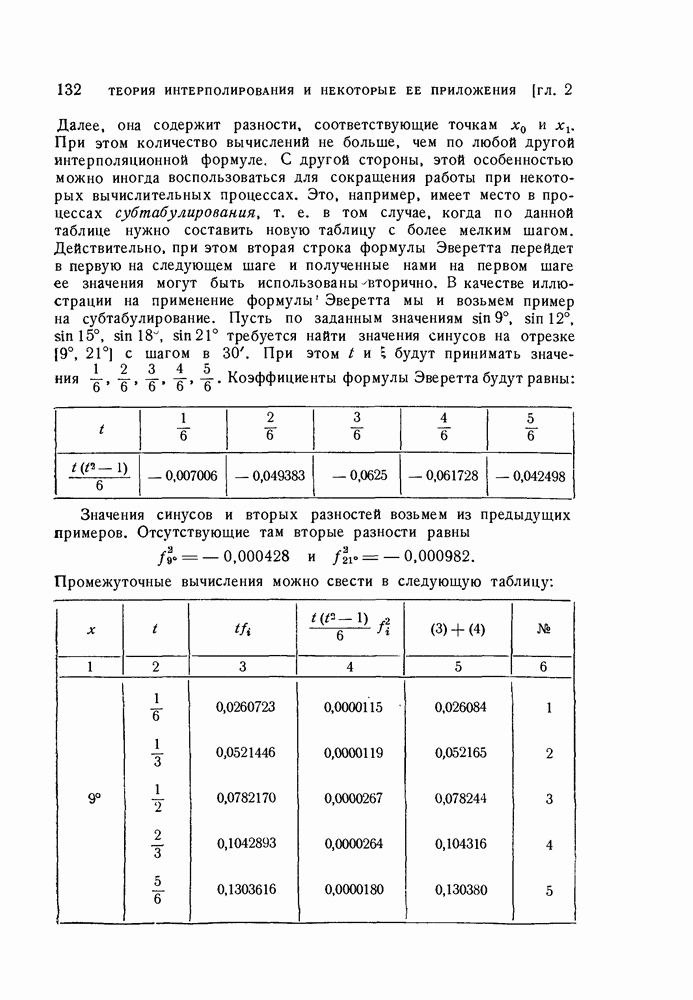
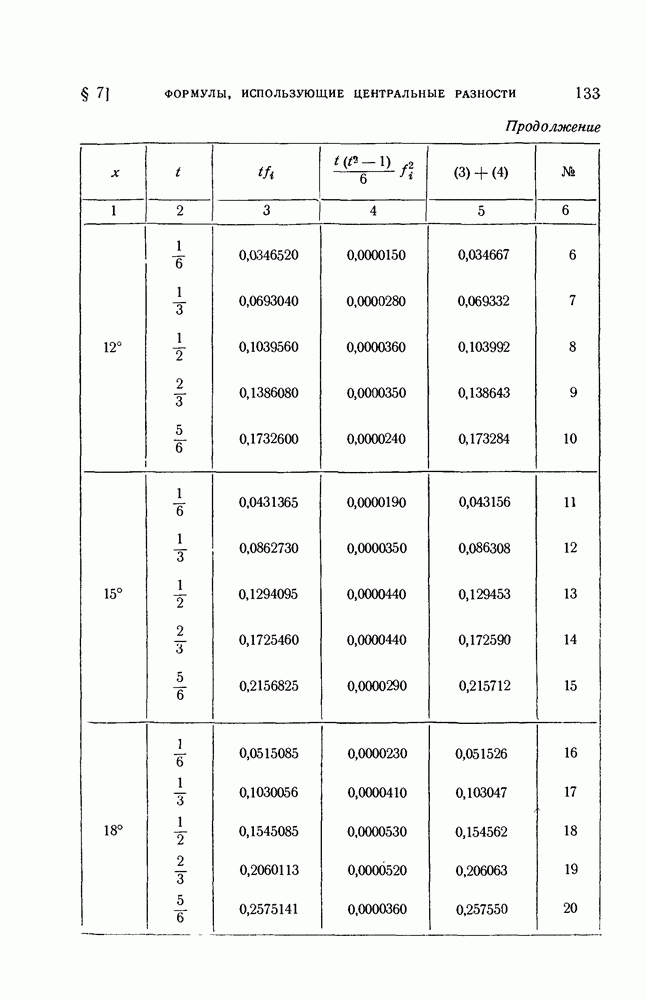
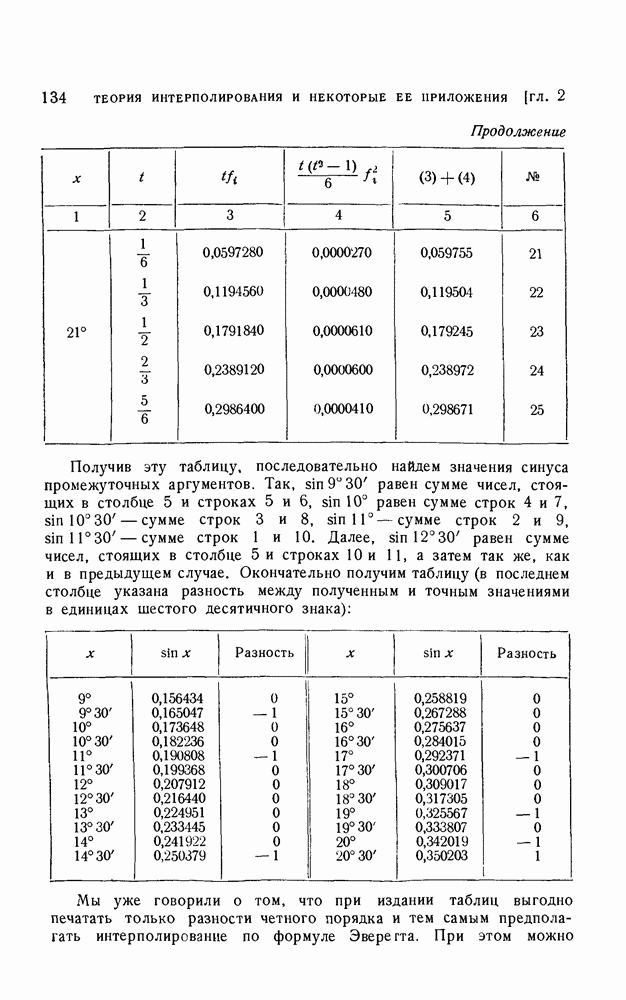
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
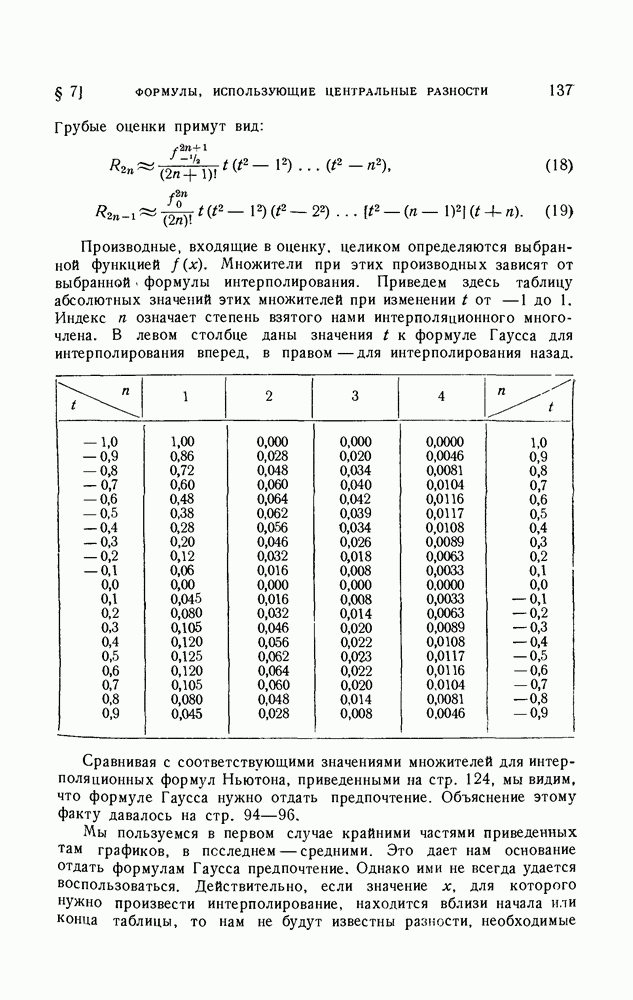
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
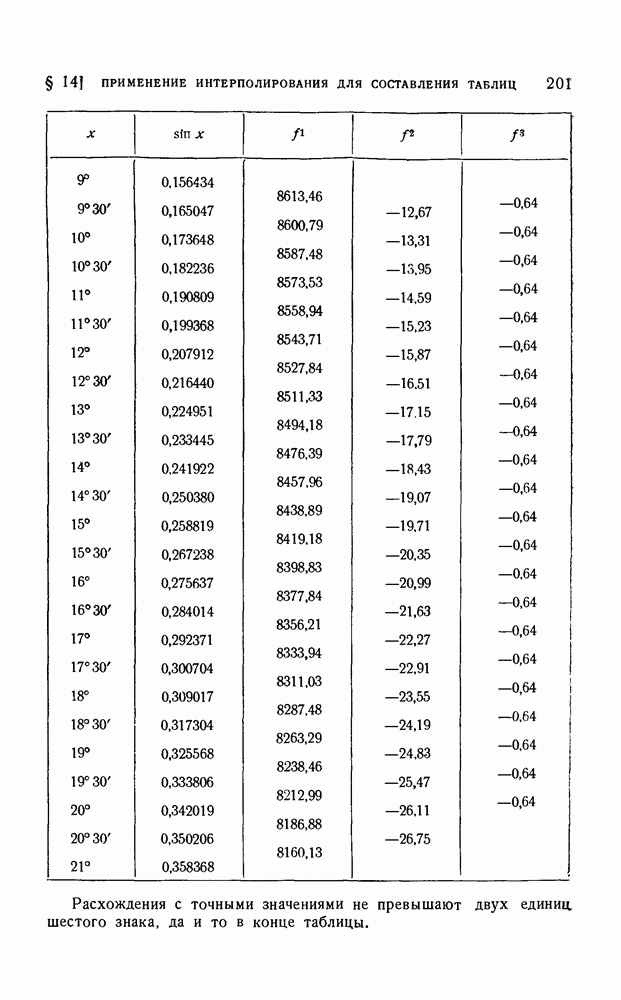
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
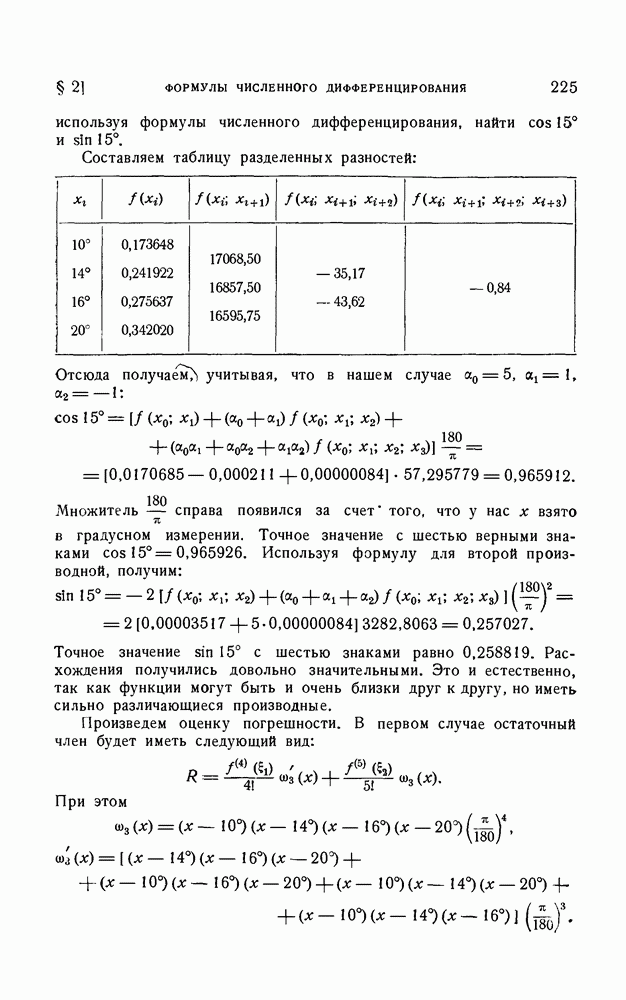
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
- § 3. Задача численного интегрирования
- § 4. Формулы Ньютона — Котеса
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
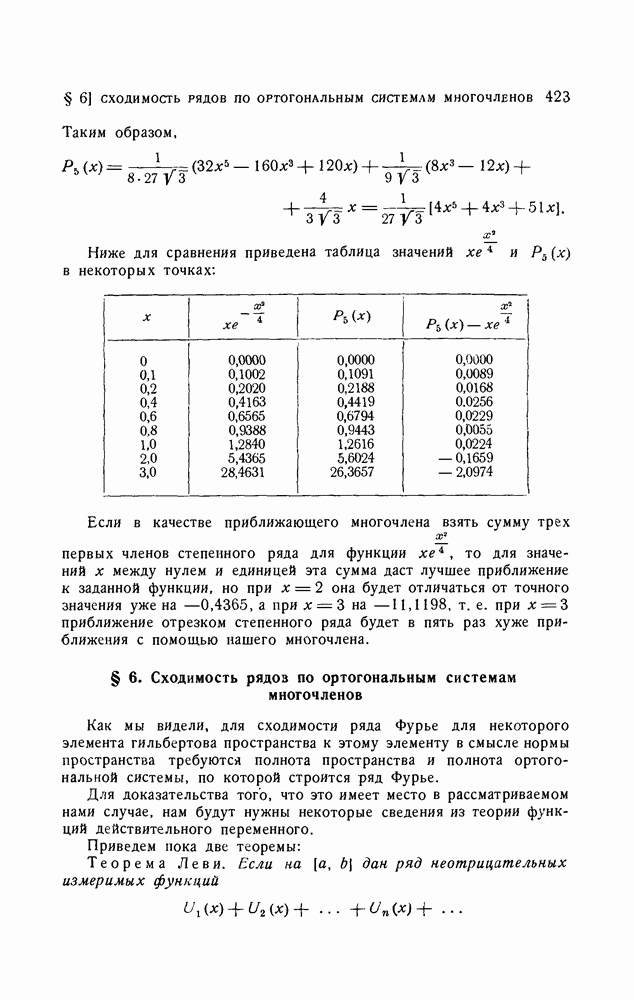
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
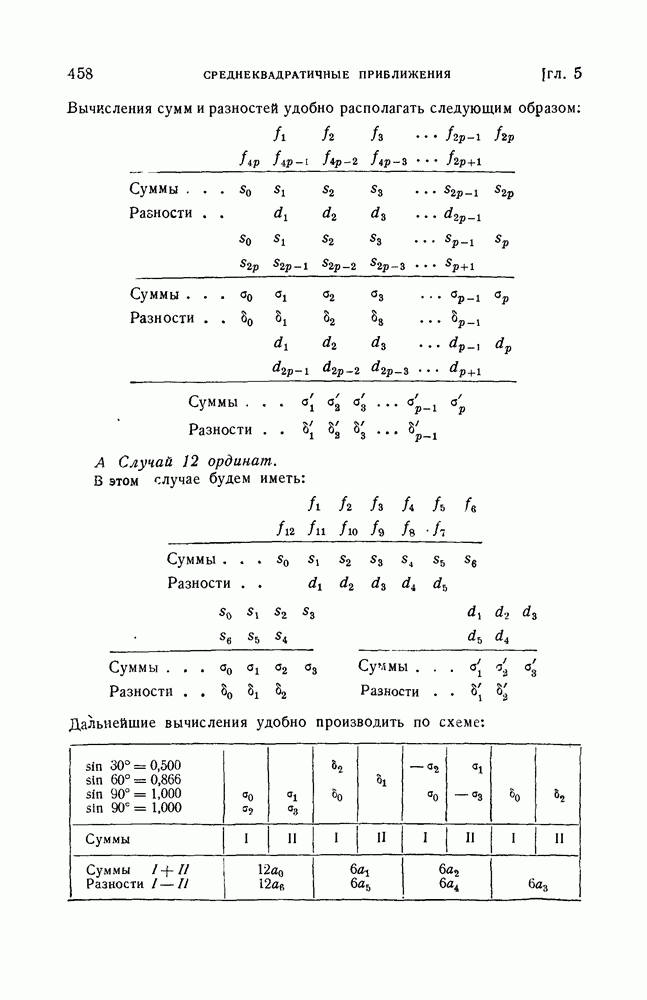
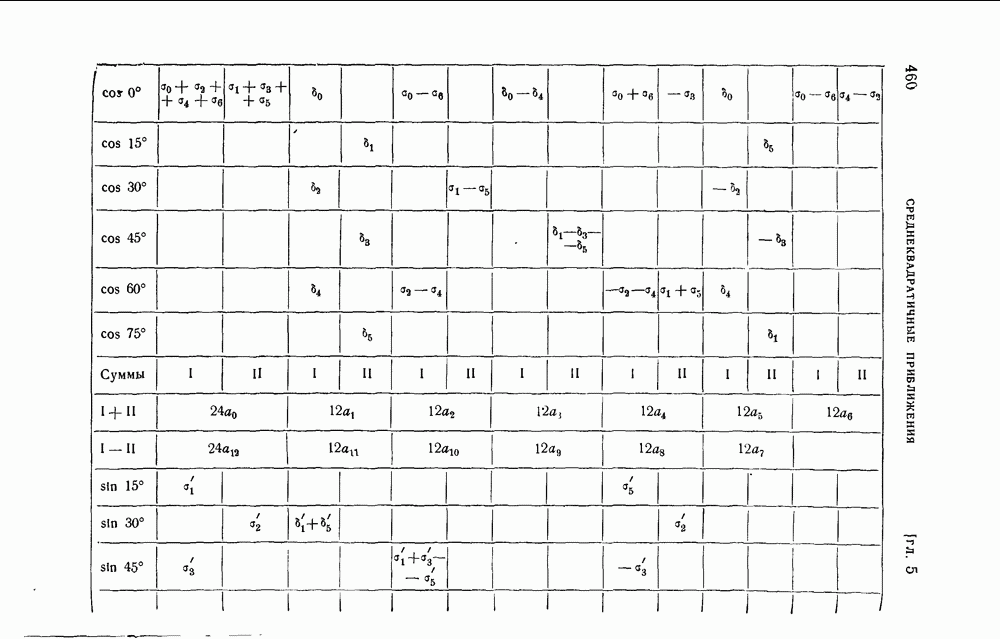
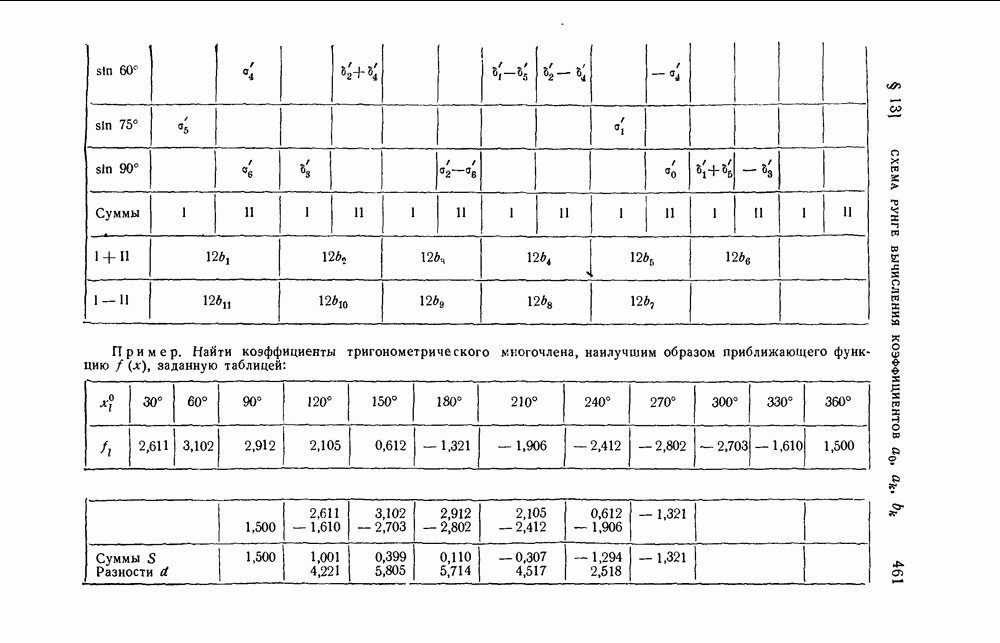
- § 13. Схема Рунге вычисления коэффициентов … в случае …