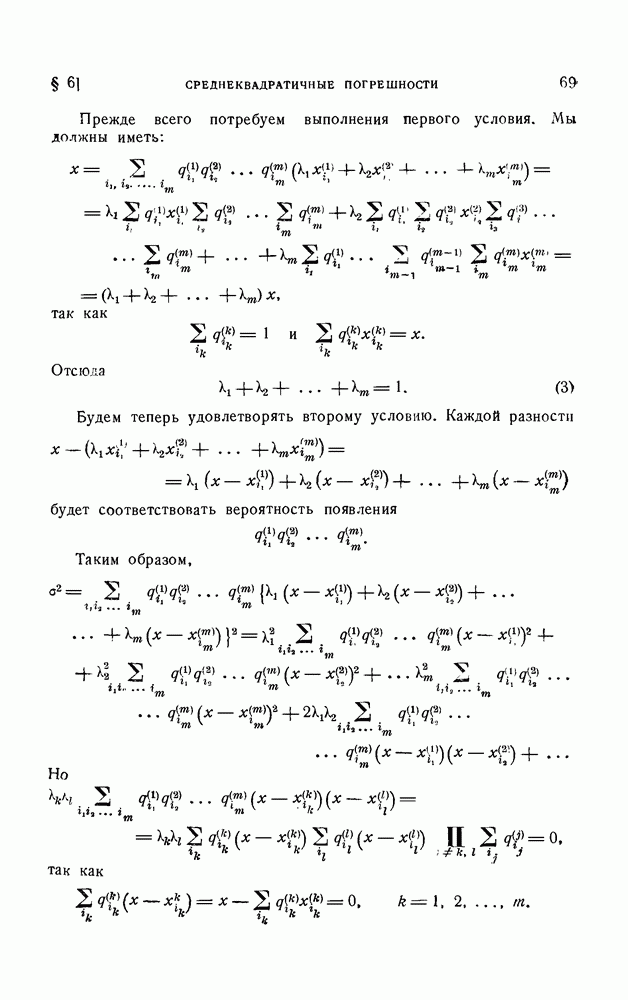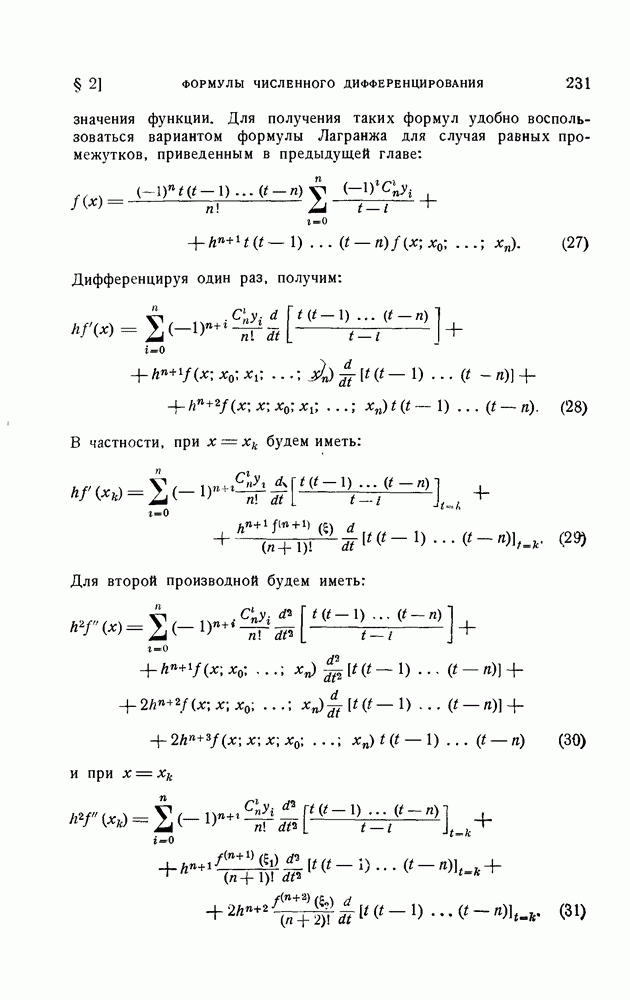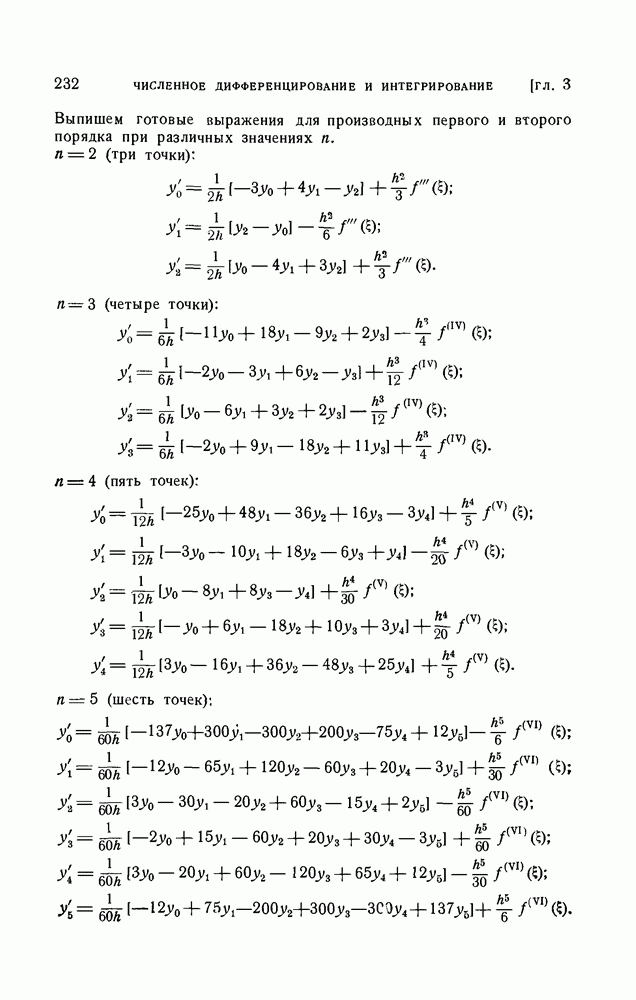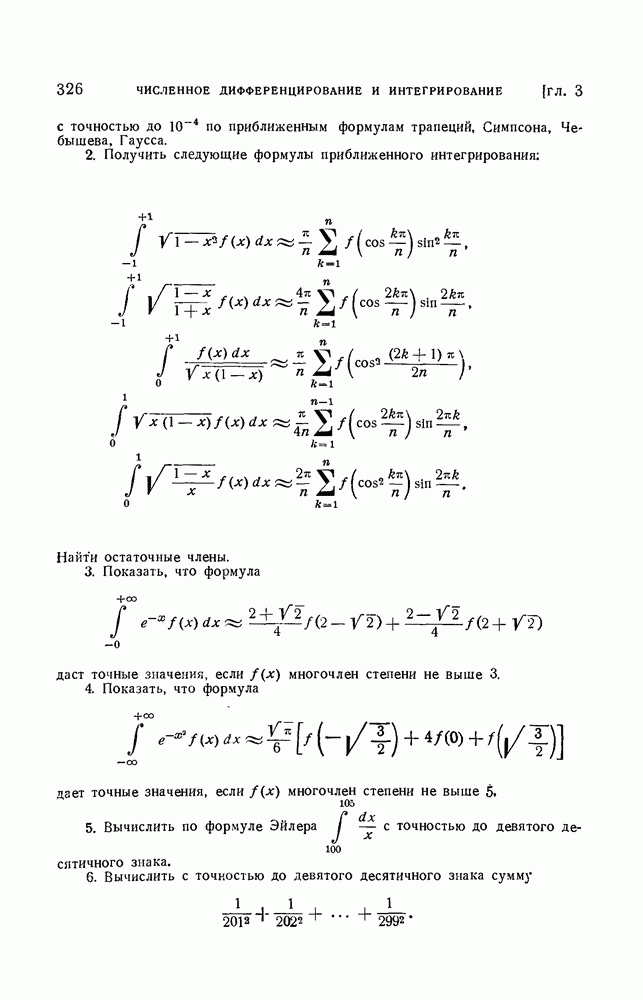| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
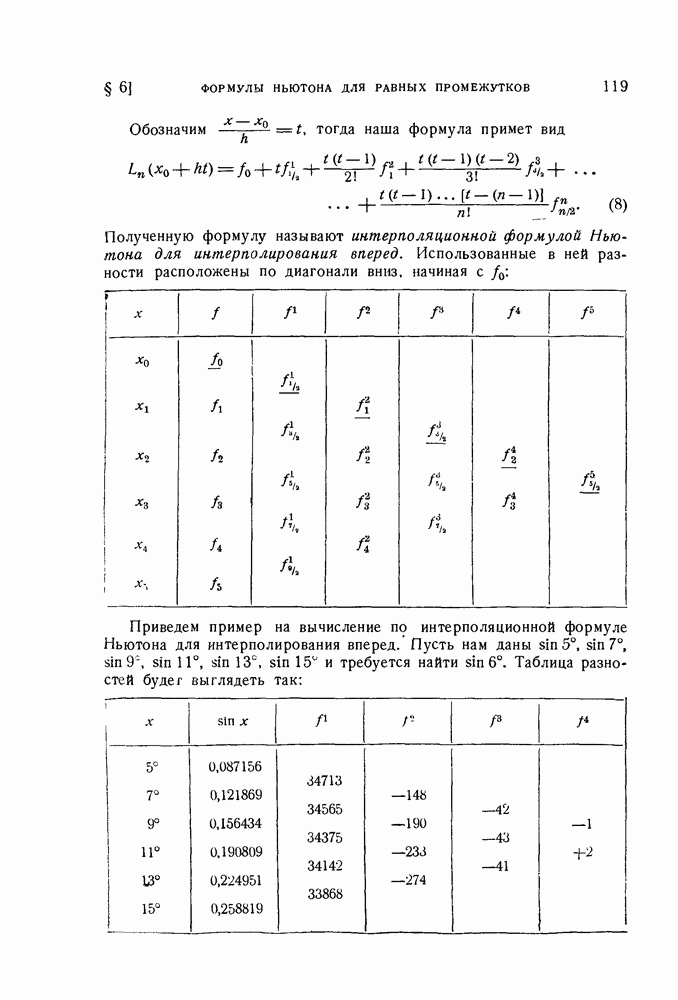
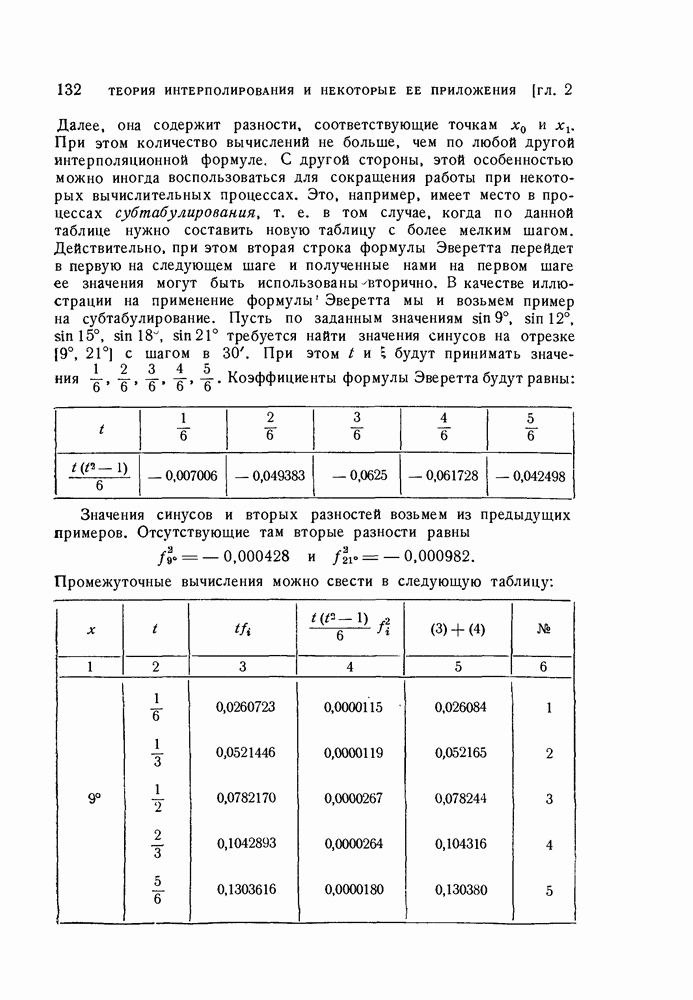
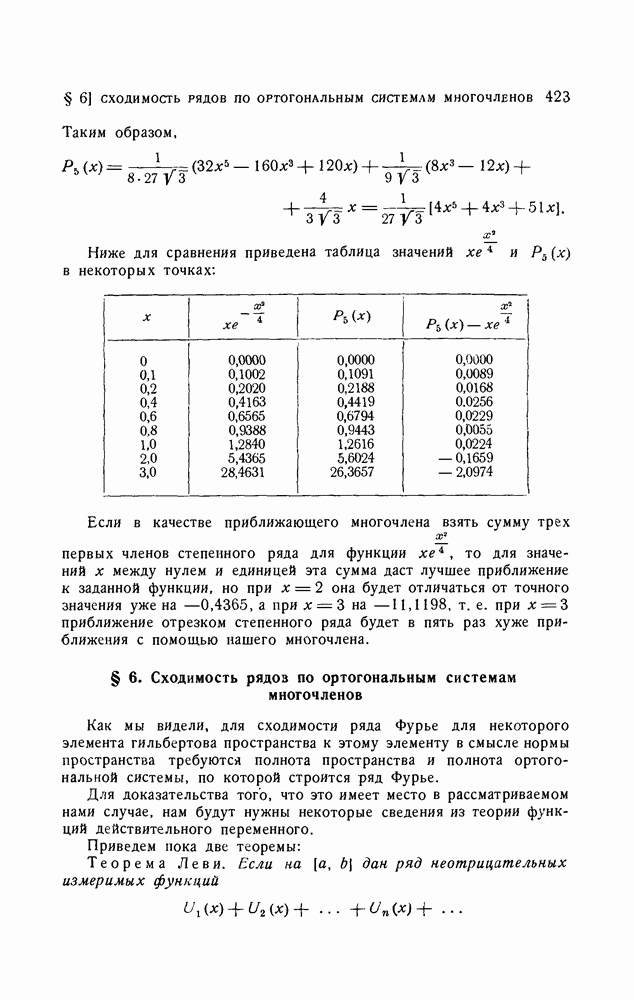
§ 6. Интерполяционные формулы Ньютона для равных промежутков
Естественно ожидать, что если промежутки между последовательными узлами интерполирования равны, т. е.  постоянная величина, то предыдущая формула упростится. Так оно и есть на самом деле. Прежде чем переходить к выводу формул, для этого случая введем понятне о конечных разностях.
постоянная величина, то предыдущая формула упростится. Так оно и есть на самом деле. Прежде чем переходить к выводу формул, для этого случая введем понятне о конечных разностях.
1. Конечные разности и их свойства.
Пусть для значений  - шаг таблицы), нам известны значения функции
- шаг таблицы), нам известны значения функции  Назовем тогда разности
Назовем тогда разности

конечными разностями первого порядка.
В литературе используются самые различные обозначения конечных разностей:

Мы будем пользоваться последним обозначением.
Из разностей первого порядка можно образовать конечные разности второго порядка:

Аналогично можно образовать разности третьего порядка, четвертого и так далее. Таблицу разностей обычно располагают следующим образом:
(см. скан)
Так, например, таблица конечных разностей для функции  будет выглядеть следующим образом:
будет выглядеть следующим образом:
(см. скан)
Практические вычисления требуют наличия контролирующих операций на всех этапах работы. Это застрахует от грубых просчетов или по крайней мере сведет их к минимуму. Такие контролирующие операции чрезвычайно просто получаются при составлении таблицы разностей. Очевидно,

т. е. сумма чисел в каждом столбце разностей равна разности крайних чисел предыдущего столбца. Поэтому целесообразно ввести в дополнение к таблице еще две строки: строку  равную сумме чисел, стоящих в столбце, и строку
равную сумме чисел, стоящих в столбце, и строку  равную разности крайних чисел столбца, и использовать предыдущие рассуждения. Для предыдущего примера эти строки будут таковы:
равную разности крайних чисел столбца, и использовать предыдущие рассуждения. Для предыдущего примера эти строки будут таковы:
(см. скан)
В некоторых интерполяционных формулах используют наряду с теми значениями и разностей, которые у нас имеются, еще
средние арифметические:

В тех случаях, когда для обозначения разностей употребляют значок  , для средних арифметических используют значок
, для средних арифметических используют значок  Так, последний столбец в этих обозначениях будет выглядеть следующим образом:
Так, последний столбец в этих обозначениях будет выглядеть следующим образом:

Разберем теперь некоторые свойства конечных разностей. Прежде всего найдем выражение разности любого порядка непосредственно через значения функции. Будем иметь:

Покажем, что общее выражение для  будет:
будет:

Для 1, 2, 3 эта формула верна, что видно из предыдущих выражений. Предположим, что она верна для всех  и докажем, что тогда она справедлива и для
и докажем, что тогда она справедлива и для  Разность порядка
Разность порядка  будет равна
будет равна

Но

Следовательно,

что и требовалось доказать.
Из полученной формулы, в силу линейной зависимости  от
от  выводим:
выводим:
Следствие 1. Конечные разности  суммы или разности функций
суммы или разности функций  равны сумме или разности конечных разностей функций
равны сумме или разности конечных разностей функций 

Следствие 2. При умножении функции на постоянный множитель конечные разности умножаются на тот же множитель.
Установим еще связь между конечными разностями и разделенными разностями для того случая, когда —  постоянна. Будем иметь:
постоянна. Будем иметь:

Вообще,

Доказательство опять будем вести методом индукции. Предполагая формулу справедливой для  докажем ее справедливость для
докажем ее справедливость для 
Действительно,

Как следствие этой формулы и результатов, полученных ранее для разделенных разностей, получаем:
Следствие 3. Конечные разности  порядка от многочлена степени
порядка от многочлена степени  постоянны, а конечные разности
постоянны, а конечные разности  порядка равны нулю.
порядка равны нулю.
Последнее свойство позволяет дать простой способ составления таблиц многочленов. Непосредственно вычисляем значения многочлена для и.  значений аргумента. По этим данным составляем таблицу разностей. В нее войдут разности до
значений аргумента. По этим данным составляем таблицу разностей. В нее войдут разности до  порядка. Далее, заполняем столбец разностей
порядка. Далее, заполняем столбец разностей  порядка, пользуясь тем, что они постоянны, затем заполняем столбец разностей
порядка, пользуясь тем, что они постоянны, затем заполняем столбец разностей  порядка. Для их получения складываем соответствующие разности
порядка. Для их получения складываем соответствующие разности  порядка с разностями
порядка с разностями  порядка. Затем последовательно заполняем столбец разностей
порядка. Затем последовательно заполняем столбец разностей  порядка,
порядка,  порядка и так далее, пока не получим столбец
порядка и так далее, пока не получим столбец  Так, например, полученная нами таблица функции
Так, например, полученная нами таблица функции  будет продолжаться следующим образом:
будет продолжаться следующим образом:
(см. скан)
При практическом применении этого приема с целью исключения грубых просчетов целесообразно время от времени производить вычисления многочленов непосредственно. Это обеспечит и от накопления ошибок округления, если мы ведем вычисления не точно, а с каким-то заданным количеством десятичных знаков.
Интересно проследить распространение ошибки, сделанной при вычислении  на конечные разности различных порядков. В приведенной ниже таблице это указано в предположении, что ошибка величины
на конечные разности различных порядков. В приведенной ниже таблице это указано в предположении, что ошибка величины  сделана при вычислении
сделана при вычислении
(см. скан)
Таким образом, ошибка с коэффициентами  распространится на разности порядка
распространится на разности порядка  При этом максимальные по модулю ошибки будут иметь разности, ближайшие к строке, в которой находится Этот результат можно так же получить из формулы, связывающей конечные разности непосредственно со значениями функции.
При этом максимальные по модулю ошибки будут иметь разности, ближайшие к строке, в которой находится Этот результат можно так же получить из формулы, связывающей конечные разности непосредственно со значениями функции.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
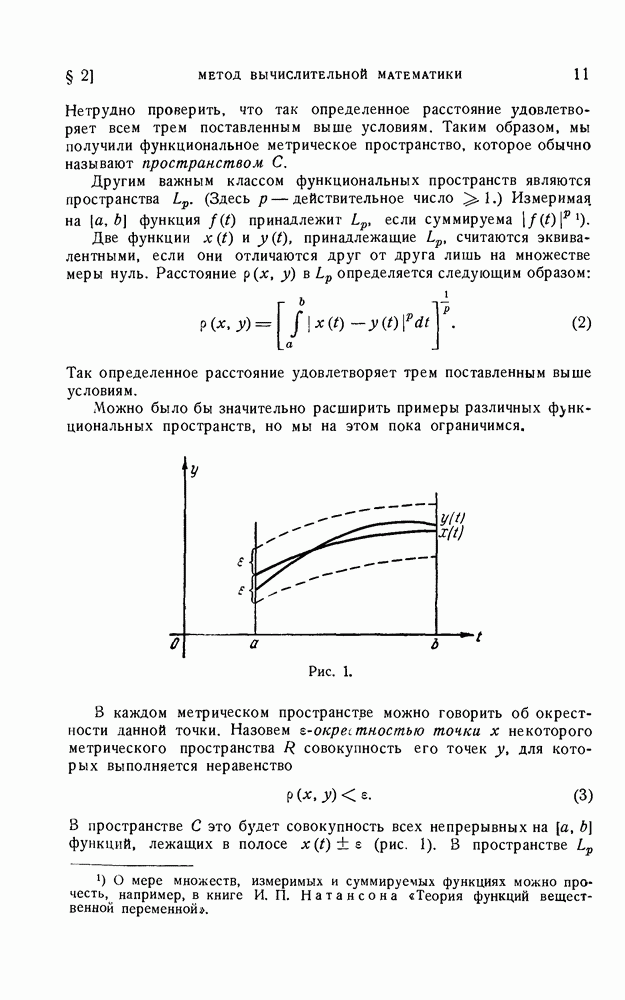
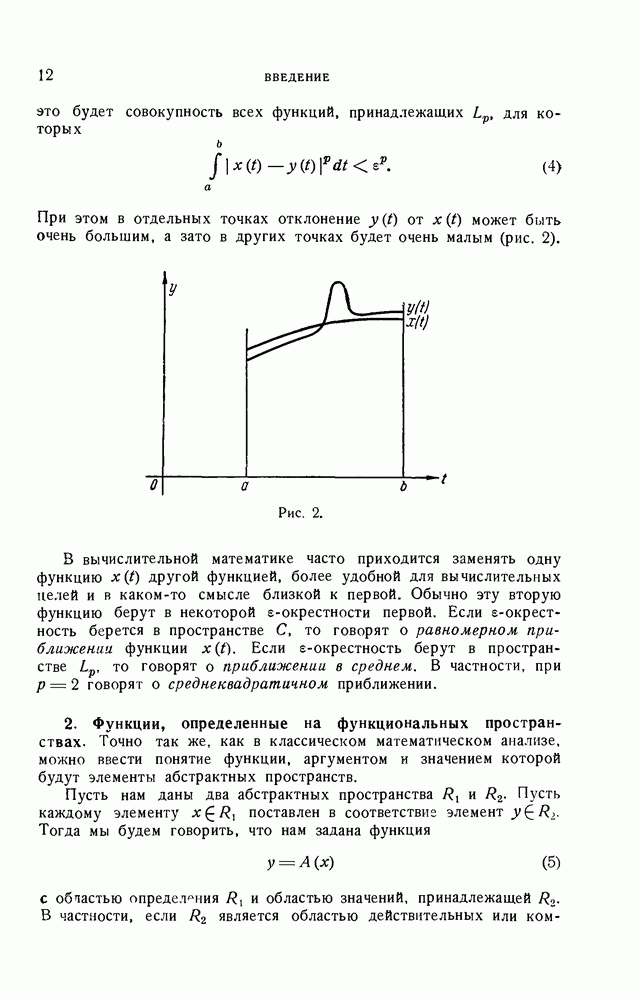
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
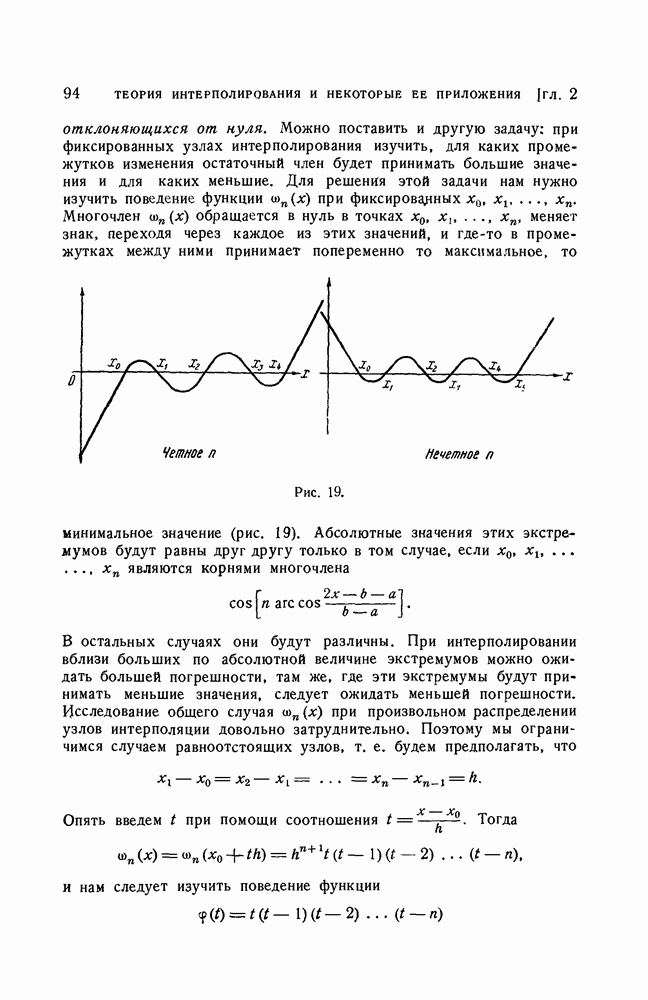
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
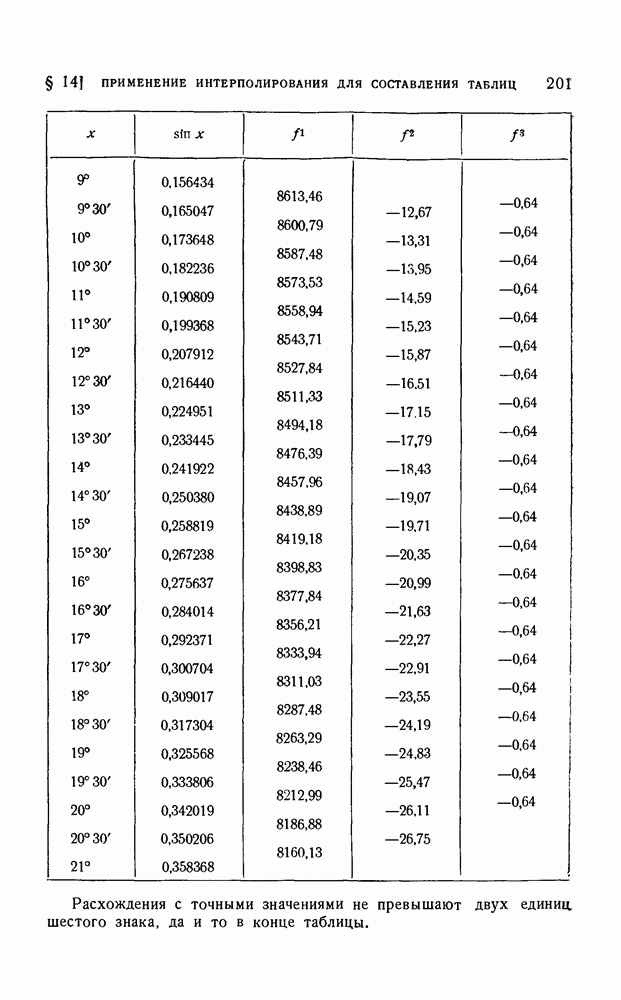
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
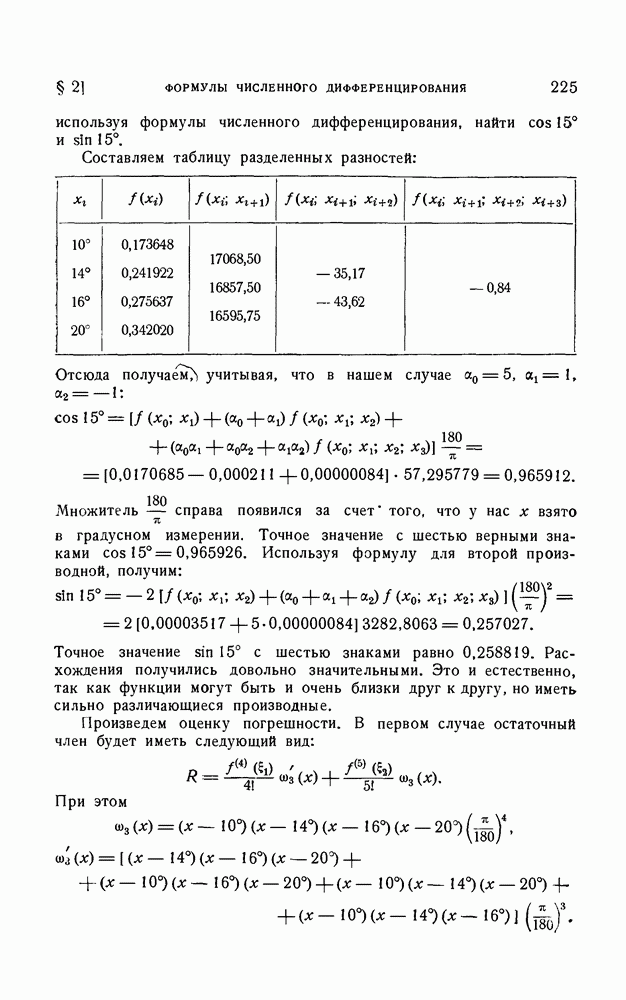
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
- § 3. Задача численного интегрирования
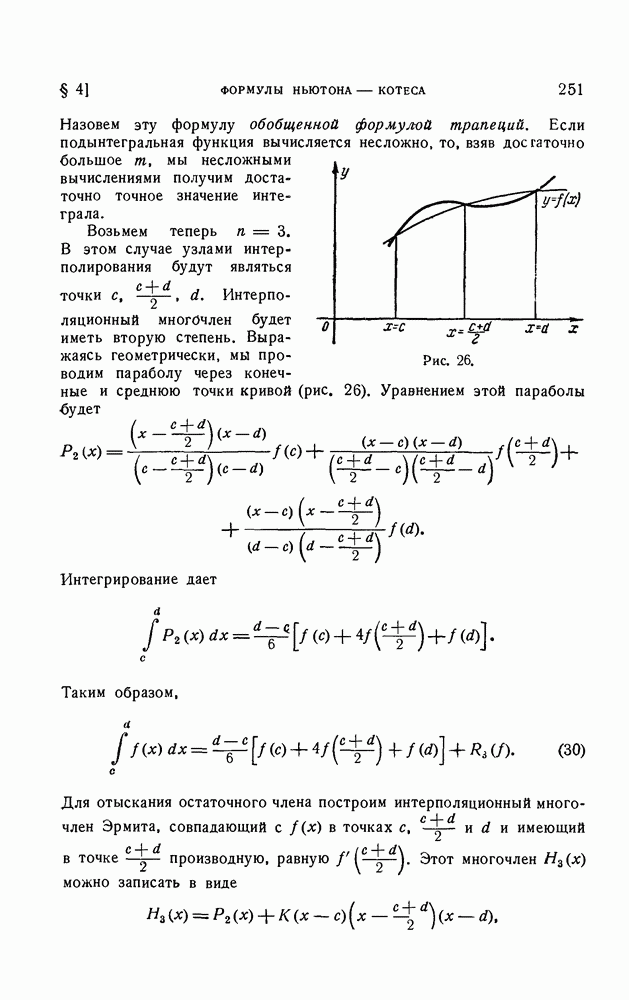
- § 4. Формулы Ньютона — Котеса
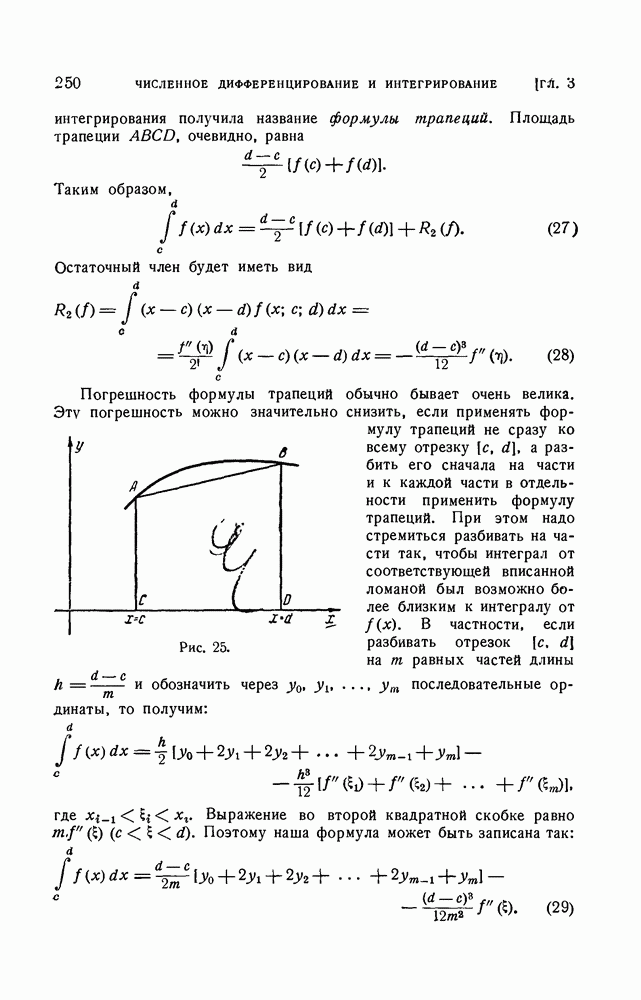
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
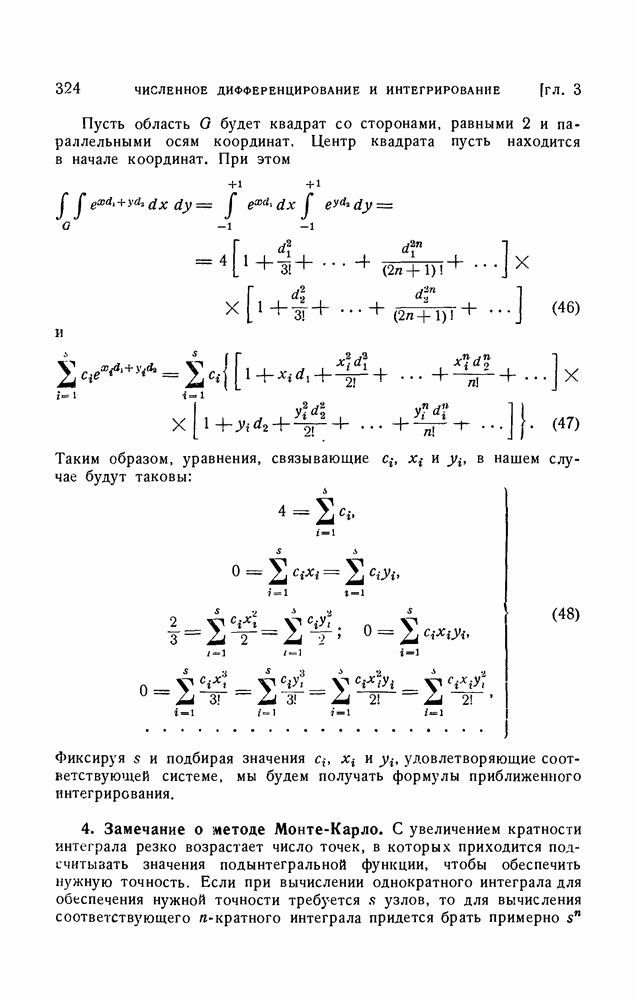
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
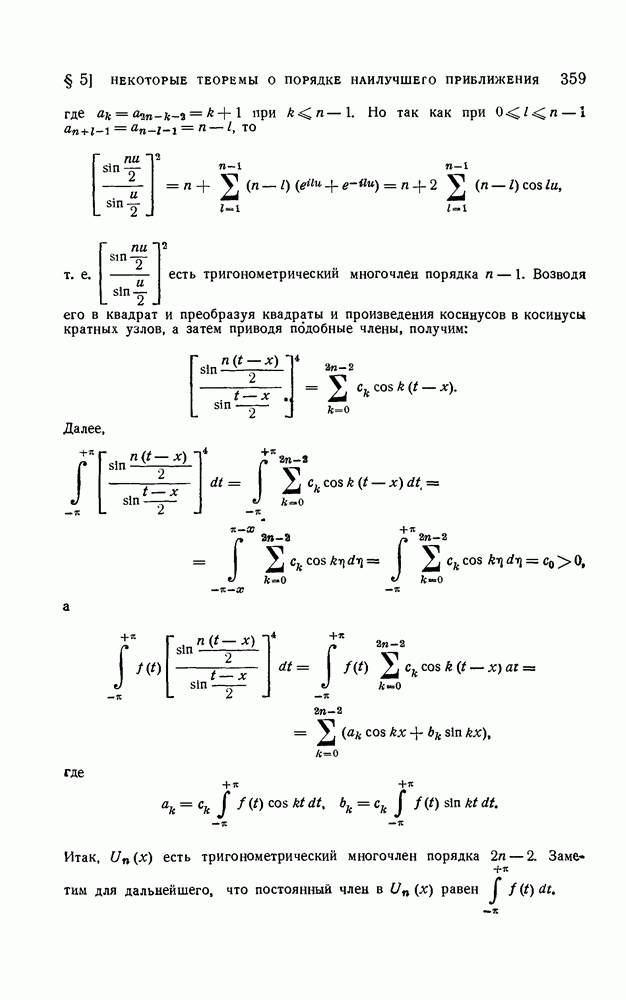
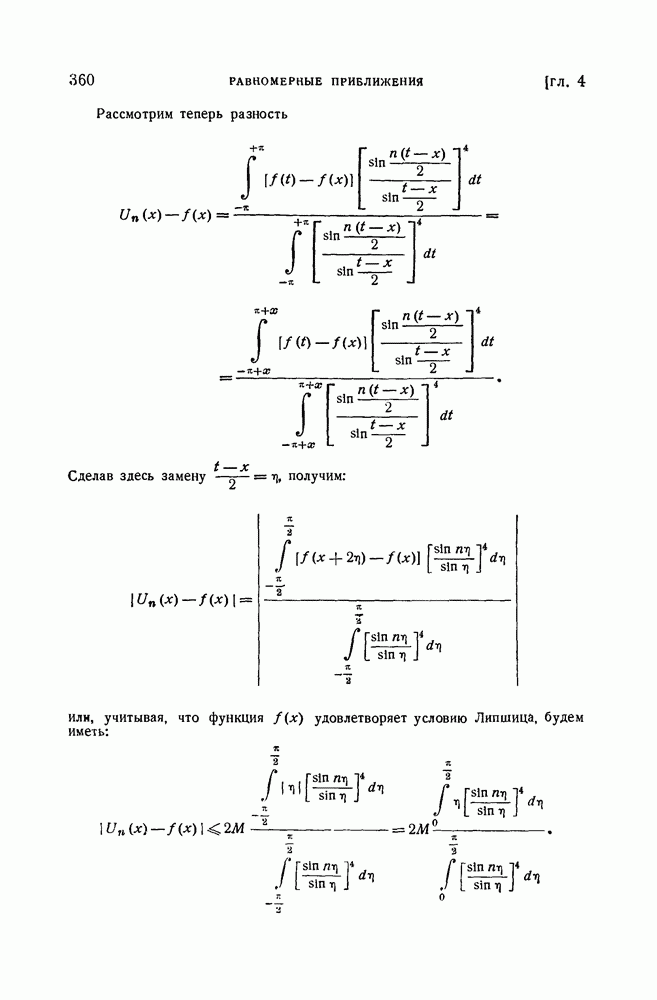
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
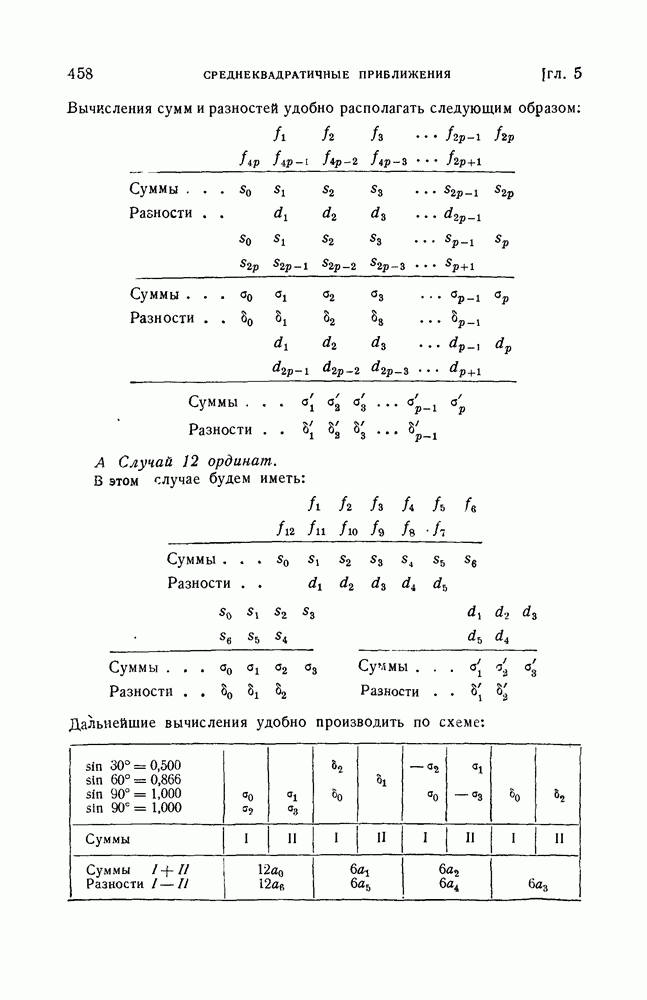
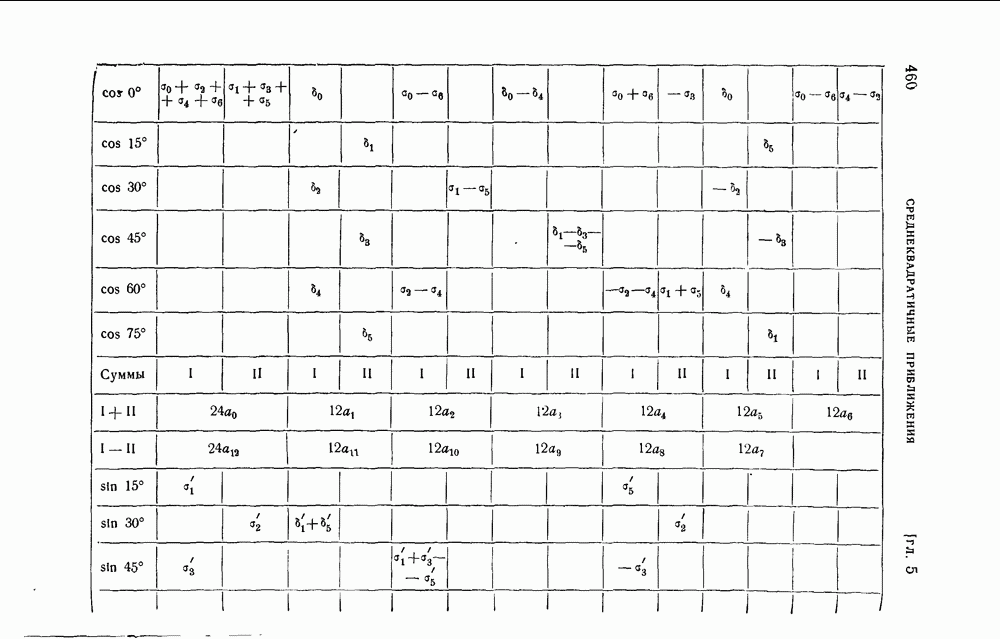
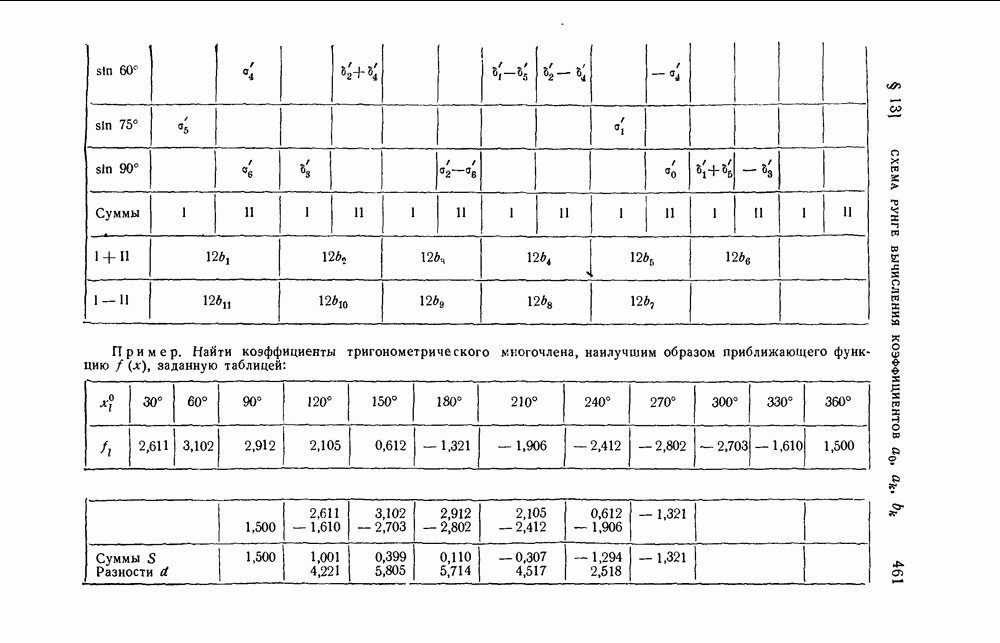
- § 13. Схема Рунге вычисления коэффициентов … в случае …