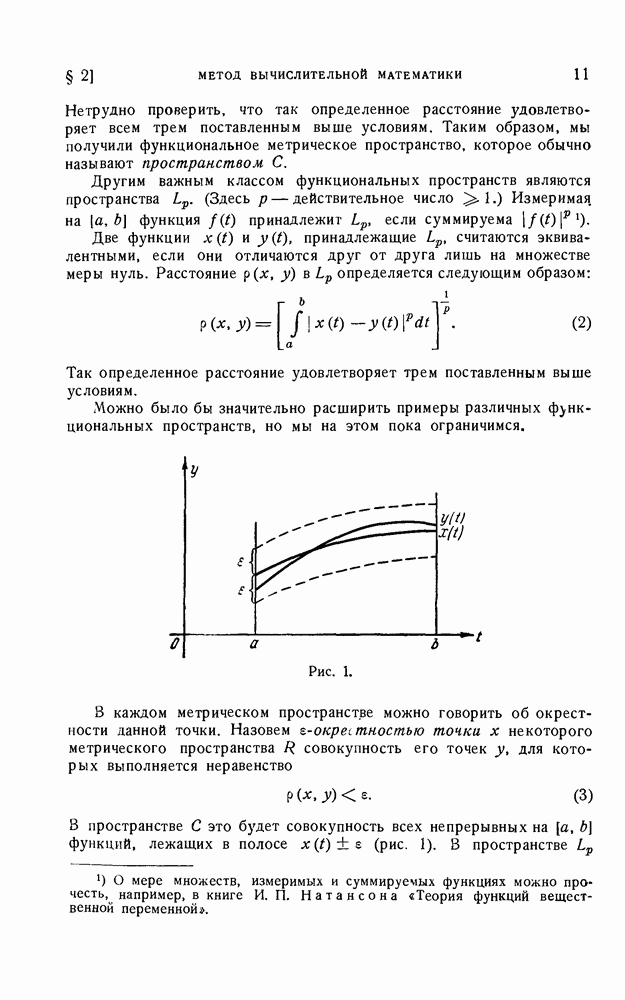
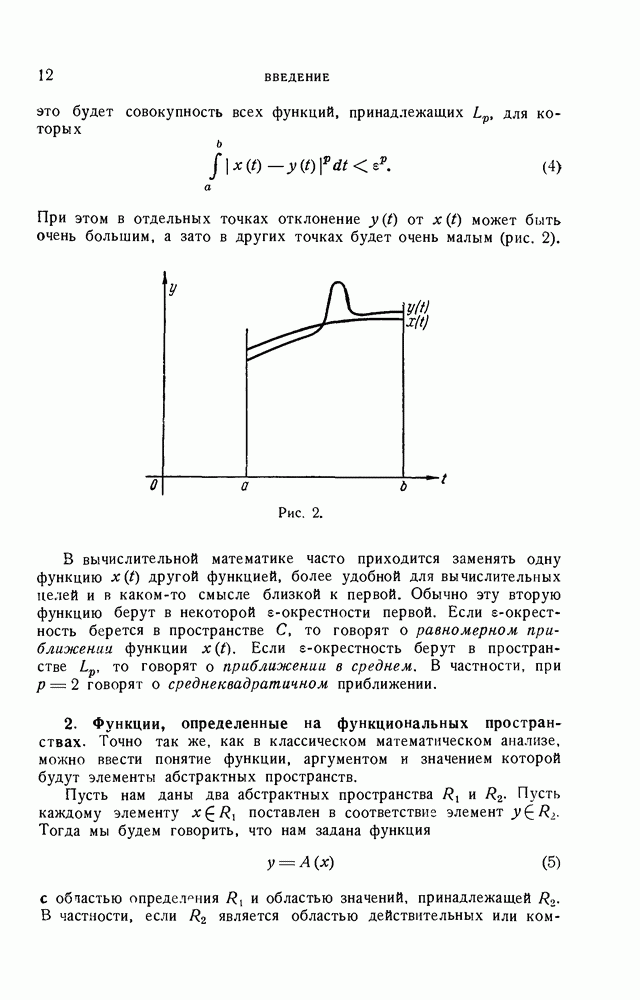
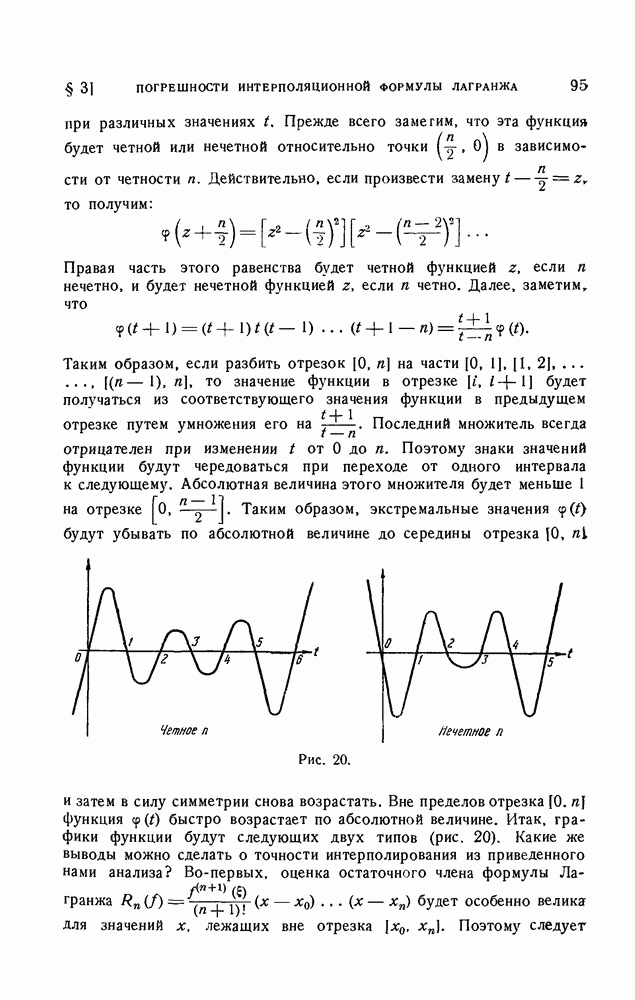
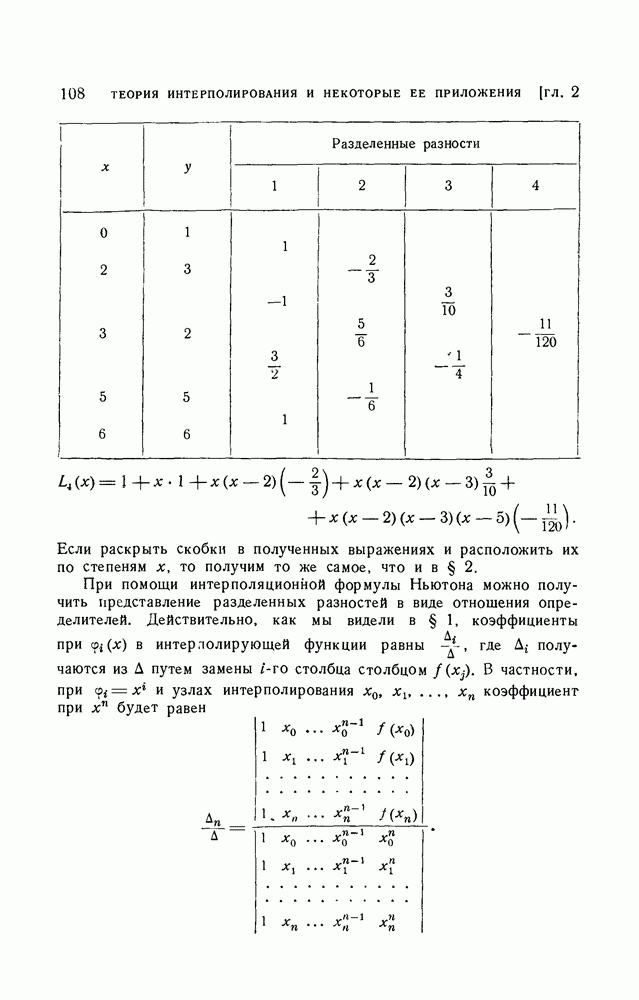
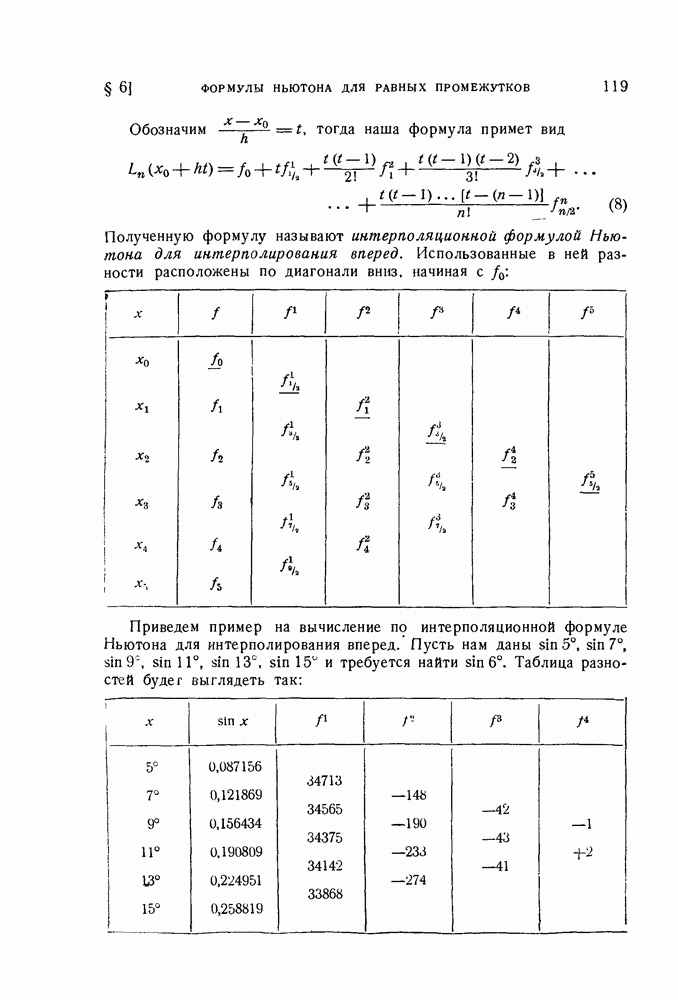
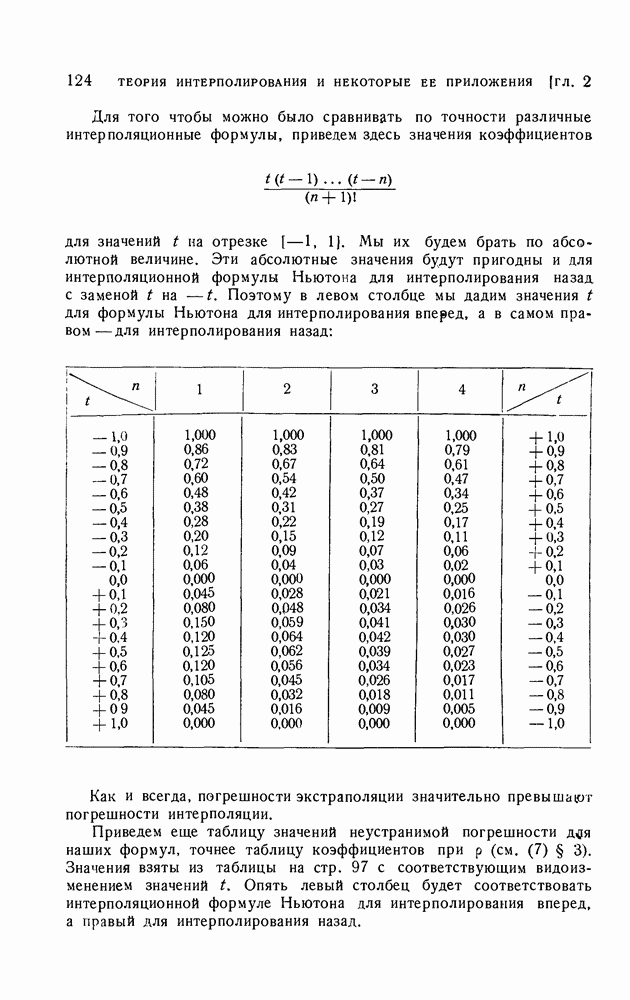
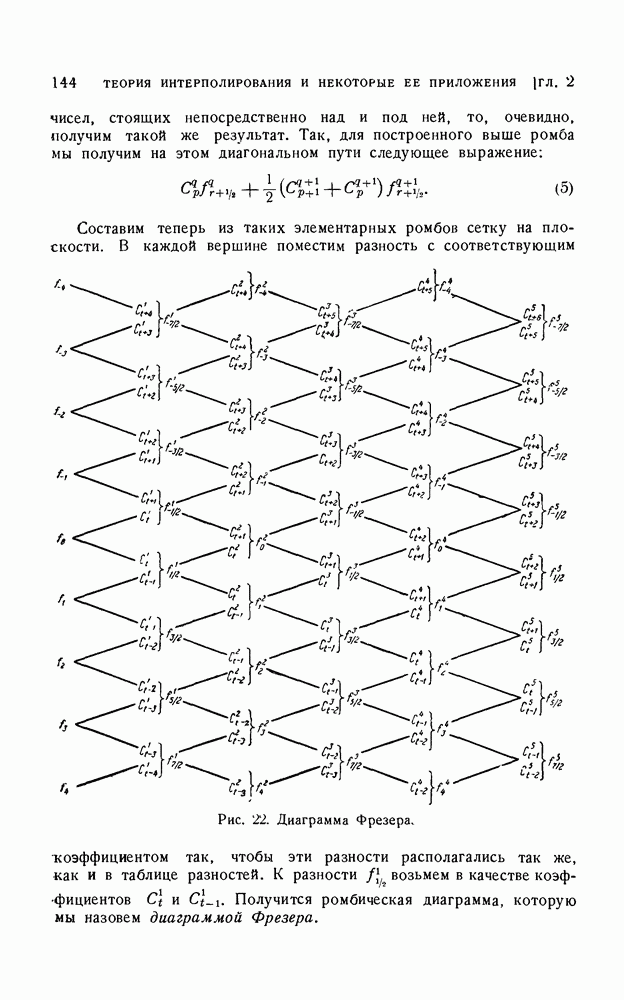
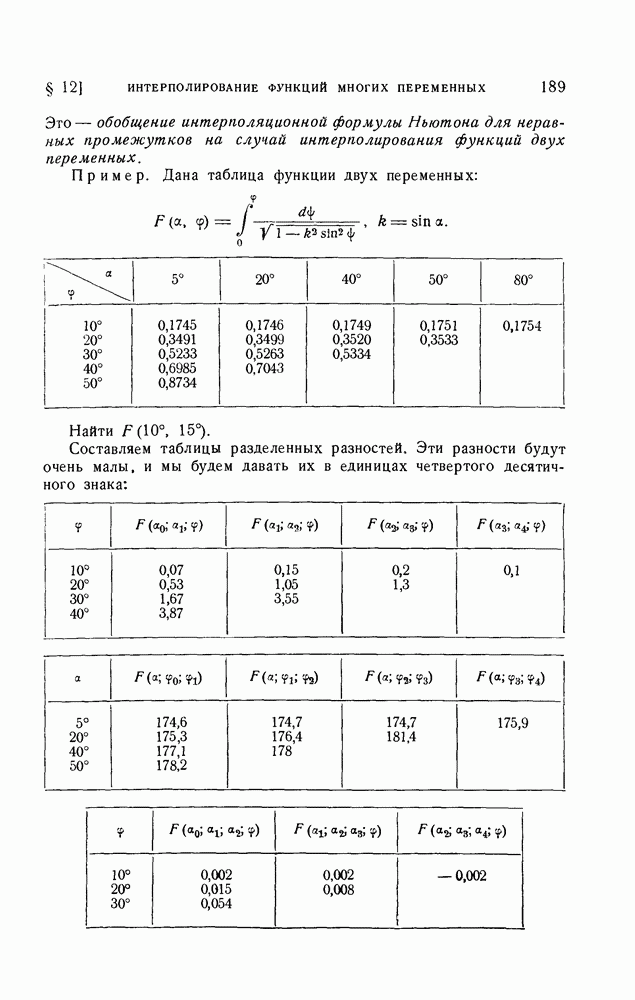
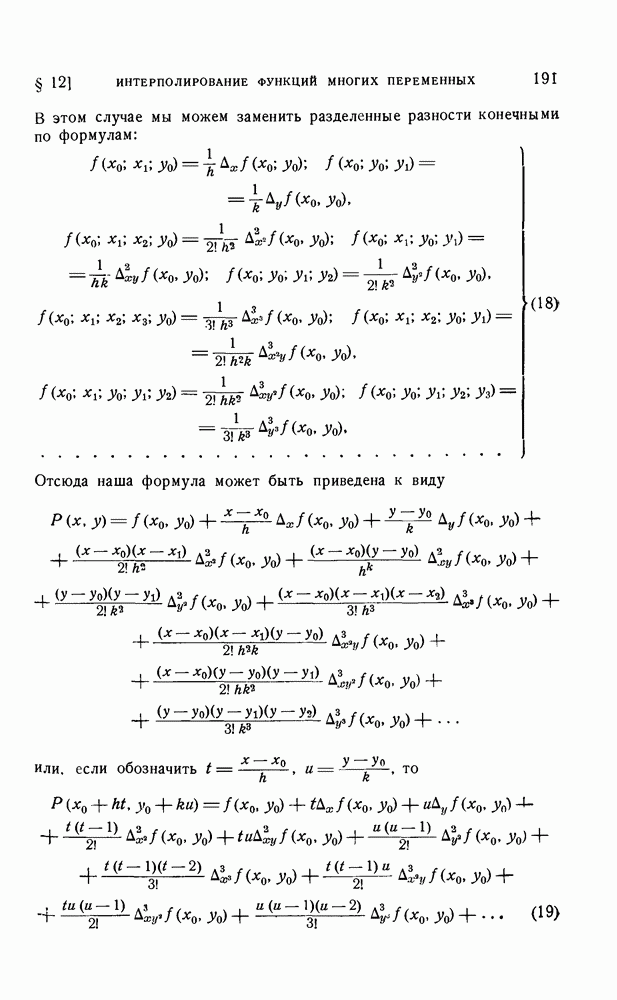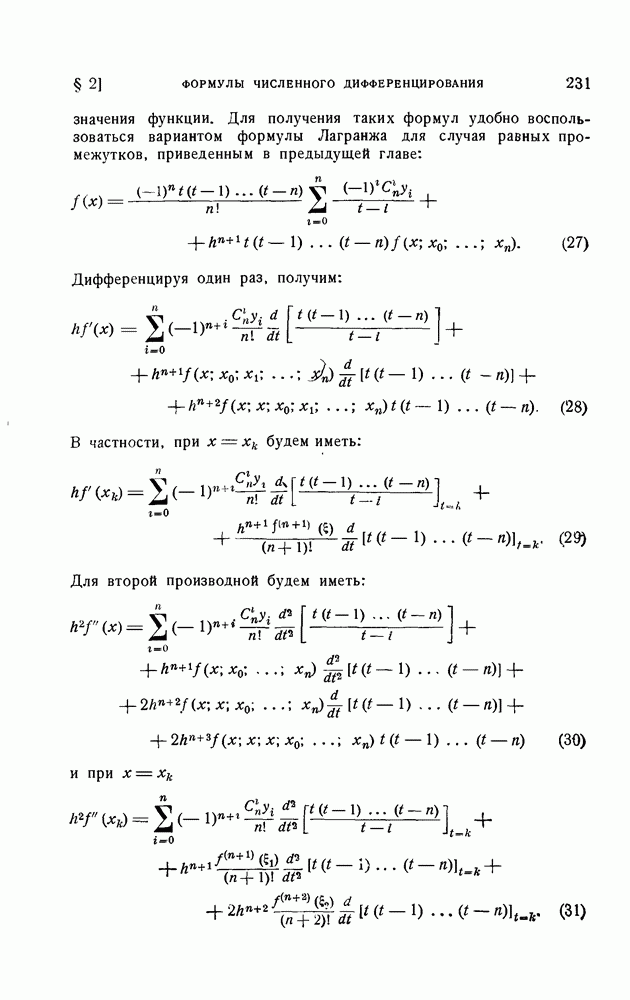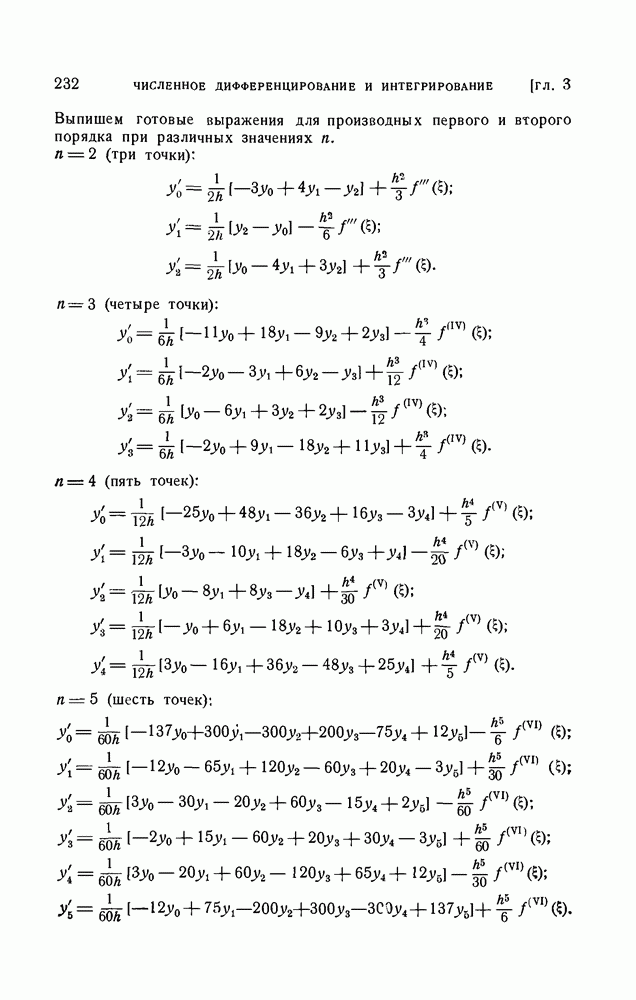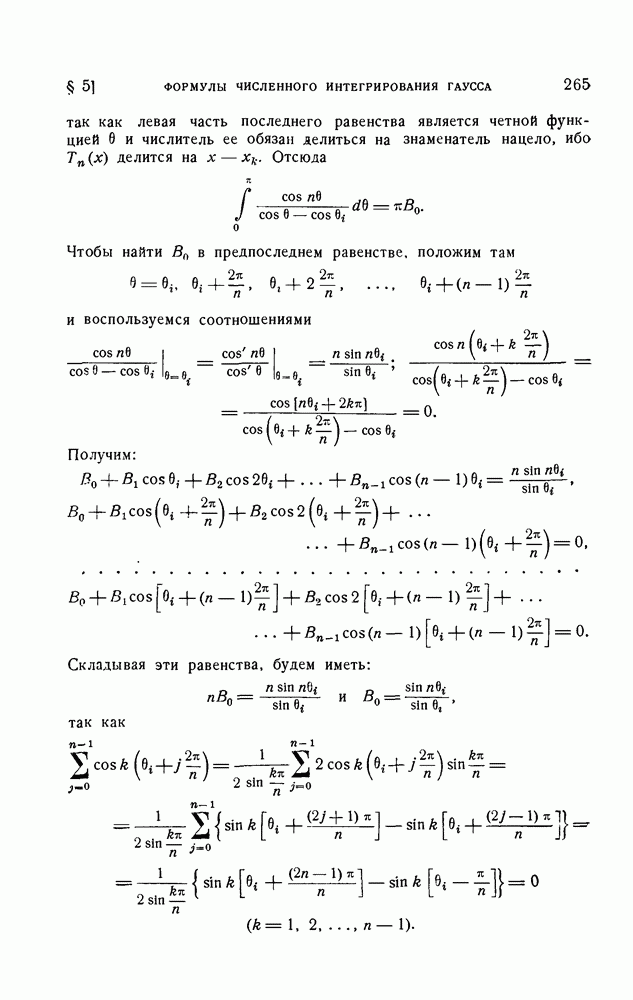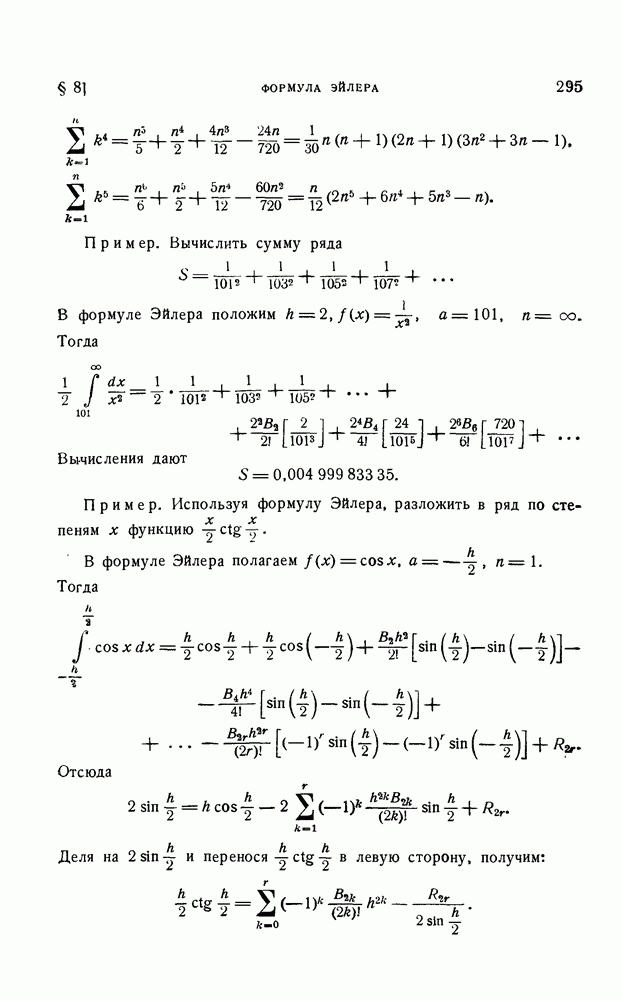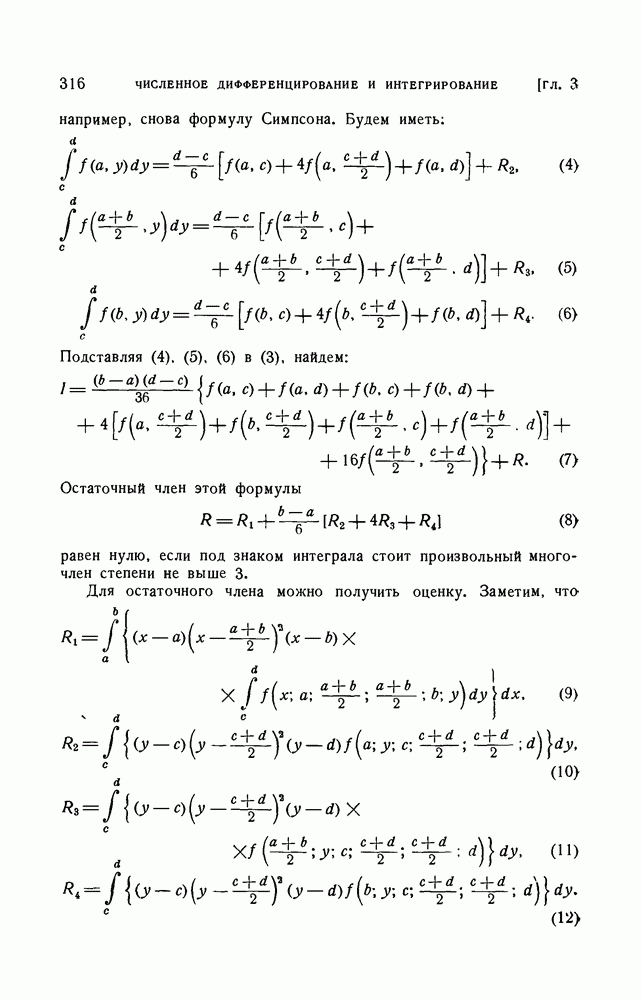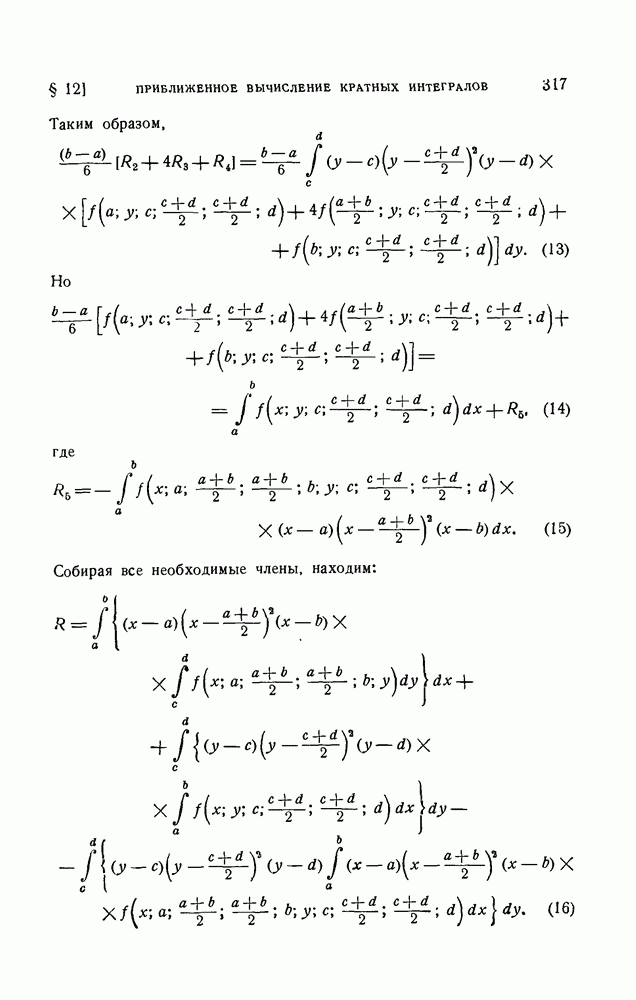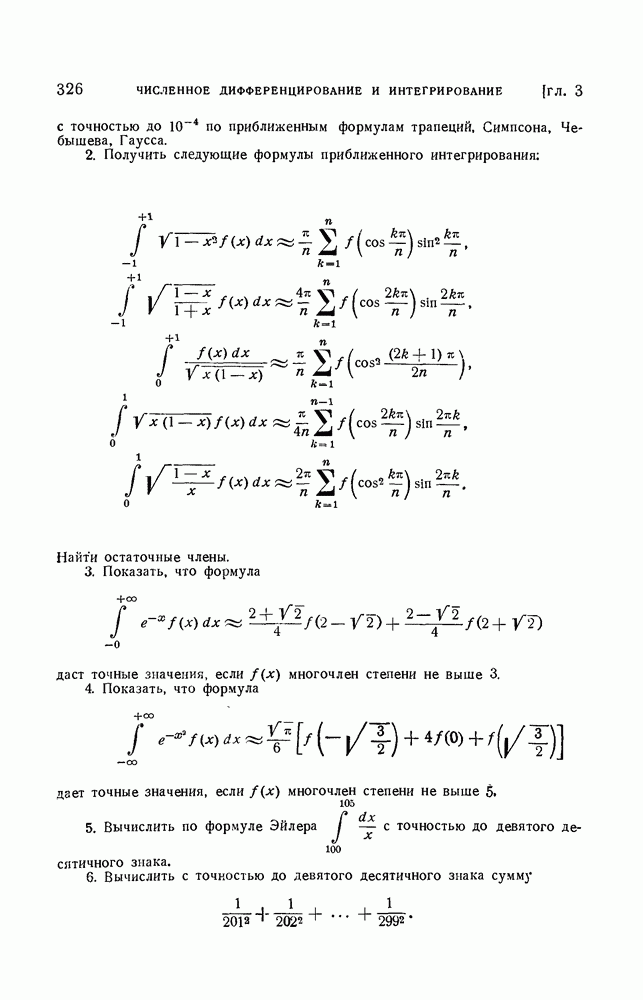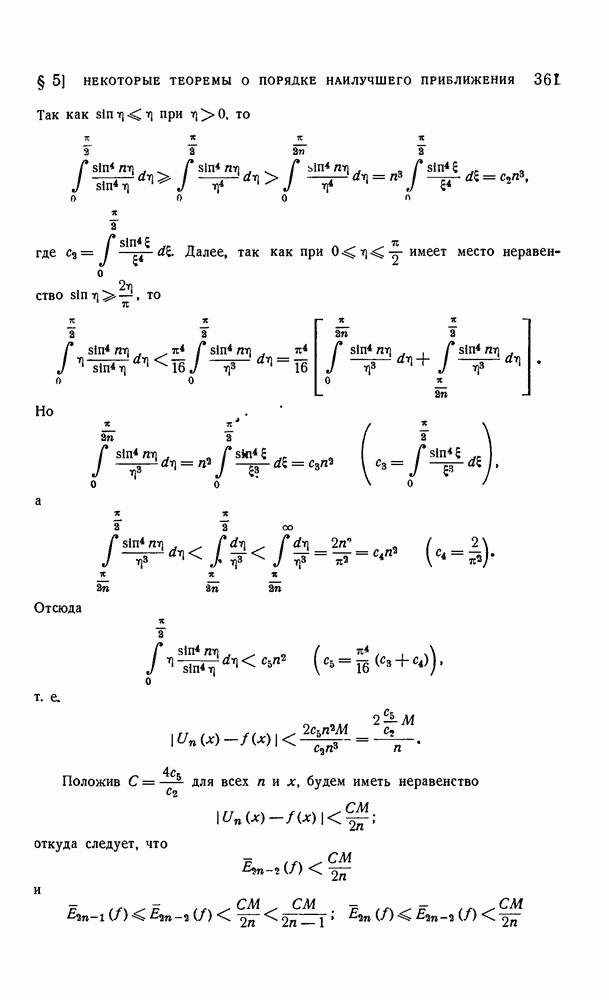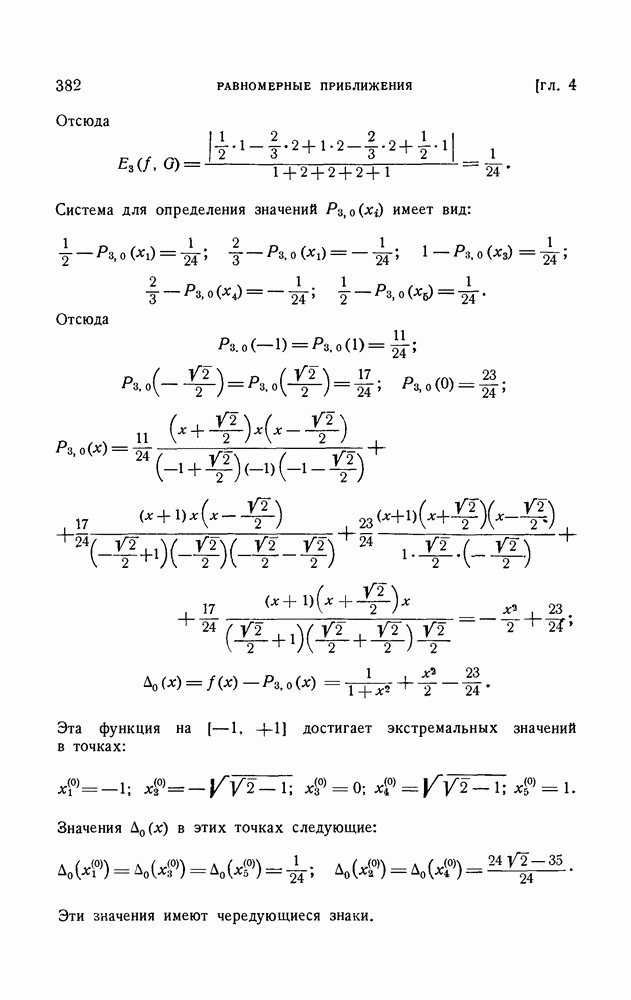| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 8. Формула Эйлера
Формула, к выводу которой мы хотим приступить, имеет самые разнообразные применения: численное интегрирование, суммирование рядов, разложение функций в ряд и т. д. Ее часто называют формулой Эйлера — Маклорена, хотя впервые она была получена Эйлером. Формула Эйлера не связана непосредственно с теорией интерполирования и потребует некоторых сведений о многочленах и числах Бернулли.
1. Числа и многочлены Бернулли.
Рассмотрим функцию

Она может быть разложена в ряд по возрастающим степеням х, равномерно сходящийся при  так как ближайшей к началу координат особой точкой этой функции является
так как ближайшей к началу координат особой точкой этой функции является

Запишем ряд в виде

 называются многочленами Бернулли. Что они действительно являются многочленами, мы обнаружим немного позднее. Многочлены Бернулли широко используются в теории чисел. При
называются многочленами Бернулли. Что они действительно являются многочленами, мы обнаружим немного позднее. Многочлены Бернулли широко используются в теории чисел. При  получим:
получим:

где через  обозначено
обозначено  Числа
Числа  называются числами Бернулли. Прежде всего убедимся, что
называются числами Бернулли. Прежде всего убедимся, что  -многочлены, и укажем более удобную, чем (1), формулу для их получения. Умножая обе части равенства (1) на
-многочлены, и укажем более удобную, чем (1), формулу для их получения. Умножая обе части равенства (1) на  и разлагая
и разлагая  и
и  в ряды по степеням х, получим;
в ряды по степеням х, получим;

Приравнивая коэффициенты при  в левой части и в правой, после умножения рядов будем иметь:
в левой части и в правой, после умножения рядов будем иметь:

или

Отсюда при  получаем
получаем  полагая далее
полагая далее  будем последовательно получать все
будем последовательно получать все  При этом непосредственно видно, что все
При этом непосредственно видно, что все  будут многочленами.
будут многочленами.
Многочлены Бернулли обладают двумя характеристическими свойствами. Рассмотрим

С одной стороны, эта разность равна

с другой,

Приравнивая коэффициенты при  имеем:
имеем:

Это и есть одно из характеристических свойств  Продифференцируем теперь (1) по
Продифференцируем теперь (1) по  Получим:
Получим:

или

Приравнивая опять коэффициенты при  будем иметь:
будем иметь:

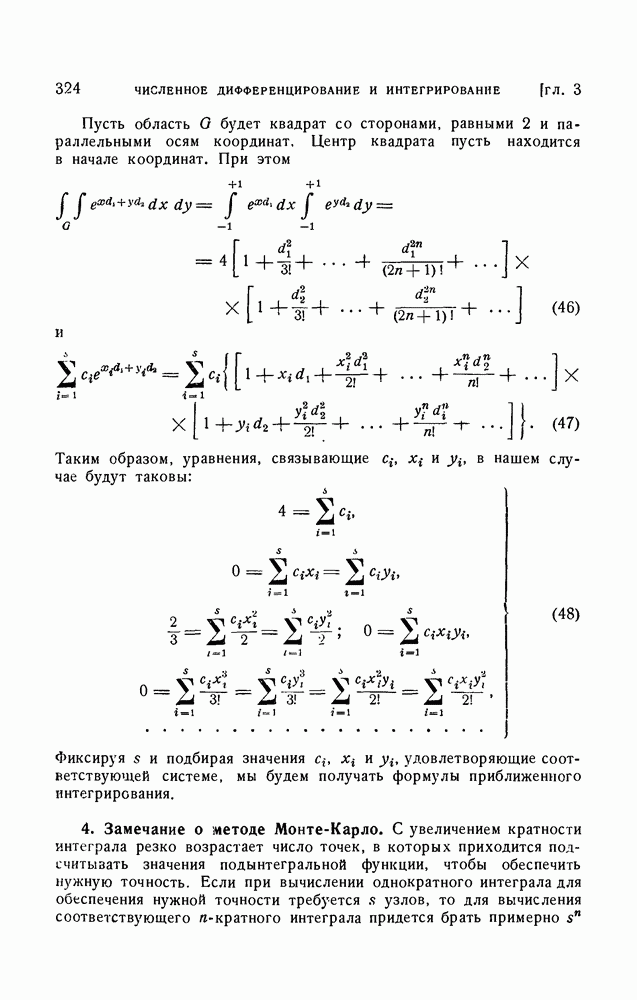
Это — второе характеристическое свойство многочленов Бернулли. Свойства (4) и (5) в свою очередь определяют  В самом деле, на основании формулы Тейлора
В самом деле, на основании формулы Тейлора

Используя (5), получим:

Следовательно,

Снова получили (3), однозначно определяющее  Рассмотрим еще ряды
Рассмотрим еще ряды

Сравнивая (6), (7) с (1) и (2), видим, что  если
если 
Изучим свойства и  Заменим в
Заменим в  на
на  Получим: слева
Получим: слева

и справа

Следовательно, все  с нечетными индексами равны нулю:
с нечетными индексами равны нулю:

Найдем теперь 

Таким образом, для всех 

При  получим
получим  Из (3) следует
Из (3) следует

Итак,

Положим в  Получим:
Получим:

Следовательно,

Полагая в  будем иметь:
будем иметь:

Следовательно,

Положим еще в  получим:
получим:

Заменим здесь х на 

Вычитая друг из друга последние два равенства, будем иметь:

Итак,

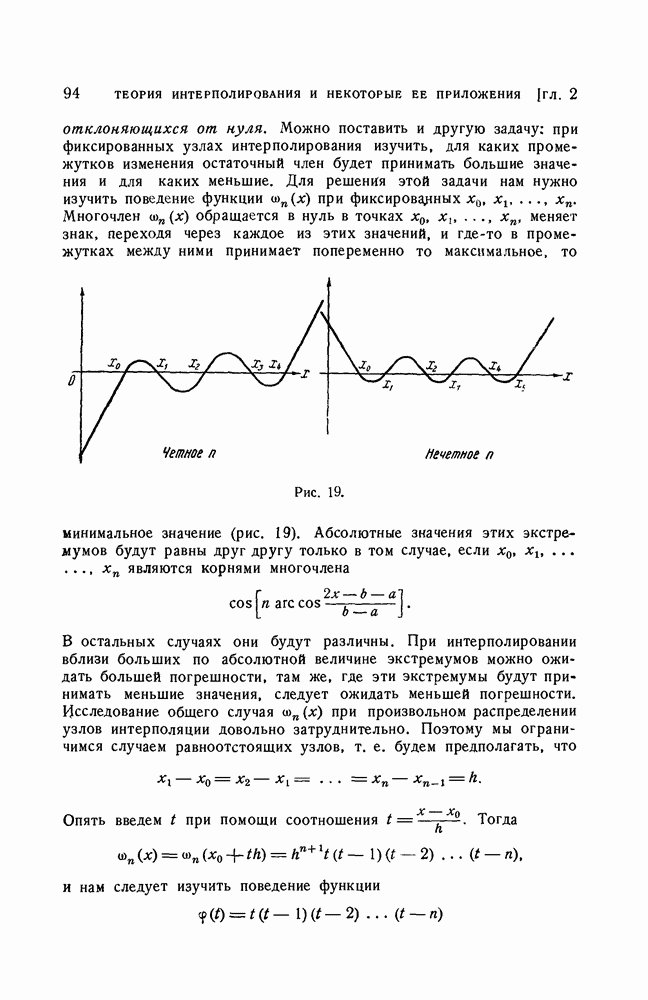
Покажем теперь, что при  нигде не обращается в нуль на отрезке [0, 1] кроме точек
нигде не обращается в нуль на отрезке [0, 1] кроме точек  а
а  нигде не обращается в нуль, кроме
нигде не обращается в нуль, кроме  и 1. Из (10) следует
и 1. Из (10) следует

а из  Следовательно, для
Следовательно, для  наше утверждение справедливо.
наше утверждение справедливо.  будет многочленом третьей степени и в силу (11), (12), (13) обращается в нуль при
будет многочленом третьей степени и в силу (11), (12), (13) обращается в нуль при  Других нулей
Других нулей  иметь не может и для него утверждение также справедливо. Допустим теперь, что утверждение справедливо для
иметь не может и для него утверждение также справедливо. Допустим теперь, что утверждение справедливо для  Положим, для определенности, что
Положим, для определенности, что  при
при  Тогда в силу (8), (9), (11) и (12):
Тогда в силу (8), (9), (11) и (12):

 Следовательно,
Следовательно,  имеет максимум при
имеет максимум при  и этот максимум единственный на [0, 1].
и этот максимум единственный на [0, 1].  не обращается в нуль на [0, 1] и имеет знак где
не обращается в нуль на [0, 1] и имеет знак где  некоторая точка отрезка
некоторая точка отрезка  Далее,
Далее,

Так как  на интервале
на интервале  обращается в нуль только водной точке, то
обращается в нуль только водной точке, то  может обращаться в нуль на отрезке [0, 1] только в двух точках, а
может обращаться в нуль на отрезке [0, 1] только в двух точках, а  только в трех точках. Следовательно,
только в трех точках. Следовательно,  являются единственными нулями
являются единственными нулями  Так как знак
Так как знак  не меняется на отрезке [0, 1], а знак
не меняется на отрезке [0, 1], а знак  меняется, то
меняется, то  имеет знак, противоположный знаку
имеет знак, противоположный знаку  и по абсолютной величине меньше, чем
и по абсолютной величине меньше, чем  Поэтому нуль
Поэтому нуль  при
при  простой. Далее,
простой. Далее,  Следовательно,
Следовательно,  а поэтому и
а поэтому и  при близких к нулю, имеет знак
при близких к нулю, имеет знак  противоположный знаку
противоположный знаку  а следовательно и знаку
а следовательно и знаку  Таким образом,
Таким образом,  будут иметь чередующиеся по к знаки. Это же будет справедливо и для
будут иметь чередующиеся по к знаки. Это же будет справедливо и для 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
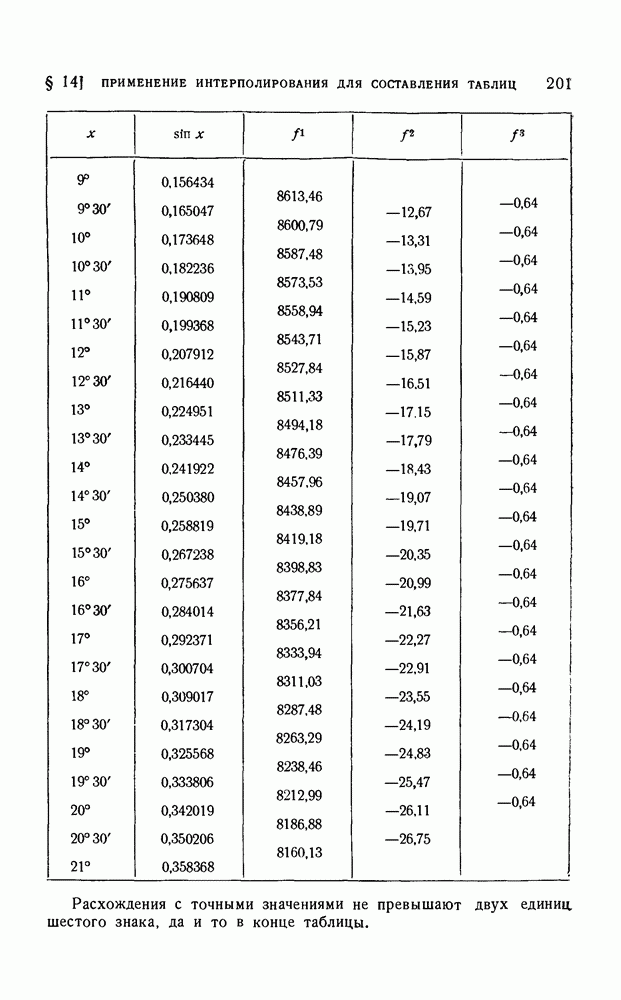
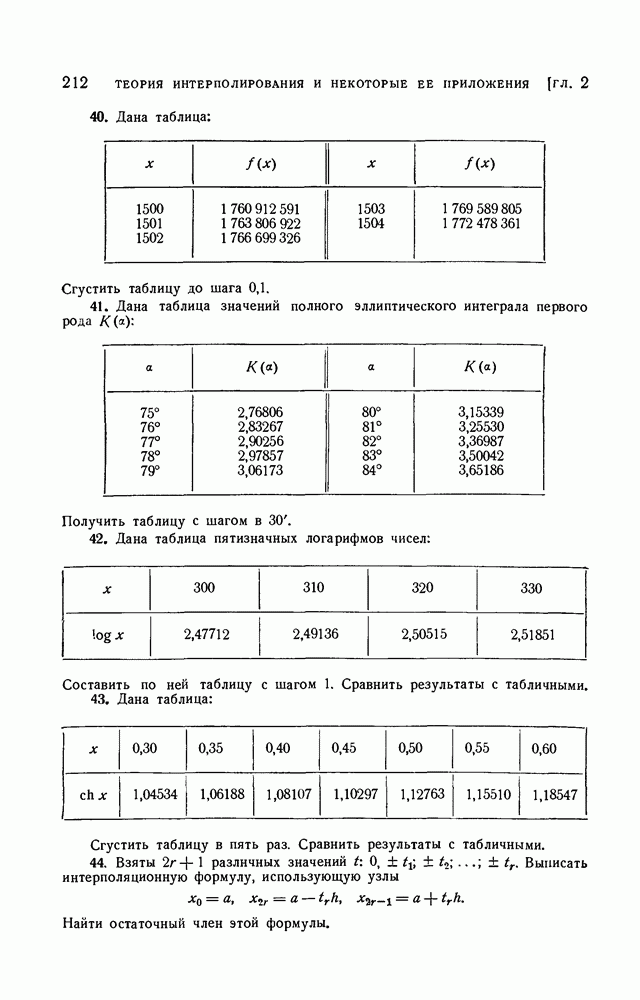
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
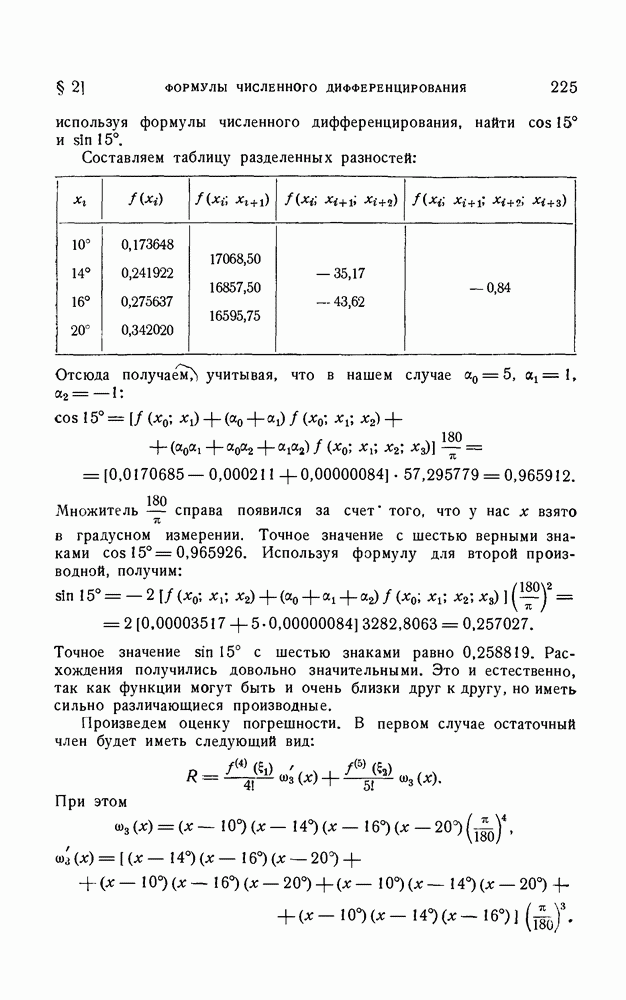
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
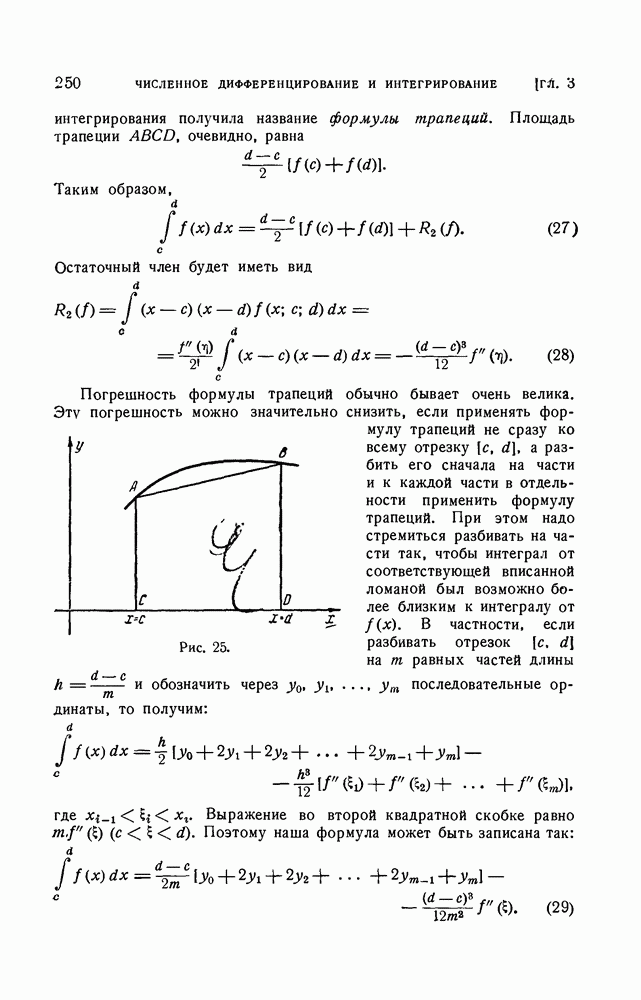
- § 3. Задача численного интегрирования
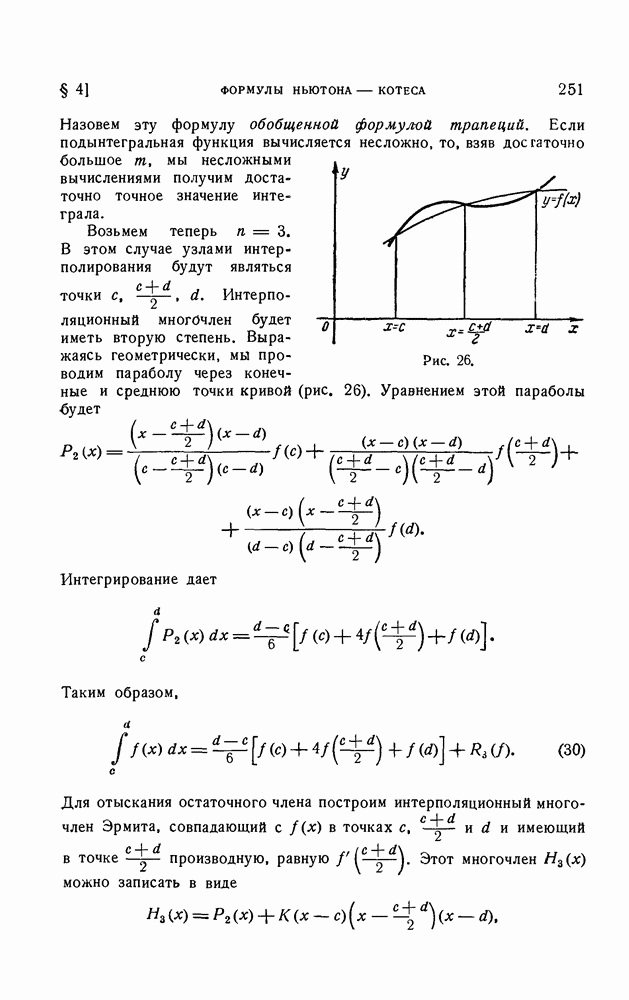
- § 4. Формулы Ньютона — Котеса
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
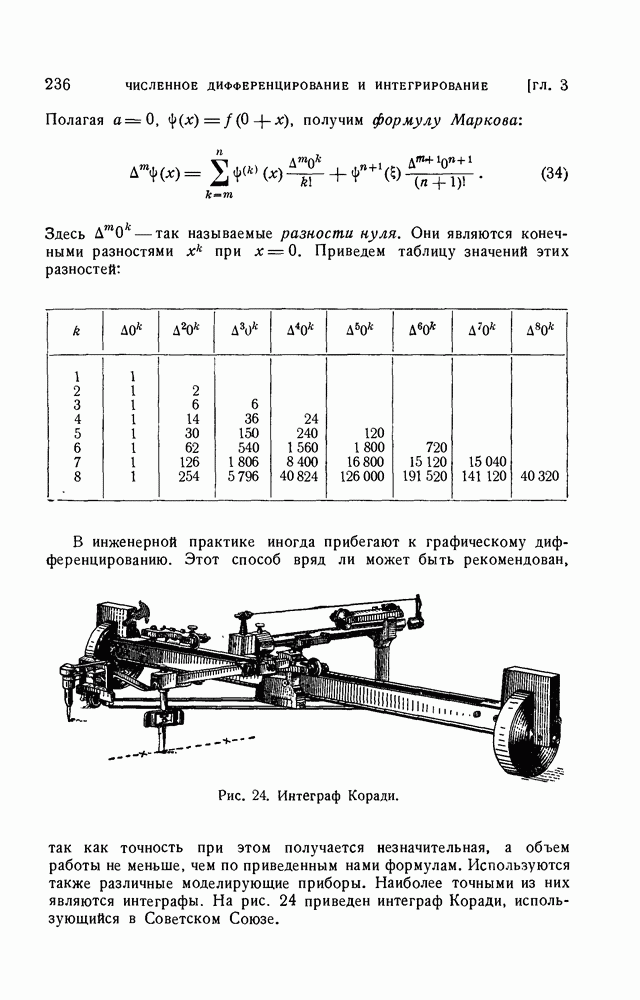
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
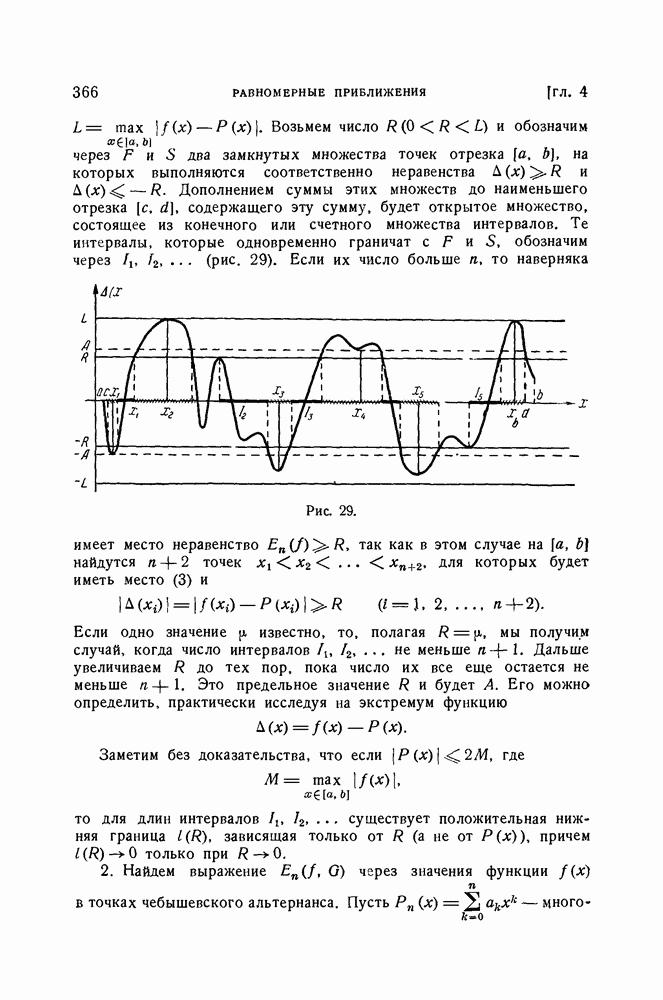
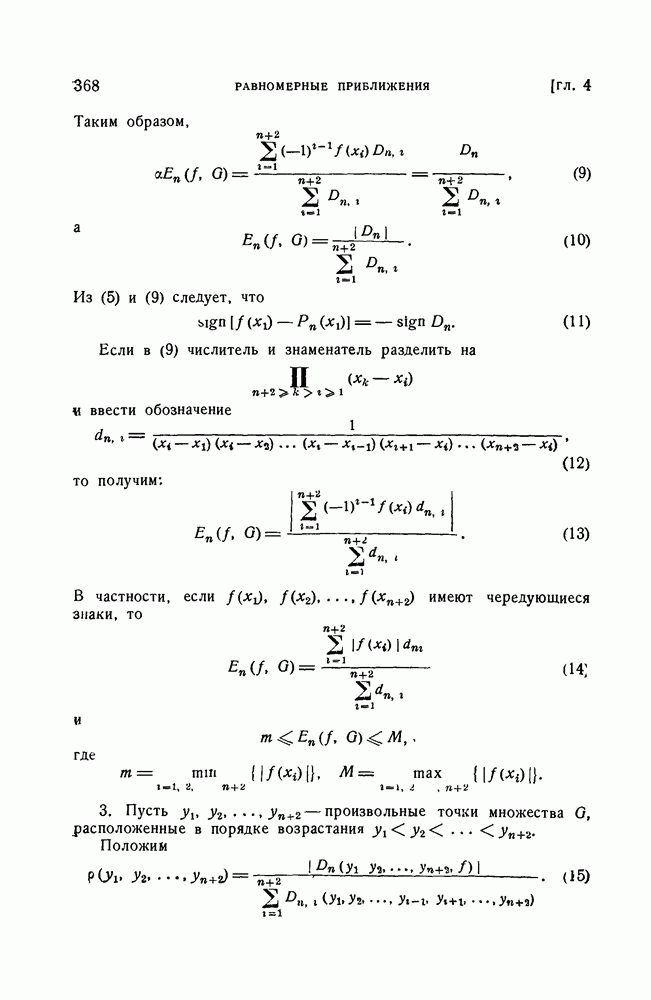
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
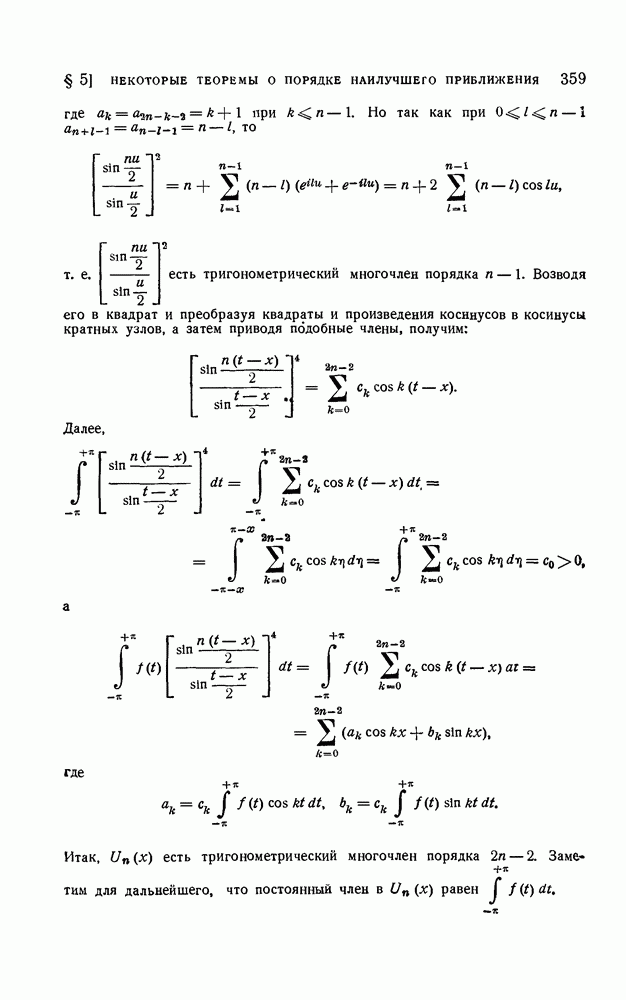
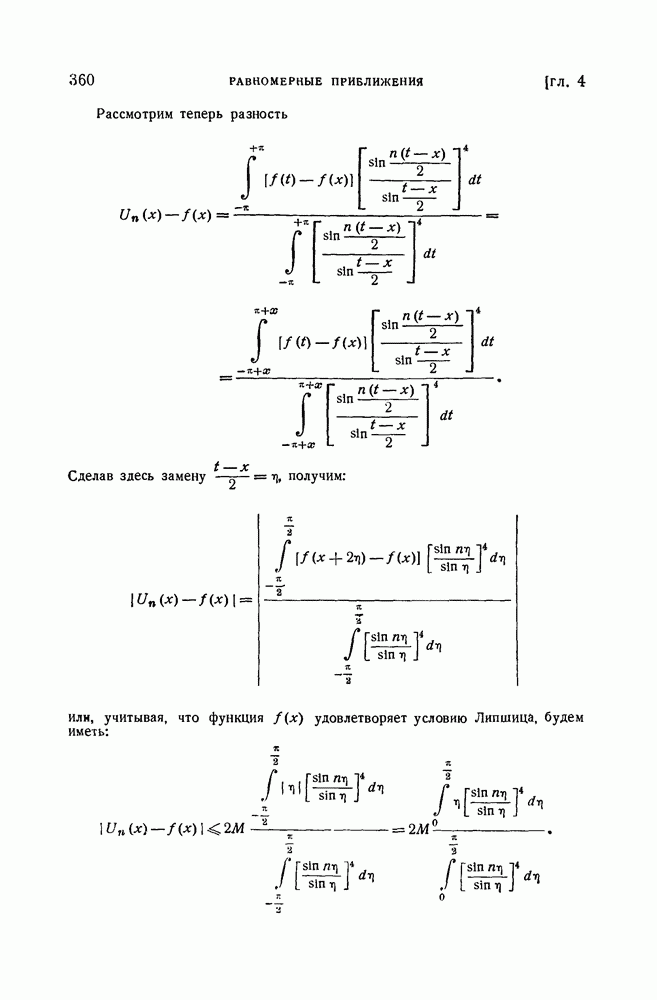
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
- § 13. Схема Рунге вычисления коэффициентов … в случае …