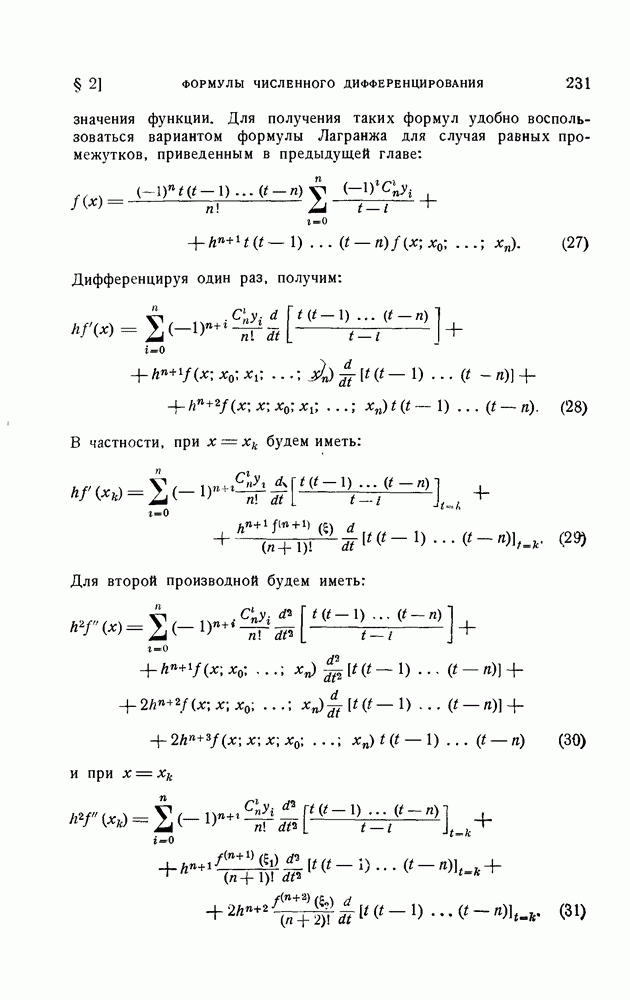| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
Перейдем теперь к отысканию областей неопределенности функций приближенных аргументов. Как мы уже говорили ранее, задача по существу сводится к отысканию экстремальных значений функций и может быть решена методами математического анализа. Здесь мы будем изучать более грубые способы определения абсолютной и относительной погрешностей функций. Для их применения нужно наложить некоторые ограничения на изучаемые функции и погрешности аргументов. Мы будем предполагать, что наши функции непрерывно дифференцируемы в рассматриваемых областях. Предположим также, что погрешности, с которыми мы будем иметь дело, определяются с небольшой точностью — один-два верных знака. Это позволит нам сократить работу по вычислению самих погрешностей. Далее, будем предполагать, что погрешности значительно меньше приближенных величин, так что ими можно пренебрегать в суммах, содержащих одновременно приближенную величину и ее погрешность. Это условие на практике обычно выполняется. Нам часто придется встречаться с значениями функций и их производных в некоторых точках области, определяемой областями неопределенности аргументов. Пользуясь нашими предположениями, мы будем фактически рассматривать их в других точках, более удобных для наших целей.
Найдем абсолютную и относительную погрешности функции  считая, что погрешности аргументов заданы. По формуле конечных приращений получим:
считая, что погрешности аргументов заданы. По формуле конечных приращений получим:

где  значения производных
значения производных  взятых в некоторой точке отрезка, соединяющего точки
взятых в некоторой точке отрезка, соединяющего точки  Используя последнее замечание предыдущего абзаца, заменим
Используя последнее замечание предыдущего абзаца, заменим  на
на  При этом получим:
При этом получим:

Таким образом,

Легко видеть, что при соответствующем выборе а правая часть последнего неравенства будет равна  Отсюда
Отсюда

Теперь нетрудно найти и относительную погрешность. Она будет равна

или

Если нам нужно выразить относительную погрешность функции через относительные погрешности аргументов, то мы запишем наше выражение так:

Отсюда

Мы получили общие выражения для абсолютной и относительной погрешностей функции нескольких приближенных аргументов и предположении малости погрешностей аргументов.
Применим теперь наши общие формулы к некоторым частным случаям. Начнем с простейших арифметических операций. Пусть нам требуется найти сумму нескольких приближенных величин

Мы будем отдельно рассматривать разность приближенных величин и поэтому предполагаем, что все  . В нашем случае все
. В нашем случае все  равны 1, а все
равны 1, а все  Отсюда
Отсюда

Таким образом, при сложении приближенных величин их абсолютные погрешности складываются. Заметим, что это равенство не является грубым и не зависит от тех предположений, которые мы высказали ранее.
Пусть  соответственно наибольшая и наименьшая из относительных погрешностей слагаемых. Тогда на основании второго равенства получим:
соответственно наибольшая и наименьшая из относительных погрешностей слагаемых. Тогда на основании второго равенства получим:

и аналогично

Таким образом, при сложении приближенных величин относительная погрешность суммы будет заключена между наибольшей и наименьшей относительными погрешностями слагаемых.
При производстве вычислений на автоматических вычислительных машинах нет смысла производить округления слагаемых перед производством сложения, если только они помещаются в машине. Это не ускорит вычислений, но расширит область неопределенности слагаемых, а следовательно и суммы. Другое дело при производстве вычислений вручную или на неавтоматической вычислительной машине. В этом случае большое количество разрядов будет связано с длительной установкой чисел, длительными вычислениями и громоздкими записями. Поэтому при вычислениях вручную или на неавтоматических вычислительных машинах производят предварительное округление слагаемых. При этом слагаемое, имеющее наименьшее количество десятичных знаков, оставляют неокругленным, а в остальных слагаемых оставляют на один или два десятичных знака больше.
Обратимся теперь к вычитанию. Рассмотрим разность

предполагая, что  Тогда
Тогда

И в этом случае абсолютная погрешность будет равна сумме абсолютных погрешностей уменьшаемого и вычитаемого, но относительная погрешность будет уже больше, чем каждая из относительных погрешностей. Если уменьшаемое значительно больше вычитаемого, то знаменатель последней дроби близок к х и сама дробь близка к  В этом случае нужно действовать также, как и при сложении. Совершенно другая картина получится, когда уменьшаемое и вычитаемое близки друг к другу. В этом случае знаменатель дроби очень мал и, следовательно, дробь будет очень велика. Получается большая потеря верных знаков. Поэтому там, где это возможно, надо стараться избегать вычитания близких по абсолютной величине чисел. Этого иногда удается достичь заменой вычитания близких чисел непосредственными измерениями или некоторым преобразованием формул. Так, например, пусть нам требуется вычислить объем, заключенный между двумя сферами с общим центром, если дан радиус меньшей сферы
В этом случае нужно действовать также, как и при сложении. Совершенно другая картина получится, когда уменьшаемое и вычитаемое близки друг к другу. В этом случае знаменатель дроби очень мал и, следовательно, дробь будет очень велика. Получается большая потеря верных знаков. Поэтому там, где это возможно, надо стараться избегать вычитания близких по абсолютной величине чисел. Этого иногда удается достичь заменой вычитания близких чисел непосредственными измерениями или некоторым преобразованием формул. Так, например, пусть нам требуется вычислить объем, заключенный между двумя сферами с общим центром, если дан радиус меньшей сферы  и разность радиусов сфер равна а. Искомый объем будет равен
и разность радиусов сфер равна а. Искомый объем будет равен

и если а мало, то вычитание даст большую потерю точности. Выгоднее вычислять результат по формуле

Заметим, что формулы для вычисления погрешностей суммы и разности являются абсолютно точными и не используют тех предположений, о которых говорилось выше.
Рассмотрим теперь произведение приближенных величин. Пусть

Тогда

Таким образом, при умножении приближенных величин относительные погрешности складываются. Оценим грубо число верных знаков в произведении  множителей, заданных в десятичной системе счисления, имеющих одинаковое число
множителей, заданных в десятичной системе счисления, имеющих одинаковое число  верных знаков, если
верных знаков, если  невелико (меньше 10). Обозначим через
невелико (меньше 10). Обозначим через  первые цифры сомножителей, отличные от нуля (их называют первыми значащими цифрами). Тогда по данной ранее приближенной формуле
первые цифры сомножителей, отличные от нуля (их называют первыми значащими цифрами). Тогда по данной ранее приближенной формуле

Отсюда

Обозначив через  первую значащую цифру произведения, будем иметь:
первую значащую цифру произведения, будем иметь:

Заменим в правой части  на
на  на 1. Получим:
на 1. Получим:

Так как  не превышает 10, то
не превышает 10, то

Таким образом, мы будем иметь по крайней мере  верных знаков. Наша оценка очень груба, и практически мы будем иметь
верных знаков. Наша оценка очень груба, и практически мы будем иметь  верных знаков, а иногда и
верных знаков, а иногда и 
При умножении вручную или на неавтоматических вычислительных машинах двух сомножителей с целью экономии времени и сокращения записей более точный сомножитель округляют так, чтобы число его верных знаков было на 1 больше, чем у менее точного.
В случае частного двух величин

будем иметь:

Таким образом, и в этом случае относительные погрешности будут складываться и будут действовать те же правила, что и при умножении.
Рассмотрим еще пример трансцендентной функции. Пусть

Тогда

Таким образом, абсолютная погрешность десятичного логарифма примерно равна половине относительной погрешности числа, стоящего под знаком логарифма. Если х имеет  верных знаков, то
верных знаков, то

Итак, у будет иметь примерно  верных десятичных знаков. Обратно, по
верных десятичных знаков. Обратно, по  -значным таблицам логарифмов можно найти само число с точностью до
-значным таблицам логарифмов можно найти само число с точностью до  верных знаков. Отсюда вывод. Чтобы не затруднять свою работу, с одной стороны, и не уменьшать точность, с другой, мы должны брать таблицы с таким количеством десятичных знаков, каково число верных знаков в аргументе под знаком логарифма.
верных знаков. Отсюда вывод. Чтобы не затруднять свою работу, с одной стороны, и не уменьшать точность, с другой, мы должны брать таблицы с таким количеством десятичных знаков, каково число верных знаков в аргументе под знаком логарифма.
Полученные нами формулы позволяют решать и обратную задачу теории погрешностей: находить допустимые погрешности одного из аргументов по заданным погрешностям функции и остальных аргументов.
В заключение еще раз хотим напомнить, что полученные в настоящем параграфе формулы и способы оценок погрешности справедливы только при тех предположениях, которые были высказаны выше. Эти предположения сводятся к тому, что при разложении разности значений функции при точных и приближенных значениях аргументов в ряд Тейлора по степеням погрешностей аргументов мы можем ограничиться только первыми членами, содержащими первые степени погрешностей аргументов. Если первыми степенями погрешностей ограничиться нельзя, то следует использовать формулу Тейлора до вторых, третьих и т. д. степеней.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
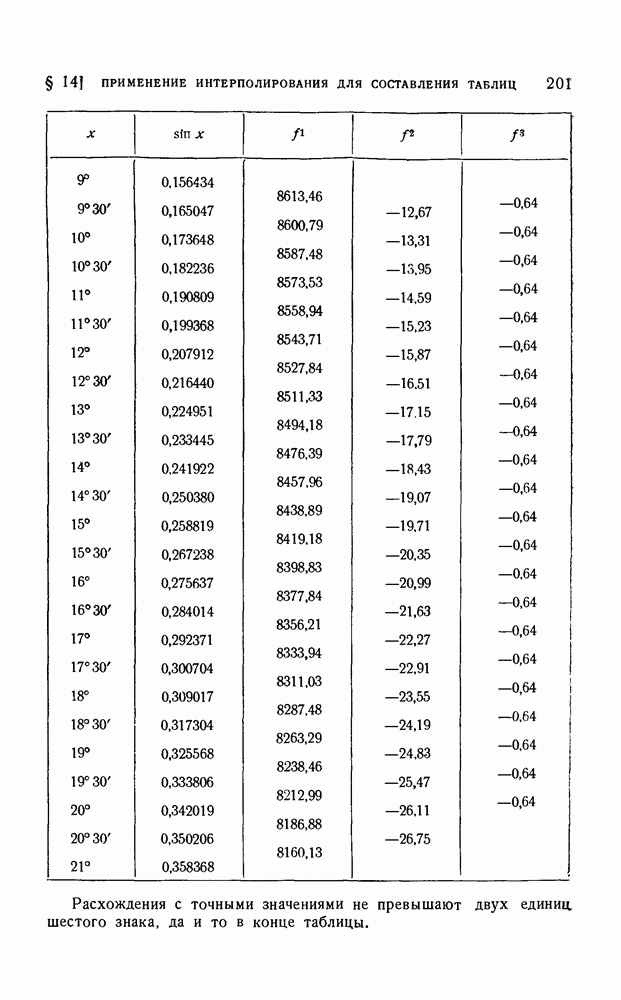
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
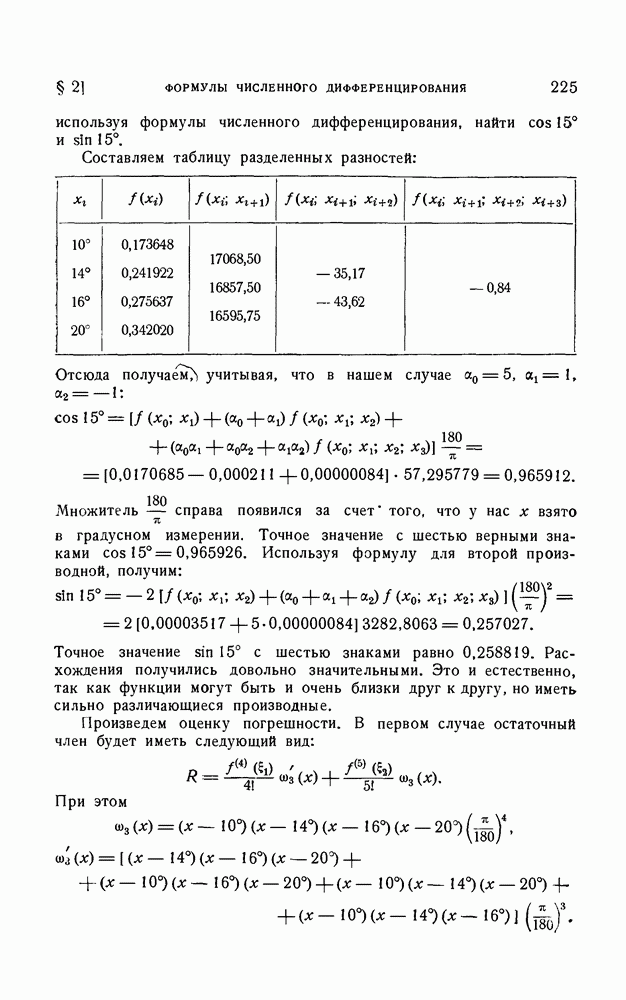
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
- § 3. Задача численного интегрирования
- § 4. Формулы Ньютона — Котеса
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
- § 13. Схема Рунге вычисления коэффициентов … в случае …