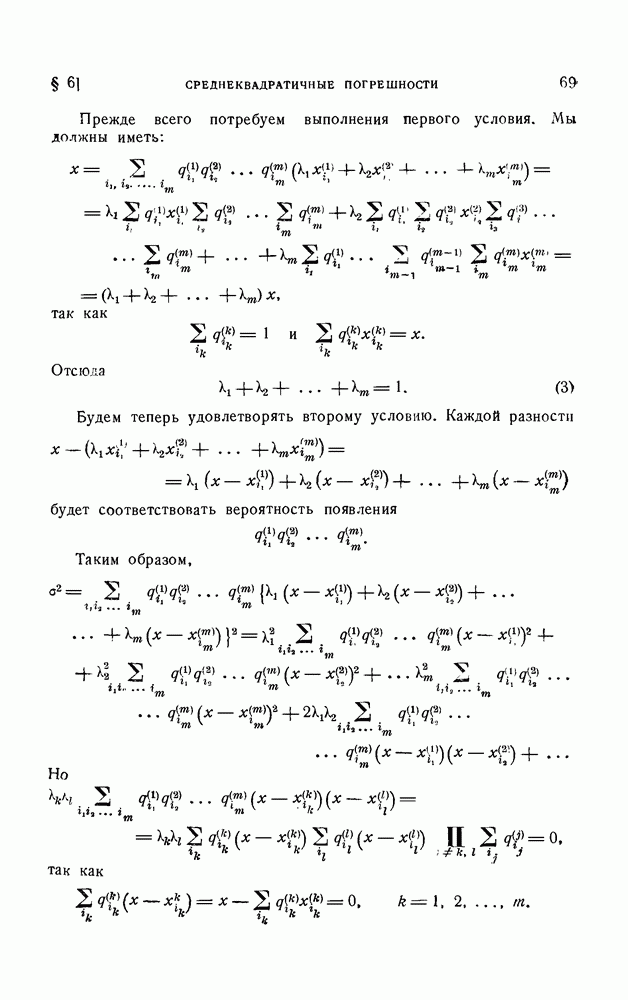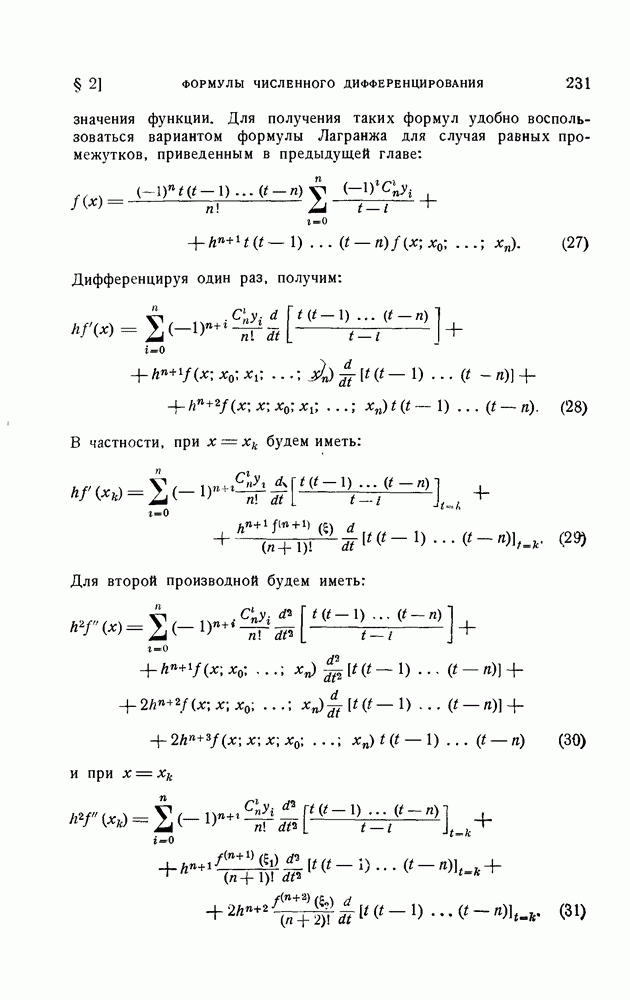| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Приближенное построение алгебраических многочленов наилучшего приближения
Как уже указывалось во Введении, в вычислительной практике часто приходится приближать трудно вычислимые, функции более простыми, например алгебраическими многочленами. При этом часто требуется приблизить функцию  на отрезке
на отрезке  алгебраическим многочленом
алгебраическим многочленом  так, чтобы его отклонение от функции
так, чтобы его отклонение от функции  по абсолютной величине не превосходило заданного числа
по абсолютной величине не превосходило заданного числа  на всем отрезке
на всем отрезке  т. е.
т. е.

Из теоремы Вейерштрасса, доказанной в этой главе, следует, что для функции  непрерывной на
непрерывной на  при любом
при любом  такой многочлен построить можно. Но для практики важно, чтобы такой многочлен имел возможно меньшую степень. Таким многочленом будет многочлен наилучшего равномерного приближения к функции
такой многочлен построить можно. Но для практики важно, чтобы такой многочлен имел возможно меньшую степень. Таким многочленом будет многочлен наилучшего равномерного приближения к функции  на отрезке
на отрезке  в совокупности
в совокупности  многочленов степени не выше
многочленов степени не выше  при таком
при таком  для которого имеет место неравенство
для которого имеет место неравенство

К сожалению, способов построения многочленов наилучшего приближения к данной функции  нет, поэтому большое значение приобретают способы приближенного построения таких многочленов. Хотя разработанные до сих пор методы приближенного построения многочленов наилучшего равномерного приближения недостаточно эффективны, так как требуют выполнения большой вычислительной работы, мы изложим два способа, сравнительно простых по идее и их осуществлению.
нет, поэтому большое значение приобретают способы приближенного построения таких многочленов. Хотя разработанные до сих пор методы приближенного построения многочленов наилучшего равномерного приближения недостаточно эффективны, так как требуют выполнения большой вычислительной работы, мы изложим два способа, сравнительно простых по идее и их осуществлению.
1. Предварительные замечания.
Сделаем несколько общих замечаний и докажем несколько существенных для дальнейшего изложения утверждений.
1. В § 2 этой главы мы отмечали, что вся теория наилучшего равномерного приближения функций  непрерывных на отрезке
непрерывных на отрезке  с помощью многочленов (в том числе и алгебраических) остается в силе, если мы будем рассматривать вместо отрезка
с помощью многочленов (в том числе и алгебраических) остается в силе, если мы будем рассматривать вместо отрезка  любое замкнутое множество
любое замкнутое множество  лишь бы оно состояло не меньше чем из
лишь бы оно состояло не меньше чем из  точек. В частности, справедлива теорема:
точек. В частности, справедлива теорема:
Для того чтобы многочлен  был многочленом наилучшего приближения к функции
был многочленом наилучшего приближения к функции  на замкнутом множестве
на замкнутом множестве  содержащем не менее
содержащем не менее  точек, необходимо и достаточно существование таких
точек, необходимо и достаточно существование таких  точек
точек

что

где  При этом
При этом  наилучшее приближение функции
наилучшее приближение функции  на
на 
Точки (1), для которых выполняется условие (2), будем называть чебышевским альтернатом.
Справедлива также и следующая теорема (Балле — 
Если  и точки
и точки  таковы, что
таковы, что

то

При фиксированных  величина
величина  зависит от выбора комбинации
зависит от выбора комбинации  удовлетворяющей условию (3). Верхнюю границу для
удовлетворяющей условию (3). Верхнюю границу для  при выборе всевозможных таких комбинаций обозначим через А. Если
при выборе всевозможных таких комбинаций обозначим через А. Если  то А можно найти следующим образом. Рассматриваем разность
то А можно найти следующим образом. Рассматриваем разность  Пусть
Пусть
 Возьмем число
Возьмем число  и обозначим через
и обозначим через  два замкнутых множества точек отрезка
два замкнутых множества точек отрезка  на которых выполняются соответственно неравенства
на которых выполняются соответственно неравенства  Дополнением суммы этих множеств до наименьшего отрезка
Дополнением суммы этих множеств до наименьшего отрезка  содержащего эту сумму, будет открытое множество, состоящее из конечного или счетного множества интервалов. Те интервалы, которые одновременно граничат с
содержащего эту сумму, будет открытое множество, состоящее из конечного или счетного множества интервалов. Те интервалы, которые одновременно граничат с  и 5, обозначим через
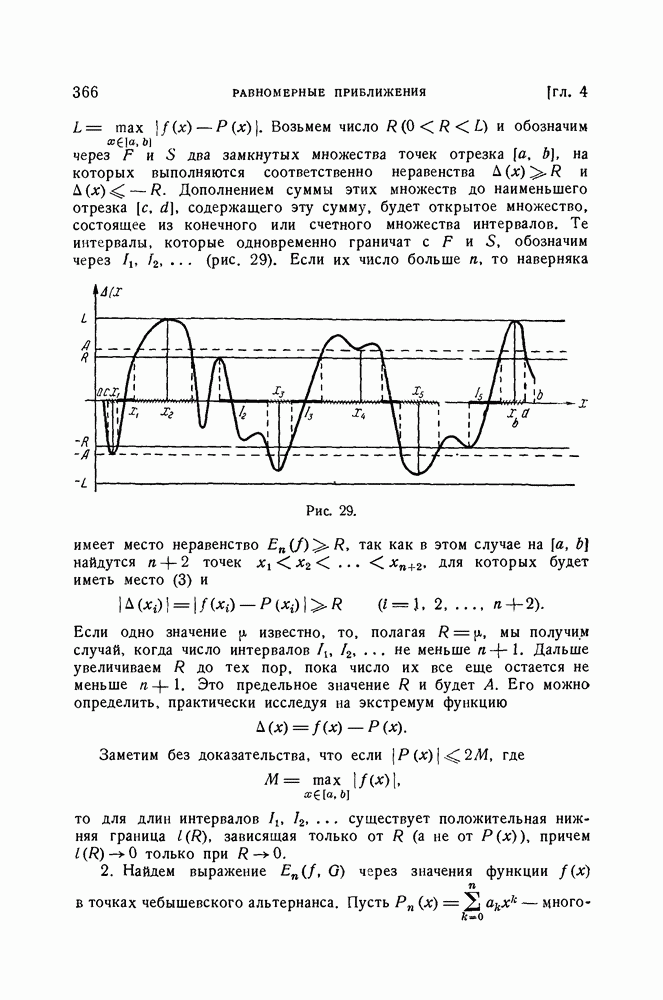
и 5, обозначим через  (рис. 29).
(рис. 29).

Рис. 29.
Если их число больше  то наверняка имеет место неравенство
то наверняка имеет место неравенство  так как в этом случае на
так как в этом случае на  найдутся
найдутся  точек
точек  для которых будет иметь место (3) и
для которых будет иметь место (3) и

Если одно значение  известно, то, полагая
известно, то, полагая  мы получим случай, когда число интервалов
мы получим случай, когда число интервалов  не меньше
не меньше  Дальше увеличиваем
Дальше увеличиваем  до тех пор, пока число их все еще остается не меньше
до тех пор, пока число их все еще остается не меньше  . Это предельное значение
. Это предельное значение  и будет А. Его можно определить, практически исследуя на экстремум функцию
и будет А. Его можно определить, практически исследуя на экстремум функцию

Заметим без доказательства, что если  где
где

то для длин интервалов  существует положительная нижняя граница
существует положительная нижняя граница  зависящая только от
зависящая только от  (а не от
(а не от  причем
причем  только при
только при 
2. Найдем выражение  через значения функции
через значения функции  в точках чебышевского альтернанса. Пусть
в точках чебышевского альтернанса. Пусть  — многочлен
— многочлен
наилучшего приближения к  на множестве
на множестве  чебышевский альтернанс для него, т. е.
чебышевский альтернанс для него, т. е.

Рассмотрим определители

Все определители  положительны, так как
положительны, так как  Далее, при
Далее, при 

Умножая (5) на  и суммируя по
и суммируя по  от 1 до
от 1 до  будем иметь:
будем иметь:

Меняя слева порядок суммирования и учитывая (7), убеждаемся в равенстве нулю левой части, 

где

Таким образом,

а

Из (5) и (9) следует, что

Если в (9) числитель и знаменатель разделить на

и ввести обозначение

то получим;

В частности, если  имеют чередующиеся знаки, то
имеют чередующиеся знаки, то

и

где

3. Пусть  произвольные точки множества
произвольные точки множества  расположенные в порядке возрастания
расположенные в порядке возрастания  -Положим
-Положим

Эта величина обладает тем свойством, что

2) существует система точек  для которой
для которой

Эта система точек образует чебышевский альтернанс и, следовательно,

где  многочлен наилучшего приближения к
многочлен наилучшего приближения к  на
на 
Для доказательства этих утверждений обозначим через 5 множество, состоящее из  указанных точек
указанных точек  через
через  многочлены наилучшего приближения к функции
многочлены наилучшего приближения к функции  соответственно на множествах
соответственно на множествах  в
в  а через
а через  соответствующие наилучшие приближения.
соответствующие наилучшие приближения.
Пусть  чебышевский альтернанс
чебышевский альтернанс  на
на  По доказанному ранее (см. (10))
По доказанному ранее (см. (10))

Так как множество  состоит только из
состоит только из  точек
точек  то они образуют чебышевский альтернанс
то они образуют чебышевский альтернанс  по отношению к 5, а следовательно,
по отношению к 5, а следовательно,

Далее,

Отсюда

и неравенство (16) доказано.
Если  есть чебышевский альтернанс функции
есть чебышевский альтернанс функции  на
на  то
то  а так как в силу теоремы существования многочлена наилучшего приближения и теоремы Чебышева он всегда существует в
а так как в силу теоремы существования многочлена наилучшего приближения и теоремы Чебышева он всегда существует в  то
то  достигает своей верхней границы на любом из этих альтернансов.
достигает своей верхней границы на любом из этих альтернансов.
Пусть теперь  есть множество точек
есть множество точек  для которых
для которых

а  многочлены наилучшего Приближения к
многочлены наилучшего Приближения к  соответственно на множествах
соответственно на множествах  и 5. Из равенства
и 5. Из равенства  следует, что
следует, что

Но  Следовательно,
Следовательно,

Но так как

то

Это означает, что  есть многочлен наилучшего приближения к
есть многочлен наилучшего приближения к  на 5 и в силу единственности многочлена наилучшего приближения
на 5 и в силу единственности многочлена наилучшего приближения

Но так как 5 состоит из  различных точек, то
различных точек, то

Это и доказывает, что множество  есть альтернанс к
есть альтернанс к  на
на  а поэтому имеет место и равенство (18) (см. (11)).
а поэтому имеет место и равенство (18) (см. (11)).
4. Предыдущие рассуждения позволяют с помощью конечного числа шагов построить многочлен наилучшего приближения к  на множестве
на множестве  состоящем из конечного числа точек
состоящем из конечного числа точек 
Рассмотрим сначала случай 
Располагая точки этого множества в порядке возрастания  вычисляем
вычисляем  используя равенства (15), (6), (8). Значение
используя равенства (15), (6), (8). Значение  Зная знак определителя
Зная знак определителя  определяем знак разности
определяем знак разности  с помощью равенства (18).
с помощью равенства (18).
Далее, пишем систему равенств

где  если
если  если
если 
Из этой системы равенств находим значения искомого многочлена  в точках
в точках 

Этими значениями многочлен полностью определяется. Найти его можно, строя интерполяционный многочлен по любым «4-1
значениям. Лишнее значение можно использовать для контроля, так как полученный интерполяционный многочлен должен принимать заранее вычисленное значение в неиспользованном узле.
Если множество  состоит из
состоит из  точек
точек  то рассматриваем всевозможные комбинации из
то рассматриваем всевозможные комбинации из  точек этого множества
точек этого множества  где
где  и для каждой из них вычисляем
и для каждой из них вычисляем  Из конечного числа значений
Из конечного числа значений  выбираем наибольшее. Система точек
выбираем наибольшее. Система точек  для которой
для которой  имеет максимальное значение, будет давать альтернанс для
имеет максимальное значение, будет давать альтернанс для  на
на  и построение многочлена наилучшего приближения к
и построение многочлена наилучшего приближения к  на
на  сводится к построению многочлена наилучшего приближения к
сводится к построению многочлена наилучшего приближения к  на множестве из этих
на множестве из этих  точек. Построение этого многочлена мы уже описали. Основная трудность заключается в том, что приходится вычислять значения
точек. Построение этого многочлена мы уже описали. Основная трудность заключается в том, что приходится вычислять значения  для всевозможных комбинаций у,
для всевозможных комбинаций у,  число которых равно т. е. при большом
число которых равно т. е. при большом  может быть очень большим.
может быть очень большим.
5. Для дальнейшего имеет важное значение следующая Теорема. Если  непрерывная на
непрерывная на  функция, а
функция, а  последовательность многочленов из
последовательность многочленов из  для которых имеет место неравенство
для которых имеет место неравенство

где  при
при  то последовательность
то последовательность  равномерно на
равномерно на  сходится к многочлену наилучшего приближения
сходится к многочлену наилучшего приближения  функции
функции  на
на 
Доказательство этой теоремы существенно опирается на лемму: Из всякой, последовательности многочленов  ограниченных на
ограниченных на  одной и той же константой
одной и той же константой  можно выбрать подпоследовательность, равномерно сходящуюся на
можно выбрать подпоследовательность, равномерно сходящуюся на  к многочлену
к многочлену 
Для доказательства леммы прежде всего докажем, что если

то существуют такие постоянные  не зависящие от
не зависящие от  что
что

В самом деле, если положить  то при
то при 

Отсюда

и неравенство (23) доказано. Для доказательства неравенства (22) возьмем на  некоторые точки
некоторые точки  при
при  Тогда по интерполяционной формуле Лагранжа
Тогда по интерполяционной формуле Лагранжа

где  многочлен степени
многочлен степени  обладающий свойством
обладающий свойством 

Пусть  Тогда
Тогда

Отсюда

Полагая  не зависит от
не зависит от  получим неравенство (22).
получим неравенство (22).
Теперь перейдем к непосредственному доказательству леммы. Многочлен  вполне определяется его коэффициентами
вполне определяется его коэффициентами  Поэтому вместо последовательности многочленов
Поэтому вместо последовательности многочленов  рассмотрим последовательность точек
рассмотрим последовательность точек  -мерного евклидова пространства. Так как
-мерного евклидова пространства. Так как  то по неравенству
то по неравенству  т. е.
т. е.  ограниченная последовательность точек, а следовательно, из нее можно выбрать некоторую подпоследовательность
ограниченная последовательность точек, а следовательно, из нее можно выбрать некоторую подпоследовательность  сходящуюся к некоторой точке
сходящуюся к некоторой точке  Рассмотрим многочлен
Рассмотрим многочлен  коэффициентами которого являются координаты точки
коэффициентами которого являются координаты точки  Из неравенства (23) следует, что
Из неравенства (23) следует, что

Правая часть стремится к нулю при  а это и означает, что
а это и означает, что  равномерно на
равномерно на  сходится к
сходится к 
Используя эту лемму, докажем сформулированную выше теорему. Из неравенства (21) и условия, что  при
при  следует существование такой постоянной К, что
следует существование такой постоянной К, что

ибо

где  верхняя грань
верхняя грань  Поэтому за К можно взять
Поэтому за К можно взять  Так как последовательность
Так как последовательность  ограничена одним и тем же числом К, то по лемме из нее можно выбрать подпоследовательность
ограничена одним и тем же числом К, то по лемме из нее можно выбрать подпоследовательность  равномерно сходящуюся к некоторому многочлену
равномерно сходящуюся к некоторому многочлену  Для этой подпоследовательности имеем:
Для этой подпоследовательности имеем:

Переходя к пределу при получим:

но так как 

и, следовательно,  есть многочлен наилучшего приближения к
есть многочлен наилучшего приближения к  на
на  в
в  В силу единственности многочлена наилучшего приближения
В силу единственности многочлена наилучшего приближения 
Таким образом, подпоследовательность  равномерно на
равномерно на  сходится к
сходится к 
Из единственности многочлена наилучшего приближения следует, что и вся последовательность  будет равномерно сходиться к
будет равномерно сходиться к  Если бы это было не так, то из нее можно было бы выделить подпоследовательность, равномерно сходящуюся к некоторому другому многочлену
Если бы это было не так, то из нее можно было бы выделить подпоследовательность, равномерно сходящуюся к некоторому другому многочлену  Этот многочлен должен был бы быть многочленом наилучшего приближения в
Этот многочлен должен был бы быть многочленом наилучшего приближения в  но это противоречит единственности многочлена наилучшего приближения.
но это противоречит единственности многочлена наилучшего приближения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
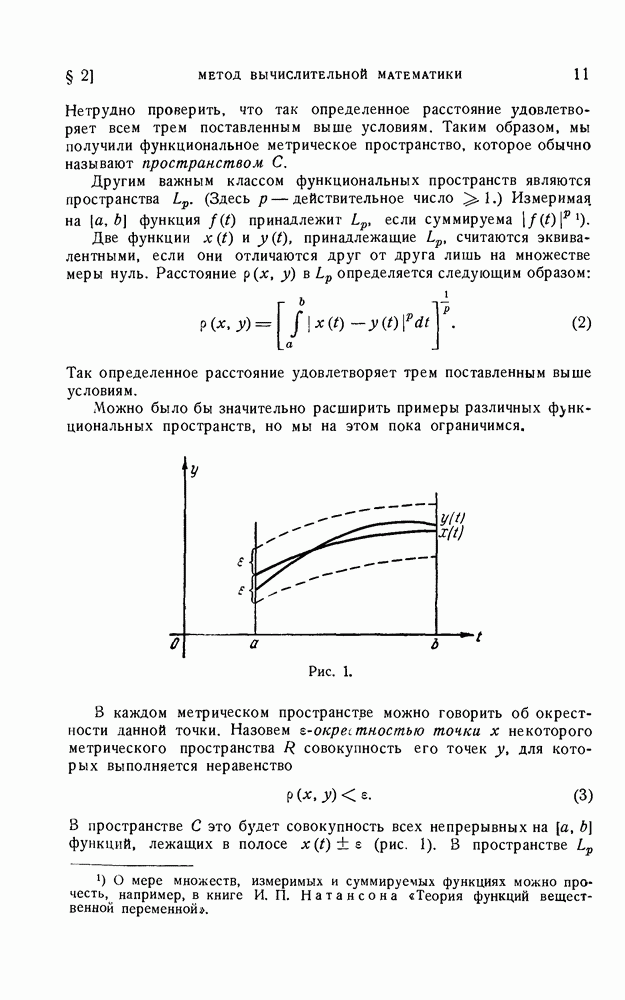
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
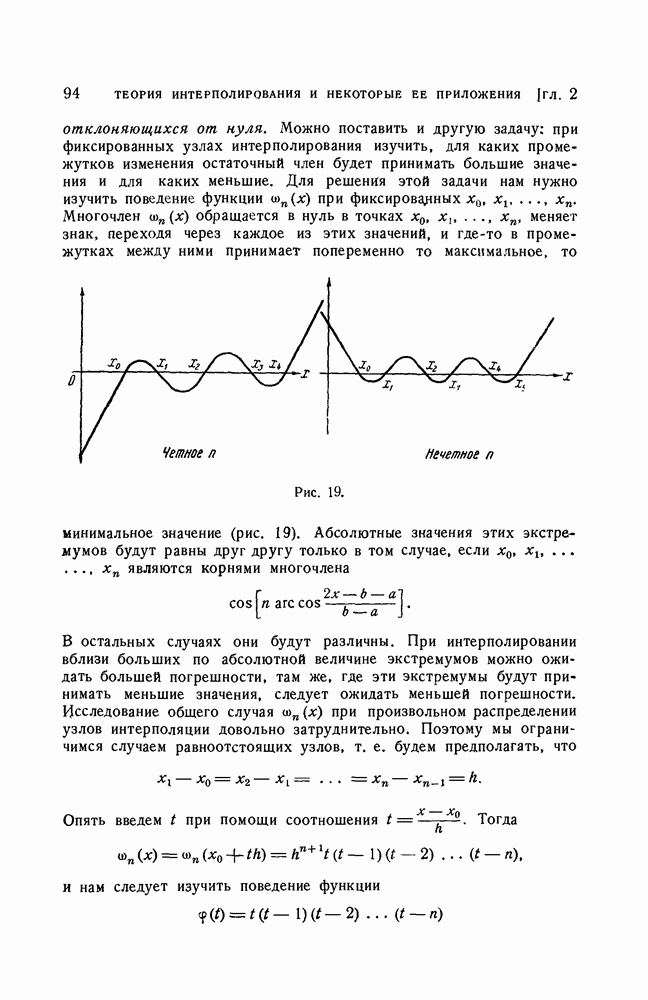
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
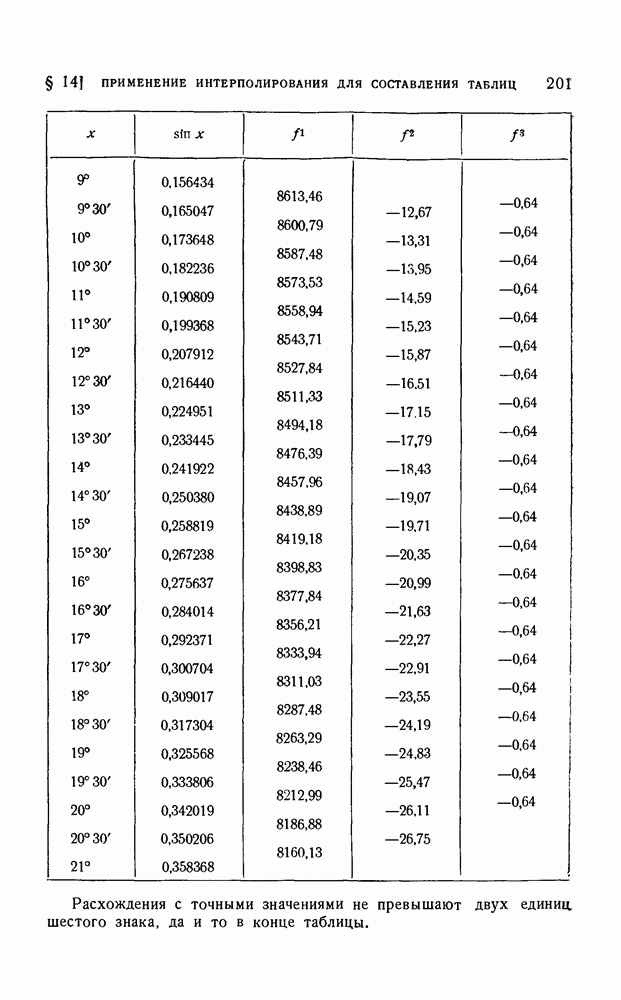
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
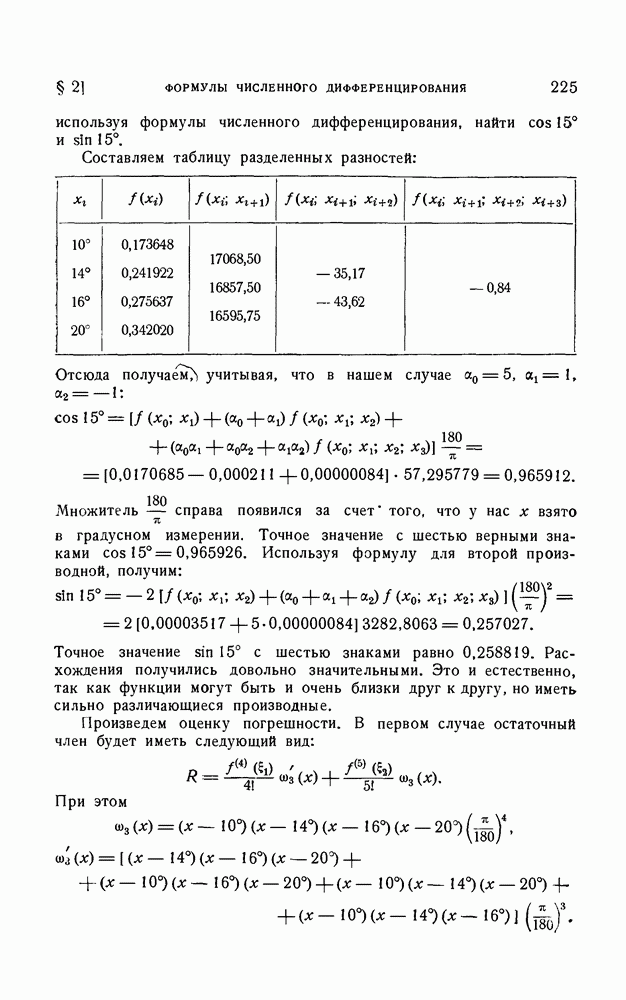
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
- § 3. Задача численного интегрирования
- § 4. Формулы Ньютона — Котеса
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
- § 13. Схема Рунге вычисления коэффициентов … в случае …