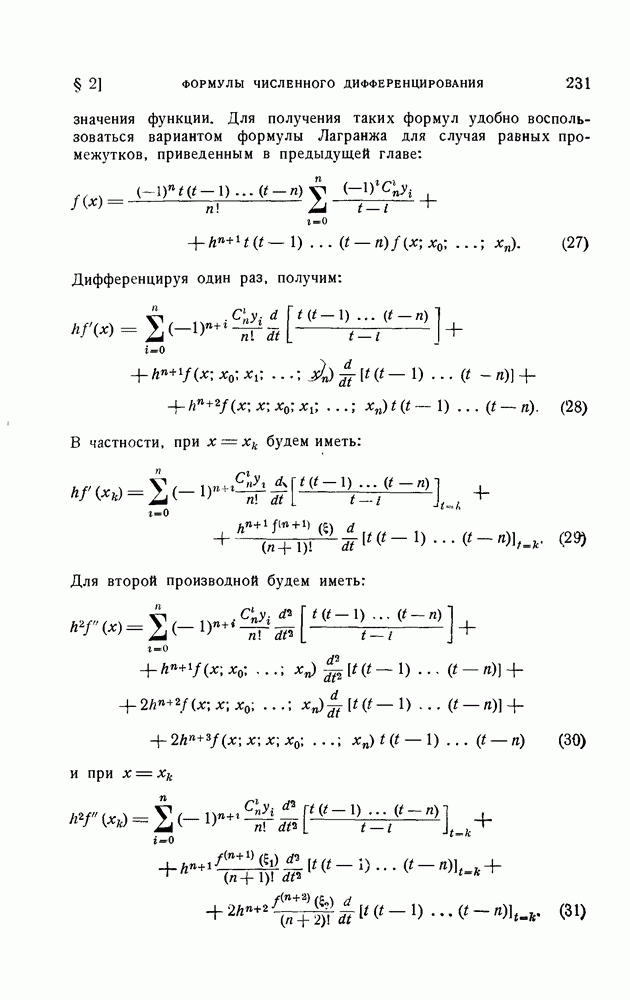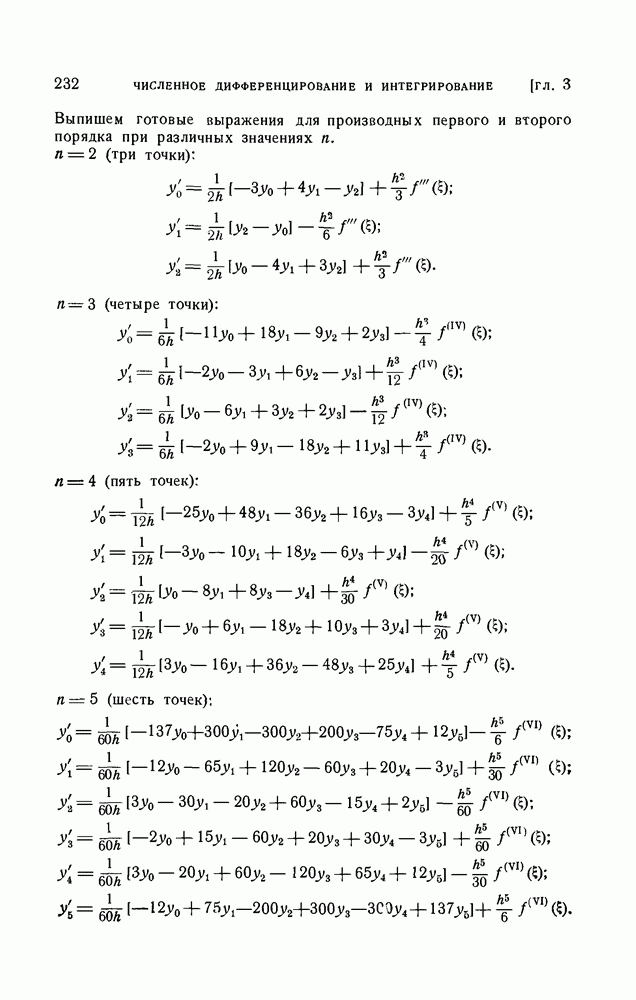| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 11. Вычисление несобственных интегралов
На практике часто приходится сталкиваться с задачами, связанными с вычислением несобственных интегралов. Это могут быть интегралы с бесконечными пределами или интегралы с конечными пределами, но подынтегральной функцией, обращающейся в бесконечность на отрезке интегрирования.
Несобственный интеграл с бесконечными пределами всегда можно преобразовать в несобственный интеграл или даже собственный с конечными пределами. Для этого достаточно произвести подходящую замену переменного под знаком интеграла или взять интеграл в конечных, но достаточно больших пределах так, что отбрасываемая часть интеграла значительно меньше, чем заданная нам точность вычисления интеграла. В последнем случае часто пользуются асимптотическими выражениями подынтегральных функций для оценки отбрасываемой части интеграла иди для учета ее вклада в интеграл.
Мы не будем подробнее останавливаться на этом вопросе, так как во многом успех при вычислении несобственного интеграла с бесконечными пределами зависит от искусства вычислителя.
1. Метод выделения особенностей.
При вычислении несобственных интегралов с конечными пределами интегрирования удобнее всего использовать метод выделения особенностей. Существует два метода выделения особенностей: мультипликативный и аддитивный.
Суть мультипликативного способа выделения особенностей состоит в следующем. Пусть нам требуется вычислить интеграл

где функция  обращается в бесконечность в одной или нескольких точках отрезка
обращается в бесконечность в одной или нескольких точках отрезка  Мы представляем эту функцию в виде
Мы представляем эту функцию в виде

где  -ограниченная функция на
-ограниченная функция на  обладающая там достаточным количеством непрерывных производных, а
обладающая там достаточным количеством непрерывных производных, а  на
на  Рассматривают
Рассматривают  как весовую функцию и строят соответствующую формулу численного интегрирования теми приемами, которые указаны выше. За приближенное значение интеграла (1) принимают результат применения полученной формулы численного интегрирования к функции
как весовую функцию и строят соответствующую формулу численного интегрирования теми приемами, которые указаны выше. За приближенное значение интеграла (1) принимают результат применения полученной формулы численного интегрирования к функции 
Пусть, например, нам нужно вычислить интеграл

Подынтегральная функция обращается в бесконечность в точках  Представим ее в виде
Представим ее в виде

и будем рассматривать функцию

как весовую. Тогда будет применима формула численного интегрирования Эрмита:

При  получим:
получим:

Значение интеграла с шестью верными знаками после запятой равно

Аддитивный способ выделения особенностей состоит в следующем. Подынтегральную функцию представляют в виде

где  не имеет особенностей и обладает достаточным числом непрерывных производных, а интеграл от
не имеет особенностей и обладает достаточным числом непрерывных производных, а интеграл от  может быть найден точными методами интегрального исчисления. Возьмем в качестве примера следующий интеграл:
может быть найден точными методами интегрального исчисления. Возьмем в качестве примера следующий интеграл:

Подынтегральную функцию представим в виде 

Тогда

Первый интеграл легко вычисляется:

Подынтегральная функция в  не имеет особенностей на отрезке интегрирования. Вычислим
не имеет особенностей на отрезке интегрирования. Вычислим  по формуле Симпсона, взяв
по формуле Симпсона, взяв  Получим:
Получим:

Таким образом,

Значение интеграла с шестью верными знаками после запятой равно

Л. В. Канторович, предложивший этот способ, указал также и на некоторые приемы представления подынтегральной функции в виде (9).
Пусть  имеет вид
имеет вид

где  может быть представлена на отрезке
может быть представлена на отрезке  формулой Тейлора по степеням
формулой Тейлора по степеням  с остаточным членом, зависящим от производной порядка
с остаточным членом, зависящим от производной порядка  Тогда
Тогда  можно записать в виде
можно записать в виде

Первая квадратная скобка правой части является степенной функцией и поэтому интегрируется без труда. Вторая квадратная скобка обращается в нуль при  вместе со всеми производными до порядка
вместе со всеми производными до порядка  включительно. Следовательно, ее произведение с
включительно. Следовательно, ее произведение с  не будет иметь никаких особенностей при
не будет иметь никаких особенностей при  Более того, при
Более того, при  это произведение будет обладать непрерывными производными до порядка
это произведение будет обладать непрерывными производными до порядка  включительно. Поэтому можно ожидать, что применение формул численного интегрирования к нему даст хорошие результаты.
включительно. Поэтому можно ожидать, что применение формул численного интегрирования к нему даст хорошие результаты.
Указанный прием можно применить и в том случае, когда подынтегральная функция имеет вид

где  натуральное число и а, с и
натуральное число и а, с и  таковы же, как и ранее. В этом случае получим разложение
таковы же, как и ранее. В этом случае получим разложение

Опять интеграл от первого слагаемого правой части выражается в конечном виде через элементарные функции, если применить Интегрирование по частям. Второе слагаемое правой части будет гладкой функцией.
Прием можно обобщить, взяв несколько особенностей на промежутке интегрирования. Пусть, например,

где  обладает на
обладает на  непрерывными производными достаточно высокого порядка. При этом последовательно исключаем особеннрсти в каждой из точек
непрерывными производными достаточно высокого порядка. При этом последовательно исключаем особеннрсти в каждой из точек  Сначала, как и при наличии одной особенности, представляем
Сначала, как и при наличии одной особенности, представляем  в виде
в виде

где  достаточно гладкая функция в точке
достаточно гладкая функция в точке  Затем таким же образом исключаем особенности в точке
Затем таким же образом исключаем особенности в точке  в точке
в точке  точке
точке  . В конце концов, дело сведется к вычислению суммы интегралов
. В конце концов, дело сведется к вычислению суммы интегралов

где  уже не имеет особенностей на
уже не имеет особенностей на 
И в этом случае можно ввести дополнительные логарифмические множители.
Рассмотрим еще один случай. Пусть

где  гладкая функция, принимающая в точке
гладкая функция, принимающая в точке  значение, при котором
значение, при котором  имеет особенность. Представим
имеет особенность. Представим  в виде
в виде

Тогда

Предполагаем, что  можно проинтегрировать в конечном виде. Интегрирование второго слагаемого можно осуществить по формулам численного интегрирования, так как фигурная скобка не имеет особенности при
можно проинтегрировать в конечном виде. Интегрирование второго слагаемого можно осуществить по формулам численного интегрирования, так как фигурная скобка не имеет особенности при  Приведенный выше пример (10) принадлежит как раз к такому типу.
Приведенный выше пример (10) принадлежит как раз к такому типу.
Данные нами методы выделения особенностей можно применять не только для вычисления несобственных интегралов,  том случае, когда подынтегральная функция ограничена, но не обладает достаточно большим числом ограниченных производных. При этом, как показывают выражения остаточных членов, формулы численного
том случае, когда подынтегральная функция ограничена, но не обладает достаточно большим числом ограниченных производных. При этом, как показывают выражения остаточных членов, формулы численного
интегрирования дадут, вообще говоря, большую погрешность. Метод выделения особенностей позволит иногда представить подынтегральное выражение в виде суммы функции, интегрируемой в конечном виде, и достаточно гладкой функции.
2. Специальные приемы.
Если известен характер поведения подынтегральной функции вблизи особенности, то можно построить специальные формулы, учитывающие особенность и позволяющие получить значение интеграла на некотором небольшом отрезке, содержащем особенность. Интеграл по остальной части отрезка интегрирования будет вычисляться по обычным формулам численного интегрирования. Пусть, например, левый конец отрезка интегрирования есть  и функция
и функция  вблизи него может быть представлена в виде
вблизи него может быть представлена в виде

Подберем коэффициенты  так, чтобы имело место
так, чтобы имело место 

при любых  Из (28) следует
Из (28) следует

Отсюда

или

Итак, в нашем случае

Аналогично находим:


Во всех этих случаях  означает подынтегральную функцию. Точно таким же способом можно получить формулы для вычисления интегралов вблизи особенностей другого характера.
означает подынтегральную функцию. Точно таким же способом можно получить формулы для вычисления интегралов вблизи особенностей другого характера.
В качестве примера используем формулу (32) для вычисления интеграла

Подынтегральная функция имеет особенность при  как раз такого характера, который учитывается этой формулой. Возьмем
как раз такого характера, который учитывается этой формулой. Возьмем  и представим интеграл (38) в виде
и представим интеграл (38) в виде

Первый интеграл вычислим по формуле (32). Это даст 

Второй интеграл вычислим по формуле Симпсона, взяв  Получим:
Получим:

Таким образом,

Точное значение интеграла таково:

Приемы и методы вычисления несобственных интегралов, приведенные в этом параграфе, не могут исчерпать всего многообразия случаев, которые могут встретиться на практике. Да и невозможно в одной книге, какая объемистая бы она не была, дать рецепты на все случаи жизни. Однако высказанные здесь идеи могут помочь читателю найти подход к решению конкретной задачи, с которой  встретится.
встретится.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
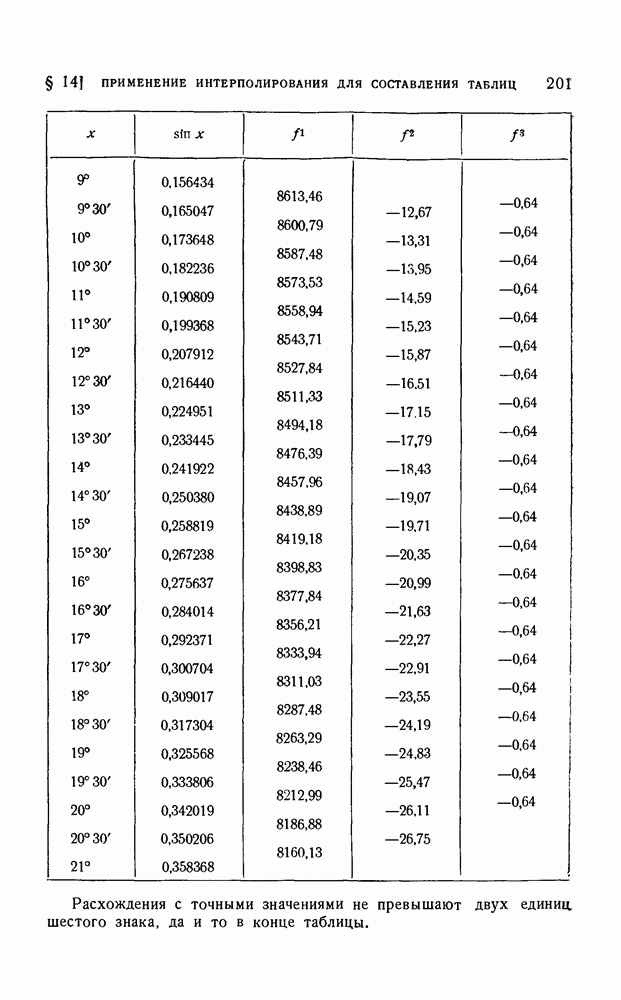
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
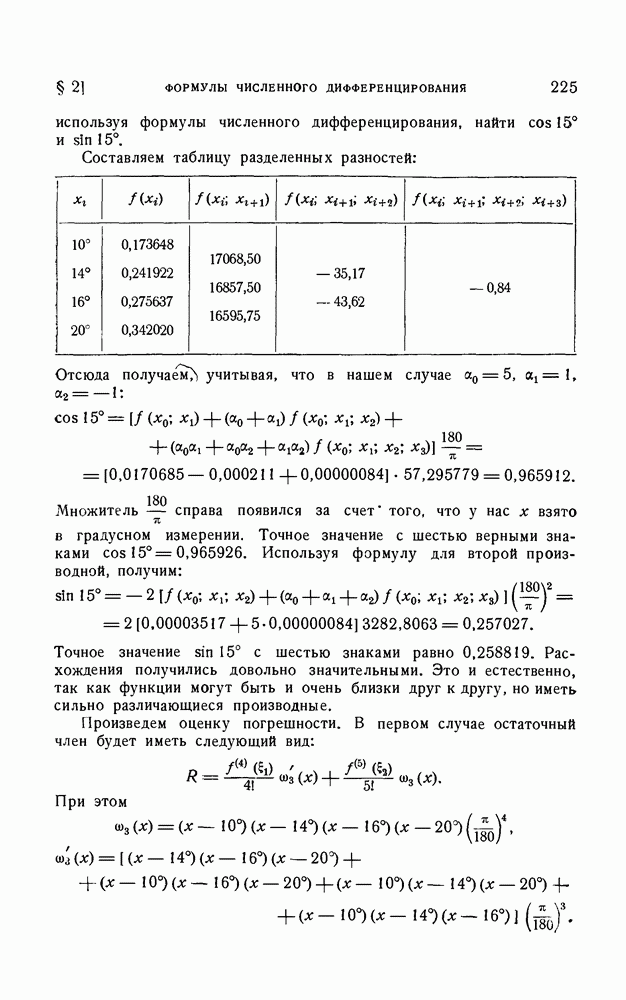
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
- § 3. Задача численного интегрирования
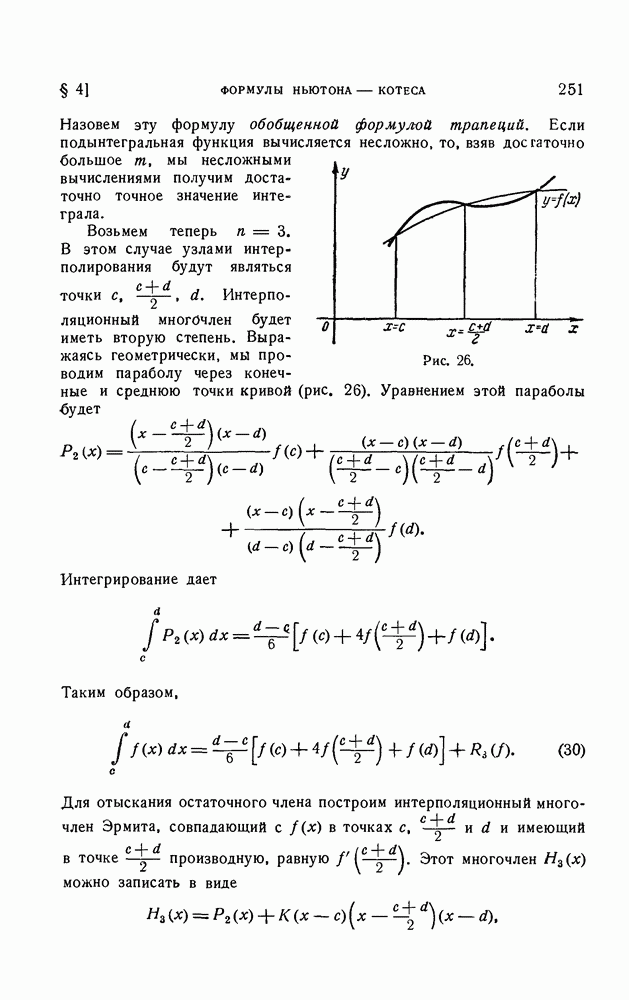
- § 4. Формулы Ньютона — Котеса
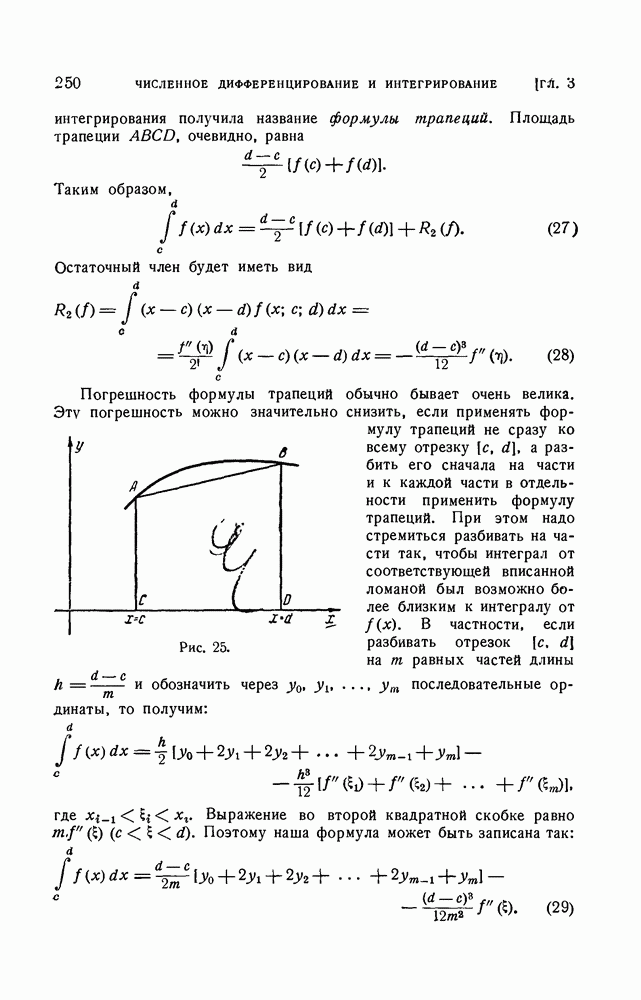
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
- § 13. Схема Рунге вычисления коэффициентов … в случае …