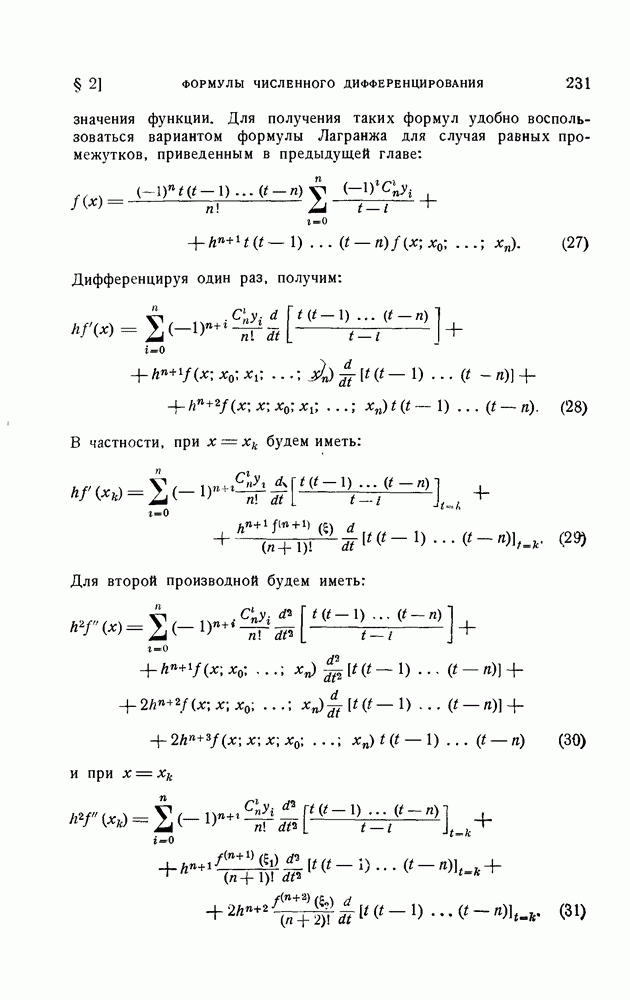| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Полная погрешность
Мы уже говорили о том, что при решении математической задачи мы получаем приближенные результаты в силу различных причин: заданная нам задача заменяется другой, и в силу этого мы получаем ошибку — погрешность метода-, числовые данные, с которыми производятся вычисления, неточны, и в силу этого измененная задача не может быть решена точно и возникает новая ошибка — неустранимая погрешность, и наконец, приближенные исходные данные будут подвергаться не тем операциям, которые требуются для измененной задачи, а псевдооперациям, так как мы вынуждены производить округления, и возникает третья ошибка — погрешность округления. Рассмотрим теперь, как будет складываться полная погрешность из отдельных погрешностей.
Пусть нам требуется решить задачу

Для того чтобы эта задача могла быть численно решена, мы приводим ее к виду

Далее, благодаря неточности исходных данных и процессам округления мы фактически решим задачу

Пусть для определенности, нам нужно по х найти у. Тогда

Первая из скобок справа и даст ошибку метода, вторая скобка определит влияние неустранимой погрешности и погрешности округления. Мы ее назовем вычислительной погрешностью. Таким образом, полная погрешность является суммой погрешности метода и. вычислительной погрешности.
При анализе погрешности метода мы должны учитывать способ замены  на
на  и замены А на А. При анализе вычислительной погрешности мы должны глубже учесть структуру функций
и замены А на А. При анализе вычислительной погрешности мы должны глубже учесть структуру функций  Действительно, как это мы видели в предыдущем параграфе, величина погрешности округления существенно зависит от последовательности операций, производимых над числами. Поэтому мы будем рассматривать вычислительную погрешность лишь в том случае, когда над двумя приближенными числами производится одна операция. Пусть х и у — те числа, над которыми должна быть произведена некоторая операция
Действительно, как это мы видели в предыдущем параграфе, величина погрешности округления существенно зависит от последовательности операций, производимых над числами. Поэтому мы будем рассматривать вычислительную погрешность лишь в том случае, когда над двумя приближенными числами производится одна операция. Пусть х и у — те числа, над которыми должна быть произведена некоторая операция  Фактически мы будем производить операцию не над ними, а над некоторыми приближениями к ним х и у. Кроме того, в действительности вследствие ошибок округления мы произведем не операцию
Фактически мы будем производить операцию не над ними, а над некоторыми приближениями к ним х и у. Кроме того, в действительности вследствие ошибок округления мы произведем не операцию  а другую операцию
а другую операцию  Таким образом, вместо
Таким образом, вместо  мы получим
мы получим  Но
Но

Первая скобка в правой части в этом случае даст неустранимую погрешность одного шага программы, а вторая — погрешность округления. Таким образом, на одном шаге вычислительного процесса вычислительная погрешность будет складываться из неустранимой погрешности, и погрешности округления.
При составлении программы желательно процесс вести так, чтобы одни погрешности компенсировали другие. Правда, часто это связано с большими затратами труда и времени на составление программы. Однако некоторые программы используются очень часто и следует хотя бы один раз произвести для них полный анализ погрешностей.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
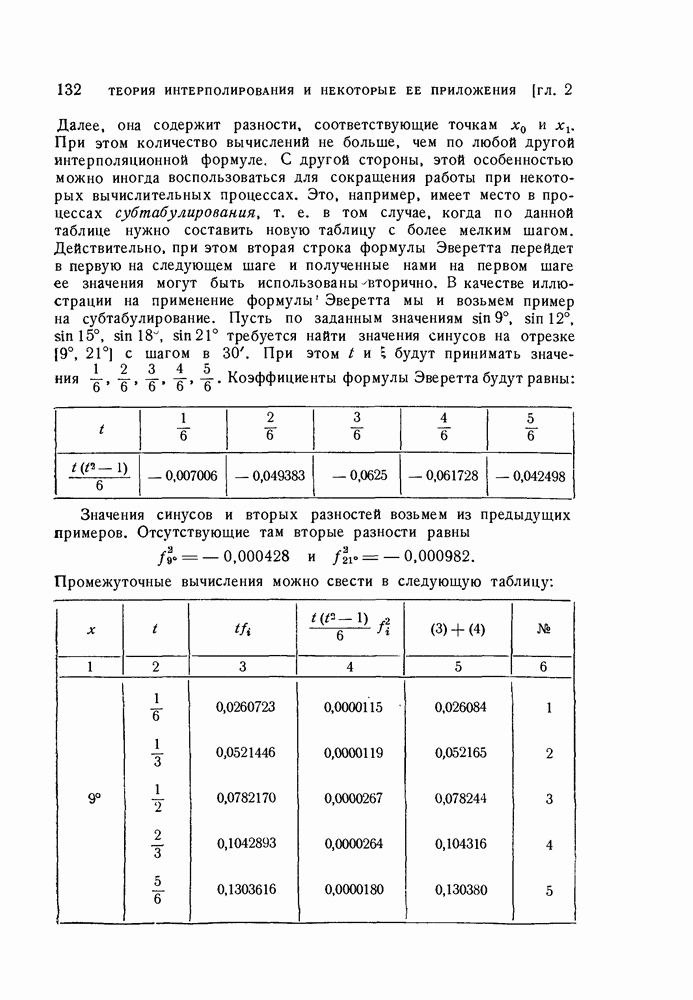
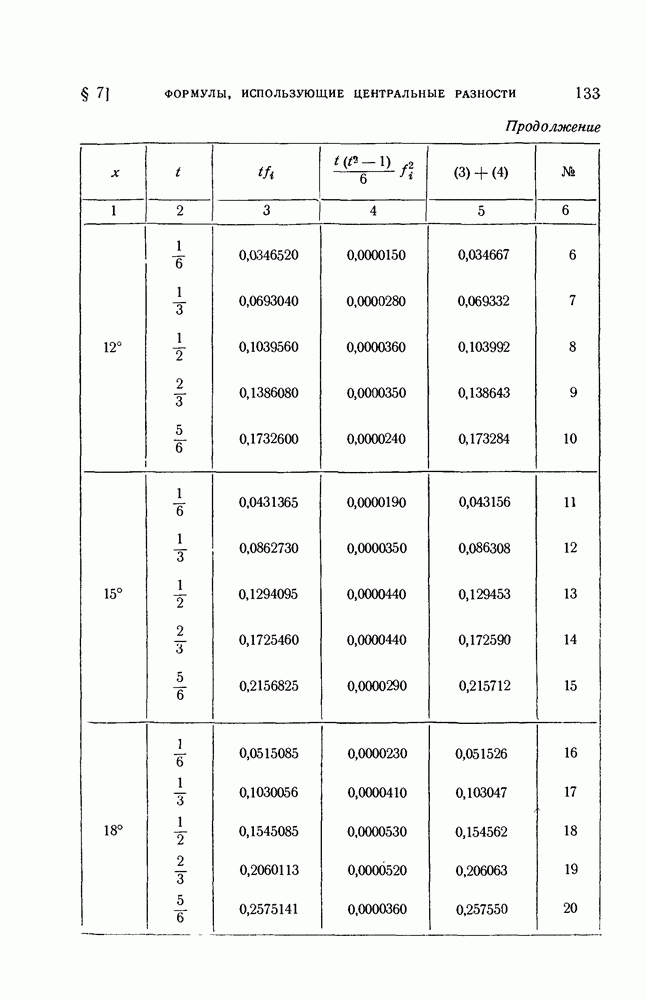
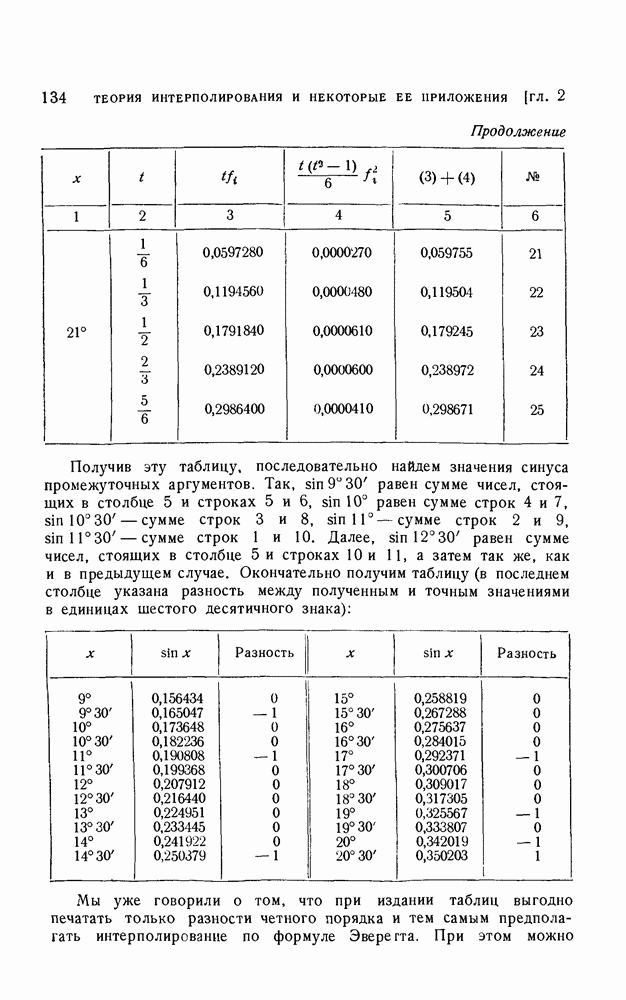
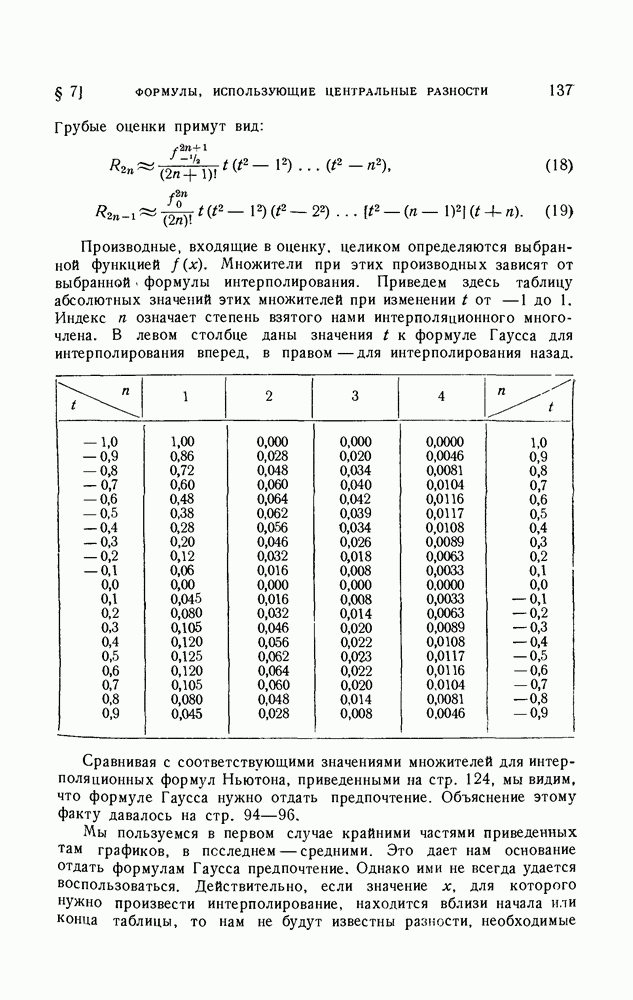
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
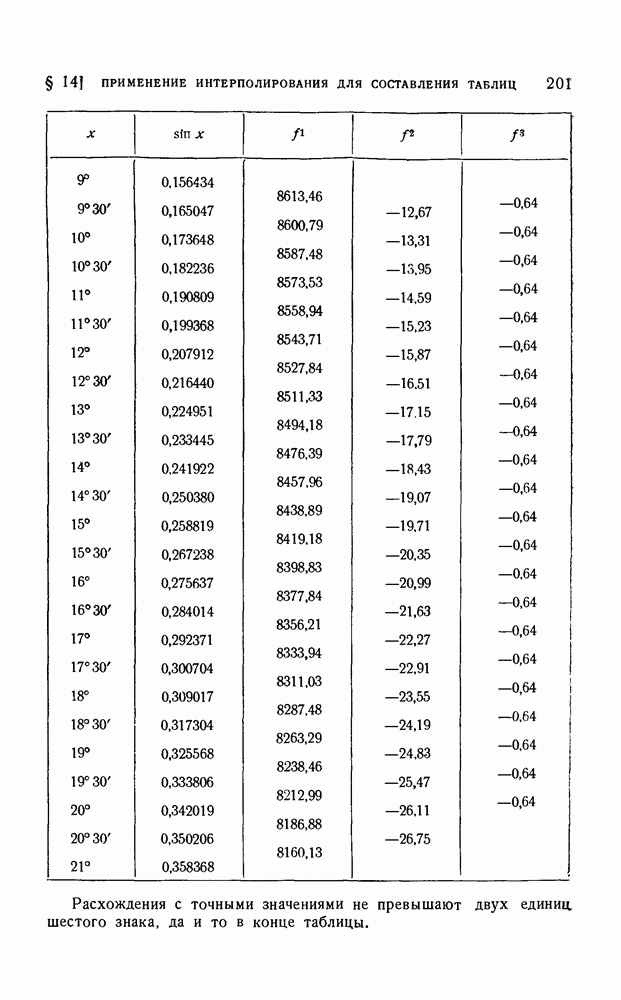
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
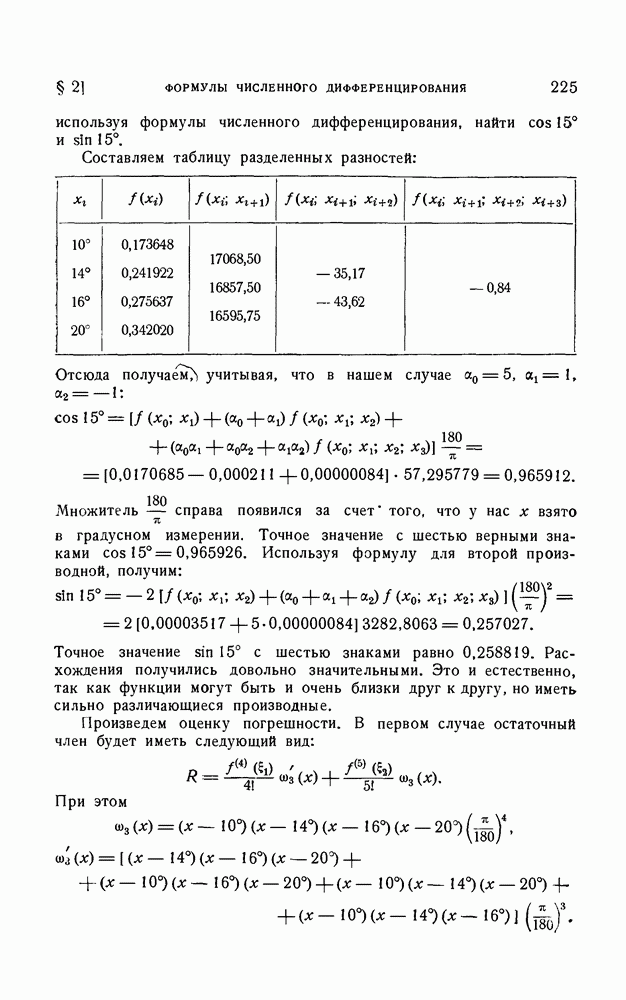
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
- § 3. Задача численного интегрирования
- § 4. Формулы Ньютона — Котеса
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
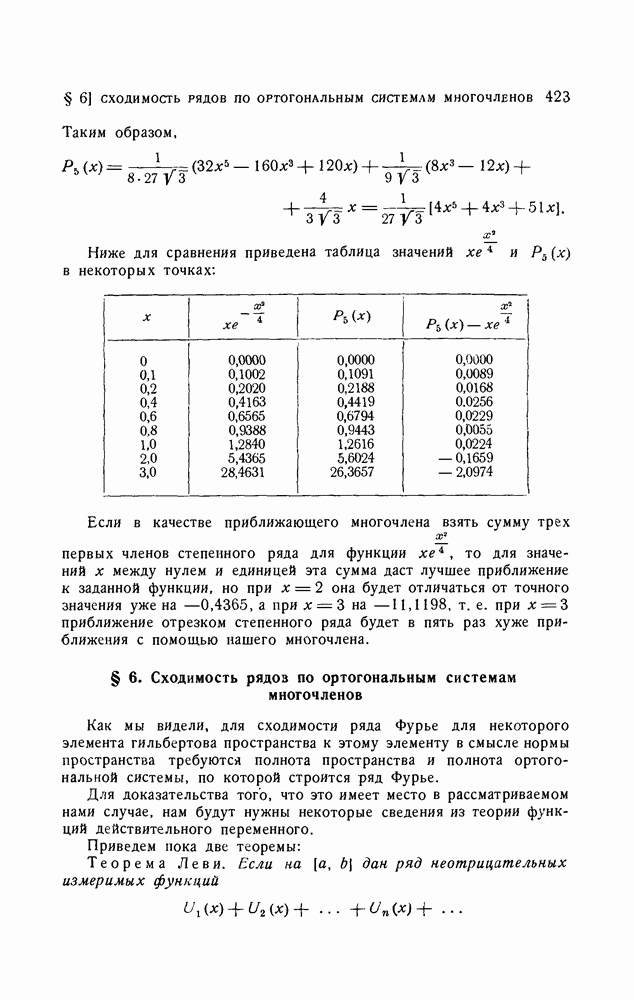
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
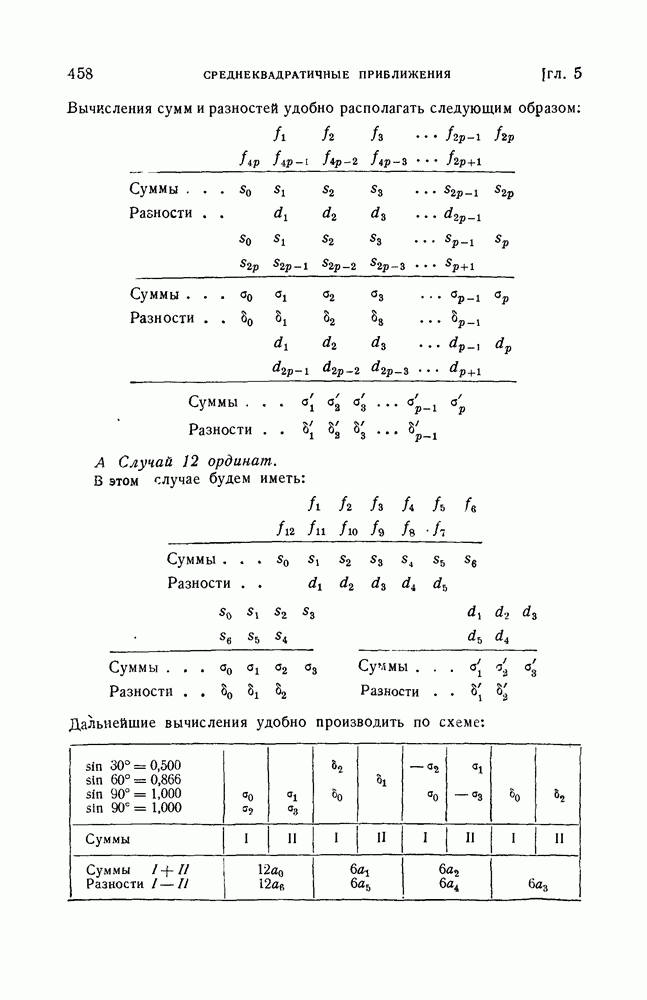
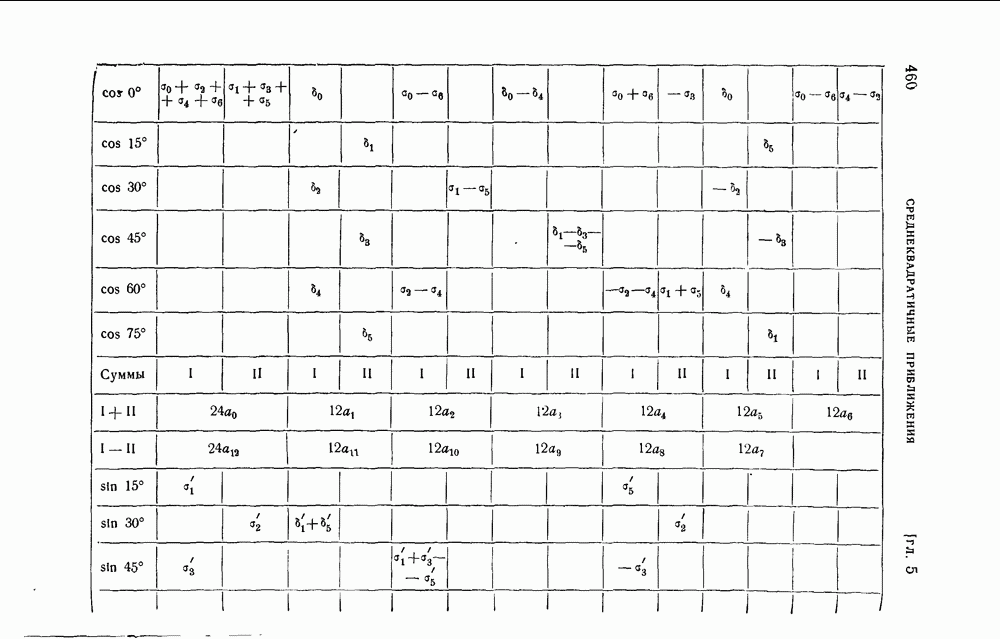
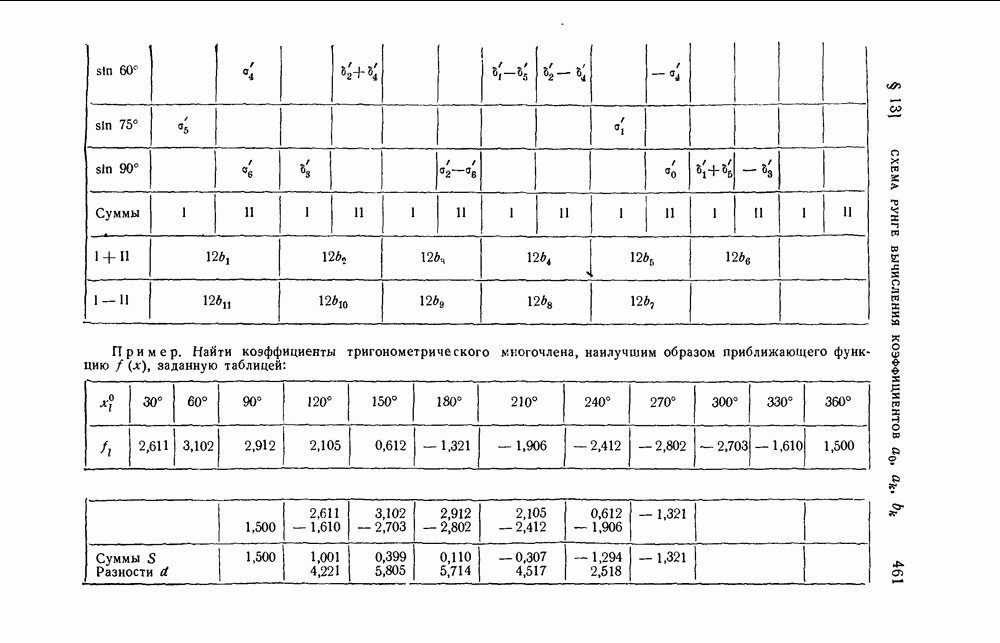
- § 13. Схема Рунге вычисления коэффициентов … в случае …