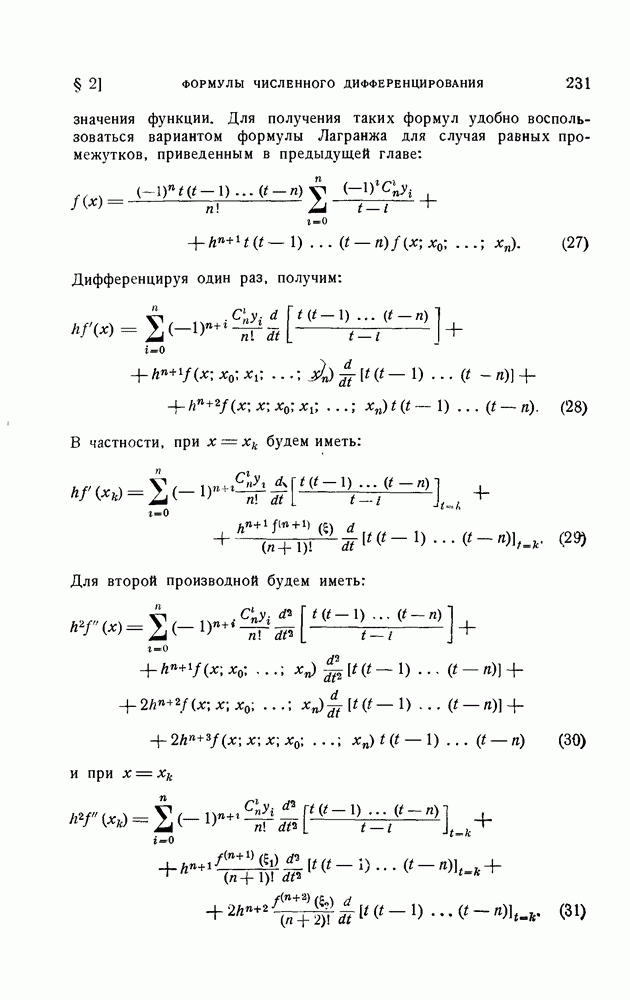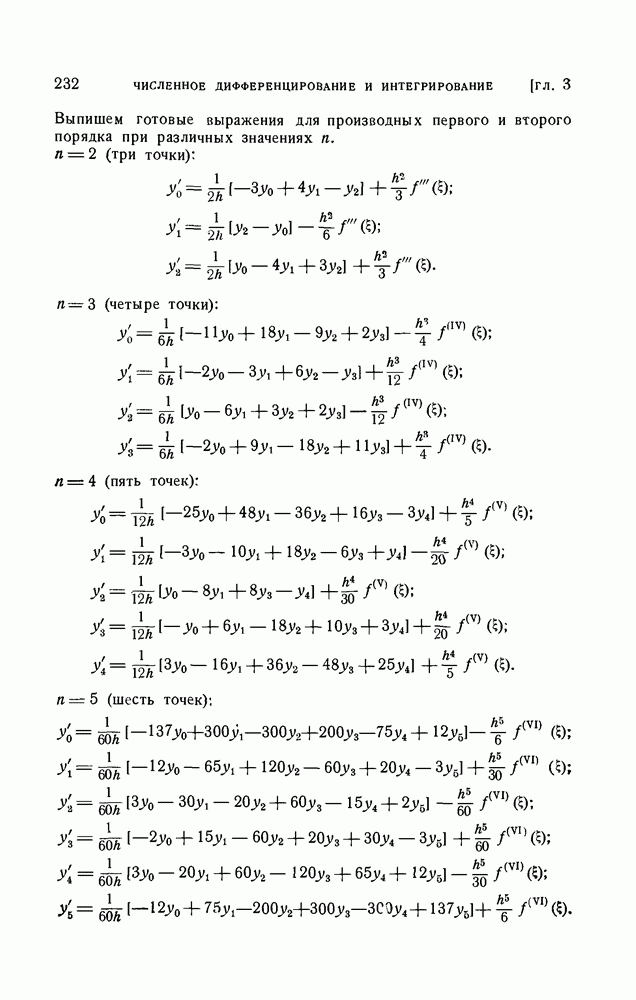| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Погрешности округления
В предыдущем параграфе мы уже говорили о том, как погрешности округления влияют на абсолютную погрешность. В этом параграфе мы коснемся некоторых вопросов, связанных с округлениями, производимыми внутри быстродействующей вычислительной машины. Эти вопросы в настоящее время разработаны еще очень
слабо. Поэтому мы ограничимся лишь самыми предварительными соображениями.
Влияние округлений внутри машины на результат вычислений в различных машинах будет различное. Поэтому мы должны условиться, с какой машиной будем иметь дело. Для упрощения последующих рассуждений возьмем самый простой образец автоматической машины. Будем предполагать, что у нас имеется машина с фиксированной запятой, в которой все числа удовлетворяют условию  Пусть машина имеет запоминающее устройство, в котором могут храниться числа, имеющие
Пусть машина имеет запоминающее устройство, в котором могут храниться числа, имеющие  разрядов. Предположим, что машина может производить операции сложения, вычитания и умножения, результаты которых помещаются в специальном накопителе, имеющем
разрядов. Предположим, что машина может производить операции сложения, вычитания и умножения, результаты которых помещаются в специальном накопителе, имеющем  разрядов. Если в этом накопителе перед началом выполнения очередной операции уже имелось какое-то число, то результат операции либо прибавляется к числу, имеющемуся в накопителе, либо вычитается из него. Пусть наша машина может производить и операцию деления, причем она помещает первые
разрядов. Если в этом накопителе перед началом выполнения очередной операции уже имелось какое-то число, то результат операции либо прибавляется к числу, имеющемуся в накопителе, либо вычитается из него. Пусть наша машина может производить и операцию деления, причем она помещает первые  разрядов величины
разрядов величины  в специальный счетчик. Последнее наше предположение будет состоять в том, что наша машина может округлять числа в накопителе путем прибавления к ним
в специальный счетчик. Последнее наше предположение будет состоять в том, что наша машина может округлять числа в накопителе путем прибавления к ним  и отбрасывания последних
и отбрасывания последних  разрядов.
разрядов.
Для того чтобы можно было произвести на нашей машине действия сложения и вычитания, нужно только потребовать, чтобы

Округлять при этом не придется, и следовательно, ошибок округления не возникает.
Если нам нужно перемножить два каких-то числа, находящихся в каких-то ячейках запоминающего устройства, то модуль результата всегда будет меньше 1, а сам результат не может иметь более  разрядов. Таким образом, и в этом случае округлений не потребуется. Но если этот результат придется выводить в какую-то ячейку запоминающего устройства или выводить из машины, то придется сделать округление. При этом мы уже не получим точного произведения. Результат такой операции будем обозначать
разрядов. Таким образом, и в этом случае округлений не потребуется. Но если этот результат придется выводить в какую-то ячейку запоминающего устройства или выводить из машины, то придется сделать округление. При этом мы уже не получим точного произведения. Результат такой операции будем обозначать  отличая его тем самым от точного произведения
отличая его тем самым от точного произведения  и будем называть псевдопроизведением. Итак,
и будем называть псевдопроизведением. Итак,

где  введено для упрощения последующих записей.
введено для упрощения последующих записей.
Точно так же при делении х на у мы будем получать не точное частное  а псевдочастное
а псевдочастное  причем
причем

Пусть теперь нам нужно образовать сумму произведений. При этом мы можем сначала получить в специальном накопителе точную сумму произведений и лишь затем произвести округление. Такую псевдооперацию будем обозначать  . Таким образом,
. Таким образом,

Интересно отметить, что не все свойства обычных арифметических операций сохранятся для псевдоопераций. Так, например, имеет место с дистрибутивным законом. Выражение  может отличаться от
может отличаться от  на
на  от
от  на
на  так как в первом случае производится одно псевдоумножение, а во втором два. Таким образом,
так как в первом случае производится одно псевдоумножение, а во втором два. Таким образом,

Но числа, разность которых стоит под знаком модуля, могут отличаться друг от друга лишь на величину, кратную  (кратную единице последнего разряда), и следовательно,
(кратную единице последнего разряда), и следовательно,

Мы получили, что разность величин, стоящих под знаком модуля, не может превышать единицы последнего разряда. Что такая разность действительно может возникнуть, подтверждается простым примером. Предположим, что  и нам нужно найти
и нам нужно найти

При

а

Мы как раз получили разницу в единицу последнего знака.
Порядок, в котором производятся операции умножения и деления, также будет иметь значение. Пусть нам требуется найти величину  При этом
При этом

и следовательно,

Аналогично получим.

Отсюда

Проводя те же рассуждения, что и в предыдущем случае, найдем:

И здесь нетрудно привести пример, когда такая разность достигается. Пусть  и нам нужно найти произведение
и нам нужно найти произведение  При этом
При этом

и

В то же время

и

Рассмотрим еще один пример. Пусть нам требуется вычислить выражение

Будем предполагать, что х,  положительны и все операции возможно произвести на нашей машине. При вычислении этого выражения в различной последовательности получим разные результаты. Вычислим сначала у X и затем найдем
положительны и все операции возможно произвести на нашей машине. При вычислении этого выражения в различной последовательности получим разные результаты. Вычислим сначала у X и затем найдем  При этом
При этом

Второй член правой части оценивается без труда:

Оценим первый член, предполагая, что  мало, т. е. близко к
мало, т. е. близко к  Для того чтобы было возможно произвести деление, придется потребовать, чтобы х было близко к
Для того чтобы было возможно произвести деление, придется потребовать, чтобы х было близко к  Так как
Так как

то  может быть близким к
может быть близким к  или
или  В первом случае оцениваемый член будет близок к
В первом случае оцениваемый член будет близок к

во втором — к

Точное частное при  будет 2/6 и погрешность составляет около 25%.
будет 2/6 и погрешность составляет около 25%.
Так как для некоторых значений х, у, z мы получили неудовлетворительный результат, то возьмем другую последовательность операций. Разделим сначала х на у и результат поделим на  Оценим
Оценим

Опять следует рассмотреть только первый член. Результат будет зависеть от того, что больше: у или z. Лучший результат получится при  Это мы будем предполагать. Так как
Это мы будем предполагать. Так как

(иначе деление невозможно было бы выполнить на машине), то

Можно считать, что  следовательно,
следовательно,

Отсюда

Этот результат лучше, чем предыдущий. Если  немало, то первый способ вычислений может оказаться лучше второго.
немало, то первый способ вычислений может оказаться лучше второго.
Приведенные здесь рассуждения относятся к конкретной машине, данные о которой приведены в начале параграфа, и являются примерными. До тех пор, пока не выработается стандарт в конструкции автоматических машин, необходимо производить аналогичный анализ для каждой машины в отдельности. Чтобы при этом не затрачивать чересчур много времени при разработке каждой частной программы, целесообразно провести его заранее для типичных вычислительных процессов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
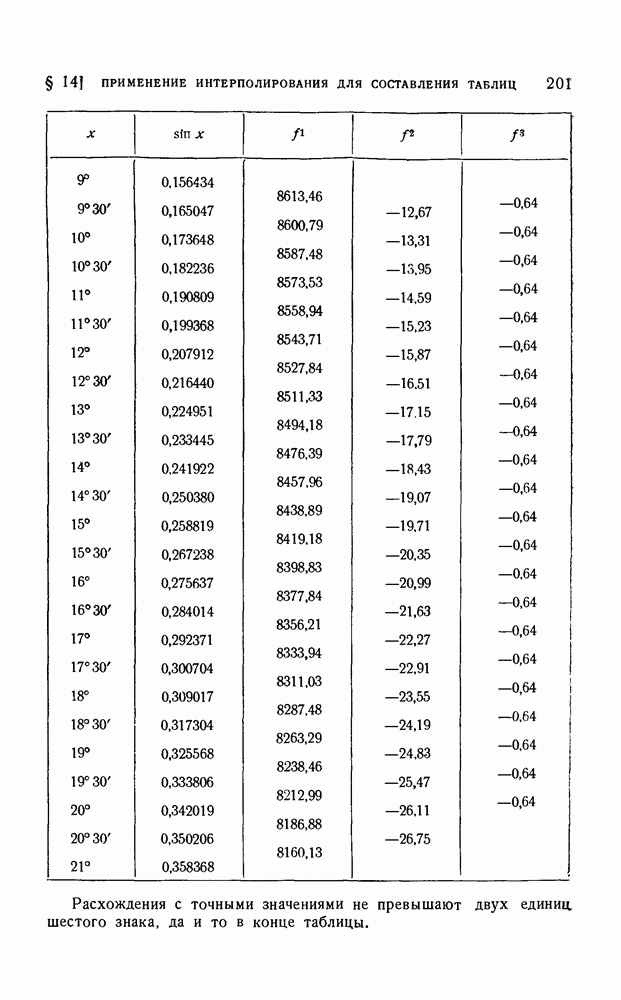
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
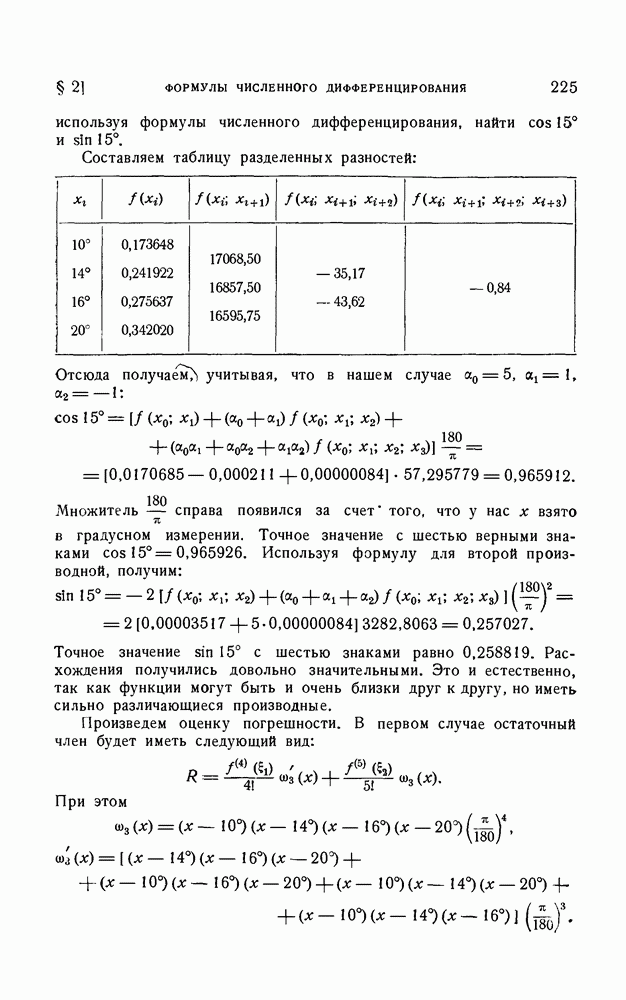
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
- § 3. Задача численного интегрирования
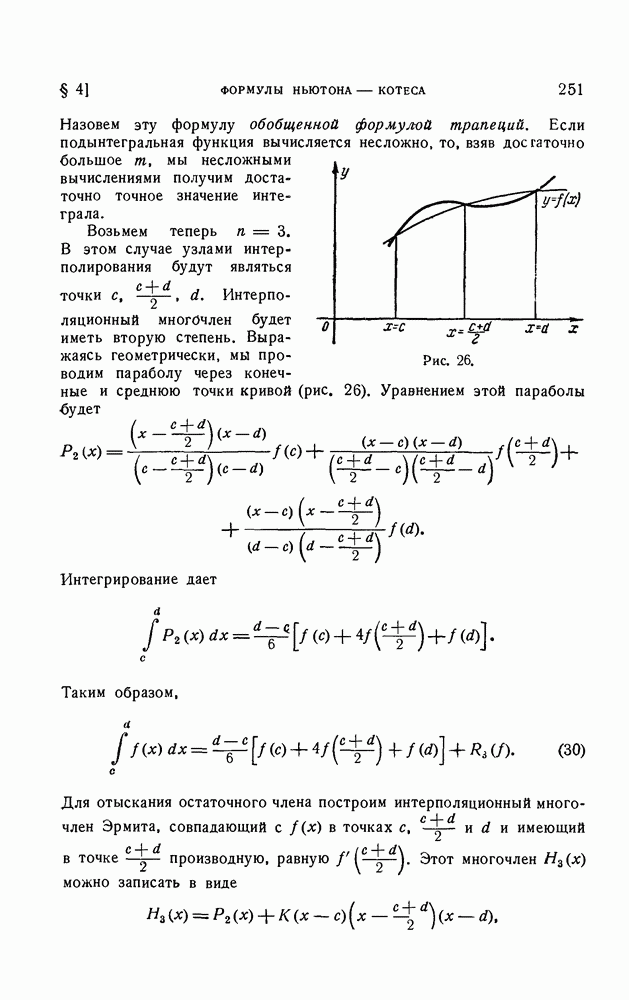
- § 4. Формулы Ньютона — Котеса
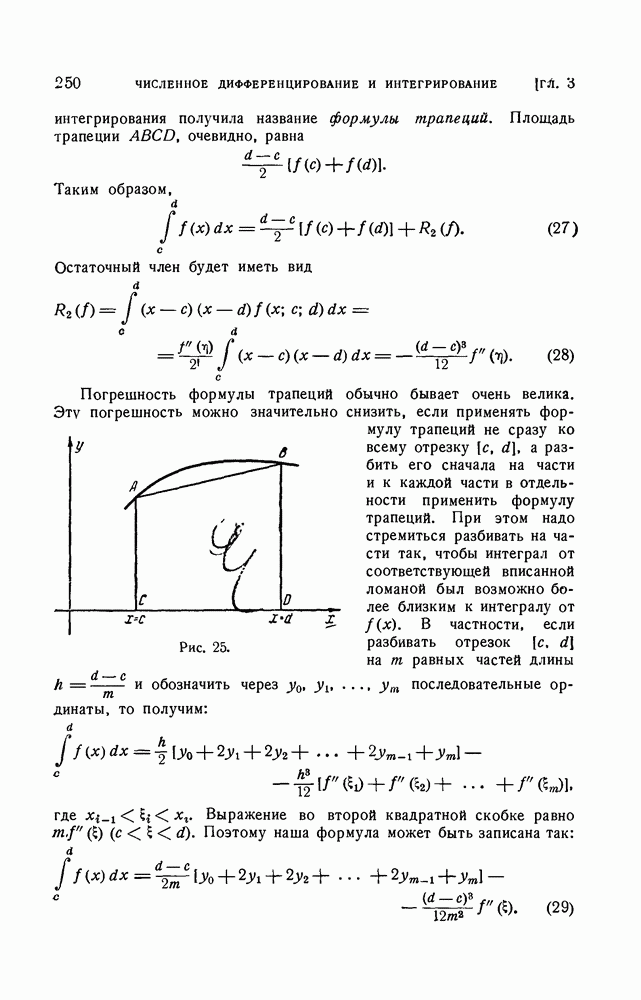
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
- § 13. Схема Рунге вычисления коэффициентов … в случае …