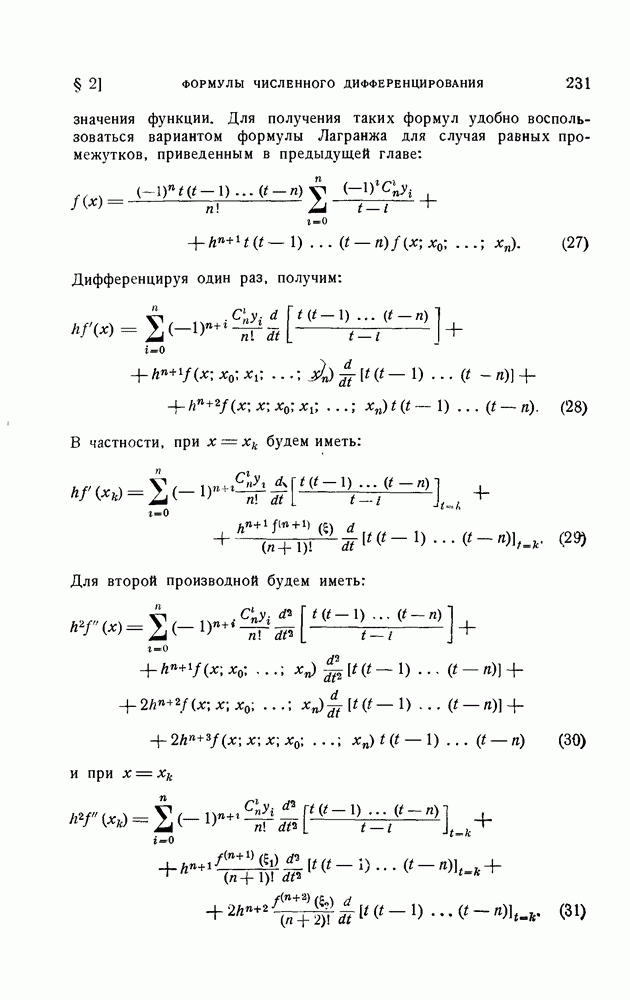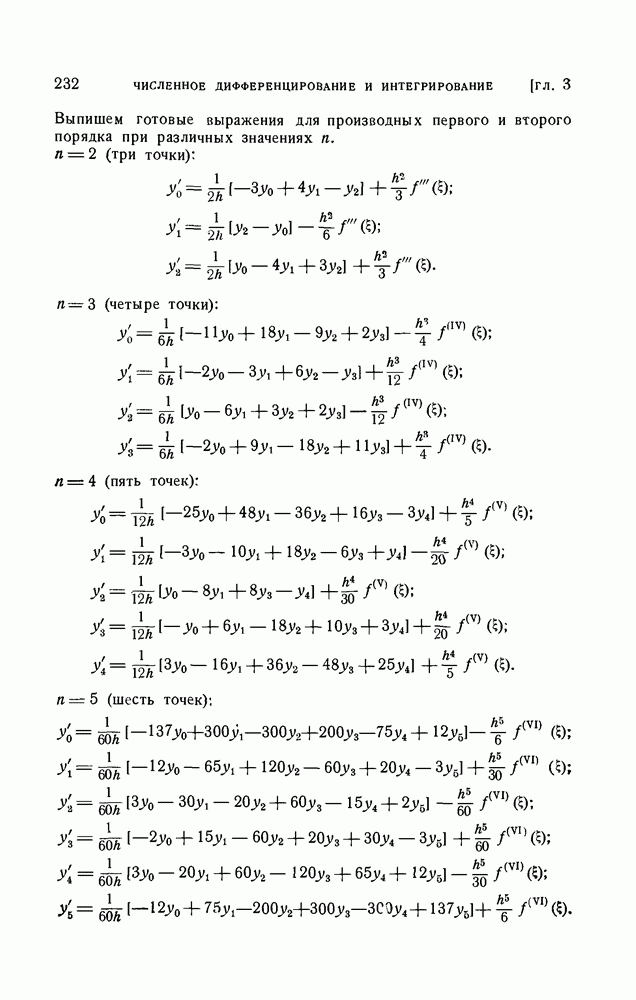| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Метод вычислительной математики
Круг задач, с которыми приходится сталкиваться в вычислительной математике, очень широк. Разнообразны и методы, применяемые для решения этих задач. Однако можно заметить одну общую идею этих методов. Эта идея отчетливее всего выражается в терминах функционального анализа. Поэтому мы введем предварительно некоторые важнейшие понятия функционального анализа.
1. Функциональные метрические пространства.
Основным предметом исследования в классическом математическом анализе является числовая функция. С появлением понятия функции одной и нескольких переменных, функции точки в евклидовом пространстве начался современный этап развития математики. Начиная с работ Ньютона и Лейбница и до конца XIX века подавляющее большинство математических исследований так или иначе было связано с этим понятием. Главным предметом изучения были числовые функции и их системы, заданные в  -мерной области, т. е. на некотором множестве
-мерной области, т. е. на некотором множестве  -мерного евклидова пространства.
-мерного евклидова пространства.
Двадцатый век внес много нового в эту картину. Особо важную роль начинает играть понятие о функциональном множестве, о функциональных I ространствах и о функциональных операторах, т. е. о функциях, аргументами которых также являются элементы функциональных пространств. Вместо евклидовых пространств рассматриваются абстрактные пространства, элементы которых могут иметь самую различную природу. Так, например, вводится понятие метрического пространства  как абстрактного множества, для любых двух элементов х и у которого определено понятие расстояния
как абстрактного множества, для любых двух элементов х и у которого определено понятие расстояния  удовлетворяющее следующим условиям:
удовлетворяющее следующим условиям:
1.  , причем
, причем  тогда и только тогда, когда х совпадает с у.
тогда и только тогда, когда х совпадает с у.

3.  для любых трех элементов х, у, z, принадлежащих
для любых трех элементов х, у, z, принадлежащих  (аксиома треугольника).
(аксиома треугольника).
Евклидовы пространства с обычным определением расстояния в  удовлетворяют всем Этим условиям. Но могут быть и другие метрические пространства. Так, рассмотрим множество всевозможных непрерывных функций, заданных на отрезке
удовлетворяют всем Этим условиям. Но могут быть и другие метрические пространства. Так, рассмотрим множество всевозможных непрерывных функций, заданных на отрезке  Для любых двух таких функций
Для любых двух таких функций  и
и  определим расстояние
определим расстояние  равенством
равенством

Нетрудно проверить, что так определенное расстояние удовлетворяет всем трем поставленным выше условиям. Таким образом, мы получили функциональное метрическое пространство, которое обычно называют пространством С.
Другим важным классом функциональных пространств являются пространства  (Здесь
(Здесь  действительное число Измеримая, на
действительное число Измеримая, на  функция
функция  принадлежит
принадлежит  если суммируема
если суммируема 
Две функции  принадлежащие
принадлежащие  считаются эквивалентными, если они отличаются друг от друга лишь на множестве меры нуль. Расстояние р(х, у) в
считаются эквивалентными, если они отличаются друг от друга лишь на множестве меры нуль. Расстояние р(х, у) в  определяется следующим образом:
определяется следующим образом:

Так определенное расстояние удовлетворяет трем поставленным выше условиям.
Можно было бы значительно расширить примеры различных функциональных пространств, но мы на этом пока ограничимся.

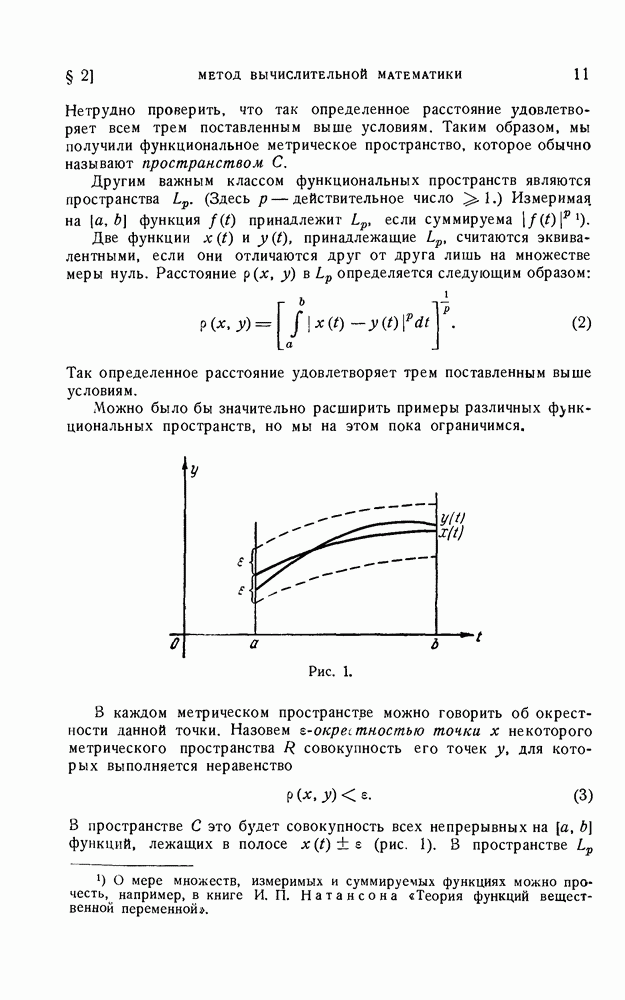
Рис. 1.
В каждом метрическом пространстве можно говорить об окрестности данной точки. Назовем  тностью точки х некоторого метрического пространства
тностью точки х некоторого метрического пространства  совокупность его точек у, для которых выполняется неравенство
совокупность его точек у, для которых выполняется неравенство

В пространстве С это будет совокупность всех непрерывных на  функций, лежащих в полосе
функций, лежащих в полосе  (рис. 1). В пространстве
(рис. 1). В пространстве 
это будет совокупность всех функций, принадлежащих  для которых
для которых

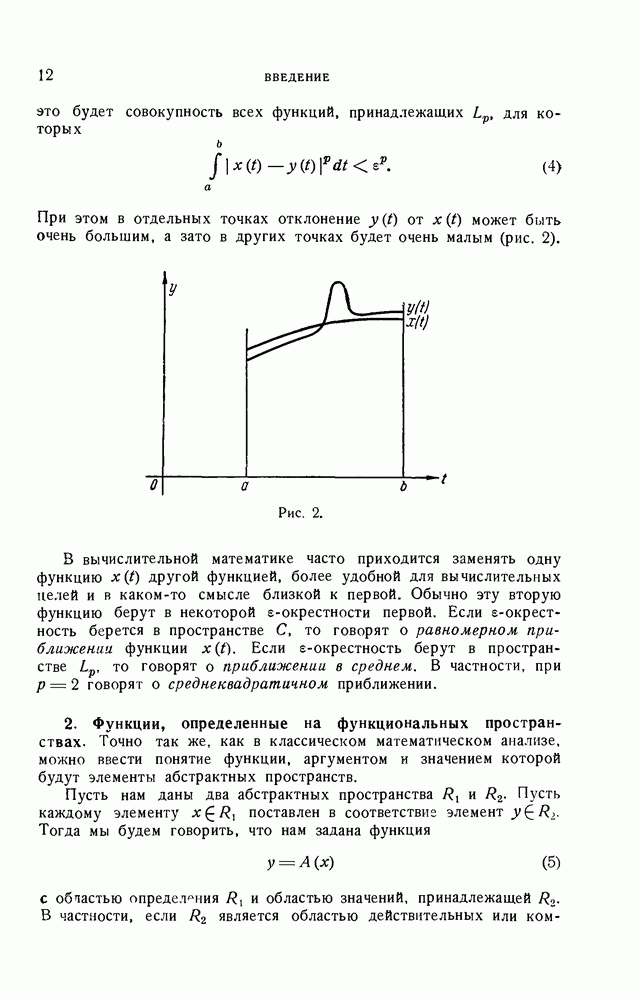
При этом в отдельных точках отклонение  от
от  может быть очень большим, а зато в других точках будет очень малым (рис. 2).
может быть очень большим, а зато в других точках будет очень малым (рис. 2).

Рис. 2.
В вычислительной математике часто приходится заменять одну функцию  другой функцией, более удобной для вычислительных целей и в каком-то смысле близкой к первой. Обычно эту вторую функцию берут в некоторой
другой функцией, более удобной для вычислительных целей и в каком-то смысле близкой к первой. Обычно эту вторую функцию берут в некоторой  -окрестности первой. Если
-окрестности первой. Если  -окрестность берется в пространстве С, то говорят о равномерном приближении функции
-окрестность берется в пространстве С, то говорят о равномерном приближении функции  Если
Если  -окрестность берут в пространстве
-окрестность берут в пространстве  то говорят о приближении в среднем. В частности, при
то говорят о приближении в среднем. В частности, при  говорят о среднеквадратичном приближении.
говорят о среднеквадратичном приближении.
2. Функции, определенные на функциональных пространствах.
Точно так же, как в классическом математическом анализе, можно ввести понятие функции, аргументом и значением которой будут элементы абстрактных пространств.
Пусть нам даны два абстрактных пространства  Пусть каждому элементу
Пусть каждому элементу  поставлен в соответствие элемент
поставлен в соответствие элемент  Тогда мы будем говорить, что нам задана функция
Тогда мы будем говорить, что нам задана функция

с обпастью определения  и областью значений, принадлежащей
и областью значений, принадлежащей  В частности, если
В частности, если  является областью действительных или
является областью действительных или
комплексных чисел, то  называется функционалом. Простейшим примером функционала в пространстве С будет являться
называется функционалом. Простейшим примером функционала в пространстве С будет являться

Пространство  может совпадать с пространством
может совпадать с пространством  и тогда будем называть
и тогда будем называть  оператором. Область математики, изучающая свойства функциональных пространств и заданных на них функций, и носит название функционального анализа.
оператором. Область математики, изучающая свойства функциональных пространств и заданных на них функций, и носит название функционального анализа.
3. Метод вычислительной математики.
Теперь можно охарактеризовать метод вычислительной математики.
В вычислительной математике приходится сталкиваться с самыми различными задачами. Но большинство этих задач может быть записано в виде

где х и у принадлежат заданным пространствам  некоторая заданная функция. Задача состоит либо в отыскании у по заданному х, либо в отыскании х по заданному у. В нашем курсе мы будем иметь дело только с такими задачами. Далеко не всегда с помощью средств современной математики удается точно решить эти задачи, применяя конечное число шагов. В этих случаях и прибегают к вычислительной математике. Иногда задача и может быть решена точно, но методы классической математики дают ответ после громоздких и трудоемких вычислений. Поэтому и задачи вычислительной математики входит также разработка приемов и методов наиболее рационального решения конкретных задач. Как это делается в различных случаях, будет видно из дальнейшего курса. Сейчас же мы выскажем некоторые общие сообщения.
некоторая заданная функция. Задача состоит либо в отыскании у по заданному х, либо в отыскании х по заданному у. В нашем курсе мы будем иметь дело только с такими задачами. Далеко не всегда с помощью средств современной математики удается точно решить эти задачи, применяя конечное число шагов. В этих случаях и прибегают к вычислительной математике. Иногда задача и может быть решена точно, но методы классической математики дают ответ после громоздких и трудоемких вычислений. Поэтому и задачи вычислительной математики входит также разработка приемов и методов наиболее рационального решения конкретных задач. Как это делается в различных случаях, будет видно из дальнейшего курса. Сейчас же мы выскажем некоторые общие сообщения.
Основным методом, при помощи которого в вычислительной математике решают поставленные выше задачи, является замена пространств и  и функции А некоторыми другими пространствами и
и функции А некоторыми другими пространствами и  и функцией А, более удобными для вычислительных целей. Иногда бывает достаточно произвести замену пространств
и функцией А, более удобными для вычислительных целей. Иногда бывает достаточно произвести замену пространств  или даже одного из них. Иногда достаточно заменить только функцию А. Замена должна быть сделана так, чтобы решение новой задачи
или даже одного из них. Иногда достаточно заменить только функцию А. Замена должна быть сделана так, чтобы решение новой задачи 

 было в каком-то смысле близким к точному решению исходной задачи (7) и его возможно было бы практически отыскать с сравнительно небольшими трудностями.
было в каком-то смысле близким к точному решению исходной задачи (7) и его возможно было бы практически отыскать с сравнительно небольшими трудностями.
Например, пусть необходимо вычислить интеграл

где  непрерывная функция, причем неопределенный интеграл не берется в элементарных функциях. Чтобы получить достаточно точное приближенное значение интеграла, можно идти двумя путями.
непрерывная функция, причем неопределенный интеграл не берется в элементарных функциях. Чтобы получить достаточно точное приближенное значение интеграла, можно идти двумя путями.
1. Заменим функцию  алгебраическим многочленом
алгебраическим многочленом  равномерно приближающим функцию
равномерно приближающим функцию  на отрезке
на отрезке  с необходимой степенью точности. Как будет показано в главе 4, это всегда сделать можно. Вместо интеграла
с необходимой степенью точности. Как будет показано в главе 4, это всегда сделать можно. Вместо интеграла  будем находить интеграл
будем находить интеграл  вычисление которого не составляет труда. Здесь мы, не меняя функционала
вычисление которого не составляет труда. Здесь мы, не меняя функционала  заменяем пространство С, которому принадлежит
заменяем пространство С, которому принадлежит  пространством многочленов и вместо функции
пространством многочленов и вместо функции  берем многочлен
берем многочлен  из некоторой ее
из некоторой ее  -окрестности.
-окрестности.
2. Из определения интеграла  следует, что всегда можно построить интегральную сумму
следует, что всегда можно построить интегральную сумму  которая будет достаточно близка к значению интеграла. Следовательно, вместо вычисления интеграла
которая будет достаточно близка к значению интеграла. Следовательно, вместо вычисления интеграла  можно решать другую задачу — задачу вычисления конечной суммы
можно решать другую задачу — задачу вычисления конечной суммы

Здесь мы уже заменяем функцию  новой функцией
новой функцией 
Для успешного применения указанного выше метода вычислительной математики необходимо в первую очередь иметь рациональные способы замены пространства  другим пространством
другим пространством 
Часто для этой цели в пространстве  отыскивают конечное множество элементов
отыскивают конечное множество элементов

которые бы, с одной стороны, достаточно хорошо аппроксимировали каждый элемент пространства  а с другой стороны, были бы достаточно удобны для вычислительной работы. При этом в качестве
а с другой стороны, были бы достаточно удобны для вычислительной работы. При этом в качестве  берут пространство, состоящее из этого конечного числа элементов, и элементу
берут пространство, состоящее из этого конечного числа элементов, и элементу  ставят в соответствие ближайший элемент срили один из ближайших, если таких элементов несколько. В дальнейшем мы увидим много примеров того, как это осуществляется.
ставят в соответствие ближайший элемент срили один из ближайших, если таких элементов несколько. В дальнейшем мы увидим много примеров того, как это осуществляется.
Такой прием не всегда применим. Для того чтобы им можно было воспользоваться, необходимо наложить дополнительные ограничения на метрическое пространство  Не вдаваясь в подробности, укажем на те свойства, которыми в этом случае должно обладать пространство
Не вдаваясь в подробности, укажем на те свойства, которыми в этом случае должно обладать пространство  Для любого
Для любого  должны существовать элементы
должны существовать элементы  такие, что какой бы элемент
такие, что какой бы элемент  мы ни взяли, найдется такой элемент
мы ни взяли, найдется такой элемент  для которого
для которого

В этом случае элементы  называют
называют  -сетью пространства
-сетью пространства  Из наличия
Из наличия  -сети при любом
-сети при любом  будет вытекать компактность пространства
будет вытекать компактность пространства  в себе. Это означает, что из любой последовательности элементов
в себе. Это означает, что из любой последовательности элементов  принадлежащих
принадлежащих  можно выделить фундаментальную подпоследовательность, т. е. такую подпоследовательность
можно выделить фундаментальную подпоследовательность, т. е. такую подпоследовательность  Для любого
Для любого  найдется целое положительное
найдется целое положительное  что при
что при  имеет место неравенство
имеет место неравенство

Из наличия  -сети при любом
-сети при любом  следует также сепарабельность пространства
следует также сепарабельность пространства  что означает существование счетного всюду плотного в
что означает существование счетного всюду плотного в  множества элементов, т. е. такого множества, что в любой окрестности элемента
множества элементов, т. е. такого множества, что в любой окрестности элемента  найдется хотя бы один элемент этого множества.
найдется хотя бы один элемент этого множества.
Однако из предыдущих рассуждений нельзя делать вывода, что конечные аппроксимирующие группы можно использовать только Для компактных в себе пространств. Во-первых, нужно заметить, что современный функциональный анализ не связан каким-либо одним способом метризуемости. Наоборот, одна и та же функция может служить элементом самых различных пространств. Функциональные пространства могут целиком вкладываться в другие функциональные пространства с сохранением или потерей понятия близости, расстояния и других. Иногда возможно рассматривать пространство  как предельное множество его подпространств
как предельное множество его подпространств  обладающих нужными нам свойствами.
обладающих нужными нам свойствами.
Можно было бы многое говорить относительно различных применений функционального анализа в вычислительной математике. Однако удобнее это сделать при изложении конкретного материала курса.
Резюмируя сказанное выше, мы отметим, что в настоящее время перед вычислительной математикой стоят следующие основные задачи:
1. Приближение множеств в функциональных пространствах.
2. Приближение функций, заданных на функциональных пространствах.
3. Разработка рациональных алгоритмов и методов решения задач в условиях применения современных вычислительных машин.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
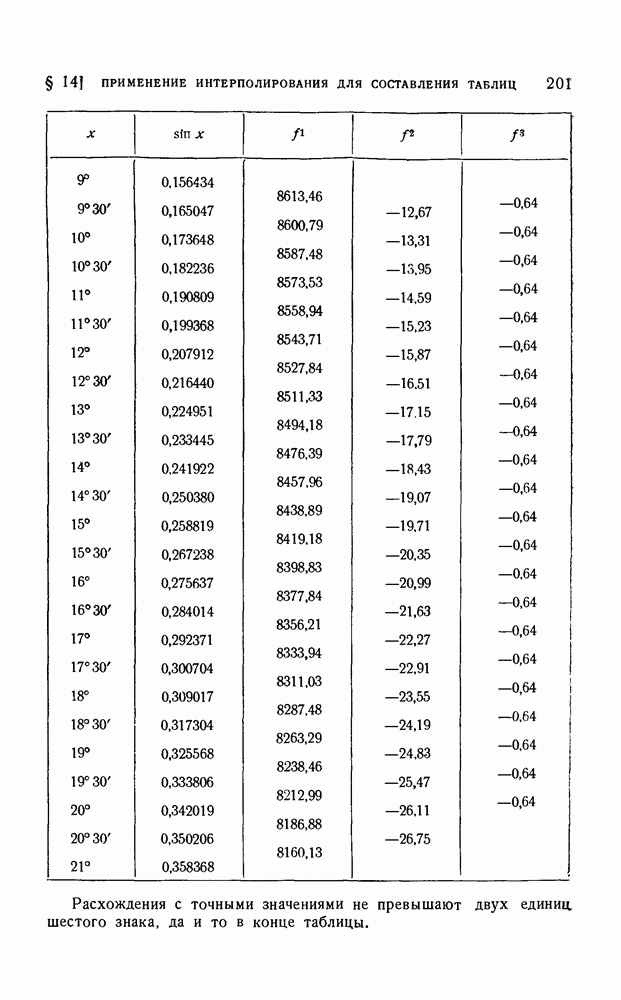
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
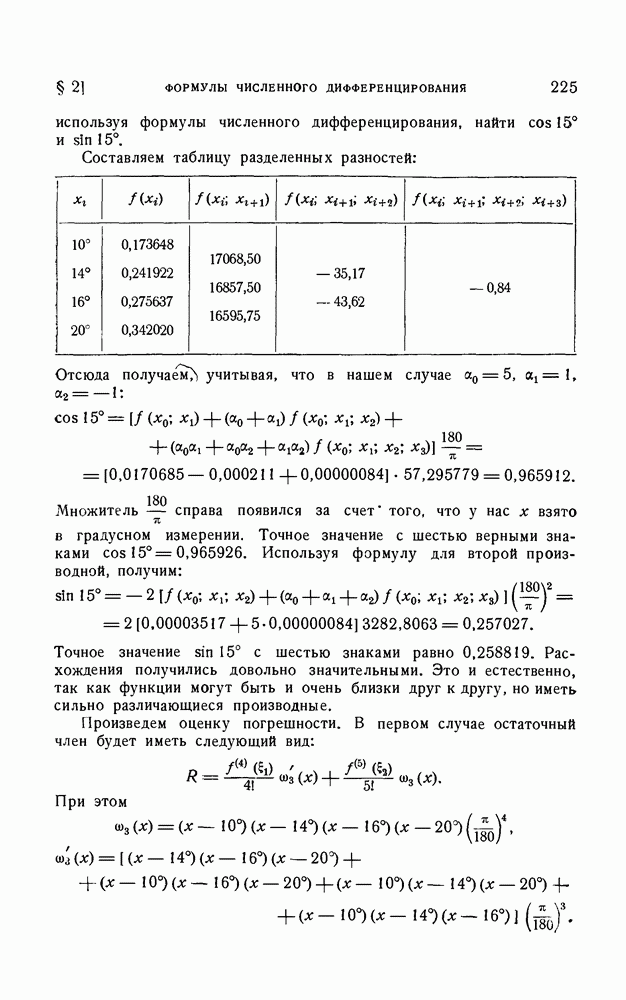
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
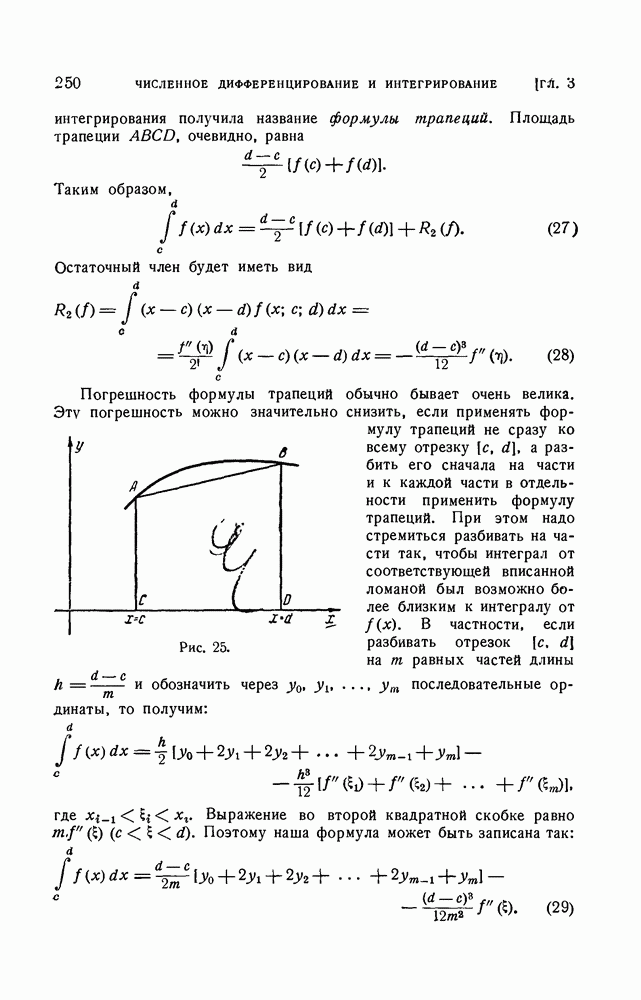
- § 3. Задача численного интегрирования
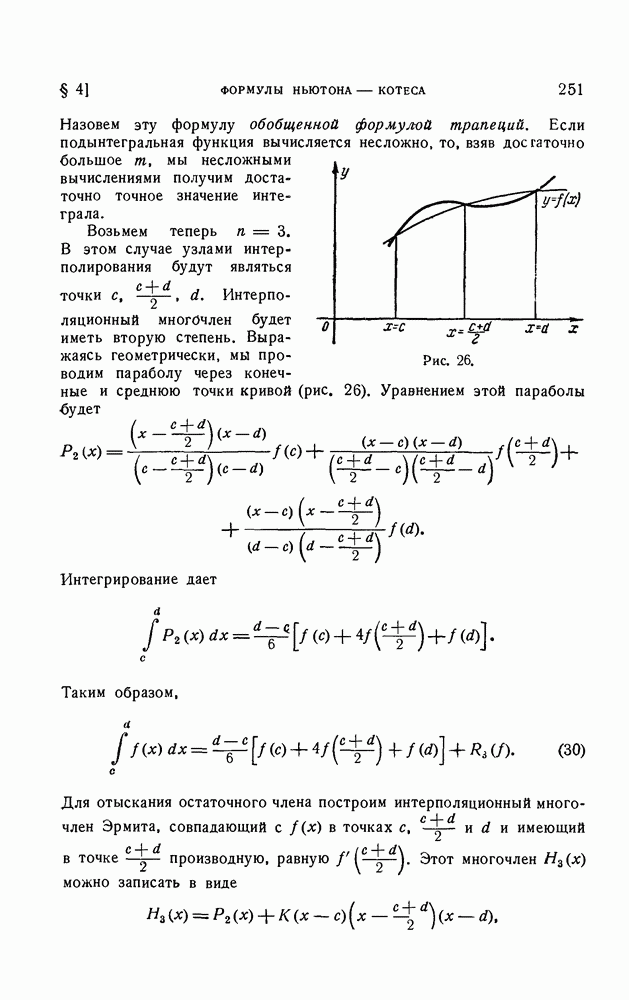
- § 4. Формулы Ньютона — Котеса
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
- § 13. Схема Рунге вычисления коэффициентов … в случае …