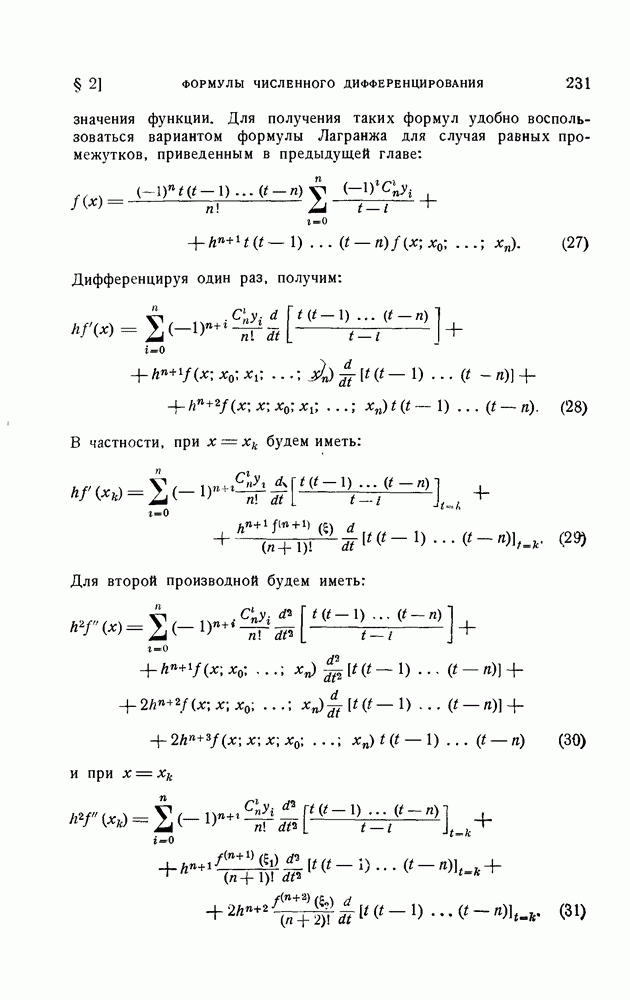| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
Пусть две переменные х и у связаны известной функциональной зависимостью

содержащей  параметров
параметров  Пусть при
Пусть при  известны с некоторой точностью значения
известны с некоторой точностью значения  Требуется найти значения параметров
Требуется найти значения параметров 
С такой задачей приходится встречаться при построении эмпирических формул, выражающих в аналитической форме закономерность изменения одной величины в зависимости от изменения другой, если в результате наблюдений получена таблица значений величины у при соответствующих значениях х.
Вид функциональной зависимости  и число параметров
и число параметров  в некоторых случаях известны из каких-либо дополнительных соображений, в других случаях вид функциональной зависимости усматривается из графика, построенного по наблюденным значениям
в некоторых случаях известны из каких-либо дополнительных соображений, в других случаях вид функциональной зависимости усматривается из графика, построенного по наблюденным значениям  а число параметров и их значения подбираются так, чтобы эмпирическая формула наилучшим образом отображала результаты наблюдений и была достаточно проста. В некоторых случаях, когда не удается построить достаточно простую эмпирическую формулу, выражающую достаточно просто зависимость у от х на всем диапазоне изменения аргумента х, прибегают к построению ряда эмпирических формул, выражающих эту зависимость в опреде генных более узких пределах изменения х.
а число параметров и их значения подбираются так, чтобы эмпирическая формула наилучшим образом отображала результаты наблюдений и была достаточно проста. В некоторых случаях, когда не удается построить достаточно простую эмпирическую формулу, выражающую достаточно просто зависимость у от х на всем диапазоне изменения аргумента х, прибегают к построению ряда эмпирических формул, выражающих эту зависимость в опреде генных более узких пределах изменения х.
Вернемся к поставленной задаче. Если бы значения  при
при  были известны точно, то задача принципиально решалась бы просто. Нужно было бы из системы
были известны точно, то задача принципиально решалась бы просто. Нужно было бы из системы

взять  уравнений и найти из них значения параметров
уравнений и найти из них значения параметров  (предполагается, что эта система имеет единственное решение). При этих значениях параметров были бы в точности удовлетворены все остальные уравнения системы. Если же
(предполагается, что эта система имеет единственное решение). При этих значениях параметров были бы в точности удовлетворены все остальные уравнения системы. Если же  как и бывает практически, являются приближенными значениями, то, найдя из каких-либо
как и бывает практически, являются приближенными значениями, то, найдя из каких-либо  уравнений значения параметров
уравнений значения параметров  мы столкнемся с тем фактом, что эти значения параметров не будут удовлетворять остальным уравнениям, причем разность между правой и левой частями для некоторых уравнений может быть значительной. Наша система чаще всего будет несовместна. Возникает задача так определить значения параметров, чтобы в некотором смысле все уравнения системы были удовлетворены с наименьшей погрешностью, т. е. найти те значения параметров, при которых искомая эмпирическая формула наилучшим образом согласуется с результатами наблюдений.
мы столкнемся с тем фактом, что эти значения параметров не будут удовлетворять остальным уравнениям, причем разность между правой и левой частями для некоторых уравнений может быть значительной. Наша система чаще всего будет несовместна. Возникает задача так определить значения параметров, чтобы в некотором смысле все уравнения системы были удовлетворены с наименьшей погрешностью, т. е. найти те значения параметров, при которых искомая эмпирическая формула наилучшим образом согласуется с результатами наблюдений.
Одним из способов отыскания этих значений параметров  является следующий. Отыскиваются приближенные значения параметров
является следующий. Отыскиваются приближенные значения параметров  например решая систему, составленную из каких-либо
например решая систему, составленную из каких-либо  уравнений системы. Далее, ищутся поправки к этим значениям
уравнений системы. Далее, ищутся поправки к этим значениям

Предполагая, что поправки  достаточно малы, а функция
достаточно малы, а функция  достаточно гладкая функция, разлагают правые части уравнений системы в ряд Тейлора в окрестности точки
достаточно гладкая функция, разлагают правые части уравнений системы в ряд Тейлора в окрестности точки  удерживая лишь члены первого порядка относительно поправок, т. е.
удерживая лишь члены первого порядка относительно поправок, т. е. 

Вводя для сокращения записи обозначения:

Вернемся к поставленной задаче. Если бы значения  при
при  были известны точно, то задача принципиально решалась бы просто. Нужно было бы из системы
были известны точно, то задача принципиально решалась бы просто. Нужно было бы из системы

взять  уравнений и найти из них значения параметров
уравнений и найти из них значения параметров  (предполагается, что эта система имеет единственное решение). При этих значениях параметров были бы в точности удовлетворены все остальные уравнения системы. Если же
(предполагается, что эта система имеет единственное решение). При этих значениях параметров были бы в точности удовлетворены все остальные уравнения системы. Если же  как и бывает практически, являются приближенными значениями, то, найдя из каких-либо
как и бывает практически, являются приближенными значениями, то, найдя из каких-либо  уравнений значения параметров
уравнений значения параметров  мы столкнемся с тем фактом, что эти значения параметров не будут удовлетворять остальным уравнениям, причем разность между правой и левой частями для некоторых уравнений может быть значительной. Наша система чаще всего будет несовместна. Возникает задача так определить значения параметров, чтобы в некотором смысле все уравнения системы были удовлетворены с наименьшей погрешностью, т. е. найти те значения параметров, при которых искомая эмпирическая формула наилучшим образом согласуется с результатами наблюдений.
мы столкнемся с тем фактом, что эти значения параметров не будут удовлетворять остальным уравнениям, причем разность между правой и левой частями для некоторых уравнений может быть значительной. Наша система чаще всего будет несовместна. Возникает задача так определить значения параметров, чтобы в некотором смысле все уравнения системы были удовлетворены с наименьшей погрешностью, т. е. найти те значения параметров, при которых искомая эмпирическая формула наилучшим образом согласуется с результатами наблюдений.
Одним из способов отыскания этих значений параметров  является следующий. Отыскиваются приближенные значения параметров
является следующий. Отыскиваются приближенные значения параметров  например решая систему, составленную из каких-либо
например решая систему, составленную из каких-либо  уравнений системы. Далее, ищутся поправки к этим значениям
уравнений системы. Далее, ищутся поправки к этим значениям

Предполагая, что поправки  достаточно малы, а функция
достаточно малы, а функция  достаточно гладкая функция, разлагают правые части уравнений системы в ряд Тейлора в окрестности точки
достаточно гладкая функция, разлагают правые части уравнений системы в ряд Тейлора в окрестности точки  удерживая лишь члены первого порядка относительно поправок, т. е.
удерживая лишь члены первого порядка относительно поправок, т. е.

Вводя для сокращения записи обозначения:

Решая систему нормальных уравнений одним из известных способов (подробнее об этом будет рассказываться в следующей главе), найдем значения неизвестных  которые для нашей исходной задачи являются поправками к начальным значениям параметров, а суммы
которые для нашей исходной задачи являются поправками к начальным значениям параметров, а суммы  можно принять за искомые значения параметров
можно принять за искомые значения параметров  в эмпирической формуле.
в эмпирической формуле.
Предыдущий способ дает удовлетворительные результаты только в том случае, когда результаты измерений  имеют одинаковую точность, т. е. их среднеквадратичные погрешности примерно одинаковы (см. гл. 1). Если этого нет, то целесообразно сначала все условные уравнения привести к «одинаковому весу». Это делается следующим способом. Пусть среднеквадратичные ошибки величин
имеют одинаковую точность, т. е. их среднеквадратичные погрешности примерно одинаковы (см. гл. 1). Если этого нет, то целесообразно сначала все условные уравнения привести к «одинаковому весу». Это делается следующим способом. Пусть среднеквадратичные ошибки величин

суть

Вычисляем величину

и находим веса

Затем каждое условное уравнение умножаем на соответствующее  Очевидно, получим систему, эквивалентную исходной, в которой правыми частями будут величины
Очевидно, получим систему, эквивалентную исходной, в которой правыми частями будут величины

имеющие одну и ту же среднюю ошибку 
Это равносильно составлению нормальных уравнений из условия минимума

Заметим, что для упрощения вычислений вместо среднеквадратичных ошибок можно брать величины, им пропорциональные, так как это не меняет нормальной системы.
Наконец, отметим, что на задачу приближения функций, заданной таблицей значений, с помощью алгебраического многочлена степени  по методу наименьших квадратов можно смотреть как на задачу построения эмпирической формулы в виде многочлена степени
по методу наименьших квадратов можно смотреть как на задачу построения эмпирической формулы в виде многочлена степени  Роль параметров в этом случае играют коэффициенты многочлена, причем система условных уравнений будет иметь вид
Роль параметров в этом случае играют коэффициенты многочлена, причем система условных уравнений будет иметь вид

а коэффициенты многочлена наилучшего приближения в смысле метода наименьших квадратов будут находиться как решение системы нормальных уравнений.
Пример. Известно, что некоторая величина  зависит от времени
зависит от времени  следующим образом:
следующим образом:

Измерения величины  произведенные с одинаковой точностью, дали следующую таблицу зависимости
произведенные с одинаковой точностью, дали следующую таблицу зависимости  от
от 
(см. скан)
Найти значение параметров  в этой функциональной зависимости.
в этой функциональной зависимости.
Исходные уравнения будут иметь вид

Решая приближенно первые два уравнения, найдем:

Ищем поправки

Так как

то

Система условных уравнений запишется так:

Система нормальных уравнений принимает вид:

или

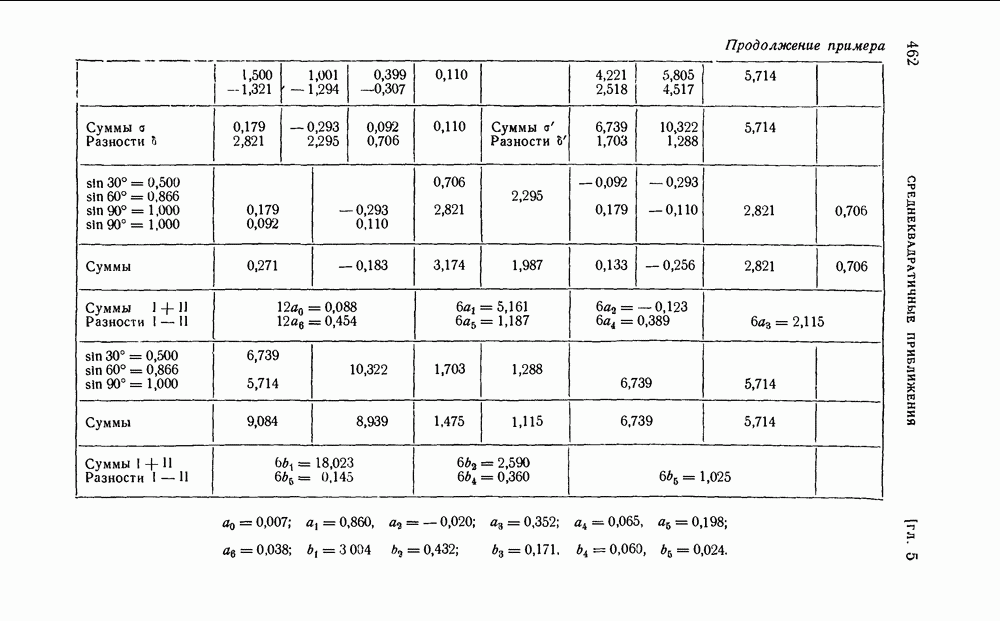
откуда

а

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
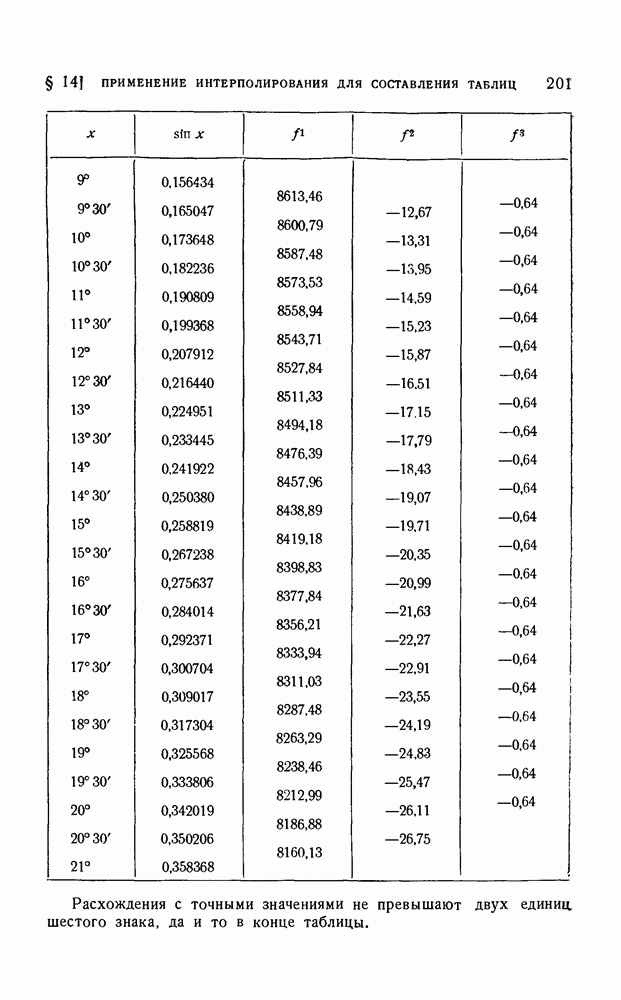
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
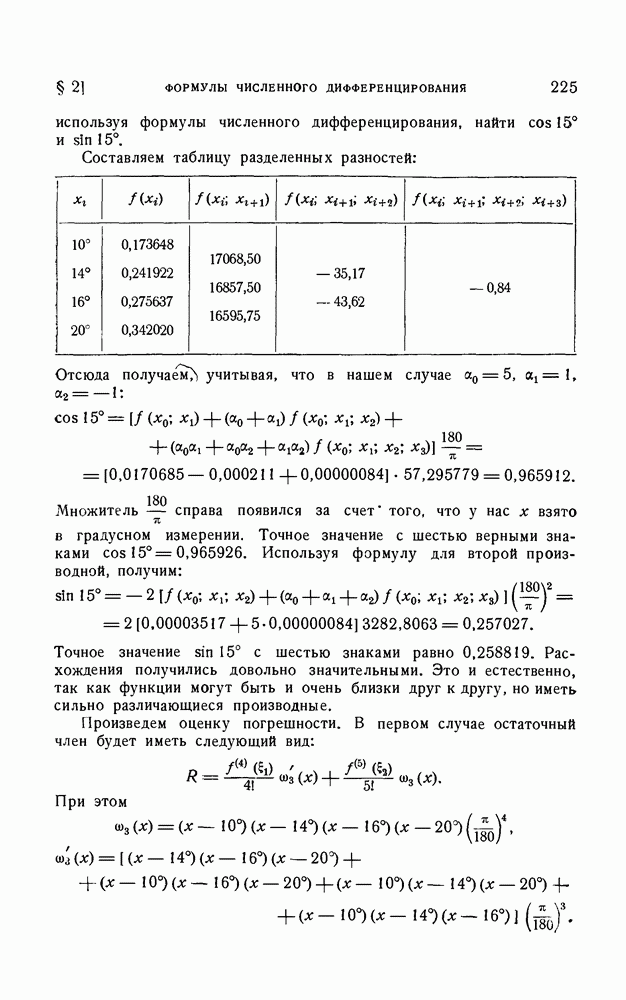
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
- § 3. Задача численного интегрирования
- § 4. Формулы Ньютона — Котеса
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
- § 13. Схема Рунге вычисления коэффициентов … в случае …