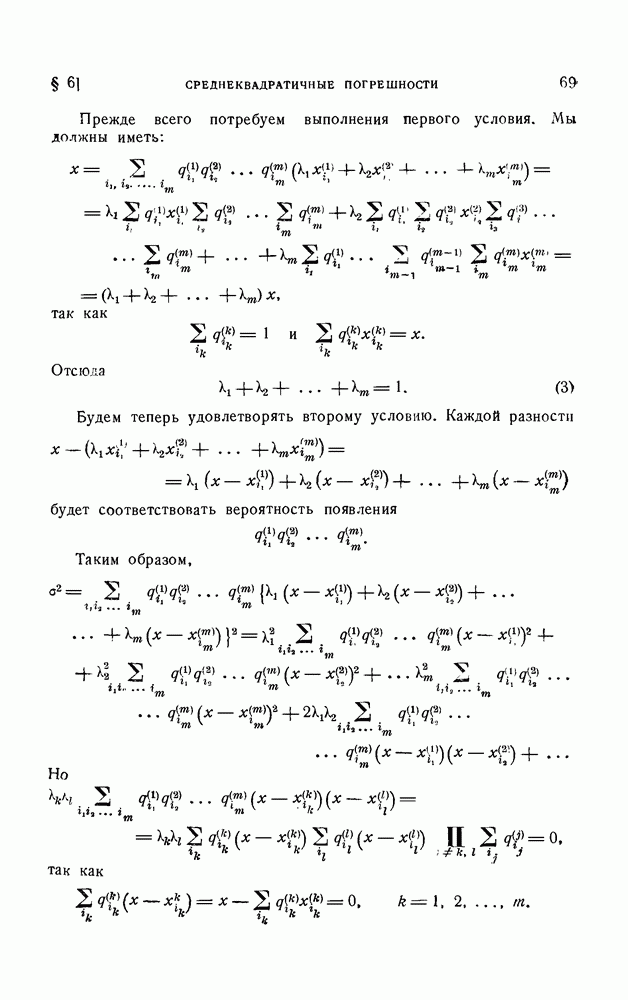| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Интерполяционные формулы, использующие центральные разности
1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
Опять воспользуемся интерполяционной формулой Ньютона для неравных промежутков ((6) § 5) и возьмем в качестве узлов  точки
точки 
Тогда

Используя симметричность разделенных разностей относительно своих аргументов и их связь с конечными разностями, получим:


Отсюда

Обозначив, как и ранее,

получим:

Это — интерполяционная формула Гаусса. В ней используются следующие разности (подчеркнуты черточкой):
(см. скан)
Если бы мы взяли узлы интерполирования в другом порядке, а именно:  то совершенно аналогично получили бы вторую формулу Гаусса:
то совершенно аналогично получили бы вторую формулу Гаусса:

Для того чтобы их можно было различить, будем называть первую из них интерполяционной формулой Гаусса для интерполирования вперед, вторую — для интерполирования назад. Интерполяционная формула Гаусса для интерполировачия назад использует следующие разности:
(см. скан)
Полусумма двух интерполяционных формул Гаусса даст нам: 

так как

а

Мы получили формулу Стирлинга. В ней используются разности четного порядка с индексом  и полусуммы разностей нечетного порядка с индексами и
и полусуммы разностей нечетного порядка с индексами и  как
как  показано в следующей таблице:
показано в следующей таблице:
(см. скан)
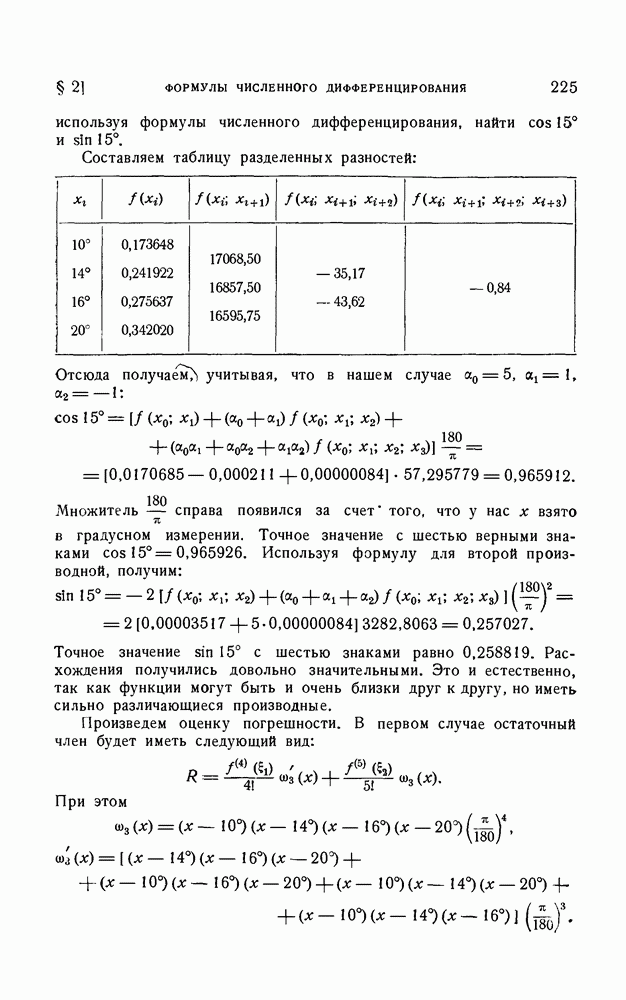
Приведем пример на вычисление по формуле Стирлинга. Пусть требуется найти  по значениям
по значениям  Таблица разностей будет такова:
Таблица разностей будет такова:
(см. скан)
За  возьмем ближайшее к х узловое значение, т. е. 15°. Тогда
возьмем ближайшее к х узловое значение, т. е. 15°. Тогда  и вычисления дадут:
и вычисления дадут:

Все знаки верны.
Получим еще одну важную интерполяционную формулу. Для этого применим интерполяционную формулу Гаусса для интерполирования назад (6) к точке  Тогда
Тогда

В этой формуле для обозначения параметра мы использовали  вместо
вместо  так как он равен
так как он равен  а не
а не  Легко видеть, что
Легко видеть, что  Сделаем замену
Сделаем замену  на Тогда получим:
на Тогда получим:

Полусумма этой формулы и формулы Гаусса для интерполирования вперед (5) даст

так как

а

Эта формула носит имя Бесселя. Она особенно удобна для интерполирования на середину, т. е. для Действительно, в этом случае все члены, содержащие разности нечетного порядка, обратятся в нуль. В формуле Бесселя используются следующие разности:
(см. скан)
В качестве примера на применение формулы Бесселя вычислим  по данным предыдущего примера. При этом, если в качестве
по данным предыдущего примера. При этом, если в качестве  взять снова 15°, то
взять снова 15°, то  Вычисления дают:
Вычисления дают:

Получили тсчное значение с шестью десятичными знаками.
Из используемых часто формул нам осталось получить еще только формулу Эверетта. Чтобы вывести ее, исключим разности нечетного порядка из формулы Гаусса для интерполирования вперед (5) при помощи соотношения

При этом у нас появятся члены с разностями  имеющие коэффициент
имеющие коэффициент

и разности  с коэффициентом
с коэффициентом

Преобразуем последнее выражение, заменив  на 1 — Получим:
на 1 — Получим:

Окончательно формула Эверетта примет вид

В этой формуле используются разности, подчеркнутые в таблице черточкой:
(см. скан)
Формула Эверетта имеет некоторые особенности, отличающие ее от других выведенных нами формул. Прежде всего она содержит только разности четного порядка. Это особенно удобно при печатании таблиц, если в них необходимо поместить также и разности.
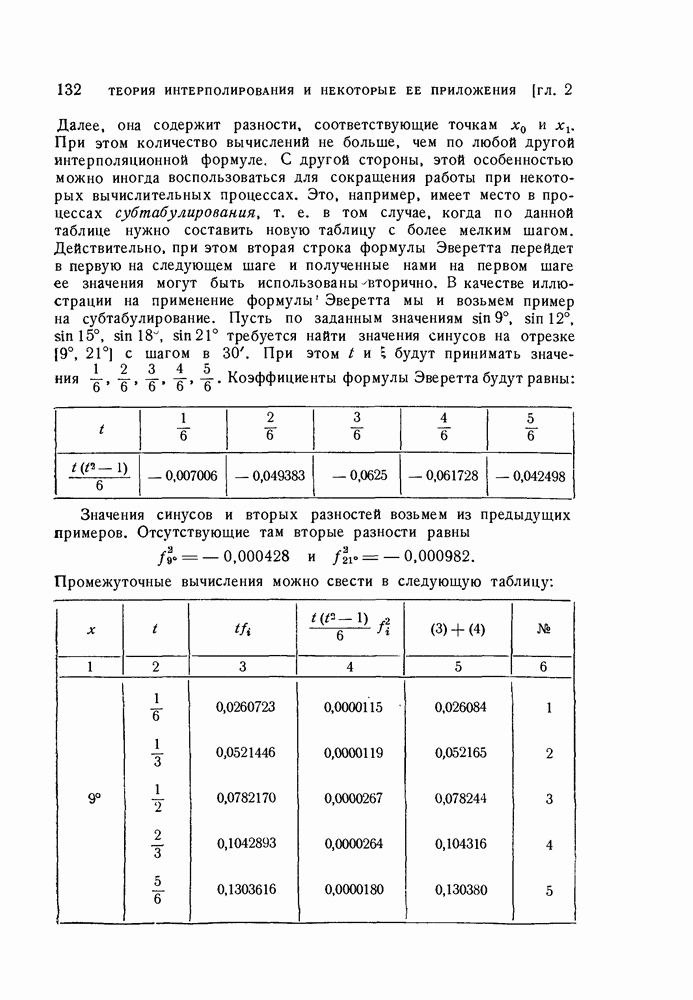
Далее, она содержит разности, соответствующие точкам  При этом количество вычислений не больше, чем по любой другой интерполяционной формуле. С другой стороны, этой особенностью можно иногда воспользоваться для сокращения работы при некоторых вычислительных процессах. Это, например, имеет место в процессах субтабулирования, т. е. в том случае, когда по данной таблице нужно составить новую таблицу с более мелким шагом. Действительно, при этом вторая строка формулы Эверетта перейдет в первую на следующем шаге и полученные нами на первом шаге ее значения могут быть использованы вторично. В качестве иллюстрации на применение формулы Эверетта мы и возьмем пример на субтабулирование. Пусть по заданным значениям
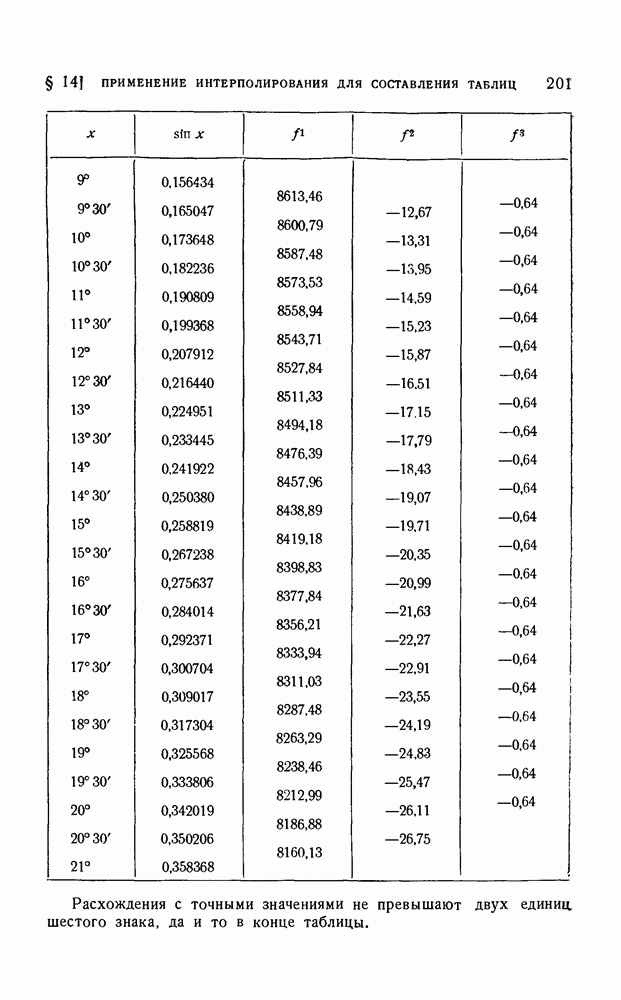
При этом количество вычислений не больше, чем по любой другой интерполяционной формуле. С другой стороны, этой особенностью можно иногда воспользоваться для сокращения работы при некоторых вычислительных процессах. Это, например, имеет место в процессах субтабулирования, т. е. в том случае, когда по данной таблице нужно составить новую таблицу с более мелким шагом. Действительно, при этом вторая строка формулы Эверетта перейдет в первую на следующем шаге и полученные нами на первом шаге ее значения могут быть использованы вторично. В качестве иллюстрации на применение формулы Эверетта мы и возьмем пример на субтабулирование. Пусть по заданным значениям  требуется найти значения синусов на отрезке
требуется найти значения синусов на отрезке  с шагом в 30. При этом
с шагом в 30. При этом  будут принимать значения
будут принимать значения  . Коэффициенты формулы Эверетта будут равны:
. Коэффициенты формулы Эверетта будут равны:
(см. скан)
Значения синусов и вторых разностей возьмем из предыдущих примеров. Отсутствующие там вторые разности равны

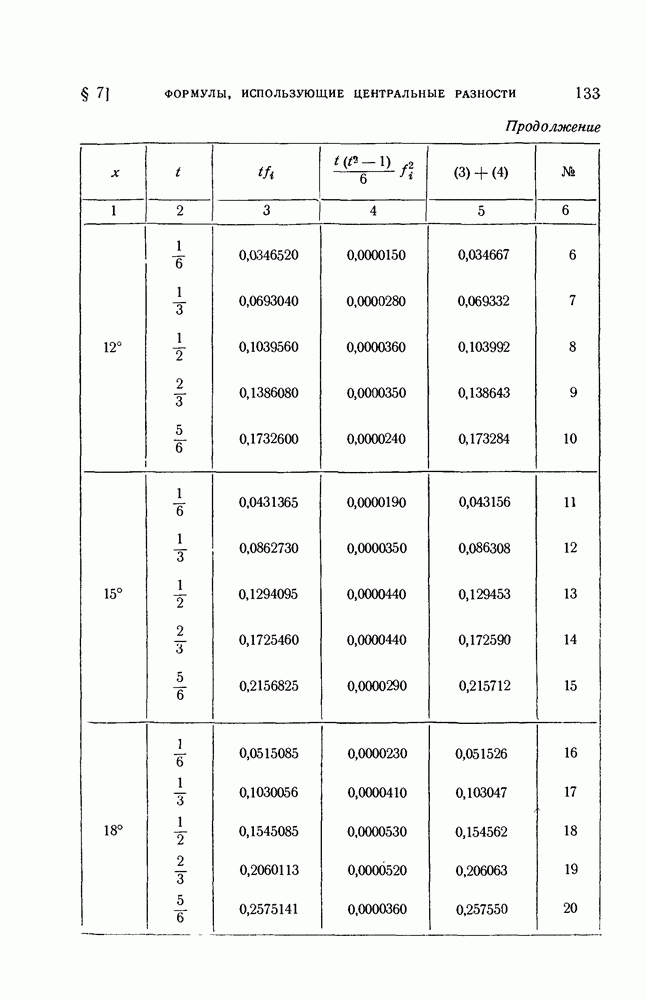
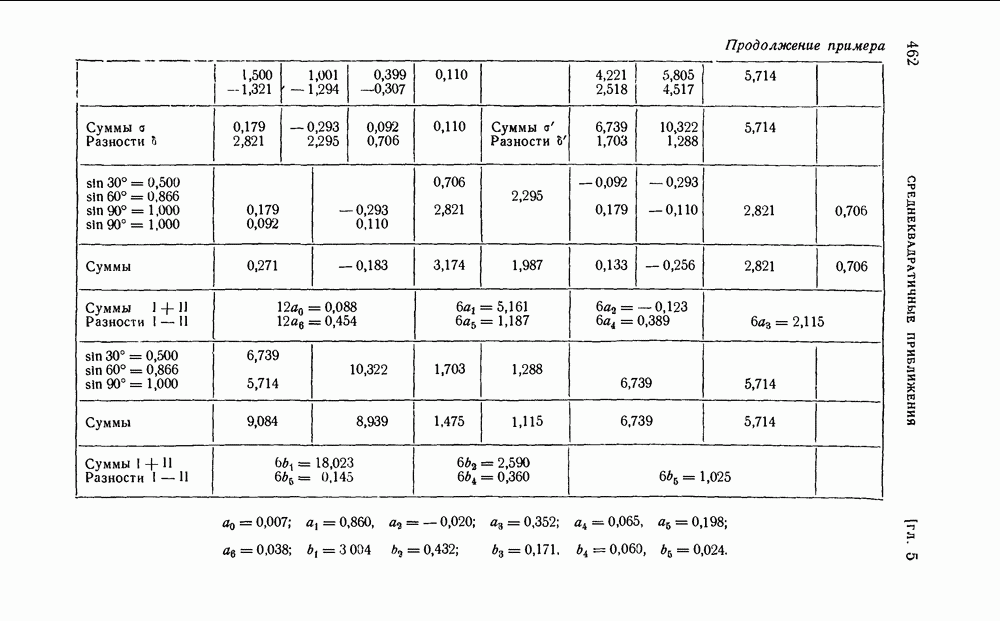
Промежуточные вычисления можно свести в следующую таблицу:
(см. скан)
(см. скан)
(см. скан)
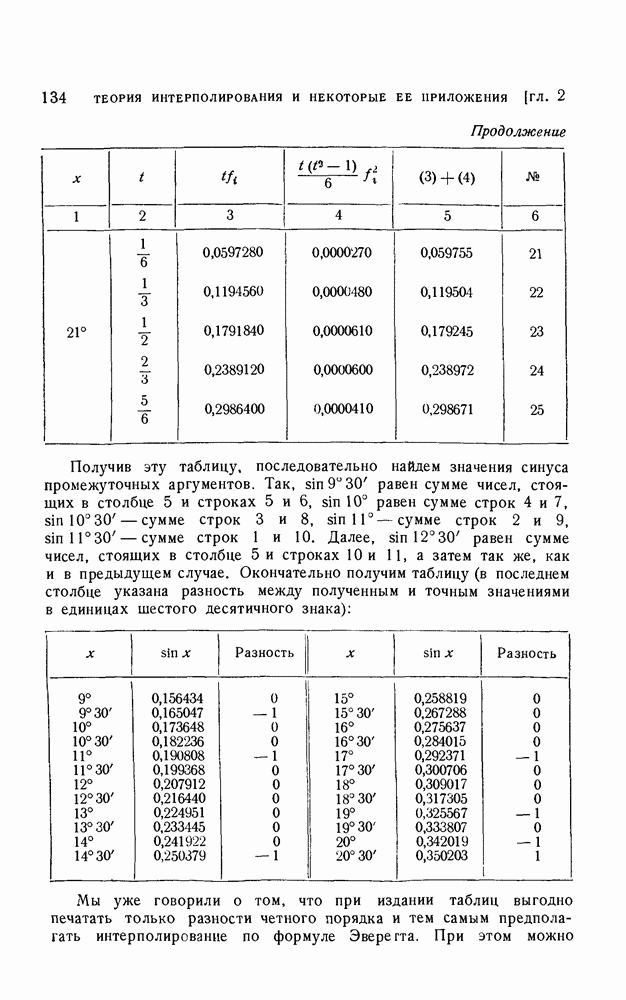
Получив эту таблицу, последовательно найдем значения синуса промежуточных аргументов. Так,  равен сумме чисел, стоящих в столбце 5 и строках
равен сумме чисел, стоящих в столбце 5 и строках  равен сумме строк
равен сумме строк  сумме строк 3 и 8,
сумме строк 3 и 8,  - сумме строк
- сумме строк  сумме строк 1 и 10. Далее,
сумме строк 1 и 10. Далее,  равен сумме чисел, стоящих в столбце 5 и строках 10 и 11, а затем так же, как и в предыдущем случае. Окончательно получим таблицу (в последнем столбце указана разность между полученным и точным значениями в единицах шестого десятичного знака):
равен сумме чисел, стоящих в столбце 5 и строках 10 и 11, а затем так же, как и в предыдущем случае. Окончательно получим таблицу (в последнем столбце указана разность между полученным и точным значениями в единицах шестого десятичного знака):
(см. скан)
Мы уже говорили о том, что при издании таблиц выгодно печатать только разности четного порядка и тем самым предполагать интерполирование по формуле Эверегта. При этом можно
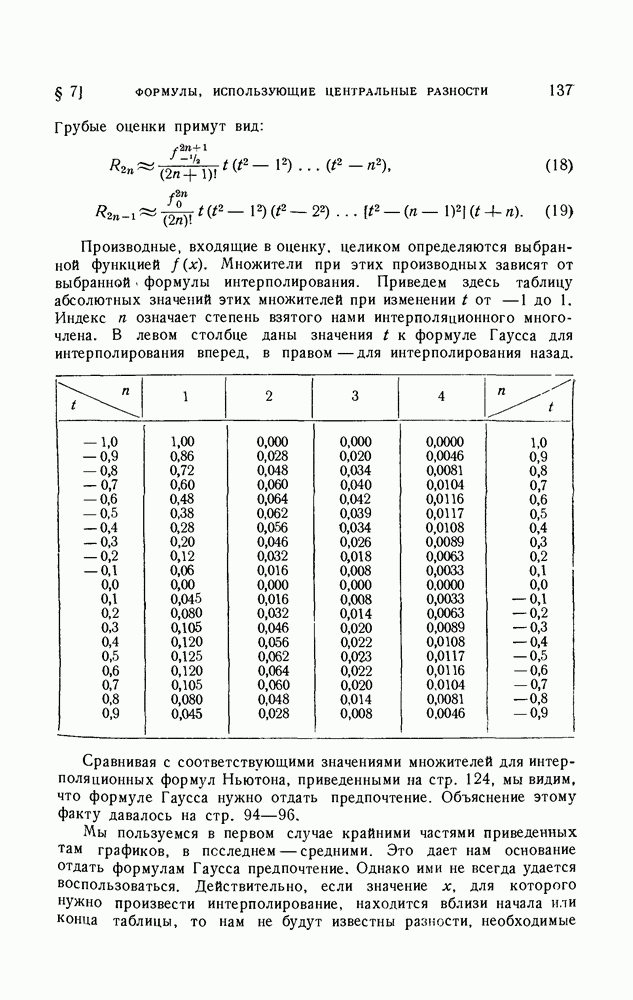
достичь дальнейших упрощений. Пусть мы хотим использовать формулу Эверетта до членов с четвертыми разностями:

Последние два члена первой и второй строк можно записать в виде

и

где  некоторая постоянная. Выражения
некоторая постоянная. Выражения  и
и  стоящие в последних квадратных скобках, изменяются незначительно при изменении
стоящие в последних квадратных скобках, изменяются незначительно при изменении  в промежутке (
в промежутке ( в котором обычно используют формулу Эверетта. Поэтому можно так подобрать
в котором обычно используют формулу Эверетта. Поэтому можно так подобрать  что множители при четвертых разностях в последних членах будут очень малы. Если при этом и сами четвертые разности не очень велики, так что их произведение с этими множителями не окажет влияния на верные десятичные знаки
что множители при четвертых разностях в последних членах будут очень малы. Если при этом и сами четвертые разности не очень велики, так что их произведение с этими множителями не окажет влияния на верные десятичные знаки  то последние члены можно целиком отбросить. Тогда мы можем печатать в таблице вместо настоящих вторых разностей модифицированные разности
то последние члены можно целиком отбросить. Тогда мы можем печатать в таблице вместо настоящих вторых разностей модифицированные разности  и использовать формулу Эверетта только до вторых разностей. Выберем
и использовать формулу Эверетта только до вторых разностей. Выберем  так, чтобы
так, чтобы

был равен нулю. Это даст

На практике используют значение  При этом
При этом  изменяются в пределах от —0,016 до 0,034. Коэффициенты при меняются от —0,00077 до 0,00053. Следовательно, даже если четвертые разности достигают 600 единиц последнего знака, наш прием будет применим.
изменяются в пределах от —0,016 до 0,034. Коэффициенты при меняются от —0,00077 до 0,00053. Следовательно, даже если четвертые разности достигают 600 единиц последнего знака, наш прием будет применим.
Сказанное здесь о формуле Эверетта можно частично перенести и на другие интерполяционные формулы. Так можно использовать модифицированные разности и с другими формулами. Можно использовать симметрию коэффициентов многих интерполяционных формул.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
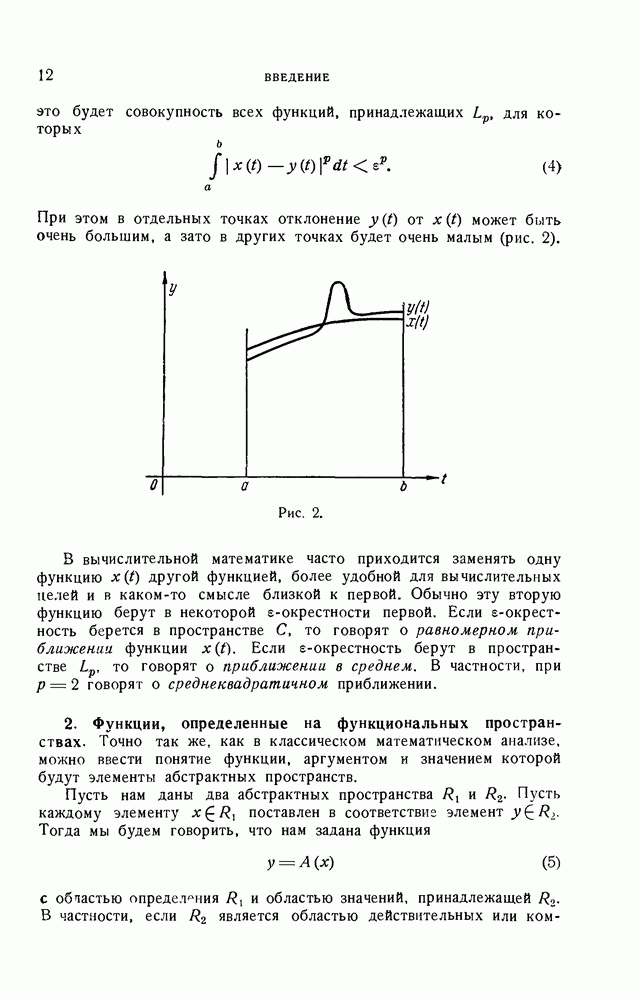
- ВВЕДЕНИЕ
- § 1. Предмет вычислительной математики
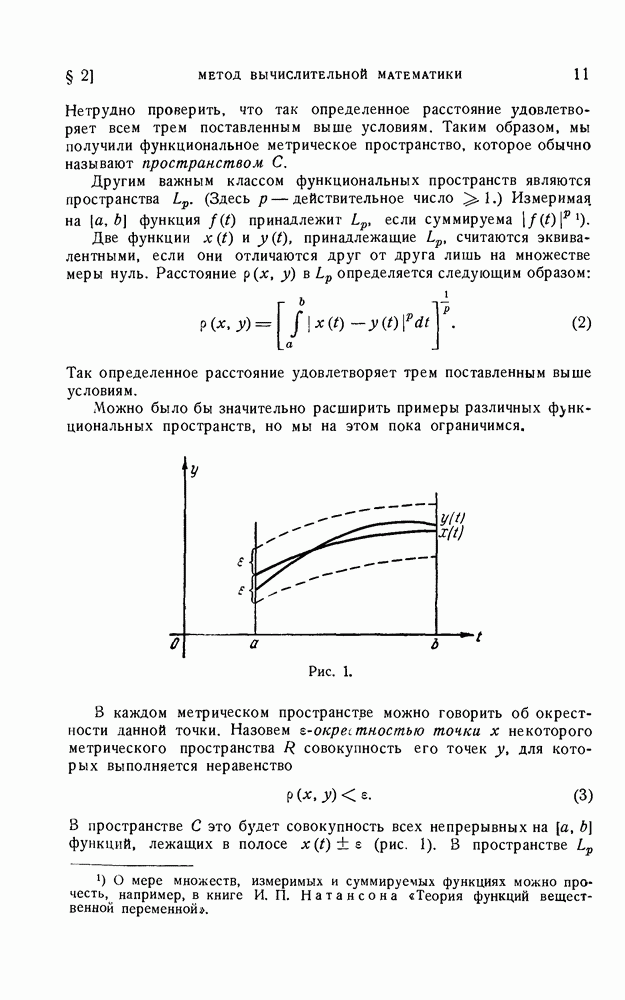
- § 2. Метод вычислительной математики
- § 3. Средства вычислений
- § 4. Методы вычислений как раздел вычислительной математики. Краткое содержание курса
- ГЛАВА 1. ДЕЙСТВИЯ С ПРИБЛИЖЕННЫМИ ВЕЛИЧИНАМИ
- 1. Источники погрешности результатов вычислений.
- 2. Задачи, возникающие при работе с приближенными величинами.
- 3. Правила округления чисел.
- 4. Классификация погрешностей.
- § 2. Неустранимая погрешность
- 1. Абсолютная и относительная погрешности числа.
- 2. Верные знаки числа.
- 3. Неустранимая погрешность значения функции для приближенных значений аргументов. Погрешности результатов арифметических операций.
- § 3. Погрешности округления
- § 4. Полная погрешность
- § 5. Понятие о статистических методах оценки погрешностей
- § 6. Среднеквадратичные погрешности
- 1. Систематические и случайные ошибки.
- 2. Среднеквадратичные погрешности.
- 3. Обработка результатов по методу наименьших квадратов.
- 4. Среднеквадратичная погрешность функции.
- 5. Среднеквадратичная погрешность равномерно распределенной величины.
- ГЛАВА 2. ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ И НЕКОТОРЫЕ ЕЕ ПРИЛОЖЕНИЯ
- 1. Линейные множества. Линейно независимые системы элементов.
- 2. Задача интерполирования.
- 3. Построение интерполирующей функции.
- 4. Системы Чебышева.
- 5. Основные вопросы теории интерполирования.
- § 2. Интерполяционный многочлен Лагранжа
- 2. Интерполяционный многочлен Лагранжа для равноотстоящих узлов.
- 3. Интерполяционная схема Эйткена.
- § 3. Погрешности интерполяционной формулы Лагранжа
- 1. Остаточный член формулы Лагранжа и его оценки.
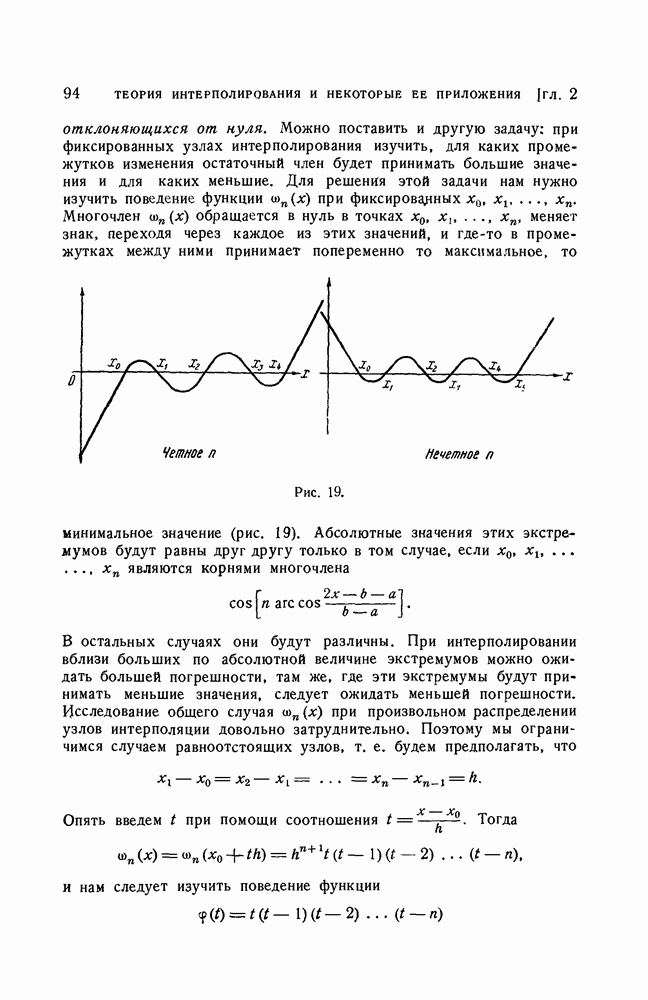
- 2. Выбор узлов интерполирования.
- 3. Неустранимая погрешность формулы Лагранжа.
- § 4. Остаточный член общей интерполяционной формулы
- § 5. Интерполяционная формула Ньютона для неравных промежутков
- 2. Вывод формулы Ньютона для неравных промежутков.
- 3. Остаточный член формулы Ньютона.
- § 6. Интерполяционные формулы Ньютона для равных промежутков
- 2. Вывод интерполяционных формул Ньютона.
- 3. Остаточные члены интерполяционных формул Ньютона.
- § 7. Интерполяционные формулы, использующие центральные разности
- 1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя и Эверетта.
- 2. Остаточные члены интерполяционных формул с центральными разностями.
- § 8. Некоторые другие подходы к выводу формул интерполирования для равных промежутков
- 2. Понятие об операторном методе вывода формул интерполирования.
- § 9. Сходимость интерполяционного процесса
- § 10. Интерполирование периодических функций
- § 11. Общая задача интерполирования алгебраическими многочленами
- 1. Интерполяционный многочлен Эрмита.
- 2. Общий вид интерполяционного многочлена Эрмита.
- 3. Остаточный член интерполяционной формулы Эрмита.
- 4. Разделенные разности с повторяющимися значениями аргумента.
- 5. Обобщенная интерполяционная формула Ньютона с разделенными разностями.
- § 12. Интерполирование функций многих независимых переменных
- 2. Обобщение интерполяционных формул Ньютона на случай функции многих переменных.
- 3. Другие способы построения интерполяционных многочленов для функций многих переменных.
- § 13. Интерполирование функций комплексного переменного
- § 14. Применение интерполирования для составления таблиц
- § 15. Обратное интерполирование
- ГЛАВА 3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
- § 2. Формулы численного дифференцирования
- 1. Формулы численного дифференцирования для неравноотстоящих узлов.
- 2. Формулы численного дифференцирования для равноотстоящих узлов.
- 3. Безразностные формулы численного дифференцирования.
- 4. Метод неопределенных коэффициентов.
- 5. Выражение разностей через производные.
- § 3. Задача численного интегрирования
- § 4. Формулы Ньютона — Котеса
- 3. Формула трапеций и формула Симпсона.
- § 5. Формулы численного интегрирования Гаусса
- 2. Остаточный член формул Гаусса.
- 3. Коэффициенты формул Гаусса.
- 4. Формула численного интегрирования Эрмита.
- 5. Формулы численного интегрирования Маркова.
- § 6. Формулы численного интегрирования Чебышева
- 2. Остаточный член формул Чебышева.
- § 7. Сходимость квадратурных процессов
- § 8. Формула Эйлера
- 1. Числа и многочлены Бернулли.
- 2. Формула Эйлера и примеры ее применения.
- § 9. Формулы численного интегрирования, содержащие разности подынтегральной функции
- 1. Формула Грегори.
- 2. Формула Лапласа и другие формулы.
- § 10. Некоторые замечания по поводу формул численного интегрирования
- 1. Метод Рунге приближенной оценки погрешности численного интегрирования.
- § 11. Вычисление несобственных интегралов
- § 12. Приближенное вычисление кратных интегралов
- 2. Метод замены подынтегральной функции интерполяционным многочленом.
- 3. Метод Л. А. Люстерника и В. А. Диткина.
- 4. Замечание о методе Монте-Карло.
- ГЛАВА 4. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Наилучшее приближение в линейных нормированных пространствах
- 4. Единственность элемента наилучшего приближения.
- § 2. Наилучшее равномерное приближение непрерывных функций обобщенными многочленами
- 3. Теорема Чебышева.
- § 3. Алгебраические многочлены наилучшего равномерного приближения
- 1. Теорема Вейерштрасса.
- 2. Теоремы о порядке приближения с помощью многочленов Бернштейна.
- § 4. Тригонометрические многочлены наилучшего приближения
- § 5. Некоторые теоремы о порядке наилучшего равномерного приближения непрерывных функций
- § 6. Приближенное построение алгебраических многочленов наилучшего приближения
- 2. Первый способ приближенного построения многочлена наилучшего приближения.
- 3. Второй способ приближенного построения многочлена наилучшего приближения.
- ГЛАВА 5. СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ
- § 1. Гильбертовы пространства
- § 2. Ортонормированные системы в гильбертовом пространстве Ряды Фурье
- § 3. Приближения в гильбертовом пространстве
- 1. Построение элемента наилучшего приближения.
- § 4. Среднеквадратичные приближения функций алгебраическими многочленами
- 1. Ортогональные системы многочленов.
- 2. Рекуррентные соотношения для ортогональных многочленов.
- 3. Тождество Кристофеля — Дарбу.
- 4. Свойства корней ортогональных многочленов.
- 5. Дифференциальные уравнения, которым удовлетворяют ортогональные многочлены.
- § 5. Некоторые частные случаи ортогональных систем многочленов
- 1. Многочлены Якоби.
- 2. Многочлены Лежандра.
- 3. Многочлены Чебышева первого и второго рода.
- 4. Многочлены Лагерра и Эрмита.
- § 6. Сходимость рядов по ортогональным системам многочленов
- § 7. Среднеквадратичные приближения функций тригонометрическими многочленами
- § 8. Приближение функций, заданных таблицей, по методу наименьших квадратов
- § 9. Приближения по методу наименьших квадратов алгебраическими многочленами
- § 10. Применение метода наименьших квадратов для сглаживания результатов наблюдения
- § 11. Применение метода наименьших квадратов к построению эмпирических формул. Решение систем линейных алгебраических уравнений по методу наименьших квадратов
- § 12. Приближение функций, заданных таблицей, тригонометрическими многочленами по методу наименьших квадратов
- § 13. Схема Рунге вычисления коэффициентов … в случае …