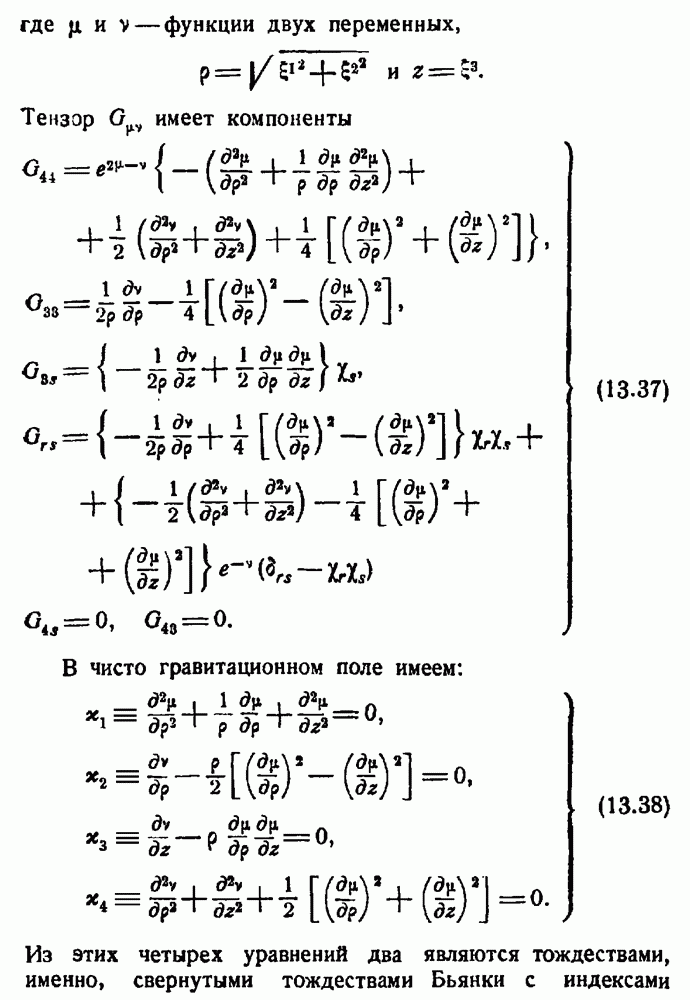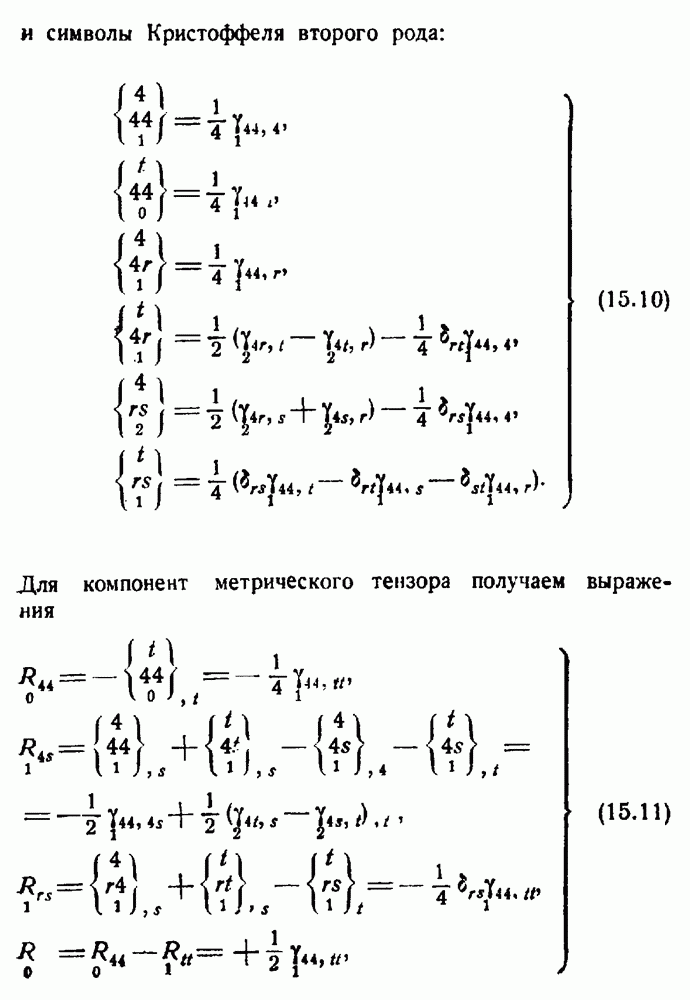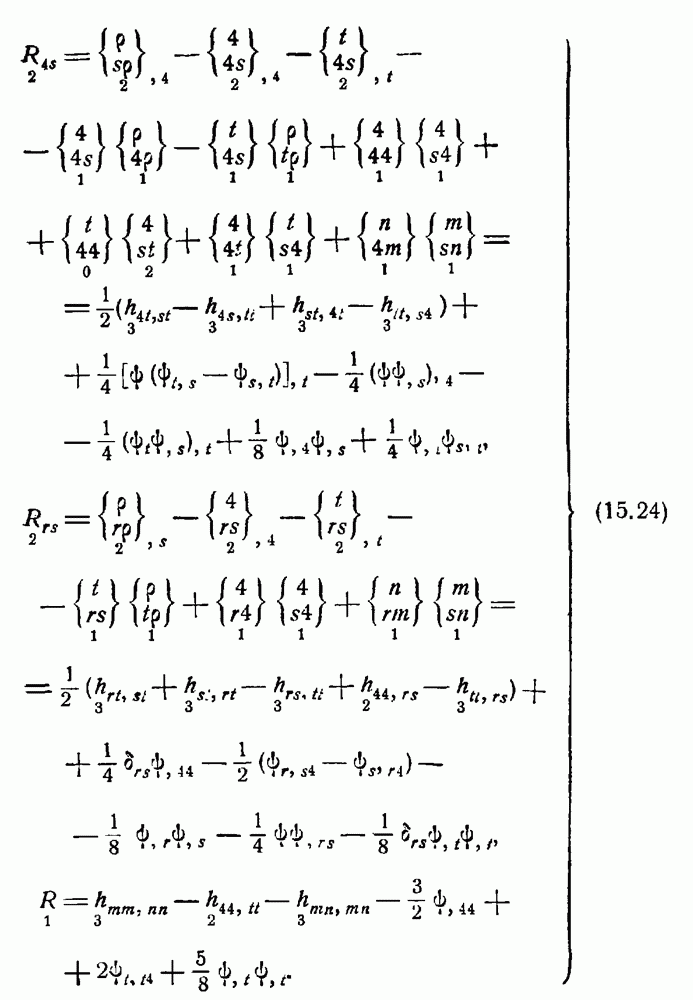| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Уравнения поля общей теории относительности нелинейны. Пока мы нашли решения только приближенных линейных уравнений. В этой главе будут рассмотрены случаи, в которых возможно решение точных уравнений в конечном виде.
Общего метода нахождения точных решений уравнений поля не существует. Однако точное решение возможно в тех немногих случаях, когда число переменных можно уменьшить, используя условия симметрии.
Решение Шварцшильда.
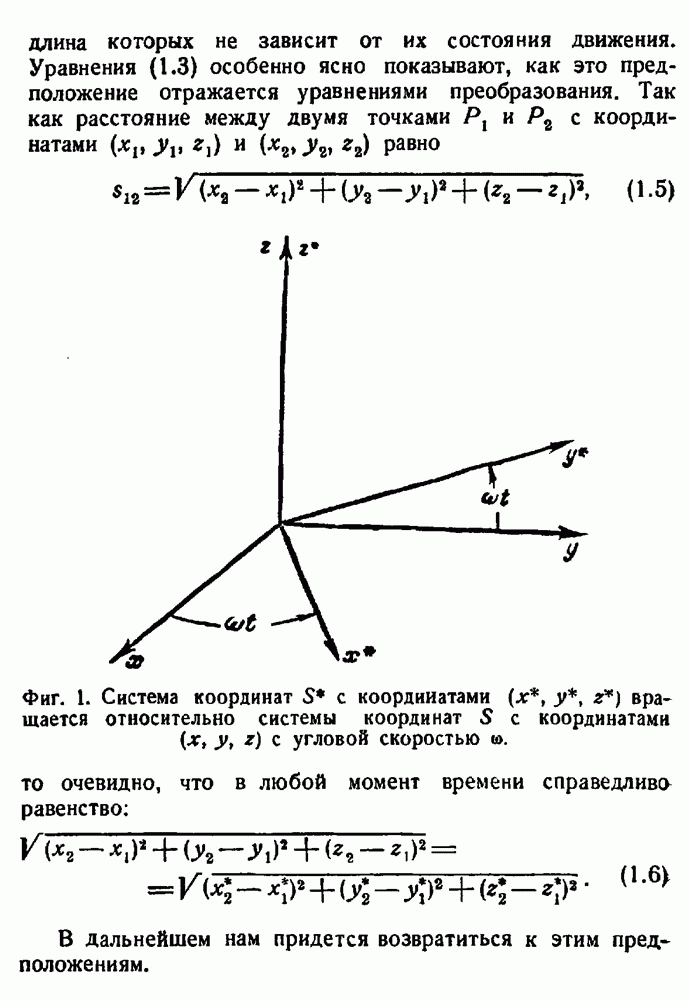
Рассмотрим сначала решение, соответствующее покоящейся точечной массе. Предположим, что решение сферически симметрично и что ни одна из переменных не зависит от  . Если ввести переменную
. Если ввести переменную

наиболее общим видом линейного элемента с указанными свойствами будет

где А, В, С и D являются функциями от  . Этот линейный элемент не меняет своего вида при повороте пространственных координат
. Этот линейный элемент не меняет своего вида при повороте пространственных координат  вокруг оси, проходящей через начало координат.
вокруг оси, проходящей через начало координат.
Подходящим преобразованием координат можно исключить две из четырех неизвестных функций А, В, С и D,
не нарушая при этом статического характера задачи и сферической симметрии линейного элемента. Производя сначала лреобразование координат

можно исключить члены, содержащие произведения  Компоненты
Компоненты  преобразуются при этом согласно уравнению
преобразуются при этом согласно уравнению

или

Выбирая  так, чтобы оно удовлетворяло уравнению
так, чтобы оно удовлетворяло уравнению

можно исключить член, содержащий В.
Рассмотрим далее метрику с компонентами

Преобразуя пространственные координаты следующим образом

получим новую систему координат, в которой метрика сохраняет прежний вид (13.6), но где функция С — постоянная и равна единице. Компоненты  преобразуются
преобразуются
по закону

В полученной системе координат С будет равно единице, если  в (13.7) выбрать следующим образом:
в (13.7) выбрать следующим образом:

Остаются только две неизвестные функции А и  Вместо них введем две другие функции от
Вместо них введем две другие функции от  функции —
функции —  и V, с помощью которых решение уравнений поля значительно упрощается. Новые функции зададим уравнениями:
и V, с помощью которых решение уравнений поля значительно упрощается. Новые функции зададим уравнениями:

Для компонент контравариантного метрического тензора получим:

Найдем теперь символы Кристоффеля и компоненты тензора  Для символов Кристоффеля первого рода имеем
Для символов Кристоффеля первого рода имеем

где штрихами обозначено дифференцирование по  Компоненты, в которые индекс 4 входит нечетное число раз, равны нулю. Символы Кристоффеля второго рода имеют следующий вид:
Компоненты, в которые индекс 4 входит нечетное число раз, равны нулю. Символы Кристоффеля второго рода имеют следующий вид:

Как и в предыдущем случае, компоненты, в которые индекс 4 входит нечетное число раз, обращаются в нуль.
Вычислим компоненты свернутого тензора кривизны 

тогда компоненты тензора будут равны

Рассмотрим сначала гравитационное поле в пустоте, где удовлетворяются уравнения (12.4). Нужно решить следующие три уравнения для двух неизвестных:

Эти три уравнения не независимы, так как они должны удовлетворять свернутым тождествам Бьянки (11.46).
Из первого и второго уравнений видно, что сумма  равна нулю:
равна нулю:

Решим первое уравнение относительно V. Для этого введем величину х:

Тогда вместо первого уравнения (13.16) получим уравнение для

решением которого будет

где а — постоянная интегрирования. В силу (13.17) функция может быть представлена в виде:

где  — новая постоянная. Решения (13.19) и (13.20) удовлетворяют и третьему уравнению (13.16). Таким образом, для компонент метрического тензора находим:
— новая постоянная. Решения (13.19) и (13.20) удовлетворяют и третьему уравнению (13.16). Таким образом, для компонент метрического тензора находим:

При больших  компоненты метрического тензора должны стремиться к значениям уравнения (12.7). Для этого необходимо положить
компоненты метрического тензора должны стремиться к значениям уравнения (12.7). Для этого необходимо положить  равной нулю. Оставшаяся постоянная а должна характеризовать массу частицы, образующей поле (13.21).
равной нулю. Оставшаяся постоянная а должна характеризовать массу частицы, образующей поле (13.21).
Согласно (12.13) ньютоновский потенциал, создаваемый точечной массой поля (13.21), равен

С другой стороны, О связано с массой уравнением

откуда находим связь постоянной а с массой  :
:

Гравитационное поле точечной шссы поэтому дается выражениями

Это решение было получено Шварцшильдом.
Решение Шварцшильда замечательно тем, что оно представляет собой единственное статическое сферически симметричное решение уравнений поля в пустоте, переходящее в плоскую метрику на бесконечности. Остальные решения уравнений поля в пустоте, обладающие теми же свойствами» получаются из решения Шварцшильда путем преобразования координат. Более того, Биркгоффом было показано, что все сферически симметричные решения уравнений поля в пустоте, удовлетворяющие граничным условиям на бесконечности, эквивалентны полю Шварцшильда, т. е. что их зависимость от времени может быть исключена подходящим преобразованием координат.
Пусть ограниченная область пространства заполнена материей, создающей сферически симметричную метрику. Тогда согласно сказанному выше гравитационное поле вне области, занятой материей, должно быть полем Шварцшильда. Создающая поле материя может даже пульсировать (сферически симметрично), не меняя поля вне ее. При этом, конечно, предполагается, что нет потока материи или электромагнитного излучения из области, занятой материей, наружу.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
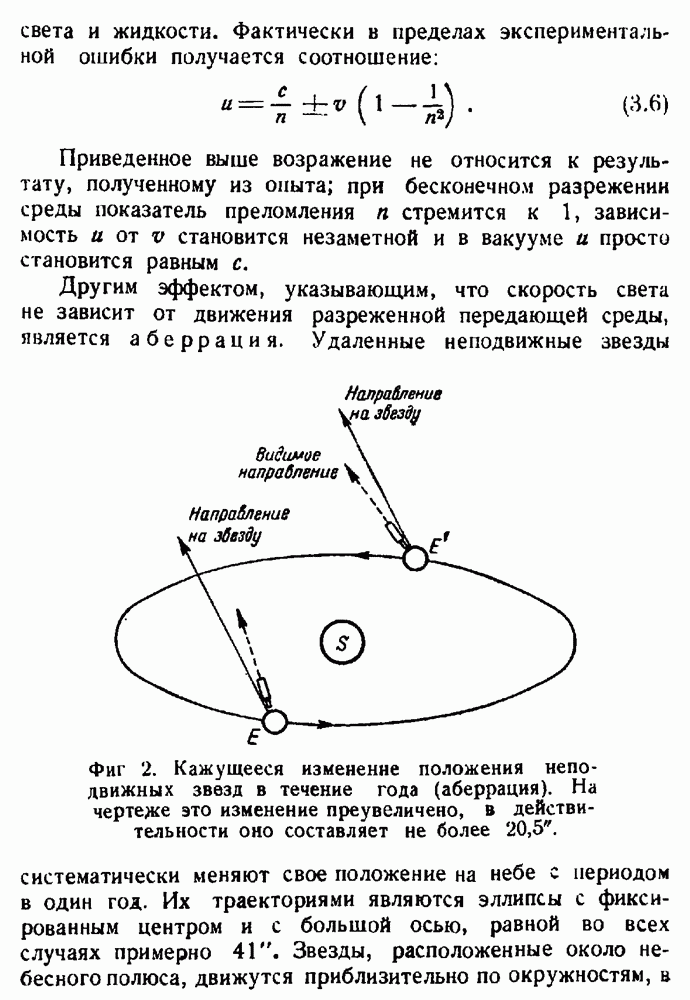
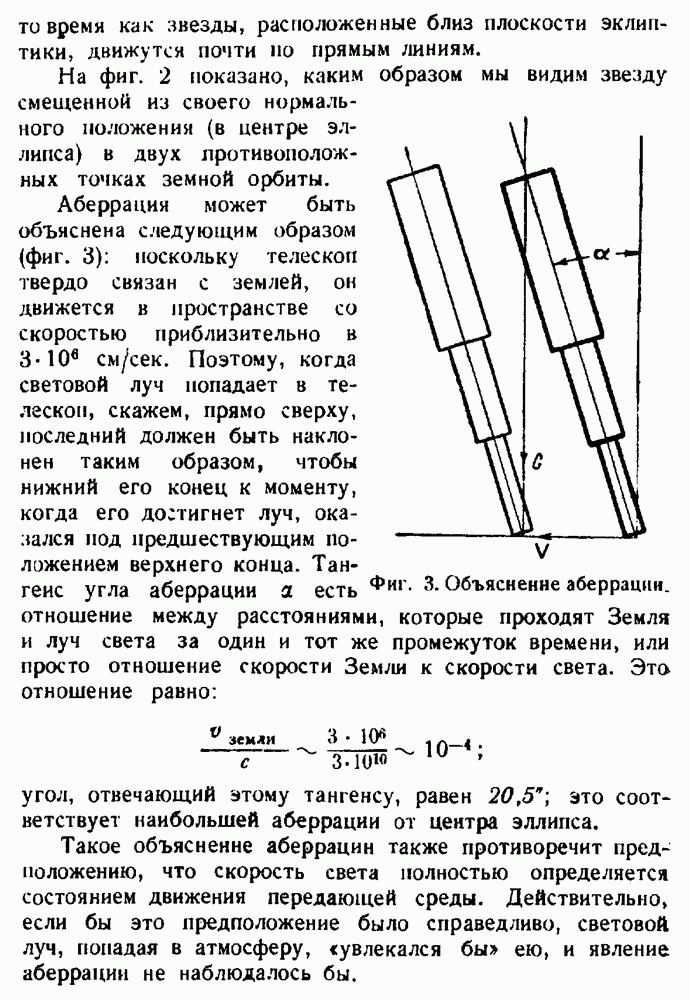
- Передающая среда как система отсчета.
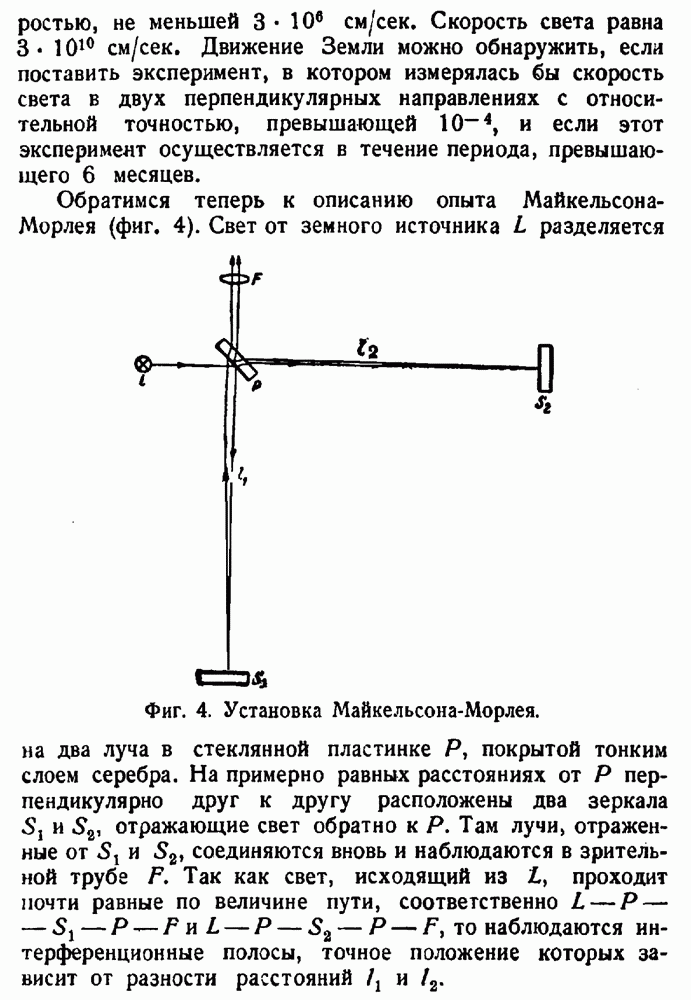
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
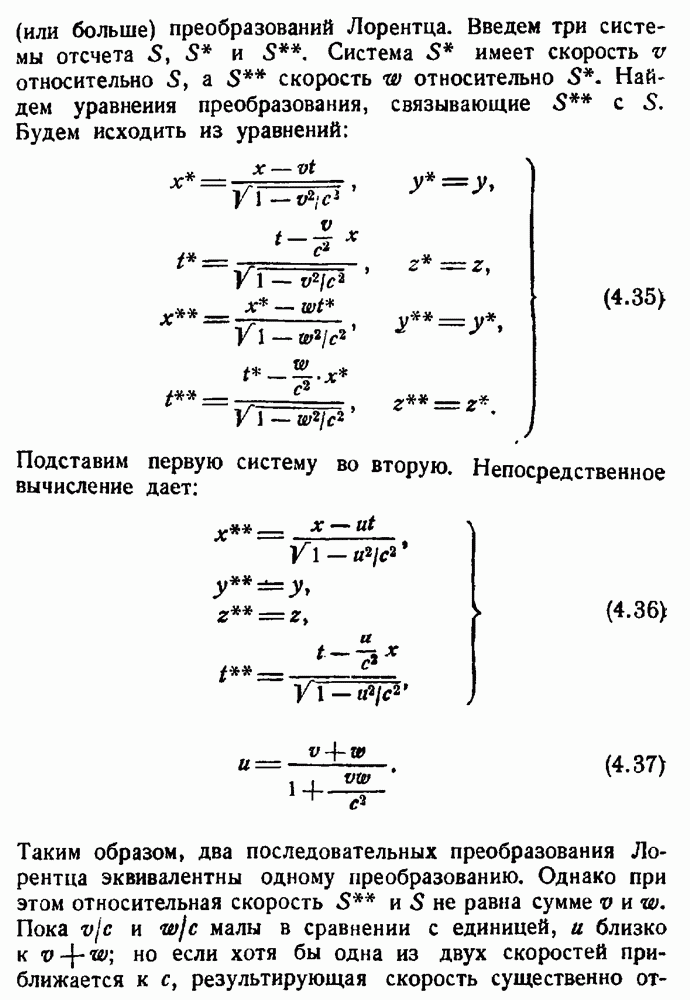
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
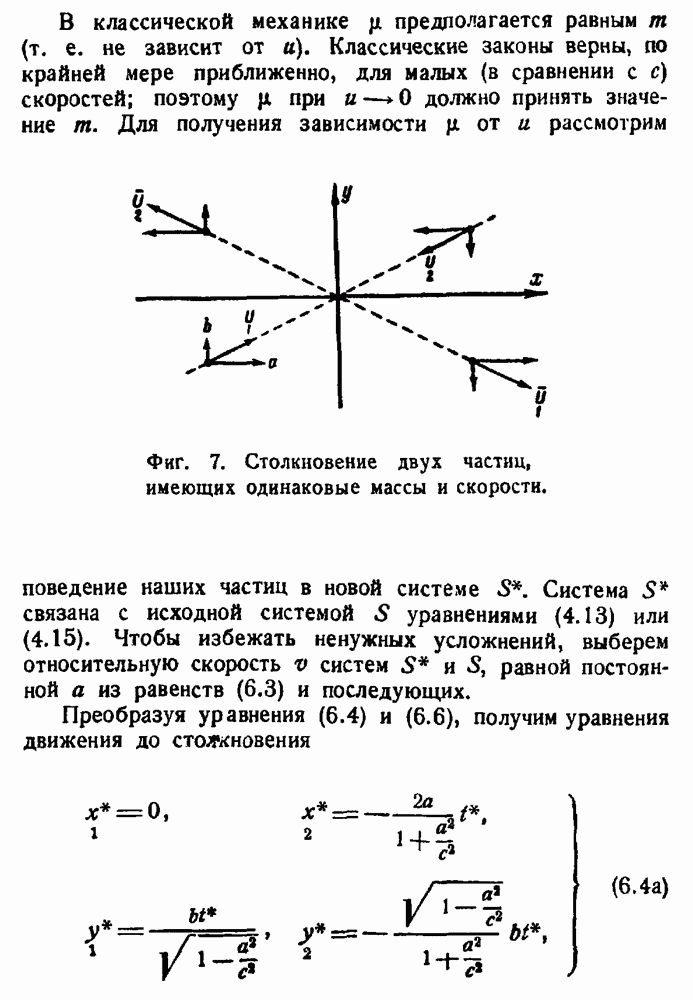
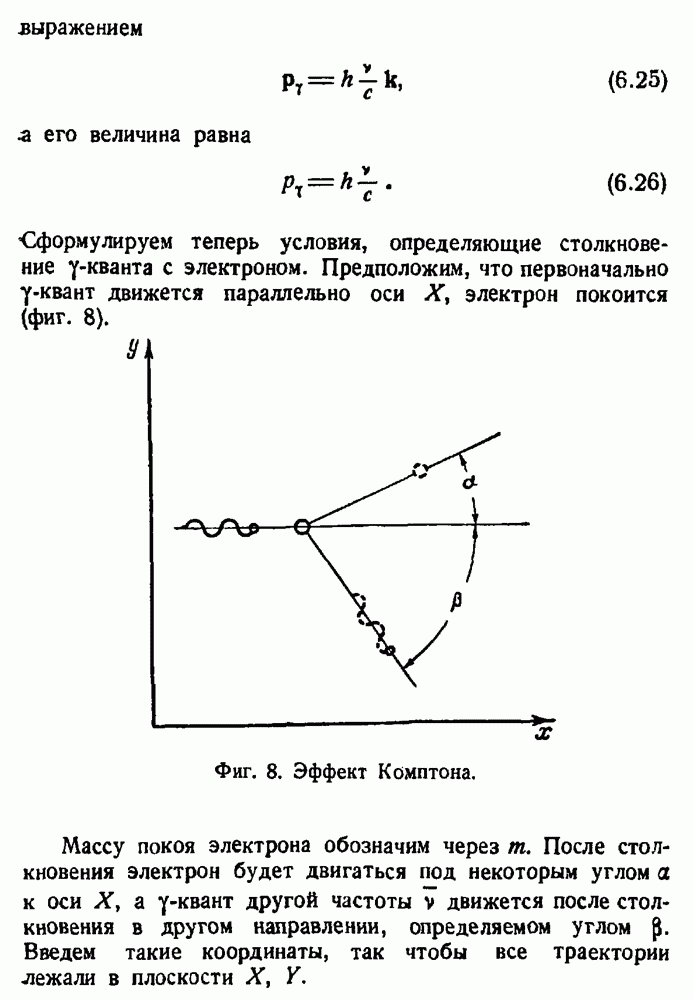
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
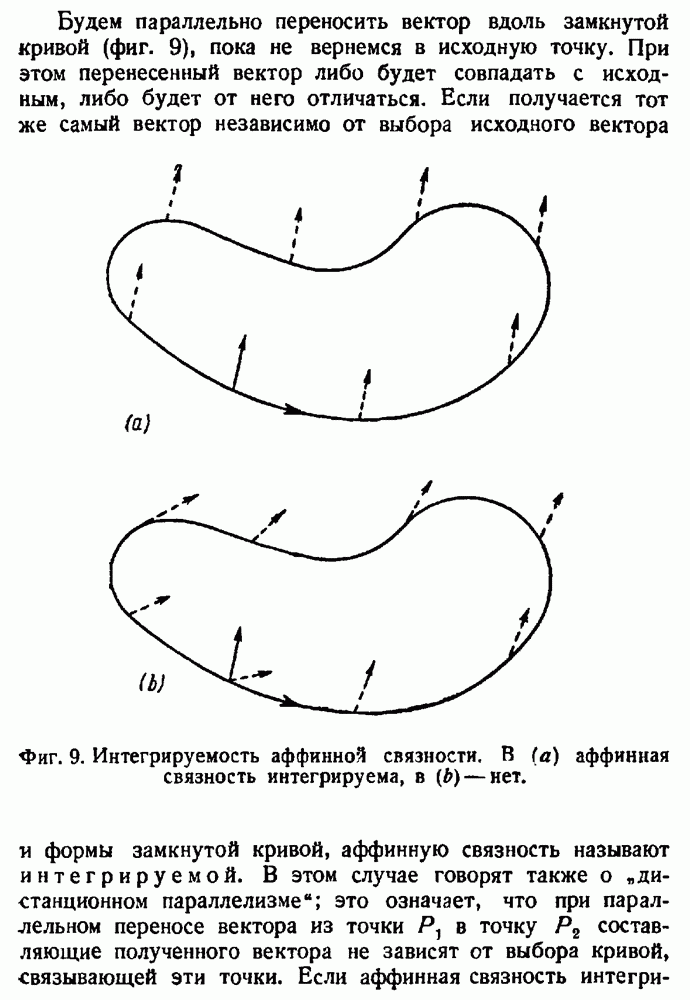
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.