| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Вариационный принцип Вейля.
Вейль стремился получить уравнения поля, как уравнения Лагранжа-Эйлера вариационного принципа. Покажем следующее: если вариационный принцип инвариантен относительно преобразования координат, то эти уравнения всегда удовлетворяют необходимому количеству тождеств.
Рассмотрим вариационный принцип в виде:

где индексы  служат для нумерации переменных поля у. Если варьировать
служат для нумерации переменных поля у. Если варьировать  так, чтобы вариации и их производные вплоть до нужного порядка исчезали на границе области
так, чтобы вариации и их производные вплоть до нужного порядка исчезали на границе области  то вариация интеграла (16.26) примет вид
то вариация интеграла (16.26) примет вид

и уравнения

будут уравнениями Эйлера-Лагранжа вариационного принципа (16.26). Будем изменять переменные  на величины, соответствующие бесконечно малым преобразованиям координат
на величины, соответствующие бесконечно малым преобразованиям координат

Если и их производные исчезают на границе V, то значение  не изменится при вариации, независимо от того, удовлетворяются уравнения (16.28) или нет.
не изменится при вариации, независимо от того, удовлетворяются уравнения (16.28) или нет.
При преобразовании координат (16.29) функции  претерпевают бесконечно малые изменения
претерпевают бесконечно малые изменения  которые зависят от
которые зависят от  и от специального вида закона преобразования
и от специального вида закона преобразования  Рассмотрим случай, когда некоторые из
Рассмотрим случай, когда некоторые из  являются компонентами контравариантного вектора
являются компонентами контравариантного вектора  При переходе
При переходе
от координат  к координатам
к координатам  преобразованные компоненты вектора станут новыми функциями от
преобразованные компоненты вектора станут новыми функциями от  ; кроме того, аргументы этих функций
; кроме того, аргументы этих функций  должны быть заменены на Если выразить преобразованные компоненты векторного поля
должны быть заменены на Если выразить преобразованные компоненты векторного поля  как функции первоначальных координат, получим
как функции первоначальных координат, получим

В каждой мировой точке величины  равны
равны  т. е.
т. е.

где  — соответственно первоначальные и новые координаты в одной и той же мировой точке. Чтобы найти разность значений функций
— соответственно первоначальные и новые координаты в одной и той же мировой точке. Чтобы найти разность значений функций  для одинаковых значений соответствующих аргументов, нужно сравнить
для одинаковых значений соответствующих аргументов, нужно сравнить  в мировой точке с координатами
в мировой точке с координатами  в мировой точке с координатами
в мировой точке с координатами  Тогда получим
Тогда получим

и поэтому бесконечно малым изменением функции  будет
будет

Вообще говоря, компоненты тензоров и тензорных плотностей преобразуются согласно законам типа

где постоянные зависят от особенностей законов преобразования. В законе преобразования имеется один член, не относящийся к типу (16.34). Чтобы его учесть, предположим, что рассматриваемые переменные поля преобразуются согласно закону

где  — добавочные постоянные.
— добавочные постоянные.
Чтобы найти условие инвариантности  относительно общих преобразований координат, заменим
относительно общих преобразований координат, заменим  в (16.27) его выражением (16.35). Тогда
в (16.27) его выражением (16.35). Тогда  должно обращаться в нуль при произвольных
должно обращаться в нуль при произвольных  если только
если только  и его первые и вторые производные исчезают на границе области V. Имеем
и его первые и вторые производные исчезают на границе области V. Имеем

Производя ряд интегрирований по частям, получим отсюда

и если  произвольны внутри V, то уравнения Эйлера-Лагранжа должны удовлетворять четырем дифференциальным тождествам
произвольны внутри V, то уравнения Эйлера-Лагранжа должны удовлетворять четырем дифференциальным тождествам

Рассмотрим теперь вариационный принцип в градиентно-инвариантной теории Вейля. Подинтегральное выражение инвариантного интеграла должно быть скалярной плотностью с весом  Скалярная плотность кривизны
Скалярная плотность кривизны

имеет вес  Поэтому лангранжиан вариационного принципа должен быть квадратичной функцией кривизны. Существует несколько скалярных плотностей с весом
Поэтому лангранжиан вариационного принципа должен быть квадратичной функцией кривизны. Существует несколько скалярных плотностей с весом  которые могут быть образованы из компонент тензора кривизны, именно:
которые могут быть образованы из компонент тензора кривизны, именно:

Первые три из них являются дифференциальными величинами четвертого порядка относительно  Наиболее общий лагранжиан такого порядка должен быть линейной комбинацией четырех выражений (16.39). Вариации десяти
Наиболее общий лагранжиан такого порядка должен быть линейной комбинацией четырех выражений (16.39). Вариации десяти
 независимы друг от друга, но связаны добавочным условием неизменности нормировки детерминанта
независимы друг от друга, но связаны добавочным условием неизменности нормировки детерминанта 

Это дополнительное условие легко учесть, применяя метод неопределенных множителей Лагранжа. Появляющийся, таким образом, в уравнениях добавочный параметр можно, однако, исключить, тогда в конечном счете получим тринадцать дифференциальных уравнений для тринадцати переменных  удовлетворяет условию (16.1)). Эти тринадцать уравнений удовлетворяют четырем дифференциальным тождествам (16.37).
удовлетворяет условию (16.1)). Эти тринадцать уравнений удовлетворяют четырем дифференциальным тождествам (16.37).
Существуют два основных возражения относительно уравнений этого типа. Во-первых, они являются дифференциальными уравнениями четвертого порядка относительно  Имеются все основания полагать, что уравнения такого высокого порядка имеют гораздо больше решений, чем уравнения поля второго порядка, поэтому очень трудно объяснить, почему решения этих гипотетических уравнений четвертого порядка так хорошо аппроксимируются в природе решениями уравнений второго порядка. Во-вторых, лагранжиан вариационного принципа не является однозначно определенным, так как для него годится любая линейная комбинация выражений (16.39). Таким образом, не достигается желательной унификации поля, так как остается еще чисто «электромагнитная скалярная плотность [последнее выражение (16.39)], которая может входить в лагранжиан с произвольным коэфициентом.
Имеются все основания полагать, что уравнения такого высокого порядка имеют гораздо больше решений, чем уравнения поля второго порядка, поэтому очень трудно объяснить, почему решения этих гипотетических уравнений четвертого порядка так хорошо аппроксимируются в природе решениями уравнений второго порядка. Во-вторых, лагранжиан вариационного принципа не является однозначно определенным, так как для него годится любая линейная комбинация выражений (16.39). Таким образом, не достигается желательной унификации поля, так как остается еще чисто «электромагнитная скалярная плотность [последнее выражение (16.39)], которая может входить в лагранжиан с произвольным коэфициентом.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
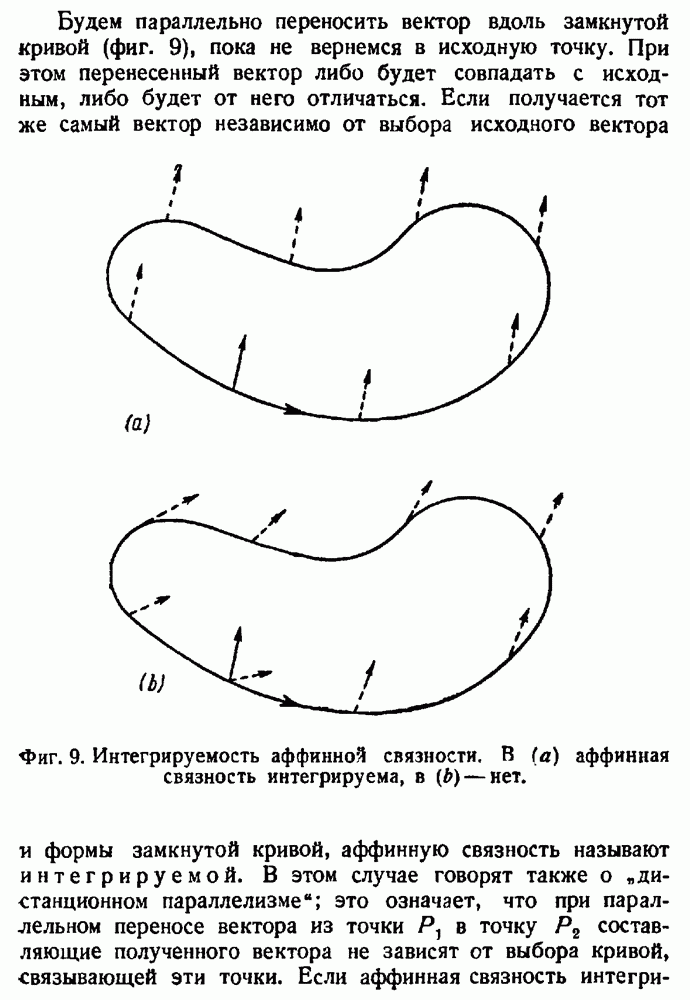
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.