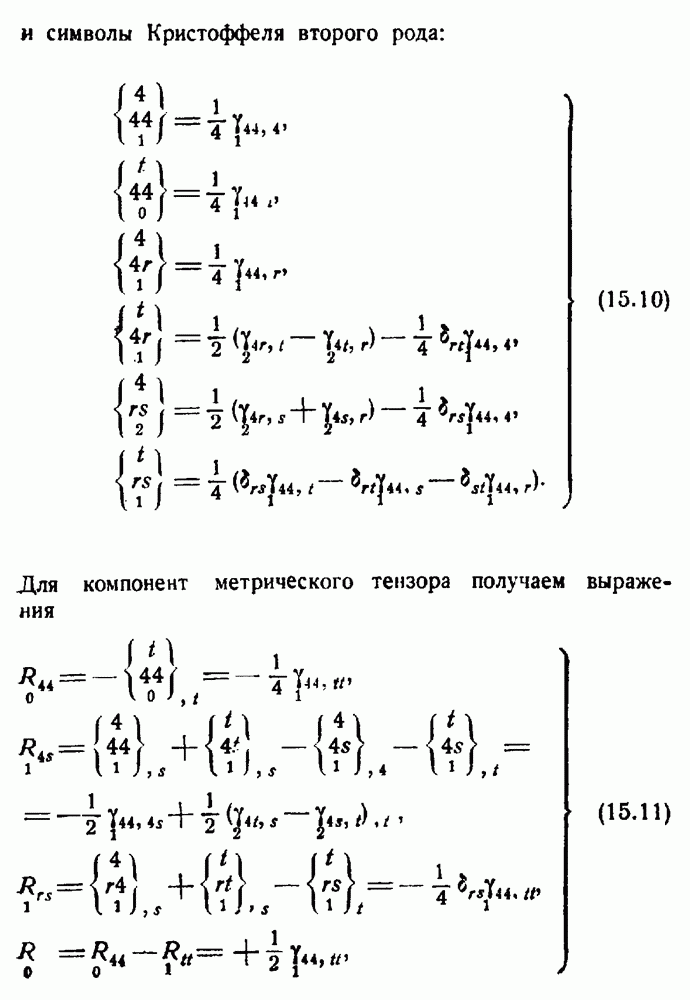| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Первое приближение и закон сохранения массы.
В первом приближении используем следующие значения компонент:

С их помощью образуем символы Кристоффеля первого рода:

и символы Кристоффеля второго рода:

Для компонент метрического тензора получаем выражения

а уравнения поля в первом приближении запишутся в виде:

В качестве решения первого уравнения можно выбрать выражение

Это решение соответствует случаю  точечных масс. Все полюса высших порядков мы из рассмотрения исключили. Масса
точечных масс. Все полюса высших порядков мы из рассмотрения исключили. Масса  точечной массы, согласно (12.34), равна:
точечной массы, согласно (12.34), равна:

Возможно предположить, что эта масса может еще зависеть от временной координаты  но вскоре будет показано, что в действительности массы постоянны.
но вскоре будет показано, что в действительности массы постоянны.  функций у от
функций у от  определяют положения
определяют положения  точечных масс в каждый момент времени
точечных масс в каждый момент времени 
Докажем теперь с помощью трех уравнений  что параметры
что параметры  (а поэтому и массы М) постоянны. Это
(а поэтому и массы М) постоянны. Это
доказательство проводится с помощью метода, последующий этап приближения которого способствует нам в выводе (классических) уравнений движения. Прежде всего докажем следующую лемму: если выражение, зависящее от нескольких индексов, антисимметрично по отношению к двум из них, скажем  и t, то его обыкновенная дивергенция по одному из этих индексов, скажем по
и t, то его обыкновенная дивергенция по одному из этих индексов, скажем по  эквивалентна ротору, компоненты которого характеризуются вторым (не немым) антисимметричным индексом (в нашем случае
эквивалентна ротору, компоненты которого характеризуются вторым (не немым) антисимметричным индексом (в нашем случае  ). При этом, как обычно, предполагается, что
). При этом, как обычно, предполагается, что  пробегают значения от 1 до 3. Доказательство проводится путем непосредственного составления интересующих нас величин. Пусть
пробегают значения от 1 до 3. Доказательство проводится путем непосредственного составления интересующих нас величин. Пусть  антисимметрично в
антисимметрично в  и
и  Обозначим
Обозначим

Выражения  тогда равны следующим:
тогда равны следующим:

аналогичные соотношения справедливы и для других двух дивергенций.
Вернемся к уравнениям  Они содержат величину
Они содержат величину  являющуюся дивергенцией антисимметричного выражения. Эта дивергенция эквивалентна ротору, компоненты которого нумеруются индексом
являющуюся дивергенцией антисимметричного выражения. Эта дивергенция эквивалентна ротору, компоненты которого нумеруются индексом  По теореме Стокса интеграл ротора по замкнутой поверхности равен нулю. Другими словами,
По теореме Стокса интеграл ротора по замкнутой поверхности равен нулю. Другими словами,

здесь  означает косинус угла между координатой и нормалью к элементу поверхности
означает косинус угла между координатой и нормалью к элементу поверхности  Применим (15.16) к замкнутой поверхности, окружающей
Применим (15.16) к замкнутой поверхности, окружающей  особенность, но выбранную так, чтобы на самой поверхности не было особенностей. На поверхности (но не внутри ее) должны удовлетворяться уравнения поля, поэтому имеем
особенность, но выбранную так, чтобы на самой поверхности не было особенностей. На поверхности (но не внутри ее) должны удовлетворяться уравнения поля, поэтому имеем

Это уравнение выражает собой то условие, что параметры  остаются постоянными, ибо интеграл
остаются постоянными, ибо интеграл  представляет собой просто «число силовых линий», исходящих из области S, и поэтому пропорционален
представляет собой просто «число силовых линий», исходящих из области S, и поэтому пропорционален  Уравнение (15.17) соответствует условию
Уравнение (15.17) соответствует условию

Последнее, что можно сделать в первом приближении, это решить дифференциальные уравнения  относительно
относительно 

где  теперь рассматриваются как постоянные. Уравнения (15.6) и (15.7) показывают, что эти уравнения
теперь рассматриваются как постоянные. Уравнения (15.6) и (15.7) показывают, что эти уравнения
удовлетворяются выражениями:

(точкой обозначено дифференцирование по  ), что доказывается просто подстановкой в (15.19).
), что доказывается просто подстановкой в (15.19).
Для получения уравнений движения необходимо перейти ко второму приближению.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
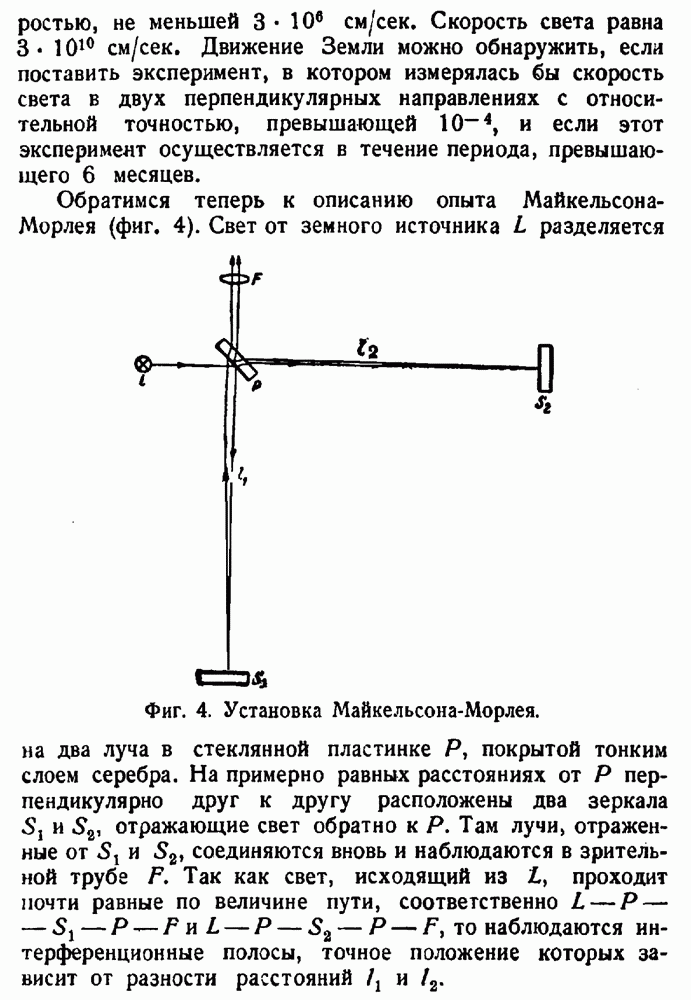
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
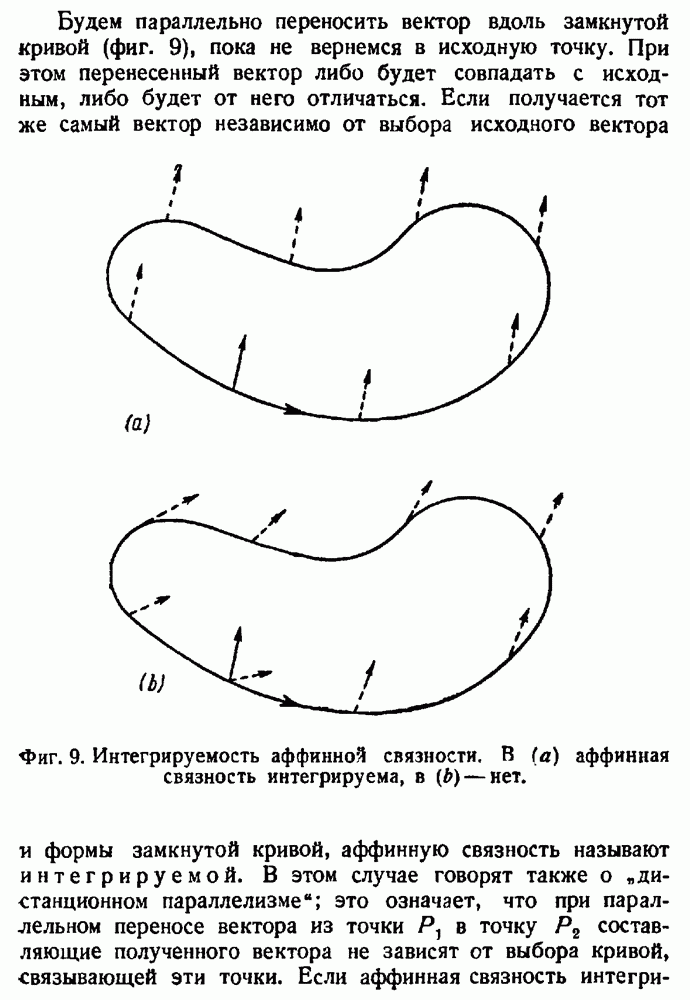
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.