| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приближенный метод.
В релятивистской теории гравитации, так же как в электродинамике, электрические заряды и массы представляются особыми точками переменных поля. При наличии особенностей изменение поля во времени полностью не определяется. Рассмотрим, например, поле Шварцшильда. Вблизи начала координат имеется особая область, сферическая поверхность г=2хт. Окружим эту особую область небольшой двумерной поверхностью S, снаружи которой поле везде регулярно и удовлетворяет уравнениям поля.
Поле Шварцшильда статично. Однако если мы ничего не знаем относительно поля внутри S, то может возникнуть излучение электромагнитных или гравитационных волн через поверхность S изнутри наружу. Если это излучение имеет преимущественное направление, произойдет „отдача”, т. е. ускорение всей особой области в противоположном направлении.
Другими словами, нельзя ожидать, что закон движения справедлив для всякой особенности. Движение особенности
может быть определено, если она не является источником излучения. Поэтому закон движения может быть получен только в предположении, что особенность является и остается простым полюсом (уравнения поля могут также иметь решения, соответствующие «диполям масс и т. п.) и что не происходит спонтанного излучения.
Эти условия трудно сформулировать инвариантным образом. Существуют, например, гравитационные волны, связанные с ускоренным движением точечной массы. Различие между в спонтанными волнами и „гравитационным тормозным излучением имеет простой физический смысл, однако его математическая формулировка не представляется возможной.
Чтобы избежать этих трудностей, Эйнштейн и его сотрудники вынуждены были получать законы движения с помощью приближенного метода, при котором математическая формулировка необходимых предположений значительно проще.
Их метод аппроксимации аналогичен обычному методу, описанному в главе XII, который в первом приближении приводит к „линеаризации уравнений поля. Однако он отличается от последнего одним важным обстоятельством. Предположение, что спонтанного излучения не происходит, эквивалентно предположению, что переменные поля меняются со временем не быстрее, чем этого требует движение особенности. Скорость последнего мала в сравнении со скоростью света. Поэтому предполагается, что дифференцирование по  (измеренному в релятивистских единицах) приводит к величинам высшего порядка.
(измеренному в релятивистских единицах) приводит к величинам высшего порядка.
Это предположение можно сформулировать несколько иным способом. Если снова ввести метрические единицы (т. е. если в качестве метрического тензора плоского пространства использовать  вместо
вместо  скорости материальных тел будут порядка единицы, а дифференцирование переменных поля по
скорости материальных тел будут порядка единицы, а дифференцирование переменных поля по  не будет менять их порядка величины. С другой стороны,
не будет менять их порядка величины. С другой стороны,  будет тогда рассматриваться, как малая величина, которая может служить параметром разложения переменных поля в степенные ряды
будет тогда рассматриваться, как малая величина, которая может служить параметром разложения переменных поля в степенные ряды
(параметр X главы XII). Тензор  например, примет вид
например, примет вид

Член  опускается, так как в противном случае
опускается, так как в противном случае  было бы порядка единицы, в связи с чем первое приближение стало бы нелинейным. Как и в главе XII, введем величины
было бы порядка единицы, в связи с чем первое приближение стало бы нелинейным. Как и в главе XII, введем величины  помощи уравнений
помощи уравнений

Y также разложим в степенные ряды по 

Покоящиеся точечные массы представляются решениями уравнений поля, которые в первом приближении даются уравнениями (12.31а) и (12.34) или в метрических единицах выражениями

Поэтому предположим, что величины  равны нулю. Для получения в том же приближении поля точечной массы
равны нулю. Для получения в том же приближении поля точечной массы
нужно произвести преобразование Лорентца; преобразуется согласно закону:

где  имеют те же значения, что и в главе V (уравнение (5.111)). Величины
имеют те же значения, что и в главе V (уравнение (5.111)). Величины 

преобразуется по тому же закону, что и  так как закон преобразования линеен, и
так как закон преобразования линеен, и  остаются неизменными.
остаются неизменными.
По тому же закону преобразуются и  что может быть проверено непосредственным вычислением. Применяя эти законы преобразования к уравнению (15.4), получим следующие выражения:
что может быть проверено непосредственным вычислением. Применяя эти законы преобразования к уравнению (15.4), получим следующие выражения:

Коэфициенты  отличаются от единицы только малыми величинами порядка
отличаются от единицы только малыми величинами порядка  Коэфициенты
Коэфициенты  представляются выражениями
представляются выражениями

и таким образом являются малыми величинами порядка  Отсюда видно, что величины у, к которым приводит преобразование, того же порядка, а величины
Отсюда видно, что величины у, к которым приводит преобразование, того же порядка, а величины  — порядка
— порядка  Величины
Величины  для поля точечной массы исчезают, даже если эта масса движется.
для поля точечной массы исчезают, даже если эта масса движется.
В первом приближении естественно принять, что полное поле является просто суммой полей различных точечных масс. Разложение  будем начинать, согласно сказанному, с члена, содержащего
будем начинать, согласно сказанному, с члена, содержащего 
Подставляя разложения (15.1) и (15.3) в уравнения поля и приравнивая коэфициенты при членах с одинаковыми степенями  получим ряд систем уравнений. Метод
получим ряд систем уравнений. Метод
Эйнштейна, Инфельда и Гофмана и заключается в получении и решении таких систем уравнений. Каждая последующая система уравнений содержит ряд величин  не входивших в предыдущие системы, и, кроме того, ряд других
не входивших в предыдущие системы, и, кроме того, ряд других  определенных ранее. Новые“ величины всегда входят линейно, так что на каждой последующей стадии приближенного метода приходится решать только линейные неоднородные дифференциальные уравнения.
определенных ранее. Новые“ величины всегда входят линейно, так что на каждой последующей стадии приближенного метода приходится решать только линейные неоднородные дифференциальные уравнения.
Определение движения особенностей производится следующим образом. На каждой стадии метода приближения нужно решить десять линейных неоднородных уравнений относительно десяти величин  Левые части этих уравнений, содержащие еще неизвестные величины, не независимы друг от друга, а удовлетворяют четырем дифференциальным тождествам. Если правые части (которые содержат уже определенные величины) не удовлетворяли бы тем же тождествам, дифференциальные уравнения были бы не совместимы друг с другом. Таким образом, каждая стадия приближенного метода налагает условия на предыдущую. В отсутствии особенностей эти условия ничего не дают, однако при наличии особенностей они являются как раз уравнениями движения.
Левые части этих уравнений, содержащие еще неизвестные величины, не независимы друг от друга, а удовлетворяют четырем дифференциальным тождествам. Если правые части (которые содержат уже определенные величины) не удовлетворяли бы тем же тождествам, дифференциальные уравнения были бы не совместимы друг с другом. Таким образом, каждая стадия приближенного метода налагает условия на предыдущую. В отсутствии особенностей эти условия ничего не дают, однако при наличии особенностей они являются как раз уравнениями движения.
Эйнштейн и его сотрудники при помощи этого метода довели вычисления до той стадии, на которой начинают сказываться релятивистские эффекты. Мы ограничимся приближением, приводящим к классическим уравнениям движения, так как на этой стадии уже можно видеть связь между уравнениями поля и уравнениями движения.
Разложим компоненты тензора кривизны, символы Кристоффеля и ковариантные и контравариантные компоненты метрического тензора в степенные ряды по  и приравняем коэфициенты разложения по индексам, написанным под каждым символом, причем нижний индекс
и приравняем коэфициенты разложения по индексам, написанным под каждым символом, причем нижний индекс  будет относиться к коэфициенту при
будет относиться к коэфициенту при  Например, будет означать ту часть
Например, будет означать ту часть  которая умножается на
которая умножается на 
 ту часть
ту часть  которая умножается на
которая умножается на  и так далее.
и так далее.
Используя выражения для метрического тензора (15.1), найдем, что разложения в ряды компонент начинаются со следующих степеней  . В дальнейшем нам понадобятся только первые неисчезающие члены разложения каждой компоненты, т. е.
. В дальнейшем нам понадобятся только первые неисчезающие члены разложения каждой компоненты, т. е.  , кроме того, величина
, кроме того, величина  Чтобы получить их значения, вычислим
Чтобы получить их значения, вычислим  символы Кристоффеля первого и второго рода и с точностью до членов с
символы Кристоффеля первого и второго рода и с точностью до членов с 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
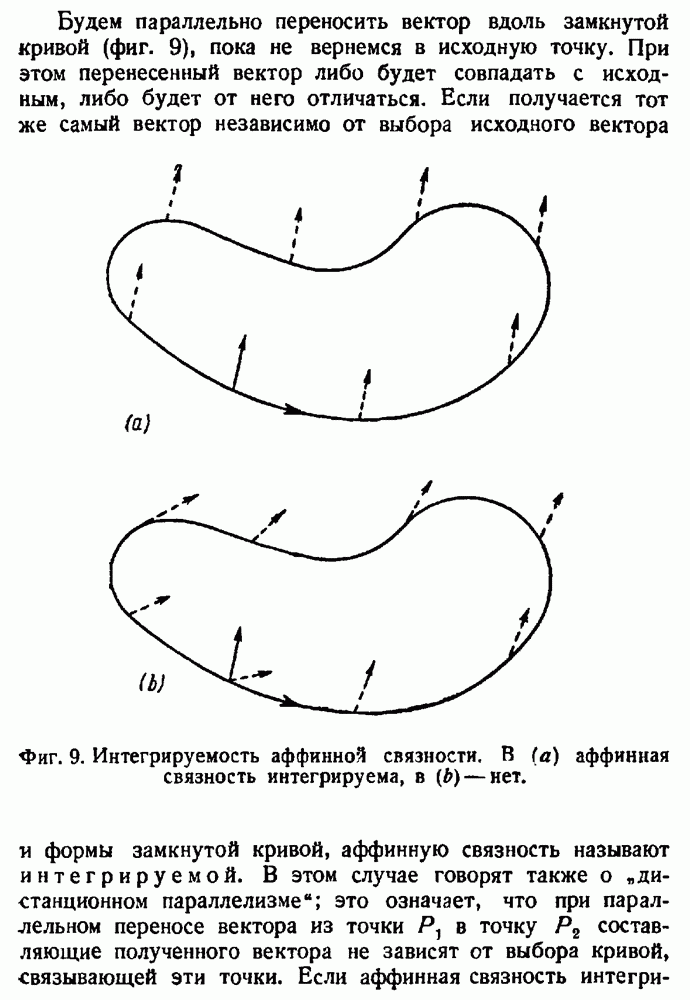
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.