| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Движение перигелия Меркурия.
Рассмотрим движение небольшого тела в поле Шварцшильда, создаваемом телом массы значительно большего размера. При этом удобно ввести полярные координаты, определяемые следующими уравнениями:

В этих координатах метрический тензор имеет вид:

а все остальные его компоненты равны нулю.
Уравнениями движения малой частицы в этом поле Шварцшильда будут

Вычислим символы Кристоффеля  Если для краткости ввести обозначение
Если для краткости ввести обозначение

для неисчезающих символов Кристоффеля получим:

Если упростить нашу механическую задачу, предполагая, что движение происходит в плоскости  то уравнения движения получим в виде следующих дифференциальных уравнений:
то уравнения движения получим в виде следующих дифференциальных уравнений:

Один из интегралов этих уравнений дает определение дифференциала собственного времени

Первое уравнение (14.6) имеет интеграл

Последнее уравнение (14.6) дает интеграл момента количества движения

Интеграл (14.8) соответствует интегралу энергии. Три уравнения (14.7), (14.8) и (14.9) заменяют уравнения второго порядка (14.6). Наконец, с помощью уравнения (14.8) можно исключить координатное время t, в результате чего получаем два уравнения:

где  заменено его значением 1—5. Отличие этих уравнений от классических уравнений движения тела в ньютоновском поле состоит в том, что последний член первого уравнения (14.10) отсутствует в нерелятивистских уравнениях и что дифференцирование производится по собственному времени, а не по координатному. Классическими интегралами энергии и момента количества движения будут
заменено его значением 1—5. Отличие этих уравнений от классических уравнений движения тела в ньютоновском поле состоит в том, что последний член первого уравнения (14.10) отсутствует в нерелятивистских уравнениях и что дифференцирование производится по собственному времени, а не по координатному. Классическими интегралами энергии и момента количества движения будут

где  — масса движущегося тела.
— масса движущегося тела.
Уравнения (14.10) нельзя решить точно. Однако возможно найти такое приближенное решение, в котором первое приближение соответствует классической траектории тела, а второе приближение показывает отклонение решений релятивистских уравнений (14.10) от классических (14.11).
Умножим первое уравнение (14.10) на и подставим значение этого множителя из второго уравнения. Тогда
получим дифференциальное уравнение

которое после введения функции  переходит в
переходит в

Дифференцируя по  получим отсюда уравнение второго порядка:
получим отсюда уравнение второго порядка:

Отличие этого релятивистского уравнения от соответствующего классического обусловлено вторым членом в круглых скобках,  Согласно (14.9) этот член равен
Согласно (14.9) этот член равен

другими словами, он приблизительно пропорционален квадрату компоненты скорости, перпендикулярной радиусу-вектору. В „релятивистских единицах" времени, в которых скорость света равна единице, скорость звезд, например, мала по сравнению с единицей. Релятивистский член в уравнении (14.14) является поэтому поправкой высшего порядка. Решением уравнения

будет

где  — постоянные интегрирования,
— постоянные интегрирования,  представляет собой эксцентриситет эллипса, а
представляет собой эксцентриситет эллипса, а  определяет положение перигелия.
определяет положение перигелия.
Решения уравнений (14.14), которые апроксимируются эллипсами, являются периодическими. Уравнение (14.13)
каждому значению а ставит в соответствие два значения отличающиеся только знаком. Решения будут периодическими, если правая часть уравнения (14.13) имеет два нуля в области положительных значений и и положительна между этими двумя нулями. В этом случае решение будет осциллировать между этими двумя нулями. Приближенное решение (14.17) имеет период  т. е. представляется замкнутыми орбитами. Периоды точных решений уравнения (14.14) будут, однако, отличаться от
т. е. представляется замкнутыми орбитами. Периоды точных решений уравнения (14.14) будут, однако, отличаться от  малой величиной. Разложим периодические решения уравнения
малой величиной. Разложим периодические решения уравнения

в ряды Фурье

Если  малая постоянная, решение может быть апроксимировано выражением
малая постоянная, решение может быть апроксимировано выражением

Предположим поэтому, что  в этом приближении равно а, а
в этом приближении равно а, а  и другие коэфициенты, по крайней мере, порядка X. Иначе говоря, выражение (14.19) мы заменяем рядом
и другие коэфициенты, по крайней мере, порядка X. Иначе говоря, выражение (14.19) мы заменяем рядом

Подставим это выражение в (14.18), пренебрегая членами второго и высшего порядков относительно  Для а" получим
Для а" получим

Для  имеем
имеем

Уравнение (14.18) поэтому переходит в

Приравнивая постоянные члены и коэфициенты при  и при
и при  , получим соотношения
, получим соотношения

Нас интересует только второе соотношение, определяющее  . Легко видеть, что
. Легко видеть, что  мало отличается от единицы:
мало отличается от единицы:

Подставляя для X и а их значения, определяемые (14.14), найдем

Угол между двумя последовательными перигелиями поэтому равен

Смещение перигелия планетной орбиты на  радиан за время полного оборота может быть наблюдаемо у Меркурия, для которого оно составляет
радиан за время полного оборота может быть наблюдаемо у Меркурия, для которого оно составляет  в столетие. Предсказываемое и наблюдаемое значения смещения хороша согласуются в пределах экспериментальных ошибок астрономических наблюдений.
в столетие. Предсказываемое и наблюдаемое значения смещения хороша согласуются в пределах экспериментальных ошибок астрономических наблюдений.
Специальная теория относительности также предсказывает прецессионный эффект при движении тела в поле  потенциалом у. Однако количественно она дает результат, отличный от полученного в общей теории относительности.
потенциалом у. Однако количественно она дает результат, отличный от полученного в общей теории относительности.
Чтобы убедиться в этом, возвратимся к рассмотренной в главе IX релятивистской трактовке атома водорода, данной Зоммерфельдом. Уравнения (9.27) соответствуют уравнениям (14.7), (14.8) и (14.9) настоящей главы. Их можно записать в виде:

в последнем уравнении можно заменить его выражением из первого уравнения, что приводит к уравнению, не содержащему t:

Умножая это уравнение на

получим:

Вводя опять новую функцию  , найдем дифференциальное уравнение для а:
, найдем дифференциальное уравнение для а:

Дифференцирование по  приводит к уравнению второго порядка
приводит к уравнению второго порядка

которое имеет следующие решения:

Отсюда получаем величину смещения перигелия за один период

Чтобы сравнить это выражение с (14.24), нужно заменить  (коэфициент кулоновского взаимодействия) на
(коэфициент кулоновского взаимодействия) на  (коэффициент гравитационного взаимодействия в законе Ньютона).
(коэффициент гравитационного взаимодействия в законе Ньютона).
Далее, постоянную К нужно положить равной  постоянная, фигурирующая в уравнении (14.24)], так как
постоянная, фигурирующая в уравнении (14.24)], так как  в уравнении (14.25) измеряется в метрических единицах. Таким образом, вместо (14.32) получаем
в уравнении (14.25) измеряется в метрических единицах. Таким образом, вместо (14.32) получаем

т. е. смещение, в шесть раз меньшее, чем в общей теории от нос ительности.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
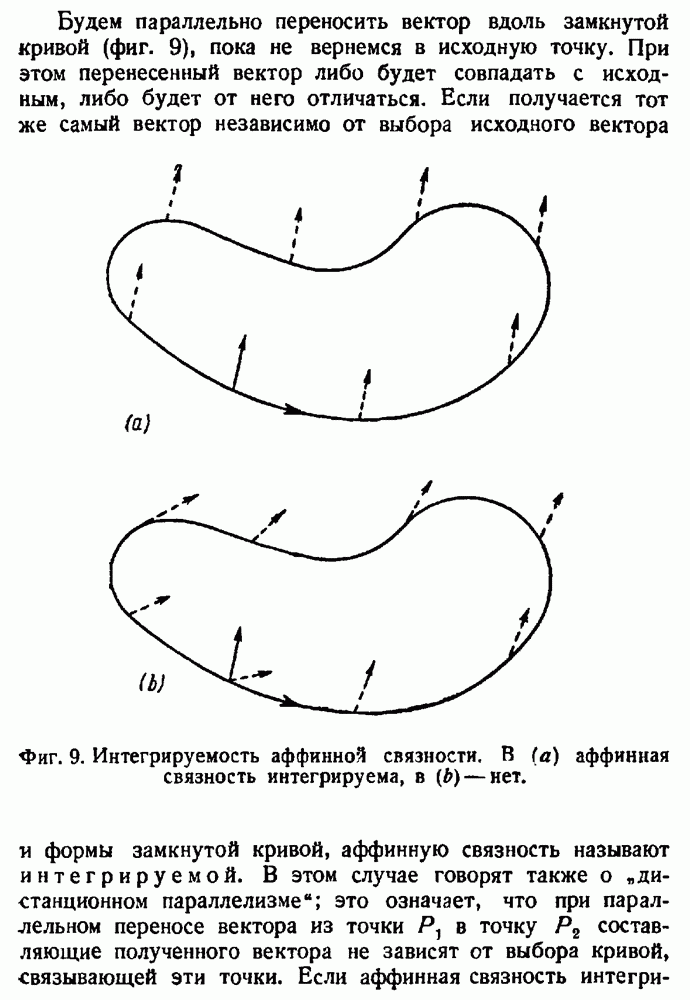
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.