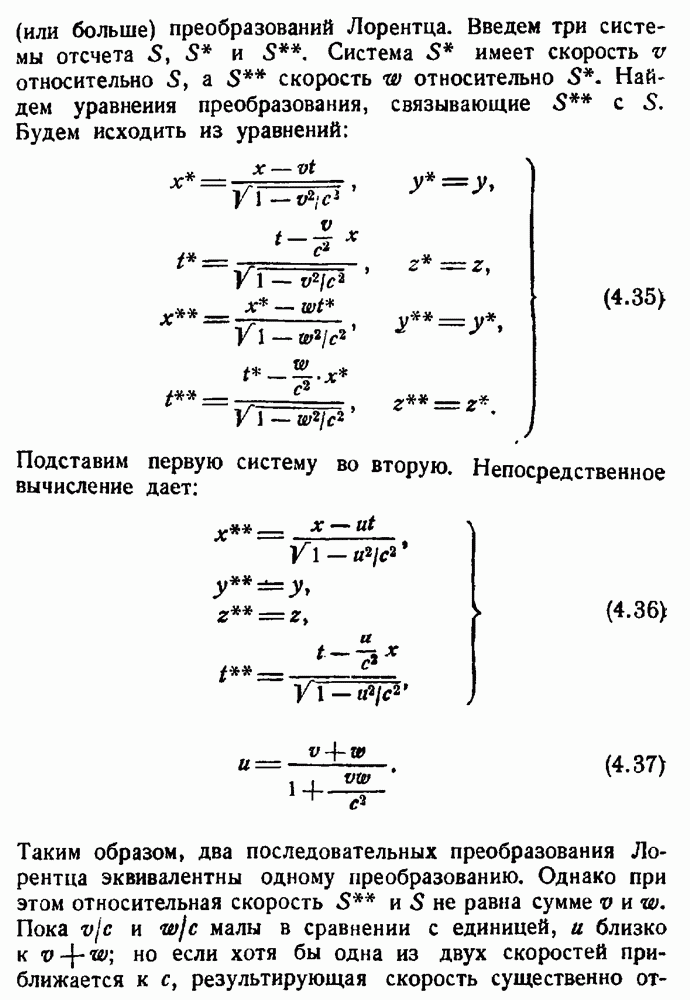
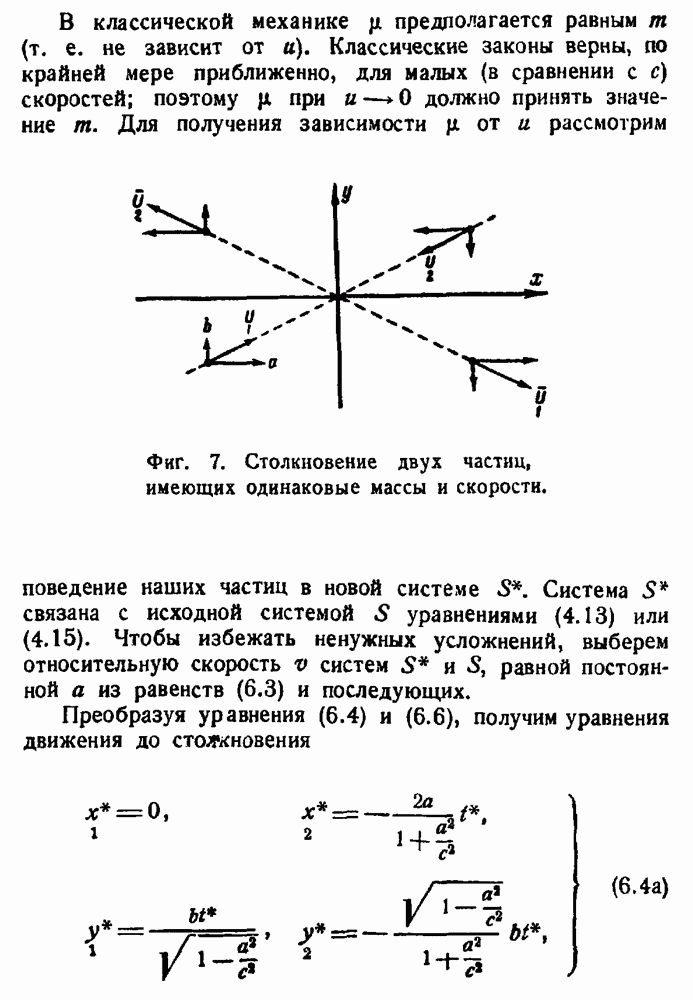
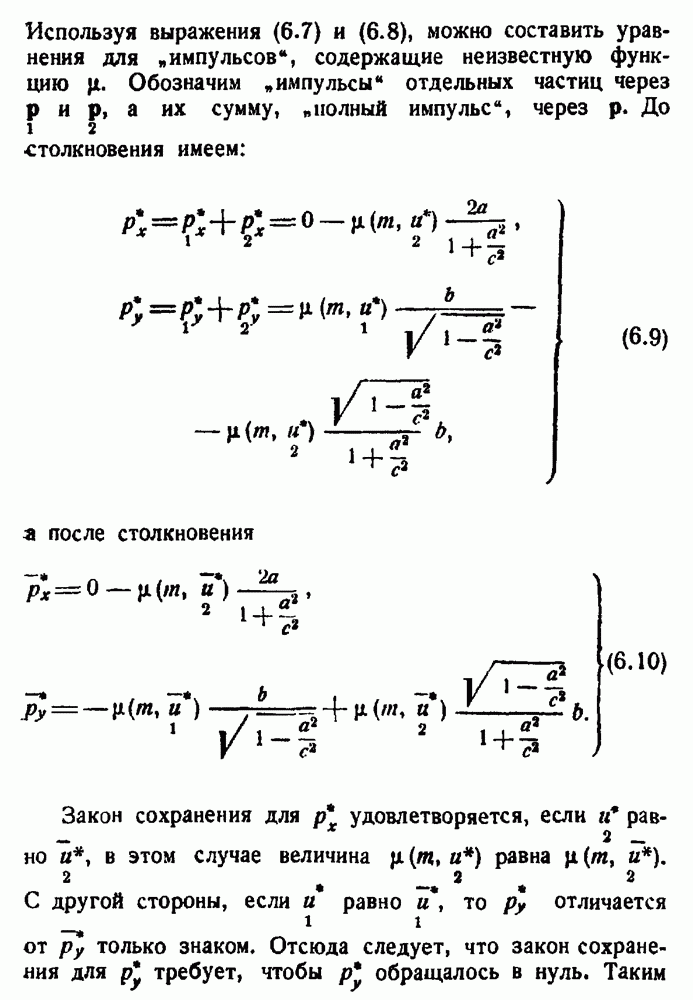
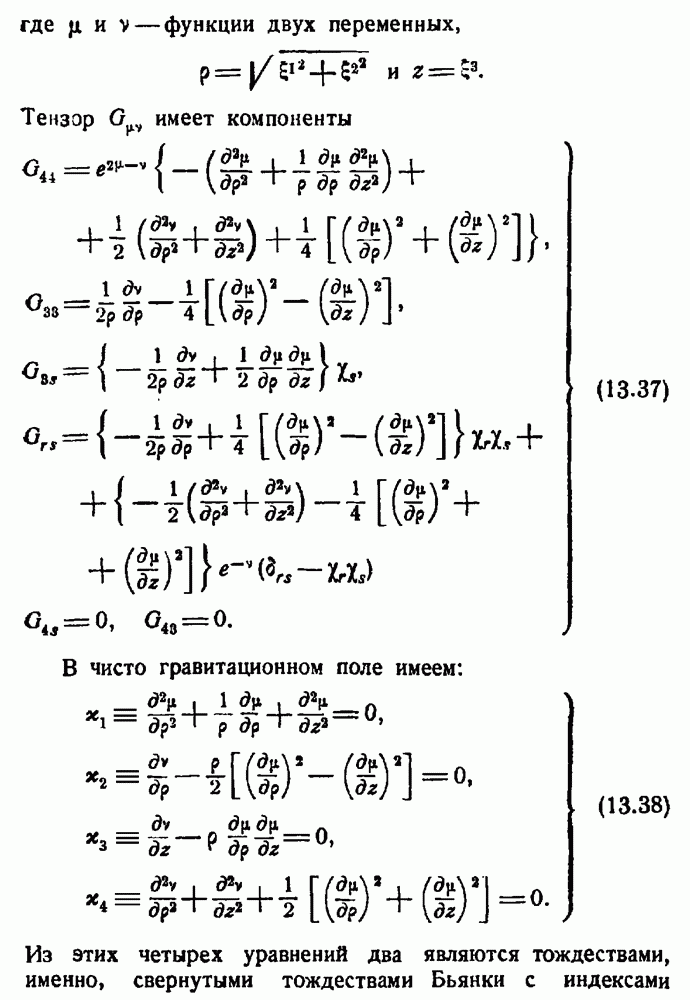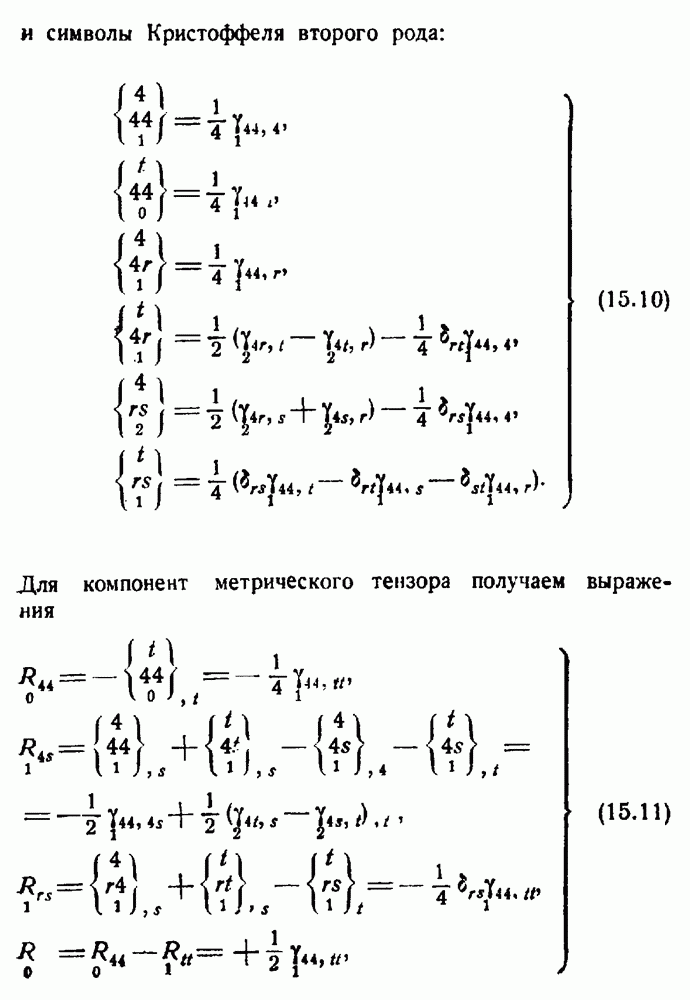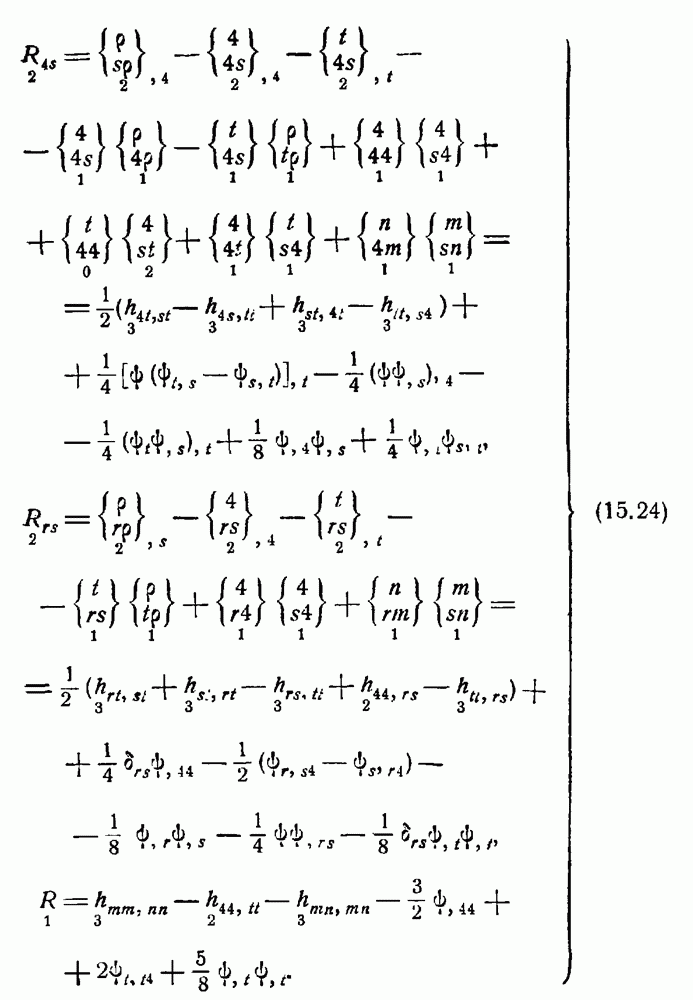| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
Проблемы, стоящие перед классической оптикой.
В течение XIX в. развилась новая отрасль физики, не укладывающаяся в рамки классической механики. Этой отраслью была электродинамика. Пока были известны только эффекты электростатического и магнитостатического характера, они могли трактоваться в рамках механики путем введения электростатических и магнитостатических потенциалов, зависящих лишь от расстояний между электрическими зарядами или магнитными полюсами.
Взаимосвязь электрических и магнитных полей требует иной трактовки. Это ясно следует уже из эксперимента Эрстеда, обнаружившего, что магнитная стрелка отклоняется от своего нормального направления север—юг током, текущим в том же направлении. С изменением направления тока, знак отклонения меняется на обратный. Очевидно, что магнитное действие электрических токов, т. е. движущихся зарядов, зависит не только от расстояния, но также и от скорости этих зарядов. Более того, сила в заданной точке не направлена по прямой, соединяющей эту точку с зарядом. Таким образом, идеи ньютоновской механики оказались здесь уже не применимыми.
Максвеллу удалось сформулировать законы электромагнетизма введением нового понятия — понятия о поле. Как мы видели в предыдущей главе, в механике система полностью описывается заданием положений составляющих ее точечных масс как функций времени. В теории Максвелла мы имеем дело с рядом переменных поля, каковыми являются компоненты напряженностей электрического и магнитного полей. В то время как координаты точек в механике определяются только как функции времени, переменные
поля определяются для всех значений, как временной координаты, так и трех пространственных координат, и являются, таким образом, функциями четырех независимых переменных.
В максвелловской теории поля предполагается далее, что изменение переменных поля во времени в заданной точке пространства зависит только от непосредственной окрестности этой точки. Возмущение поля в некоторой точке вызывает изменение поля в соседних точках, которые в свою очередь передают его дальше; таким образом, первоначальное возмущение распространяется с конечной скоростью и в конце концов передается на большие расстояния. Таким образом, «дальнодействие» может быть осуществлено полем, но всегда за конечный промежуток времени. Законы теории поля представляются дифференциальными уравнениями в частных производных, содержащими частные производные переменных поля по пространственным координатам и времени.
Сила, действующая на точечную массу, определяется полем в непосредственной окрестности этой точки. Наоборот, присутствие точечной массы может изменить и обычно изменяет поле.
Так как характер максвелловской теории электромагнетизма существенно отличен от механики Ньютона, то из справедливости принципа относительности в механике ни в коем случае не вытекает его справедливость в электродинамике. Вопрос о том, насколько применим этот принцип к электродинамике, должен быть предметом специального исследования.
Полное исследование такого рода должно было бы установить законы преобразования для интенсивностей
электрического и магнитного полей при преобразовании Галилея, а затем выяснить, подчиняются ли эти трансформированные величины тем же законам в новых координатах. Такое исследование было осуществлено различными учеными, в частности Герцом и Лорентцом; однако наиболее важные результаты их исследований мы здесь получим более простым путем.
Вместо того чтобы исследовать уравнения Максвелла в общем виде, мы ограничимся рассмотрением одного частного случая, именно уравнения распространения электромагнитных волн.
Уже сам Максвелл установил, что электромагнитные возмущения, подобные тем, которые вызываются колеблющимися зарядами, распространяются в пространстве со скоростью, зависящей от свойств среды, заполняющей пространство. В пустоте их скорость распространения не зависит от направления и равна примерно 3-1010 см/сек. Это есть скорость света, поэтому Максвелл предположил, что свет является одним из видов электромагнитного излучения. С тех пор как Герцу при помощи специальной установки удалось получить электромагнитное излучение, максвелловская теория электромагнитного поля и электромагнитная теория света стали составной частью нашего физического мировоззрения.
Электромагнитное излучение распространяется в пустоте с постоянной скоростью (в дальнейшем обозначаемой через с). Это заключение может быть формулировано без рассмотрения внутренней связи между электрическими и магнитными полями. Оно ценно для нас потому, что мы можем изучать трансформационные свойства этого закона распространения света, не прибегая к рассмотрению законов преобразования переменных поля.
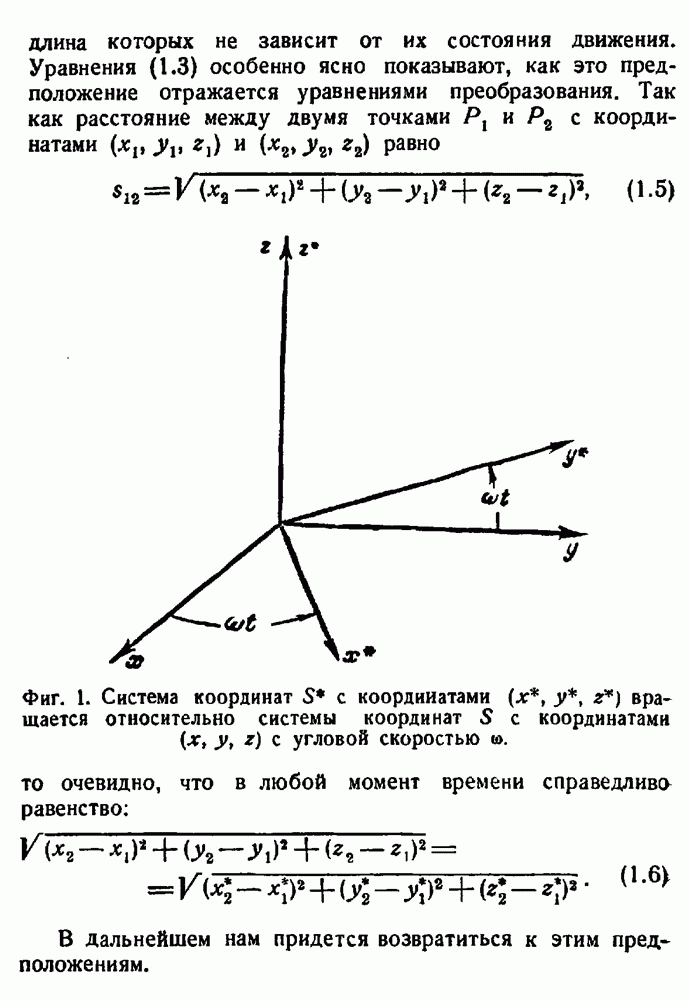
Теперь можно решить, будут ли законы электромагнитного поля ковариантны относительно преобразования Галилея. Рассмотрим систему координат S, по отношению к которой справедлив закон постоянства скорости света. Проведя преобразование Галилея типа (1.3), соответствующее равномерному прямолинейному движению новой
системы S относительно S, получим, что скорость одного и того же светового луча в новой системе S не может быть равна с во всех направлениях. Если направление светового луча в системе координат S характеризовать углами этого луча с осями  , то компоненты его скорости в этой системе будут:
, то компоненты его скорости в этой системе будут:

где

Согласно (2.9), компоненты скорости в новой системе S получим в виде:

отсюда скорость света зависит от направления и определяется уравнением

Она равна с только на некотором конусе направлений, осью которого является вектор V. В направлении  скорость света в системе S равна
скорость света в системе S равна  в противоположном направлении она равна
в противоположном направлении она равна 
Принцип относительности, таким образом, оказывается несовместимым с законами электромагнитного излучения, а потому и с теорией электромагнитного поля. Если принять, что уравнения Максвелла верны, то должуа существовать система отсчета, скажем, инерциальная система, в которой они принимают свою обычную форму. Всякая
другая система отсчета, движущаяся относительно вышеупомянутой, являлась бы менее удобной, по крайней мере с точки зрения электродинамики, даже если бы ее движение было равномерным и прямолинейным. Принцип относительности в таком виде, как мы его сформулировали в предыдущей главе, был бы в этом случае применим только к механике, но не ко всей физике.
С таким заключением трудно согласиться. Механика всегда считалась наиболее заслуживающей доверия областью физики, а принцип относительности—фундаментальным принципом всей природы. Было сделано много попыток преодолеть возникшие трудности. Мы рассмотрим наиболее важные из них.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
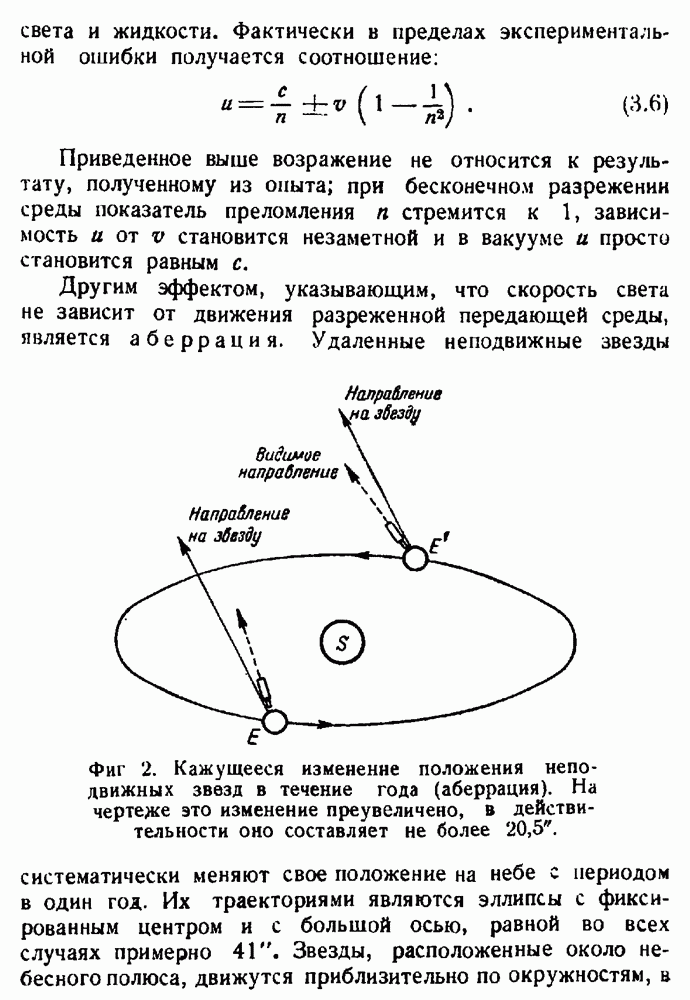
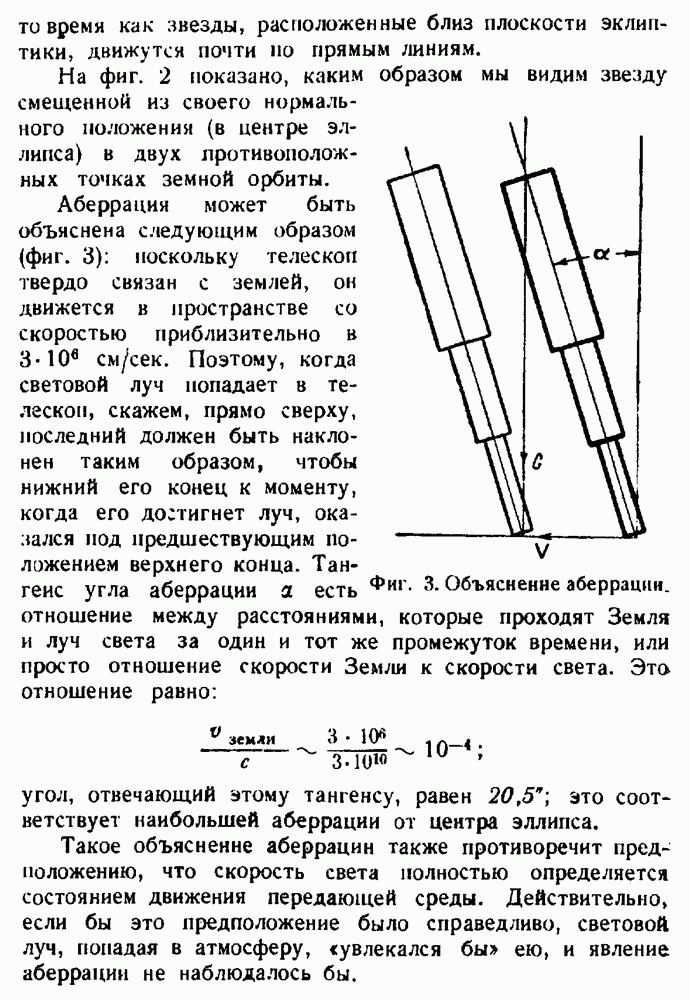
- Передающая среда как система отсчета.
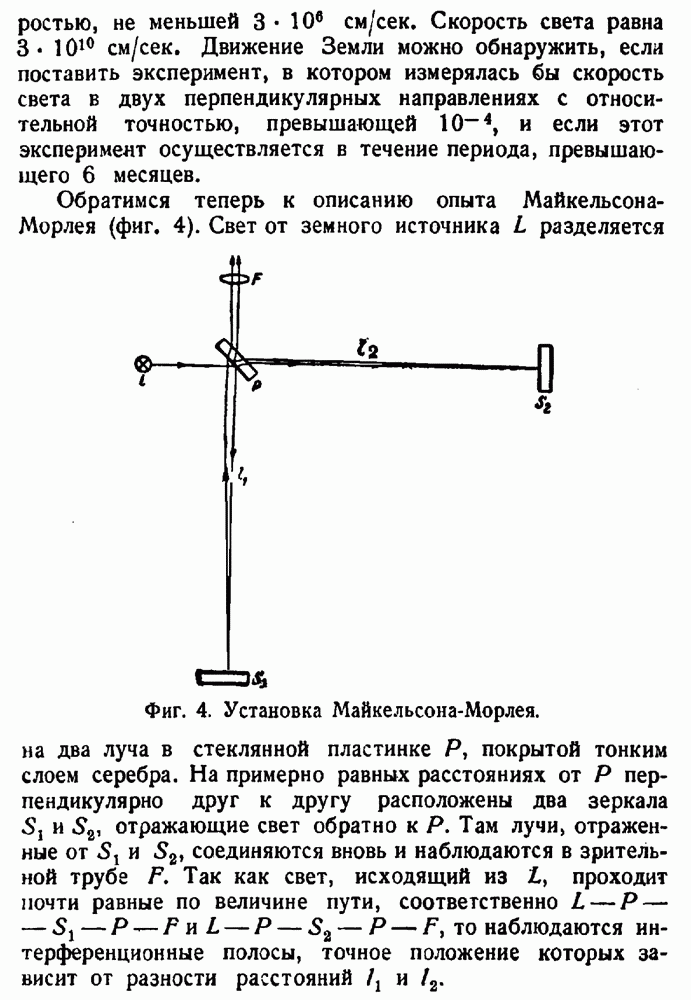
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
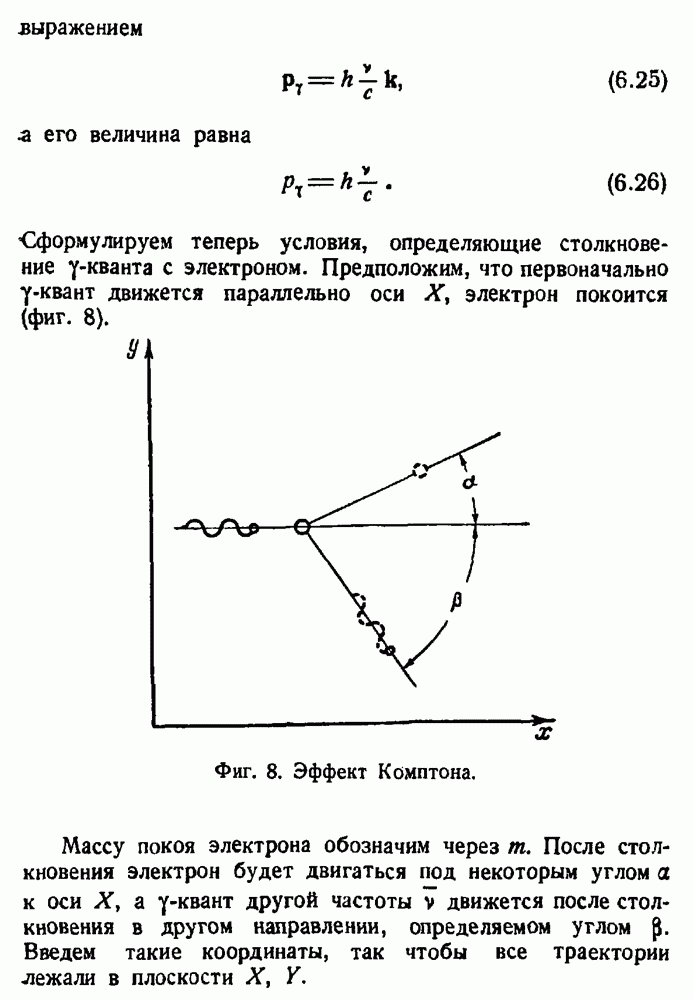
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
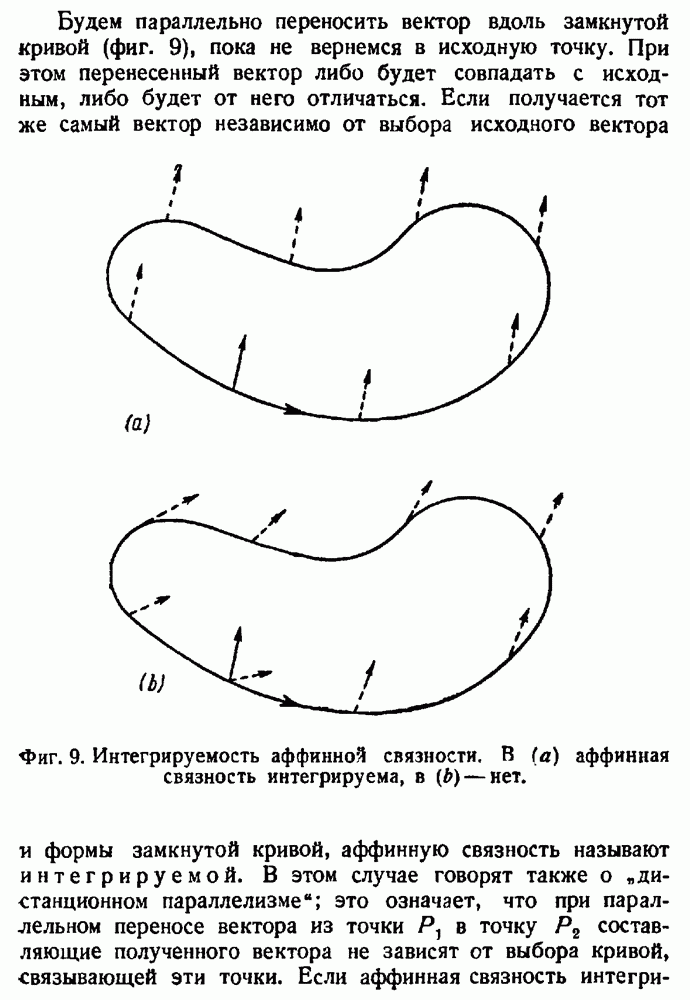
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.