| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Геометрия замкнутого пятимерного мира.
В то время как проективные теории, в частности теория Эйнштейна-Майера, рассматривают пространство как четырехмерное, а пятое измерение вводят только как средство для построения нового типа тензорного анализа, теория, рассмотренная в указанных двух статьях, пытается придать пятому измерению более определенный физический смысл.
Физические соображения оправдывают создание такой теории. Не выходя за пределы четырехмерной теории поля, представляется невозможным даже принять во внимание результаты квантовой теории, в частности принцип неопределенности Гейзенберга. Так как описание пятимерного мира при помощи четырехмерного формализма является неполным, была надежда, что из неопределенности „четырехмерных законов можно получить принцип неопределенности и что квантовые явления в конце концов смогут быть объяснены теорией поля. В настоящее время очевидно, что эти смелые надежды не оправдались. Вообще, вопрос о том, выдержит ли какой-либо пятимерный подход проверку времени, покажет будущее.
Во всяком случае, макроскопический мир четырехмерен» поэтому пятимерный мир должен быть, по крайней мере, приближенно цилиндрическим относительно пятого измерения. Из этих соображений Эйнштейн и его сотрудники предположили, что мир является замкнутым по отношению к пятой координате и представляет собой нечто вроде трубы.
Если вырезать из пятимерного континуума тонкий бесконечно протяженный слой и отождествить его две открытые (четырехмерные) поверхности, получится модель такого замкнутого пятимерного пространства. Все функции поля предполагаются, конечно, непрерывными при переходе через шов“, и поэтому, если трубка достаточно узка (т. е. если слой достаточно тонок), изменение величин поля поперек нее будет мало по сравнению с их изменениями вдоль трубки.
Геометрия замкнутого пятимерного пространства предполагается римановой. Это налагает еще одно
ограничительное условие, которое уменьшает число переменных поля от 15 до 14. Метрику теории Калуза мы называли А-цилиндрической. Другими словами, пространство Калуза является цилиндрическим не только относительно некоторого векторного поля, но и относительна поля единичных векторов А. В силу этого А-кривые Калуза являются геодезическими, и в специальной системе координат  равна единице. В рассматриваемой геометрии условие цилиндричности Калуза заменяется условием замкнутости пятимерного пространства. Кроме того, предполагается, что геодезические линии вокруг цилиндра, соединяющие данную точку с нею же самой, пересекаются под углом, равным нулю, т. е. являются замкнутыми непрерывными кривыми. Это условие заменяет условие Калуза о цилиндричности его пространства относительно поля единичных векторов.
равна единице. В рассматриваемой геометрии условие цилиндричности Калуза заменяется условием замкнутости пятимерного пространства. Кроме того, предполагается, что геодезические линии вокруг цилиндра, соединяющие данную точку с нею же самой, пересекаются под углом, равным нулю, т. е. являются замкнутыми непрерывными кривыми. Это условие заменяет условие Калуза о цилиндричности его пространства относительно поля единичных векторов.
Через каждую точку пятимерного пространства проходит одна и только одна замкнутая геодезическая линия.
Длину такой линии, один раз обходящей вокруг цилиндра и возвращающейся в исходную точку, будем называть „периметром" пространства в пятом измерении. Докажем теперь, что этот периметр везде имеет одну и ту же величину.
Рассмотрим замкнутую геодезическую линию, проходящую через точку Р. Ее длина S равна

где  — произвольная функция координат; путь интегрирования является замкнутой геодезической линией. Изменим теперь координаты каждой точки вдоль этой замкнутой геодезической линии на бесконечно малую величину так, чтобы получить новую линию. „Конечная точка" Р не считается при этом фиксированной. Разность между длиной
— произвольная функция координат; путь интегрирования является замкнутой геодезической линией. Изменим теперь координаты каждой точки вдоль этой замкнутой геодезической линии на бесконечно малую величину так, чтобы получить новую линию. „Конечная точка" Р не считается при этом фиксированной. Разность между длиной
новой линии и длиной старой линии будет равна:

где точки означают дифференцирование по  угловому расстоянию от Р. Интегрируя по частям, получим:
угловому расстоянию от Р. Интегрируя по частям, получим: 

Выражение в круглых скобках равно нулю, так как первоначальная линия геодезическая. Поэтому вариация  зависит только от вариации координат в двойной конечной точке
зависит только от вариации координат в двойной конечной точке

Выражение в квадратных скобках является скалярным произведением двух векторов:  и поэтому инвариантно. Так как на двух границах в действительности представляет одно и то же бесконечно малое смещение, а
и поэтому инвариантно. Так как на двух границах в действительности представляет одно и то же бесконечно малое смещение, а  — то же направление, оба члена взаимно уничтожаются и
— то же направление, оба члена взаимно уничтожаются и  обращается в нуль. Таким образом, S остается постоянным при таком переходе от одной замкнутой
обращается в нуль. Таким образом, S остается постоянным при таком переходе от одной замкнутой
геодезической линии к другой, когда варьирование происходит так, чтобы все промежуточные линии были геодезическими.
Периметр замкнутого пространства, в котором все пересекающие сами себя геодезические линии являются замкнутыми и непрерывными (без разрывов производной), является, таким образом, постоянной, характеризующей пространство.
Векторы, касательные к замкнутым геодезическим  образуют поле единичных векторов. Обозначим это поле через А и применим к замкнутому пятимерному пространству формализм, рассмотренный в предыдущей главе.
образуют поле единичных векторов. Обозначим это поле через А и применим к замкнутому пятимерному пространству формализм, рассмотренный в предыдущей главе.
Так как  -поле состоит из векторов, касательных к геодезическим, оно удовлетворяет дифференциальным уравнениям.
-поле состоит из векторов, касательных к геодезическим, оно удовлетворяет дифференциальным уравнениям.

что означает согласно уравнениям (17.17) и (17.21), что Л-метрика.

является А-цилиндрической. Уравнение (18.6) принимает особенно простой вид в специальной системе координат.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
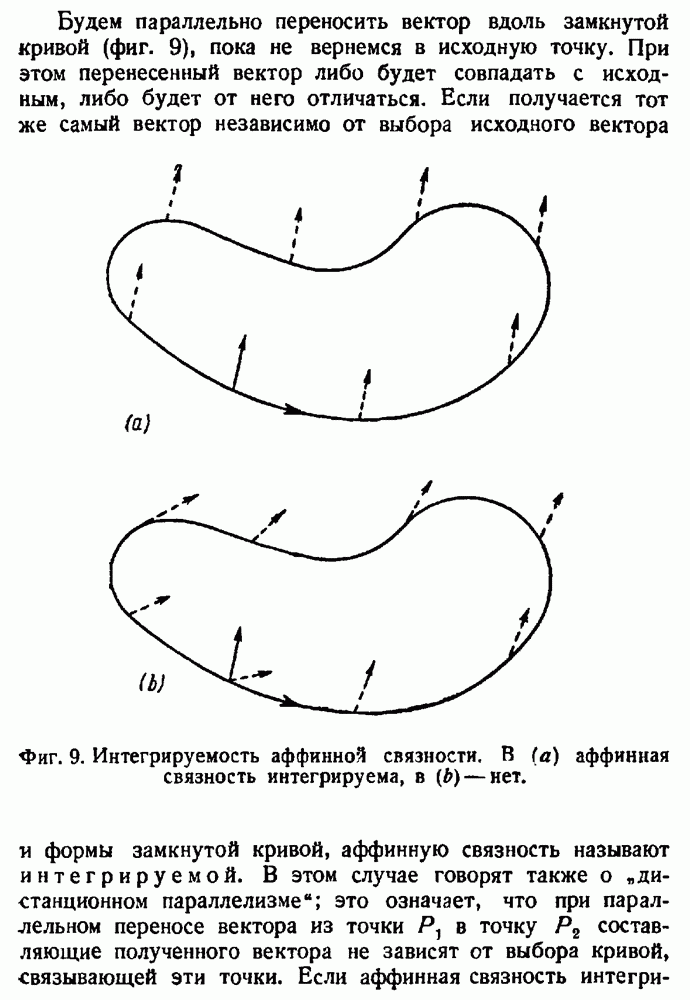
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.