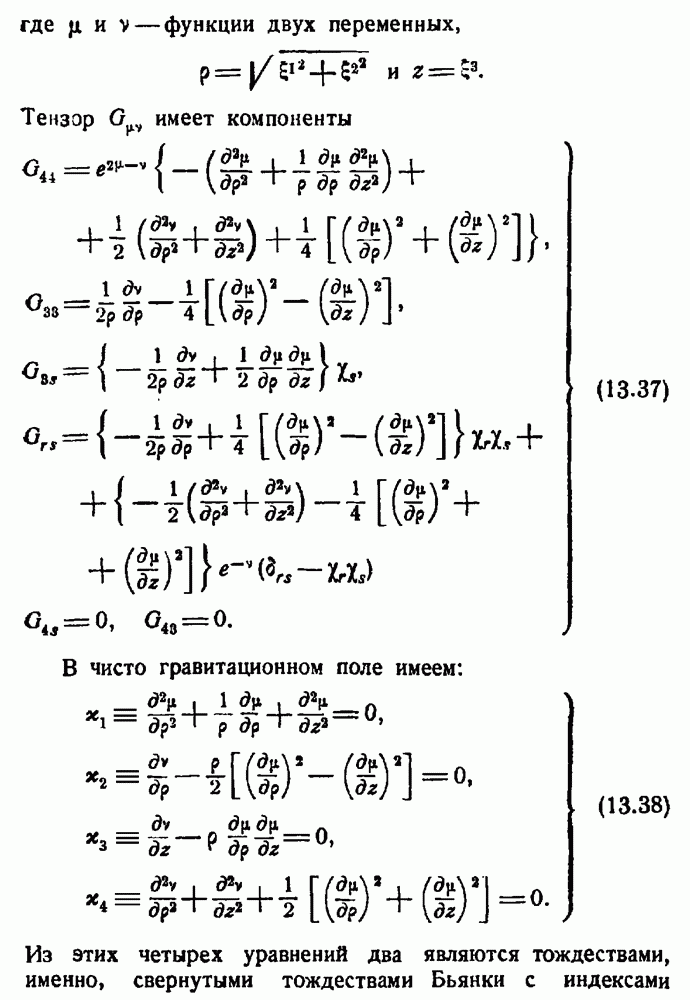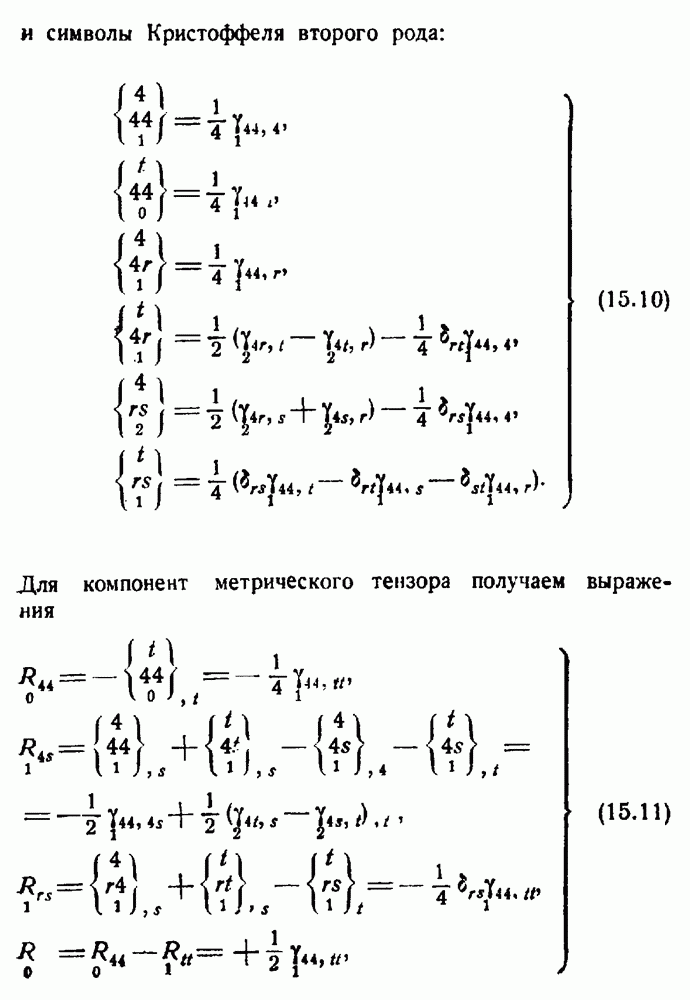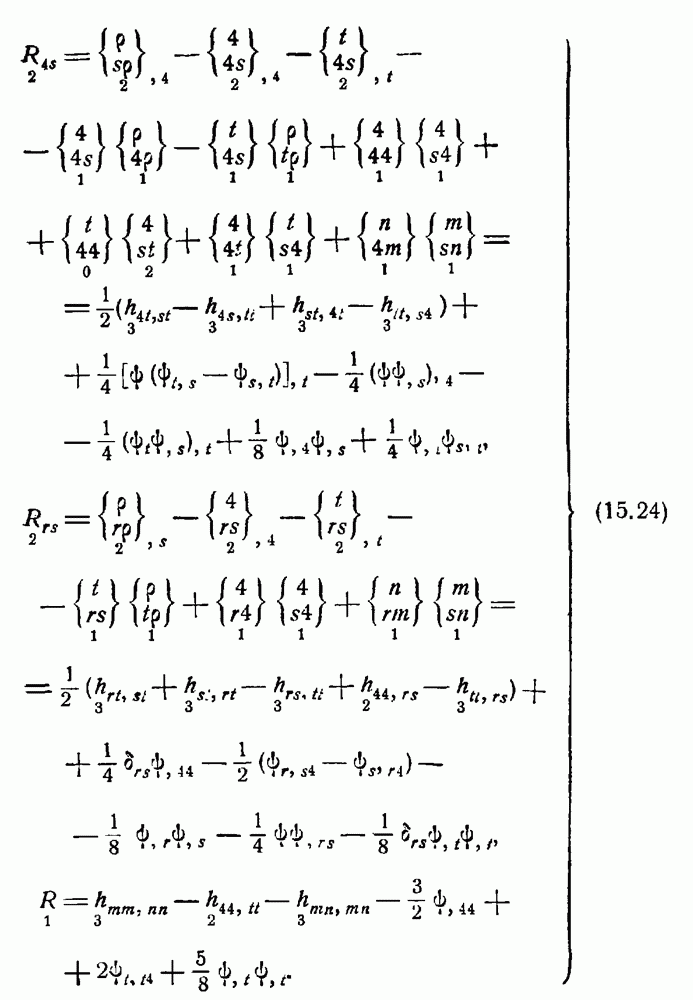| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ВВЕДЕНИЕ
Почти все законы физики служат для описания поведения некоторых объектов в пространстве и во времени. Положение тела или местонахождение события можно определить только как положение относительно какого-либо другого, подходящего для этого тела. Например, в опыте с машиной Атвуда скорости и ускорения гирь измеряются относительно самой машины, т. е., в конечном счете, относительно земли. Астроном может описывать движение планет относительно центра тяжести Солнца. Всякое движение описывается как движение относительно некоторого тела отсчета.
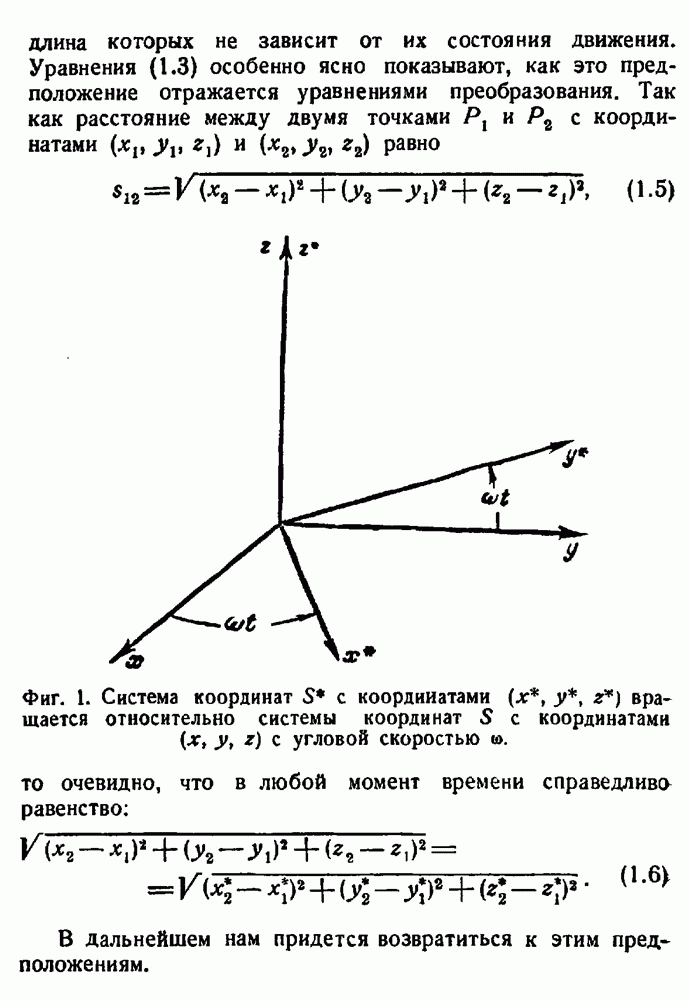
Представим себе, по крайней мере умозрительно, что с этим телом отсчета твердо связан простирающийся в пространстве каркас из прямых прутьев. Используя этот воображаемый каркас в качестве декартовой системы координат в трех измерениях, мы сможем любое положение описывать тремя числами, координатами соответствующей точки пространства. Такой воображаемый каркас, твердо связанный с некоторым материальным телом и с какой-либо строго определенной точкой пространства, часто называют системой отсчета.
Некоторые тела с успехом могут быть использованы для установления системы отсчета, другие же тела для этого непригодны. Даже до построения теории относительности вопрос о выборе подходящей системы отсчета сыграл весьма важную роль в развитии науки. Галилей, создатель послесредневековой физики, считал выбор гелиоцентрической системы настолько важным, что рисковал свободой и даже жизнью ради того, чтобы новая система отсчета была принята его современниками. В сущности
говоря, вопрос о выборе тела, с которым связывается система отсчета, и явился причиной его конфликта с властями.
После тех всеобъемлющих обобщений, которые сделал Ньютон в современной ему физике, гелиоцентрическая система отсчета стала общепринятой. Однако еще сам Ньютон чувствовал, что необходимо дальнейшее рассмотрение этого вопроса. Чтобы показать, что одни системы отсчета являются более подходящими для описания явлений природы, чем другие, он придумал знаменитый эксперимент с ведром, наполненным водой. Закручиванием поддерживающей ведро веревки, Ньютон заставлял его вращаться вокруг своей оси. По мере того как вода начинала принимать участие во вращении, ее поверхность меняла свою форму от плоской к параболической. Когда вода принимала ту же скорость, что и ведро, последнее останав-вливалось экспериментатором. По мере того как вода прекращала свое вращение, ее поверхность становилась опять все более плоской.
Это описание произведено с точки зрения системы отсчета, связанной с Землей. Закон, по которому изменяется поверхность воды, может быть сформулирован следующим образом: пока вода не вращается, ее поверхность представляет собой плоскость. При вращении воды ее поверхность является параболоидом. Состояние движения ведра не влияет на форму поверхности воды.
Опишем теперь тот же эксперимент с точки зрения системы отсчета, вращающейся относительно Земли с постоянной угловой скоростью, равной максимальной скорости вращения ведра. Вначале веревка, ведро и вода «вращаются” с некоторой постоянной угловой скоростью относительно новой системы отсчета. При этом поверхность воды представляет собой плоскость. Затем веревка, а вслед за ней и ведро „останавливаются"; при этом вода постепенно „замедляется”, а ее поверхность становится параболоидом. После того как вода приходит в состояние „полного покоя", ее поверхность еще является параболоидальной. Затем веревка, а также ведро снова начинают „вращаться”
относительно нашей системы отсчета (т. е. останавливаются относительно земли); вода начинает постепенно участвовать во „вращении", причем поверхность ее выпрямляется. В конце концов, когда вся система вращается с первоначальной угловой скоростью, поверхность воды становится опять плоской. Относительно этой системы отсчета тот же закон можно сформулировать следующим образом: поверхность воды является плоской только тогда, когда вода „вращается" с некоторой угловой скоростью. Отклонение формы поверхности от плоской возрастает с отклонением от такого состояния движения. В состоянии покоя поверхностью также является параболоид. Вращение ведра опять-таки не играет никакой роли.
Ньютоновский эксперимент с ведром очень ясно показывает, что понимается под „подходящей" системой отсчета. Можно описывать явления природы и управляющие ими законы, пользуясь произвольно выбранной системой отсчета. Однако может существовать система (или системы), в которой законы природы имеют особенно простой вид, т. е. содержат меньшее количество составных элементов, чем в других системах. Возьмем, например, ньютоновское вращающееся ведро. Если бы описание явлений природы производилось в системе отсчета, связанной с ведром, то многие физические законы должны были бы содержать добавочный элемент, угловую скорость <о ведра относительно „более удобной" системы отсчета, скажем, Земли.
Законы движения планет существенно упрощаются, если пользоваться гелиоцентрической системой отсчета, а не геоцентрической. Поэтому система Коперника и Галилея была предпочтительнее системы Птоломея еще до того, как Кеплером и Ньютоном были установлены законы движения планет.
Как только стало ясным, что выбор системы отсчета определяет форму законов природы, были предприняты исследования, имеющие целью выразить влияние выбора системы отсчета в математической форме.
Первой областью физики, все законы которой были полностью сформулированы математически, была механика.
Среди всех мыслимых систем отсчета существует совокупность таких систем, в которых закон инерции принимает свою обычную форму: в отсутствии сил пространственные координаты точечной массы являются линейными функциями времени. Эти системы отсчета называются инерциальными системами. Было установлено, что если законы механики сформулировать в одной из таких систем, то они будут иметь тот же вид во всех остальных инерциальных системах. В других системах отсчета физическое и математическое описание будет более сложным, как, например, в системе отсчета, связанной с ньютоновским вращающимся ведром. Описывать движение точечных масс в отсутствии сил можно и в этой системе отсчета, но математическая форма закона инерции усложнится. В этом случае пространственные координаты уже не будут линейными функциями времени.
Так как законы механики имеют один и тот же вид во всех инерциальных системах отсчета, то все инерциальные системы эквивалентны с точки зрения механики. Движется ли данное тело ускоренно, можно определить, сравнивая его движение с движением точечной массы, не находящейся под действием сил. Но установить, «покоится» данное тело или движется „равномерно", таким образом нельзя, так как это зависит от выбора инерциальной системы, в которой явление описывается. Термины „покой" и „равномерное движение" не имеют абсолютного смысла. Принцип, устанавливающий, что при описании явлений природы все инерциальные системы эквивалентны, называется принципом относительности.
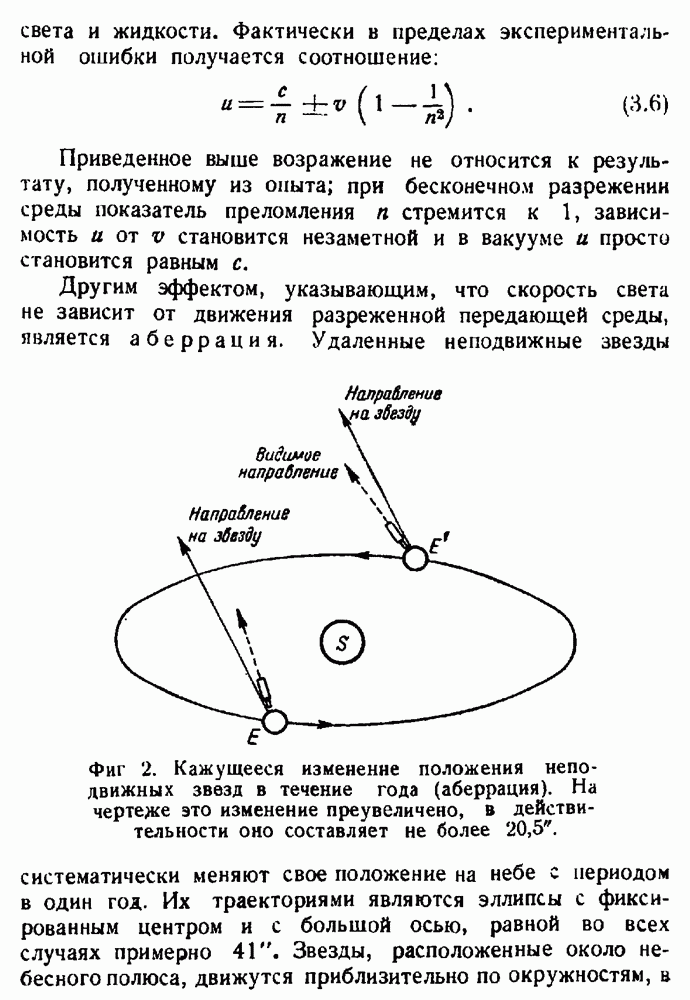
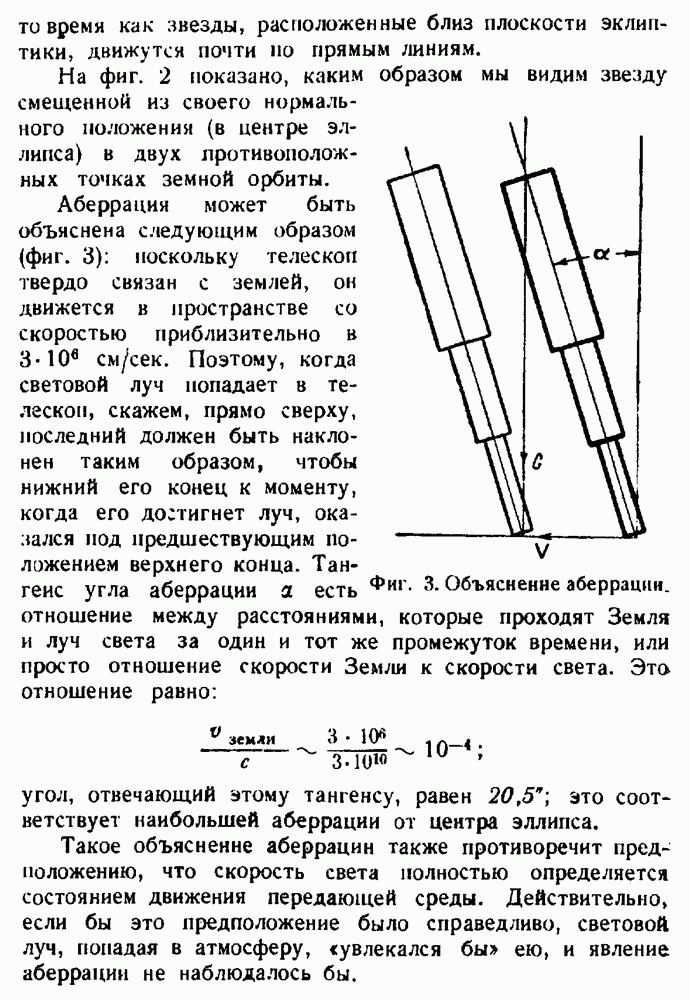
Когда Максвеллом были установлены уравнения электромагнитного поля, казалось, что они не совместимы с принципом относительности. Так, согласно теории Максвелла, электромагнитные волны должны распространяться в пустоте с универсальной постоянной скоростью с, равной примерно 3.1010 см/сек, что представлялось невозможным одновременно по отношению к двум инерциальным системам, движущимся друг относительного друга. Если бы существовала одна система отсчета, в которой скорость
электромагнитных волн была бы одной и той же во всех направлениях, ее можно было бы использовать для определения «абсолютного покоя" и абсолютного движения. Многие экспериментаторы упорно пытались найти такую систему отсчета и определить движение Земли относительно нее.
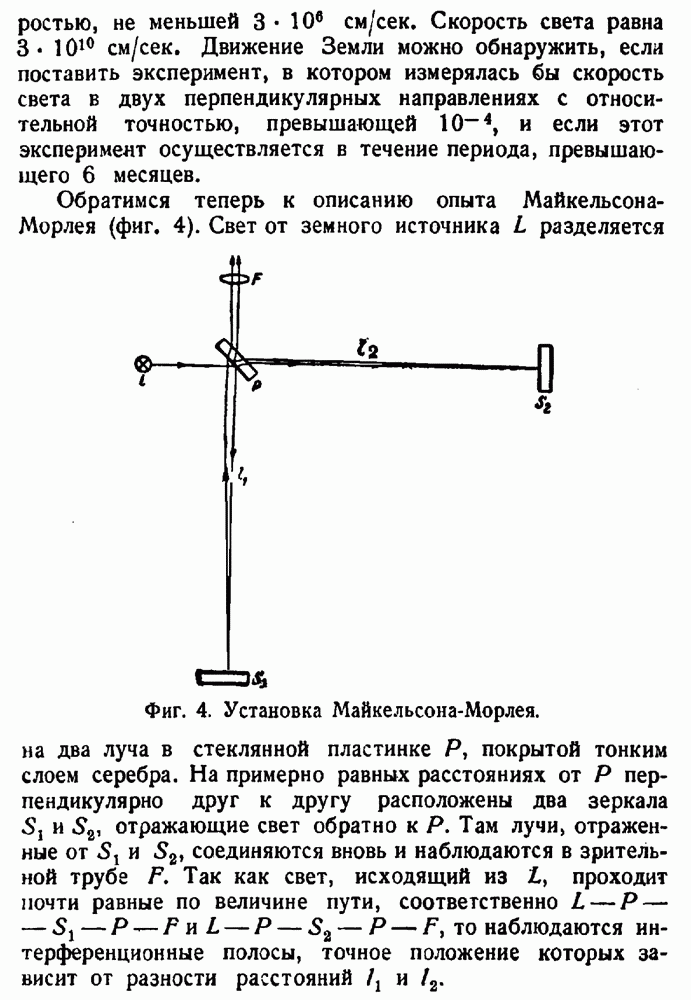
Однако все эти попытки были безуспешны. Более того, все эксперименты, казалось, говорили о том, что принцип относительности так же хорошо применим к законам электродинамики, как и к законам механики. Г. А. Лорентц предложил новую теорию, в которой принималось существование одной привилегированной системы отсчета и в то же время объяснялось, почему ее нельзя обнаружить экспериментальным путем. Однако Лорентц должен был ввести ряд предположений, правильность которых нельзя было проверить ни при каких мыслимых экспериментах. С этой точки зрения его теория не вполне удовлетворительна. Только Эйнштейн полностью осознал, что лишь при помощи ревизии основных представлений о пространстве и времени можно устранить несоответствие между теорией и экспериментом. Лишь после того как такая ревизия была осуществлена, принцип относительности был распространен на всю физику. Соответствующая теория носит теперь название специальной теории относительности. Она устанавливает полную эквивалентность всех инерциальных систем, но полностью сохраняет их привилегированное положение по отношению к остальным системам отсчета. В так называемой общей теории относительности обсуждается, а затем устраняется привилегированный характер инерциальных систем, что дает возможность создать теорию гравитации.
В этой книге сначала будет рассмотрена с классической точки зрения роль различных систем отсчета в механике и, до некоторой степени, в электродинамике. Только после того, как читатель полностью осознает, какие неразрешимые противоречия возникают между выводами теории и результатами эксперимента в классической электродинамике, он сможет понять необходимость пересмотра
классической физики с точки зрения теории относительности, Лишь усвоив новые представления о пространстве и времени, легко понять „релятивистскую механику и „релятивистскую электродинамику.
Вторая часть книги посвящена общей теории относительности; в третьей части рассматриваются некоторые недавние попытки распространить теорию гравитации на электродинамику.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
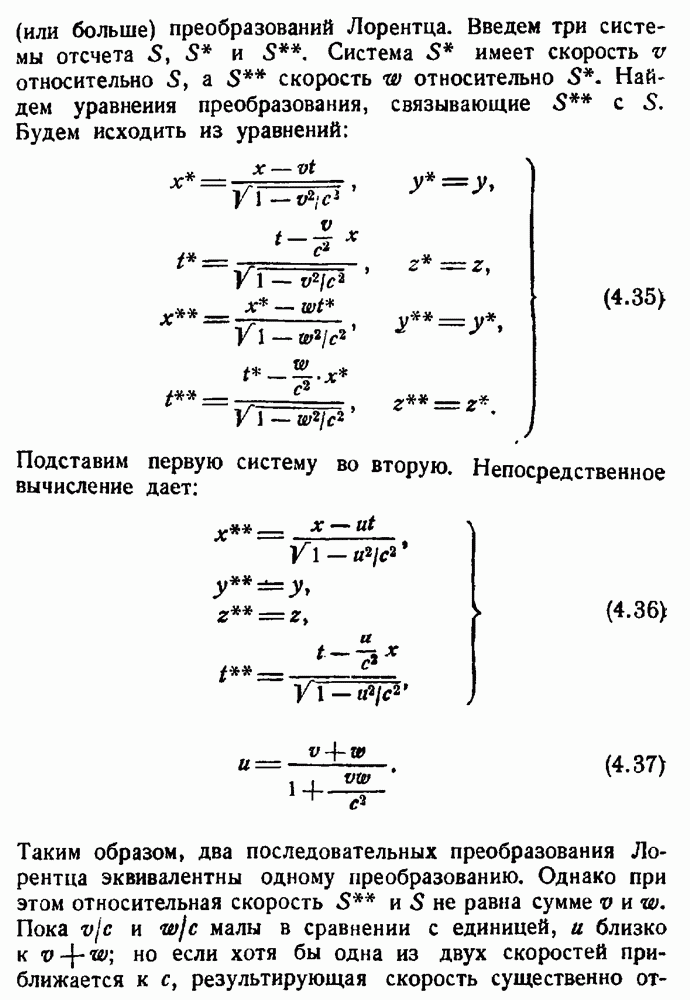
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
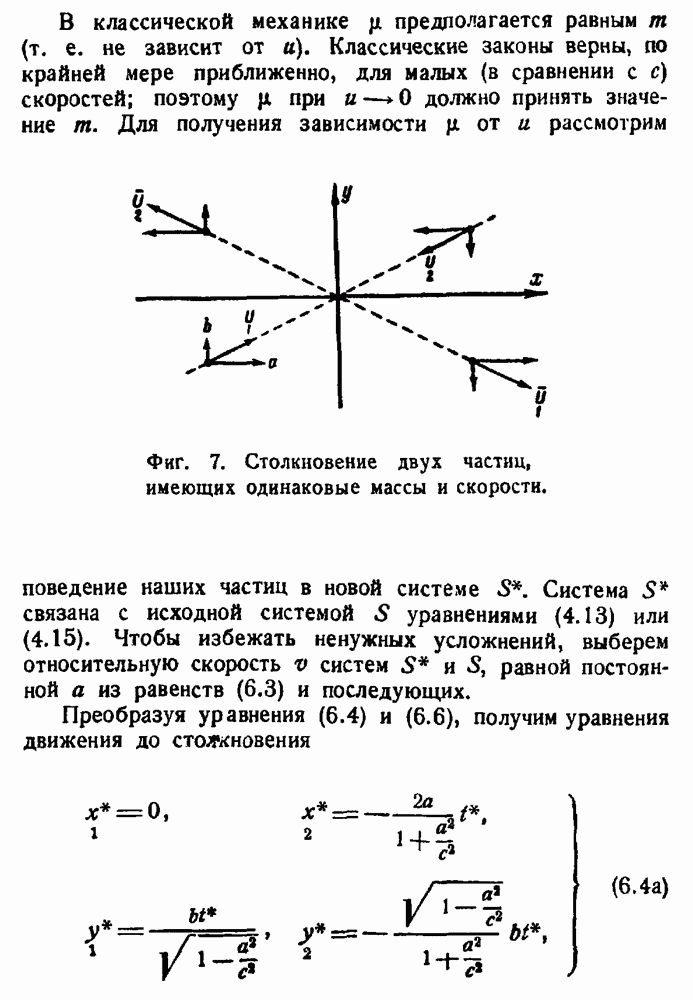
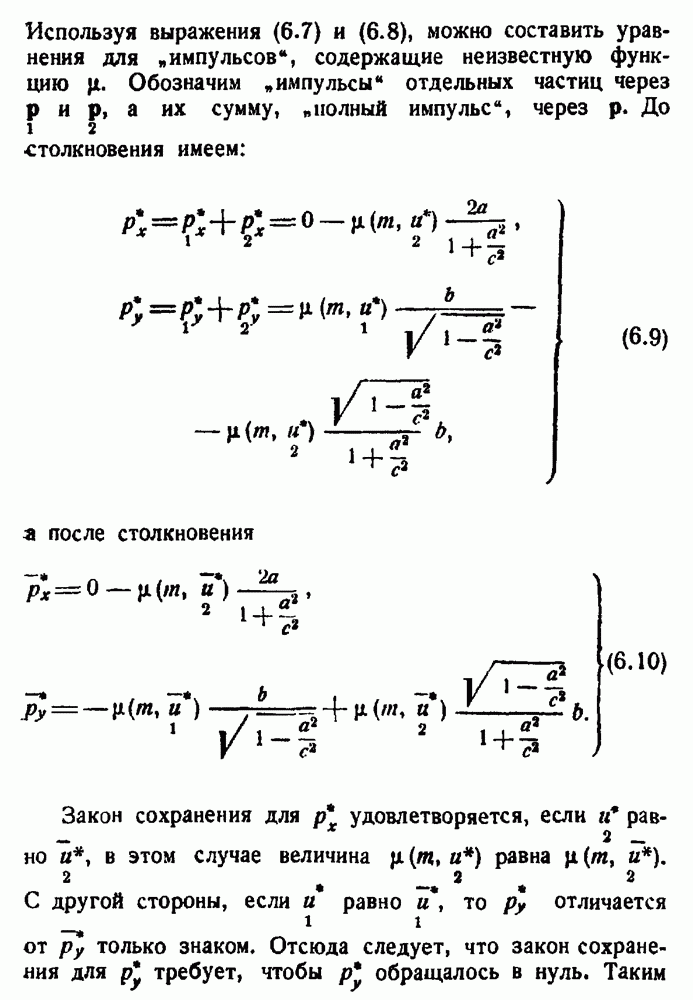
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
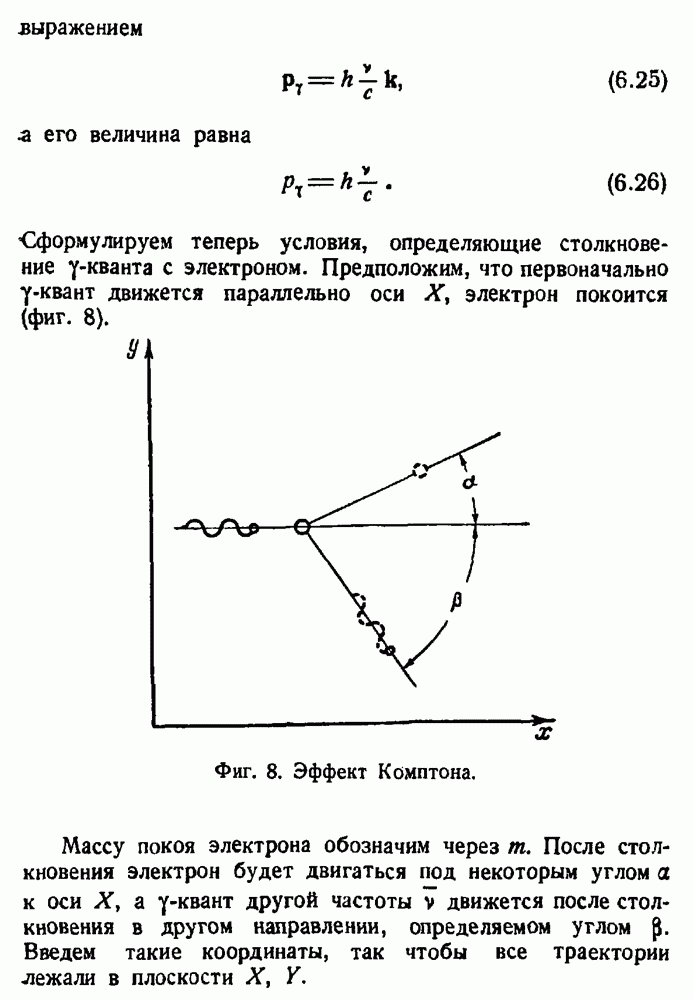
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
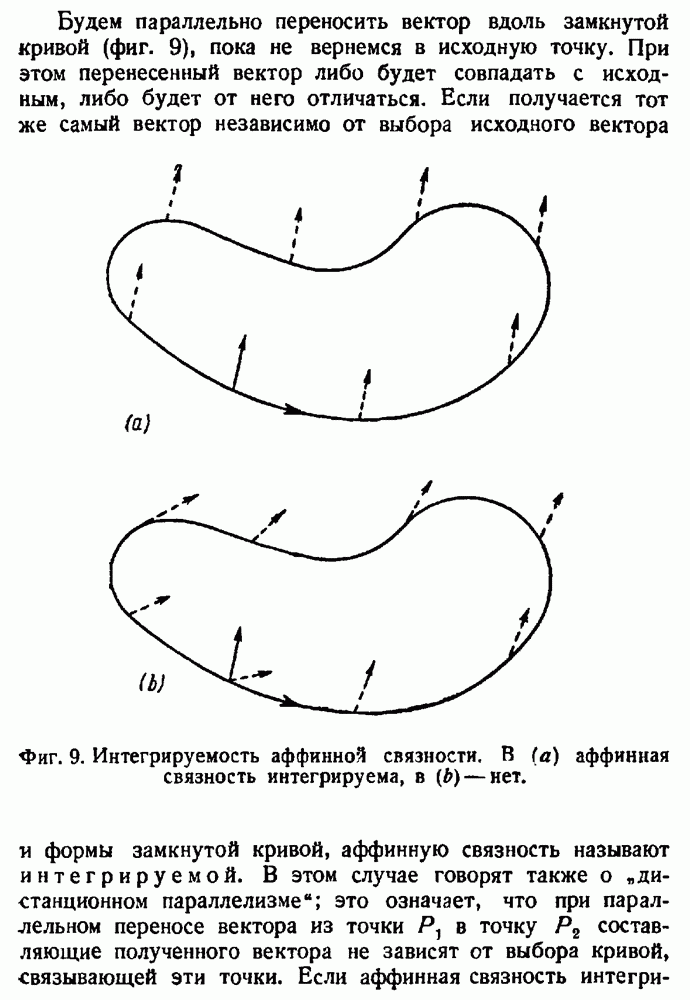
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.