| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Дифференциальные тождества.
Такой физический закон, как уравнения гравитационного поля, не может быть получен путем чисто логических рассуждений. Однако класс возможных уравнений поля уже ограничен нашими требованиями того, что поле должно представляться десятью дифференциальными уравнениями второго порядка относительно  ковариантными по отношению к общему преобразованию координат. В этом разделе мы наложим на уравнения поля дополнительное условие, которое исключит все возможности, кроме одной.
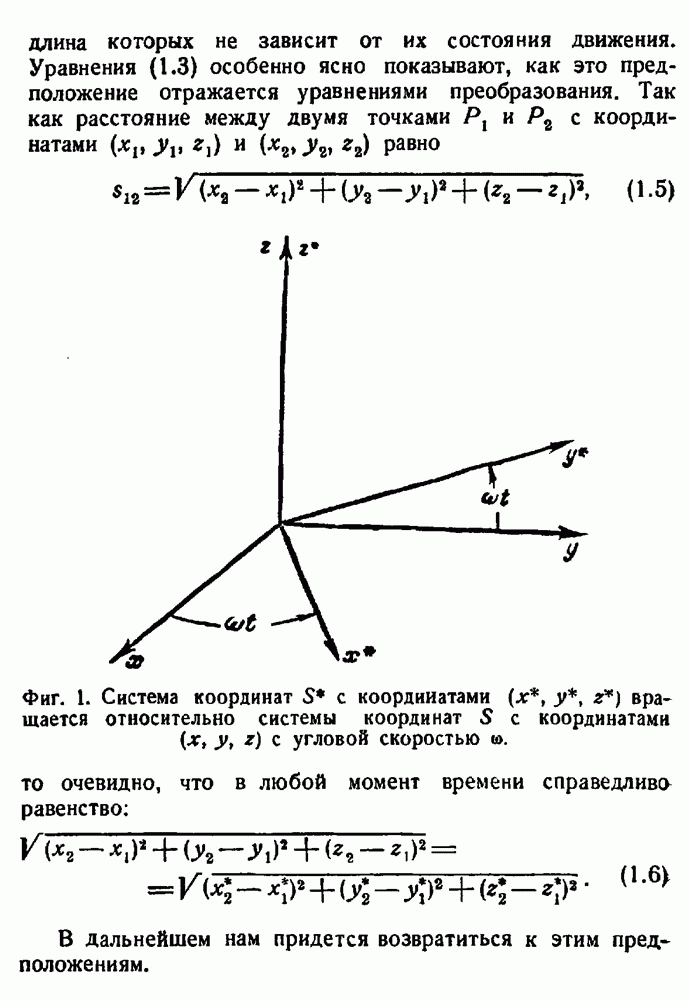
ковариантными по отношению к общему преобразованию координат. В этом разделе мы наложим на уравнения поля дополнительное условие, которое исключит все возможности, кроме одной.
Десять дифференциальных уравнений для  не могут быть полностью независимы друг от друга, они должны удовлетворять четырем тождествам. Это условие непосредственно связано с условием общей ковариантности. Предположим, что нами получена система десяти ковариантных уравнений для и что известно одно из решений этих уравнений. В этом случае новые решения этих уравнений можно получить просто преобразованием координат. Зависимость преобразованных компонент метрического тензора от
не могут быть полностью независимы друг от друга, они должны удовлетворять четырем тождествам. Это условие непосредственно связано с условием общей ковариантности. Предположим, что нами получена система десяти ковариантных уравнений для и что известно одно из решений этих уравнений. В этом случае новые решения этих уравнений можно получить просто преобразованием координат. Зависимость преобразованных компонент метрического тензора от  будет иной, чем зависимость
будет иной, чем зависимость  от
от  Эти формально
Эти формально
различные решения в сущности являются эквивалентными представлениями одного и того же физического состояния, так как их различие отражает только возможность произвольного выбора систем отсчета, в которых может быть описано гравитационное поле. Таким образом, действительно отличных друг от друга гравитационных полей гораздо меньше, чем формально различных решений уравнений пиля.
Чтобы ограничить число формальных решений, на систему координат следует наложить дополнительное условие. Так как преобразования координат содержат четыре произвольные функции (в четырехмерном пространстве), то можно составить четыре уравнения для  которые не должны быть ковариантными. Эти уравнения должны быть выбраны таким образом, чтобы, исходя из произвольной совокупности
которые не должны быть ковариантными. Эти уравнения должны быть выбраны таким образом, чтобы, исходя из произвольной совокупности  им можно было бы удовлетворить после соответствующего преобразования координат. Такие уравнения называются координатными условиями.
им можно было бы удовлетворить после соответствующего преобразования координат. Такие уравнения называются координатными условиями.
При добавлении к десяти ковариантным уравнениям поля четырех координатных условий получается система из четырнадцати уравнений, имеющая то же множество неэквивалентных решений, что и система десяти уравнений поля, взятая отдельно, но с меньшим числом формально различных решений.
Четырнадцать полностью независимых уравнений для десяти переменных имели бы слишком мало решений. Эти решения соответствуют либо плоской метрике, либо, в лучшем случае, они определяют значительно меньшее количество действительно различных состояний, чем то, которое можно получить, допуская произвольное распределение материи в пространстве. Поэтому, кроме четырнадцати уравнений,  должны удовлетворять четырем тождествам.
должны удовлетворять четырем тождествам.
Четыре координатные условия являются в значительной степени произвольными. Они могут быть любыми нековариантными уравнениями, содержащими  которые можно удовлетворить любой метрикой после соответствующего выбора системы координат. Так как выбор конкретных координатных условий не влияет на характер решений,
которые можно удовлетворить любой метрикой после соответствующего выбора системы координат. Так как выбор конкретных координатных условий не влияет на характер решений,
необходимо, чтобы тождества содержали только ковариантные уравнения поля и чтобы они были независимы от координатных условий.
Предыдущие рассуждении показывают, что десять уравнений поля в силу их ковариантности должны удовлетворять четырем тождествам. Однако до сих пор мы еще ничего не знаем о форме самих уравнений и природе соответствующих им тождеств. Чтобы решить эти вопросы, используем свойства тензора Р. Если рассматривать материю как сплошную среду, правыми частями уравнений гравитационного поля будут величины  подобно тому, как компоненты мирового вектора тока образуют правые части уравнений Максвелла. Аналогично тому, что закон сохранения электрического заряда выражается уравнением
подобно тому, как компоненты мирового вектора тока образуют правые части уравнений Максвелла. Аналогично тому, что закон сохранения электрического заряда выражается уравнением

Закон сохранения энергии и импульса может быть выражен уравнением

Поэтому можно ожидать, что десять величин, стоящих в левых частях уравнений поля, являются компонентами симметричного тензора второго ранга, а четыре тождества имеют вид дивергенций.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
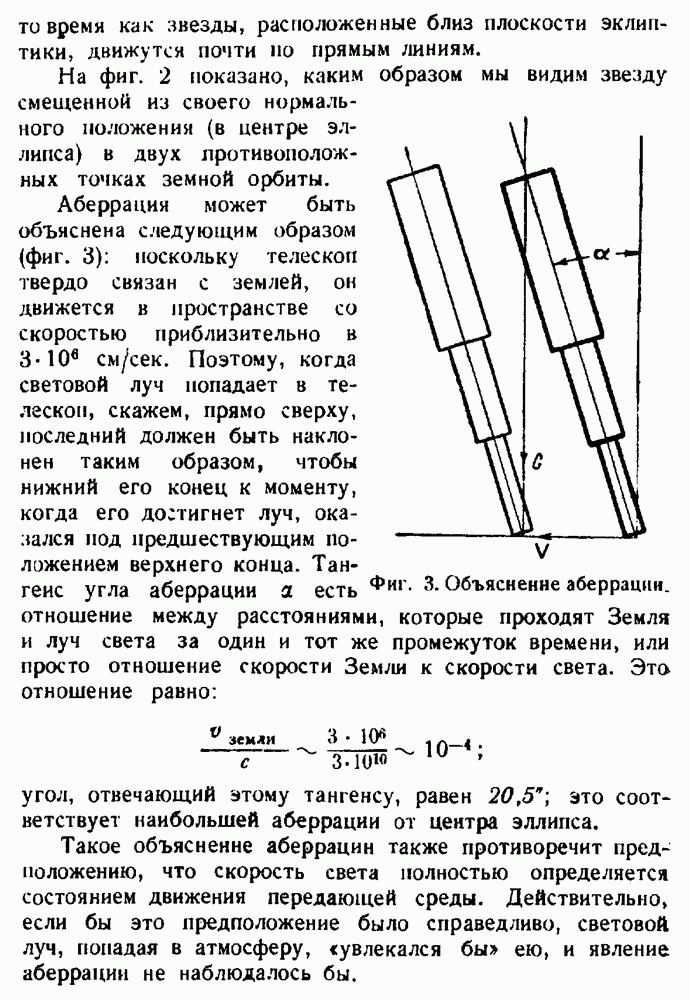
- Корпускулярная гипотеза.
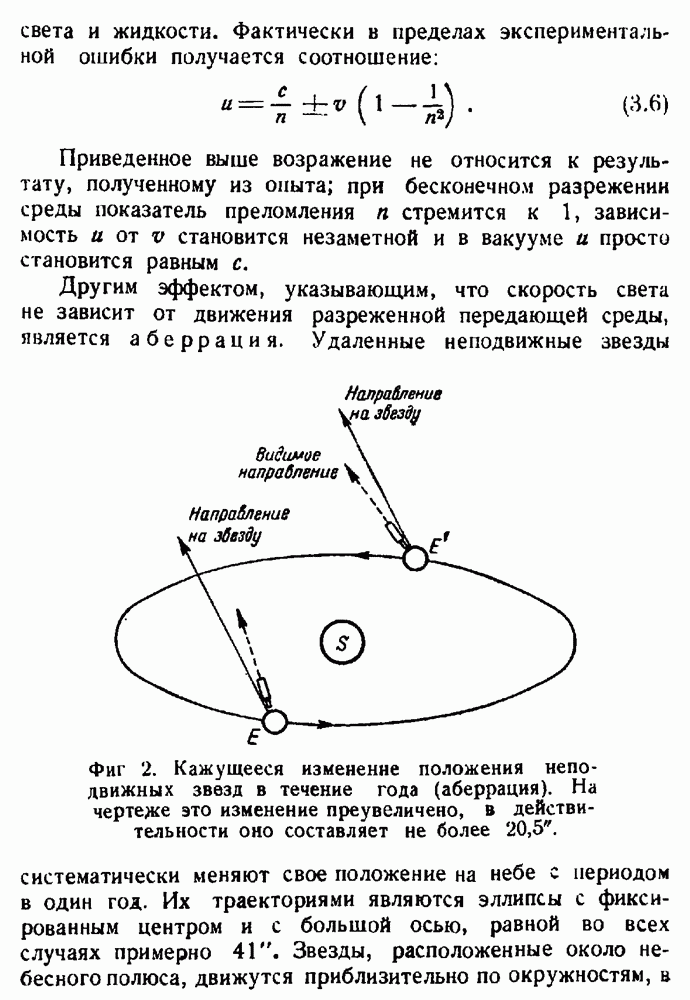
- Передающая среда как система отсчета.
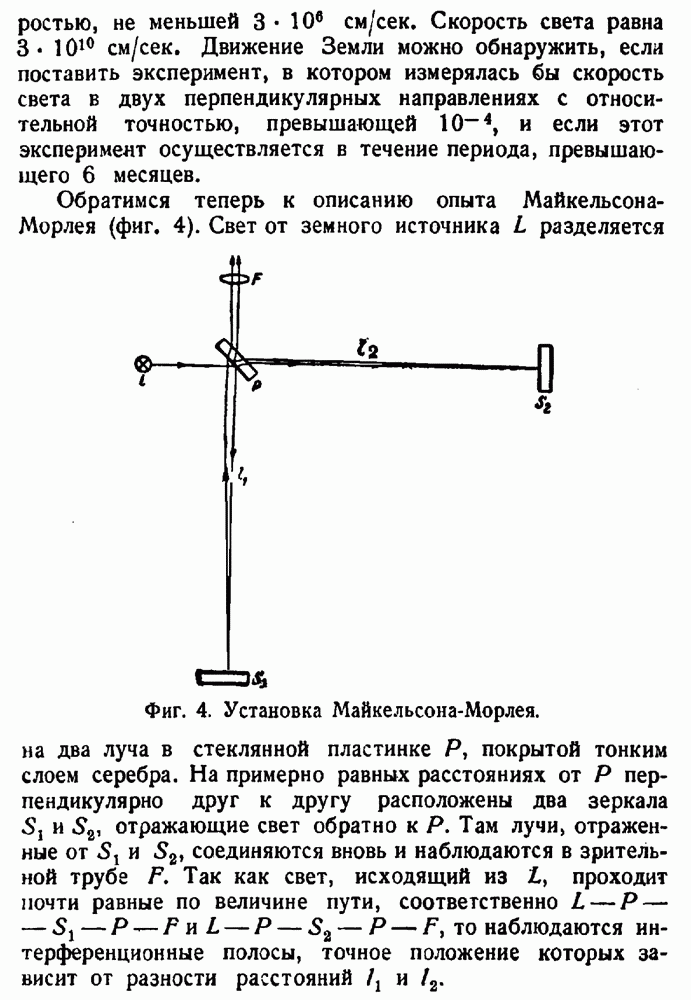
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
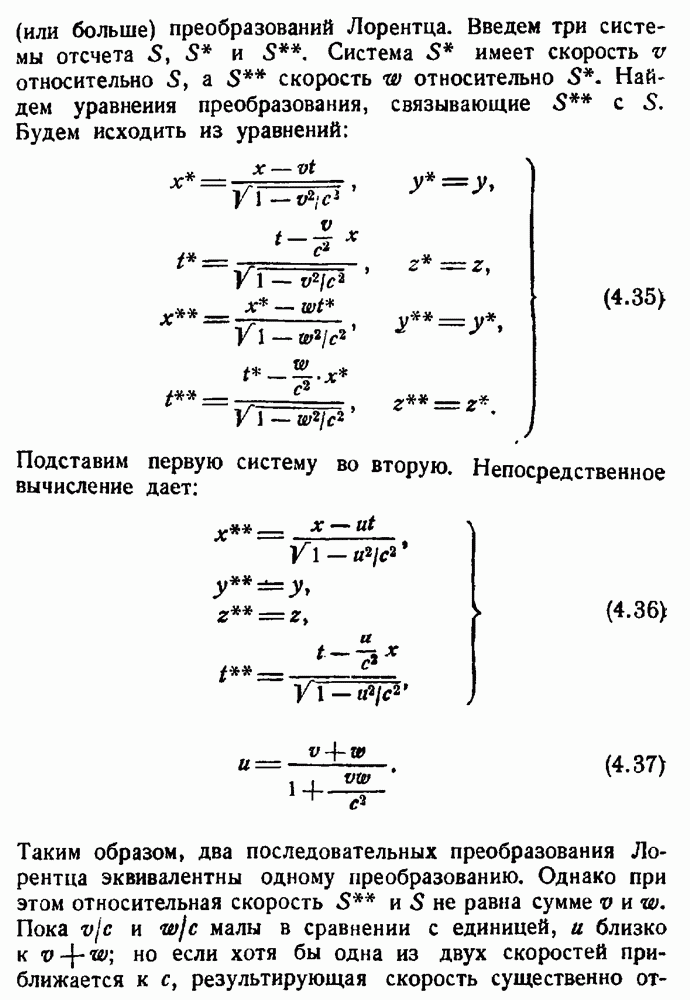
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
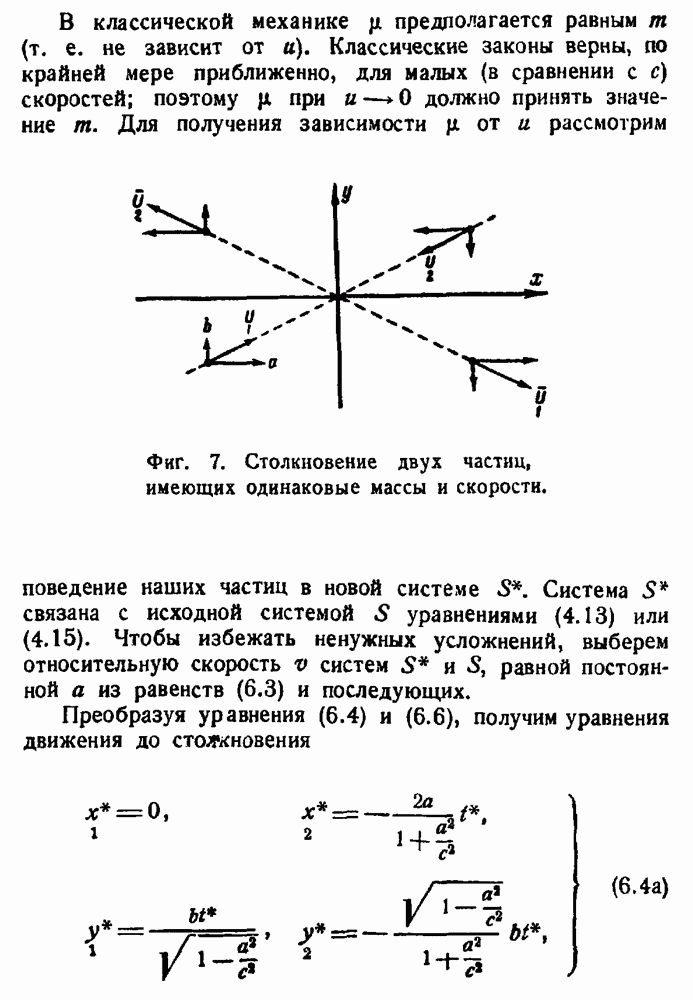
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
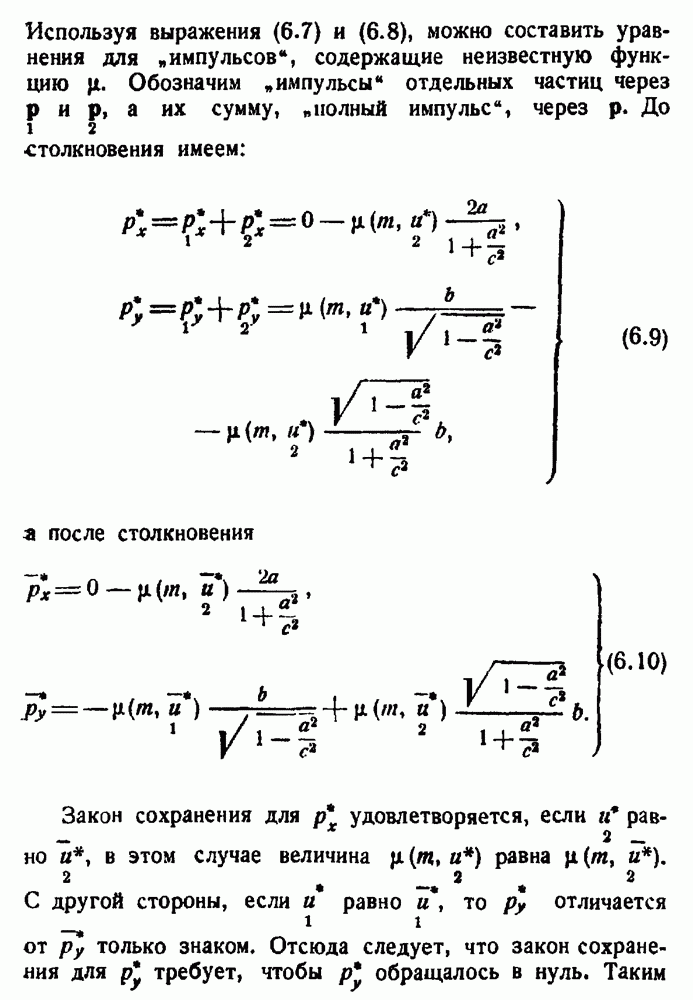
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
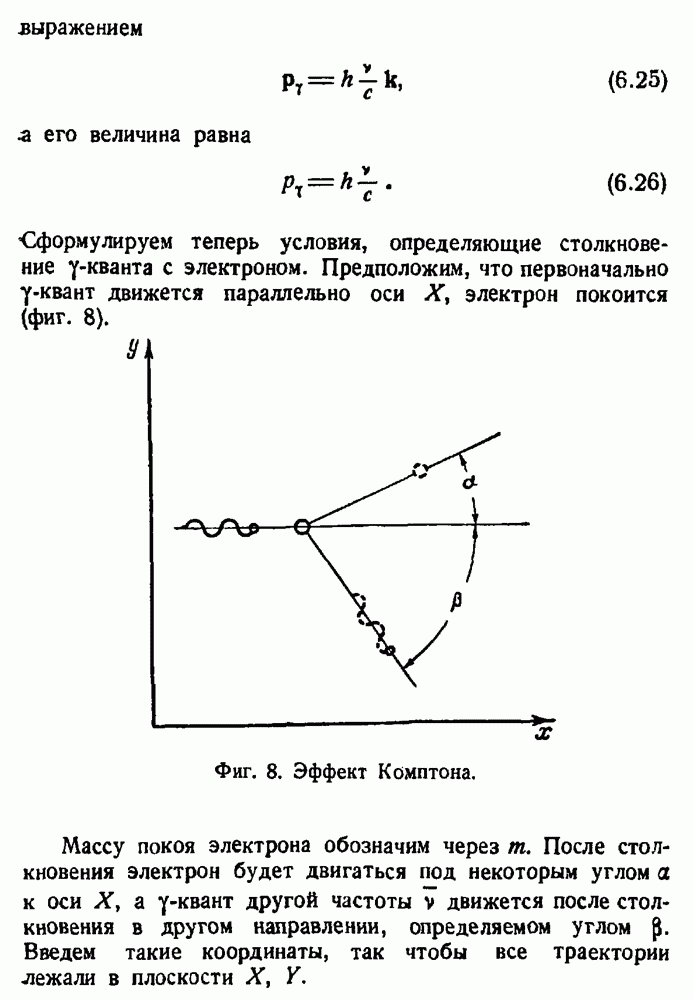
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
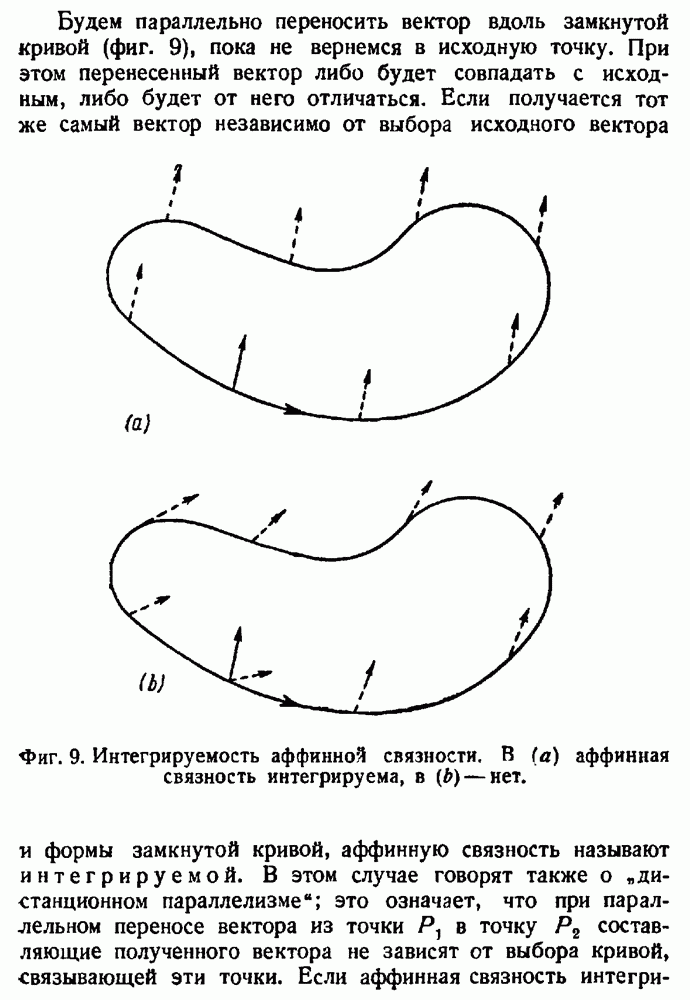
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.