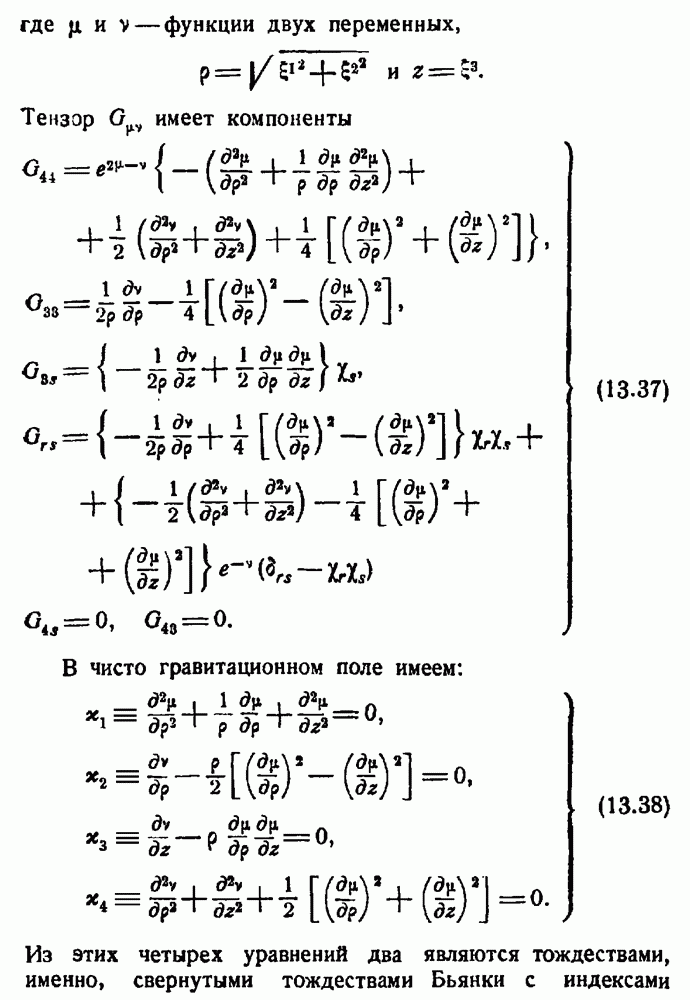| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Решение с осевой симметрией.
Вейлю и Леви-Чивита удалось найти статические решения, обладающие только осевой симметрией, но не сферической. Если с самого начала предположить, что „статичность” означает как независимость  от
от  так и обращение в нуль компонент
так и обращение в нуль компонент  то можно показать, что метрический тензор с осевой симметрией может быть представлен в виде:
то можно показать, что метрический тензор с осевой симметрией может быть представлен в виде:

где  — функции двух переменных,
— функции двух переменных,

Тензор  имеет компоненты
имеет компоненты

В чисто гравитационном поле имеем:

Из этих четырех уравнений два являются тождествами, именно, свернутыми тождествами Бьянки с индексами
3 и  Можно убедиться, что последнее уравнение (13.38) вытекает из трех предыдущих:
Можно убедиться, что последнее уравнение (13.38) вытекает из трех предыдущих:

Первые три уравнения в свою очередь связаны соотношением

Две функции  и
и  должны обращаться в нуль на бесконечности. Далее, из уравнений (13.36) видно, что
должны обращаться в нуль на бесконечности. Далее, из уравнений (13.36) видно, что  имеют особенность (т. е. неопределенны) на оси
имеют особенность (т. е. неопределенны) на оси  если, только
если, только  не обращается на ней в нуль, т. е. если
не обращается на ней в нуль, т. е. если  не равно нулю при
не равно нулю при 
Первое уравнение (13.38),  является линейным однородным уравнением только для
является линейным однородным уравнением только для  кроме того, оно является уравнением Лапласа в цилиндрических координатах для функций, обладающих осевой симметрией. Известно, что решения уравнения Лапласа, не считая решения
кроме того, оно является уравнением Лапласа в цилиндрических координатах для функций, обладающих осевой симметрией. Известно, что решения уравнения Лапласа, не считая решения  , удовлетворяют граничным условиям на бесконечности только в том случае, если они имеют особенность в какой-либо точке, находящейся на конечном расстоянии от начала координат. Особенности вне оси
, удовлетворяют граничным условиям на бесконечности только в том случае, если они имеют особенность в какой-либо точке, находящейся на конечном расстоянии от начала координат. Особенности вне оси  всегда представляют собой, окружности, в то время как на оси
всегда представляют собой, окружности, в то время как на оси  могут быть особенности точечного типа, вида
могут быть особенности точечного типа, вида  или
или  производные по
производные по  от таких „полюсов.
от таких „полюсов.
Однако не все эти решения совместимы с дифференциальными уравнениями для  Если уравнение
Если уравнение  удовлетворяется в некоторой односвязной области пространства
удовлетворяется в некоторой односвязной области пространства  то в силу (13.40) уравнения для
то в силу (13.40) уравнения для  имеют решения. Но при наличии особенностей пространство
имеют решения. Но при наличии особенностей пространство  уже не будет односвязным.
уже не будет односвязным.
Рассмотрим сначала особенности вне оси  Если выбрать решение
Если выбрать решение  уравнения
уравнения  с произвольной окружностью особых точек, интеграл по замкнутому контуру,
с произвольной окружностью особых точек, интеграл по замкнутому контуру,
окружающему такую особенность в плоскости 

вообще говоря, не будет обращаться в нуль. Однако если интеграл (13.41) не исчезает, функция  не будет однозначно определена вне особенности; иначе говоря, обращение в нуль интеграла (13.41) является необходимым условием существования решения.
не будет однозначно определена вне особенности; иначе говоря, обращение в нуль интеграла (13.41) является необходимым условием существования решения.
Перейдем к рассмотрению особенностей на оси  . Вне особенности равно нулю на оси
. Вне особенности равно нулю на оси  следовательно, если предположить, что
следовательно, если предположить, что  обращается в нуль в некоторой точке на оси
обращается в нуль в некоторой точке на оси  оно будет равно нулю на всей оси
оно будет равно нулю на всей оси  до особой точки. Сама особая точка должна быть такова, что должен обращаться в нуль интеграл от дифференциала
до особой точки. Сама особая точка должна быть такова, что должен обращаться в нуль интеграл от дифференциала

взятый по малой полуокружности около особенности от одной точки пересечения этой полуокружности с осью  до другой.
до другой.
Рассмотрим типичную особенность на оси 

Производные от  равны
равны 

Дифференциал (13.42) принимает вид:

Проведем интегрирование по малой полуокружности. Для этого введем угол 

Подставляя эти выражения в уравнение (13.44), получим:

Интегрирование производим от  до
до  . Имеем
. Имеем 

Решение  [уравнение (13.43)] совместимо с условиями регулярности для V.
[уравнение (13.43)] совместимо с условиями регулярности для V.
Рассмотрим теперь случай наличия двух особенностей. В одной особой точке решение с особенностью в другой точке можно разложить в степенной ряд по  и предположить, что вблизи от начала координат
и предположить, что вблизи от начала координат  имеет вид
имеет вид

Перед тем как снова вычислять интеграл, заметим, что только некоторые коэфициенты разложения могут входить в интеграл по полуокружности. Значение интеграла, конечно, не зависит от размеров полуокружности, т. е. от  до тех пор, пока эта окружность не охватывает никакой другой особой точки, кроме первоначальной
до тех пор, пока эта окружность не охватывает никакой другой особой точки, кроме первоначальной  . Поэтому не должны рассматриваться все коэфициенты
. Поэтому не должны рассматриваться все коэфициенты  делающие значение интеграла зависящим от
делающие значение интеграла зависящим от  . Кроме того, регулярная часть
. Кроме того, регулярная часть  сама по себе не может ничего прибавить к неисчезающему интегралу, поэтому нужно
сама по себе не может ничего прибавить к неисчезающему интегралу, поэтому нужно
рассматривать только перекрестные произведения сингулярной и регулярной частей  Производные сингулярной части
Производные сингулярной части  (при заданном
(при заданном  ) убывают как
) убывают как  . Они умножаются на
. Они умножаются на  на дифференциалы координат
на дифференциалы координат  и эти дифференциалы возрастают, как
и эти дифференциалы возрастают, как  и на производные от регулярной части
и на производные от регулярной части  Поэтому для нас представляют интерес только те члены разложения, производные которых зависят только от
Поэтому для нас представляют интерес только те члены разложения, производные которых зависят только от  но не от
но не от  Единственным таким членом будет
Единственным таким членом будет  Заменим поэтому выражение (13.47) на
Заменим поэтому выражение (13.47) на

Вычислим выражение

Только выписанные члены могут привести к неисчезающим значениям интеграла. Получим:

Интеграл этого выражения в пределах от  до
до  не равен нулю.
не равен нулю.
Мы нашли, что в окрестности одной из особых точек производная по z от регулярной части  должна обращаться в нуль. Это исключает возможность одновременного существования нескольких особых точек на оси
должна обращаться в нуль. Это исключает возможность одновременного существования нескольких особых точек на оси  Это выглядит так, как будто сами уравнения поля исключают движения точечных масс, не совместимые с уравнениями движения. В главе XV мы увидим, что это действительно так.
Это выглядит так, как будто сами уравнения поля исключают движения точечных масс, не совместимые с уравнениями движения. В главе XV мы увидим, что это действительно так.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
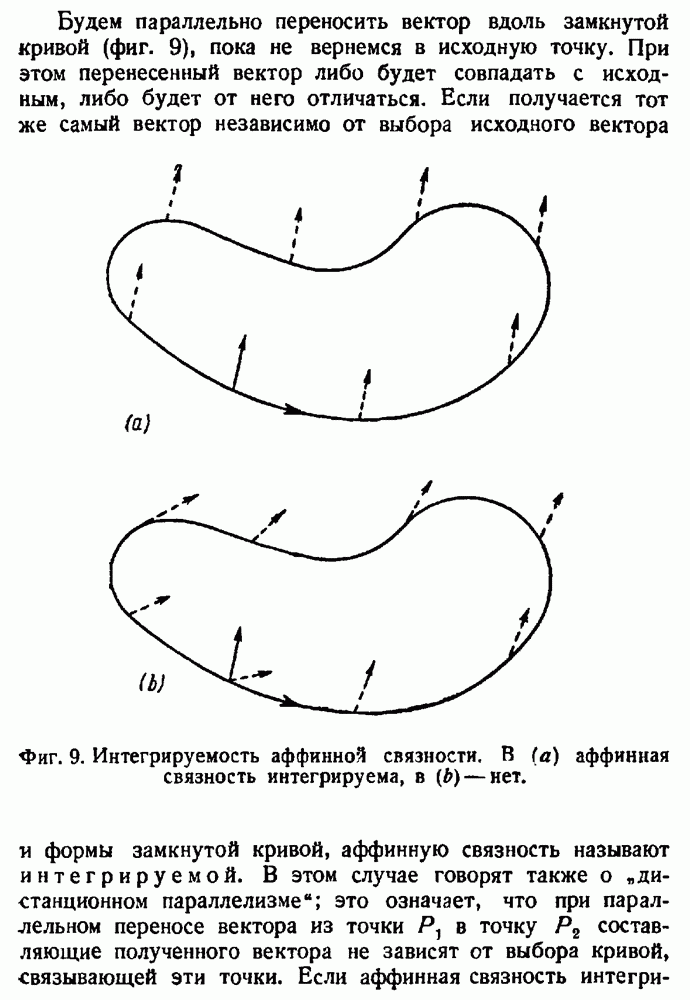
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.