| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
Закон инерции, инерциальные системы.
Механика Галилея — Ньютона была первой областью физики, ставшей наиболее развитой экспериментальной наукой. Прежде всего был установлен закон инерции: тела, не взаимодействующие с другими телами, продолжают оставаться в состоянии покоя или равномерного прямолинейного движения. Другими словами, движение таких тел является неускоренным.
Чтобы выразить закон инерции в математической форме, мы будем описывать положение тела его тремя координатами:  . Если тело не находится в состоянии покоя, его координаты являются функциями времени. Согласно закону инерции, когда на тело не действуют силы, вторые производные этих трех функций, т. е. ускорения, обращаются в нуль:
. Если тело не находится в состоянии покоя, его координаты являются функциями времени. Согласно закону инерции, когда на тело не действуют силы, вторые производные этих трех функций, т. е. ускорения, обращаются в нуль:

Мы пользуемся обычным обозначением х вместо 
Первый интеграл уравнений (2.1) выражает постоянство трех компонент скорости:

Уравнения, выражающие закон инерцин, содержат координаты и относятся поэтому к определенной системе координат. Пока система координат не выбрана, закон инерции в том виде, как он сформулирован выше (см. курсив), еще не имеет точного смысла. Для любого тела мы всегда можем ввести систему отсчета, в которой оно покоится и, следовательно, не ускорено. Правильная
формулировка такова: существует система (или системы) координат, относительно которой все тела, не испытывающие действия сил, движутся неускоренно. Системы координат, обладающие такими свойствами, и соответствующие им системы отсчета называются инерциальными системами.
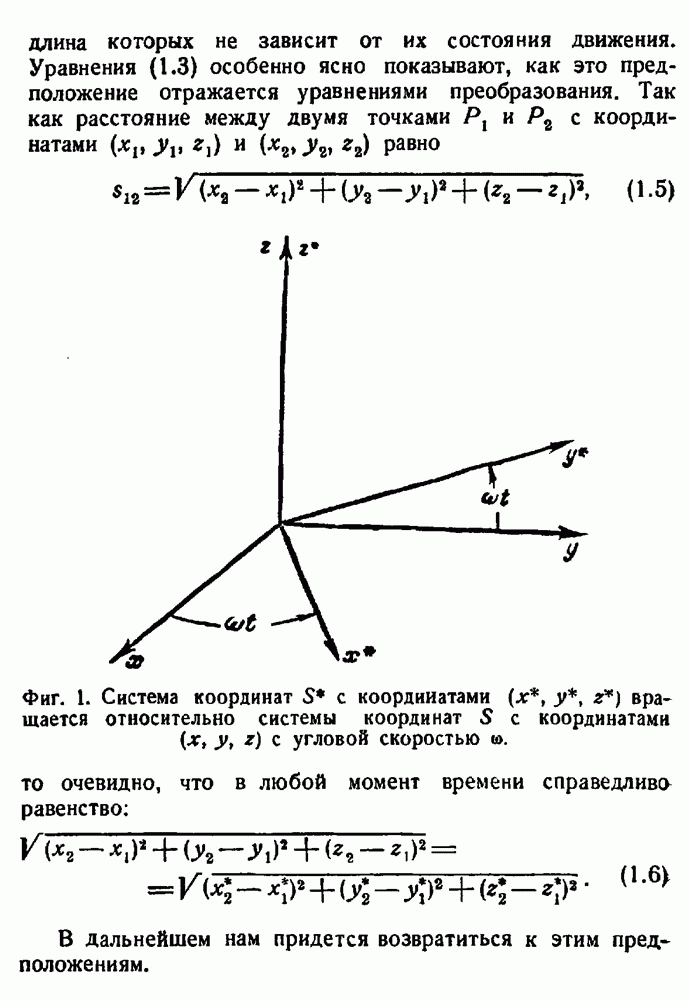
Конечно, не все системы отсчета являются инерциальными. Например, будем исходить из инерциальной системы координат S и произведем преобразование (1.2) к системе S, вращающейся с постоянной угловой скоростью  относительно S. Чтобы получить законы преобразования уравнений (2.1) и (2.2), продифференцируем уравнения преобразования (1.2) сначала один, а затем второй раз по времени
относительно S. Чтобы получить законы преобразования уравнений (2.1) и (2.2), продифференцируем уравнения преобразования (1.2) сначала один, а затем второй раз по времени  Получающиеся уравнения содержат
Получающиеся уравнения содержат  и их первые и вторые производные по времени.
и их первые и вторые производные по времени.
Мы предположили, что система координат S инерциальна. Поэтому подставим вместо х, у и z и х, у и z соответственно выражения (2.1) и (2.2). Таким образом, получаем для координат, отмеченных звездочкой и их производных,

и

Оказывается, что в системе координат S не все вторые производные по времени исчезают. Иногда бывает удобно перейти к системе отсчета, в которой появляющиеся ускорения обусловлены не действительным взаимодействием тел. Умноженные на массы, эти ускорения трактуются как
реальные силы и большей частью носят название «сил инерции». Несмотря на это название, они не являются настоящими силами; они только формально входят в уравнения так же, как обычные силы. В нашем случае первые члены  умноженные на массу, называются „центробежными силами”, а последние члены, также умноженные на массу, называются силами Кориолиса.
умноженные на массу, называются „центробежными силами”, а последние члены, также умноженные на массу, называются силами Кориолиса.
С другой стороны, существуют типы преобразований координат, оставляющие формы закона инерции (2.1) неизмененными. В качестве такого случая рассмотрим раньше всего преобразования типа (1.1), не связанные с переходом к новой системе отсчета. Дифференцированием (1.1) с подстановкой  и так далее из (2.1) и (2.2) получаем уравнения:
и так далее из (2.1) и (2.2) получаем уравнения:

и

Компоненты скорости, как и следовало ожидать, преобразуются, как компоненты вектора, а уравнения (2.1) воспроизводятся в новых координатах без изменения своего вида.
Другое преобразование, сохраняющее вид закона инерции, есть преобразование типа (1.3). Оно соответствует переходу от одной системы отсчета к другой, движущейся относительно первой равномерно и прямолинейно. Дифференцируя (1.3) два раза, получим:

и, если движение тела в системе S подчиняется закону инерции (2.1), мы имеем также:

в то время как первые производные отмеченных звездочкой координат [если уравнения (2.2) относятся к неотмеченным, звездочкой координатам] равны:

Уравнения (2.8) показывают, что закон инерции выполняется в новой системе так же, как и в старой. Уравнения (2.9) выражают тот факт, что скорость в новой координатной системе S равна разности скорости в старой системе и относительной скорости обеих систем. Этот закон часто называют (классическим) законом сложения скоростей.
Системы отсчета и системы координат, в которых справедлив закон (2.1), являются инерциальными системами. Все декартовы системы координат, покоящиеся относительно инерциальной системы координат, сами являются также инерциальными системами. Декартовы системы координат, связанные с системой отсчета, равномерно и прямолинейно движущейся относительно некоторой инерциальной системы, также являются инерциальными системами. С другой стороны, если мы перейдем к новой системе отсчета, ускоренно движущейся относительно первой, то преобразования координат в этой новой системе не приведут к уравнениям (2.1). Ускорение новой системы отсчета относительно инерциальной системы проявляется в появлении ускорения тел, не связанного с наличием реальных сил.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
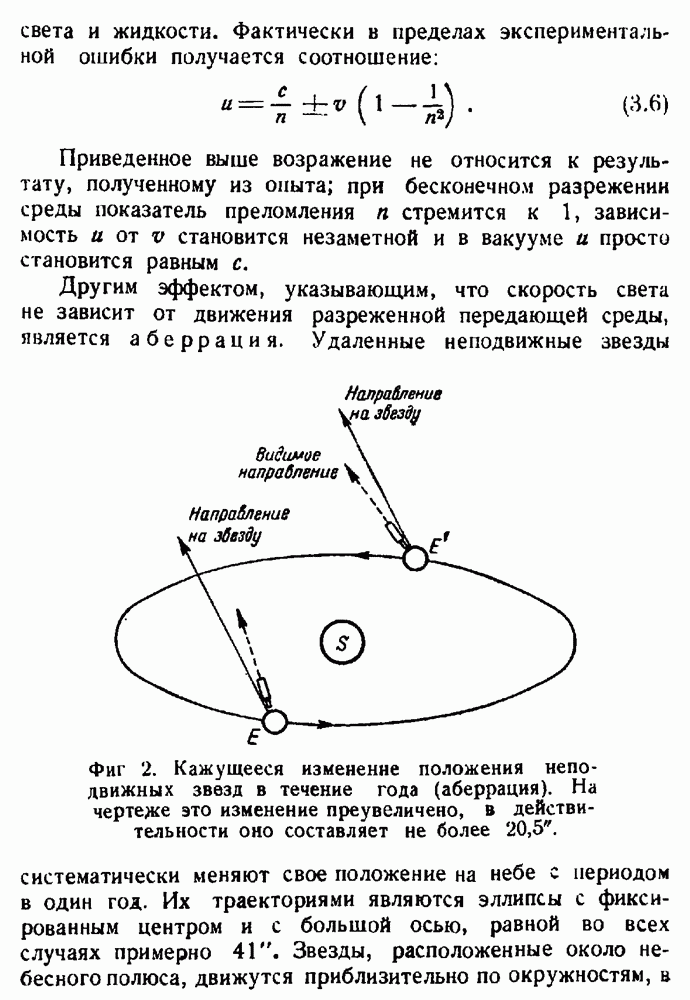
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
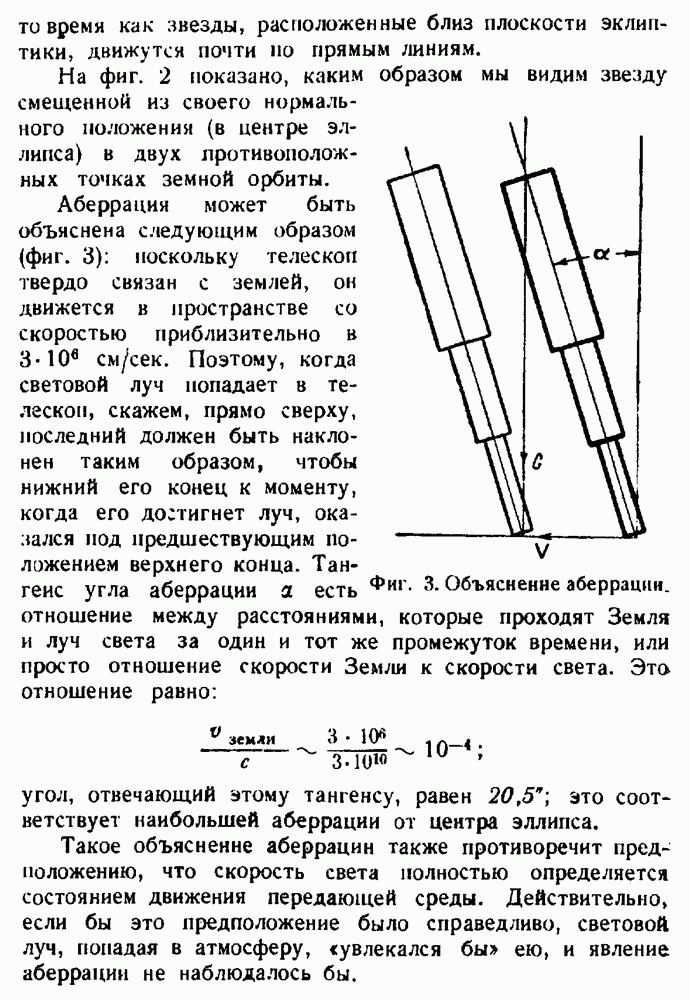
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
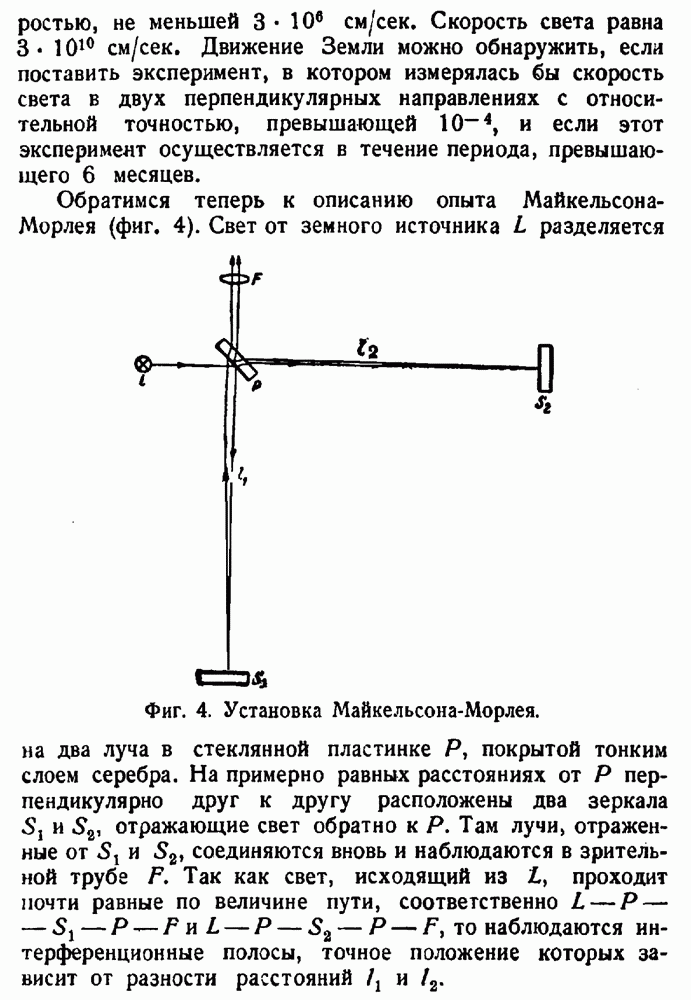
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
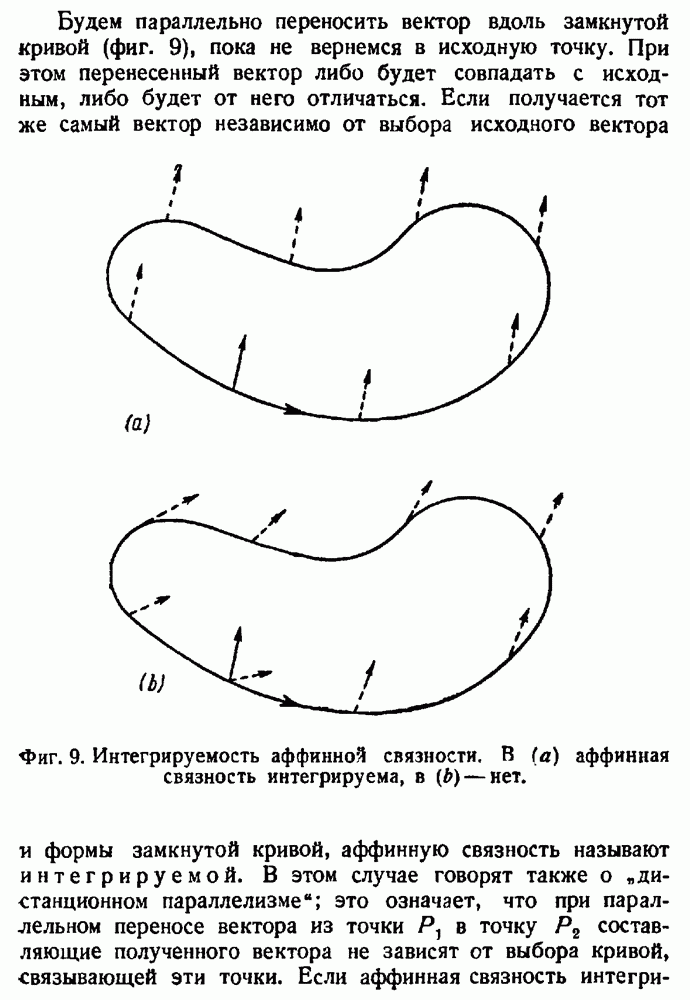
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.