| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Анализ в p-формализме.
Кроме дифференциальных ковариантов риманова пятимерного пространства, существуют еще дифференциальные коварианты, свойственные только рассматриваемому здесь формализму. Рассмотрим каждый из них в отдельности.
Внутреннее произведение (обычной) производной  -тензора на вектор
-тензора на вектор 

является  -тензором того же типа. Доказательство проводится непосредственным вычислением. Будем называть этот тип ковариантного дифференцирования - дифференцированием,
-тензором того же типа. Доказательство проводится непосредственным вычислением. Будем называть этот тип ковариантного дифференцирования - дифференцированием,  -тензор,
-тензор,  -производная которого равна нулю, будем называть полем, цилиндрическим относительно
-производная которого равна нулю, будем называть полем, цилиндрическим относительно  -поля, или, короче, — цилиндрическим.
-поля, или, короче, — цилиндрическим.
Рассмотрим теперь некоторые из таких  -производных. В первую очередь остановимся на
-производных. В первую очередь остановимся на  -производной метрического
-производной метрического  -тензора,
-тензора,  Покажем, что она может быть выражена через ковариантные производные
Покажем, что она может быть выражена через ковариантные производные  -поля. Величины
-поля. Величины  можно заменить выражением
можно заменить выражением

Преобразуем произведение, стоящее справа от точки:

Теперь можно сгруппировать члены таким образом, чтобы получить выражение (пятимерного) тензора:

где  — соответственно тензор и вектор, определяемые выражениями:
— соответственно тензор и вектор, определяемые выражениями:

Для  -производной метрического тензора, находим, таким образом:
-производной метрического тензора, находим, таким образом:

Квадрат линейного элемента

равен сумме квадратов  -линейного элемента
-линейного элемента

и компоненты дифференциала координатного вектора в А-направлении

Рассмотрим произвольную кривую в пятимерном пространстве, конечные точки которой суть  Если всю кривую сместить так, чтобы все ее точки сдвинулись вдоль
Если всю кривую сместить так, чтобы все ее точки сдвинулись вдоль  -кривых на одно и то же расстояние, то
-кривых на одно и то же расстояние, то  -длина кривой
-длина кривой

останется неизменной, если  -метрика является Л-цилиндрической.
-метрика является Л-цилиндрической.  -длина кривой останется неизменной, если вектор В равен нулю:
-длина кривой останется неизменной, если вектор В равен нулю:

а (пятимерная) длина кривой не изменится, если А-поле удовлетворяет уравнению Киллинга

Для того, чтобы  -метрика была цилиндрической, достаточно, чтобы правая часть уравнения (17.15) равнялась нулю. Это условие слабее, чем условие Киллинга, так как произведение правой части уравнения (17.15) на А? тождественно равно нулю; другими словами, существует только десять алгебраически независимых компонент уравнения (17.15), в то время как уравнения Киллинга имеют пятнадцать компонент. Очевидно, что из одновременной цилиндричности
-метрика была цилиндрической, достаточно, чтобы правая часть уравнения (17.15) равнялась нулю. Это условие слабее, чем условие Киллинга, так как произведение правой части уравнения (17.15) на А? тождественно равно нулю; другими словами, существует только десять алгебраически независимых компонент уравнения (17.15), в то время как уравнения Киллинга имеют пятнадцать компонент. Очевидно, что из одновременной цилиндричности  -метрики и цилиндричности , А-метрики“ следует цилиндричность (пятимерной) метрики, и наоборот.
-метрики и цилиндричности , А-метрики“ следует цилиндричность (пятимерной) метрики, и наоборот.
Далее рассмотрим  -производную от антисимметричного
-производную от антисимметричного  -тензора
-тензора 

Этот тензор  впоследствии будет интерпретирован, как тензор электромагнитного поля. Его А-производными будут
впоследствии будет интерпретирован, как тензор электромагнитного поля. Его А-производными будут

В квадратных скобках исключим  Это можно сделать при помощи следующего преобразования:
Это можно сделать при помощи следующего преобразования:

Поэтому имеем:

Так как произведение  на
на  равно нулю, имеем
равно нулю, имеем

Чтобы вычислить выражение в квадратных скобках, примем во внимание, что циклическая производная от равна нулю и что  также равно нулю. Учитывать при этом нужно только те члены, в которых один из двух множителей заменем на
также равно нулю. Учитывать при этом нужно только те члены, в которых один из двух множителей заменем на  а другой — на
а другой — на  Тогда получим
Тогда получим

После проведения дифференцирования большинство членов выпадает, либо в силу того, что  равно нулю, либо благодаря тому, что непродифференцированные
равно нулю, либо благодаря тому, что непродифференцированные  умножаются на
умножаются на  Окончательным результатом будет
Окончательным результатом будет

Рассмотрев  -дифференцирование
-дифференцирование  перейдем к рассмотрению другой дифференциальной операции,
перейдем к рассмотрению другой дифференциальной операции,  -дифференцирования". Назовем выражение
-дифференцирования". Назовем выражение

 -производной от V по
-производной от V по  . Если функция А-цилнндриче-ская,
. Если функция А-цилнндриче-ская,  -производная будет обычной производной от V по аргументу
-производная будет обычной производной от V по аргументу  . (А-цилиндрическая функция может рассматриваться как функция только параметров
. (А-цилиндрическая функция может рассматриваться как функция только параметров  -производные скаляра образуют
-производные скаляра образуют  -вектор.
-вектор.
Вообще говоря,  -производные не коммутируют. Их перестановочными соотношениями будут
-производные не коммутируют. Их перестановочными соотношениями будут

Если V А-цилиндрическая функция, ее  -производные, являющиеся обычными производными, должны коммутировать, т. е. правая часть уравнения (17.26) обращается в нуль. Поэтому выражение в скобках пропорционально
-производные, являющиеся обычными производными, должны коммутировать, т. е. правая часть уравнения (17.26) обращается в нуль. Поэтому выражение в скобках пропорционально 

 можно найти, умножая уравнение (17.27) на
можно найти, умножая уравнение (17.27) на 

Отсюда имеем:

и

 -производные от
-производные от  -тензора, вообще говоря, не ковариантны. Однако антисимметричные
-тензора, вообще говоря, не ковариантны. Однако антисимметричные  -производные от
-производные от  -вектора образуют
-вектора образуют  -тензор, а циклическая
-тензор, а циклическая  -производная антисимметричного
-производная антисимметричного  -тензора второго ранга также является
-тензора второго ранга также является  -тензором.
-тензором.
Особенный интерес представляет собой  -тензор
-тензор  Этот тензор можно выразить через антисимметричные производные от
Этот тензор можно выразить через антисимметричные производные от 

В силу того, что циклическая производная  равна нулю, нужно оставить только следующие члены:
равна нулю, нужно оставить только следующие члены:

Пользуясь (17.28), антисимметричные  -производные от
-производные от  можно исключить и окончательным результатом будет
можно исключить и окончательным результатом будет

Введем теперь понятие ковариантного дифференцирования  -тензоров. Если
-тензоров. Если  является
является  -вектором, то легко показать, что дифференциальные выражения
-вектором, то легко показать, что дифференциальные выражения

образуют смешанный тензор  -вектор относительно а, вектор относительно
-вектор относительно а, вектор относительно  если коэфициенты преобразуются согласно закону
если коэфициенты преобразуются согласно закону

Имеется  величин
величин  . Чтобы их найти, нужно задать такое же количество связывающих их соотношений. У словия
. Чтобы их найти, нужно задать такое же количество связывающих их соотношений. У словия

слишком жестки, так как их больше, чем нужно, с другой стороны, условий

слишком мало. Необходимые условия должны зависеть от трех индексов, одного координатного и двух параметрических. Условия

являются как раз условиями такого типа. Непосредственное вычисление показывает, что эти условия удовлетворяются, если  принимают значения
принимают значения

Можно также показать, что при таком выборе  удовлетворяются и условия (17.32). Однако условия (17.31) не удовлетворяются, вместо них имеем
удовлетворяются и условия (17.32). Однако условия (17.31) не удовлетворяются, вместо них имеем

Ковариантную  -производную тензора или
-производную тензора или  -тензора по
-тензора по  определим, как ковариантную производную по
определим, как ковариантную производную по  , умноженную на
, умноженную на

и

симметричны в  Известно также, что выражения
Известно также, что выражения  равны нулю, если они образованы с помощью выражений (17.34). Отсюда следует, что имеют значения
равны нулю, если они образованы с помощью выражений (17.34). Отсюда следует, что имеют значения

Обратимся теперь к различным типам тензоров кривизны, которые можно образовать с помощью различных типов аффинной связности. Наиболее просто получить их, составляя различные перестановочные соотношения. В первую
очередь естественно отметить перестановочное соотношение Римана

Для получения перестановочных соотношений для производных  -векторов понадобятся ковариантные производные от
-векторов понадобятся ковариантные производные от 

Отсюда получаем перестановочные соотношения:

Выражение  может быть преобразовано следующим образом:
может быть преобразовано следующим образом:

так как здесь скобки второй строки обращаются в нуль. Подставляя это в (17.41), после небольших преобразований получим:

«Смешанный» тензор кривизны  также может быть выражен через
также может быть выражен через 

Найдем далее перестановочные соотношения для ковариантных  -производных (обычного) вектора:
-производных (обычного) вектора:

Аналогичные вычисления дают перестановочные соотношения для  -производных
-производных  -вектора:
-вектора:

С другой стороны, эти же перестановочные соотношения можно выразить через

Сравнение правых частей уравнений (17.47), (17.46) (17.43) дает соотношения, связывающие величины  и
и

Особенно существенными для применения этого формализма к теории Калуза являются выражения, получающиеся в результате двойного свертывания этих уравнений;

Член  входящий в это выражение, представим в несколько иной форме:
входящий в это выражение, представим в несколько иной форме:

Подставляя (17.50) в (17.49), найдем, что скалярная  -кривизна связана с (обычной) скалярной кривизной соотношением
-кривизна связана с (обычной) скалярной кривизной соотношением

Следует подчеркнуть, что с точки зрения теории инвариантов развитый здесь формализм представляет собой не что иное, как теорию поля единичных векторов в метрическом пространстве. Значение такого представления состоит в том, что в единых теориях поля, использующих
пятимерный формализм для описания физического мира, четыре параметра х предполагаются представляющими четыре координаты нашего физического пространства.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
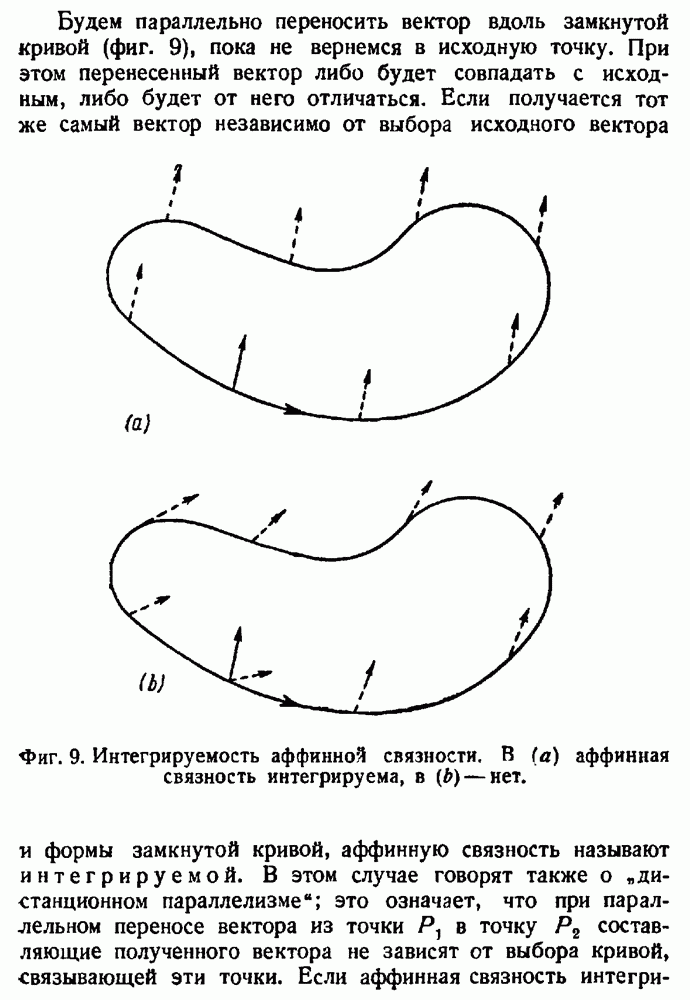
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.