| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Заряженные частицы в электромагнитном поле.
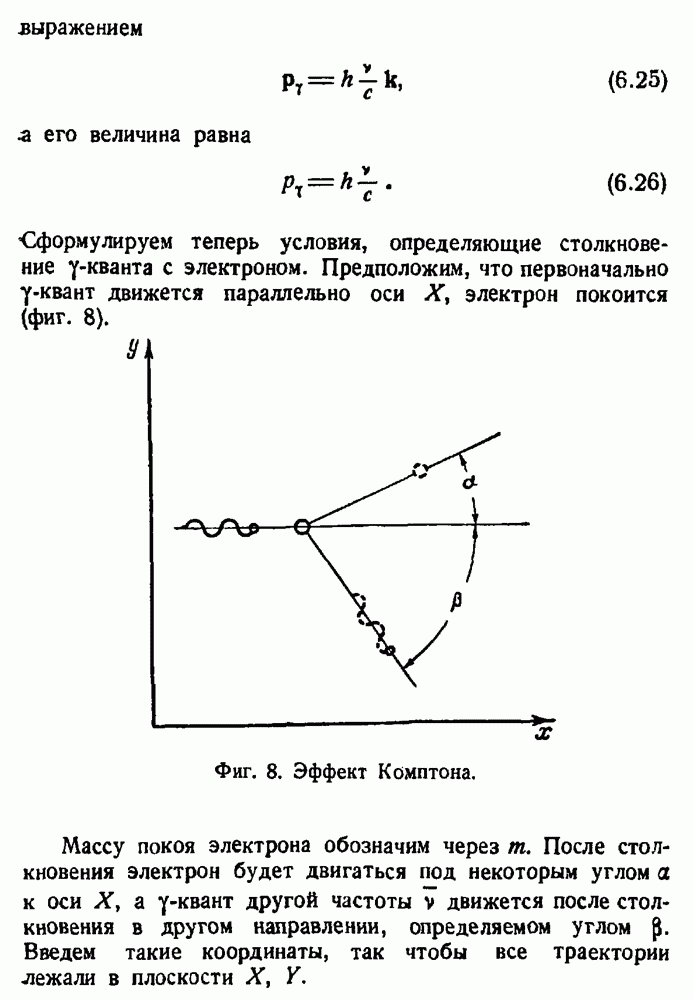
Дальнейшая проверка специальной теории относительности основывается на изучении поведения частиц под действием сил. В главе IV был рассмотрен эффект Комптона, то есть столкновения у-квантов с электронами. Теперь рассмотрим действие стационарных электромагнитных полей на заряженные частицы. Уравнениями движения будут уравнения (7.44):

Для получения закона сохранения энергии умножим это уравнение скалярно на и и проинтегрируем обе стороны по частям. Слева получим

а справа

Таким образом, изменение энергии вдоль пути частицы определяется выражением

Рассматривая изменение потенциала  вдоль пути, можно выделить полный дифференциал из выражения
вдоль пути, можно выделить полный дифференциал из выражения 

Уравнение (9.5) принимает тогда вид

В статическом поле, где  и А не меняются во времени, выражение слева в квадратных скобках остается постоянным.
и А не меняются во времени, выражение слева в квадратных скобках остается постоянным.
Уравнение (9.7) дает возможность определить скорость частиц, попадающих в сильное электрическое поле с весьма малыми начальными скоростями. Их кинетическая энергия после прохождения разности потенциалов V будет

а их скорость

Классическая формула

является хорошим приближением, когда  мало в сравнении с единицей.
мало в сравнении с единицей.
Формула (9.8) показывает, что изменение энергии частицы равно произведению ее заряда на разность потенциалов. Этой формулой пользуются во всех случаях, когда энергия частицы при эксперименте определяется ускоряющей разностью потенциалов, как, скажем, это имеет место в электростатическом генераторе Ван-де-Граафа.
В камере Вильсоиа скорость заряженной частицы обычно определяется измерением радиуса кривизны ее траектории в постоянном магнитном поле, перпендикулярном направлению скорости. Определим этот радиус.
Ускорение заряженной частицы в магнитном поле определяется уравнением (9.3)

Из уравнения (9.7) видно, что, когда Н не зависит от времени, скорость а остается постоянной. Поэтому можно заменить вектор  произведением постоянной скорости и на единичный вектор
произведением постоянной скорости и на единичный вектор  параллельный и и меняющий с течением времени свое направление. Левая часть уравнения (9.10) переходит в
параллельный и и меняющий с течением времени свое направление. Левая часть уравнения (9.10) переходит в

а правая равна:

так что для (9.10) получаем

Заменим теперь дифференцирование по t дифференцированием по длине дуги  Так как есть скорость и, те вместо (9.10а) получим
Так как есть скорость и, те вместо (9.10а) получим

где  — единичный касательный вектор вдоль пути и, следовательно, является кривизной, обратная величина которой представляет собой радиус кривизны
— единичный касательный вектор вдоль пути и, следовательно, является кривизной, обратная величина которой представляет собой радиус кривизны  Отсюда имеем
Отсюда имеем

Угол  постоянен вдоль пути. В этом легко убедиться путем скалярного умножения уравнения (9.10а) на Н, при этом правая часть обращается в нуль, в левую же часть в качестве множителя войдет производная от
постоянен вдоль пути. В этом легко убедиться путем скалярного умножения уравнения (9.10а) на Н, при этом правая часть обращается в нуль, в левую же часть в качестве множителя войдет производная от  по
по  Поэтому частица будет двигаться по винтовой линии. Если
Поэтому частица будет двигаться по винтовой линии. Если  и Н взаимно перпендикулярны, траекторией будет окружность. В этом случае произведение
и Н взаимно перпендикулярны, траекторией будет окружность. В этом случае произведение  определяет величину релятивистского импульса частицы
определяет величину релятивистского импульса частицы

Зная  можно найти скорость и энергию частицы.
можно найти скорость и энергию частицы.
Иногда определяют отклонение заряженной частицы в электрическом поле, перпендикулярном ее траектории. Ускорение попрежнему определяется уравнением (9.3)

Пока Е и и взаимно перпендикулярны, скорость и остается постоянной. Вводя опять единичный вектор  вместо (9.14), получим:
вместо (9.14), получим:

Переход к переменной длины дуги I приводит к уравнению

или, вводя радиус кривизны 

В случае электрического поля траектории, конечно, не являются кругами. Уравнение (9.15) дает радиус кривизны только той части траектории, в которой направление движения перпендикулярно силовым линиям.
Для определения как массы покоя, так и скорости частицы необходимо исследовать ее поведение одновременно в электрическом и в магнитном полях. Можно, например, сообщить частице определенную энергию, ускоряя ее заданной разностью потенциалов [уравнение (9.8)], а затем по отклонению в магнитном поле определит ее импульс [уравнение (9.13)]; в таком случае одновременна вычисляются и масса и импульс частицы.
Опыты подобного рода использовались и для проверки релятивистских законов движения; при этом исследовалось множество частиц одного сорта, но обладавших различными скоростями. Все эти эксперименты подтвердили правильность релятивистских законов. Подробное описание этих экспериментов можно найти в статье В. Герлаха.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
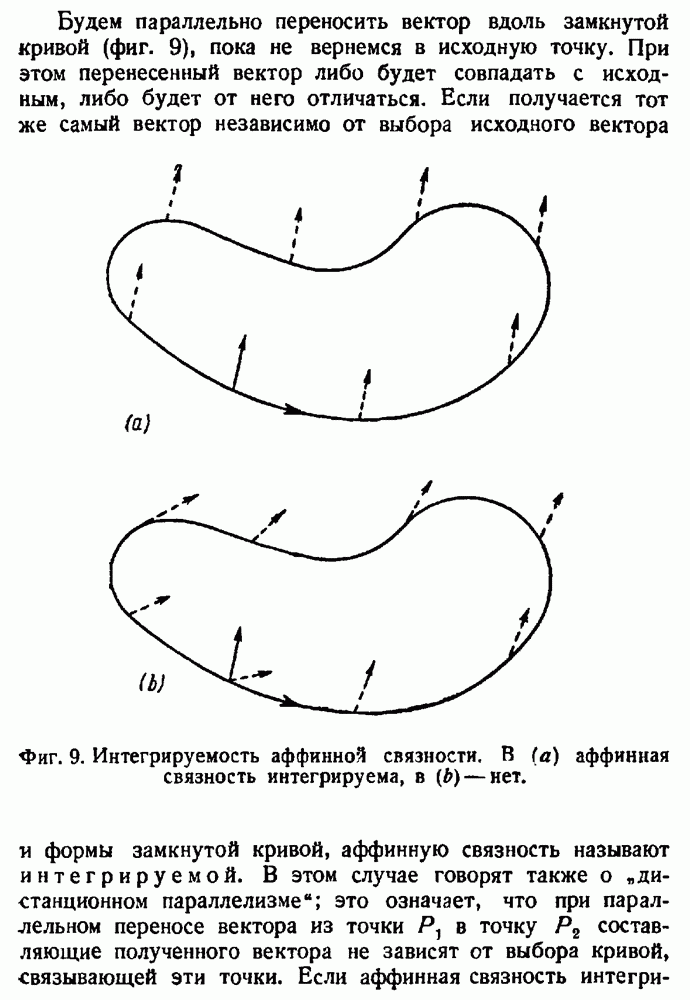
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.