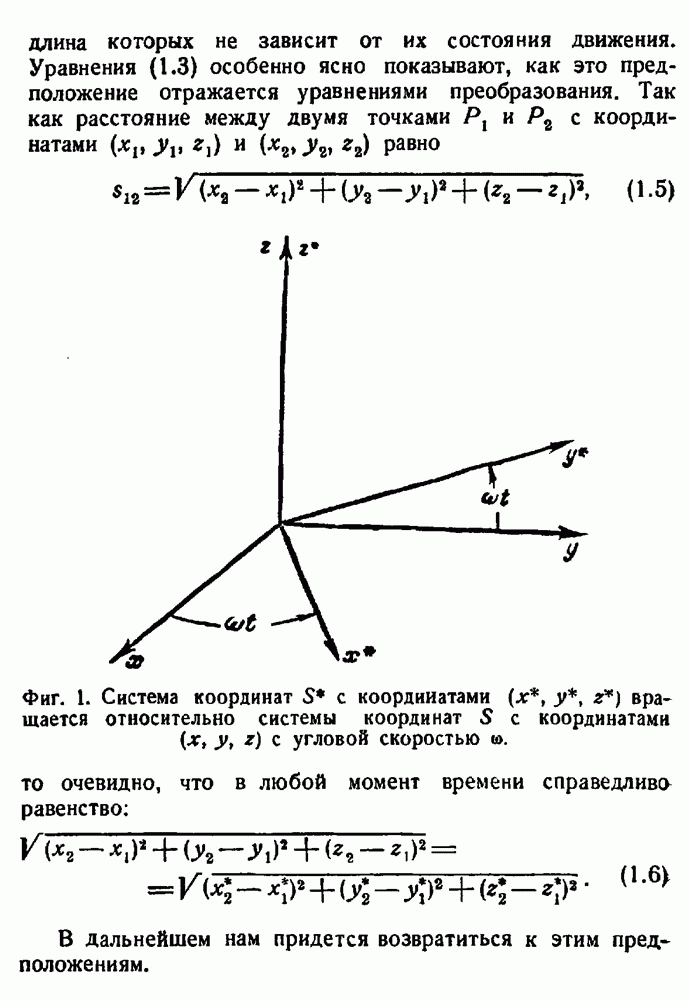
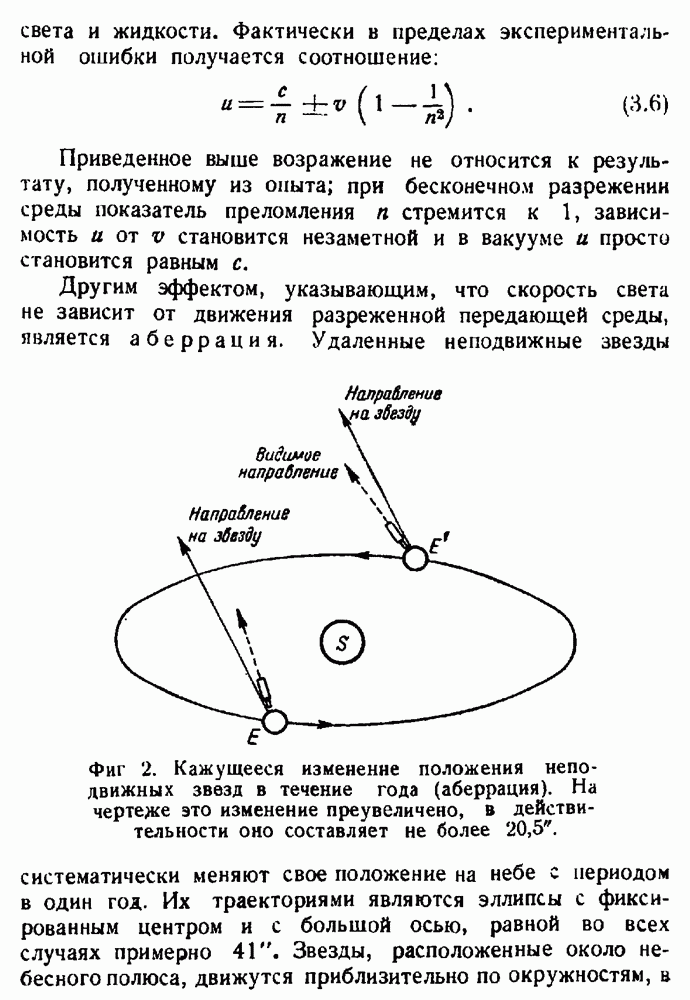
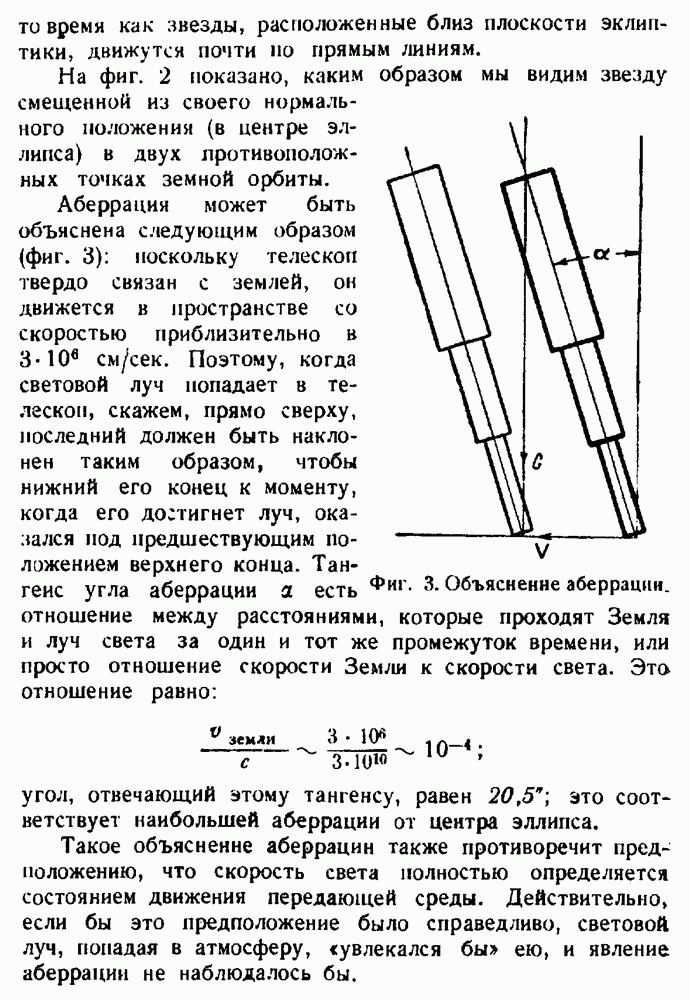
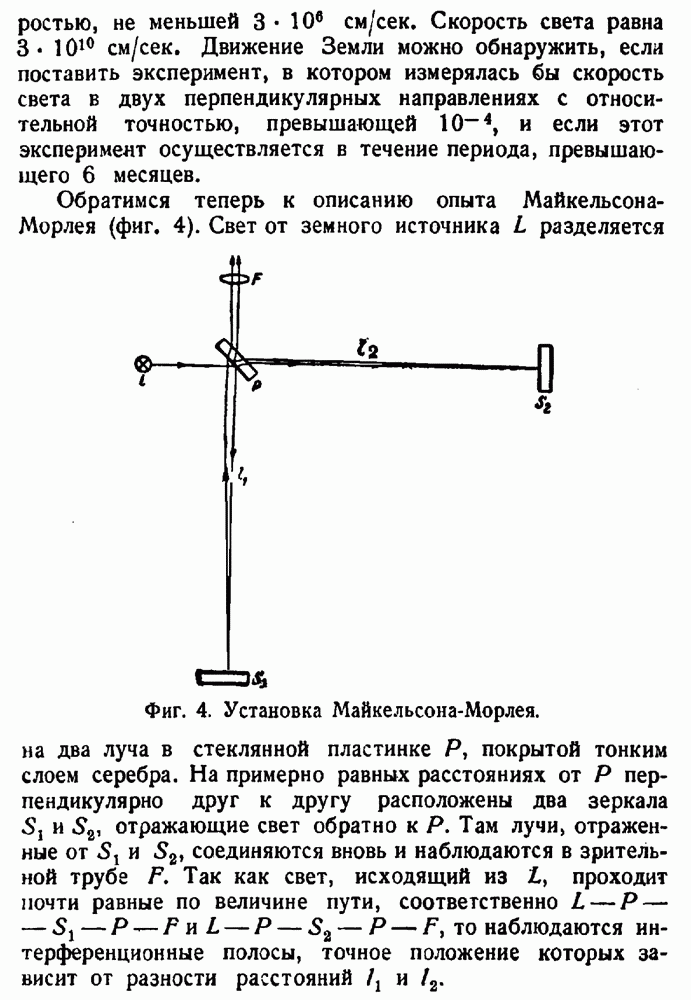
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Заключение.
Очень важно выяснить, почему в одной теории поля (теории гравитации) уравнения движения получаются из уравнений поля, в то время как в другой теории (теории Максвелла) этого не происходит. Основная причина состоит в том, что уравнения гравитационного поля удовлетворяют четырем тождествам, тогда как уравнения Максвелла только одному. Значение этих тождеств для уравнений движения было показано как Вейлем при исследовании точных решений с осевой симметрией, так и Эйнштейном, Инфельдом и Гофманом в их приближенном методе.
Благодаря этим тождествам уравнения поля общей теории относительности являются одновременно как бы «переопределенными» и «недоопределенными». Уравнения поля линейны относительно вторых производных. Однако разрешить их относительно второй производной такой координаты, как  невозможно, так как четыре из десяти уравнений поля,
невозможно, так как четыре из десяти уравнений поля,  содержат только первые производные по 5. Поэтому невозможно произвольно задать все переменные поля и их первые производные по
содержат только первые производные по 5. Поэтому невозможно произвольно задать все переменные поля и их первые производные по  на некоторой гиперповерхности
на некоторой гиперповерхности  на этой гиперповерхности эти величины должны удовлетворять четырем условиям. В этом смысле уравнения переопределены.
на этой гиперповерхности эти величины должны удовлетворять четырем условиям. В этом смысле уравнения переопределены.
Но в то же время, если задать переменные и их первые производные по  на гиперповерхности
на гиперповерхности  в согласии с четырьмя уравнениями
в согласии с четырьмя уравнениями  то останутся только шесть уравнений, определяющих поведение десяти переменных в направлении
то останутся только шесть уравнений, определяющих поведение десяти переменных в направлении  вторые производные по
вторые производные по  от четырех переменных остаются произвольными. В этом смысле уравнения недоопределены. Однако можно показать, что благодаря четырем свернутым тождествам Бьянки четыре уравнения
от четырех переменных остаются произвольными. В этом смысле уравнения недоопределены. Однако можно показать, что благодаря четырем свернутым тождествам Бьянки четыре уравнения  продолжают удовлетворяться и вне выбранной гиперповерхности в том случае, если они удовлетворяются на этой гиперповерхности и если шесть уравнений
продолжают удовлетворяться и вне выбранной гиперповерхности в том случае, если они удовлетворяются на этой гиперповерхности и если шесть уравнений  удовлетворяются во всем пространстве.
удовлетворяются во всем пространстве.
Если же на выбранной гиперповерхности  имеются изолированные области, в которых уравнения не удовлетворяются, то эти области можно окружить (пространственными) поверхностями, так что тождества заменятся условиями обращения в нуль четырех интегралов по этим поверхностям. Одно тождество, которому удовлетворяют уравнения Максвелла, дает для изолированных областей, только одно условие — условие сохранения заряда (см» главу XII). Однако в этом случае количество тождеств недостаточно для получения уравнений движения.
имеются изолированные области, в которых уравнения не удовлетворяются, то эти области можно окружить (пространственными) поверхностями, так что тождества заменятся условиями обращения в нуль четырех интегралов по этим поверхностям. Одно тождество, которому удовлетворяют уравнения Максвелла, дает для изолированных областей, только одно условие — условие сохранения заряда (см» главу XII). Однако в этом случае количество тождеств недостаточно для получения уравнений движения.
Уравнения гравитационного поля отличаются от уравнений электромагнитного поля Максвелла и в другом отношении: они нелинейны. В силу этого линейная комбинация нескольких решений не является решением уравнений. Если бы
решения получались как линейные комбинации, это означало бы отсутствие взаимодействия точечных масс друг с другом. Приближенный метод Эйнштейна, Инфельда и Гофмана показывает, что даже классическое взаимодействие точечных масс обусловлено нелинейными членами в уравнениях поля.
Отсюда явствует, что из теории поля законы движения вытекают только в том случае, когда уравнения поля нелинейны и удовлетворяют, по крайней мере, четырем тождествам. В общей теории относительности нелинейность уравнений поля обусловлена их ковариантностью относительно общих преобразований координат. Взаимодействие точечных масс является, таким образом, еще одним аргументом в пользу принципа общей ковариантности.
Прежде чем закончить обсуждение общей теории относительности, отметим еще некоторые возникающие здесь проблемы. Общая теория относительности дает нам логически стройную теорию гравитации. Однако электромагнитное поле остается логически независимым от гравитационного; общей теории относительности не удалось объединить эти два типа полей в единое целое. Был предпринят ряд попыток создать „единую теорию поля, в которой и электромагнитное и гравитационное поля являлись бы составными частями геометрической структуры пространства. Некоторые из этих попыток будут рассмотрены в третьей части книги.
Далее, общая теория относительности не дает нам удовлетворительной теории строения материи. Существующие в природе элементарные частицы обладают определенными характеристическими массами, зарядами и т. д. Однако теория относительности, в которой частицы представляют собой особенности поля, не может объяснить этого обстоятельства.
Квантовые явления целиком находятся вне сферы рассмотрения общей теории относительности. Волновая механика является нерелятивистской, так как она не может обойтись без представления о действии на расстоянии. Первоначальная теория электрона Дирака описывает лорентц-ковариантным образом действие электромагнитного поля на
один электрон; однако, поскольку само поле неквантовано, эта теория не определяет надлежащим образом поля самого электрона, поэтому в ней не могут рассматриваться проблемы, касающиеся взаимодействия нескольких заряженных частиц.
Попытки получения релятивистской квантовой теории квантованием самого электромагнитного поля оказались весьма успешными. Однако все «квантовые теории поля" неудовлетворительны с математической точки зрения в том отношении, что их решения всегда расходятся. Таким образом, в настоящее время не существует удовлетворительной квантовой теории, лорентц-ковариантной или ковариантной относительно общих преобразований координат.
И теория относительности и квантовая теория являются огромными достижениями современной физики по сравнению с физикой девятнадцатого столетия. Однако эти достижения поставили нас лицом к лицу с новыми, в настоящее время еще не решенными проблемами. Невозможно предсказать, как будут преодолены возникшие трудности, несомненно, однако, что будущие теории включат то лучшее, что имеется в квантовой теории и в теории относительности.
Задача
Получить уравнения движения электрически заряженных точечных масс (закон Кулона).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
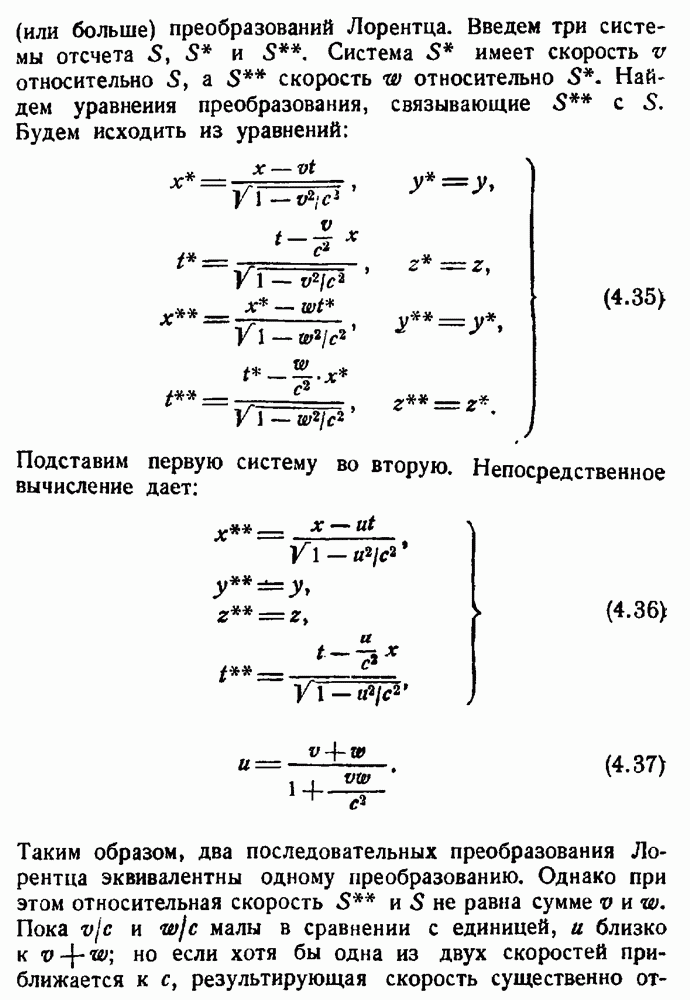
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
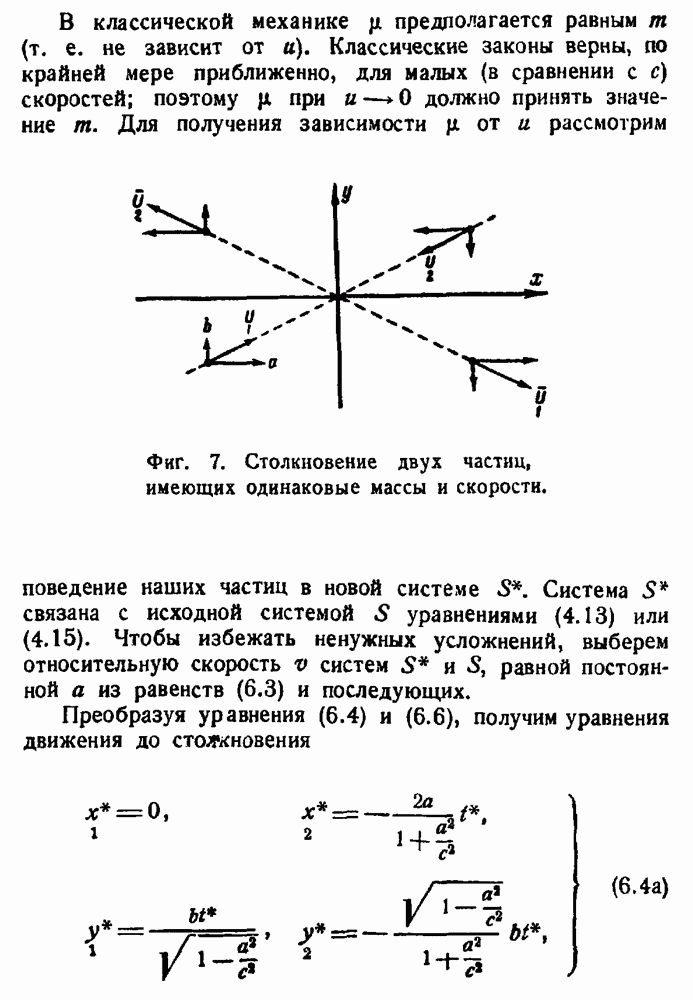
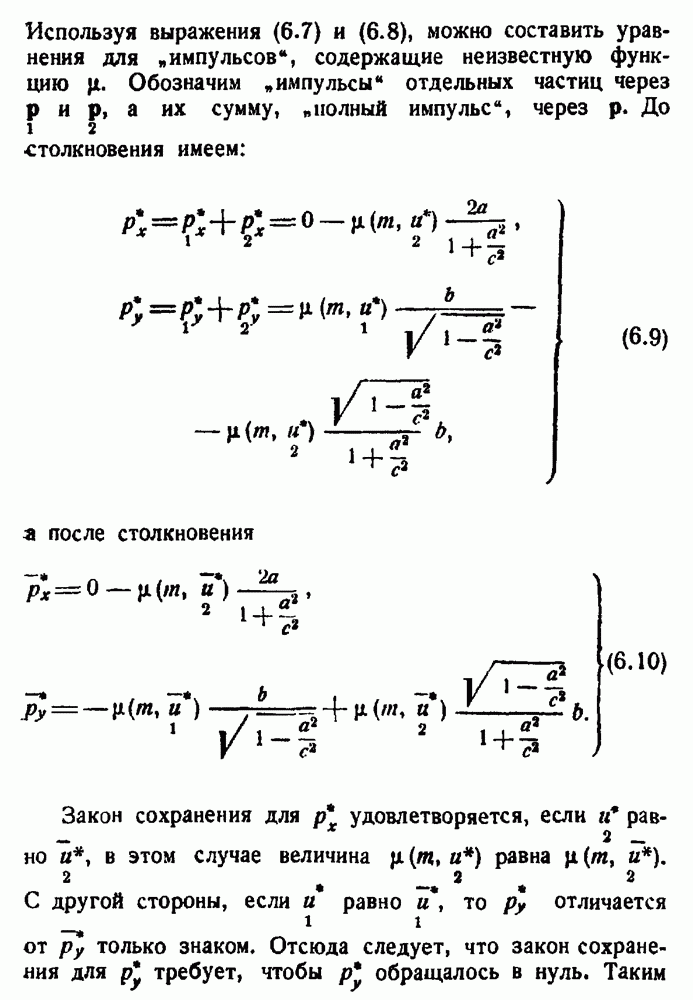
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
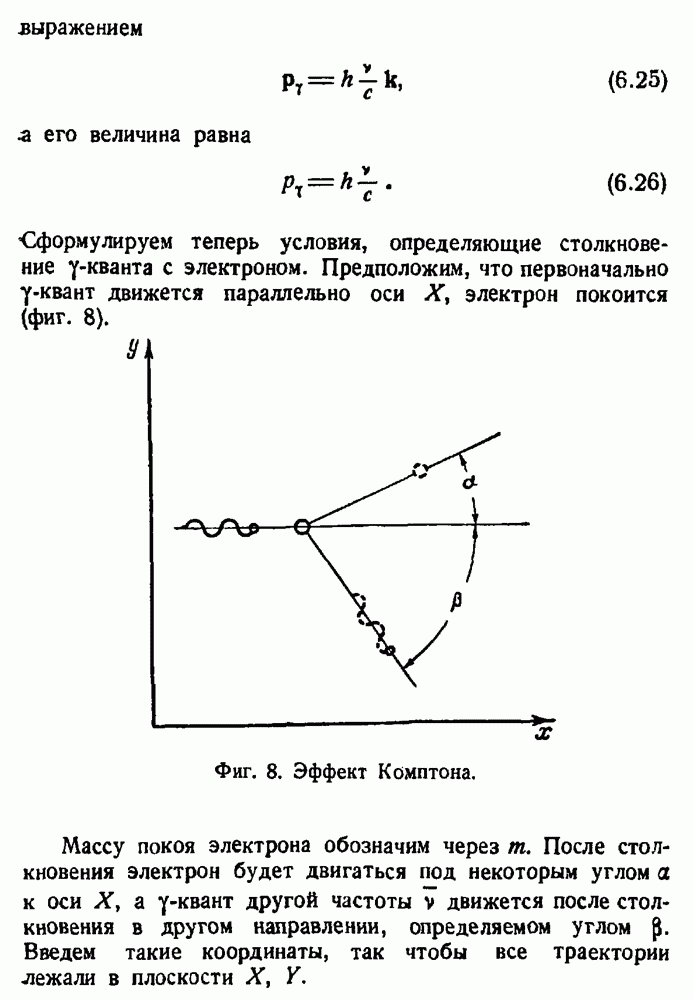
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
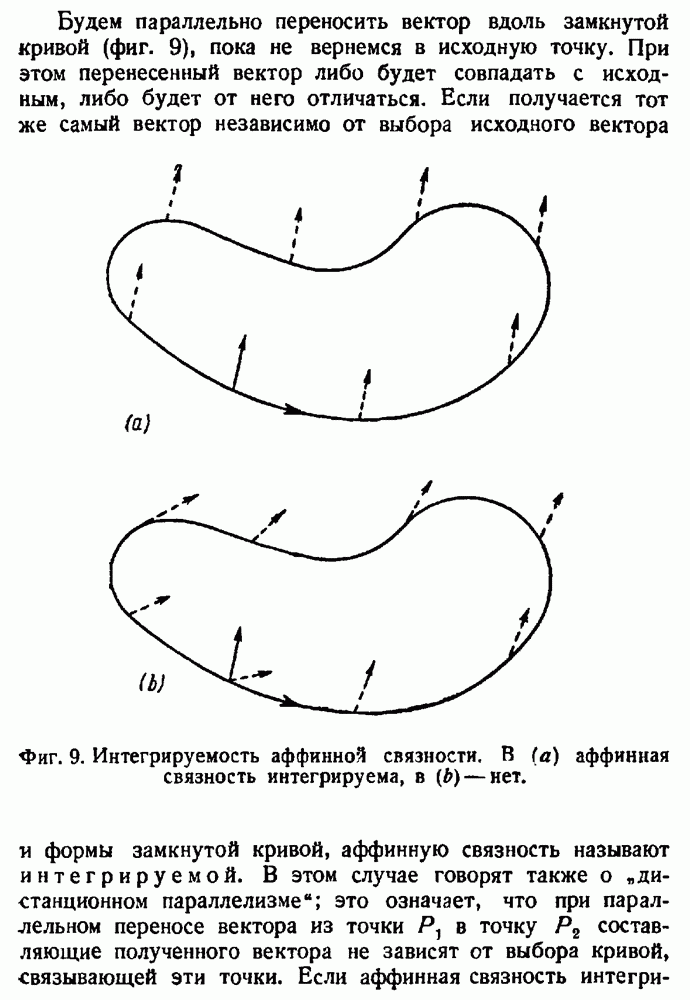
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.