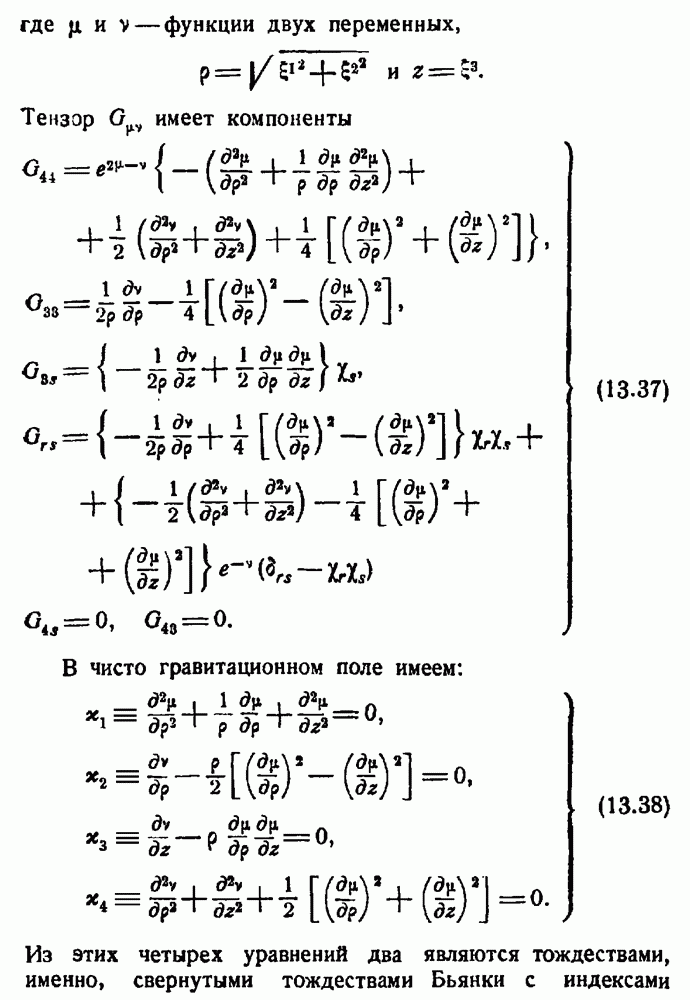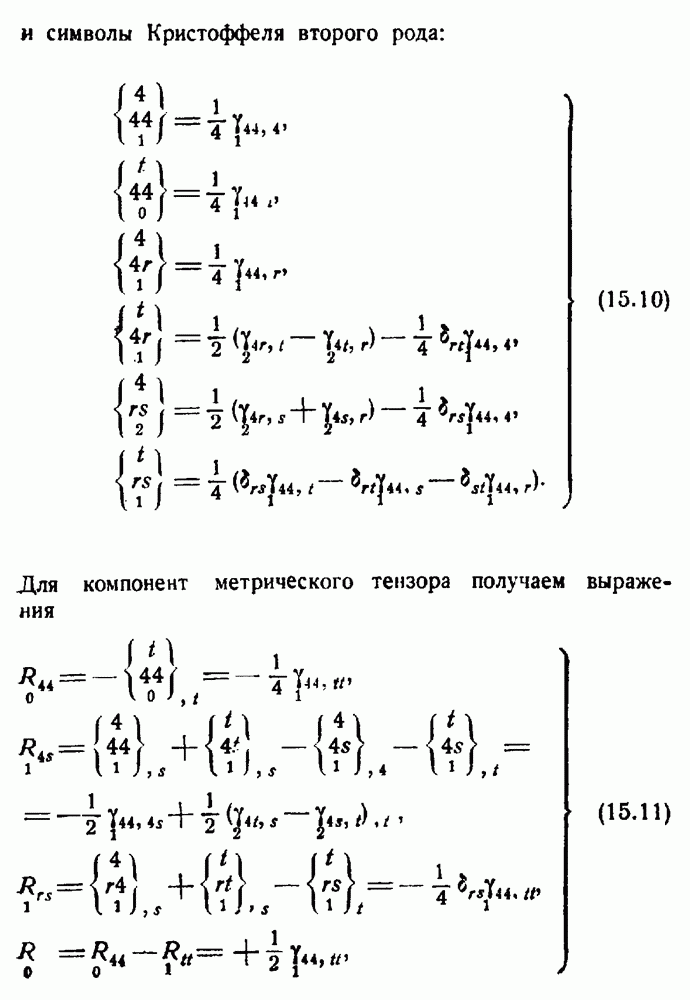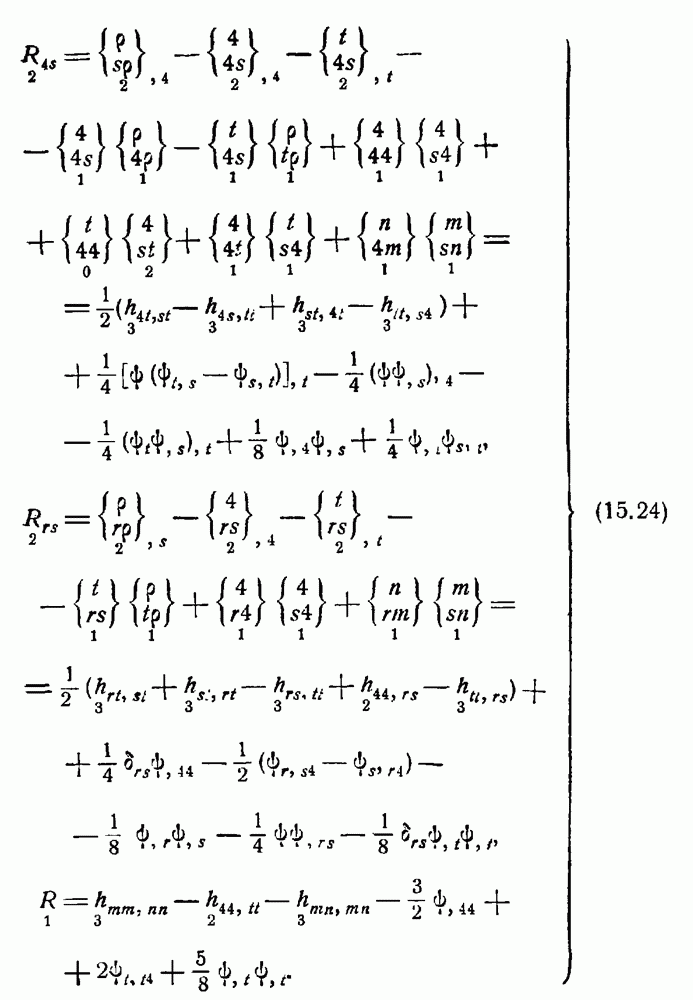| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Второе приближение и уравнения движения.
Во втором приближении необходимо использовать следующие контравариантные компоненты метрического тензора:

С их помощью находим выражения для символов Кристоффеля:


(кликните для просмотра скана)

(кликните для просмотра скана)
Для получения уравнений движения необходимо иметь выражения для  :
:

Некоторые члены этих выражений могут быть представлены как дивергенции антисимметричных величин. Поэтому для квадратной скобки имеем:

и кроме того,

С этого момента доказательство проводится так же, как и доказательство закона сохранения массы. Интегралы от  по замкнутой поверхности S, на которой
по замкнутой поверхности S, на которой
нет особенностей, должны равняться нулю. С другой стороны, интегралы от выражений, эквивалентных ротору, независимо обращаются в нуль. Поэтому должны сами по себе обращаться в иуль и интегралы от остальных членов. Эти оставшиеся члены состоят только из величин, найденных в первом приближении. Если существует второе приближение, то равенство нулю интеграла от оставшихся членов является тем интегральным условием, которому должны удовлетворять величины первого приближения. Следующие три интеграла должны обращаться в нуль:

Если внутри поверхности S нет особенностей, условия (15.28) удовлетворяются тождественно, так как в этом случае, пользуясь теоремой Гаусса, поверхностный интеграл можно преобразовать в объемный, подинтегральное выражение которого тождественно равно нулю. Обозначая подинтегральное выражение поверхностного интеграла через  , получим
, получим

Покажем с помощью тождеств Бьянки, что подинтегральное выражение  равно нулю. Обозначим еще выражения
равно нулю. Обозначим еще выражения  через
через  Разлагая В в степенные ряды по
Разлагая В в степенные ряды по
 для
для  получим
получим

Так как уже предполагается, что уравнения первого приближения  удовлетворяются в области V, то аходим, что первый член, —
удовлетворяются в области V, то аходим, что первый член, —  обращается в нуль, даже если уравнения второго и высших приближений не удовлетворяются.
обращается в нуль, даже если уравнения второго и высших приближений не удовлетворяются.
Усливия (15.28) существенны, только если внутри поверхности S имеются особые точки. Значение интегралов (15.28) зависит от особенностей, находящихся внутри 5, но не зависит от формы и размеров этой поверхности. Выберем 5 в виде малой сферы радиуса  центром которой является
центром которой является  -особенность.
-особенность.
Вычислим далее явно три интеграла (15.28). Для  выражений
выражений  являющихся косинусами углов
являющихся косинусами углов  введем сокращенные обозначения
введем сокращенные обозначения  Производными от
Производными от  по
по  будут:
будут:

Вычисление упрощается, если подинтегральные выражения уравнений (15.28) разложить в степенные ряды по  Поэтому удобно вместо трех координат
Поэтому удобно вместо трех координат  ввести радиус
ввести радиус  и направляющие косинусы
и направляющие косинусы  удовлетворяющие соотношению
удовлетворяющие соотношению

Поскольку значения интегралов не зависят от формы и размеров поверхности S, они не зависят также и от  Бели подинтегральные выражения
Бели подинтегральные выражения  разложить в
разложить в
степенные ряды по  (степенные ряды, содержащие и положительные и отрицательные степени), то будут отличны от нуля только интегралы от членов, содержащих
(степенные ряды, содержащие и положительные и отрицательные степени), то будут отличны от нуля только интегралы от членов, содержащих  Это объясняется тем, что „площадь” поверхности S пропорциональна
Это объясняется тем, что „площадь” поверхности S пропорциональна  и только члены подинтегрального выражения, пропорциональные
и только члены подинтегрального выражения, пропорциональные  могут сделать интегралы, не зависящими от
могут сделать интегралы, не зависящими от  Поэтому необходимые вычисления можно сократить, разлагая подинтегральные выражения
Поэтому необходимые вычисления можно сократить, разлагая подинтегральные выражения  в ряды и отбрасывая все члены, которые не умножаются на
в ряды и отбрасывая все члены, которые не умножаются на 
Далее, если бы  обращались в нуль, т. е. если бы
обращались в нуль, т. е. если бы  особенность не существовала, интегралы (15.28) равнялись бы нулю тождественно. В силу этого, все члены, не зависящие от
особенность не существовала, интегралы (15.28) равнялись бы нулю тождественно. В силу этого, все члены, не зависящие от  в значение интегралов ничего не вносят, и, следовательно, ими можно пренебречь. Разложим
в значение интегралов ничего не вносят, и, следовательно, ими можно пренебречь. Разложим  и каждую на две части:
и каждую на две части:

где сумма распространяется на все значения  кроме
кроме  .
.
В  входят как линейные относительно
входят как линейные относительно  и члены, так и квадратичные. В линейных членах нужно рассматривать только выражения, зависящие от
и члены, так и квадратичные. В линейных членах нужно рассматривать только выражения, зависящие от  и
и  Имеем:
Имеем:

Линейные члены, интеграл которых не равен нулю, умноженные на

равны

После интегрирования по S они дают

Обратимся теперь к квадратичным членам,  и
и  умножаются на
умножаются на  их первые производные по пространственным координатам — на
их первые производные по пространственным координатам — на  и их вторые производные — на
и их вторые производные — на  Очевидно, что все члены, квадратичные относительно
Очевидно, что все члены, квадратичные относительно  умножаются на
умножаются на  и поэтому ничего не вносят в интегралы. Таким образом, необходимо рассматривать только члены, билинейные относительно выражений
и поэтому ничего не вносят в интегралы. Таким образом, необходимо рассматривать только члены, билинейные относительно выражений  Кроме выражений t, нам еще понадобятся
Кроме выражений t, нам еще понадобятся  которые имеют вид:
которые имеют вид:

Эти  -выражения умножаются на X и ее производные. Само X умножается на вторые производные t, т. е. на выражения, пропорциональные
-выражения умножаются на X и ее производные. Само X умножается на вторые производные t, т. е. на выражения, пропорциональные  Поэтому для вычисления интеграла существенны только те члены в степенном разложении которые пропорциональны
Поэтому для вычисления интеграла существенны только те члены в степенном разложении которые пропорциональны  По тем же причинам для вычисления интегралов (15.28) будут существенны только те члены первых производных от X, которых умножаются на
По тем же причинам для вычисления интегралов (15.28) будут существенны только те члены первых производных от X, которых умножаются на  эти члены являются первыми производными от интересующих нас членов в разложении самого X. Наконец, во вторых производных нас интересовали бы члены, пропорциональные
эти члены являются первыми производными от интересующих нас членов в разложении самого X. Наконец, во вторых производных нас интересовали бы члены, пропорциональные  но они равны нулю, так как X регулярна внутри S.
но они равны нулю, так как X регулярна внутри S.
Для получения степенных рядов для I, разложим  к сперва выражения
к сперва выражения  Запишем
Запишем  в виде
в виде

Обозначим „координатные расстояния" между  точечными массами
точечными массами  через
через  тогда для
тогда для  получим степенное разложение:
получим степенное разложение:

а разложение для X примет вид

Только второй член этого разложения

существен для интегралов (15.28). Его производные равны

Нелинейными членами в интегралах (15.28) тогда будут

Подставляя выражения (15.36) и (15.41) в уравнение (15.42), получим для 

а для произведения  на
на 

Это выражение нужно проинтегрировать по поверхности S. Для этого рассмотрим интеграл

Нужно отдельно вычислить два интеграла: 

и

Сферу S можно разделить на две полусферы, на одной из которых  положительно, а на другой — отрицательно,
положительно, а на другой — отрицательно,  в свою очередь будет положительно на одной половине каждой полусферы и отрицательно — на другой. Интеграл (15.46) обращается в нуль, так как интегралы по соответствующим четвертям сфер взаимно уничтожаются. Для вычисления интеграла (15.45) введем полярные координаты с полюсами в двух точках
в свою очередь будет положительно на одной половине каждой полусферы и отрицательно — на другой. Интеграл (15.46) обращается в нуль, так как интегралы по соответствующим четвертям сфер взаимно уничтожаются. Для вычисления интеграла (15.45) введем полярные координаты с полюсами в двух точках  . Тогда получим:
. Тогда получим:

Наконец, находим, что интеграл от выражения (15.44) равен

Наше условие заключается в том, что сумма из  выражения (15.35) и
выражения (15.35) и  должна равняться нулю:
должна равняться нулю:

Деля это уравнение на  и подставляя вместо
и подставляя вместо  его значение из уравнения (15.14), получим классические уравнения движения
его значение из уравнения (15.14), получим классические уравнения движения

Метод Эйнштейна, Инфельда и Гофмана применим также и при наличии одновременно гравитационного и электромагнитного полей. И в этом случае во втором приближении уравнения поля имеют решения только тогда, когда первое приближение удовлетворяет некоторым интегральным условиям. Эти условия эквивалентны уравнению (15.48). с добавочным членом, соответствующим кулонову полю.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.