| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Релятивистская аналитическая механика.
Теперь можно перейти к рассмотрению основ релятивистской аналитической механики. При этом предполагается, что читатель хорошо знаком с основными положениями классической аналитической механики, в силу чего последующий обзор будет затрагивать только те вопросы, которые имеют непосредственное отношение к содержанию этой книги.
Дифференциальные уравнения движения механической (классической) системы, подвергающейся действию консервативных сил, записываются в виде

где Т — кинетическая, а  - потенциальная энергия. Записанные так уравнения движения ковариантны не только относительно ортогональных преобразований пространственных координат, но и относительно произвольных преобразований
- потенциальная энергия. Записанные так уравнения движения ковариантны не только относительно ортогональных преобразований пространственных координат, но и относительно произвольных преобразований  координат, соответствующих
координат, соответствующих  степеням свободы системы.
степеням свободы системы.
Это так называемые уравнения Эйлера-Лагранжа для вариационной проблемы. Вариационная проблема — это проблема нахождения таких кривых, соединяющих две фиксированные точки, вдоль которых данный криволинейный интеграл принимает экстремальное значение. Рассмотрим  -мерное пространство с координатами
-мерное пространство с координатами  и t и криволинейный интеграл
и t и криволинейный интеграл

подинтегральная функция которого вдоль пути интегрирования зависит от координат  (и, возможно, t) и производных Варьируя при фиксированных конечных точках путь интегрирования на бесконечно малую величину, получим
(и, возможно, t) и производных Варьируя при фиксированных конечных точках путь интегрирования на бесконечно малую величину, получим

где  обозначает
обозначает  . Отсюда видно, что вдоль путей интегрирования, на которых величина
. Отсюда видно, что вдоль путей интегрирования, на которых величина  экстремальна, справедливы уравнения (6.36).
экстремальна, справедливы уравнения (6.36).
Импульсы определяются уравнениями

С помощью этих соотношений  дифференциальных уравнений (6.36) второго порядка могут быть преобразованы в
дифференциальных уравнений (6.36) второго порядка могут быть преобразованы в  уравнений первого порядка. Для этого нужно решить
уравнений первого порядка. Для этого нужно решить  уравнений (6.39) относительно
уравнений (6.39) относительно  и образовать так называемую функцию Гамильтона
и образовать так называемую функцию Гамильтона

где  предполагаются замененными решениями уравнений (6.39). Уравнения движения принимают теперь каноническую форму:
предполагаются замененными решениями уравнений (6.39). Уравнения движения принимают теперь каноническую форму:

Этот формализм в целом ковариантен относительно общих преобразований трех пространственных координат (в действительности, даже относительно более общих преобразований). Особенностью, представляющей для нас специфический интерес, является возможность введения вместо времени t другого параметра. Обозначим этот параметр через  и определим его уравнением
и определим его уравнением

где предполагается заданным. Производные по t будем обозначать точками, а по  — штрихами. Тогда имеем:
— штрихами. Тогда имеем:

Теперь уравнения Эйлера-Лагранжа можно выразить через новый лагранжиан от  . Производными от
. Производными от  по его аргументам будут
по его аргументам будут

В силу

уравнения Эйлера-Лагранжа приводятся к виду:

Отметим, что определение импульсов (6.39) инвариантно относительно такого преобразования параметра. Однако, помимо импульсов, нужно рассматривать также компоненту, канонически сопряженную времени  Она равна—Н. Обозначим эту новую компоненту через
Она равна—Н. Обозначим эту новую компоненту через
 уравнения, определяющие импульсы, могут быть опять решены относительно
уравнения, определяющие импульсы, могут быть опять решены относительно  величины
величины  и новый гамильтониан может быть определен как
и новый гамильтониан может быть определен как

Этот гамильтониан равен нулю. Однако если  рассматривать как независимую переменную, его частные производные не исчезают. Они связаны с производными гамильтониана (6.40) следующим образом:
рассматривать как независимую переменную, его частные производные не исчезают. Они связаны с производными гамильтониана (6.40) следующим образом:

Таким образом, мы можем прибавить к уравнениям (6.41) следующее:

Гамильтониан (6.40) представляет собой сумму кинетической и потенциальной энергий. Эта полная энергия изменяется во времени со скоростью Уравнение (6.48) не независимо от уравнений (6.41). Его можно получить из последних, не прибегая к методу преобразования параметра. Действительно, полный дифференциал Н равен

и в силу (6.41)

Делением на  получаем отсюда (6.48).
получаем отсюда (6.48).
Преобразование параметра полезно в том отношении, что позволяет переходить от одного параметра t к другому параметру  Оба представления при этом эквивалентны.
Оба представления при этом эквивалентны.
Перейдем к рассмотрению релятивистской механики, причем сначала изучим движение частиц, на которые не действуют силы. Лагранжиан является некоторой функцией от (если за параметр выбрано  или от (если параметр есть
или от (если параметр есть  ). В дальнейшем точками будем обозначать дифференцирование по t, а штрихами по собственному времени частицы т. Производные лагранжиана по этим переменным дают значения импульсов. Импульсы, канонически сопряженные координатам
). В дальнейшем точками будем обозначать дифференцирование по t, а штрихами по собственному времени частицы т. Производные лагранжиана по этим переменным дают значения импульсов. Импульсы, канонически сопряженные координатам  определяются формулами (6.15). Четвертая компонента импульса (канонически сопряженная времени) согласно (6.44) равна
определяются формулами (6.15). Четвертая компонента импульса (канонически сопряженная времени) согласно (6.44) равна

где  лагранжиан, соответствующий параметру
лагранжиан, соответствующий параметру 
Примем сначала за параметр время t. Из дифференциальных уравнений

видим, что  равно:
равно:

где  — постоянная интегрирования. При этом интеграл
— постоянная интегрирования. При этом интеграл  принимает значение 11
принимает значение 11

где  — собственное время вдоль пути интегрирования между двумя конечными точками
— собственное время вдоль пути интегрирования между двумя конечными точками  . Этот интеграл лорентц-инвариантен, если
. Этот интеграл лорентц-инвариантен, если  равно нулю. Выражение
равно нулю. Выражение

не зависит от пути интегрирования. Поэтому этот член ничего не дает для вариации  если пределы интеграла не варьируются. Мы увидим, что величина
если пределы интеграла не варьируются. Мы увидим, что величина  определяет значение постоянной интегрирования
определяет значение постоянной интегрирования  в (6.17). Поскольку этот член неинвариантен, мы его опустим при переходе к четырехмерному представлению.
в (6.17). Поскольку этот член неинвариантен, мы его опустим при переходе к четырехмерному представлению.
Уравнения

могут быть разрешены относительно 

Гамильтониан определяется уравнением (6.40). В этом случае он равен

Если  выбрать равным 1, равен релятивистской кинетической энергии; а при
выбрать равным 1, равен релятивистской кинетической энергии; а при  равным нулю, — полной энергии.
равным нулю, — полной энергии.
Для уравнений Гамильтона получаем 

Перейдем теперь к параметру  . Согласно (6.43)
. Согласно (6.43)

Отсюда импульсы равны

Корни, входящие в уравнения (6.55) и (6.56), равны 1 [(см. (5.127)]. Если этого не учесть, решение уравнений (6.56) относительно  станет невозможным. Вообще говоря, можно было бы выбрать некоторый другой параметр вместо
станет невозможным. Вообще говоря, можно было бы выбрать некоторый другой параметр вместо  скажем
скажем  . При этом уравнения (6.56) имели бы точно такой же вид, только штрихи означали бы дифференцирование по
. При этом уравнения (6.56) имели бы точно такой же вид, только штрихи означали бы дифференцирование по  . Однако в этом случае оказалось бы невозможным выразить
. Однако в этом случае оказалось бы невозможным выразить  только через
только через  . В рассмотренном же
. В рассмотренном же
случае мы используем то обстоятельство, что  являются контравариантными компонентами единичного вектора, а
являются контравариантными компонентами единичного вектора, а  ковариантными компонентами того же единичного вектора,
ковариантными компонентами того же единичного вектора,  идентично с
идентично с  Решение может быть записано в виде:
Решение может быть записано в виде:

который аналогичен (6.156). Однако такой способ записи решения совершенно произволен.
Квадратный корень в знаменателе постоянен:

Поэтому решение может быть записано в общем виде:

где  обращается в 1, когда аргумент равен 1, а в остальном совершенно произвольна. Используя (6.57а), получим для
обращается в 1, когда аргумент равен 1, а в остальном совершенно произвольна. Используя (6.57а), получим для 

Для краткости будем в дальнейшем обозначать квадратный корень через  . Для уравнений Гамильтона имеем
. Для уравнений Гамильтона имеем

где  означает производную от
означает производную от  по ее аргументу. Первый член справа исчезает, так как выражение в квадратных скобках равно нулю. Второй член равен [см. (6.57а)]:
по ее аргументу. Первый член справа исчезает, так как выражение в квадратных скобках равно нулю. Второй член равен [см. (6.57а)]:

 Появление произвольной функции
Появление произвольной функции  не случайно. Интеграл (6.52) при
не случайно. Интеграл (6.52) при  равен длине дуги мировой линии в пространстве Минковского. Уравнения Эйлера-Лагранжа являются дифференциальными уравнениями геодезических линий, соответствующих уравнениям (5.99).
равен длине дуги мировой линии в пространстве Минковского. Уравнения Эйлера-Лагранжа являются дифференциальными уравнениями геодезических линий, соответствующих уравнениям (5.99).
Дифференциальные уравнения (5.99) можно получить не только из вариационного интеграла (5.93), так как любой вариационный интеграл

имеет вариацию

т. е. приводит к тем же уравнениям геодезических линий.
В нашем случае в качестве лагранжиана можно использовать любую функцию

при этом импульсы определяются как

где Ф — производная Ф по ее аргументу. Эти величины  идентичны импульсам (6.56), если
идентичны импульсам (6.56), если

Таким же образом в качестве гамильтониана можно использовать любую функцию импульсов вида

Уравнениями, связывающими импульсы и скорости, будут:

Величины  идентичны с
идентичны с  если
если

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
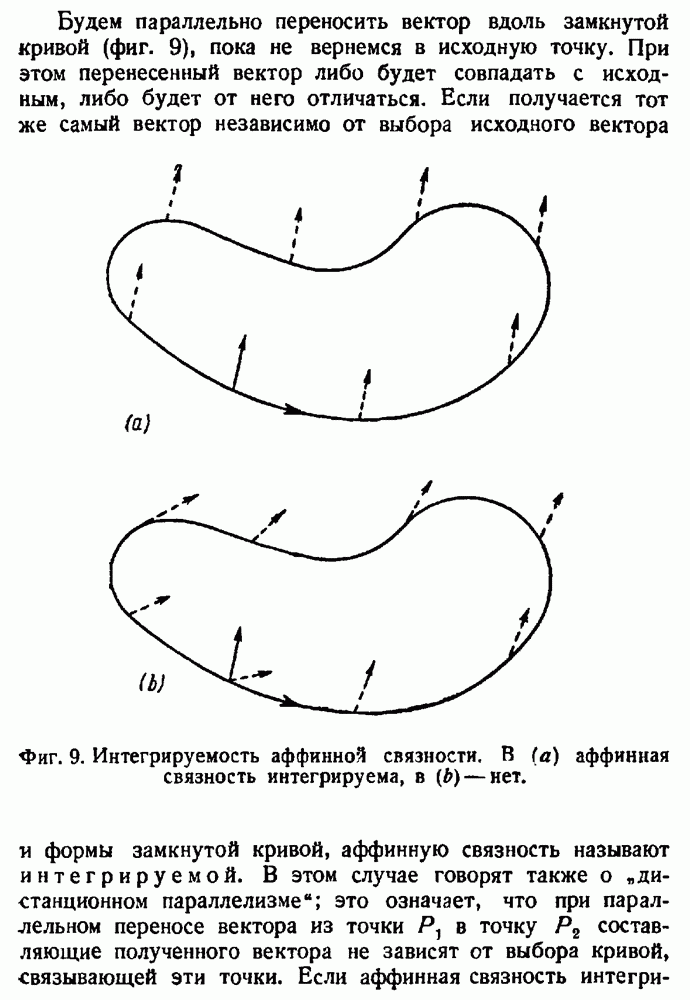
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.