| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Тензорный анализ.
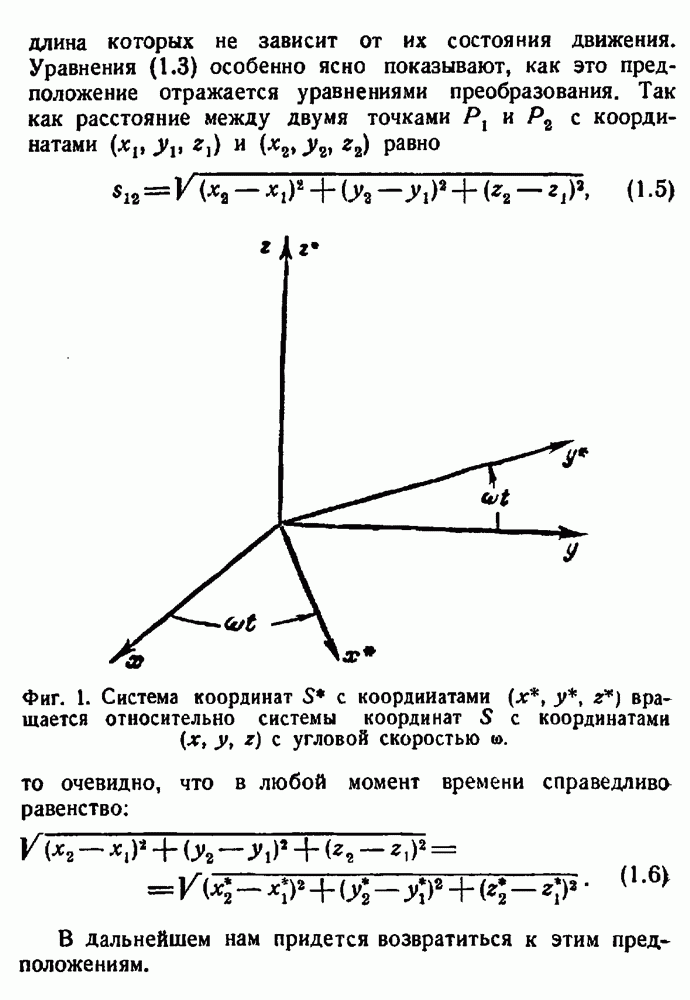
Рассмотрением тензорных плотностей мы полностью завершили изложение тензорной алгебры; точнее, мы описали последнюю настолько полно, насколько это нам потребуется. Теперь мы перейдем к тензорному анализу. Мы уже видели, что обыкновенные производные скалярного поля представляют собой компоненты ковариантного векторного поля. Однако в общем случае производные тензорного поля не образуют нового тензорного поля.
Рассмотрим производную вектора. Производная связывает значение вектора в одной точке с его значением в другой бесконечно близкой к ней точке. При преобразовании координат векторы в обеих точках имеют различные коэфициенты преобразования, так как последние являются функциями координат. Поэтому производные коэфициентов преобразования входят в закон преобразования производных вектора.
Однако существует способ получения новых тензоров в результате дифференцирования. Этот способ основан на аналогии с дифференцированием в декартовых координатах. Там мы получали производные вектора или тензора следующим образом: сначала вектор переносился в „соседнюю" точку без изменения величины своих компонент, т. е. параллельно самому себе. (Пока мы пользуемся декартовой системой координат, это понятие имеет инвариантный смысл, так как коэфициенты преобразования одинаковы в обеих точках.) Затем этот параллельно перенесенный вектор сравнивается с вектором (как функцией координат) в этой же точке. Их разность представляется как  Если бы было возможно в соседней точке ввести понятия „тот же вектор” или „параллельный вектор, разность между параллельно перенесенным вектором
Если бы было возможно в соседней точке ввести понятия „тот же вектор” или „параллельный вектор, разность между параллельно перенесенным вектором
и вектором поля в этой точке преобразовывалась бы как вектор в этой же точке.
Определение параллельного переноса действительна можно ввести сравнительно простым образом. При этом величина смещенного вектора зависит как от исходного вектора, так и от направления переноса. Рассмотрим сперва эвклидово пространство, в котором можно ввести декартову систему координат. В этой системе закон параллельного переноса имеет вид

где  представляет собой бесконечно малое смещение.
представляет собой бесконечно малое смещение.
Введем теперь произвольное преобразование координат (5.46). Компоненты вектора в новой системе координат отметим штрихами. Мы имеем:

Так как  преобразуется согласно (5.48), получим
преобразуется согласно (5.48), получим

Величины  являются приращениями
являются приращениями  в результате смещения и могут быть обозначены чарез
в результате смещения и могут быть обозначены чарез  Умножая правую часть уравнения (5.76а) на
Умножая правую часть уравнения (5.76а) на  получим окончательно (так как —
получим окончательно (так как — 

Если нельзя ввести декартову систему координат, мы, сохраняя линейную форму последнего уравнения, предположим, что при параллельном переносе бесконечно малые изменения компонент вектора являются билинейной функцией компонент вектора и компонент бесконечно малого смещения:

Коэфициенты  этих новых предполагаемых законов остаются пока совершенно неопределенными. Однако можно найти их законы преобразования.
этих новых предполагаемых законов остаются пока совершенно неопределенными. Однако можно найти их законы преобразования.  является разностью векторов в двух точках с координатами и
является разностью векторов в двух точках с координатами и  При преобразовании координат новые
При преобразовании координат новые  получаются следующим образом:
получаются следующим образом:

Уже указывалось, что  не преобразуется как вектор, что явилось источником наших затруднений.
не преобразуется как вектор, что явилось источником наших затруднений.
Подставим (5.80) в левую часть уравнения

и заменим  их выражениями из (5.51) и (5.50). Тогда получим:
их выражениями из (5.51) и (5.50). Тогда получим:

Подставляя далее  из (5.78), найдем
из (5.78), найдем

Так как и  произвольны, коэфициеиты при них должны быть равны:
произвольны, коэфициеиты при них должны быть равны:

Закон преобразования для  получается после умножения
получается после умножения 

Последний член справа может быть записан в несколько мной форме:

Первый член справа равен нулю, так как выражение в круглых скобках постоянно. (5.81), таким образом, дает:

Аналогичными рассуждениями из (5.79) получим закон  преобразования для
преобразования для  Он таков же, как и для
Он таков же, как и для 
Теперь можно наложить на  условия, совместимые с их законами преобразования. Эти формулы преобразования содержат два члена. Один из них зависит от
условия, совместимые с их законами преобразования. Эти формулы преобразования содержат два члена. Один из них зависит от  в старой системе координат и имеет тот же вид, что и закон преобразования тензоров. Второй член не зависит от и симметричен в своих иижних индексах. Поэтому, если и равны нулю в одной системе координат, они все же будут отличны от нуля в другой системе. Однако симметрия
в старой системе координат и имеет тот же вид, что и закон преобразования тензоров. Второй член не зависит от и симметричен в своих иижних индексах. Поэтому, если и равны нулю в одной системе координат, они все же будут отличны от нуля в другой системе. Однако симметрия  по отношению к нижним индексам
по отношению к нижним индексам
сохраняется во всех системах координат, если она существует хотя бы в одной из них. Это, в частности, справедливо, когда исчезает в одной из систем. Далее, если и  равны в одной системе, они остаются равными при произвольном преобразовании координат. Мы увидим, что геометрические соображения приводят нас только к таким системам
равны в одной системе, они остаются равными при произвольном преобразовании координат. Мы увидим, что геометрические соображения приводят нас только к таким системам  которые обладают обоими упомянутыми свойствами.
которые обладают обоими упомянутыми свойствами.
Произведем параллельный перенос двух векторов а, и  на бесконечно малое расстояние
на бесконечно малое расстояние  Изменение их скалярного произведения
Изменение их скалярного произведения  будет равно
будет равно

При параллельном переносе двух векторов  скалярное произведение остается постоянным тогда и только тогда, когда Г, соответственно равны
скалярное произведение остается постоянным тогда и только тогда, когда Г, соответственно равны 
Фактически предположение о равенстве  основывается не только на том обстоятельстве, что в декартовых координатах скалярное произведение двух постоянных векторов постоянно, но и на более общих соображениях, не связанных с декартовыми системами координат.
основывается не только на том обстоятельстве, что в декартовых координатах скалярное произведение двух постоянных векторов постоянно, но и на более общих соображениях, не связанных с декартовыми системами координат.
Обобщая закон или определение „параллельного" переноса (5.78), (5.79) на тензоры, будем производить „параллельное" смещение согласно следующему правилу:

Это правило основывается на том предположении, что „параллельный перенос" произведения производится по тому же закону, и что дифференцирование произведения:

При параллельном переносе тензора Кронекера, согласно (5.84), получим:

Далее, из (5.86) и (5.85) имеем для «параллельного переноса” произведения

С другой стороны, это произведение равно а. Отсюда:

и в силу этого  должно обращаться в нуль. Соответственно имеем:
должно обращаться в нуль. Соответственно имеем:

В дальнейшем различительные индексы I и II будем опускать.
Как уже отмечалось,  симметричны в своих нижних индексах, если возможно ввести такую систему координат, в которой
симметричны в своих нижних индексах, если возможно ввести такую систему координат, в которой  равны нулю, хотя бы в локальной области. С этого момента следует все время иметь в виду, что в дальнейшем будут рассматриваться только симметричные
равны нулю, хотя бы в локальной области. С этого момента следует все время иметь в виду, что в дальнейшем будут рассматриваться только симметричные  При этом Г остаются еще в значительной степени произвольными. Однако они определятся однозначно, если их связать с метрическим тензором
При этом Г остаются еще в значительной степени произвольными. Однако они определятся однозначно, если их связать с метрическим тензором  с помощью следующего условия: результат параллельного смещения вектора а должен быть одним и тем же как при применении закона (5.78) к его контравариантным координатам, так и при применении закона (5.79) к его ковариантным координатам. В этих двух представлениях
с помощью следующего условия: результат параллельного смещения вектора а должен быть одним и тем же как при применении закона (5.78) к его контравариантным координатам, так и при применении закона (5.79) к его ковариантным координатам. В этих двух представлениях  соответственно имеют в точке
соответственно имеют в точке  значения
значения  где
где  даются с помощью (5.78) и (5.79). Условие того, что эти
даются с помощью (5.78) и (5.79). Условие того, что эти
два вектора являются представлениями одного и того же вектора  в точке
в точке  выражается формулой:
выражается формулой:

где

С точностью до членов высшего порядка по отношению к дифференциалам формула (5.88) должна быть справедлива для произвольных  и Раскрывая скобки в правой части (5.88), получим:
и Раскрывая скобки в правой части (5.88), получим:

Подставляя  из (5.78) и (5.79), найдем
из (5.78) и (5.79), найдем

или

где  произвольны; поэтому выражение в скобках должно равняться нулю.
произвольны; поэтому выражение в скобках должно равняться нулю.
Далее используем условия симметрии и выпишем обращающееся в нуль выражение, три раза переставляяя индексы:

Первое уравнение вычитаем из суммы двух других. После приведения подобных членов получим уравнение:

Отсюда умножением на  найдем окончательное выражение для
найдем окончательное выражение для 

Это выражение обычно называют символом Кристоффеля второго рода и обозначают знаком

Левая часть уравнения (5.89) называется символом Кристоффеля первого рода. Он обозначается знаком 

В декартовых координатах оба символа Кристоффел обращаются в нуль.
Понятие параллельного переноса является независимым от существования метрического тензора. Пространство, в котором определен закон параллельного переноса, назовем пространством аффинной связности, а  коэфициентами аффинной связности (affipe connection). Когда задана метрика, ковариантные и контравариантные векторы эквивалентны; при этом
коэфициентами аффинной связности (affipe connection). Когда задана метрика, ковариантные и контравариантные векторы эквивалентны; при этом  принимает значение так что параллельный перенос вектора не зависит от выбора одного из двух возможных представлений..
принимает значение так что параллельный перенос вектора не зависит от выбора одного из двух возможных представлений..
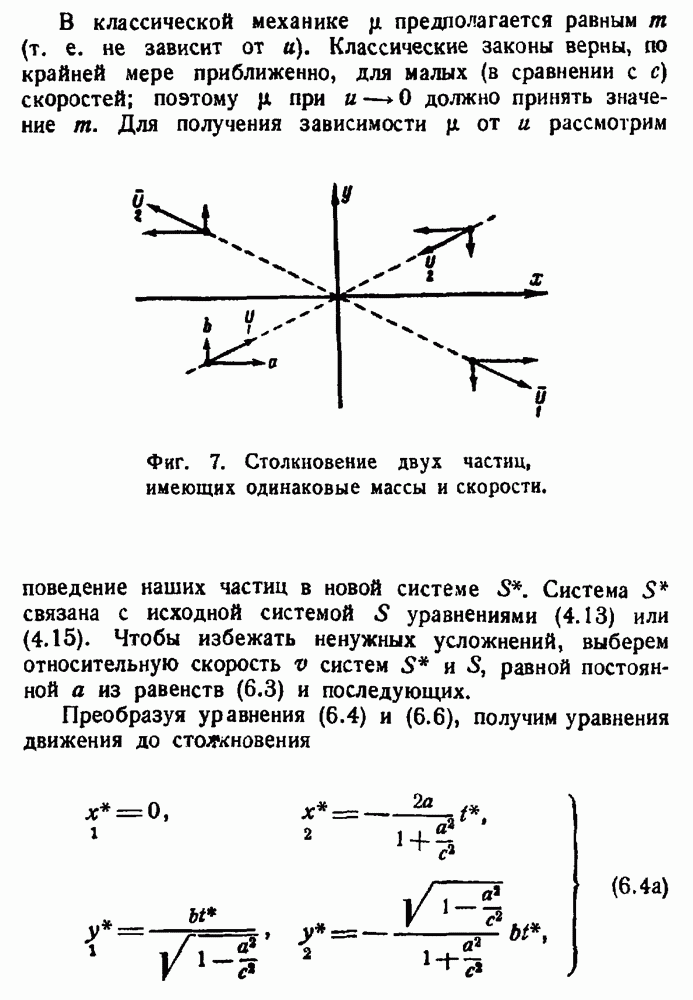
Вернемся теперь к нашей первоначальной задаче — к образованию новых тензоров при помощи дифференцирования. Рассмотрим тензорное поле, т. е. тензор, компоненты которого являются функциями координат. Возьмем тензор в точке  и сместим его параллельно самому себе в точку
и сместим его параллельно самому себе в точку  Вычтем из величины тензорного поля в точке
Вычтем из величины тензорного поля в точке  тензор, параллельно перенесенный в эту точку; эта разность также будет тензором. В случае смешанного тензора второго ранга его значение в точке
тензор, параллельно перенесенный в эту точку; эта разность также будет тензором. В случае смешанного тензора второго ранга его значение в точке  будет
будет

а для значения параллельно перенесенного тензора найдем:

разность этих двух выражений равна

То, что это выражение является тензором, видно из метода его получения. Так как  — произвольный вектор, выражение в скобках также является тензором. Этот тензор называется ковариантной производной от
— произвольный вектор, выражение в скобках также является тензором. Этот тензор называется ковариантной производной от  по S. Ковариантная производная идентична с обычной производной, если
по S. Ковариантная производная идентична с обычной производной, если  обращается в нуль, как это имеет место, например, в декартовых координатах. Приведем два из часто встречающихся обозначений ковариантной производной
обращается в нуль, как это имеет место, например, в декартовых координатах. Приведем два из часто встречающихся обозначений ковариантной производной  Мы будем употреблять последнее.
Мы будем употреблять последнее.
Ковариантные производные произвольного тензора получаются прибавлением к обычным производным добавочных членов. Каждому контравариантному индексу соответствует добавочный член вида

а к ковариантному индексу член вида

Это определение удовлетворяет правилу дифференциро-Бания произведения

независимо от того, будут ли некоторые из индексов у  немыми.
немыми.
Ковариантные производные метрического тензора равны нулю, так как равно нулю выражение в скобках в (5.88а), В силу того, что ковариантное дифференцирование согласуется с законом дифференцирования произведения, можно поднимать и опускать индексы под знаком дифференцирования:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
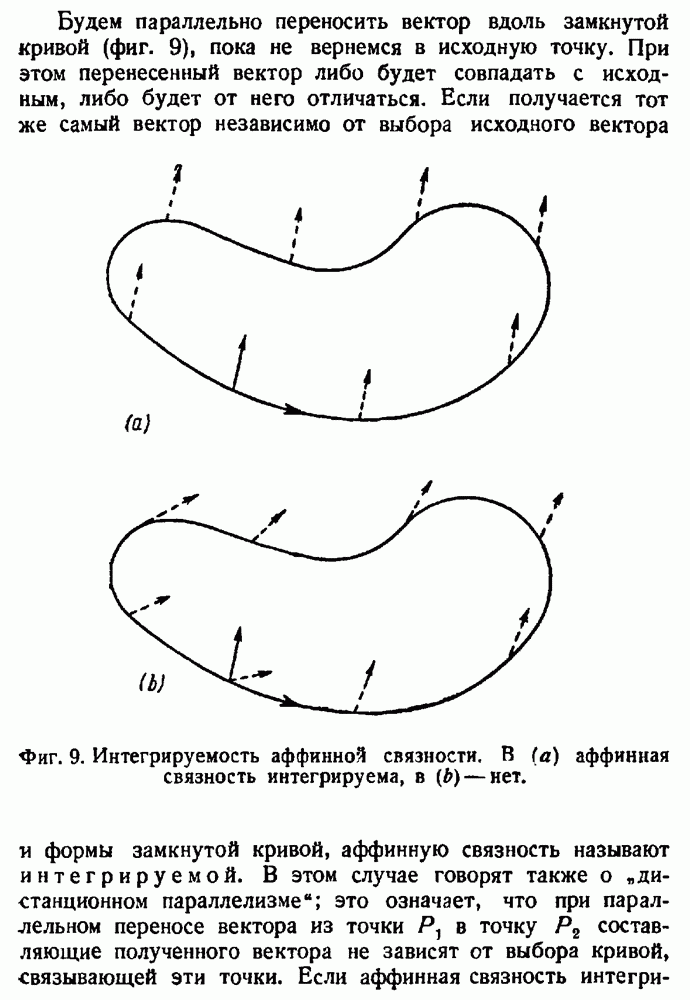
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.