| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Нерелятивистская трактовка.
При описании поведения так называемых сплошных сред — упругих тел, жидкостей и газов внимание фиксируется не на индивидуальных частицах, а на некотором выделенном элементе объема. С течением времени одни частицы попадают в этот объем, а другие его покидают. Движение каждой молекулы подчиняется общим законам механики, однако важно сформулировать эти законы так, чтобы в них входили не точечные массы и их положения, а локальные плотности массы, импульса и т. д. „Элемент объема должен содержать достаточно большое количество отдельных частиц, чтобы средние значения имели смысл и являлись разумными непрерывными функциями четырех координат: х, у, z и t. Предположим, что можно определить локальные средние плотность и скорость. Вначале будем придерживаться нерелятивистской точки зрения. Обозначим плотность через  , а среднюю скорость через и. Изменение плотности
, а среднюю скорость через и. Изменение плотности  в данном элементе объема определяется количеством втекающего в него вещества
в данном элементе объема определяется количеством втекающего в него вещества

Это уравнение, уравнение непрерывности, выражает закон сохранения массы.
Чтобы получить уравнения движения, введем понятия «частного» («локального») и «полного» («материального») дифференцирования по времени. Рассмотрим некоторую характеристику среды  (скаляр, компонента вектора и т. д.) и ее изменение во времени. Если описывается ее изменение во времени в фиксированной точке
(скаляр, компонента вектора и т. д.) и ее изменение во времени. Если описывается ее изменение во времени в фиксированной точке  то в качестве производной нужно взять „частную или локальную да производную
то в качестве производной нужно взять „частную или локальную да производную  . С другой стороны, это изменение можно относить к системе координат, движущейся вместе с выделенным элементом объема среды; иначе говоря, изменение
. С другой стороны, это изменение можно относить к системе координат, движущейся вместе с выделенным элементом объема среды; иначе говоря, изменение  можно описывать так, как это представляется наблюдателю, движущемуся вместе с выделенным элементом материи. Тогда надо брать «полную или материальную
можно описывать так, как это представляется наблюдателю, движущемуся вместе с выделенным элементом материи. Тогда надо брать «полную или материальную
производную, обозначаемую через Последняя связана с частной производной соотношением

Обозначим силу, действующую на единичный объем материи, через  Тогда уравнениями движения будут
Тогда уравнениями движения будут

или, используя (8.2), получим:

Левую часть можно преобразовать к виду:

В силу уравнения непрерывности (8.1) выражение в квадратных скобках обращается в нуль, и мы имеем

Сами силы могут быть двух типов. Во-первых, среда может подвергаться действию гравитационных, электрических или тому подобных полей, в которых сила, действующая на заданный бесконечно малый элемент объема, пропорциональна его величине. Такие силы называются «объемными силами". Будем обозначать их через  Кроме того, нужно принять во внимание и другой тип сил, являющихся результатом возникающих внутри материальной среды напряжений. Частицы, принадлежащие двум смежным элементам объема, могут взаимодействовать друг с другом, причем сила их взаимодействия будет пропорциональна
Кроме того, нужно принять во внимание и другой тип сил, являющихся результатом возникающих внутри материальной среды напряжений. Частицы, принадлежащие двум смежным элементам объема, могут взаимодействовать друг с другом, причем сила их взаимодействия будет пропорциональна
площади соприкосновения этих объемов. Такие силы называются поэтому „поверхностными силами". Компоненты поверхностной силы  линейно зависят от компонент вектора ориентированной площадки
линейно зависят от компонент вектора ориентированной площадки 

где вектор  перпендикулярен площадке, а длина его равна площади последней. Сила
перпендикулярен площадке, а длина его равна площади последней. Сила  является линейной функцией
является линейной функцией  в силу того, что полная сила, действующая на бесконечно малый объем, зависит от его размера, но не от формы. Знак
в силу того, что полная сила, действующая на бесконечно малый объем, зависит от его размера, но не от формы. Знак  выбирается так, чтобы при направлении вектора
выбирается так, чтобы при направлении вектора  по внешней нормали получалась сила, действующая со стороны окружающей среды на выбранный элемент объема. Это обычно принимаемое условие ведет к тому, что компоненты тензора напряжений, соответствующего обыкновенному изотропному давлению, становятся положительными.
по внешней нормали получалась сила, действующая со стороны окружающей среды на выбранный элемент объема. Это обычно принимаемое условие ведет к тому, что компоненты тензора напряжений, соответствующего обыкновенному изотропному давлению, становятся положительными.
 должен быть симметричным в своих индексах:
должен быть симметричным в своих индексах:

В противном случае момент количества движения изолированного тела  будет меняться во времени:
будет меняться во времени:

где интегрирование производится по объему тела).
Сила, действующая на материю, заключенную в конечном объеме, равна:

где  — плотность объемных сил. С помощью теоремы Гаусса второй интеграл по замкнутой поверхности можно преобразовать в объемный:
— плотность объемных сил. С помощью теоремы Гаусса второй интеграл по замкнутой поверхности можно преобразовать в объемный:

Таким образом, для плотности силы получаем:

Сравнивая последнее уравнение с (8.5), получим нерелятивистские уравнения движения:

Эти три уравнения вместе с уравнением непрерывности (8.1) определяют поведение сплошной среды под действием напряжений и других сил.
Кроме того, существует закон сохранения энергии, согласно которому изменение энергии в элементе объема определяется балансом потока энергии, протекающего через этот элемент.
Поведение механической системы может быть полностью определено только в том случае, если известны  Объемные силы определяются внешними условиями, скажем, наличием гравитационного поля, в то время как напряжения зависят от внутренних деформаций или от потока материи. Например, в случае идеальной жидкости
Объемные силы определяются внешними условиями, скажем, наличием гравитационного поля, в то время как напряжения зависят от внутренних деформаций или от потока материи. Например, в случае идеальной жидкости  равно давлению
равно давлению  умноженному на тензор Кронекера
умноженному на тензор Кронекера  Само давление
Само давление  является функцией плотности
является функцией плотности  и температуры, которая определяется из уравнения состояния жидкости. Нет необходимости определять компоненты напряжения, так как нас будут интересовать только их трансформационные свойства.
и температуры, которая определяется из уравнения состояния жидкости. Нет необходимости определять компоненты напряжения, так как нас будут интересовать только их трансформационные свойства.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АЛЬБЕРТА ЭЙНШТЕЙНА
- ПРЕДИСЛОВИЕ АВТОРА
- ВВЕДЕНИЕ
- Часть I. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава I. СИСТЕМЫ ОТСЧЕТА, СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- Преобразования координат, содержащие время.
- Глава II. КЛАССИЧЕСКАЯ МЕХАНИКА
- Закон инерции, инерциальные системы.
- Преобразования Галилея.
- Закон сил и его трансформационные свойства.
- Глава III. РАСПРОСТРАНЕНИЕ СВЕТА
- Корпускулярная гипотеза.
- Передающая среда как система отсчета.
- Эксперимент Майкельсона — Морлея.
- Гипотеза эфира.
- Глава IV. ПРЕОБРАЗОВАНИЯ ЛОРЕНТЦА
- Относительный характер одновременности.
- Длина масштабов.
- Ход часов.
- Преобразования Лорентца.
- «Кинематические» эффекты при преобразованиях Лорентца.
- Собственное время.
- Релятивистский закон сложения скоростей.
- Собственное время материального тела.
- Задача
- Глава V. ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ В n-МЕРНОМ ПРОСТРАНСТВЕ
- Ортогональные преобразования.
- Детерминант преобразования.
- Сокращенные обозначения.
- Векторы.
- Векторный анализ.
- Тензоры.
- Тензорный анализ.
- Тензорные плотности.
- Тензорная плотность Леви-Чивита.
- Векторное произведение и ротор.
- Обобщение.
- n-мерное пространство.
- Обобщенные преобразования.
- Векторы.
- Тензоры.
- Метрический тензор, римановы пространства.
- Поднятие и опускание индексов.
- Тензорные плотности. Тензорная плотность Леви-Чивита.
- Тензорный анализ.
- Геодезические линии.
- Мир Минковского и преобразования Лорентца.
- Траектории, мировые линии.
- Глава VI. РЕЛЯТИВИСТСКАЯ МЕХАНИКА ТОЧЕЧНЫХ МАСС
- Законы сохранения.
- Нахождение выражения для импульса.
- Лорентц-ковариантность новых законов сохранения.
- Связь между энергией и массой.
- Эффект Комптона.
- Релятивистская аналитическая механика.
- Сила в релятивистской механике.
- Глава VII. РЕЛЯТИВИСТСКАЯ ЭЛЕКТРОДИНАМИКА
- Предварительные замечания о трансформационных свойствах.
- Представление четырехмерных тензоров в трех плюс одном измерениях.
- Лорентц-ковариантность уравнений Максвелла.
- Физический смысл законов преобразования.
- Градиентное преобразование.
- Уравнения движения.
- Глава VIII. МЕХАНИКА СПЛОШНЫХ СРЕД
- Нерелятивистская трактовка.
- Специальная система координат.
- Тензорная форма уравнений.
- Тензор энергии-импульса электромагнитного поля.
- Глава IX. ПРИМЕНЕНИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Заряженные частицы в электромагнитном поле.
- Поле быстро движущейся частицы.
- Теория Зоммерфельда тонкой структуры водородных линий.
- Волны де Бройля.
- Часть II. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- Глава X. ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- Принцип эквивалентности.
- Предварительные соображения о релятивистской, теории гравитации.
- Об инерциальных системах.
- «Лифт» Эйнштейна.
- Принцип общей ковариантности.
- Природа гравитационного поля.
- Глава XI. ТЕНЗОР КРИВИЗНЫ РИМАНА-КРИСТОФФЕЛЯ
- Характерные особенности римановых пространств.
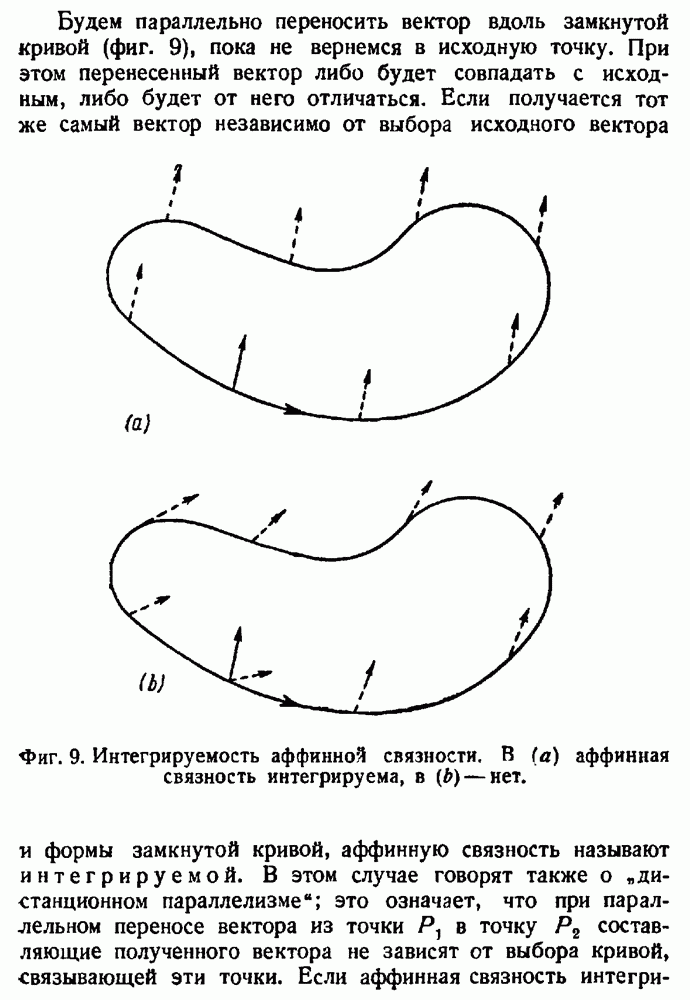
- Интегрируемость аффинной связности.
- Эвклидовость и интегрируемость.
- Критерий интегрируемости.
- Перестановочные соотношения для ковариантного дифференцирования, тензорный характер.
- Свойства тензора кривизны.
- Ковариантная форма тензора кривизны.
- Свертывание тензора кривизны.
- Свернутые тождества Бьянки.
- Число алгебраически независимых компонент тензора кривизны.
- Глава XII. УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Уравнение движения в гравитационном поле.
- Представление материи в уравнениях поля.
- Дифференциальные тождества.
- Уравнения поля.
- Линейное приближение и нормальные координатные условия.
- Решение линеаризованных уравнений поля.
- Поле точечной массы.
- Гравитационные волны.
- Вариационный принцип.
- Наличие одновременно гравитационного и электромагнитного поля.
- Законы сохранения в общей теории относительности.
- Глава XIII. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Особенность решения Шварцшильда.
- Поле электрически заряженной точечной массы.
- Решение с осевой симметрией.
- Глава XIV. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Движение перигелия Меркурия.
- Отклонение света в шварцшильдовском поле.
- Гравитационное смещение спектральных линий.
- Глава XV. УРАВНЕНИЯ ДВИЖЕНИЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Закон движения в общей теории относительности.
- Приближенный метод.
- Первое приближение и закон сохранения массы.
- Второе приближение и уравнения движения.
- Заключение.
- Часть III. ЕДИНЫЕ ТЕОРИИ ПОЛЯ
- Глава XVI. ГРАДИЕНТНО-ИНВАРИАНТНАЯ ГЕОМЕТРИЯ ВЕЙЛЯ
- Производные в градиентно-инвариантной геометрии.
- Физическая интерпретация геометрии Вейля.
- Вариационный принцип Вейля.
- Уравнения.
- Глава XVII. ПЯТИМЕРНАЯ ТЕОРИЯ КАЛУЗА И ПРОЕКТИВНЫЕ ТЕОРИИ ПОЛЯ
- Четырехмерный формализм в пятимерном пространстве.
- Анализ в p-формализме.
- Специальный тип системы координат.
- Ковариантная формулировка теории Калуза.
- Проективные теории поля.
- Глава XVIII. ОБОБЩЕНИЕ ТЕОРИИ КАЛУЗА
- Геометрия замкнутого пятимерного мира.
- Введение специальной системы координат.
- Получение уравнений поля из вариационного принципа.
- Дифференциальные уравнения поля.