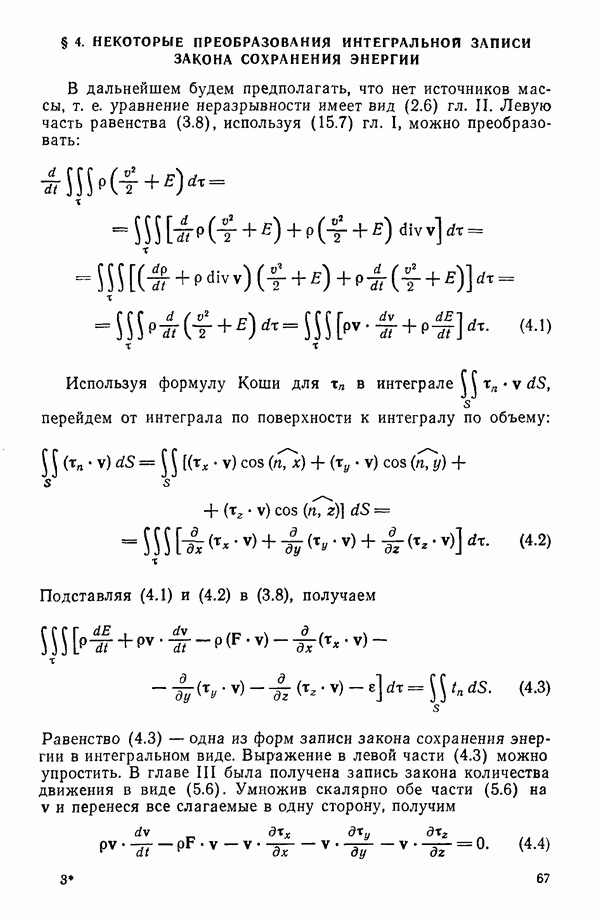| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ
Рассмотрим установившееся течение вязкой жидкости в круглой трубе радиуса R (рис. 54). Труба неподвижна, ось х совпадает с осью трубы. Для определения поля скоростей надо решить уравнение (1.13) при условии, что в любом поперечном сечении на контуре трубы  скорость равна нулю.
скорость равна нулю.  ввести цилиндрические координаты. Переходя от координат у, z к координатам
ввести цилиндрические координаты. Переходя от координат у, z к координатам  , получим
, получим 

Исследуемое течение осесимметрично, поэтому  зависит лишь от
зависит лишь от  . Уравнение (1.13) при этом становится обыкновенным дифференциальным уравнением второго порядка.
. Уравнение (1.13) при этом становится обыкновенным дифференциальным уравнением второго порядка.
Таким образом, задача свелась к решению уравнения

при условии

Уравнение (4.1) можно переписать в виде

Интегрируя, получим

Постоянную  следует положить равной нулю, так как иначе на оси трубы
следует положить равной нулю, так как иначе на оси трубы  скорость будет неограниченной величиной, что не имеет физического смысла. Постоянную
скорость будет неограниченной величиной, что не имеет физического смысла. Постоянную  находим из граничного условия (4.2):
находим из граничного условия (4.2):

Таким образом, для поля скоростей вязкой жидкости внутри трубы имеем формулу

Формула  - формула Пуазейля.
- формула Пуазейля.
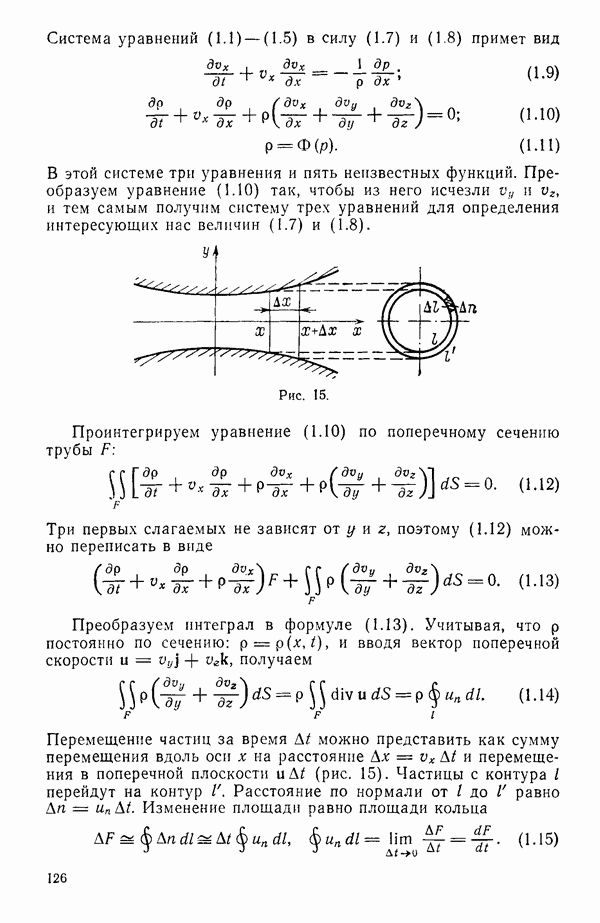
Подсчитаем расход жидкости через поперечное сечение трубы:

Таким образом, расход пропорционален падению давления, четвертой степени радиуса трубы и обратно пропорционален коэффициенту вязкости. Обычно интересуются падением давления  в зависимости от
в зависимости от  . Формула (4.7) используется также для экспериментального определения коэффициента вязкости.
. Формула (4.7) используется также для экспериментального определения коэффициента вязкости.
Полученное решение (как и решение предыдущей задачи в § 3) не всегда хорошо согласуется с экспериментом. Оказывается, что качественная картина течения существенно зависит от безразмерного параметра  , введенного Рейнольдсом. Числом Рейнольдса называют величину
, введенного Рейнольдсом. Числом Рейнольдса называют величину  ; где v и
; где v и  - характерные для данного течения скорость и размер.
- характерные для данного течения скорость и размер.
Для течений в трубах за характерную скорость принимают среднюю скорость

Если  , то имеется хорошее совпадение теории с экспериментом. При
, то имеется хорошее совпадение теории с экспериментом. При  происходит резкое изменение картины течения. При небольших
происходит резкое изменение картины течения. При небольших  каждая частица жидкости движется по прямой, движение слоистое, спокойное. Такое течение называется ламинарным. При
каждая частица жидкости движется по прямой, движение слоистое, спокойное. Такое течение называется ламинарным. При  каждая из частиц жидкости совершает хаотическое движение, течение перестает быть одномерным и стационарным. На среднюю скорость накладываются дополнительные составляющие, зависящие от времени и координат. Такое течение называется турбулентным.
каждая из частиц жидкости совершает хаотическое движение, течение перестает быть одномерным и стационарным. На среднюю скорость накладываются дополнительные составляющие, зависящие от времени и координат. Такое течение называется турбулентным.
Формулы (3.6), (4.6) справедливы только для ламинарных течений. Число  , при котором происходит переход течения от ламинарного режима к турбулентному, называется критическим числом Рейнольдса. Цифра
, при котором происходит переход течения от ламинарного режима к турбулентному, называется критическим числом Рейнольдса. Цифра  , которая приводилась выше, относится к обычным технически гладким трубам. Однако на самом деле переход ламинарного режима в турбулентный — явление сложное. В частности, число
, которая приводилась выше, относится к обычным технически гладким трубам. Однако на самом деле переход ламинарного режима в турбулентный — явление сложное. В частности, число  при специальных условиях может быть сильно увеличено. Рейнольдсом был проведен следующий опыт. Брались специальным образом подготовленные очень гладкие трубы с очень гладким входом. Жидкость подавалась в трубу из специальных баков, в которых она отстаивалась в течение 2—3 недель. Тогда критическое число
при специальных условиях может быть сильно увеличено. Рейнольдсом был проведен следующий опыт. Брались специальным образом подготовленные очень гладкие трубы с очень гладким входом. Жидкость подавалась в трубу из специальных баков, в которых она отстаивалась в течение 2—3 недель. Тогда критическое число  возрастало до
возрастало до  . Таким образом, переход к турбулентному режиму существенно зависит от уровня начальных возмущений. Кроме того, существует и нижняя граница
. Таким образом, переход к турбулентному режиму существенно зависит от уровня начальных возмущений. Кроме того, существует и нижняя граница  Если
Если  то течение всегда ламинарное. Известно также, что задержке перехода к турбулентному режиму способствует добавление в жидкость молекул полимеров.
то течение всегда ламинарное. Известно также, что задержке перехода к турбулентному режиму способствует добавление в жидкость молекул полимеров.
Примечание. Решение (4.4), полученное для осесимметричных течений в круглой трубе, содержит две произвольные постоянные. В этом решении равенство нулю постоянной  обеспечивало ограниченность скорости внутри трубы. Для случая осесимметричных установившихся течений жидкости внутри кольцевой трубы
обеспечивало ограниченность скорости внутри трубы. Для случая осесимметричных установившихся течений жидкости внутри кольцевой трубы  решение (4.4) также справедливо, только постоянные
решение (4.4) также справедливо, только постоянные  должны быть определены из условий прилипания жидкости к каждой из стенок трубы
должны быть определены из условий прилипания жидкости к каждой из стенок трубы  . В самом общем случае эти условия имеют вид
. В самом общем случае эти условия имеют вид

где  — скорости, с которыми трубы движутся параллельно своей оси (оси х). Если стенки труб неподвижны
— скорости, с которыми трубы движутся параллельно своей оси (оси х). Если стенки труб неподвижны  то движение жидкости может иметь место только за счет
то движение жидкости может иметь место только за счет
(отсутствует страница)
шается с угловой скоростью  , а внешний — со скоростью
, а внешний — со скоростью  . Для решения задачи удобно ввести цилиндрические координаты
. Для решения задачи удобно ввести цилиндрические координаты  и записать в этих координатах систему уравнений вязкой жидкости. Для этого надо найти выражения
и записать в этих координатах систему уравнений вязкой жидкости. Для этого надо найти выражения  в этой системе координат. Естественно предполагать, что скорость направлена по касательной к окружности
в этой системе координат. Естественно предполагать, что скорость направлена по касательной к окружности  и зависит так же, как и давление, только от
и зависит так же, как и давление, только от  , т. е.
, т. е.  . Полученная система уравнений применительно к рассматриваемой задаче, когда движение установившееся, принимает простой вид и позволяет сразу получить решение задачи в виде
. Полученная система уравнений применительно к рассматриваемой задаче, когда движение установившееся, принимает простой вид и позволяет сразу получить решение задачи в виде

Постоянные  определяются из граничных условий. Однако для решения рассматриваемой задачи мы используем другой путь.
определяются из граничных условий. Однако для решения рассматриваемой задачи мы используем другой путь.
Чтобы найти зависимости  запишем закон сохранения момента количества движения в слое
запишем закон сохранения момента количества движения в слое  (рис. 55). Пусть М — момент сил, действующих на этот слой. Поскольку течение плоское, вектор М направлен по оси
(рис. 55). Пусть М — момент сил, действующих на этот слой. Поскольку течение плоское, вектор М направлен по оси  . В силу стационарности движения имеем равенство
. В силу стационарности движения имеем равенство  . Очевидно, что
. Очевидно, что  , где
, где  — момент сил, действующих на внутренний цилиндр,
— момент сил, действующих на внутренний цилиндр,  — момент сил вязкого трения, приложенных к цилиндру радиуса
— момент сил вязкого трения, приложенных к цилиндру радиуса  . Величина этого вектора
. Величина этого вектора


Рис. 55.
Здесь  — проекция на ось
— проекция на ось  (т. е. на направление v) напряжения, действующего на площадку с нормалью
(т. е. на направление v) напряжения, действующего на площадку с нормалью  . При наших предположениях оно зависит только от
. При наших предположениях оно зависит только от  , поэтому
, поэтому

Таким образом, закон сохранения момента дает равенство

Пусть угол  отсчитывается от оси у. Очевидно, что
отсчитывается от оси у. Очевидно, что

Поскольку  не зависит от
не зависит от  , последнее соотношение верно при всех
, последнее соотношение верно при всех  . Таким образом,
. Таким образом,

Далее имеем  и
и

Используя эти равенства, на основании (6.2) получим

Подставляя (6.4) в (6.1), получим уравнение для отыскания 

Общее решение этого уравнения дается формулой

где  . Постоянные
. Постоянные  определяются из граничных условий
определяются из граничных условий

или, более подробно,

Решая систему (6.8), получим

Таким образом, распределение скоростей между соосными цилиндрами дается формулой

Имея формулу (6.10), легко вычислить  и
и

где  имеет вид (6.9).
имеет вид (6.9).
Заметим также, что, измеряя в эксперименте  можно определить вязкость.
можно определить вязкость.
Отметим частные случаи течения.
а) Оба цилиндра вращаются с одинаковой угловой скоростью:  . Для этого случая из (6.10) получаем
. Для этого случая из (6.10) получаем

Вязкая жидкость вращается как твердое тело с той же угловой скоростью.
б) Жидкость заполняет безграничное пространство вне цилиндра  . В этом случае
. В этом случае

в) Один из цилиндров неподвижен, например  . Тогда
. Тогда

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ КИНЕМАТИКИ ЖИДКОСТИ
- § 1. ПЕРЕМЕННЫЕ ЛАГРАНЖА И ЭЙЛЕРА
- § 2. ПЕРЕХОД ОТ ПЕРЕМЕННЫХ ЛАГРАНЖА К ПЕРЕМЕННЫМ ЭЙЛЕРА И ОБРАТНО
- § 3. ИНДИВИДУАЛЬНАЯ И МЕСТНАЯ ПРОИЗВОДНЫЕ
- § 4. УСТАНОВИВШЕЕСЯ И НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЯ
- § 5. СКОРОСТИ И УСКОРЕНИЯ
- § 6. ТРАЕКТОРИИ, ЛИНИИ ТОКА, КРИТИЧЕСКИЕ ТОЧКИ
- § 7. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ТЕНЗОРАХ
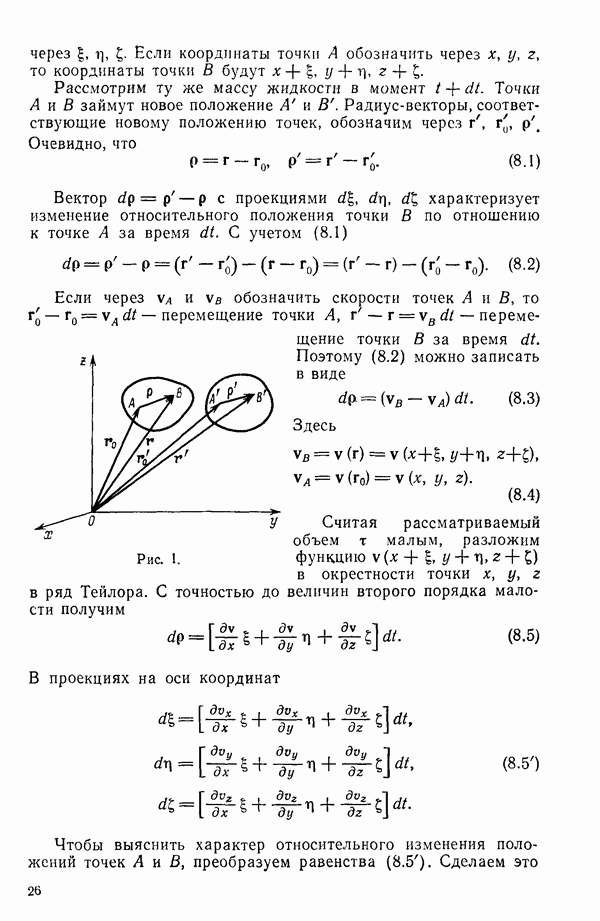
- § 8. СКОРОСТИ И ПЕРЕМЕЩЕНИЯ ТОЧЕК БЕСКОНЕЧНО МАЛОГО ОБЪЕМА СПЛОШНОЙ СРЕДЫ
- § 9. ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИЙ И ЕГО ИНВАРИАНТЫ
- § 10. СМЫСЛ КОМПОНЕНТ ТЕНЗОРА СКОРОСТЕЙ ДЕФОРМАЦИЙ
- § 11. СМЫСЛ КОМПОНЕНТ ВИХРЯ СКОРОСТИ
- § 12. ВИХРЕВЫЕ ЛИНИИ, ВИХРЕВЫЕ ТРУБКИ
- § 13. ЦИРКУЛЯЦИЯ СКОРОСТИ
- § 14. СКОРОСТЬ ОБЪЕМНОГО РАСШИРЕНИЯ ЖИДКОСТИ
- ГЛАВА II. ЗАКОН СОХРАНЕНИЯ МАСС
- § 1. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ МАСС
- § 2. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ МАСС В ПЕРЕМЕННЫХ ЭЙЛЕРА (УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ПЕРЕМЕННЫХ ЭЙЛЕРА)
- § 3. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ПЕРЕМЕННЫХ ЛАГРАНЖА
- § 4. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- ГЛАВА III. ЗАКОН КОЛИЧЕСТВА ДВИЖЕНИЯ ДЛЯ СПЛОШНОЙ СРЕДЫ
- § 1 СИЛЫ МАССОВЫЕ И ПОВЕРХНОСТНЫЕ
- § 2. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. ФОРМУЛА КОШИ
- § 4. ТЕНЗОР НАПРЯЖЕНИЙ
- § 5. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА КОЛИЧЕСТВА ДВИЖЕНИЯ
- ГЛАВА IV. ЗАКОН МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 1. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 2. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- ГЛАВА V. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 1. ВНУТРЕННЯЯ ЭНЕРГИЯ
- § 2. ПОЛНАЯ ЭНЕРГИЯ
- § 3. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- § 4. НЕКОТОРЫЕ ПРЕОБРАЗОВАНИЯ ИНТЕГРАЛЬНОЙ ЗАПИСИ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- § 5. ВЕКТОР ПОТОКА ТЕПЛА
- § 6. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- ГЛАВА VI. ПРОСТЕЙШИЕ МОДЕЛИ ЖИДКИХ СРЕД
- § 1. ИДЕАЛЬНАЯ ЖИДКОСТЬ И ТЕНЗОР НАПРЯЖЕНИИ ДЛЯ НЕЕ
- § 2. ВЯЗКАЯ (НЬЮТОНОВСКАЯ) ЖИДКОСТЬ И ТЕНЗОР НАПРЯЖЕНИЙ ДЛЯ НЕЕ
- § 3. НЕТЕПЛОПРОВОДНАЯ ЖИДКОСТЬ
- § 4. ЖИДКОСТЬ, ПОДЧИНЯЮЩАЯСЯ ЗАКОНУ ТЕПЛОПРОВОДНОСТИ ФУРЬЕ
- § 5. НЕСЖИМАЕМАЯ ЖИДКОСТЬ
- § 6. СЖИМАЕМАЯ ЖИДКОСТЬ
- ГЛАВА VII. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОЙ ЖИДКОСТИ И ПОСТАНОВКА ЗАДАЧ ДЛЯ НЕЕ
- § 1. СИСТЕМА УРАВНЕНИИ ГИДРОМЕХАНИКИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОИ ЖИДКОСТИ
- § 2. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ УСТАНОВИВШИХСЯ ТЕЧЕНИИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
- § 3. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ НЕУСТАНОВИВШИХСЯ ТЕЧЕНИИ ИДЕАЛЬНОИ НЕТЕПЛОПРОВОДНОИ ЖИДКОСТИ
- ГЛАВА VIII. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ВЯЗКОЙ ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ И ПОСТАНОВКА ЗАДАЧ ДЛЯ НЕЕ
- § 1. ОБЩАЯ СИСТЕМА УРАВНЕНИИ ГИДРОМЕХАНИКИ ВЯЗКОЙ ЖИДКОСТИ
- § 2. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ОДНОРОДНОЙ НЕСЖИМАЕМОЙ ВЯЗКОЙ ЖИДКОСТИ
- § 3. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ ТЕЧЕНИИ ВЯЗКОЙ ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
- ЧАСТЬ II. ОСНОВЫ ГИДРОСТАТИКИ
- § 1. УРАВНЕНИЯ РАВНОВЕСИЯ
- § 2. УСЛОВИЕ ДЛЯ СИЛ
- § 3. УСЛОВИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ДВУХ ЖИДКОСТЕЙ
- § 4. РАВНОВЕСИЕ ОДНОРОДНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 5. РАВНОВЕСИЕ БАРОТРОПНОИ ЖИДКОСТИ
- § 6. ОБЩИЙ СЛУЧАЙ РАВНОВЕСИЯ ЖИДКОСТИ В КОНСЕРВАТИВНОМ СИЛОВОМ ПОЛЕ
- § 7. ОБЩИЕ ФОРМУЛЫ ДЛЯ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИЛ ДАВЛЕНИИ
- § 8. ЗАКОН АРХИМЕДА
- ЧАСТЬ III. ГИДРОМЕХАНИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 1. АДИАБАТА
- § 2. ИНТЕГРАЛ БЕРНУЛЛИ
- § 3. ИНТЕГРАЛ БЕРНУЛЛИ В СЛУЧАЕ ДВИЖЕНИЯ ГАЗА С УСЛОЖНЕННОЙ ТЕРМОДИНАМИКОЙ
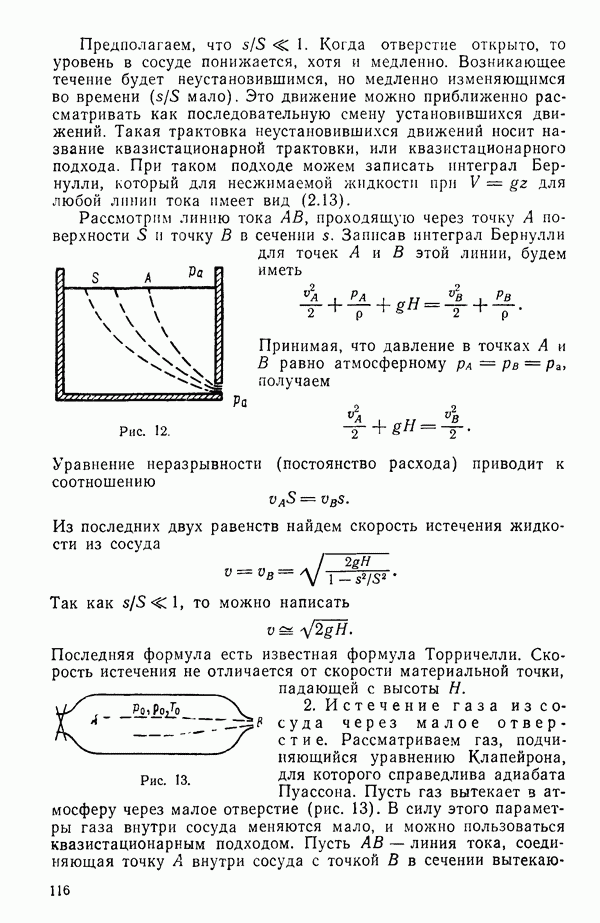
- § 4. ДВА ПРИМЕРА НА ПРИМЕНЕНИЕ ИНТЕГРАЛА БЕРНУЛЛИ
- § 5. УРАВНЕНИЯ ЭЙЛЕРА В ФОРМЕ ГРОМЕКИ — ЛЭМБА
- § 6. ПОТЕНЦИАЛЬНЫЕ, ИЛИ БЕЗВИХРЕВЫЕ, ДВИЖЕНИЯ
- § 7. ИНТЕГРАЛ ЛАГРАНЖА
- § 8. ИНТЕГРАЛ ЭЙЛЕРА-БЕРНУЛЛИ
- § 9. УРАВНЕНИЯ ДЛЯ ПОТЕНЦИАЛА СКОРОСТЕЙ
- ГЛАВА XI. ОБОБЩЕННЫЕ ОДНОМЕРНЫЕ ДВИЖЕНИЯ
- § 2. ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
- § 3. ДВИЖЕНИЕ СЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ. СОПЛО ЛАВАЛЯ
- ГЛАВА XII. ПЛОСКИЕ БЕЗВИХРЕВЫЕ УСТАНОВИВШИЕСЯ ТЕЧЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 1. СИСТЕМА УРАВНЕНИЙ
- § 2. ПОТЕНЦИАЛ СКОРОСТЕЙ
- § 3. ФУНКЦИЯ ТОКА
- § 4. КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ И КОМПЛЕКСНАЯ СКОРОСТЬ
- § 4. КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ И КОМПЛЕКСНАЯ СКОРОСТЬ
- § 6. ПОТЕНЦИАЛЬНОЕ ОБТЕКАНИЕ КРУГОВОГО ЦИЛИНДРА ПОТОКОМ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 7. МЕТОД КОНФОРМНЫХ ОТОБРАЖЕНИЙ
- § 8. ОБТЕКАНИЕ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА
- § 9. ПОСТУЛАТ ЧАПЛЫГИНА — ЖУКОВСКОГО
- § 10. ФОРМУЛЫ ЧАПЛЫГИНА — БЛАЗИУСА
- § 11. ИНТЕГРАЛ ОТ КОМПЛЕКСНОЙ СКОРОСТИ
- § 12. ТЕОРЕМА ЖУКОВСКОГО
- § 13. ФОРМУЛА ДЛЯ МОМЕНТА
- § 14. ОБТЕКАНИЕ ПЛАСТИНКИ
- § 15. ОБТЕКАНИЕ ПРОФИЛЕЙ ЖУКОВСКОГО
- § 16. ОБТЕКАНИЕ ПРОИЗВОЛЬНОГО ПРОФИЛЯ. МЕТОД НУЖИНА
- § 17. НЕКОТОРЫЕ ОБЩИЕ ЗАМЕЧАНИЯ О ПЛОСКИХ ПОТЕНЦИАЛЬНЫХ ДВИЖЕНИЯХ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- ГЛАВА XIII. ТЕОРИЯ ТОНКОГО КРЫЛА
- § 1. ПОНЯТИЕ ТОНКОГО КРЫЛА И УСЛОВИЯ ОБТЕКАНИЯ ДЛЯ ТОНКОГО ПРОФИЛЯ
- § 2. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ТОНКОГО ПРОФИЛЯ МЕТОДОМ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ
- § 3. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОФИЛЯ С НУЛЕВОЙ ТОЛЩИНОЙ
- § 5. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОИЗВОЛЬНОГО ТОНКОГО ПРОФИЛЯ
- ГЛАВА XIV. ОСЕСИММЕТРИЧНЫЕ ПОТЕНЦИАЛЬНЫЕ ТЕЧЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 1. ИСТОЧНИКИ В ПРОСТРАНСТВЕ
- § 2. ДИПОЛЬ В ПРОСТРАНСТВЕ
- § 3. ОБТЕКАНИЕ СФЕРЫ
- § 4. ФУНКЦИЯ ТОКА ДЛЯ ОСЕСИММЕТРИЧНЫХ ТЕЧЕНИЙ
- § 5. ПРОДОЛЬНОЕ ОБТЕКАНИЕ ТЕЛА ВРАЩЕНИЯ. МЕТОД ИСТОЧНИКОВ И СТОКОВ
- § 6. ПОПЕРЕЧНОЕ ОБТЕКАНИЕ ТЕЛА ВРАЩЕНИЯ
- § 7. ОБЩИЙ СЛУЧАЙ ОБТЕКАНИЯ ТЕЛА ВРАЩЕНИЯ
- ГЛАВА XV. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- § 1. ОБЩИЙ ВИД ПОТЕНЦИАЛА СКОРОСТЕЙ
- § 2. ПОВЕДЕНИЕ ПОТЕНЦИАЛА СКОРОСТЕЙ В ОКРЕСТНОСТИ БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКИ
- § 3. РАСЧЕТ ГИДРОДИНАМИЧЕСКИХ РЕАКЦИИ ПРИ ДВИЖЕНИИ ТЕЛА
- § 4. УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- ГЛАВА XVI. ВИХРЕВЫЕ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 1. ТЕОРЕМА ТОМСОНА
- § 2. ТЕОРЕМА ЛАГРАНЖА
- § 3. ТЕОРЕМЫ ГЕЛЬМГОЛЬЦА
- § 4. О ВОЗНИКНОВЕНИИ ВИХРЕЙ
- § 5. УРАВНЕНИЯ ДЛЯ ВИХРЯ
- § 6. ОПРЕДЕЛЕНИЕ ВЕКТОРА СКОРОСТИ ПО ВИХРЮ И ДИВЕРГЕНЦИИ
- § 7. СКОРОСТИ, ИНДУЦИРУЕМЫЕ ВИХРЕВОЙ НИТЬЮ
- § 8. ПРЯМОЛИНЕЙНАЯ ВИХРЕВАЯ НИТЬ
- § 9. ВИХРЕВОЙ СЛОЙ
- ГЛАВА XVII. ТЕОРИЯ КРЫЛА КОНЕЧНОГО РАЗМАХА
- § 2. ВИХРЕВАЯ СИСТЕМА КРЫЛА И ОСНОВНЫЕ ФОРМУЛЫ
- § 3. КРЫЛО С ЭЛЛИПТИЧЕСКИМ РАСПРЕДЕЛЕНИЕМ ЦИРКУЛЯЦИИ
- § 4. ПАРАБОЛА ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ И ПЕРЕСЧЕТ КРЫЛА С ОДНОГО УДЛИНЕНИЯ НА ДРУГОЕ
- § 5. ОПРЕДЕЛЕНИЕ ЦИРКУЛЯЦИИ Г(z) В ТЕОРИИ КРЫЛА КОНЕЧНОГО РАЗМАХА
- ЧАСТЬ IV. ГИДРОМЕХАНИКА ВЯЗКОЙ ЖИДКОСТИ
- ГЛАВА XVIII. ОБЩИЕ СВОЙСТВА ДВИЖЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 2. НЕОБРАТИМОСТЬ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
- § 3. ЗАВИХРЕННОСТЬ ТЕЧЕНИЙ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 4. ДИССИПАЦИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ В ВЯЗКОЙ ЖИДКОСТИ
- ГЛАВА XIX. ТОЧНЫЕ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 1. ПОСТАНОВКА ЗАДАЧИ ОБ ОТЫСКАНИИ ОДНОМЕРНЫХ ТЕЧЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 2. ПРИМЕРЫ ОДНОМЕРНЫХ НЕСТАЦИОНАРНЫХ ТЕЧЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 3. УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ МЕЖДУ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
- § 4. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ
- § 7. ПРИМЕР ПРОСТЕЙШЕГО УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ С ПЕРЕМЕННОЙ ВЯЗКОСТЬЮ
- ГЛАВА XX. ПОДОБИЕ ТЕЧЕНИИ ВЯЗКОЙ ЖИДКОСТИ
- § 1. СХОДСТВЕННЫЕ ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ТОЧКИ
- § 2. ЗАПИСЬ УРАВНЕНИИ ГИДРОМЕХАНИКИ ВЯЗКОЙ ЖИДКОСТИ В БЕЗРАЗМЕРНОМ ВИДЕ
- § 3. ПОДОБИЕ УСТАНОВИВШИХСЯ ТЕЧЕНИЙ
- § 5 ТЕЧЕНИЕ В ТРУБЕ ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ
- § 6. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ МЕЖДУ ДВУМЯ ВРАЩАЮЩИМИСЯ СООСНЫМИ ЦИЛИНДРАМИ
- ГЛАВА XXI. ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ ПРИ БОЛЬШИХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 1. ОСНОВНЫЕ ПРЕДПОЛОЖЕНИЯ И СИСТЕМА УРАВНЕНИИ ПОГРАНИЧНОГО СЛОЯ
- § 2. ПОГРАНИЧНЫЙ СЛОЙ ОКОЛО ПОЛУБЕСКОНЕЧНОЙ ПЛАСТИНКИ
- ГЛАВА XXII. ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ ПРИ МАЛЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 1. УРАВНЕНИЯ СТОКСА
- § 2. ОБТЕКАНИЕ СФЕРЫ ПРИ МАЛЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 3. ПАРАДОКС СТОКСА
- § 4. УРАВНЕНИЯ ОЗИНА
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА