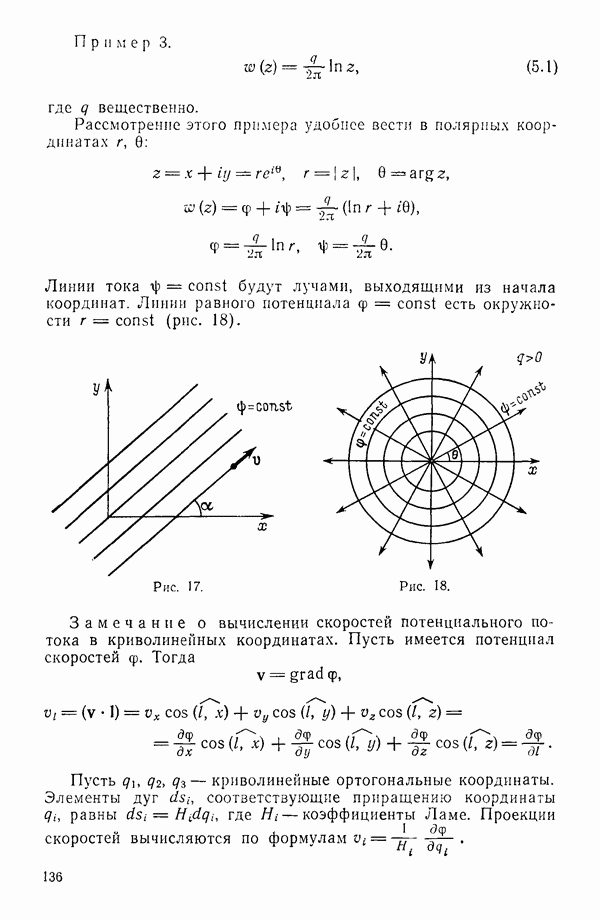
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. ВЯЗКАЯ (НЬЮТОНОВСКАЯ) ЖИДКОСТЬ И ТЕНЗОР НАПРЯЖЕНИЙ ДЛЯ НЕЕ
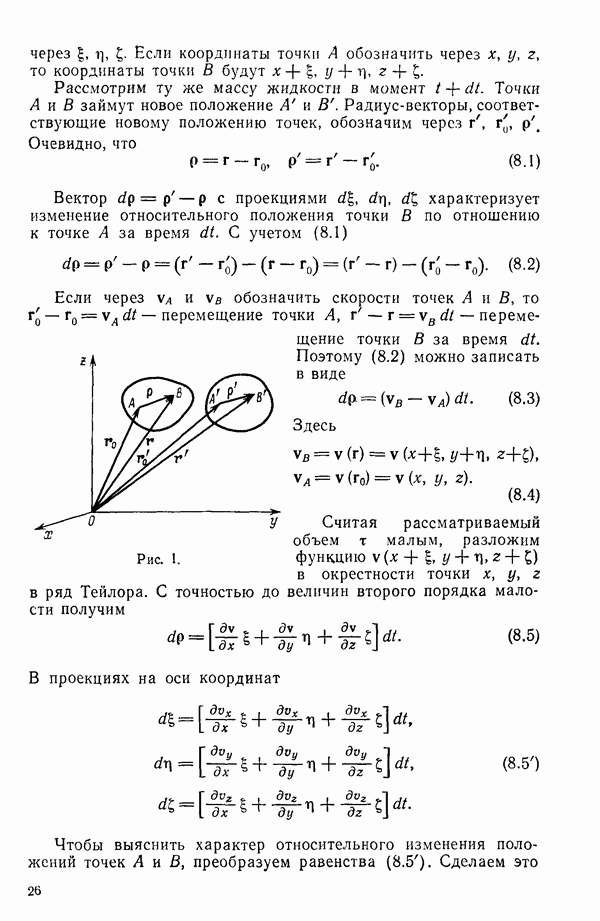
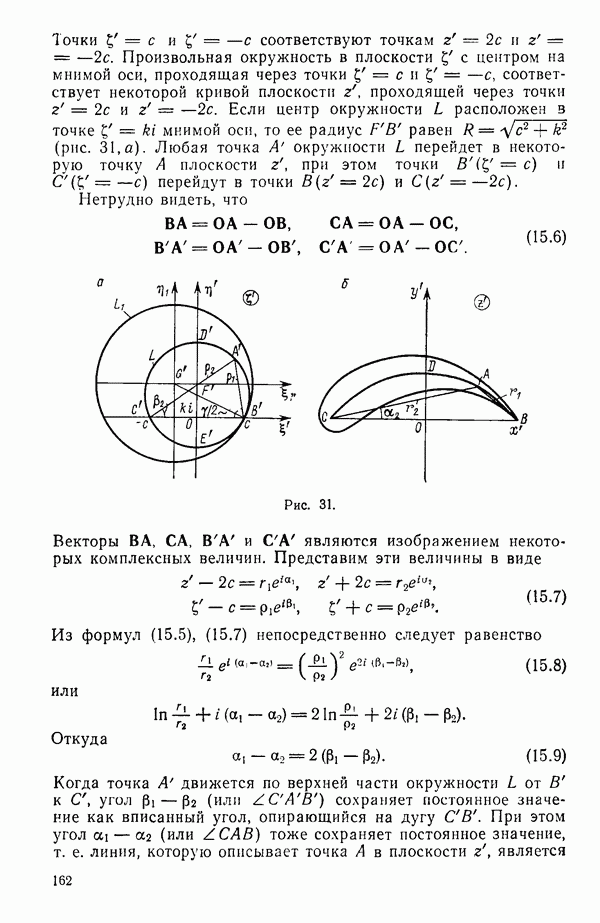
Вязкой называют жидкость, в которой при движении кроме нормальных напряжений наблюдаются и касательные напряжения. Рассмотрим эксперимент, который проводил еще Ньютон. Имеются две плоскости, между которыми находится жидкость. Нижняя пластина закреплена, верхняя движется параллельно нижней на расстоянии h со скоростью v (рис. 10).
Опыт показывает, что сила f, которую надо приложить к верхней пластине,  где S — площадь пластины. Сила, приходящаяся на единицу площади, в нашем случае касательное напряжение
где S — площадь пластины. Сила, приходящаяся на единицу площади, в нашем случае касательное напряжение

Здесь  — коэффициент, который зависит от свойств жидкости.
— коэффициент, который зависит от свойств жидкости.
Этот же опыт дает распределение скоростей жидкости: на неподвижной пластине скорость жидкости равна нулю, на верхней — равна скорости пластины. Распределение скоростей поперек линейно зависит от расстояния

В силу (2.2) — и выражение для  можно записать в виде
можно записать в виде

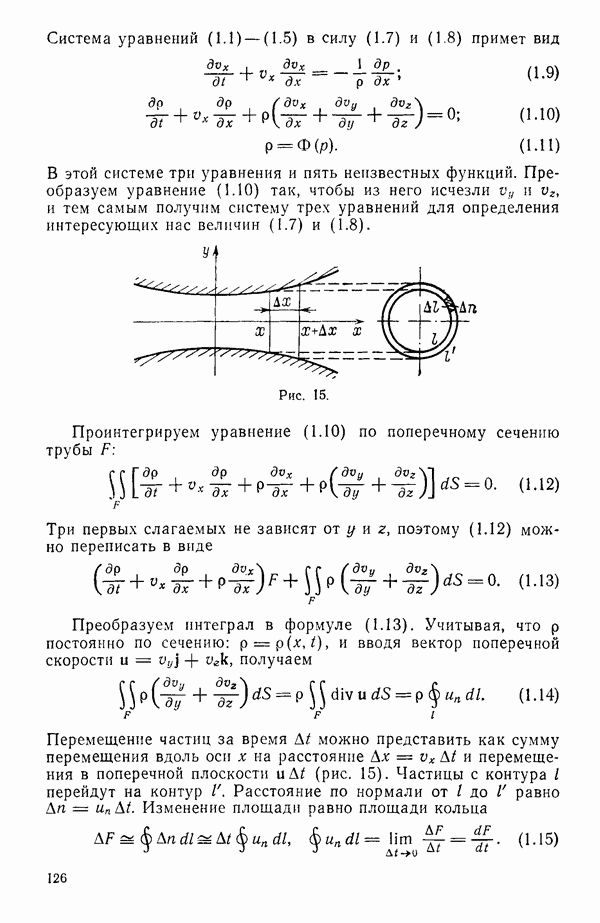
Для многих жидкостей равенство (2.1) выполняется с большой степенью точности. Коэффициент  называется коэффициентом вязкости. Причиной вязкости (касательных напряжений) является хаотическое движение молекул, переход которых из слоя в слой создает торможение этих движущихся слоев относительно друг друга.
называется коэффициентом вязкости. Причиной вязкости (касательных напряжений) является хаотическое движение молекул, переход которых из слоя в слой создает торможение этих движущихся слоев относительно друг друга.
Так как в рассматриваемом движении  и, следовательно,
и, следовательно,  то, как следует из (2.3), в этом случае справедливо соотношение
то, как следует из (2.3), в этом случае справедливо соотношение


Рис. 10.
В соответствии с рассмотренным опытом можно вывести связь между тензором напряжений и тензором скоростей деформаций в общем случае.
Жидкость называется вязкой ньютоновской, если выполнены следующие условия:
1) в жидкости, когда она движется как абсолютно твердое тело или находится в покое, наблюдаются только нормальные напряжения;
2) компоненты тензора напряжений есть линейные функции компонент тензора скоростей деформаций;
3) жидкость изотропна, т. е. ее свойства одинаковы по всем направлениям.
Условие 1) означает, что  при
при  если все
если все  .
.
Условие 2) означает, что тмогут быть представлены через  в виде (учитывая симметрию тензора напряжений)
в виде (учитывая симметрию тензора напряжений)

Условие 3) означает, что коэффициенты а в (2.5) не зависят от выбора системы координат.
Предположим, что жидкость покоится или движется как абсолютно твердое тело. В этом случае все  . Из формул (2.5) тогда будет следовать, что
. Из формул (2.5) тогда будет следовать, что

Но по условию 1) все касательные напряжения при этом обращаются в нуль. Следовательно,

Нормальные напряжения в этом случае не зависят от ориентировки площадки. Обозначим общую величину этих напряжений через —р. Тогда

Перейдем к системе координат х, у, z, оси которой являются главными осями для тензора скоростей деформаций. Обозначим  Выпишем выражения для
Выпишем выражения для  и
и  в этих координатах, учитывая (2.7) и (2.8):
в этих координатах, учитывая (2.7) и (2.8):

Рассмотрим формулу (2.9). Покажем, что  . Для этого введем новые оси координат
. Для этого введем новые оси координат

Оси  — тоже главные оси тензора скоростей деформаций. В этих осях равенство (2.9) сохраняет свой вид:
— тоже главные оси тензора скоростей деформаций. В этих осях равенство (2.9) сохраняет свой вид:

Здесь  — главные скорости деформации в осях
— главные скорости деформации в осях  . Учитывая (2.11) и определение величин
. Учитывая (2.11) и определение величин  , получим
, получим

Подставив (2.12), будем иметь

Так как оси  совпадают, то
совпадают, то  и
и 

Приравнивая (2.9) и (2.14), получим

Так как (2.16) имеет место при любых  , то, следовательно,
, то, следовательно,

Положим

Подставляя (2.18) в (2.9), получим

Аналогично получим формулы для  и
и 

Здесь  .
.
Рассмотрим теперь выражение (2.10) для касательных напряжений и покажем, что в главных осях тензора скоростей деформаций все касательные напряжения равны нулю. Наряду с системой координат х, у, z введем систему координат  :
:

Новая система координат также является главной и можно написать

Очевидно,

Подставляя (2.22) в (2.21), получаем

Но по физическому смыслу  справедливо и такое равенство:
справедливо и такое равенство:

Действительно,  величина
величина  есть проекция вектора
есть проекция вектора  на ось у, а
на ось у, а  — проекция этого же вектора на противоположное направление. Из равенств (2.23) и (2.24) следует, что
— проекция этого же вектора на противоположное направление. Из равенств (2.23) и (2.24) следует, что  .
.
Аналогично устанавливается равенство нулю и остальных касательных напряжений:

т. е. в главных осях тензора скоростей деформаций касательные напряжения в вязкой жидкости равны нулю. Но такие оси есть главные оси тензора напряжений. Следовательно, главные оси тензора скоростей деформаций одновременно являются и главными осями тензора напряжений.
Равенства (2.19) и (2.25) можно объединить, записав их в виде одного тензорного равенства:

Равенство (2.26) устанавливает связь между компонентами двух тензоров (правую часть можно записать в виде одного тензора) в главных осях. Но если два тензора равны между собой в каких-то осях координат, то они будут равны и в любых других осях координат, так как компоненты тензора при переходе к другой системе преобразуются по одним и тем же законам.
Таким образом, связь между тензором напряжений и тензором скоростей деформаций в любых осях координат имеет вид

Для составляющих получим

Используя формулы для составляющих тензора скоростей деформаций ((8.8) гл, I), получим окончательное выражение для составляющих тензора напряжений в вязкой жидкости:

В формулы (2.27), (2.28) входят два параметра:  и
и  . Если
. Если  , то тензор напряжений вязкой жидкости обращается в тензор напряжений идеальной жидкости. Коэффициент р называют коэффициентом вязкости (или сдвиговой вязкости),
, то тензор напряжений вязкой жидкости обращается в тензор напряжений идеальной жидкости. Коэффициент р называют коэффициентом вязкости (или сдвиговой вязкости),  — вторым коэффициентом вязкости (или коэффициентом объемной вязкости). Часто коэффициентом объемной вязкости называют не
— вторым коэффициентом вязкости (или коэффициентом объемной вязкости). Часто коэффициентом объемной вязкости называют не  , а величину
, а величину  Наряду с
Наряду с  для несжимаемой жидкости часто рассматривают величину v, называемую кинематическим коэффициентом вязкости
для несжимаемой жидкости часто рассматривают величину v, называемую кинематическим коэффициентом вязкости  . Коэффициент
. Коэффициент  может быть определен экспериментально; в случае, если известен закон межмолекулярного взаимодействия, его можно вычислить теоретически. Вообще говоря,
может быть определен экспериментально; в случае, если известен закон межмолекулярного взаимодействия, его можно вычислить теоретически. Вообще говоря,  но зависимость от давления слабая. Наиболее часто пользуются следующими приближенными формулами для зависимости
но зависимость от давления слабая. Наиболее часто пользуются следующими приближенными формулами для зависимости  от
от  . Для небольших интервалов температур используют линейную зависимость
. Для небольших интервалов температур используют линейную зависимость

Здесь а берется из эксперимента (для воздуха  ) — значение коэффициента вязкости при
) — значение коэффициента вязкости при  . Для более широких интервалов температур принимают
. Для более широких интервалов температур принимают  — (для воздуха
— (для воздуха  ). Часто пользуются формулой Сюзерленда
). Часто пользуются формулой Сюзерленда

Постоянная С для воздуха, азота и кислорода соответственно имеет значения 117, 110 и 127.
Второй коэффициент вязкости  исследовать трудно. В случае, если жидкость несжимаема, то
исследовать трудно. В случае, если жидкость несжимаема, то  и он выпадает из уравнений. Для случая одноатомных газов теоретически показано, что
и он выпадает из уравнений. Для случая одноатомных газов теоретически показано, что  Коэффициент
Коэффициент  существен в задаче о распространении звука.
существен в задаче о распространении звука.
Замечание. Закон связи между тензором напряжений и тензором скоростей деформаций, который мы установили исходя из закона трения Ньютона, имеет вид (2.27). Жидкости, которые подчиняются этому закону, называются ньютоновскими жидкостями. Однако существуют жидкости, которые не подчиняются закону Ньютона. Приведем примеры.
Пример 1. Для растворов полимеров (например, каучук в бензоле) и некоторых легко деформируемых металлов, которые можно рассматривать как жидкости, часто используется следующая связь между  (предполагается, что
(предполагается, что  )
)

Здесь

Тензор  — тензор второго ранга. Действительно, перемножив тензоры скоростей деформаций
— тензор второго ранга. Действительно, перемножив тензоры скоростей деформаций  получим тензор четвертого порядка с составляющими
получим тензор четвертого порядка с составляющими  Свертывая этот тензор по индексу
Свертывая этот тензор по индексу  приходим к тензору
приходим к тензору  . В выражение для
. В выражение для  тензор
тензор  входит с коэффициентом
входит с коэффициентом  Коэффициент S — новая физическая характеристика для жидкостей, он находится из эксперимента.
Коэффициент S — новая физическая характеристика для жидкостей, он находится из эксперимента.
Пример 2. Модель вязкой жидкости неприменима для описания течений разреженных газов. Степень разреженности газа и область применимости модели вязкой жидкости к газам определяются величиной числа Кнудсена  , где I — средняя длина свободного пробега молекул, L — характерный размер тела. Для слаборазреженных газов
, где I — средняя длина свободного пробега молекул, L — характерный размер тела. Для слаборазреженных газов  , коэффициенты вязкости
, коэффициенты вязкости  и теплопроводности k пропорциональны I и закон трения Ньютона верен с точностью до членов порядка
и теплопроводности k пропорциональны I и закон трения Ньютона верен с точностью до членов порядка  . Следующее приближение на этом пути (приближение Барнетта) дает один из простейших примеров неньютоновской жидкости. В этом приближении
. Следующее приближение на этом пути (приближение Барнетта) дает один из простейших примеров неньютоновской жидкости. В этом приближении

причем коэффициент С имеет порядок  — линейная комбинация вторых производных и произведений первых производных от гидродинамических величин р, Т, v.
— линейная комбинация вторых производных и произведений первых производных от гидродинамических величин р, Т, v.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ КИНЕМАТИКИ ЖИДКОСТИ
- § 1. ПЕРЕМЕННЫЕ ЛАГРАНЖА И ЭЙЛЕРА
- § 2. ПЕРЕХОД ОТ ПЕРЕМЕННЫХ ЛАГРАНЖА К ПЕРЕМЕННЫМ ЭЙЛЕРА И ОБРАТНО
- § 3. ИНДИВИДУАЛЬНАЯ И МЕСТНАЯ ПРОИЗВОДНЫЕ
- § 4. УСТАНОВИВШЕЕСЯ И НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЯ
- § 5. СКОРОСТИ И УСКОРЕНИЯ
- § 6. ТРАЕКТОРИИ, ЛИНИИ ТОКА, КРИТИЧЕСКИЕ ТОЧКИ
- § 7. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ТЕНЗОРАХ
- § 8. СКОРОСТИ И ПЕРЕМЕЩЕНИЯ ТОЧЕК БЕСКОНЕЧНО МАЛОГО ОБЪЕМА СПЛОШНОЙ СРЕДЫ
- § 9. ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИЙ И ЕГО ИНВАРИАНТЫ
- § 10. СМЫСЛ КОМПОНЕНТ ТЕНЗОРА СКОРОСТЕЙ ДЕФОРМАЦИЙ
- § 11. СМЫСЛ КОМПОНЕНТ ВИХРЯ СКОРОСТИ
- § 12. ВИХРЕВЫЕ ЛИНИИ, ВИХРЕВЫЕ ТРУБКИ
- § 13. ЦИРКУЛЯЦИЯ СКОРОСТИ
- § 14. СКОРОСТЬ ОБЪЕМНОГО РАСШИРЕНИЯ ЖИДКОСТИ
- ГЛАВА II. ЗАКОН СОХРАНЕНИЯ МАСС
- § 1. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ МАСС
- § 2. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ МАСС В ПЕРЕМЕННЫХ ЭЙЛЕРА (УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ПЕРЕМЕННЫХ ЭЙЛЕРА)
- § 3. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ПЕРЕМЕННЫХ ЛАГРАНЖА
- § 4. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- ГЛАВА III. ЗАКОН КОЛИЧЕСТВА ДВИЖЕНИЯ ДЛЯ СПЛОШНОЙ СРЕДЫ
- § 1 СИЛЫ МАССОВЫЕ И ПОВЕРХНОСТНЫЕ
- § 2. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. ФОРМУЛА КОШИ
- § 4. ТЕНЗОР НАПРЯЖЕНИЙ
- § 5. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА КОЛИЧЕСТВА ДВИЖЕНИЯ
- ГЛАВА IV. ЗАКОН МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 1. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 2. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- ГЛАВА V. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 1. ВНУТРЕННЯЯ ЭНЕРГИЯ
- § 2. ПОЛНАЯ ЭНЕРГИЯ
- § 3. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- § 4. НЕКОТОРЫЕ ПРЕОБРАЗОВАНИЯ ИНТЕГРАЛЬНОЙ ЗАПИСИ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- § 5. ВЕКТОР ПОТОКА ТЕПЛА
- § 6. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- ГЛАВА VI. ПРОСТЕЙШИЕ МОДЕЛИ ЖИДКИХ СРЕД
- § 1. ИДЕАЛЬНАЯ ЖИДКОСТЬ И ТЕНЗОР НАПРЯЖЕНИИ ДЛЯ НЕЕ
- § 2. ВЯЗКАЯ (НЬЮТОНОВСКАЯ) ЖИДКОСТЬ И ТЕНЗОР НАПРЯЖЕНИЙ ДЛЯ НЕЕ
- § 3. НЕТЕПЛОПРОВОДНАЯ ЖИДКОСТЬ
- § 4. ЖИДКОСТЬ, ПОДЧИНЯЮЩАЯСЯ ЗАКОНУ ТЕПЛОПРОВОДНОСТИ ФУРЬЕ
- § 5. НЕСЖИМАЕМАЯ ЖИДКОСТЬ
- § 6. СЖИМАЕМАЯ ЖИДКОСТЬ
- ГЛАВА VII. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОЙ ЖИДКОСТИ И ПОСТАНОВКА ЗАДАЧ ДЛЯ НЕЕ
- § 1. СИСТЕМА УРАВНЕНИИ ГИДРОМЕХАНИКИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОИ ЖИДКОСТИ
- § 2. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ УСТАНОВИВШИХСЯ ТЕЧЕНИИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
- § 3. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ НЕУСТАНОВИВШИХСЯ ТЕЧЕНИИ ИДЕАЛЬНОИ НЕТЕПЛОПРОВОДНОИ ЖИДКОСТИ
- ГЛАВА VIII. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ВЯЗКОЙ ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ И ПОСТАНОВКА ЗАДАЧ ДЛЯ НЕЕ
- § 1. ОБЩАЯ СИСТЕМА УРАВНЕНИИ ГИДРОМЕХАНИКИ ВЯЗКОЙ ЖИДКОСТИ
- § 2. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ОДНОРОДНОЙ НЕСЖИМАЕМОЙ ВЯЗКОЙ ЖИДКОСТИ
- § 3. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ ТЕЧЕНИИ ВЯЗКОЙ ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
- ЧАСТЬ II. ОСНОВЫ ГИДРОСТАТИКИ
- § 1. УРАВНЕНИЯ РАВНОВЕСИЯ
- § 2. УСЛОВИЕ ДЛЯ СИЛ
- § 3. УСЛОВИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ДВУХ ЖИДКОСТЕЙ
- § 4. РАВНОВЕСИЕ ОДНОРОДНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 5. РАВНОВЕСИЕ БАРОТРОПНОИ ЖИДКОСТИ
- § 6. ОБЩИЙ СЛУЧАЙ РАВНОВЕСИЯ ЖИДКОСТИ В КОНСЕРВАТИВНОМ СИЛОВОМ ПОЛЕ
- § 7. ОБЩИЕ ФОРМУЛЫ ДЛЯ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИЛ ДАВЛЕНИИ
- § 8. ЗАКОН АРХИМЕДА
- ЧАСТЬ III. ГИДРОМЕХАНИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 1. АДИАБАТА
- § 2. ИНТЕГРАЛ БЕРНУЛЛИ
- § 3. ИНТЕГРАЛ БЕРНУЛЛИ В СЛУЧАЕ ДВИЖЕНИЯ ГАЗА С УСЛОЖНЕННОЙ ТЕРМОДИНАМИКОЙ
- § 4. ДВА ПРИМЕРА НА ПРИМЕНЕНИЕ ИНТЕГРАЛА БЕРНУЛЛИ
- § 5. УРАВНЕНИЯ ЭЙЛЕРА В ФОРМЕ ГРОМЕКИ — ЛЭМБА
- § 6. ПОТЕНЦИАЛЬНЫЕ, ИЛИ БЕЗВИХРЕВЫЕ, ДВИЖЕНИЯ
- § 7. ИНТЕГРАЛ ЛАГРАНЖА
- § 8. ИНТЕГРАЛ ЭЙЛЕРА-БЕРНУЛЛИ
- § 9. УРАВНЕНИЯ ДЛЯ ПОТЕНЦИАЛА СКОРОСТЕЙ
- ГЛАВА XI. ОБОБЩЕННЫЕ ОДНОМЕРНЫЕ ДВИЖЕНИЯ
- § 2. ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
- § 3. ДВИЖЕНИЕ СЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ. СОПЛО ЛАВАЛЯ
- ГЛАВА XII. ПЛОСКИЕ БЕЗВИХРЕВЫЕ УСТАНОВИВШИЕСЯ ТЕЧЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 1. СИСТЕМА УРАВНЕНИЙ
- § 2. ПОТЕНЦИАЛ СКОРОСТЕЙ
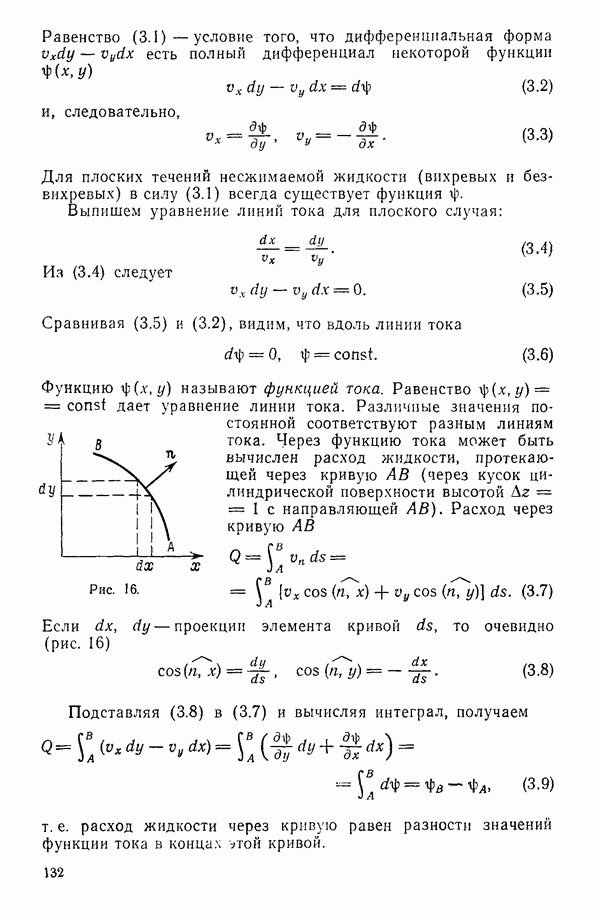
- § 3. ФУНКЦИЯ ТОКА
- § 4. КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ И КОМПЛЕКСНАЯ СКОРОСТЬ
- § 4. КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ И КОМПЛЕКСНАЯ СКОРОСТЬ
- § 6. ПОТЕНЦИАЛЬНОЕ ОБТЕКАНИЕ КРУГОВОГО ЦИЛИНДРА ПОТОКОМ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 7. МЕТОД КОНФОРМНЫХ ОТОБРАЖЕНИЙ
- § 8. ОБТЕКАНИЕ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА
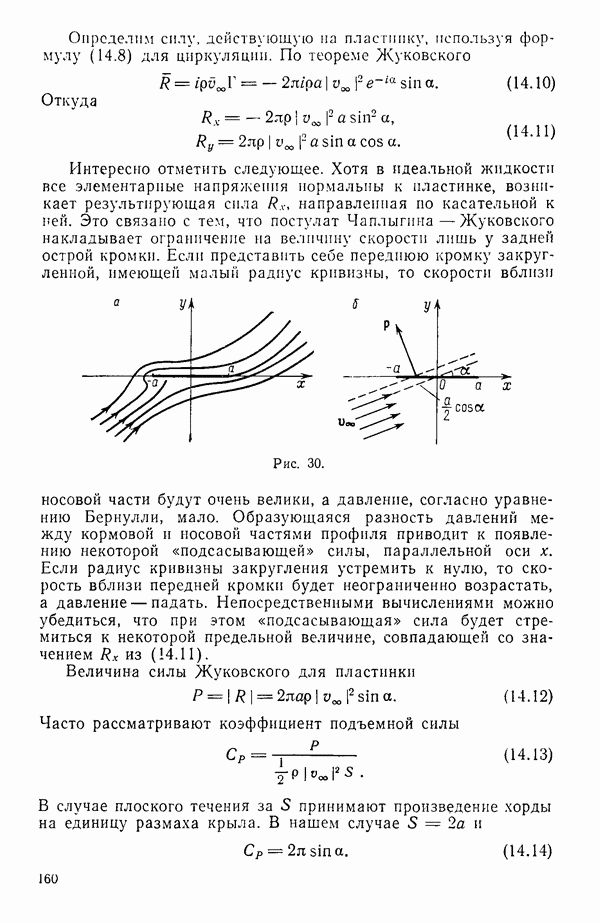
- § 9. ПОСТУЛАТ ЧАПЛЫГИНА — ЖУКОВСКОГО
- § 10. ФОРМУЛЫ ЧАПЛЫГИНА — БЛАЗИУСА
- § 11. ИНТЕГРАЛ ОТ КОМПЛЕКСНОЙ СКОРОСТИ
- § 12. ТЕОРЕМА ЖУКОВСКОГО
- § 13. ФОРМУЛА ДЛЯ МОМЕНТА
- § 14. ОБТЕКАНИЕ ПЛАСТИНКИ
- § 15. ОБТЕКАНИЕ ПРОФИЛЕЙ ЖУКОВСКОГО
- § 16. ОБТЕКАНИЕ ПРОИЗВОЛЬНОГО ПРОФИЛЯ. МЕТОД НУЖИНА
- § 17. НЕКОТОРЫЕ ОБЩИЕ ЗАМЕЧАНИЯ О ПЛОСКИХ ПОТЕНЦИАЛЬНЫХ ДВИЖЕНИЯХ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- ГЛАВА XIII. ТЕОРИЯ ТОНКОГО КРЫЛА
- § 1. ПОНЯТИЕ ТОНКОГО КРЫЛА И УСЛОВИЯ ОБТЕКАНИЯ ДЛЯ ТОНКОГО ПРОФИЛЯ
- § 2. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ТОНКОГО ПРОФИЛЯ МЕТОДОМ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ
- § 3. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОФИЛЯ С НУЛЕВОЙ ТОЛЩИНОЙ
- § 5. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОИЗВОЛЬНОГО ТОНКОГО ПРОФИЛЯ
- ГЛАВА XIV. ОСЕСИММЕТРИЧНЫЕ ПОТЕНЦИАЛЬНЫЕ ТЕЧЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 1. ИСТОЧНИКИ В ПРОСТРАНСТВЕ
- § 2. ДИПОЛЬ В ПРОСТРАНСТВЕ
- § 3. ОБТЕКАНИЕ СФЕРЫ
- § 4. ФУНКЦИЯ ТОКА ДЛЯ ОСЕСИММЕТРИЧНЫХ ТЕЧЕНИЙ
- § 5. ПРОДОЛЬНОЕ ОБТЕКАНИЕ ТЕЛА ВРАЩЕНИЯ. МЕТОД ИСТОЧНИКОВ И СТОКОВ
- § 6. ПОПЕРЕЧНОЕ ОБТЕКАНИЕ ТЕЛА ВРАЩЕНИЯ
- § 7. ОБЩИЙ СЛУЧАЙ ОБТЕКАНИЯ ТЕЛА ВРАЩЕНИЯ
- ГЛАВА XV. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- § 1. ОБЩИЙ ВИД ПОТЕНЦИАЛА СКОРОСТЕЙ
- § 2. ПОВЕДЕНИЕ ПОТЕНЦИАЛА СКОРОСТЕЙ В ОКРЕСТНОСТИ БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКИ
- § 3. РАСЧЕТ ГИДРОДИНАМИЧЕСКИХ РЕАКЦИИ ПРИ ДВИЖЕНИИ ТЕЛА
- § 4. УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- ГЛАВА XVI. ВИХРЕВЫЕ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 1. ТЕОРЕМА ТОМСОНА
- § 2. ТЕОРЕМА ЛАГРАНЖА
- § 3. ТЕОРЕМЫ ГЕЛЬМГОЛЬЦА
- § 4. О ВОЗНИКНОВЕНИИ ВИХРЕЙ
- § 5. УРАВНЕНИЯ ДЛЯ ВИХРЯ
- § 6. ОПРЕДЕЛЕНИЕ ВЕКТОРА СКОРОСТИ ПО ВИХРЮ И ДИВЕРГЕНЦИИ
- § 7. СКОРОСТИ, ИНДУЦИРУЕМЫЕ ВИХРЕВОЙ НИТЬЮ
- § 8. ПРЯМОЛИНЕЙНАЯ ВИХРЕВАЯ НИТЬ
- § 9. ВИХРЕВОЙ СЛОЙ
- ГЛАВА XVII. ТЕОРИЯ КРЫЛА КОНЕЧНОГО РАЗМАХА
- § 2. ВИХРЕВАЯ СИСТЕМА КРЫЛА И ОСНОВНЫЕ ФОРМУЛЫ
- § 3. КРЫЛО С ЭЛЛИПТИЧЕСКИМ РАСПРЕДЕЛЕНИЕМ ЦИРКУЛЯЦИИ
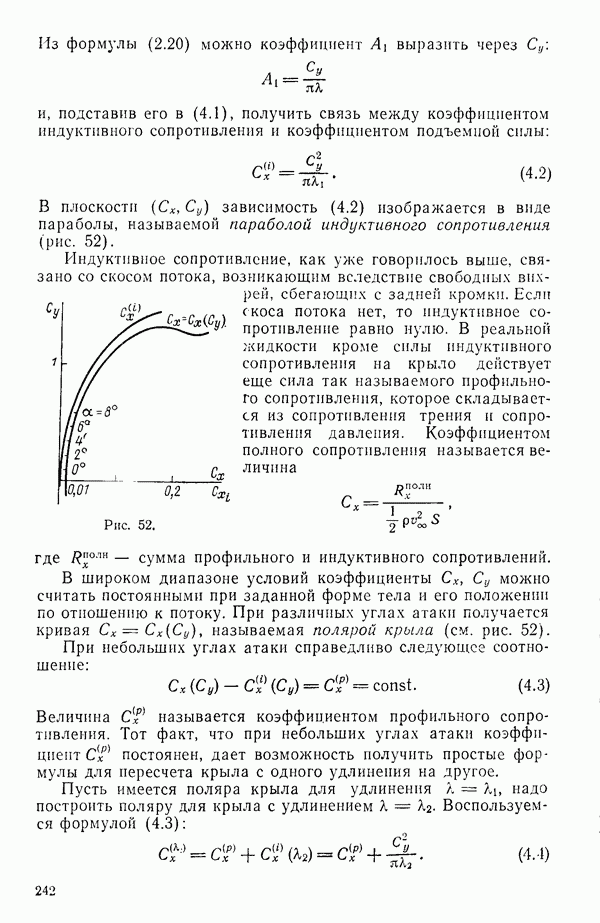
- § 4. ПАРАБОЛА ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ И ПЕРЕСЧЕТ КРЫЛА С ОДНОГО УДЛИНЕНИЯ НА ДРУГОЕ
- § 5. ОПРЕДЕЛЕНИЕ ЦИРКУЛЯЦИИ Г(z) В ТЕОРИИ КРЫЛА КОНЕЧНОГО РАЗМАХА
- ЧАСТЬ IV. ГИДРОМЕХАНИКА ВЯЗКОЙ ЖИДКОСТИ
- ГЛАВА XVIII. ОБЩИЕ СВОЙСТВА ДВИЖЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 2. НЕОБРАТИМОСТЬ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
- § 3. ЗАВИХРЕННОСТЬ ТЕЧЕНИЙ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 4. ДИССИПАЦИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ В ВЯЗКОЙ ЖИДКОСТИ
- ГЛАВА XIX. ТОЧНЫЕ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 1. ПОСТАНОВКА ЗАДАЧИ ОБ ОТЫСКАНИИ ОДНОМЕРНЫХ ТЕЧЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 2. ПРИМЕРЫ ОДНОМЕРНЫХ НЕСТАЦИОНАРНЫХ ТЕЧЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 3. УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ МЕЖДУ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
- § 4. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ
- § 7. ПРИМЕР ПРОСТЕЙШЕГО УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ С ПЕРЕМЕННОЙ ВЯЗКОСТЬЮ
- ГЛАВА XX. ПОДОБИЕ ТЕЧЕНИИ ВЯЗКОЙ ЖИДКОСТИ
- § 1. СХОДСТВЕННЫЕ ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ТОЧКИ
- § 2. ЗАПИСЬ УРАВНЕНИИ ГИДРОМЕХАНИКИ ВЯЗКОЙ ЖИДКОСТИ В БЕЗРАЗМЕРНОМ ВИДЕ
- § 3. ПОДОБИЕ УСТАНОВИВШИХСЯ ТЕЧЕНИЙ
- § 5 ТЕЧЕНИЕ В ТРУБЕ ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ
- § 6. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ МЕЖДУ ДВУМЯ ВРАЩАЮЩИМИСЯ СООСНЫМИ ЦИЛИНДРАМИ
- ГЛАВА XXI. ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ ПРИ БОЛЬШИХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 1. ОСНОВНЫЕ ПРЕДПОЛОЖЕНИЯ И СИСТЕМА УРАВНЕНИИ ПОГРАНИЧНОГО СЛОЯ
- § 2. ПОГРАНИЧНЫЙ СЛОЙ ОКОЛО ПОЛУБЕСКОНЕЧНОЙ ПЛАСТИНКИ
- ГЛАВА XXII. ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ ПРИ МАЛЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 1. УРАВНЕНИЯ СТОКСА
- § 2. ОБТЕКАНИЕ СФЕРЫ ПРИ МАЛЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 3. ПАРАДОКС СТОКСА
- § 4. УРАВНЕНИЯ ОЗИНА
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА