| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 2. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ОДНОРОДНОЙ НЕСЖИМАЕМОЙ ВЯЗКОЙ ЖИДКОСТИ
Рассматриваем однородную несжимаемую жидкость. Для нее  — уравнение состояния. Будем предполагать, что коэффициенты вязкости
— уравнение состояния. Будем предполагать, что коэффициенты вязкости  и теплопроводности k являются постоянными:
и теплопроводности k являются постоянными:
 (2.1)
(2.1)
Так как  и уравнение неразрывности принимает вид
и уравнение неразрывности принимает вид

Тензор напряжений в силу (2.2) будет

Рассмотрим уравнение движения (1.2). Запишем его проекцию на ось х и подставим вместо m выражения (2.3). учитывая при этом (2.1), получим


В силу (2.2) уравнение (2.4) примет вид

Аналогично запишутся два других уравнения — проекции на оси у и z. Вводя обозначения

перепишем уравнения движения вязкой несжимаемой жидкости в виде

Уравнения (2.6) равносильны одному векторному уравнению

Уравнения (2.6) носят название уравнений Навье—Стокса.
Уравнение неразрывности (2.2) и уравнения Навье—Стокса (2.6) образуют систему четырех уравнений для отыскания  и р, т. е. для несжимаемой вязкой жидкости при
и р, т. е. для несжимаемой вязкой жидкости при  задача об отыскании поля скоростей и давлений может быть решена независимо от задачи отыскания поля температур. После того как функции v и р будут найдены из (2.2) и (2.6), можно искать температуру, решая уравнение энергии.
задача об отыскании поля скоростей и давлений может быть решена независимо от задачи отыскания поля температур. После того как функции v и р будут найдены из (2.2) и (2.6), можно искать температуру, решая уравнение энергии.
В отличие от уравнений Эйлера в уравнения Навье—Стокса входят производные второго порядка. Это должно отразиться на постановке граничных условий.
Если же  , то уравнения Навье—Стокса переходят в уравнения Эйлера.
, то уравнения Навье—Стокса переходят в уравнения Эйлера.
Обратимся к уравнению энергии (1.3). Подставим выражения (2.3) для тензора напряжений в группу слагаемых, входящих в уравнение энергии:

В силу  . Через Ф обозначена сумма
. Через Ф обозначена сумма

Используя закон теплопроводности Фурье (1.5) и предположение, что  , получаем
, получаем

Учитывая (2.7) и (2.9), перепишем уравнение энергии (1.3) в виде

Для несжимаемой жидкости  , где с — теплоемкость, и уравнение энергии примет вид
, где с — теплоемкость, и уравнение энергии примет вид

Если система уравнений (2.2), (2.6) проинтегрирована, т. е. v и р — известные функции, то уравнение (2.11) есть дифференциальное уравнение в частных производных второго порядка для отыскания температуры Т. Входящая в (2.11) функция Ф неотрицательна и обращается в нуль только в случае, когда жидкость покоится или движется как абсолютно твердое тело. Для идеальной жидкости  , так как
, так как  . Функция Ф называется диссипативной функцией.
. Функция Ф называется диссипативной функцией.
Если среда неподвижна, т. е.  , то уравнение (2.11) принимает вид известного уравнения теплопроводности
, то уравнение (2.11) принимает вид известного уравнения теплопроводности

Если коэффициент k нельзя считать постоянным, т. е.  , то уравнение запишется в виде
, то уравнение запишется в виде

Итак, уравнения (2.2), (2.6), (2.11) образуют систему уравнений вязкой несжимаемой жидкости

Функция Ф имеет вид (2.8). Система (2.12) содержит пять уравнений для отыскания пяти функций:  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ КИНЕМАТИКИ ЖИДКОСТИ
- § 1. ПЕРЕМЕННЫЕ ЛАГРАНЖА И ЭЙЛЕРА
- § 2. ПЕРЕХОД ОТ ПЕРЕМЕННЫХ ЛАГРАНЖА К ПЕРЕМЕННЫМ ЭЙЛЕРА И ОБРАТНО
- § 3. ИНДИВИДУАЛЬНАЯ И МЕСТНАЯ ПРОИЗВОДНЫЕ
- § 4. УСТАНОВИВШЕЕСЯ И НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЯ
- § 5. СКОРОСТИ И УСКОРЕНИЯ
- § 6. ТРАЕКТОРИИ, ЛИНИИ ТОКА, КРИТИЧЕСКИЕ ТОЧКИ
- § 7. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ТЕНЗОРАХ
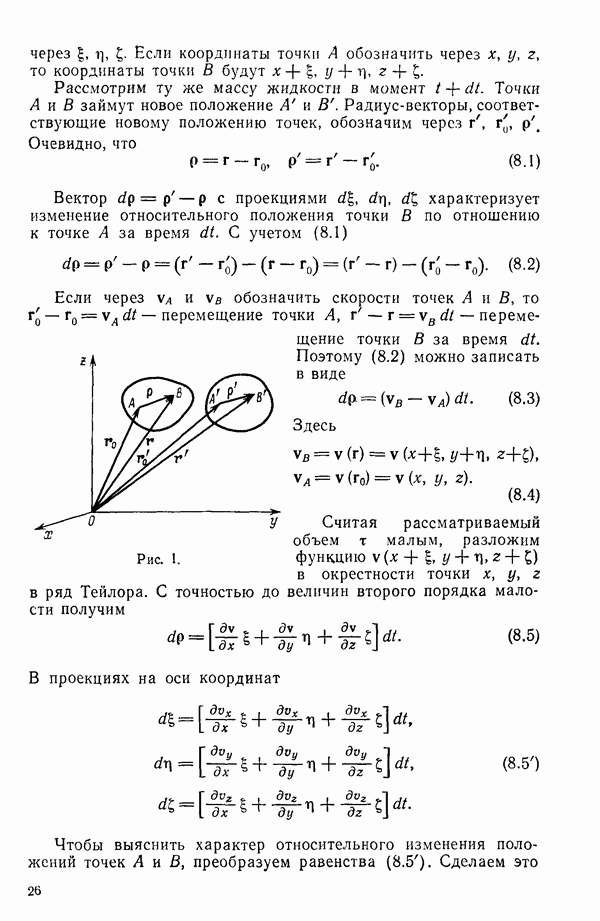
- § 8. СКОРОСТИ И ПЕРЕМЕЩЕНИЯ ТОЧЕК БЕСКОНЕЧНО МАЛОГО ОБЪЕМА СПЛОШНОЙ СРЕДЫ
- § 9. ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИЙ И ЕГО ИНВАРИАНТЫ
- § 10. СМЫСЛ КОМПОНЕНТ ТЕНЗОРА СКОРОСТЕЙ ДЕФОРМАЦИЙ
- § 11. СМЫСЛ КОМПОНЕНТ ВИХРЯ СКОРОСТИ
- § 12. ВИХРЕВЫЕ ЛИНИИ, ВИХРЕВЫЕ ТРУБКИ
- § 13. ЦИРКУЛЯЦИЯ СКОРОСТИ
- § 14. СКОРОСТЬ ОБЪЕМНОГО РАСШИРЕНИЯ ЖИДКОСТИ
- ГЛАВА II. ЗАКОН СОХРАНЕНИЯ МАСС
- § 1. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ МАСС
- § 2. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ МАСС В ПЕРЕМЕННЫХ ЭЙЛЕРА (УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ПЕРЕМЕННЫХ ЭЙЛЕРА)
- § 3. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ПЕРЕМЕННЫХ ЛАГРАНЖА
- § 4. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- ГЛАВА III. ЗАКОН КОЛИЧЕСТВА ДВИЖЕНИЯ ДЛЯ СПЛОШНОЙ СРЕДЫ
- § 1 СИЛЫ МАССОВЫЕ И ПОВЕРХНОСТНЫЕ
- § 2. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. ФОРМУЛА КОШИ
- § 4. ТЕНЗОР НАПРЯЖЕНИЙ
- § 5. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА КОЛИЧЕСТВА ДВИЖЕНИЯ
- ГЛАВА IV. ЗАКОН МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 1. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 2. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- ГЛАВА V. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 1. ВНУТРЕННЯЯ ЭНЕРГИЯ
- § 2. ПОЛНАЯ ЭНЕРГИЯ
- § 3. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- § 4. НЕКОТОРЫЕ ПРЕОБРАЗОВАНИЯ ИНТЕГРАЛЬНОЙ ЗАПИСИ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- § 5. ВЕКТОР ПОТОКА ТЕПЛА
- § 6. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- ГЛАВА VI. ПРОСТЕЙШИЕ МОДЕЛИ ЖИДКИХ СРЕД
- § 1. ИДЕАЛЬНАЯ ЖИДКОСТЬ И ТЕНЗОР НАПРЯЖЕНИИ ДЛЯ НЕЕ
- § 2. ВЯЗКАЯ (НЬЮТОНОВСКАЯ) ЖИДКОСТЬ И ТЕНЗОР НАПРЯЖЕНИЙ ДЛЯ НЕЕ
- § 3. НЕТЕПЛОПРОВОДНАЯ ЖИДКОСТЬ
- § 4. ЖИДКОСТЬ, ПОДЧИНЯЮЩАЯСЯ ЗАКОНУ ТЕПЛОПРОВОДНОСТИ ФУРЬЕ
- § 5. НЕСЖИМАЕМАЯ ЖИДКОСТЬ
- § 6. СЖИМАЕМАЯ ЖИДКОСТЬ
- ГЛАВА VII. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОЙ ЖИДКОСТИ И ПОСТАНОВКА ЗАДАЧ ДЛЯ НЕЕ
- § 1. СИСТЕМА УРАВНЕНИИ ГИДРОМЕХАНИКИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОИ ЖИДКОСТИ
- § 2. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ УСТАНОВИВШИХСЯ ТЕЧЕНИИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
- § 3. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ НЕУСТАНОВИВШИХСЯ ТЕЧЕНИИ ИДЕАЛЬНОИ НЕТЕПЛОПРОВОДНОИ ЖИДКОСТИ
- ГЛАВА VIII. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ВЯЗКОЙ ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ И ПОСТАНОВКА ЗАДАЧ ДЛЯ НЕЕ
- § 1. ОБЩАЯ СИСТЕМА УРАВНЕНИИ ГИДРОМЕХАНИКИ ВЯЗКОЙ ЖИДКОСТИ
- § 2. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ОДНОРОДНОЙ НЕСЖИМАЕМОЙ ВЯЗКОЙ ЖИДКОСТИ
- § 3. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ ТЕЧЕНИИ ВЯЗКОЙ ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
- ЧАСТЬ II. ОСНОВЫ ГИДРОСТАТИКИ
- § 1. УРАВНЕНИЯ РАВНОВЕСИЯ
- § 2. УСЛОВИЕ ДЛЯ СИЛ
- § 3. УСЛОВИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ДВУХ ЖИДКОСТЕЙ
- § 4. РАВНОВЕСИЕ ОДНОРОДНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 5. РАВНОВЕСИЕ БАРОТРОПНОИ ЖИДКОСТИ
- § 6. ОБЩИЙ СЛУЧАЙ РАВНОВЕСИЯ ЖИДКОСТИ В КОНСЕРВАТИВНОМ СИЛОВОМ ПОЛЕ
- § 7. ОБЩИЕ ФОРМУЛЫ ДЛЯ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИЛ ДАВЛЕНИИ
- § 8. ЗАКОН АРХИМЕДА
- ЧАСТЬ III. ГИДРОМЕХАНИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 1. АДИАБАТА
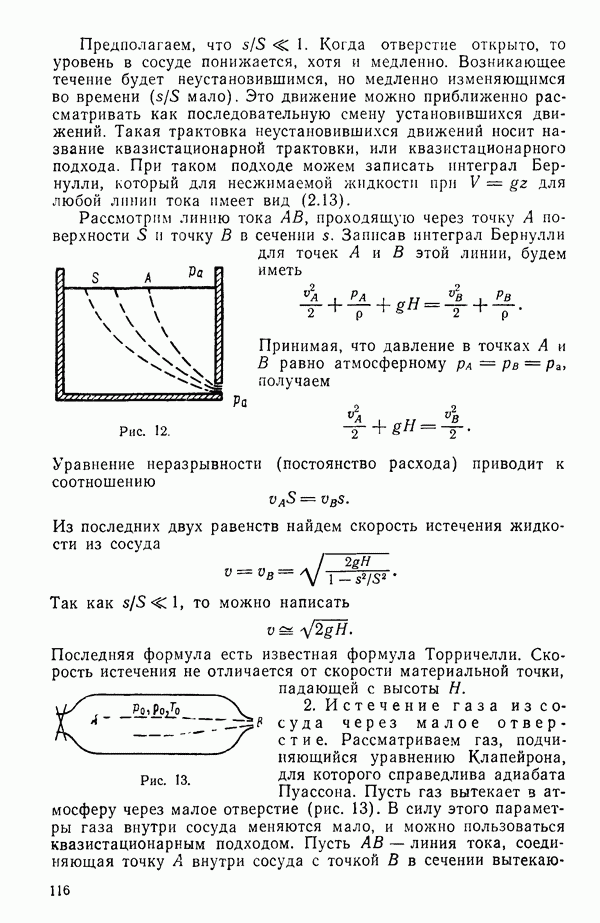
- § 2. ИНТЕГРАЛ БЕРНУЛЛИ
- § 3. ИНТЕГРАЛ БЕРНУЛЛИ В СЛУЧАЕ ДВИЖЕНИЯ ГАЗА С УСЛОЖНЕННОЙ ТЕРМОДИНАМИКОЙ
- § 4. ДВА ПРИМЕРА НА ПРИМЕНЕНИЕ ИНТЕГРАЛА БЕРНУЛЛИ
- § 5. УРАВНЕНИЯ ЭЙЛЕРА В ФОРМЕ ГРОМЕКИ — ЛЭМБА
- § 6. ПОТЕНЦИАЛЬНЫЕ, ИЛИ БЕЗВИХРЕВЫЕ, ДВИЖЕНИЯ
- § 7. ИНТЕГРАЛ ЛАГРАНЖА
- § 8. ИНТЕГРАЛ ЭЙЛЕРА-БЕРНУЛЛИ
- § 9. УРАВНЕНИЯ ДЛЯ ПОТЕНЦИАЛА СКОРОСТЕЙ
- ГЛАВА XI. ОБОБЩЕННЫЕ ОДНОМЕРНЫЕ ДВИЖЕНИЯ
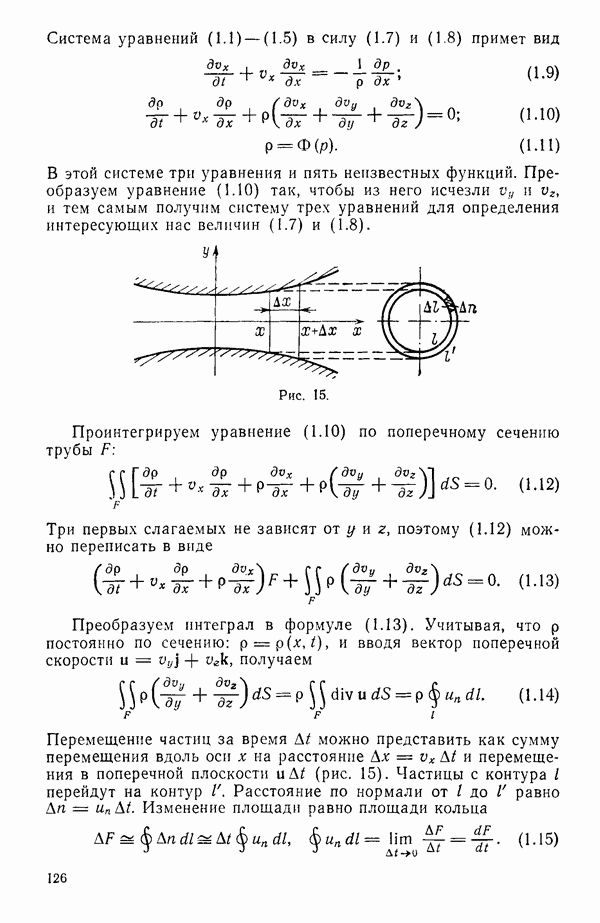
- § 2. ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
- § 3. ДВИЖЕНИЕ СЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ. СОПЛО ЛАВАЛЯ
- ГЛАВА XII. ПЛОСКИЕ БЕЗВИХРЕВЫЕ УСТАНОВИВШИЕСЯ ТЕЧЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 1. СИСТЕМА УРАВНЕНИЙ
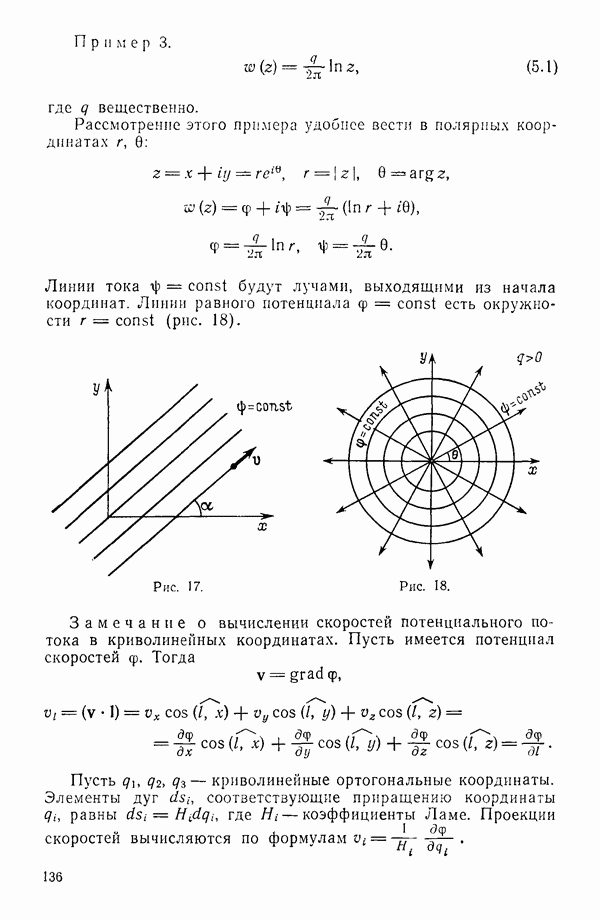
- § 2. ПОТЕНЦИАЛ СКОРОСТЕЙ
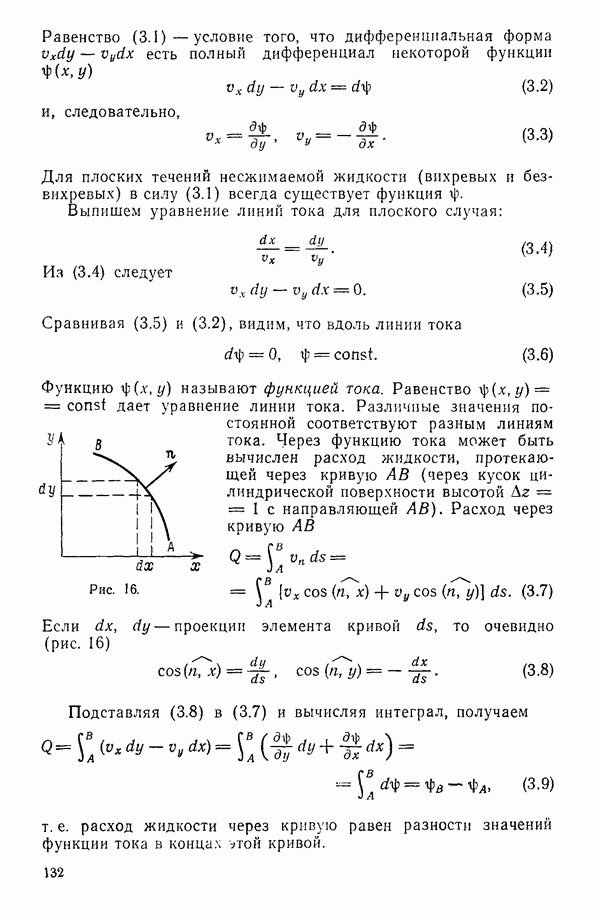
- § 3. ФУНКЦИЯ ТОКА
- § 4. КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ И КОМПЛЕКСНАЯ СКОРОСТЬ
- § 4. КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ И КОМПЛЕКСНАЯ СКОРОСТЬ
- § 6. ПОТЕНЦИАЛЬНОЕ ОБТЕКАНИЕ КРУГОВОГО ЦИЛИНДРА ПОТОКОМ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 7. МЕТОД КОНФОРМНЫХ ОТОБРАЖЕНИЙ
- § 8. ОБТЕКАНИЕ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА
- § 9. ПОСТУЛАТ ЧАПЛЫГИНА — ЖУКОВСКОГО
- § 10. ФОРМУЛЫ ЧАПЛЫГИНА — БЛАЗИУСА
- § 11. ИНТЕГРАЛ ОТ КОМПЛЕКСНОЙ СКОРОСТИ
- § 12. ТЕОРЕМА ЖУКОВСКОГО
- § 13. ФОРМУЛА ДЛЯ МОМЕНТА
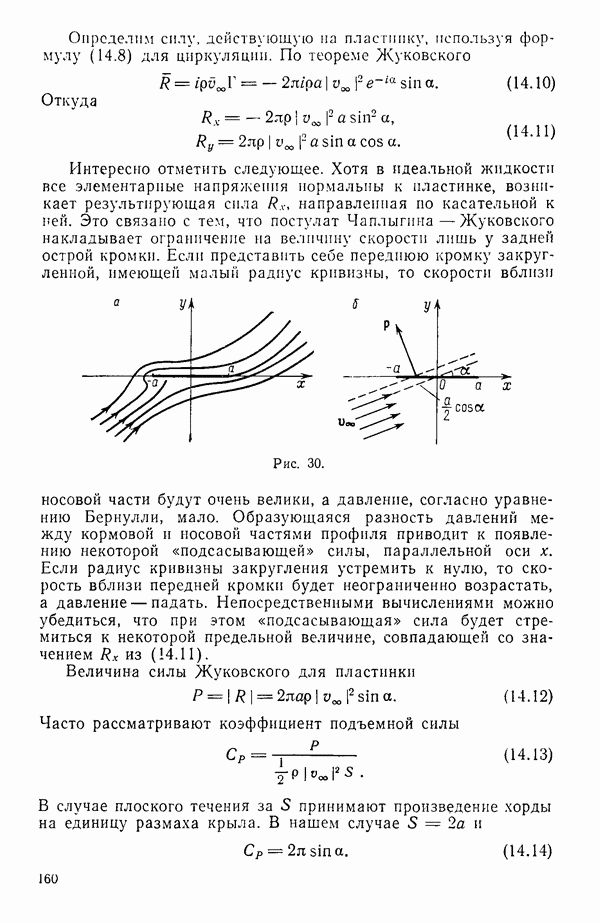
- § 14. ОБТЕКАНИЕ ПЛАСТИНКИ
- § 15. ОБТЕКАНИЕ ПРОФИЛЕЙ ЖУКОВСКОГО
- § 16. ОБТЕКАНИЕ ПРОИЗВОЛЬНОГО ПРОФИЛЯ. МЕТОД НУЖИНА
- § 17. НЕКОТОРЫЕ ОБЩИЕ ЗАМЕЧАНИЯ О ПЛОСКИХ ПОТЕНЦИАЛЬНЫХ ДВИЖЕНИЯХ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- ГЛАВА XIII. ТЕОРИЯ ТОНКОГО КРЫЛА
- § 1. ПОНЯТИЕ ТОНКОГО КРЫЛА И УСЛОВИЯ ОБТЕКАНИЯ ДЛЯ ТОНКОГО ПРОФИЛЯ
- § 2. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ТОНКОГО ПРОФИЛЯ МЕТОДОМ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ
- § 3. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОФИЛЯ С НУЛЕВОЙ ТОЛЩИНОЙ
- § 5. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОИЗВОЛЬНОГО ТОНКОГО ПРОФИЛЯ
- ГЛАВА XIV. ОСЕСИММЕТРИЧНЫЕ ПОТЕНЦИАЛЬНЫЕ ТЕЧЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 1. ИСТОЧНИКИ В ПРОСТРАНСТВЕ
- § 2. ДИПОЛЬ В ПРОСТРАНСТВЕ
- § 3. ОБТЕКАНИЕ СФЕРЫ
- § 4. ФУНКЦИЯ ТОКА ДЛЯ ОСЕСИММЕТРИЧНЫХ ТЕЧЕНИЙ
- § 5. ПРОДОЛЬНОЕ ОБТЕКАНИЕ ТЕЛА ВРАЩЕНИЯ. МЕТОД ИСТОЧНИКОВ И СТОКОВ
- § 6. ПОПЕРЕЧНОЕ ОБТЕКАНИЕ ТЕЛА ВРАЩЕНИЯ
- § 7. ОБЩИЙ СЛУЧАЙ ОБТЕКАНИЯ ТЕЛА ВРАЩЕНИЯ
- ГЛАВА XV. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- § 1. ОБЩИЙ ВИД ПОТЕНЦИАЛА СКОРОСТЕЙ
- § 2. ПОВЕДЕНИЕ ПОТЕНЦИАЛА СКОРОСТЕЙ В ОКРЕСТНОСТИ БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКИ
- § 3. РАСЧЕТ ГИДРОДИНАМИЧЕСКИХ РЕАКЦИИ ПРИ ДВИЖЕНИИ ТЕЛА
- § 4. УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- ГЛАВА XVI. ВИХРЕВЫЕ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 1. ТЕОРЕМА ТОМСОНА
- § 2. ТЕОРЕМА ЛАГРАНЖА
- § 3. ТЕОРЕМЫ ГЕЛЬМГОЛЬЦА
- § 4. О ВОЗНИКНОВЕНИИ ВИХРЕЙ
- § 5. УРАВНЕНИЯ ДЛЯ ВИХРЯ
- § 6. ОПРЕДЕЛЕНИЕ ВЕКТОРА СКОРОСТИ ПО ВИХРЮ И ДИВЕРГЕНЦИИ
- § 7. СКОРОСТИ, ИНДУЦИРУЕМЫЕ ВИХРЕВОЙ НИТЬЮ
- § 8. ПРЯМОЛИНЕЙНАЯ ВИХРЕВАЯ НИТЬ
- § 9. ВИХРЕВОЙ СЛОЙ
- ГЛАВА XVII. ТЕОРИЯ КРЫЛА КОНЕЧНОГО РАЗМАХА
- § 2. ВИХРЕВАЯ СИСТЕМА КРЫЛА И ОСНОВНЫЕ ФОРМУЛЫ
- § 3. КРЫЛО С ЭЛЛИПТИЧЕСКИМ РАСПРЕДЕЛЕНИЕМ ЦИРКУЛЯЦИИ
- § 4. ПАРАБОЛА ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ И ПЕРЕСЧЕТ КРЫЛА С ОДНОГО УДЛИНЕНИЯ НА ДРУГОЕ
- § 5. ОПРЕДЕЛЕНИЕ ЦИРКУЛЯЦИИ Г(z) В ТЕОРИИ КРЫЛА КОНЕЧНОГО РАЗМАХА
- ЧАСТЬ IV. ГИДРОМЕХАНИКА ВЯЗКОЙ ЖИДКОСТИ
- ГЛАВА XVIII. ОБЩИЕ СВОЙСТВА ДВИЖЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 2. НЕОБРАТИМОСТЬ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
- § 3. ЗАВИХРЕННОСТЬ ТЕЧЕНИЙ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 4. ДИССИПАЦИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ В ВЯЗКОЙ ЖИДКОСТИ
- ГЛАВА XIX. ТОЧНЫЕ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 1. ПОСТАНОВКА ЗАДАЧИ ОБ ОТЫСКАНИИ ОДНОМЕРНЫХ ТЕЧЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 2. ПРИМЕРЫ ОДНОМЕРНЫХ НЕСТАЦИОНАРНЫХ ТЕЧЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 3. УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ МЕЖДУ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
- § 4. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ
- § 7. ПРИМЕР ПРОСТЕЙШЕГО УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ С ПЕРЕМЕННОЙ ВЯЗКОСТЬЮ
- ГЛАВА XX. ПОДОБИЕ ТЕЧЕНИИ ВЯЗКОЙ ЖИДКОСТИ
- § 1. СХОДСТВЕННЫЕ ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ТОЧКИ
- § 2. ЗАПИСЬ УРАВНЕНИИ ГИДРОМЕХАНИКИ ВЯЗКОЙ ЖИДКОСТИ В БЕЗРАЗМЕРНОМ ВИДЕ
- § 3. ПОДОБИЕ УСТАНОВИВШИХСЯ ТЕЧЕНИЙ
- § 5 ТЕЧЕНИЕ В ТРУБЕ ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ
- § 6. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ МЕЖДУ ДВУМЯ ВРАЩАЮЩИМИСЯ СООСНЫМИ ЦИЛИНДРАМИ
- ГЛАВА XXI. ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ ПРИ БОЛЬШИХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 1. ОСНОВНЫЕ ПРЕДПОЛОЖЕНИЯ И СИСТЕМА УРАВНЕНИИ ПОГРАНИЧНОГО СЛОЯ
- § 2. ПОГРАНИЧНЫЙ СЛОЙ ОКОЛО ПОЛУБЕСКОНЕЧНОЙ ПЛАСТИНКИ
- ГЛАВА XXII. ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ ПРИ МАЛЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 1. УРАВНЕНИЯ СТОКСА
- § 2. ОБТЕКАНИЕ СФЕРЫ ПРИ МАЛЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 3. ПАРАДОКС СТОКСА
- § 4. УРАВНЕНИЯ ОЗИНА
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА