| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. ДВА ПРИМЕРА НА ПРИМЕНЕНИЕ ИНТЕГРАЛА БЕРНУЛЛИ
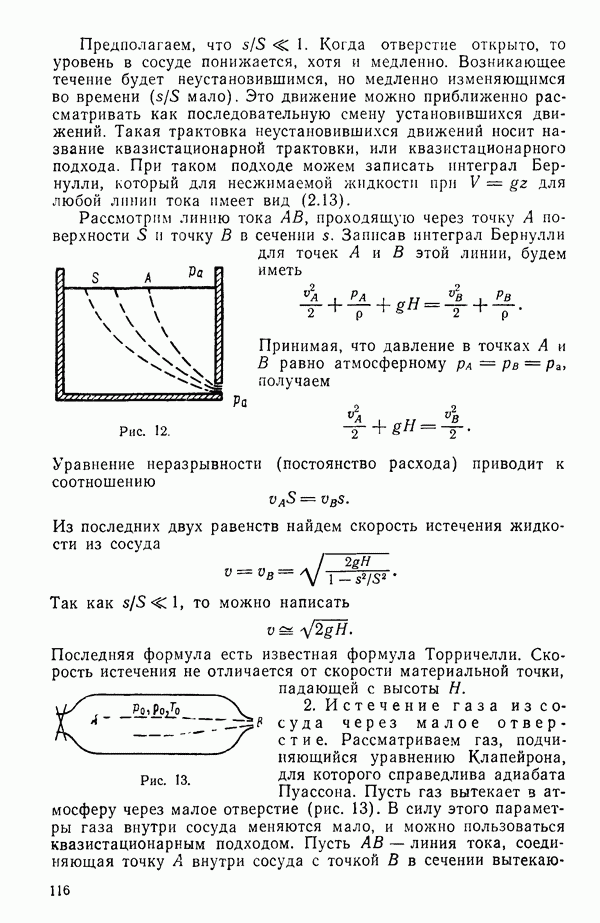
1. Истечение несжимаемой жидкости через малое отверстие. Рассмотрим истечение жидкости из сосуда через отверстие. Будем считать, что отверстие расположено вблизи дна (рис. 12). Жидкость предположим несжимаемой и находящейся в поле сил тяжести. Пусть S — площадь открытой поверхности жидкости в сосуде, s — площадь отверстия, Н — уровень жидкости в сосуде.
Предполагаем, что  . Когда отверстие открыто, то уровень в сосуде понижается, хотя и медленно. Возникающее течение будет неустановившимся, но медленно изменяющимся во времени (
. Когда отверстие открыто, то уровень в сосуде понижается, хотя и медленно. Возникающее течение будет неустановившимся, но медленно изменяющимся во времени ( мало). Это движение можно приближенно рассматривать как последовательную смену установившихся движений. Такая трактовка неустановившихся движений носит название квазистационарной трактовки, или квазистационарного подхода. При таком подходе можем записать интеграл Бернулли, который для несжимаемой жидкости при
мало). Это движение можно приближенно рассматривать как последовательную смену установившихся движений. Такая трактовка неустановившихся движений носит название квазистационарной трактовки, или квазистационарного подхода. При таком подходе можем записать интеграл Бернулли, который для несжимаемой жидкости при  для любой линии тока имеет вид (2.13).
для любой линии тока имеет вид (2.13).
Рассмотрим линию тока АВ, проходящую через точку А поверхности S и точку В в сечении s. Записав интеграл Бернулли для точек А а В этой линии, будем иметь

Принимая, что давление в точках А и В равно атмосферному  , получаем
, получаем


Рис. 12.
Уравнение неразрывности (постоянство расхода) приводит к соотношению

Из последних двух равенств найдем скорость истечения жидкости из сосуда

Так как  , то можно написать
, то можно написать

Последняя формула есть известная формула Торричелли. Скорость истечения не отличается от скорости материальной точки, падающей с высоты Н.

Рис. 13.
2. Истечение газа из сосуда через малое отверстие. Рассматриваем газ, подчиняющийся уравнению Клапейрона, для которого справедлива адиабата Пуассона. Пусть газ вытекает в атмосферу через малое отверстие (рис. 13). В силу этого параметры газа внутри сосуда меняются мало, и можно пользоваться квазистационарным подходом. Пусть АВ — линия тока, соединяющая точку А внутри сосуда с точкой В в сечении вытекающей струи.
Для точек А и В можно записать адиабату Пуассона (1.11) и интеграл Бернулли (2.19):

При большом сосуде и малом отверстии  и можно принять
и можно принять  . Обозначая
. Обозначая  получаем из интеграла Бернулли (4.1)
получаем из интеграла Бернулли (4.1)

Из условия адиабатичности следует

Подставляя (4.3) в (4.2), найдем скорость истечения

Формулы (4.3) и (4.4) дают решение задачи.
Рассмотрим полученное решение. Чтобы оно имело смысл, нужно, чтобы  . Введем величину
. Введем величину  — расход на единицу площади. Используя (4.3) и (4.4), получаем
— расход на единицу площади. Используя (4.3) и (4.4), получаем

Формула (4.5) позволяет исследовать зависимость q от  или, если
или, если  постоянно, от р — давления среды, в которую вытекает газ. При
постоянно, от р — давления среды, в которую вытекает газ. При  имеем равновесие, газ течь не будет. При уменьшении р, т. е. расход увеличивается и при некотором
имеем равновесие, газ течь не будет. При уменьшении р, т. е. расход увеличивается и при некотором  достигает максимума. При дальнейшем уменьшении
достигает максимума. При дальнейшем уменьшении  величина q уменьшается, обращаясь в нуль при
величина q уменьшается, обращаясь в нуль при  (рис. 14). Эксперименты подтверждают справедливость зависимости
(рис. 14). Эксперименты подтверждают справедливость зависимости  лишь для
лишь для  . При
. При  в действительности расход остается постоянным, равным максимальному.
в действительности расход остается постоянным, равным максимальному.

Рис. 14.
Максимальное значение расхода  достигается, когда скорость истечения оказывается равной скорости звука. Дальнейшее понижение давления р уже не оказывает влияния на истечение из отверстия — возмущения из внешней среды не проникают внутрь (скорость распространения возмущений — скорость звука — будет меньше скорости газа в струе).
достигается, когда скорость истечения оказывается равной скорости звука. Дальнейшее понижение давления р уже не оказывает влияния на истечение из отверстия — возмущения из внешней среды не проникают внутрь (скорость распространения возмущений — скорость звука — будет меньше скорости газа в струе).
При  когда струя становится сверхзвуковой, предположение об одномерности течения оказывается неверным, надо учитывать пространственный характер течения.
когда струя становится сверхзвуковой, предположение об одномерности течения оказывается неверным, надо учитывать пространственный характер течения.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ КИНЕМАТИКИ ЖИДКОСТИ
- § 1. ПЕРЕМЕННЫЕ ЛАГРАНЖА И ЭЙЛЕРА
- § 2. ПЕРЕХОД ОТ ПЕРЕМЕННЫХ ЛАГРАНЖА К ПЕРЕМЕННЫМ ЭЙЛЕРА И ОБРАТНО
- § 3. ИНДИВИДУАЛЬНАЯ И МЕСТНАЯ ПРОИЗВОДНЫЕ
- § 4. УСТАНОВИВШЕЕСЯ И НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЯ
- § 5. СКОРОСТИ И УСКОРЕНИЯ
- § 6. ТРАЕКТОРИИ, ЛИНИИ ТОКА, КРИТИЧЕСКИЕ ТОЧКИ
- § 7. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ТЕНЗОРАХ
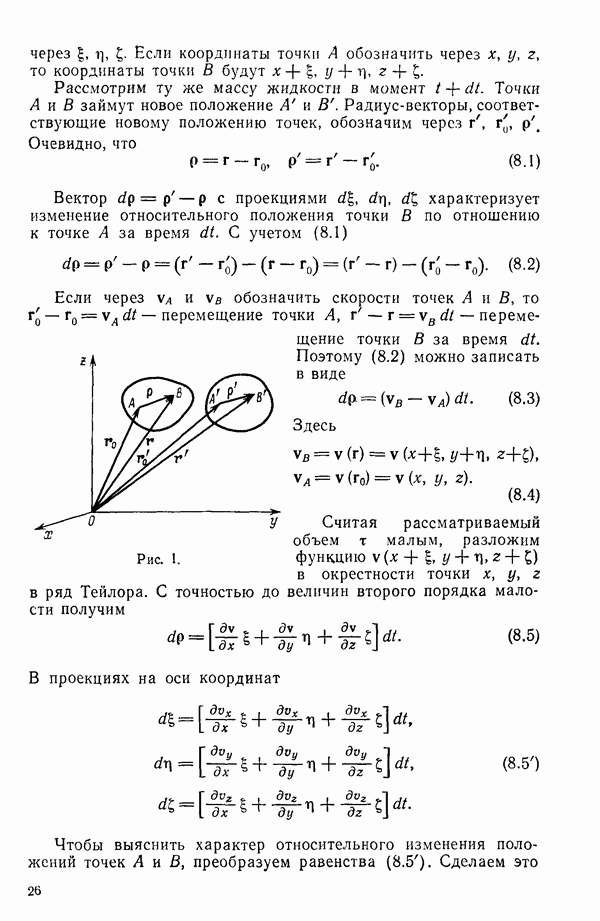
- § 8. СКОРОСТИ И ПЕРЕМЕЩЕНИЯ ТОЧЕК БЕСКОНЕЧНО МАЛОГО ОБЪЕМА СПЛОШНОЙ СРЕДЫ
- § 9. ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИЙ И ЕГО ИНВАРИАНТЫ
- § 10. СМЫСЛ КОМПОНЕНТ ТЕНЗОРА СКОРОСТЕЙ ДЕФОРМАЦИЙ
- § 11. СМЫСЛ КОМПОНЕНТ ВИХРЯ СКОРОСТИ
- § 12. ВИХРЕВЫЕ ЛИНИИ, ВИХРЕВЫЕ ТРУБКИ
- § 13. ЦИРКУЛЯЦИЯ СКОРОСТИ
- § 14. СКОРОСТЬ ОБЪЕМНОГО РАСШИРЕНИЯ ЖИДКОСТИ
- ГЛАВА II. ЗАКОН СОХРАНЕНИЯ МАСС
- § 1. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ МАСС
- § 2. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ МАСС В ПЕРЕМЕННЫХ ЭЙЛЕРА (УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ПЕРЕМЕННЫХ ЭЙЛЕРА)
- § 3. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ПЕРЕМЕННЫХ ЛАГРАНЖА
- § 4. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- ГЛАВА III. ЗАКОН КОЛИЧЕСТВА ДВИЖЕНИЯ ДЛЯ СПЛОШНОЙ СРЕДЫ
- § 1 СИЛЫ МАССОВЫЕ И ПОВЕРХНОСТНЫЕ
- § 2. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. ФОРМУЛА КОШИ
- § 4. ТЕНЗОР НАПРЯЖЕНИЙ
- § 5. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА КОЛИЧЕСТВА ДВИЖЕНИЯ
- ГЛАВА IV. ЗАКОН МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 1. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 2. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- ГЛАВА V. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 1. ВНУТРЕННЯЯ ЭНЕРГИЯ
- § 2. ПОЛНАЯ ЭНЕРГИЯ
- § 3. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- § 4. НЕКОТОРЫЕ ПРЕОБРАЗОВАНИЯ ИНТЕГРАЛЬНОЙ ЗАПИСИ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- § 5. ВЕКТОР ПОТОКА ТЕПЛА
- § 6. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- ГЛАВА VI. ПРОСТЕЙШИЕ МОДЕЛИ ЖИДКИХ СРЕД
- § 1. ИДЕАЛЬНАЯ ЖИДКОСТЬ И ТЕНЗОР НАПРЯЖЕНИИ ДЛЯ НЕЕ
- § 2. ВЯЗКАЯ (НЬЮТОНОВСКАЯ) ЖИДКОСТЬ И ТЕНЗОР НАПРЯЖЕНИЙ ДЛЯ НЕЕ
- § 3. НЕТЕПЛОПРОВОДНАЯ ЖИДКОСТЬ
- § 4. ЖИДКОСТЬ, ПОДЧИНЯЮЩАЯСЯ ЗАКОНУ ТЕПЛОПРОВОДНОСТИ ФУРЬЕ
- § 5. НЕСЖИМАЕМАЯ ЖИДКОСТЬ
- § 6. СЖИМАЕМАЯ ЖИДКОСТЬ
- ГЛАВА VII. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОЙ ЖИДКОСТИ И ПОСТАНОВКА ЗАДАЧ ДЛЯ НЕЕ
- § 1. СИСТЕМА УРАВНЕНИИ ГИДРОМЕХАНИКИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОИ ЖИДКОСТИ
- § 2. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ УСТАНОВИВШИХСЯ ТЕЧЕНИИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
- § 3. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ НЕУСТАНОВИВШИХСЯ ТЕЧЕНИИ ИДЕАЛЬНОИ НЕТЕПЛОПРОВОДНОИ ЖИДКОСТИ
- ГЛАВА VIII. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ВЯЗКОЙ ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ И ПОСТАНОВКА ЗАДАЧ ДЛЯ НЕЕ
- § 1. ОБЩАЯ СИСТЕМА УРАВНЕНИИ ГИДРОМЕХАНИКИ ВЯЗКОЙ ЖИДКОСТИ
- § 2. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ОДНОРОДНОЙ НЕСЖИМАЕМОЙ ВЯЗКОЙ ЖИДКОСТИ
- § 3. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ ТЕЧЕНИИ ВЯЗКОЙ ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
- ЧАСТЬ II. ОСНОВЫ ГИДРОСТАТИКИ
- § 1. УРАВНЕНИЯ РАВНОВЕСИЯ
- § 2. УСЛОВИЕ ДЛЯ СИЛ
- § 3. УСЛОВИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ДВУХ ЖИДКОСТЕЙ
- § 4. РАВНОВЕСИЕ ОДНОРОДНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 5. РАВНОВЕСИЕ БАРОТРОПНОИ ЖИДКОСТИ
- § 6. ОБЩИЙ СЛУЧАЙ РАВНОВЕСИЯ ЖИДКОСТИ В КОНСЕРВАТИВНОМ СИЛОВОМ ПОЛЕ
- § 7. ОБЩИЕ ФОРМУЛЫ ДЛЯ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИЛ ДАВЛЕНИИ
- § 8. ЗАКОН АРХИМЕДА
- ЧАСТЬ III. ГИДРОМЕХАНИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 1. АДИАБАТА
- § 2. ИНТЕГРАЛ БЕРНУЛЛИ
- § 3. ИНТЕГРАЛ БЕРНУЛЛИ В СЛУЧАЕ ДВИЖЕНИЯ ГАЗА С УСЛОЖНЕННОЙ ТЕРМОДИНАМИКОЙ
- § 4. ДВА ПРИМЕРА НА ПРИМЕНЕНИЕ ИНТЕГРАЛА БЕРНУЛЛИ
- § 5. УРАВНЕНИЯ ЭЙЛЕРА В ФОРМЕ ГРОМЕКИ — ЛЭМБА
- § 6. ПОТЕНЦИАЛЬНЫЕ, ИЛИ БЕЗВИХРЕВЫЕ, ДВИЖЕНИЯ
- § 7. ИНТЕГРАЛ ЛАГРАНЖА
- § 8. ИНТЕГРАЛ ЭЙЛЕРА-БЕРНУЛЛИ
- § 9. УРАВНЕНИЯ ДЛЯ ПОТЕНЦИАЛА СКОРОСТЕЙ
- ГЛАВА XI. ОБОБЩЕННЫЕ ОДНОМЕРНЫЕ ДВИЖЕНИЯ
- § 2. ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
- § 3. ДВИЖЕНИЕ СЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ. СОПЛО ЛАВАЛЯ
- ГЛАВА XII. ПЛОСКИЕ БЕЗВИХРЕВЫЕ УСТАНОВИВШИЕСЯ ТЕЧЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 1. СИСТЕМА УРАВНЕНИЙ
- § 2. ПОТЕНЦИАЛ СКОРОСТЕЙ
- § 3. ФУНКЦИЯ ТОКА
- § 4. КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ И КОМПЛЕКСНАЯ СКОРОСТЬ
- § 4. КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ И КОМПЛЕКСНАЯ СКОРОСТЬ
- § 6. ПОТЕНЦИАЛЬНОЕ ОБТЕКАНИЕ КРУГОВОГО ЦИЛИНДРА ПОТОКОМ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 7. МЕТОД КОНФОРМНЫХ ОТОБРАЖЕНИЙ
- § 8. ОБТЕКАНИЕ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА
- § 9. ПОСТУЛАТ ЧАПЛЫГИНА — ЖУКОВСКОГО
- § 10. ФОРМУЛЫ ЧАПЛЫГИНА — БЛАЗИУСА
- § 11. ИНТЕГРАЛ ОТ КОМПЛЕКСНОЙ СКОРОСТИ
- § 12. ТЕОРЕМА ЖУКОВСКОГО
- § 13. ФОРМУЛА ДЛЯ МОМЕНТА
- § 14. ОБТЕКАНИЕ ПЛАСТИНКИ
- § 15. ОБТЕКАНИЕ ПРОФИЛЕЙ ЖУКОВСКОГО
- § 16. ОБТЕКАНИЕ ПРОИЗВОЛЬНОГО ПРОФИЛЯ. МЕТОД НУЖИНА
- § 17. НЕКОТОРЫЕ ОБЩИЕ ЗАМЕЧАНИЯ О ПЛОСКИХ ПОТЕНЦИАЛЬНЫХ ДВИЖЕНИЯХ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- ГЛАВА XIII. ТЕОРИЯ ТОНКОГО КРЫЛА
- § 1. ПОНЯТИЕ ТОНКОГО КРЫЛА И УСЛОВИЯ ОБТЕКАНИЯ ДЛЯ ТОНКОГО ПРОФИЛЯ
- § 2. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ТОНКОГО ПРОФИЛЯ МЕТОДОМ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ
- § 3. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОФИЛЯ С НУЛЕВОЙ ТОЛЩИНОЙ
- § 5. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОИЗВОЛЬНОГО ТОНКОГО ПРОФИЛЯ
- ГЛАВА XIV. ОСЕСИММЕТРИЧНЫЕ ПОТЕНЦИАЛЬНЫЕ ТЕЧЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 1. ИСТОЧНИКИ В ПРОСТРАНСТВЕ
- § 2. ДИПОЛЬ В ПРОСТРАНСТВЕ
- § 3. ОБТЕКАНИЕ СФЕРЫ
- § 4. ФУНКЦИЯ ТОКА ДЛЯ ОСЕСИММЕТРИЧНЫХ ТЕЧЕНИЙ
- § 5. ПРОДОЛЬНОЕ ОБТЕКАНИЕ ТЕЛА ВРАЩЕНИЯ. МЕТОД ИСТОЧНИКОВ И СТОКОВ
- § 6. ПОПЕРЕЧНОЕ ОБТЕКАНИЕ ТЕЛА ВРАЩЕНИЯ
- § 7. ОБЩИЙ СЛУЧАЙ ОБТЕКАНИЯ ТЕЛА ВРАЩЕНИЯ
- ГЛАВА XV. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- § 1. ОБЩИЙ ВИД ПОТЕНЦИАЛА СКОРОСТЕЙ
- § 2. ПОВЕДЕНИЕ ПОТЕНЦИАЛА СКОРОСТЕЙ В ОКРЕСТНОСТИ БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКИ
- § 3. РАСЧЕТ ГИДРОДИНАМИЧЕСКИХ РЕАКЦИИ ПРИ ДВИЖЕНИИ ТЕЛА
- § 4. УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- ГЛАВА XVI. ВИХРЕВЫЕ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 1. ТЕОРЕМА ТОМСОНА
- § 2. ТЕОРЕМА ЛАГРАНЖА
- § 3. ТЕОРЕМЫ ГЕЛЬМГОЛЬЦА
- § 4. О ВОЗНИКНОВЕНИИ ВИХРЕЙ
- § 5. УРАВНЕНИЯ ДЛЯ ВИХРЯ
- § 6. ОПРЕДЕЛЕНИЕ ВЕКТОРА СКОРОСТИ ПО ВИХРЮ И ДИВЕРГЕНЦИИ
- § 7. СКОРОСТИ, ИНДУЦИРУЕМЫЕ ВИХРЕВОЙ НИТЬЮ
- § 8. ПРЯМОЛИНЕЙНАЯ ВИХРЕВАЯ НИТЬ
- § 9. ВИХРЕВОЙ СЛОЙ
- ГЛАВА XVII. ТЕОРИЯ КРЫЛА КОНЕЧНОГО РАЗМАХА
- § 2. ВИХРЕВАЯ СИСТЕМА КРЫЛА И ОСНОВНЫЕ ФОРМУЛЫ
- § 3. КРЫЛО С ЭЛЛИПТИЧЕСКИМ РАСПРЕДЕЛЕНИЕМ ЦИРКУЛЯЦИИ
- § 4. ПАРАБОЛА ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ И ПЕРЕСЧЕТ КРЫЛА С ОДНОГО УДЛИНЕНИЯ НА ДРУГОЕ
- § 5. ОПРЕДЕЛЕНИЕ ЦИРКУЛЯЦИИ Г(z) В ТЕОРИИ КРЫЛА КОНЕЧНОГО РАЗМАХА
- ЧАСТЬ IV. ГИДРОМЕХАНИКА ВЯЗКОЙ ЖИДКОСТИ
- ГЛАВА XVIII. ОБЩИЕ СВОЙСТВА ДВИЖЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 2. НЕОБРАТИМОСТЬ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
- § 3. ЗАВИХРЕННОСТЬ ТЕЧЕНИЙ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 4. ДИССИПАЦИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ В ВЯЗКОЙ ЖИДКОСТИ
- ГЛАВА XIX. ТОЧНЫЕ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 1. ПОСТАНОВКА ЗАДАЧИ ОБ ОТЫСКАНИИ ОДНОМЕРНЫХ ТЕЧЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 2. ПРИМЕРЫ ОДНОМЕРНЫХ НЕСТАЦИОНАРНЫХ ТЕЧЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 3. УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ МЕЖДУ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
- § 4. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ
- § 7. ПРИМЕР ПРОСТЕЙШЕГО УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ С ПЕРЕМЕННОЙ ВЯЗКОСТЬЮ
- ГЛАВА XX. ПОДОБИЕ ТЕЧЕНИИ ВЯЗКОЙ ЖИДКОСТИ
- § 1. СХОДСТВЕННЫЕ ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ТОЧКИ
- § 2. ЗАПИСЬ УРАВНЕНИИ ГИДРОМЕХАНИКИ ВЯЗКОЙ ЖИДКОСТИ В БЕЗРАЗМЕРНОМ ВИДЕ
- § 3. ПОДОБИЕ УСТАНОВИВШИХСЯ ТЕЧЕНИЙ
- § 5 ТЕЧЕНИЕ В ТРУБЕ ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ
- § 6. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ МЕЖДУ ДВУМЯ ВРАЩАЮЩИМИСЯ СООСНЫМИ ЦИЛИНДРАМИ
- ГЛАВА XXI. ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ ПРИ БОЛЬШИХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 1. ОСНОВНЫЕ ПРЕДПОЛОЖЕНИЯ И СИСТЕМА УРАВНЕНИИ ПОГРАНИЧНОГО СЛОЯ
- § 2. ПОГРАНИЧНЫЙ СЛОЙ ОКОЛО ПОЛУБЕСКОНЕЧНОЙ ПЛАСТИНКИ
- ГЛАВА XXII. ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ ПРИ МАЛЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 1. УРАВНЕНИЯ СТОКСА
- § 2. ОБТЕКАНИЕ СФЕРЫ ПРИ МАЛЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 3. ПАРАДОКС СТОКСА
- § 4. УРАВНЕНИЯ ОЗИНА
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА