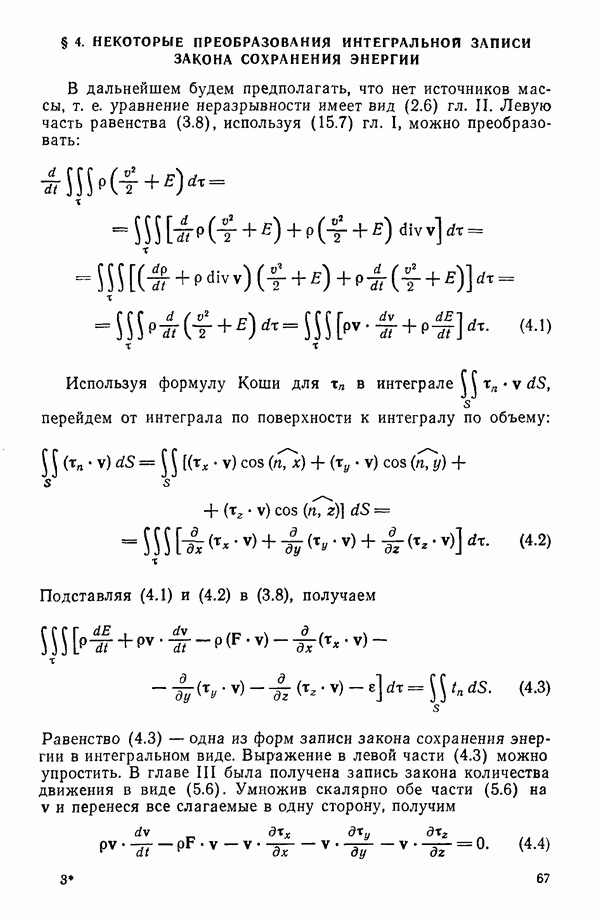| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОФИЛЯ С НУЛЕВОЙ ТОЛЩИНОЙ
В этом и следующих параграфах излагается решение задачи обтекания тонкого профиля по методу Л. И. Седова.
Заменим профиль его средней линией и рассмотрим задачу обтекания дуги  (рис. 35). В этом случае
(рис. 35). В этом случае  (см. (1.3), (1.5)).
(см. (1.3), (1.5)).
Будем искать комплексную скорость возмущении  удовлетворяющую на бесконечности условию
удовлетворяющую на бесконечности условию

и на контуре условиям (1.15), которые теперь запишем в виде

Вместо  рассмотрим вспомогательную функцию
рассмотрим вспомогательную функцию

Для однозначности выберем ту ветвь корня, которая обеспечивает его положительное значение при  Аналитическая функция f(z) определена во внешности профиля, однозначна и в силу (3.1) стремится к нулю, когда
Аналитическая функция f(z) определена во внешности профиля, однозначна и в силу (3.1) стремится к нулю, когда  стремится к бесконечности. Если найдем
стремится к бесконечности. Если найдем  , то станет известной и искомая
, то станет известной и искомая  скорость возмущении
скорость возмущении  .
.
Будем искать f(z) во внешности разреза (-а, а). Пусть  — контур, охватывающий отрезок (-а, а), и
— контур, охватывающий отрезок (-а, а), и  — точка вне этого контура. Введем функцию комплексного переменного
— точка вне этого контура. Введем функцию комплексного переменного

считая  параметром. Функция
параметром. Функция  имеет полюс первого порядка в точке
имеет полюс первого порядка в точке  . Окружим эту точку замкнутым контуром
. Окружим эту точку замкнутым контуром  и проведем кон
и проведем кон  так, чтобы он содержал внутри себя контуры
так, чтобы он содержал внутри себя контуры  . Обозначим через
. Обозначим через  разрезы, соединяющие контур
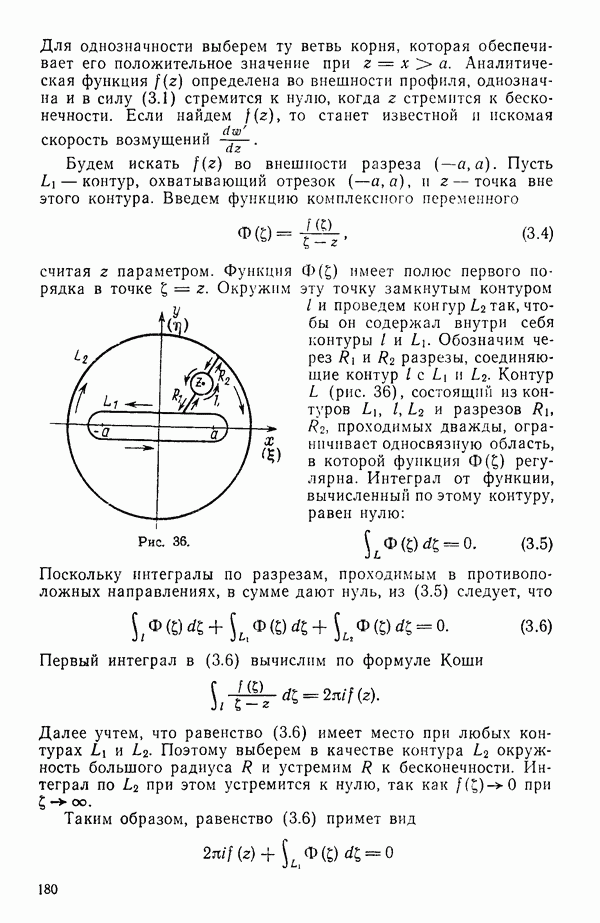
разрезы, соединяющие контур  . Контур L (рис. 36), состоящий из контуров
. Контур L (рис. 36), состоящий из контуров  и разрезов
и разрезов  проходимых дважды, ограничивает односвязную область, в которой функция
проходимых дважды, ограничивает односвязную область, в которой функция  регулярна. Интеграл от функции, вычисленный по этому контуру, равен нулю:
регулярна. Интеграл от функции, вычисленный по этому контуру, равен нулю:


Рис. 36.
Поскольку интегралы по разрезам, проходимым в противоположных направлениях, в сумме дают нуль, из (3.5) следует, что

Первый интеграл в (3.6) вычислим по формуле Коши

Далее учтем, что равенство (3.6) имеет место при любых контурах  Поэтому выберем в качестве контура
Поэтому выберем в качестве контура  окружность большого радиуса R и устремим R к бесконечности. Интеграл по
окружность большого радиуса R и устремим R к бесконечности. Интеграл по  при этом устремится к нулю, так как
при этом устремится к нулю, так как  при
при  .
.
Таким образом, равенство (3.6) примет вид

или

Специализируем теперь вид контура  . Выберем
. Выберем  в виде, указанном на рис. 37, и будем стягивать
в виде, указанном на рис. 37, и будем стягивать  к отрезку (-а, а), устремляя
к отрезку (-а, а), устремляя  к нулю. Интегралы по окружностям
к нулю. Интегралы по окружностям  и при этом будут стремиться к нулю. В результате получим
и при этом будут стремиться к нулю. В результате получим



Рис. 37.
Введем компоненты скорости  в подынтегральные выражения в (3.8). Из определения (3.3) для
в подынтегральные выражения в (3.8). Из определения (3.3) для  следует
следует

Так как на верхнем берегу разреза

а на нижнем

равенство (3.8) можно переписать в виде

Объединим в этом выражении члены с  и члены с
и члены с  :
:

Учтем теперь граничные условия (3.2) для проекции на ось у скорости возмущений

и примем, что

(отсутствует страница)
(отсутствует страница)
Подставляя (4.7) в (4.6), получаем

Так как 

Из (4.8) видно, что постулат Чаплыгина — Жуковского выполняется, если задняя кромка профиля z — a — точка возврата  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ КИНЕМАТИКИ ЖИДКОСТИ
- § 1. ПЕРЕМЕННЫЕ ЛАГРАНЖА И ЭЙЛЕРА
- § 2. ПЕРЕХОД ОТ ПЕРЕМЕННЫХ ЛАГРАНЖА К ПЕРЕМЕННЫМ ЭЙЛЕРА И ОБРАТНО
- § 3. ИНДИВИДУАЛЬНАЯ И МЕСТНАЯ ПРОИЗВОДНЫЕ
- § 4. УСТАНОВИВШЕЕСЯ И НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЯ
- § 5. СКОРОСТИ И УСКОРЕНИЯ
- § 6. ТРАЕКТОРИИ, ЛИНИИ ТОКА, КРИТИЧЕСКИЕ ТОЧКИ
- § 7. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ТЕНЗОРАХ
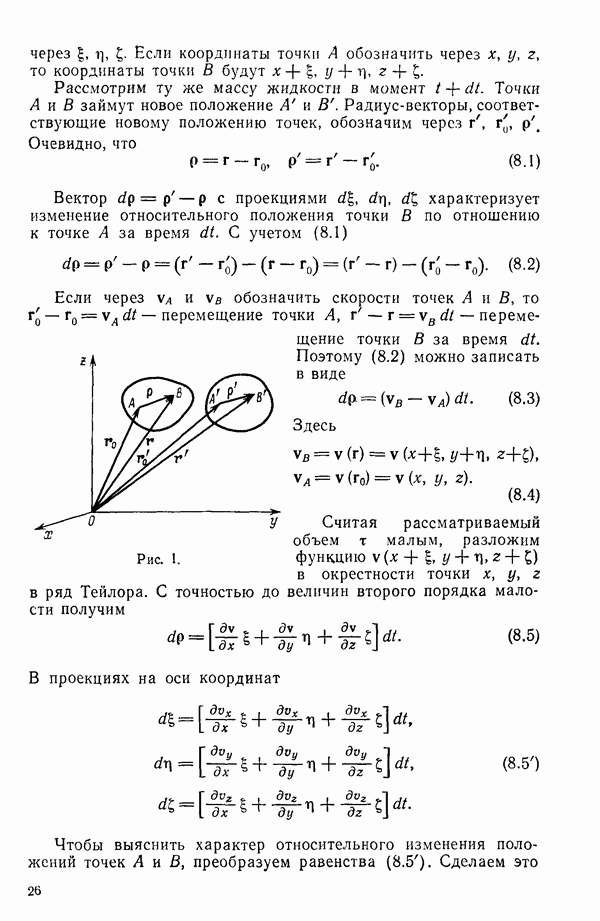
- § 8. СКОРОСТИ И ПЕРЕМЕЩЕНИЯ ТОЧЕК БЕСКОНЕЧНО МАЛОГО ОБЪЕМА СПЛОШНОЙ СРЕДЫ
- § 9. ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИЙ И ЕГО ИНВАРИАНТЫ
- § 10. СМЫСЛ КОМПОНЕНТ ТЕНЗОРА СКОРОСТЕЙ ДЕФОРМАЦИЙ
- § 11. СМЫСЛ КОМПОНЕНТ ВИХРЯ СКОРОСТИ
- § 12. ВИХРЕВЫЕ ЛИНИИ, ВИХРЕВЫЕ ТРУБКИ
- § 13. ЦИРКУЛЯЦИЯ СКОРОСТИ
- § 14. СКОРОСТЬ ОБЪЕМНОГО РАСШИРЕНИЯ ЖИДКОСТИ
- ГЛАВА II. ЗАКОН СОХРАНЕНИЯ МАСС
- § 1. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ МАСС
- § 2. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ МАСС В ПЕРЕМЕННЫХ ЭЙЛЕРА (УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ПЕРЕМЕННЫХ ЭЙЛЕРА)
- § 3. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ПЕРЕМЕННЫХ ЛАГРАНЖА
- § 4. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- ГЛАВА III. ЗАКОН КОЛИЧЕСТВА ДВИЖЕНИЯ ДЛЯ СПЛОШНОЙ СРЕДЫ
- § 1 СИЛЫ МАССОВЫЕ И ПОВЕРХНОСТНЫЕ
- § 2. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. ФОРМУЛА КОШИ
- § 4. ТЕНЗОР НАПРЯЖЕНИЙ
- § 5. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА КОЛИЧЕСТВА ДВИЖЕНИЯ
- ГЛАВА IV. ЗАКОН МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 1. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 2. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- ГЛАВА V. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 1. ВНУТРЕННЯЯ ЭНЕРГИЯ
- § 2. ПОЛНАЯ ЭНЕРГИЯ
- § 3. ИНТЕГРАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- § 4. НЕКОТОРЫЕ ПРЕОБРАЗОВАНИЯ ИНТЕГРАЛЬНОЙ ЗАПИСИ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- § 5. ВЕКТОР ПОТОКА ТЕПЛА
- § 6. ДИФФЕРЕНЦИАЛЬНАЯ ЗАПИСЬ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ
- ГЛАВА VI. ПРОСТЕЙШИЕ МОДЕЛИ ЖИДКИХ СРЕД
- § 1. ИДЕАЛЬНАЯ ЖИДКОСТЬ И ТЕНЗОР НАПРЯЖЕНИИ ДЛЯ НЕЕ
- § 2. ВЯЗКАЯ (НЬЮТОНОВСКАЯ) ЖИДКОСТЬ И ТЕНЗОР НАПРЯЖЕНИЙ ДЛЯ НЕЕ
- § 3. НЕТЕПЛОПРОВОДНАЯ ЖИДКОСТЬ
- § 4. ЖИДКОСТЬ, ПОДЧИНЯЮЩАЯСЯ ЗАКОНУ ТЕПЛОПРОВОДНОСТИ ФУРЬЕ
- § 5. НЕСЖИМАЕМАЯ ЖИДКОСТЬ
- § 6. СЖИМАЕМАЯ ЖИДКОСТЬ
- ГЛАВА VII. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОЙ ЖИДКОСТИ И ПОСТАНОВКА ЗАДАЧ ДЛЯ НЕЕ
- § 1. СИСТЕМА УРАВНЕНИИ ГИДРОМЕХАНИКИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОИ ЖИДКОСТИ
- § 2. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ УСТАНОВИВШИХСЯ ТЕЧЕНИИ ИДЕАЛЬНОЙ НЕТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
- § 3. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ НЕУСТАНОВИВШИХСЯ ТЕЧЕНИИ ИДЕАЛЬНОИ НЕТЕПЛОПРОВОДНОИ ЖИДКОСТИ
- ГЛАВА VIII. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ВЯЗКОЙ ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ И ПОСТАНОВКА ЗАДАЧ ДЛЯ НЕЕ
- § 1. ОБЩАЯ СИСТЕМА УРАВНЕНИИ ГИДРОМЕХАНИКИ ВЯЗКОЙ ЖИДКОСТИ
- § 2. СИСТЕМА УРАВНЕНИЙ ГИДРОМЕХАНИКИ ОДНОРОДНОЙ НЕСЖИМАЕМОЙ ВЯЗКОЙ ЖИДКОСТИ
- § 3. ПОСТАНОВКА ЗАДАЧ ОБ ОТЫСКАНИИ ТЕЧЕНИИ ВЯЗКОЙ ТЕПЛОПРОВОДНОЙ ЖИДКОСТИ
- ЧАСТЬ II. ОСНОВЫ ГИДРОСТАТИКИ
- § 1. УРАВНЕНИЯ РАВНОВЕСИЯ
- § 2. УСЛОВИЕ ДЛЯ СИЛ
- § 3. УСЛОВИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ДВУХ ЖИДКОСТЕЙ
- § 4. РАВНОВЕСИЕ ОДНОРОДНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 5. РАВНОВЕСИЕ БАРОТРОПНОИ ЖИДКОСТИ
- § 6. ОБЩИЙ СЛУЧАЙ РАВНОВЕСИЯ ЖИДКОСТИ В КОНСЕРВАТИВНОМ СИЛОВОМ ПОЛЕ
- § 7. ОБЩИЕ ФОРМУЛЫ ДЛЯ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИЛ ДАВЛЕНИИ
- § 8. ЗАКОН АРХИМЕДА
- ЧАСТЬ III. ГИДРОМЕХАНИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 1. АДИАБАТА
- § 2. ИНТЕГРАЛ БЕРНУЛЛИ
- § 3. ИНТЕГРАЛ БЕРНУЛЛИ В СЛУЧАЕ ДВИЖЕНИЯ ГАЗА С УСЛОЖНЕННОЙ ТЕРМОДИНАМИКОЙ
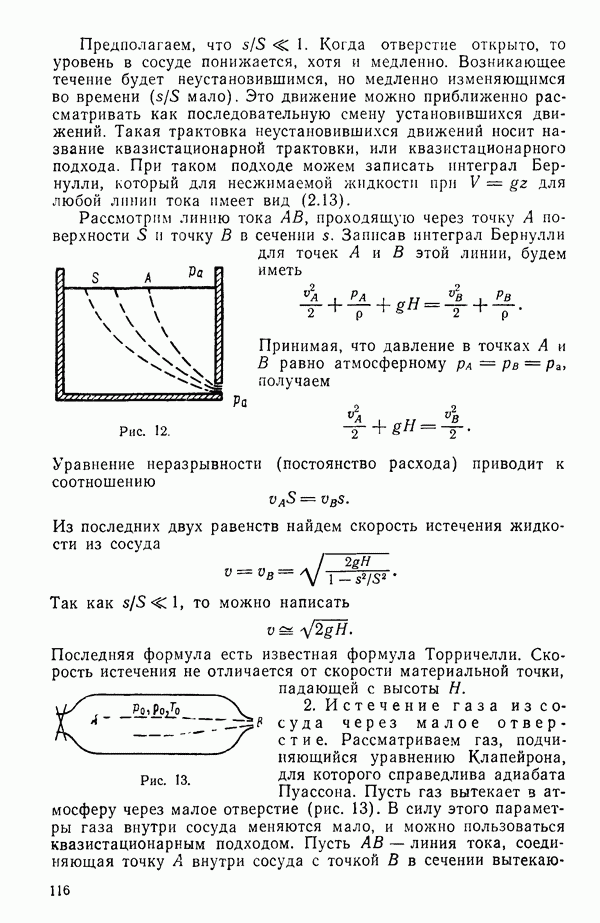
- § 4. ДВА ПРИМЕРА НА ПРИМЕНЕНИЕ ИНТЕГРАЛА БЕРНУЛЛИ
- § 5. УРАВНЕНИЯ ЭЙЛЕРА В ФОРМЕ ГРОМЕКИ — ЛЭМБА
- § 6. ПОТЕНЦИАЛЬНЫЕ, ИЛИ БЕЗВИХРЕВЫЕ, ДВИЖЕНИЯ
- § 7. ИНТЕГРАЛ ЛАГРАНЖА
- § 8. ИНТЕГРАЛ ЭЙЛЕРА-БЕРНУЛЛИ
- § 9. УРАВНЕНИЯ ДЛЯ ПОТЕНЦИАЛА СКОРОСТЕЙ
- ГЛАВА XI. ОБОБЩЕННЫЕ ОДНОМЕРНЫЕ ДВИЖЕНИЯ
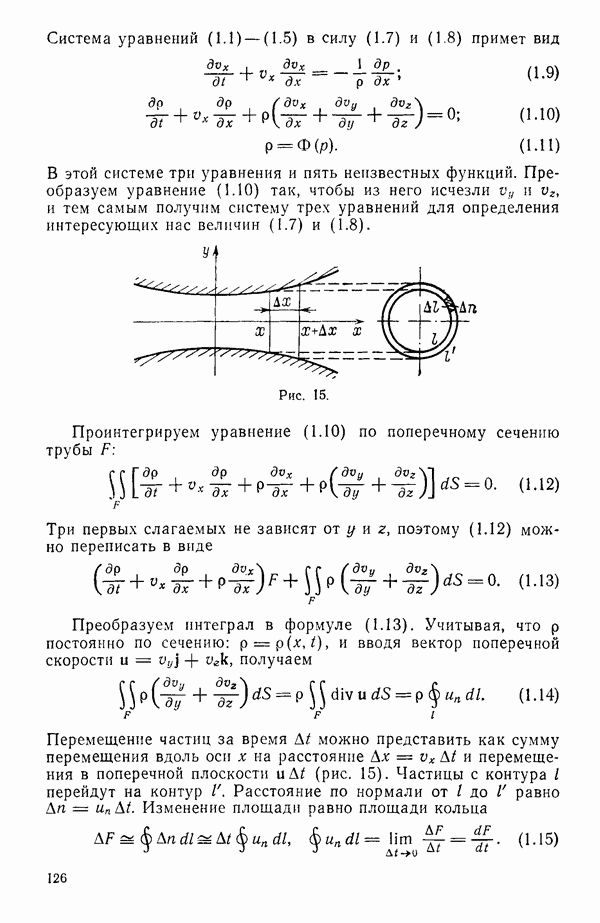
- § 2. ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ
- § 3. ДВИЖЕНИЕ СЖИМАЕМОЙ ЖИДКОСТИ В ТРУБЕ ПЕРЕМЕННОГО СЕЧЕНИЯ. СОПЛО ЛАВАЛЯ
- ГЛАВА XII. ПЛОСКИЕ БЕЗВИХРЕВЫЕ УСТАНОВИВШИЕСЯ ТЕЧЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 1. СИСТЕМА УРАВНЕНИЙ
- § 2. ПОТЕНЦИАЛ СКОРОСТЕЙ
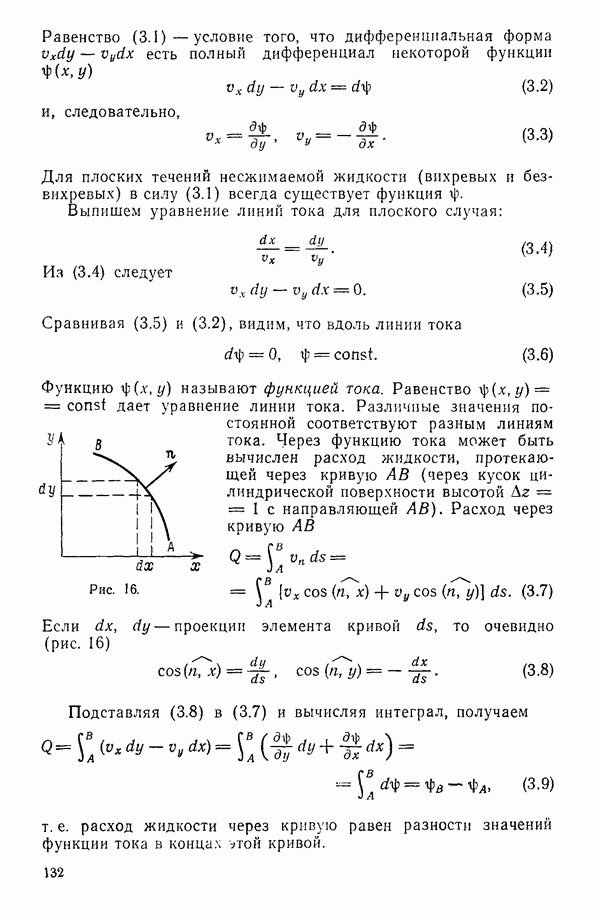
- § 3. ФУНКЦИЯ ТОКА
- § 4. КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ И КОМПЛЕКСНАЯ СКОРОСТЬ
- § 4. КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ И КОМПЛЕКСНАЯ СКОРОСТЬ
- § 6. ПОТЕНЦИАЛЬНОЕ ОБТЕКАНИЕ КРУГОВОГО ЦИЛИНДРА ПОТОКОМ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 7. МЕТОД КОНФОРМНЫХ ОТОБРАЖЕНИЙ
- § 8. ОБТЕКАНИЕ ЭЛЛИПТИЧЕСКОГО ЦИЛИНДРА
- § 9. ПОСТУЛАТ ЧАПЛЫГИНА — ЖУКОВСКОГО
- § 10. ФОРМУЛЫ ЧАПЛЫГИНА — БЛАЗИУСА
- § 11. ИНТЕГРАЛ ОТ КОМПЛЕКСНОЙ СКОРОСТИ
- § 12. ТЕОРЕМА ЖУКОВСКОГО
- § 13. ФОРМУЛА ДЛЯ МОМЕНТА
- § 14. ОБТЕКАНИЕ ПЛАСТИНКИ
- § 15. ОБТЕКАНИЕ ПРОФИЛЕЙ ЖУКОВСКОГО
- § 16. ОБТЕКАНИЕ ПРОИЗВОЛЬНОГО ПРОФИЛЯ. МЕТОД НУЖИНА
- § 17. НЕКОТОРЫЕ ОБЩИЕ ЗАМЕЧАНИЯ О ПЛОСКИХ ПОТЕНЦИАЛЬНЫХ ДВИЖЕНИЯХ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- ГЛАВА XIII. ТЕОРИЯ ТОНКОГО КРЫЛА
- § 1. ПОНЯТИЕ ТОНКОГО КРЫЛА И УСЛОВИЯ ОБТЕКАНИЯ ДЛЯ ТОНКОГО ПРОФИЛЯ
- § 2. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ТОНКОГО ПРОФИЛЯ МЕТОДОМ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ
- § 3. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОФИЛЯ С НУЛЕВОЙ ТОЛЩИНОЙ
- § 5. РЕШЕНИЕ ЗАДАЧИ ОБ ОБТЕКАНИИ ПРОИЗВОЛЬНОГО ТОНКОГО ПРОФИЛЯ
- ГЛАВА XIV. ОСЕСИММЕТРИЧНЫЕ ПОТЕНЦИАЛЬНЫЕ ТЕЧЕНИЯ ИДЕАЛЬНОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 1. ИСТОЧНИКИ В ПРОСТРАНСТВЕ
- § 2. ДИПОЛЬ В ПРОСТРАНСТВЕ
- § 3. ОБТЕКАНИЕ СФЕРЫ
- § 4. ФУНКЦИЯ ТОКА ДЛЯ ОСЕСИММЕТРИЧНЫХ ТЕЧЕНИЙ
- § 5. ПРОДОЛЬНОЕ ОБТЕКАНИЕ ТЕЛА ВРАЩЕНИЯ. МЕТОД ИСТОЧНИКОВ И СТОКОВ
- § 6. ПОПЕРЕЧНОЕ ОБТЕКАНИЕ ТЕЛА ВРАЩЕНИЯ
- § 7. ОБЩИЙ СЛУЧАЙ ОБТЕКАНИЯ ТЕЛА ВРАЩЕНИЯ
- ГЛАВА XV. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- § 1. ОБЩИЙ ВИД ПОТЕНЦИАЛА СКОРОСТЕЙ
- § 2. ПОВЕДЕНИЕ ПОТЕНЦИАЛА СКОРОСТЕЙ В ОКРЕСТНОСТИ БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКИ
- § 3. РАСЧЕТ ГИДРОДИНАМИЧЕСКИХ РЕАКЦИИ ПРИ ДВИЖЕНИИ ТЕЛА
- § 4. УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- ГЛАВА XVI. ВИХРЕВЫЕ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
- § 1. ТЕОРЕМА ТОМСОНА
- § 2. ТЕОРЕМА ЛАГРАНЖА
- § 3. ТЕОРЕМЫ ГЕЛЬМГОЛЬЦА
- § 4. О ВОЗНИКНОВЕНИИ ВИХРЕЙ
- § 5. УРАВНЕНИЯ ДЛЯ ВИХРЯ
- § 6. ОПРЕДЕЛЕНИЕ ВЕКТОРА СКОРОСТИ ПО ВИХРЮ И ДИВЕРГЕНЦИИ
- § 7. СКОРОСТИ, ИНДУЦИРУЕМЫЕ ВИХРЕВОЙ НИТЬЮ
- § 8. ПРЯМОЛИНЕЙНАЯ ВИХРЕВАЯ НИТЬ
- § 9. ВИХРЕВОЙ СЛОЙ
- ГЛАВА XVII. ТЕОРИЯ КРЫЛА КОНЕЧНОГО РАЗМАХА
- § 2. ВИХРЕВАЯ СИСТЕМА КРЫЛА И ОСНОВНЫЕ ФОРМУЛЫ
- § 3. КРЫЛО С ЭЛЛИПТИЧЕСКИМ РАСПРЕДЕЛЕНИЕМ ЦИРКУЛЯЦИИ
- § 4. ПАРАБОЛА ИНДУКТИВНОГО СОПРОТИВЛЕНИЯ И ПЕРЕСЧЕТ КРЫЛА С ОДНОГО УДЛИНЕНИЯ НА ДРУГОЕ
- § 5. ОПРЕДЕЛЕНИЕ ЦИРКУЛЯЦИИ Г(z) В ТЕОРИИ КРЫЛА КОНЕЧНОГО РАЗМАХА
- ЧАСТЬ IV. ГИДРОМЕХАНИКА ВЯЗКОЙ ЖИДКОСТИ
- ГЛАВА XVIII. ОБЩИЕ СВОЙСТВА ДВИЖЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 2. НЕОБРАТИМОСТЬ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
- § 3. ЗАВИХРЕННОСТЬ ТЕЧЕНИЙ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- § 4. ДИССИПАЦИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ В ВЯЗКОЙ ЖИДКОСТИ
- ГЛАВА XIX. ТОЧНЫЕ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 1. ПОСТАНОВКА ЗАДАЧИ ОБ ОТЫСКАНИИ ОДНОМЕРНЫХ ТЕЧЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 2. ПРИМЕРЫ ОДНОМЕРНЫХ НЕСТАЦИОНАРНЫХ ТЕЧЕНИЙ ВЯЗКОЙ ЖИДКОСТИ
- § 3. УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ МЕЖДУ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
- § 4. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ
- § 7. ПРИМЕР ПРОСТЕЙШЕГО УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ С ПЕРЕМЕННОЙ ВЯЗКОСТЬЮ
- ГЛАВА XX. ПОДОБИЕ ТЕЧЕНИИ ВЯЗКОЙ ЖИДКОСТИ
- § 1. СХОДСТВЕННЫЕ ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ТОЧКИ
- § 2. ЗАПИСЬ УРАВНЕНИИ ГИДРОМЕХАНИКИ ВЯЗКОЙ ЖИДКОСТИ В БЕЗРАЗМЕРНОМ ВИДЕ
- § 3. ПОДОБИЕ УСТАНОВИВШИХСЯ ТЕЧЕНИЙ
- § 5 ТЕЧЕНИЕ В ТРУБЕ ЭЛЛИПТИЧЕСКОГО СЕЧЕНИЯ
- § 6. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ МЕЖДУ ДВУМЯ ВРАЩАЮЩИМИСЯ СООСНЫМИ ЦИЛИНДРАМИ
- ГЛАВА XXI. ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ ПРИ БОЛЬШИХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 1. ОСНОВНЫЕ ПРЕДПОЛОЖЕНИЯ И СИСТЕМА УРАВНЕНИИ ПОГРАНИЧНОГО СЛОЯ
- § 2. ПОГРАНИЧНЫЙ СЛОЙ ОКОЛО ПОЛУБЕСКОНЕЧНОЙ ПЛАСТИНКИ
- ГЛАВА XXII. ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ ПРИ МАЛЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 1. УРАВНЕНИЯ СТОКСА
- § 2. ОБТЕКАНИЕ СФЕРЫ ПРИ МАЛЫХ ЧИСЛАХ РЕЙНОЛЬДСА
- § 3. ПАРАДОКС СТОКСА
- § 4. УРАВНЕНИЯ ОЗИНА
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА