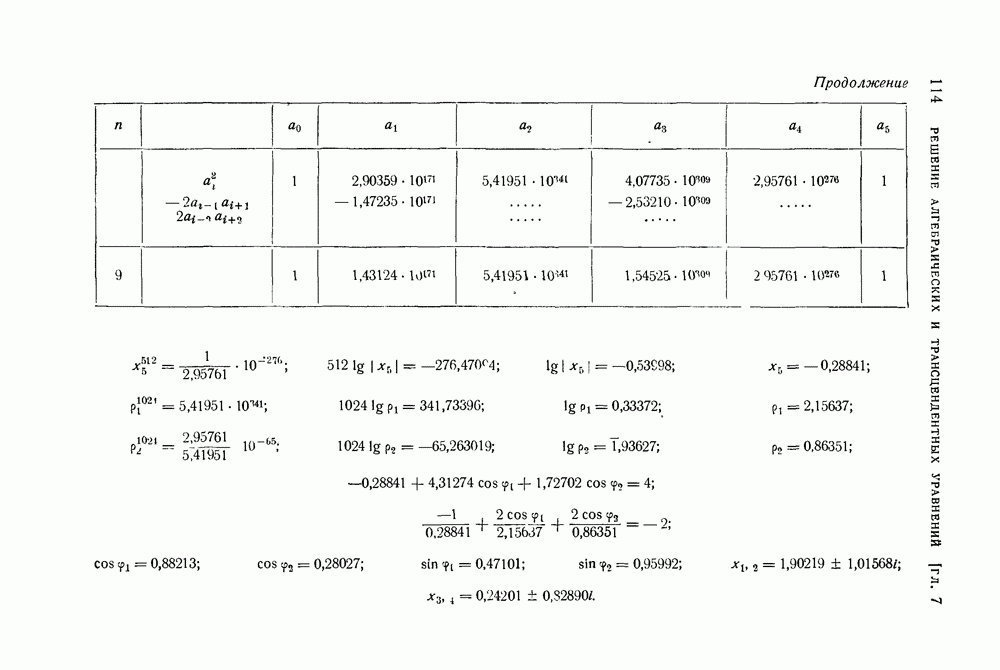
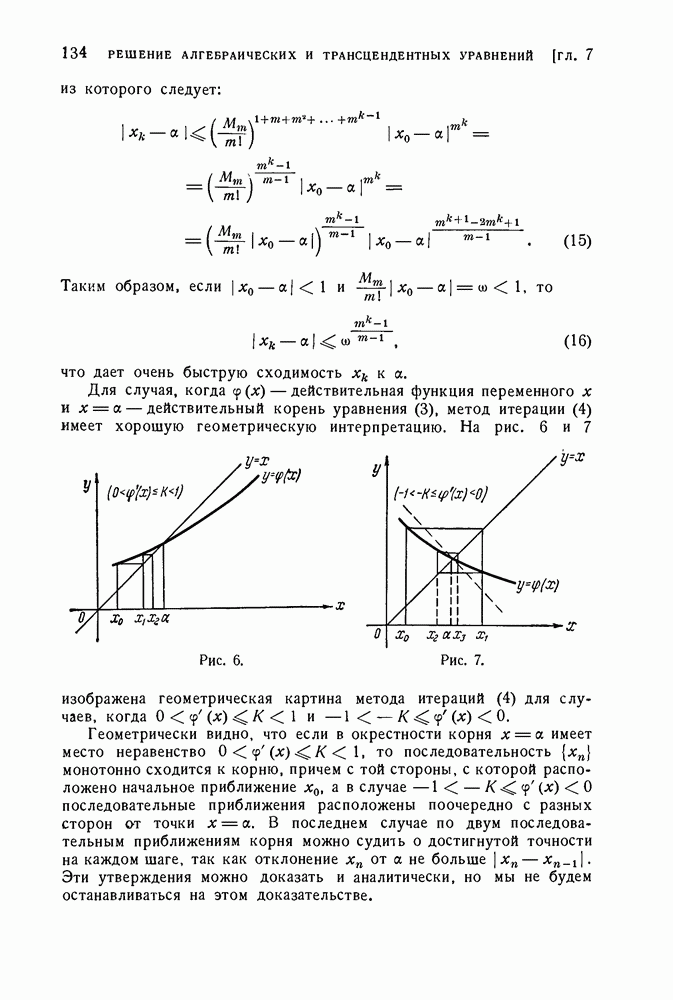
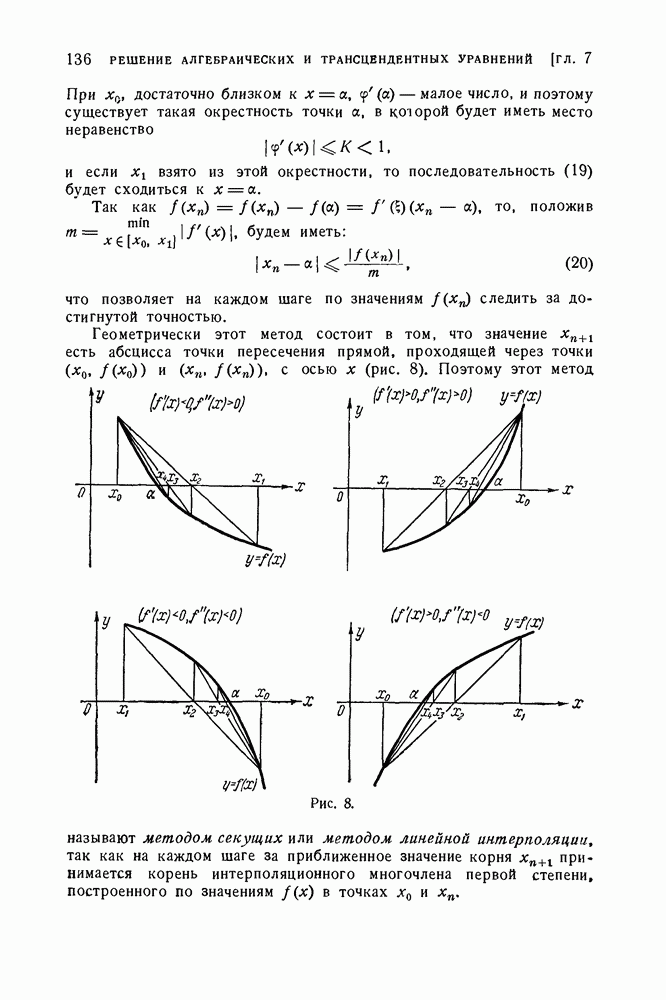
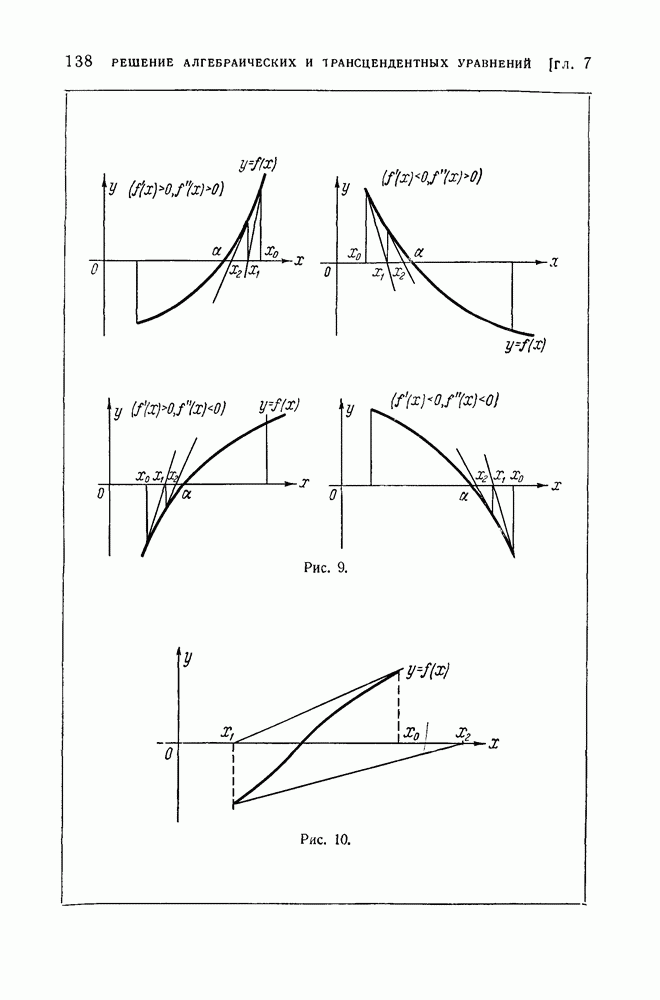
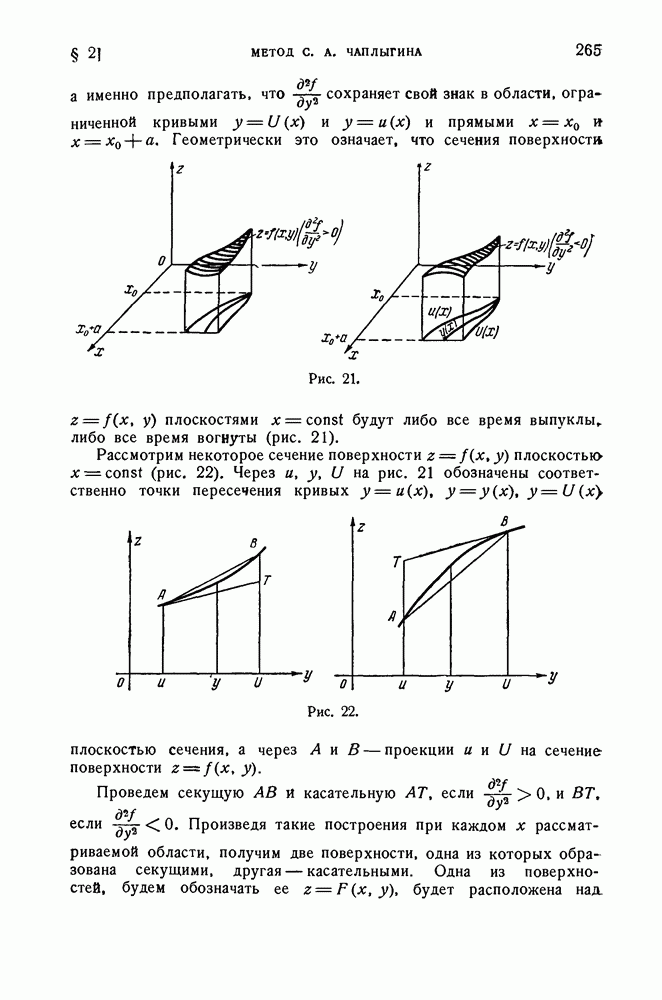
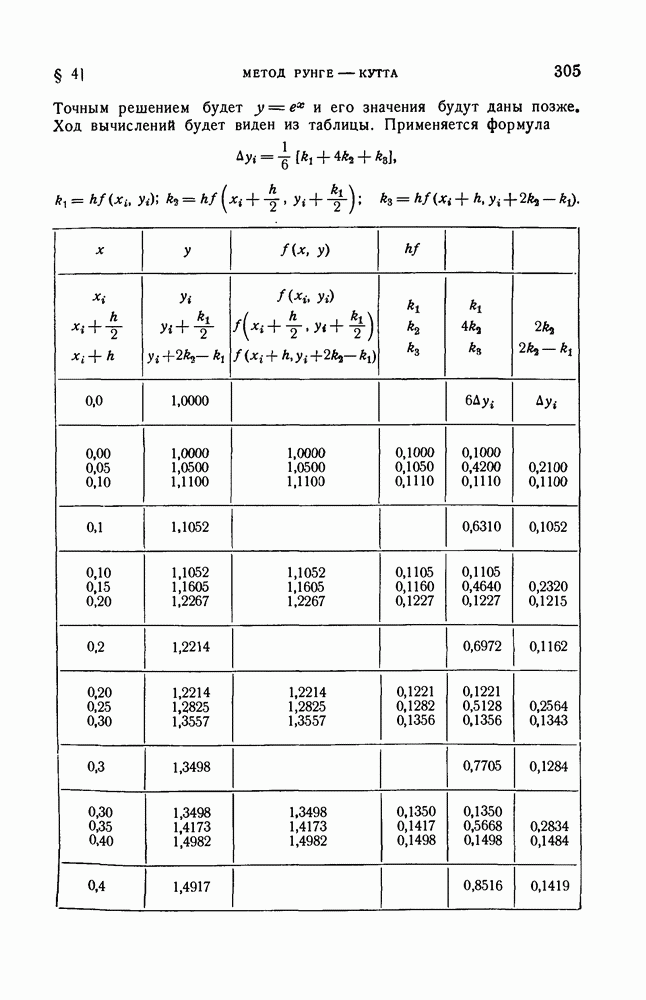
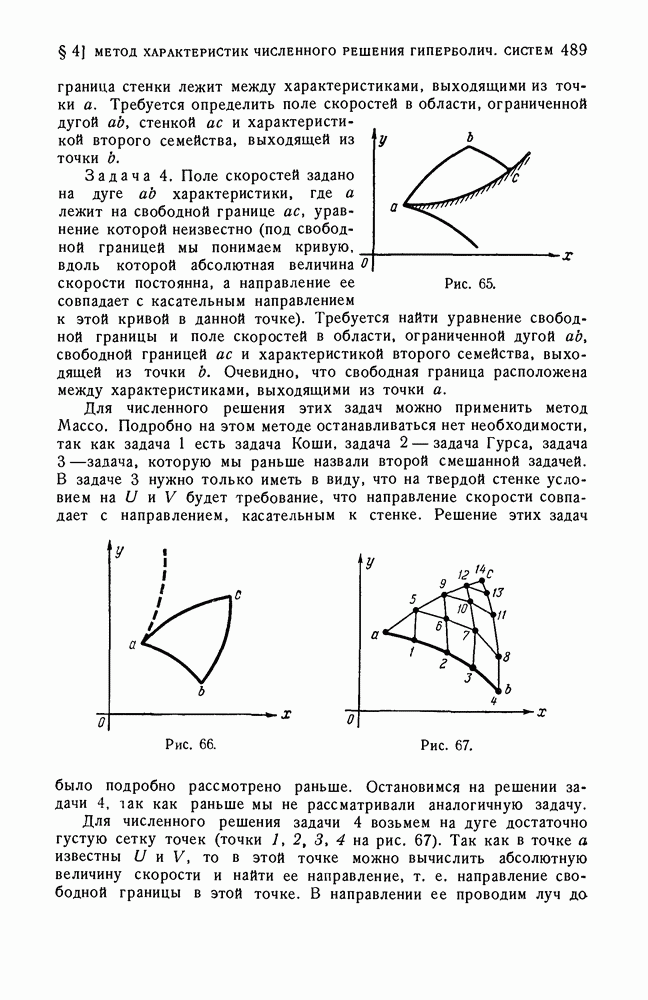
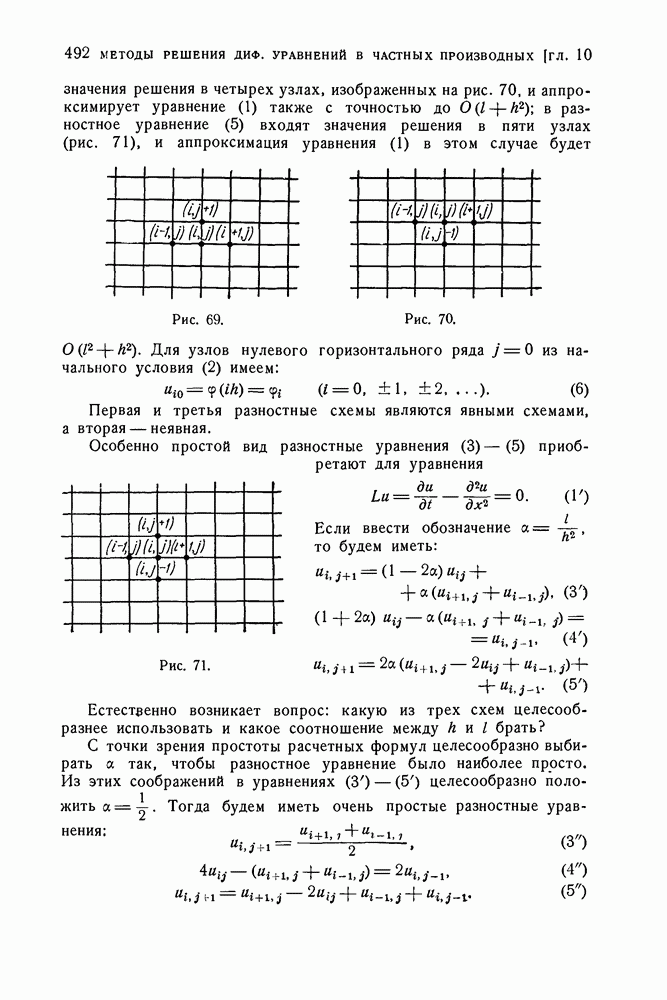
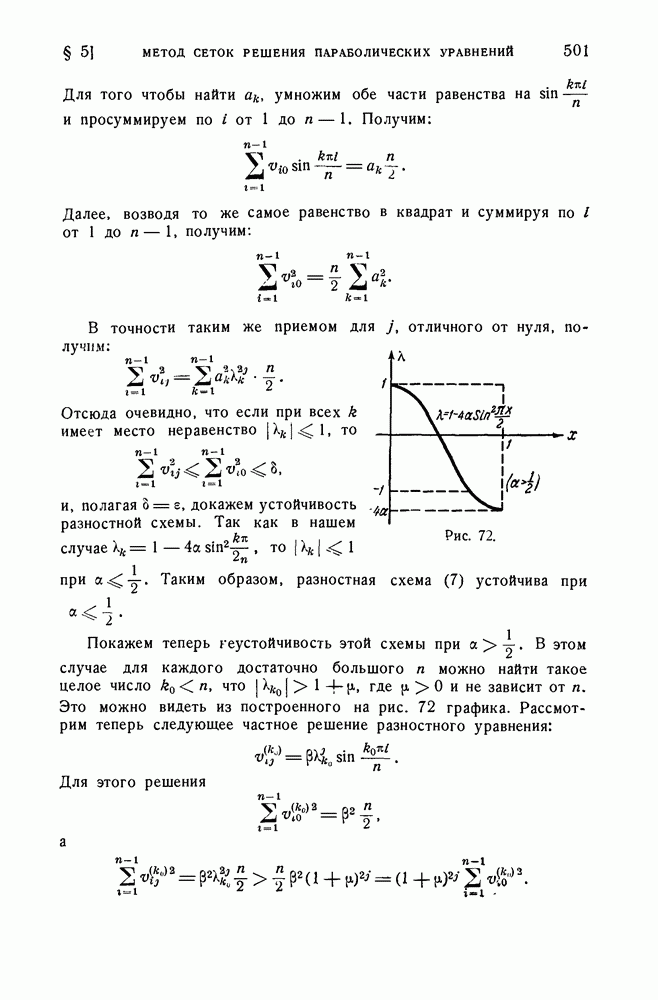
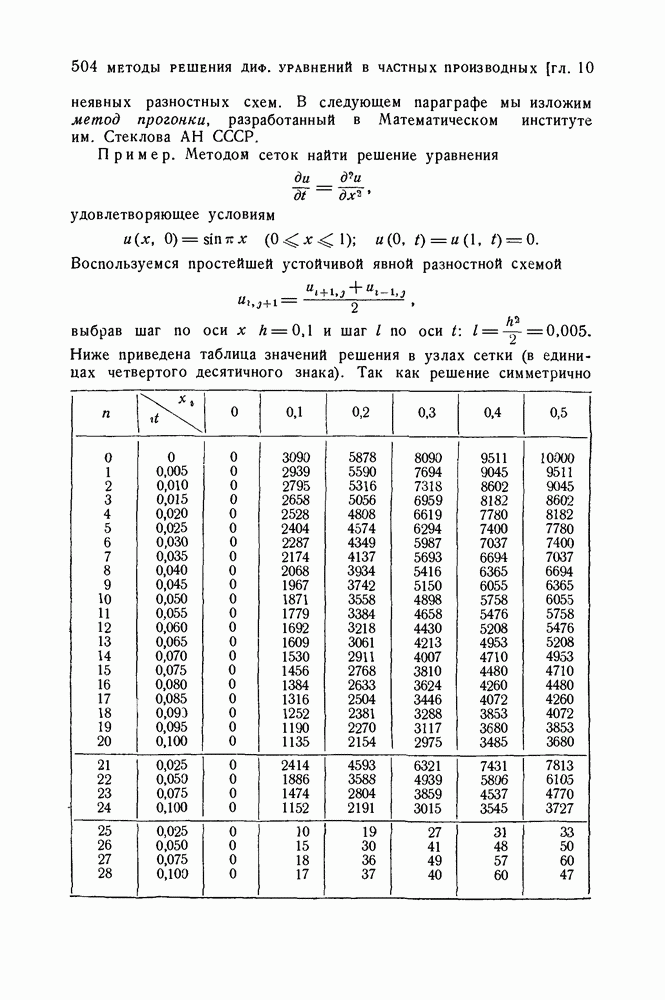
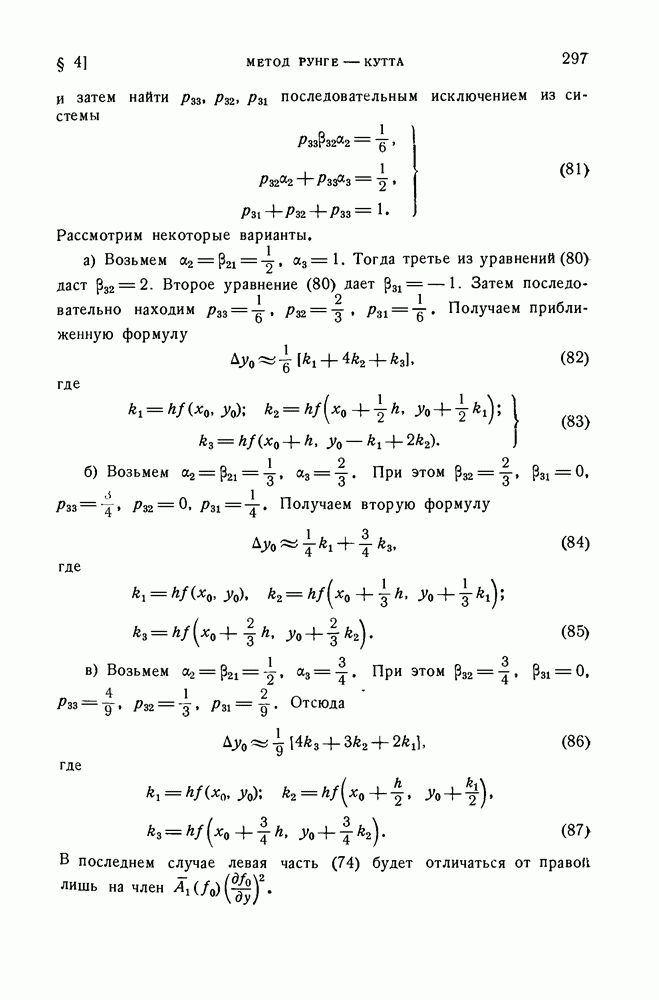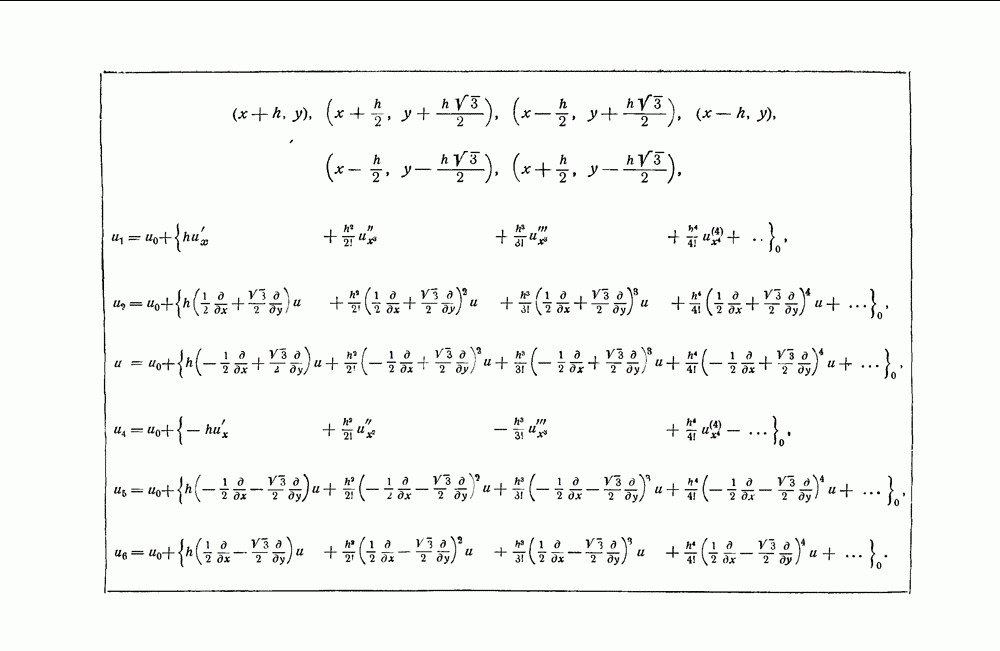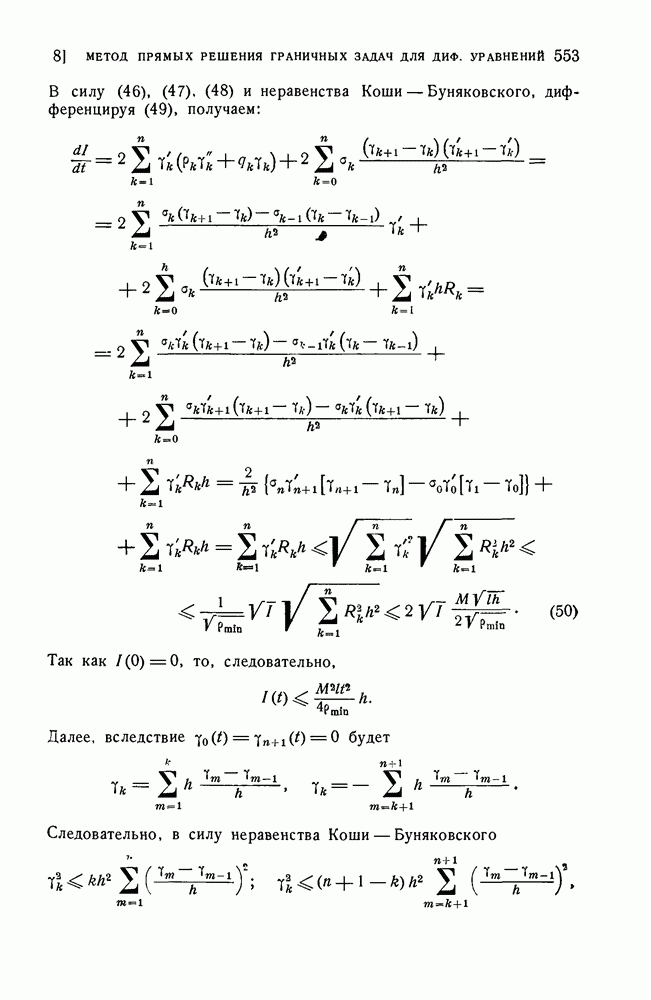| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Определение границ собственных значений
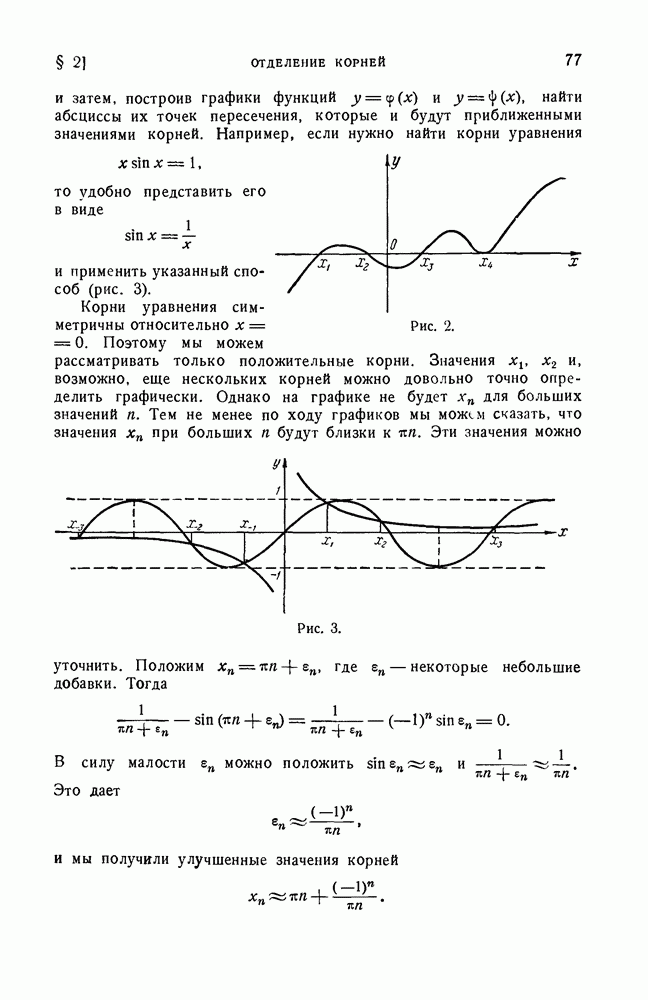
Для того чтобы решить полученное тем или иным способом характеристическое уравнение, желательно иметь представление о расположении его корней. В предыдущей главе мы уже рассматривали подобные вопросы. Однако характеристический многочлен тесно сзязан с породившей его матрицей А, и поэтому можно указать ряд методов, более приспособленных к рассматриваемому случаю. Кроме того, часто возникает необходимость знать границы собственных значений и совершенно не требуется характеристический многочлен. В связи с этим в данном параграфе будут рассмотрены методы определения границ собственных значений матрицы, не использующие ее характеристического многочлена в явном виде. Эти методы будут пригодны и для получения границ корней произвольного многочлена, если записать последний в виде характеристического многочлена некоторой матрицы. Для этого можно использовать, например, нормальную форму Фробениусэ.
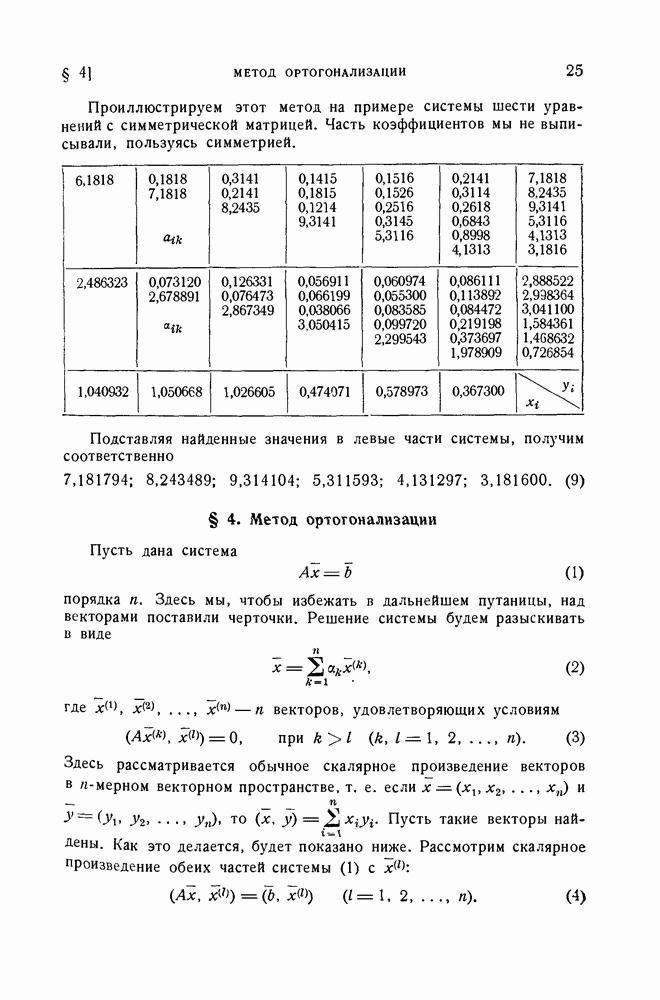
1. Случай симметрической матрицы.
Рассмотрим уравнение

где А — действительная симметрическая матрица,  вектор-столбец и X — действительное или комплексное число. Известно, что в этом случае имеется
вектор-столбец и X — действительное или комплексное число. Известно, что в этом случае имеется  действительных собственных значений
действительных собственных значений

 соответствующих им собственных векторов
соответствующих им собственных векторов  которые можно считать действительными и ортонормированными. Тогда, если
которые можно считать действительными и ортонормированными. Тогда, если  произвольный вектор-столбец:
произвольный вектор-столбец:

то

Таким образом,

или

Эти неравенства, которые иногда называют принципом Релея, дают некоторое представление о собственных значениях. Если взять в неравенстве (6) в качестве х собственные векторы, соответствующие собственным значениям  то будут выполнены знаки равенства.
то будут выполнены знаки равенства.

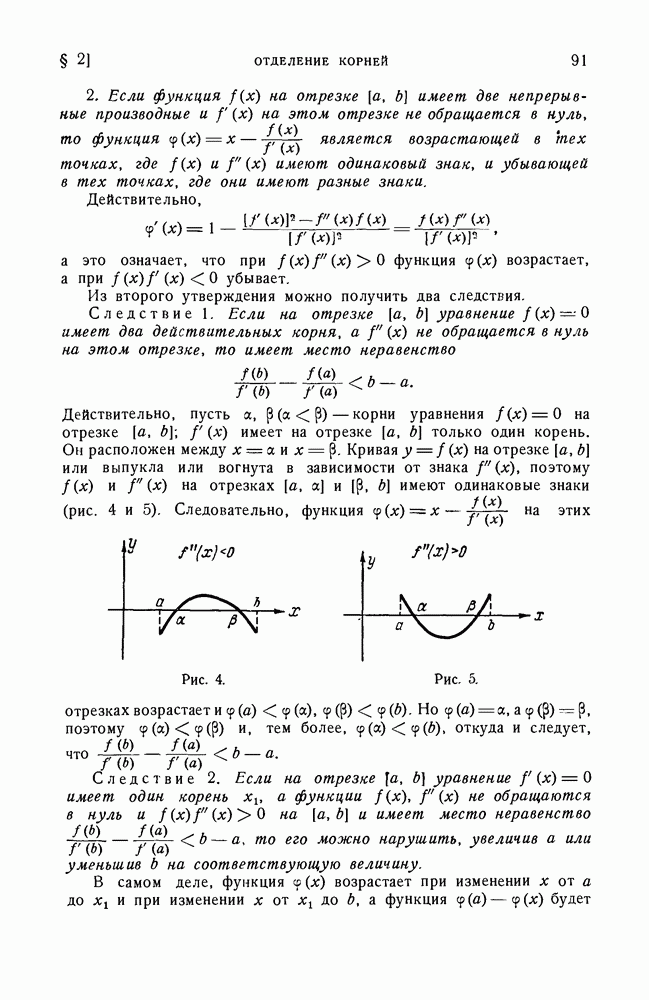
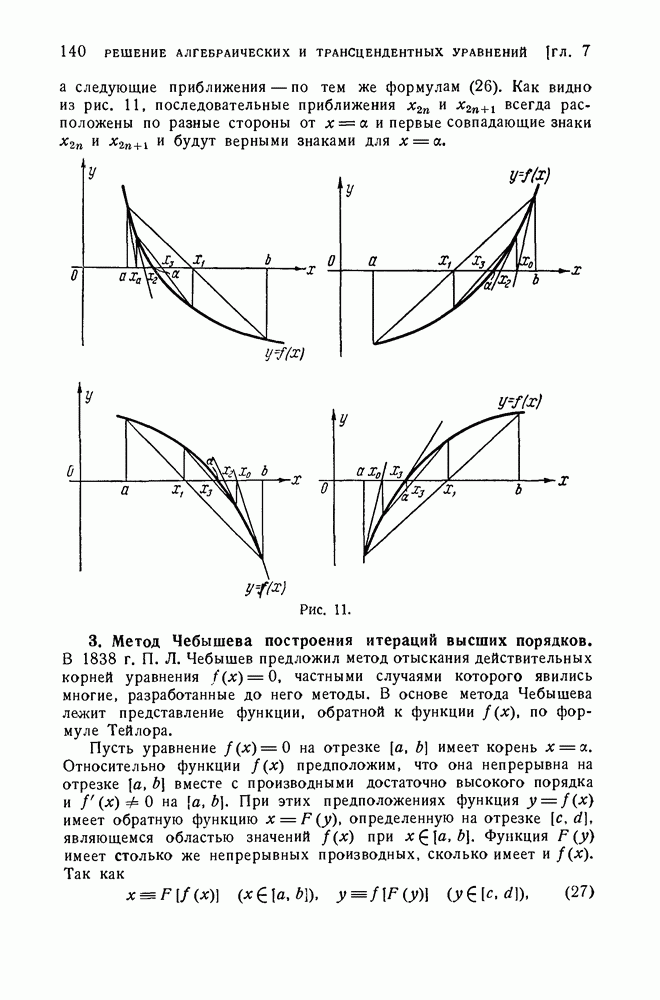
Рис. 12.
Таким образом, наибольшее собственное значение А равно верхней границе, а наименьшее собственное значение А — нижней границе отношений, стоящих в (6).
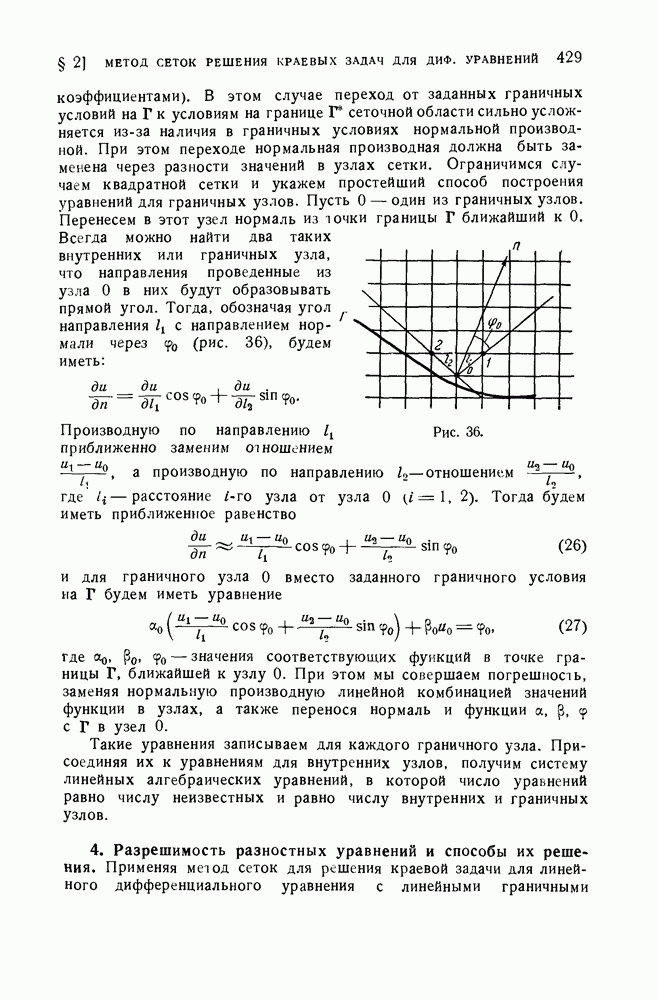
Дадим принципу Релея геометрическую интерпретацию. Пусть отрезок  изображает нормированный вектор х и
изображает нормированный вектор х и  вектор
вектор  На прямой
На прямой  отложим точки так, что
отложим точки так, что  (рис. 12).
(рис. 12).
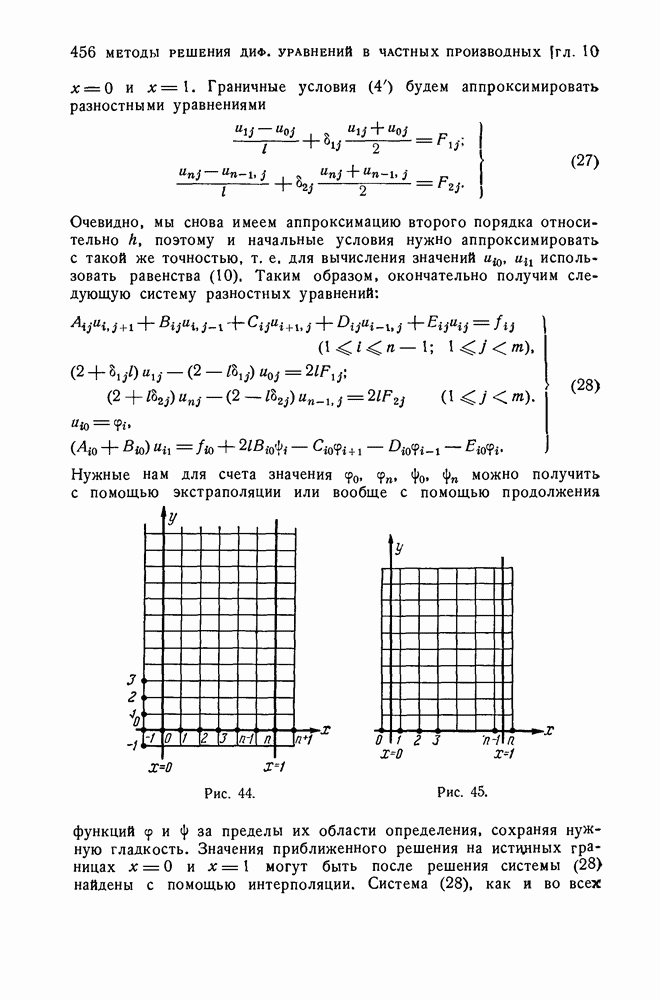
Имеем:

Отсюда

Таким образом, угол между двумя векторами  не может превышать у. Проведем перпендикуляр
не может превышать у. Проведем перпендикуляр  и заметим, что
и заметим, что

Тогда из (6) следует, что на отрезках  и
и  также имеется по крайней мере одно собственное значение.
также имеется по крайней мере одно собственное значение.

Рис. 13.
Объединяя (8) и последнее замечание, мы приходим к выводу, что если провести через точку С произвольные прямые  и
и  пересекающие прямую
пересекающие прямую  соответственно в точках
соответственно в точках  и если угол
и если угол  то на отрезке
то на отрезке  имеется по крайней мере одно собственное значение. Это и есть геометрическая интерпретация принципа Релея.
имеется по крайней мере одно собственное значение. Это и есть геометрическая интерпретация принципа Релея.
Дадим некоторые приложения этой геометрической интерпретации. Пусть опять х — произвольный вектор,  Обозначим
Обозначим

Докажем, что если  и
и

то на отрезке  имеется по крайней мере одно собственное значение А. Действительно,
имеется по крайней мере одно собственное значение А. Действительно,  Пусть
Пусть 
Тогда (рис. 13)

Отсюда и следует утверждение.
Докажем еще, что если а — произвольное действительное число,  произвольный нормированный вектор,
произвольный нормированный вектор,  то на отрезке
то на отрезке

найдется по крайней мере одно собственное значение А. Рассмотрим геометрическую картину (рис. 14).

Рис. 14.
Отрезок  берем равным а. Точки
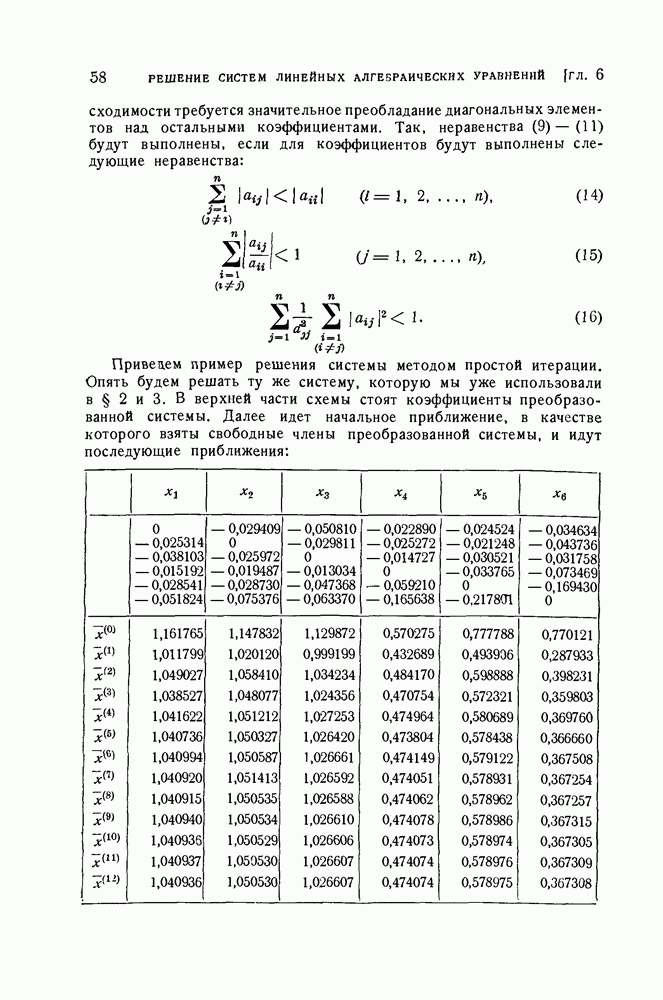
берем равным а. Точки  строим так, что
строим так, что

При

Так как угол  прямой, то утверждение доказано.
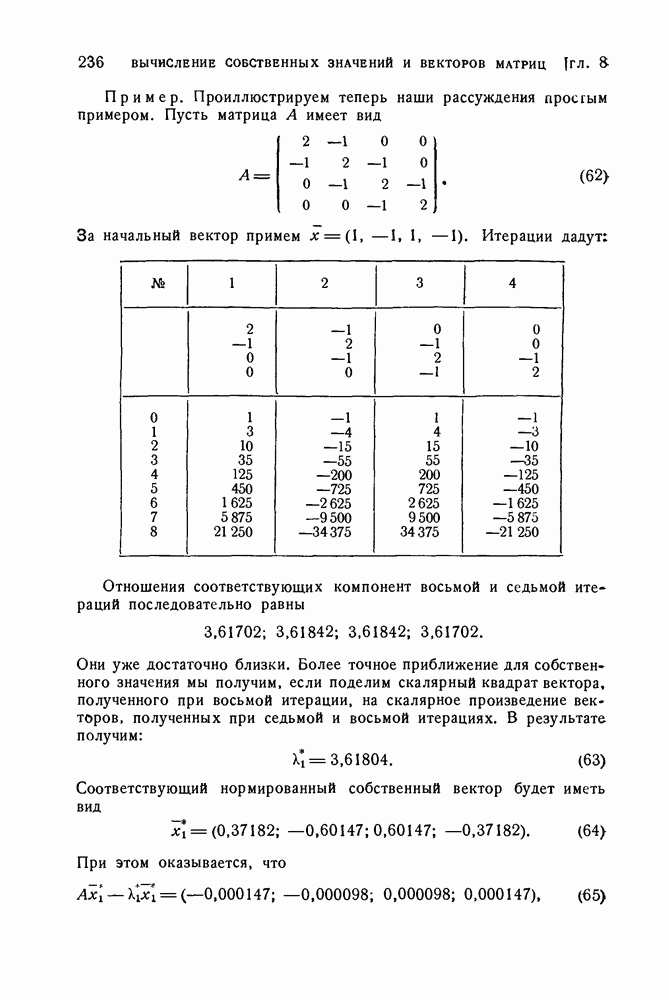
прямой, то утверждение доказано.
Дадим небольшое обобщение принципа Релея. Возьмем два многочлена

и рассмотрим

Как известно, собственные значения  матрицы
матрицы  равны
равны  Как и ранее, для произвольного
Как и ранее, для произвольного  будем иметь:
будем иметь:

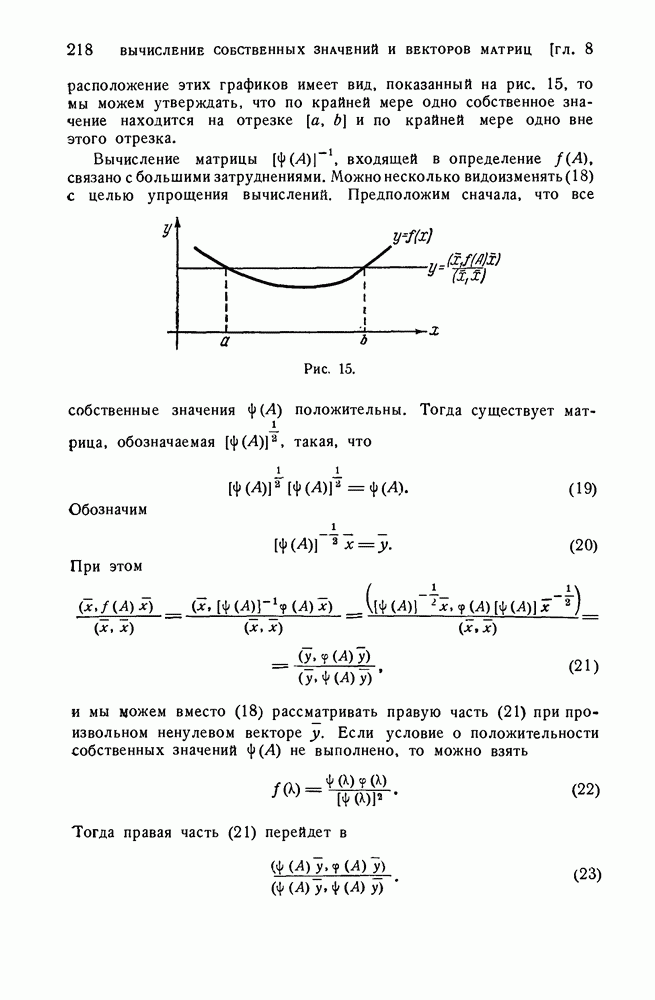
Вследствие этого, построив графики функций  сможем судить о собственных значениях А. Так, например, если
сможем судить о собственных значениях А. Так, например, если
расположение этих графиков имеет вид, показанный на рис. 15, то мы можем утверждать, что по крайней мере одно собственное значение находится на отрезке  и по крайней мере одно вне этого отрезка.
и по крайней мере одно вне этого отрезка.
Вычисление матрицы  входящей в определение
входящей в определение  связано с большими затруднениями. Можно несколько видоизменять (18) с целью упрощения вычислений. Предположим сначала, что все собственные значения
связано с большими затруднениями. Можно несколько видоизменять (18) с целью упрощения вычислений. Предположим сначала, что все собственные значения  положительны.
положительны.

Рис. 15.
Тогда существует матрица, обозначаемая  такая, что
такая, что

Обозначим

При

и мы можем вместо (18) рассматривать правую часть (21) при произвольном ненулевом векторе у. Если условие о положительности собственных значений  не выполнено, то можно взять
не выполнено, то можно взять

Тогда правая часть (21) перейдет в

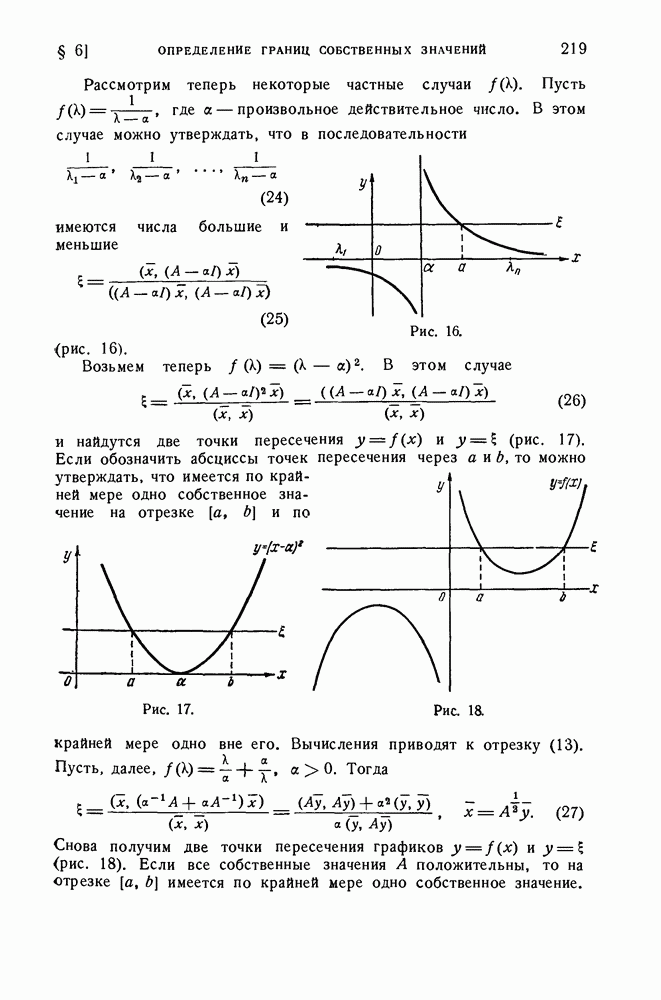
Рассмотрим теперь некоторые частные случаи  Пусть
Пусть  где а — произвольное действительное число. В этом случае можно утверждать, что в последовательности
где а — произвольное действительное число. В этом случае можно утверждать, что в последовательности

имеются числа большие и меньшие

(рис. 16).
Возьмем теперь  . В этом случае
. В этом случае

и найдутся две точки пересечения  (рис. 17). Если обозначить абсциссы точек пересечения через
(рис. 17). Если обозначить абсциссы точек пересечения через  то можно утверждать, что имеется по крайней мере одно собственное значение на отрезке
то можно утверждать, что имеется по крайней мере одно собственное значение на отрезке  и по крайней мере одно вне его. Вычисления приводят к отрезку (13).
и по крайней мере одно вне его. Вычисления приводят к отрезку (13).

Рис. 16.

Рис. 17.

Рис. 18.
Пусть, далее,  Тогда
Тогда

Снова получим две точки пересечения графиков  (рис. 18). Если все собственные значения А положительны, то на отрезке
(рис. 18). Если все собственные значения А положительны, то на отрезке  имеется по крайней мере одно собственное значение.
имеется по крайней мере одно собственное значение.
В данном случае  определяются при помощи равенств:
определяются при помощи равенств:

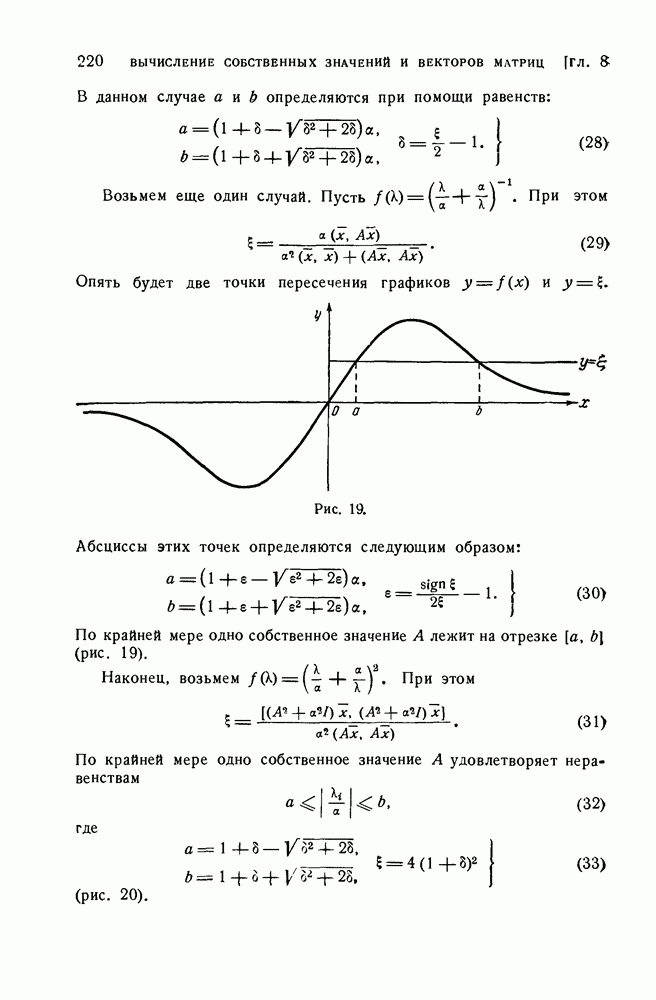
Возьмем еще один случай. Пусть  При этом
При этом

Опять будет две точки пересечения графиков 

Рис. 19.
Абсциссы этих точек определяются следующим образом:

По крайней мере одно собственное значение А лежит на отрезке  (рис. 19).
(рис. 19).
Наконец, возьмем  При этом
При этом

По крайней мере одно собственное значение А удовлетворяет неравенствам

где

(рис. 20).
На этом мы закончим рассмотрение различных случаев использования обобщенного принципа Релея.
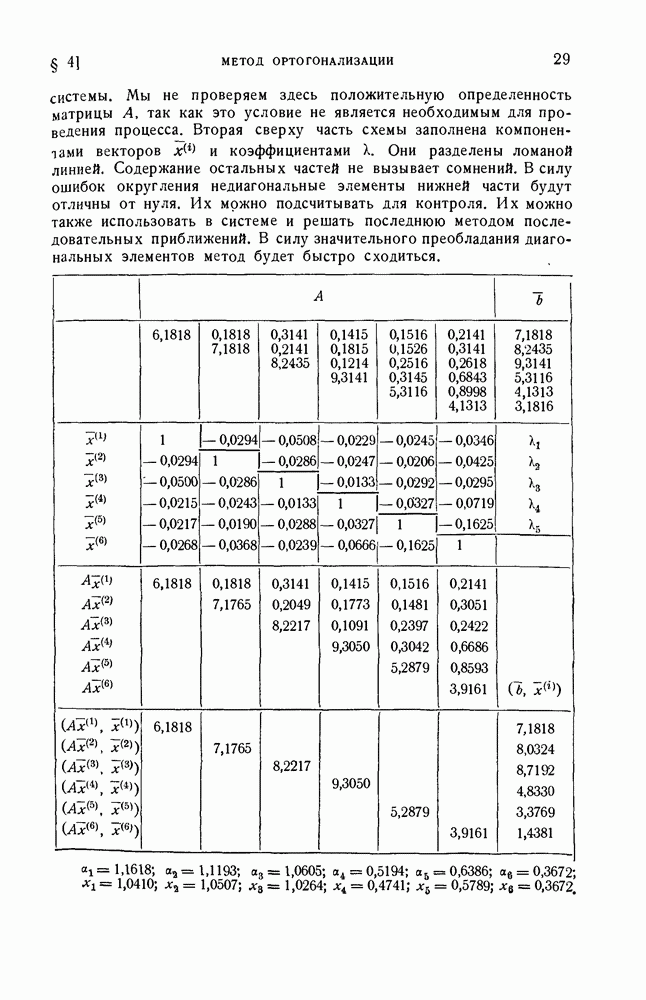
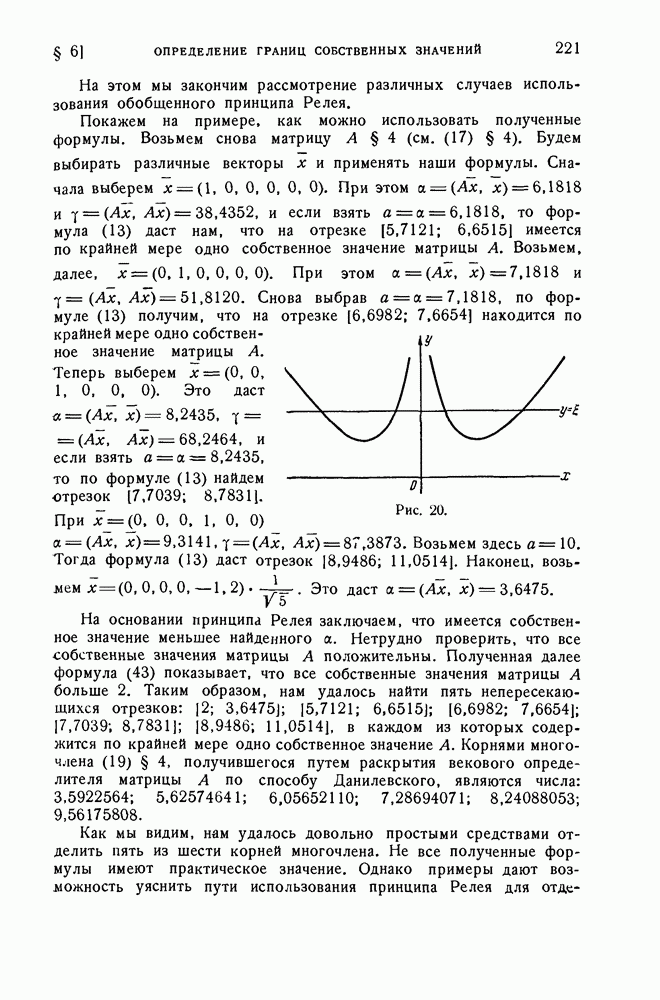
Покажем на примере, как можно использовать полученные формулы. Возьмем снова матрицу  § 4 (см. (17) § 4). Будем выбирать различные векторы х и применять наши формулы. Сначала выберем
§ 4 (см. (17) § 4). Будем выбирать различные векторы х и применять наши формулы. Сначала выберем  . При этом
. При этом  и если взять
и если взять  то формула (13) даст нам, что на отрезке [5,7121; 6,6515] имеется по крайней мере одно собственное значение матрицы А. Возьмем, далее,
то формула (13) даст нам, что на отрезке [5,7121; 6,6515] имеется по крайней мере одно собственное значение матрицы А. Возьмем, далее,  . При этом
. При этом  Снова выбрав
Снова выбрав  по формуле (13) получим, что на отрезке [6,6982; 7,6654] находится по крайней мере одно собственное значение матрицы А. Теперь выберем
по формуле (13) получим, что на отрезке [6,6982; 7,6654] находится по крайней мере одно собственное значение матрицы А. Теперь выберем  . Это даст
. Это даст  и если взять
и если взять  то по формуле (13) найдем отрезок [7,7039; 8,78311.
то по формуле (13) найдем отрезок [7,7039; 8,78311.

Рис. 20.
При  Возьмем здесь
Возьмем здесь  Тогда формула (13) даст отрезок
Тогда формула (13) даст отрезок  . Наконец, возьмем
. Наконец, возьмем  Это даст
Это даст 
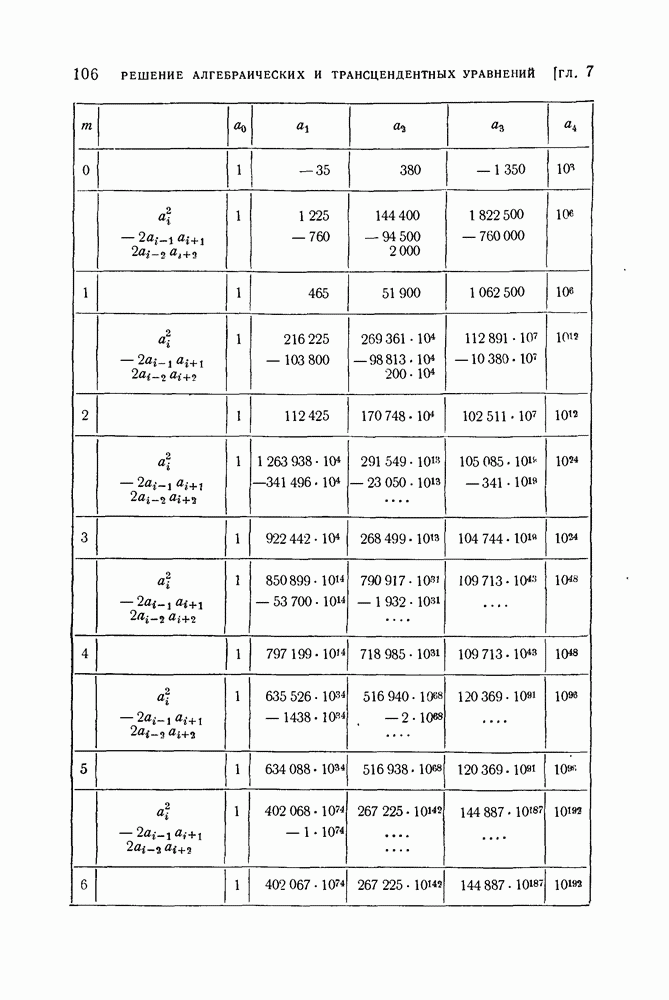
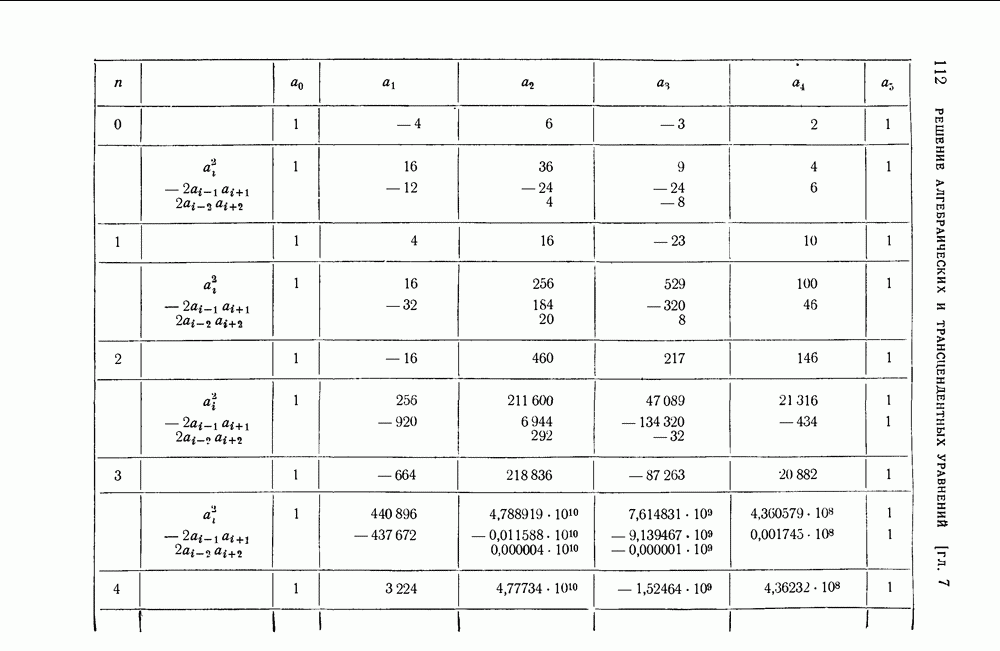
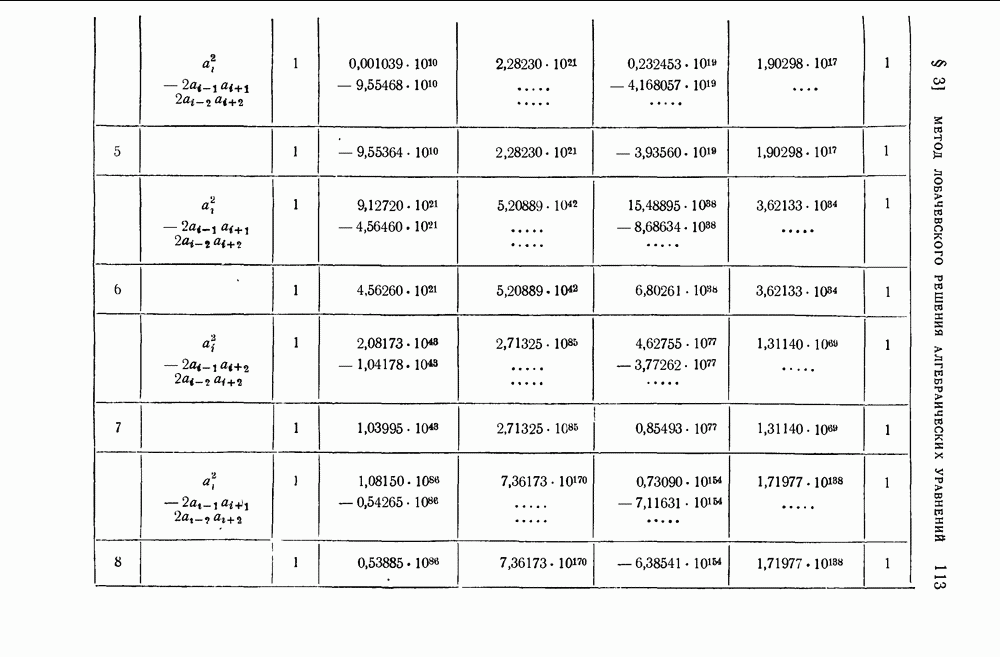
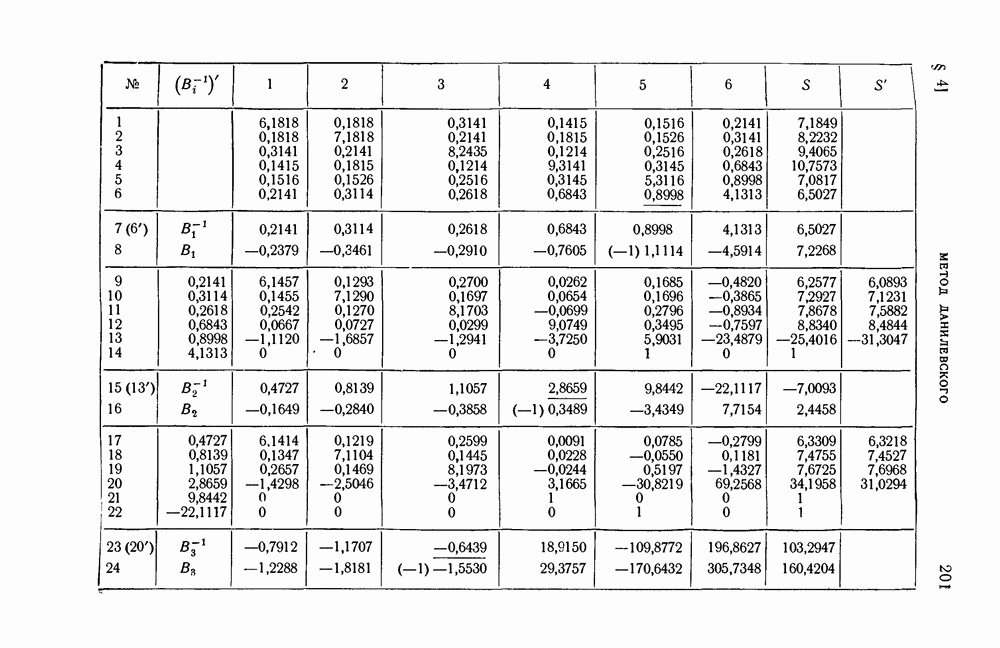
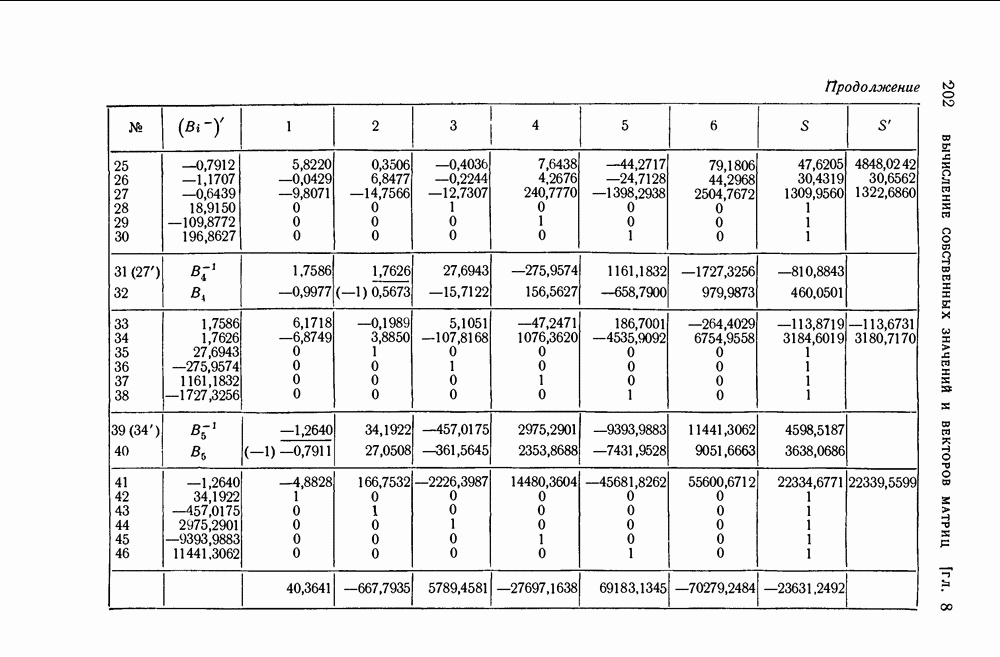
На основании принципа Релея заключаем, что имеется собственное значение меньшее найденного а. Нетрудно проверить, что все собственные значения матрицы А положительны. Полученная далее формула (43) показывает, что все собственные значения матрицы А больше 2. Таким образом, нам удалось найти пять непересекающихся отрезков:  , в каждом из которых содержится по крайней мере одно собственное значение А. Корнями многочлена (19) § 4, получившегося путем раскрытия векового определителя матрицы А по способу Данилевского, являются числа: 3,5922564; 5,62574641; 6,05652110; 7,28694071; 8,24088053; 9,56175808.
, в каждом из которых содержится по крайней мере одно собственное значение А. Корнями многочлена (19) § 4, получившегося путем раскрытия векового определителя матрицы А по способу Данилевского, являются числа: 3,5922564; 5,62574641; 6,05652110; 7,28694071; 8,24088053; 9,56175808.
Как мы видим, нам удалось довольно простыми средствами отделить пять из шести корней многочлена. Не все полученные формулы имеют практическое значение. Однако примеры дают возможность уяснить пути использования принципа Релея для
отделения собственных значений. Сформулируем теперь некоторое уточнение принципа Релея.
Рассмотрим наряду с симметрической действительной матрицей А еще положительно определенную действительную матрицу В. Будем обозначать собственные значения матрицы В через 

Собственные значения  матрицы
матрицы  также действительны и их можно определить при помощи соотношения
также действительны и их можно определить при помощи соотношения

Здесь ищется минимум при всевозможных значениях  максимумов записанного отношения для всевозможных ненулевых векторов
максимумов записанного отношения для всевозможных ненулевых векторов  компоненты которых связаны
компоненты которых связаны  соотношениями:
соотношениями:

Мы не будем приводить доказательства высказанного утверждения, так как оно довольно громоздко. Желающих ознакомиться с ними мы отсылаем к специальной литературе по теории матриц (см., например, Гантмахер Ф. Р., Теория матриц, Гостехиздат, 1953, глава X, § 7).
Из равенства (35), в частности, следует:

Неравенствами (37) можно воспользоваться, если известны собственные значения  Рассмотрим, например, такой случай. Матрица С получается из матрицы А путем деления строк А последовательно на положительные числа
Рассмотрим, например, такой случай. Матрица С получается из матрицы А путем деления строк А последовательно на положительные числа  Этот процесс можно записать как умножение А справа на
Этот процесс можно записать как умножение А справа на  где
где

Поэтому, если  собственные значения С, то
собственные значения С, то

Дадим теперь ряд оценок максимальных и минимальных собственных значений действительной положительно определенной матрицы А. Обозначим через  определитель А и через
определитель А и через  -след матрицы А. Рассмотрим
-след матрицы А. Рассмотрим

и

Так как среднее арифметическое положительных чисел не меньше чем их среднее геометрическое, то будем иметь:

Неравенство можно усилить, если заменить в левой части неравенства  на
на  а в правой части
а в правой части  на нуль. Тогда получим:
на нуль. Тогда получим:

Неравенство (43) дает оценку минимального собственного значения А снизу. Воспользуемся теперь (42) для того, чтобы получить оценку наибольшего собственного значения сверху. Преобразовывая (42), получим:

Если подставить в правую часть вместо  любое число
любое число  превышающее собственные значения А, то получим оценку сверху для собственных чисел А:
превышающее собственные значения А, то получим оценку сверху для собственных чисел А:

В качестве [а можно взять, например,  Эту оценку можно уточнить, воспользовавшись рекуррентной формулой
Эту оценку можно уточнить, воспользовавшись рекуррентной формулой

Получим убывающую последовательность чисел

для которой

Можно показать, что  где
где  является наибольшим положительным корнем уравнения
является наибольшим положительным корнем уравнения

Неравенство (43) также можно уточнить. При  имеем:
имеем:

Положим здесь  и применим (42). При этом получим:
и применим (42). При этом получим:

Зта оценка лучше, чем (43).
Последние неравенства можно использовать не только для положительно определенных матриц. Пусть А произвольная действительная неособая матрица. Матрица  будет симметрической и положительно определенной. Обозначим собственные значения
будет симметрической и положительно определенной. Обозначим собственные значения  через
через

При этом, если  -собственное значение
-собственное значение  соответствующий собственный вектор, то из
соответствующий собственный вектор, то из

следует

или

В силу принципа Релея будем иметь:

Таким образом,

где  определитель
определитель  след
след 
Полученные нами для симметрических матриц результаты переносятся и на эрмитовы, матрицы. Матрица А называется эрмитовой, если  (здесь черта над А означает комплексную сопряженность). Все собственные значения эрмитовой матрицы — действительные числа. Она имеет
(здесь черта над А означает комплексную сопряженность). Все собственные значения эрмитовой матрицы — действительные числа. Она имеет  взаимно ортогональных собственных векторов. Принцип Релея применим к эрмитовым матрицам, только вместо
взаимно ортогональных собственных векторов. Принцип Релея применим к эрмитовым матрицам, только вместо  и
и  нужно брать
нужно брать  и
и  где у — вектор, компоненты которого комплексно-сопряженные по отношению к компонентам х числа. Следовательно, все оценки, основанные на принципе Релея, сохранятся с соответствующими видоизменениями. Так же можно перенести и остальные оценки.
где у — вектор, компоненты которого комплексно-сопряженные по отношению к компонентам х числа. Следовательно, все оценки, основанные на принципе Релея, сохранятся с соответствующими видоизменениями. Так же можно перенести и остальные оценки.
2. Случай несимметрической матрицы.
В главе 6 мы доказали, что любая норма матрицы больше модулей ее собственных значений. Этим можно воспользоваться для оценки модулей собственных значений сверху. В частности, мы получим:

Если использовать третью норму матрицы, то получим уже известное неравенство (56). Неравенства (58) можно также записать в виде

Рассмотрим наряду с матрицей А еще матрицы

Это — эрмитовы матрицы. Пусть  нормированный собственный вектор А, соответствующий собственному значению
нормированный собственный вектор А, соответствующий собственному значению  Тогда
Тогда

Отсюда

где  и
и  -соответственно элементы
-соответственно элементы  Из (62) получаем:
Из (62) получаем:

Таким образом,

Аналогично найдем:

Мы получили оценки действительной и мнимой частей собственных значений.
Уточним несколько последний результат. Если обозначить собственные значения эрмитовой матрицы В через  а собственные значения эрмитовой матрицы С — через
а собственные значения эрмитовой матрицы С — через  то в силу принципа Релея из (62) следует:
то в силу принципа Релея из (62) следует:

Это — более точные оценки, чем (64) и (65), хотя их использование связано с получением собственных значений матриц В а С.
Пусть матрица А действительная. Тогда матрица В будет симметрической и для получения и  можно использовать приведенные ранее оценки. Матрица
можно использовать приведенные ранее оценки. Матрица  будет действительной кососимметрической. Такая матрица может иметь только чисто мнимые или нулевые собственные значения. Действительно, если X — ненулевое собственное значение
будет действительной кососимметрической. Такая матрица может иметь только чисто мнимые или нулевые собственные значения. Действительно, если X — ненулевое собственное значение  соответствующий собственный вектор, то будем иметь:
соответствующий собственный вектор, то будем иметь:

или

Так как элементы  действительные числа, то собственные значения будут попарно сопряжены. Обозначим ненулевые собственные значения
действительные числа, то собственные значения будут попарно сопряжены. Обозначим ненулевые собственные значения  через
через

Собственные значения С будут отличаться от собственных значений  только лишь делителем
только лишь делителем  Поэтому
Поэтому  Оценим
Оценим  Сумма попарных произведений собственных значений
Сумма попарных произведений собственных значений  будет равна
будет равна

и в то же время она равна коэффициенту при  в разложении олределителя
в разложении олределителя  по степеням
по степеням  Последний коэффициент равен сумме всех главных миноров второго порядка матрицы
Последний коэффициент равен сумме всех главных миноров второго порядка матрицы 
(Главными минорами порядка к матрицы  с элементами
с элементами  называются миноры вида
называются миноры вида

где  В нашем случае будем иметь:
В нашем случае будем иметь:

Обозначим  через
через  этом из 2) следует:
этом из 2) следует:

Отсюда

Эта оценка менее точна, но осуществляется проще.
В заключение этого параграфа покажем, что если обозначить

то каждое собственное значение X матрицы  лежит по крайней мере в одном из кругов
лежит по крайней мере в одном из кругов

и по крайней мере в одном из кругов

Пусть X — собственное значение А и  соответствующий собственный вектор. Тогда
соответствующий собственный вектор. Тогда

Пусть  При этом из
При этом из 

следует:

и так как  то получаем (76). Если провести эти же рассуждения для транспонированной матрицы, имеющей те же самые собственные значения, то получим (77). Утверждение доказано. Из (76) и (77) снова следует (59). Кроме того, если
то получаем (76). Если провести эти же рассуждения для транспонированной матрицы, имеющей те же самые собственные значения, то получим (77). Утверждение доказано. Из (76) и (77) снова следует (59). Кроме того, если

то

| << Предыдущий параграф | Следующий параграф >> |
- ГЛАВА 6. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- § 2. Метод исключения
- 1. Схема Гаусса с выбором главного элемента.
- 2. Компактная схема Гаусса.
- 3. Обращение матрицы.
- 4. Вычисление определителей.
- 5. Схема Жордана.
- 6. Схема без обратного хода.
- § 3. Метод квадратного корня
- § 4. Метод ортогонализации
- § 5. Метод сопряженных градиентов
- § 6. Метод разбиения на клетки
- § 7. Линейные операторы. Нормы операторов
- 1. Конечномерные линейные нормированные пространства.
- 2. Линейные операторы в конечномерном линейном нормированном пространстве и их связь с матрицами.
- 3. Сходимость последовательностей матриц и матричных рядов.
- § 8. Разновидности методов последовательных приближений
- § 9. Линейные полношаговые методы первого порядка
- 2. Метод Ричардсона.
- 3. Обращение матриц методом последовательных приближений.
- § 10. Линейные одношаговые методы первого порядка
- 2. Сходимость метода Зейделя.
- 3. Релаксационный метод.
- § 11. Метод скорейшего спуска
- ГЛАВА 7. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ВЫСШИХ СТЕПЕНЕЙ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
- § 2. Отделение корней
- 2. Границы расположения корней алгебраического уравнения.
- 3. Число действительных корней алгебраического уравнения.
- 4. Отделение действительных корней алгебраического уравнения.
- 5. Отделение комплексных корней алгебраических уравнений.
- § 3. Метод Лобачевского решения алгебраических уравнений
- 2. Метод Лобачевского. Случай комплексных корней.
- 3. Метод Лобачевского. Случай близких или равных корней.
- 4. Погрешность метода Лобачевского.
- 5. Видоизменение Лемера метода Лобачевского.
- § 4. Итерационные методы решения алгебраических и трансцендентных уравнений
- 2. Простейшие итерационные методы: метод секущих и метод Ньютона.
- 3. Метод Чебышева построения итераций высших порядков.
- 4. Построение итераций высших порядков с помощью теоремы Кёнига.
- 5. Метод Эйткена построения итераций высших порядков.
- 6. Пример.
- § 5. Решение систем уравнений
- 2. Метод Ньютона.
- 3. Метод скорейшего спуска.
- § 6. Отыскание корней алгебраических уравнений методом выделения множителей
- 1. Метод Лина выделения множителей.
- 2. Метод Фридмана.
- 3. Метод Хичкока выделения квадратного множителя.
- ГЛАВА 8. ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ
- § 2. Метод А. Н. Крылова
- 2. Отыскание собственных векторов матрицы.
- § 3. Метод Ланцоша
- 2. Отыскание собственных векторов.
- § 4. Метод Данилевского
- 1. Видоизменение метода Данилевского.
- § 5. Обзор других способов получения характеристического многочлена
- § 6. Определение границ собственных значений
- § 7. Итерационные методы отыскания собственных значений и собственных векторов матриц
- 2. Отыскание других собственных значений и соответствующих им собственных векторов для симметрических матриц.
- 3. Отыскание собственных значений и собственных векторов несимметрических матриц, имеющих простую структуру.
- 4. Некоторые замечания об отыскании собственных значений и собственных векторов матриц общей структуры.
- § 8. Ускорение сходимости итерационных процессов при решении задач линейной алгебры
- 2. Метод М. К. Гавурина.
- 3. Метод Л. А. Люстерника.
- 4. «дельта квадрат»-процесс Эйткена.
- 5. Улучшение сходимости итерационных процессов для отыскания собственных значений матриц.
- § 9. Неустранимая погрешность при численном решении систем линейных алгебраических уравнений
- ГЛАВА 9. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Метод С. А. Чаплыгина
- 2. Способ Чаплыгина построения улучшенных приближений.
- 3. Второй способ построения улучшенных приближений.
- 4. Метод Чаплыгина приближенного решения линейных дифференциальных уравнений второго порядка.
- § 3. Метод малого параметра
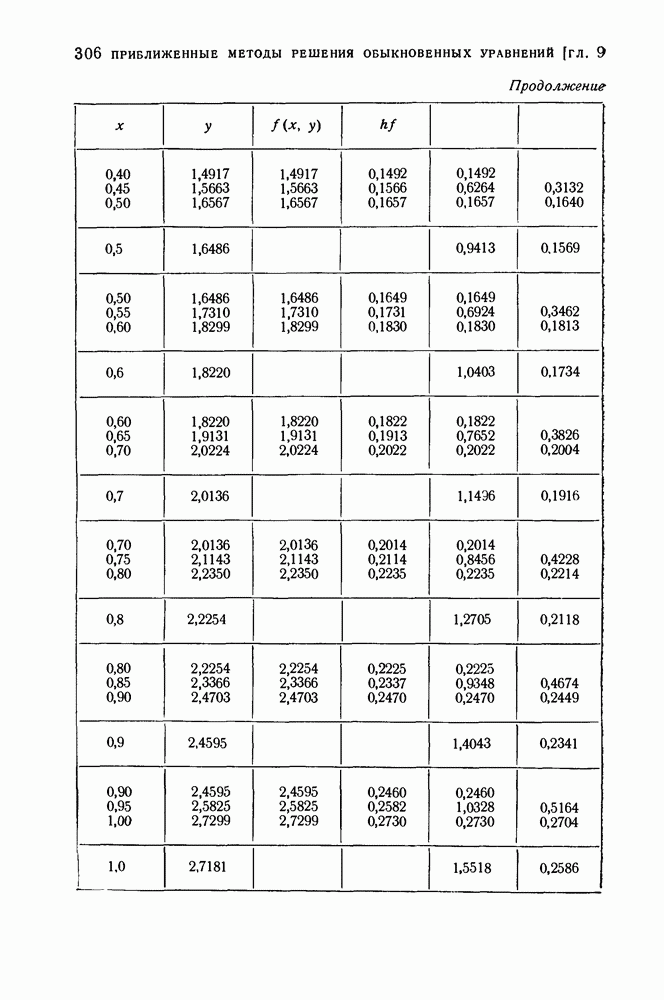
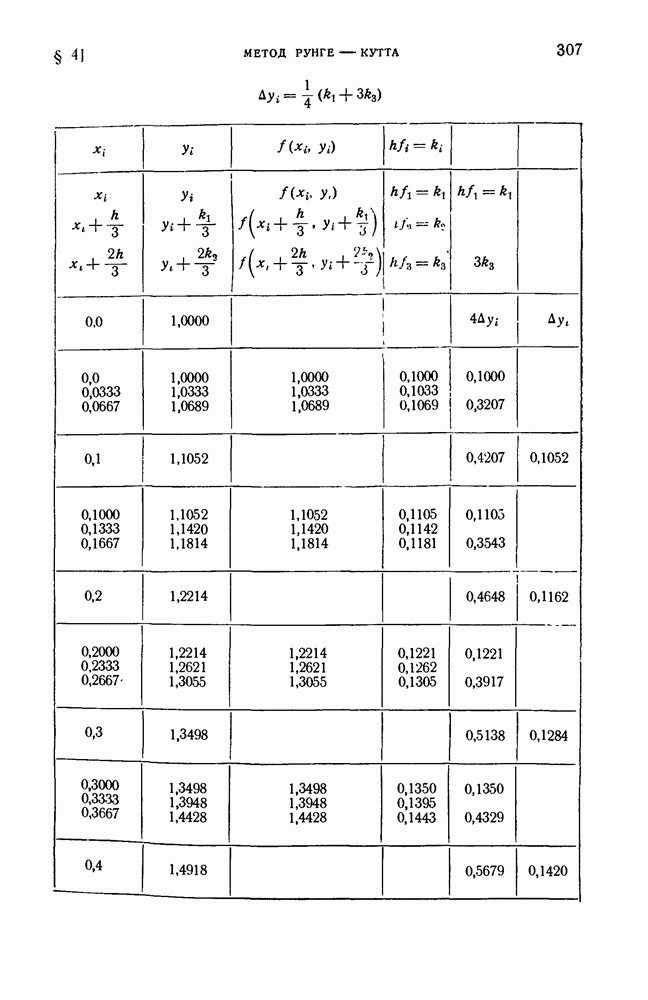
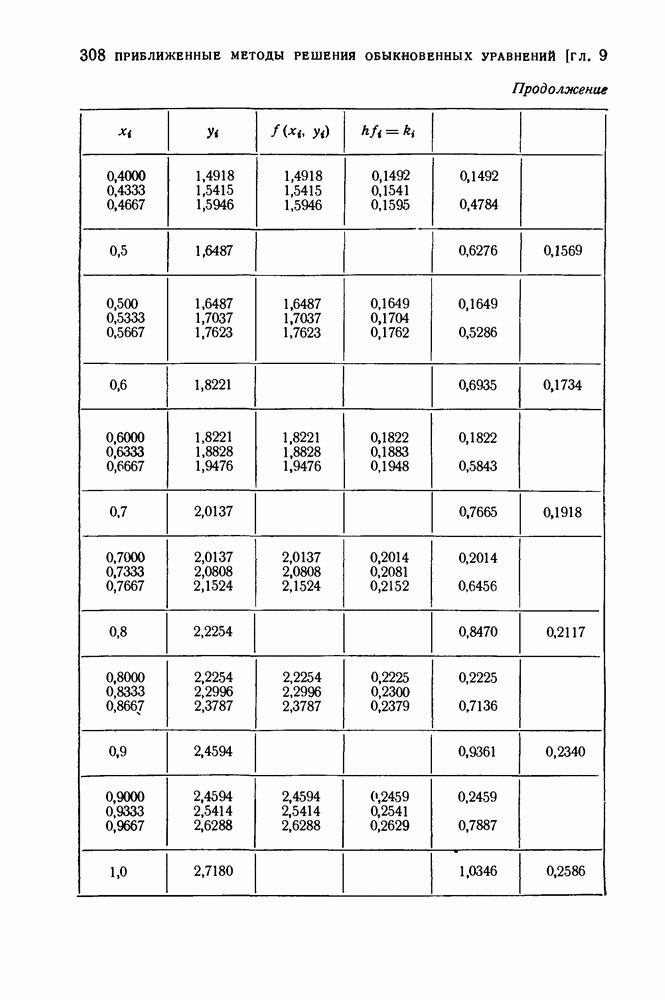
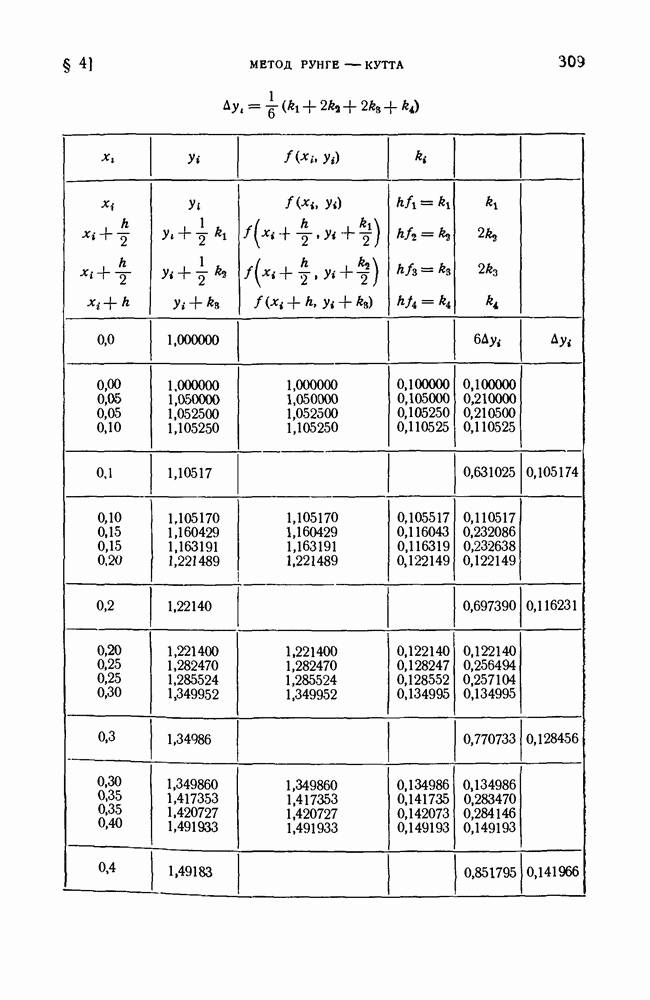
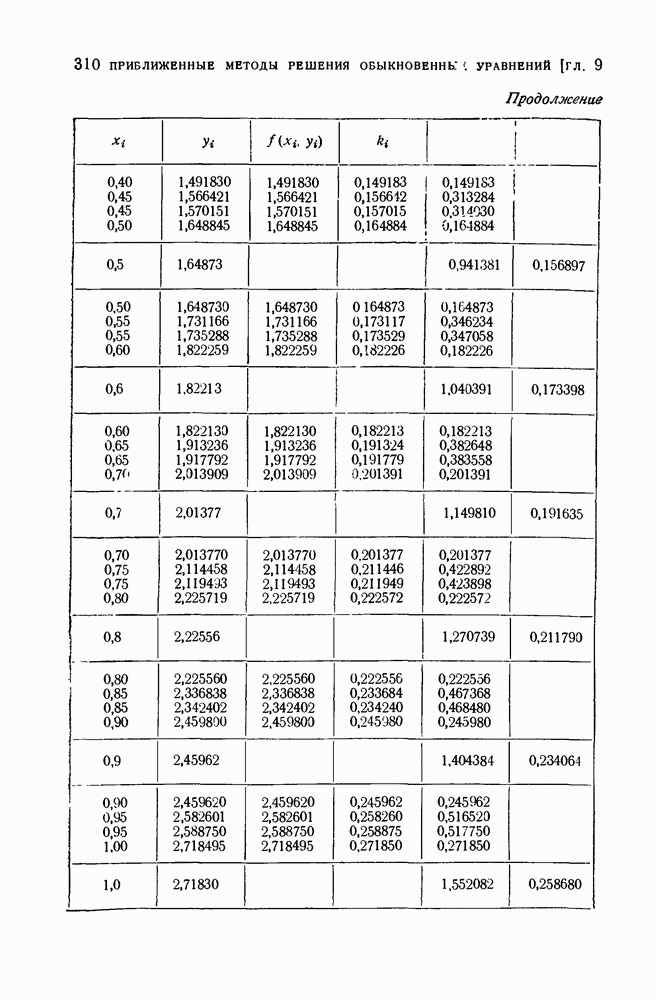
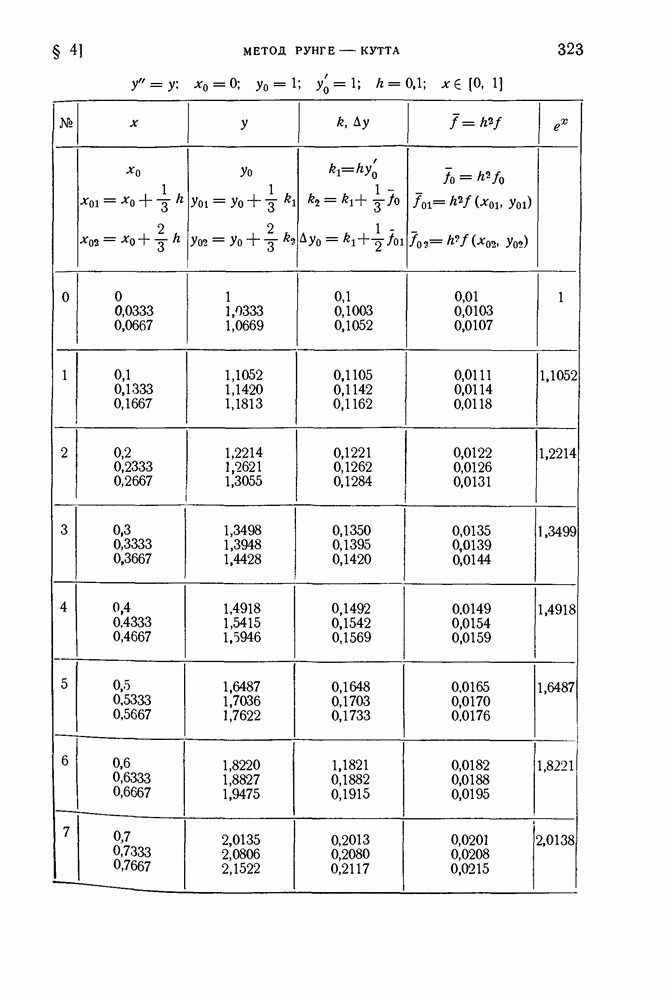
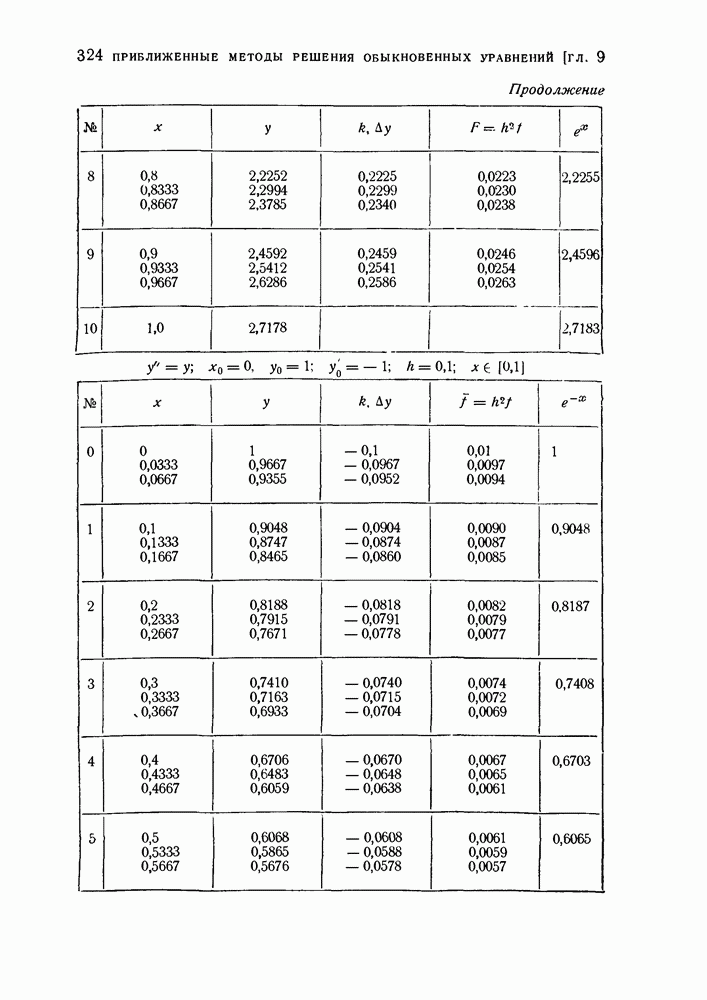
- § 4. Метод Рунге — Кутта
- 2. Метод Рунге — Кутта решения систем дифференциальных уравнений первого порядка.
- 3. Метод Рунге-Кутта решения уравнений второго порядка.
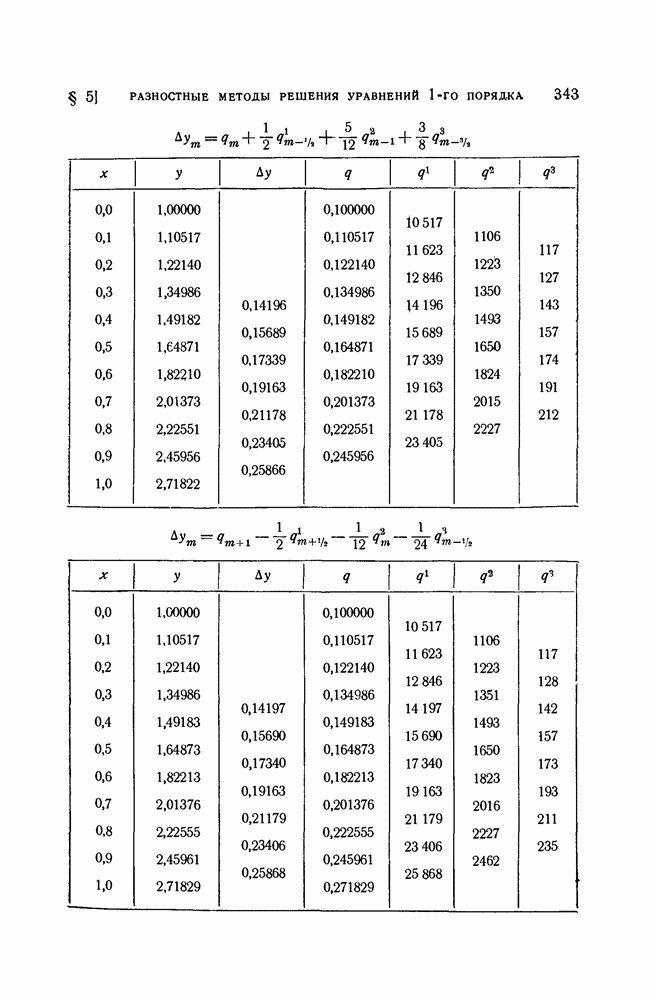
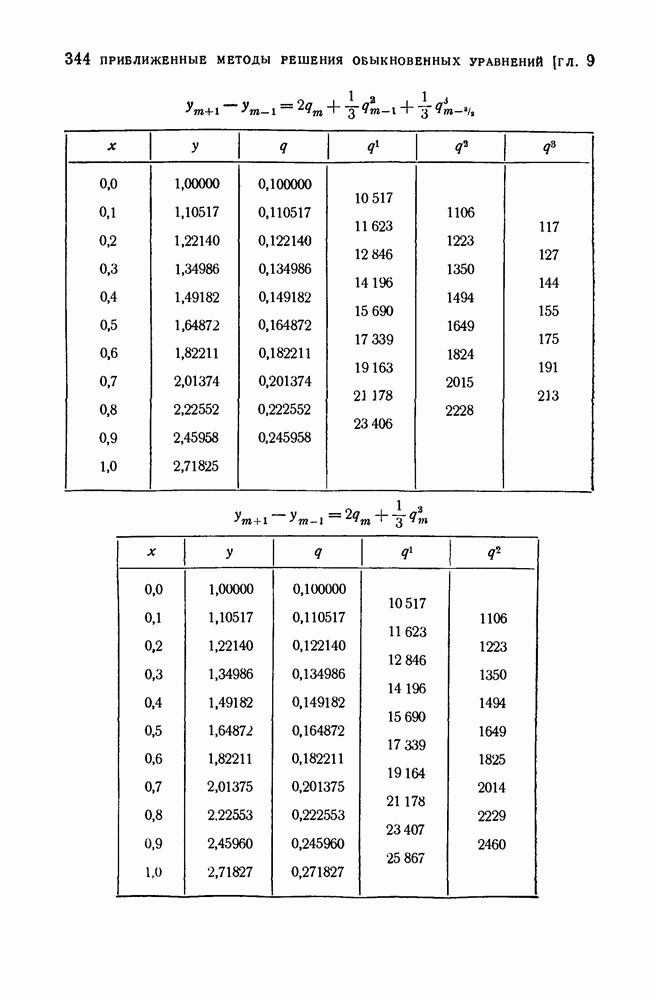
- § 5. Разностные методы решения обыкновенных дифференциальных уравнений первого порядка
- 1. Некоторые экстраполяционные формулы для интегрирования дифференциальных уравнений первого порядка.
- 2. Примеры интерполяционных формул.
- 3. Метод неопределенных коэффициентов вывода разностных формул.
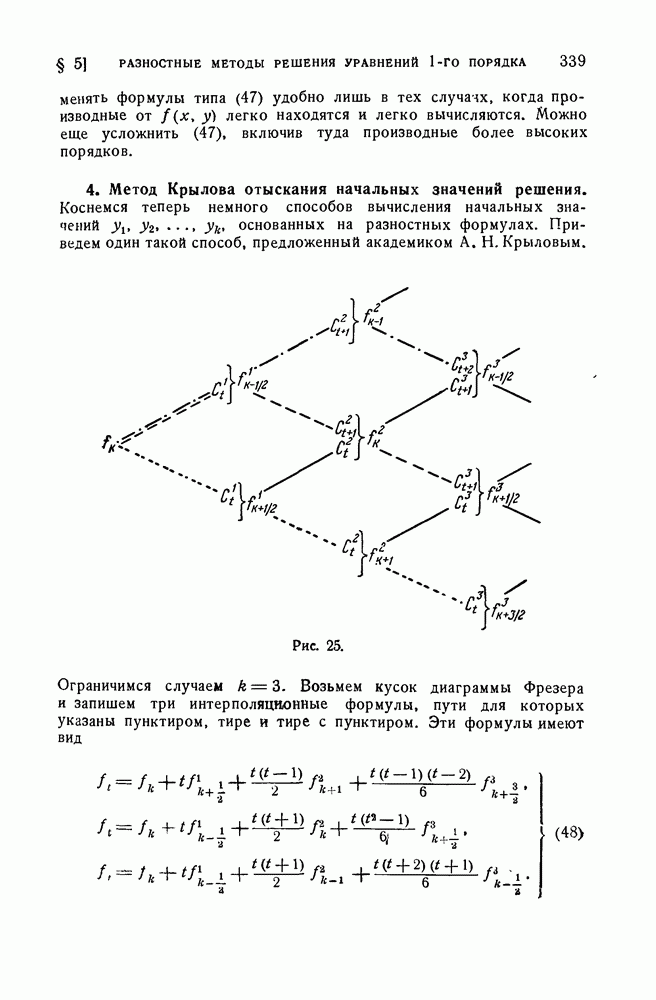
- 4. Метод Крылова отыскания начальных значений решения.
- 5. Примеры.
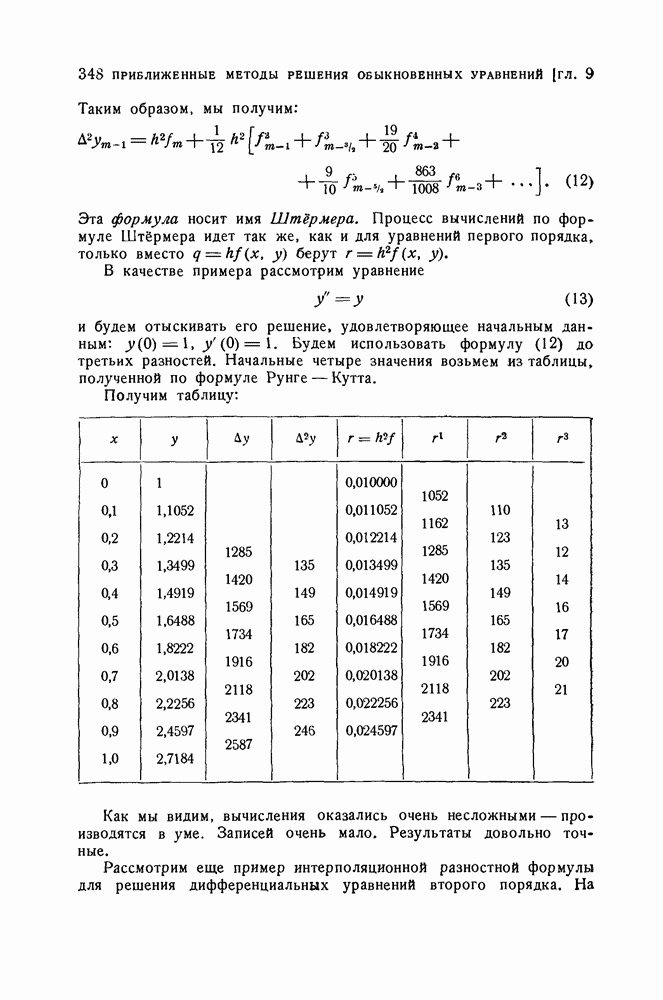
- § 6. Разностные методы решения обыкновенных дифференциальных уравнений высших порядков
- § 7. Оценка погрешности, сходимость и устойчивость разностных методов решения обыкновенных дифференциальных уравнений
- 2. Разностное уравнение для погрешности приближенного решения.
- 3. Оценки погрешности решений, получаемых по формулам Адамса.
- 4. Устойчивость разностных методов решения дифференциальных уравнений.
- 5. Оценка погрешности и сходимость устойчивых разностных методов решения дифференциальных уравнений.
- § 8. Решение краевых задач для обыкновенных дифференциальных уравнений методом конечных разностей
- 2. Метод конечных разностей решения краевых задач для нелинейных дифференциальных уравнений второго порядка.
- § 9. Метод прогонки
- § 10. Решение краевых задач для обыкновенных дифференциальных уравнений вариационными методами
- 1. Вариационные методы решения операторных уравнений в гильбертовом пространстве.
- 2. Метод Ритца решения вариационных задач.
- 3. Понятие о методе Галеркина.
- ГЛАВА 10. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ И ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
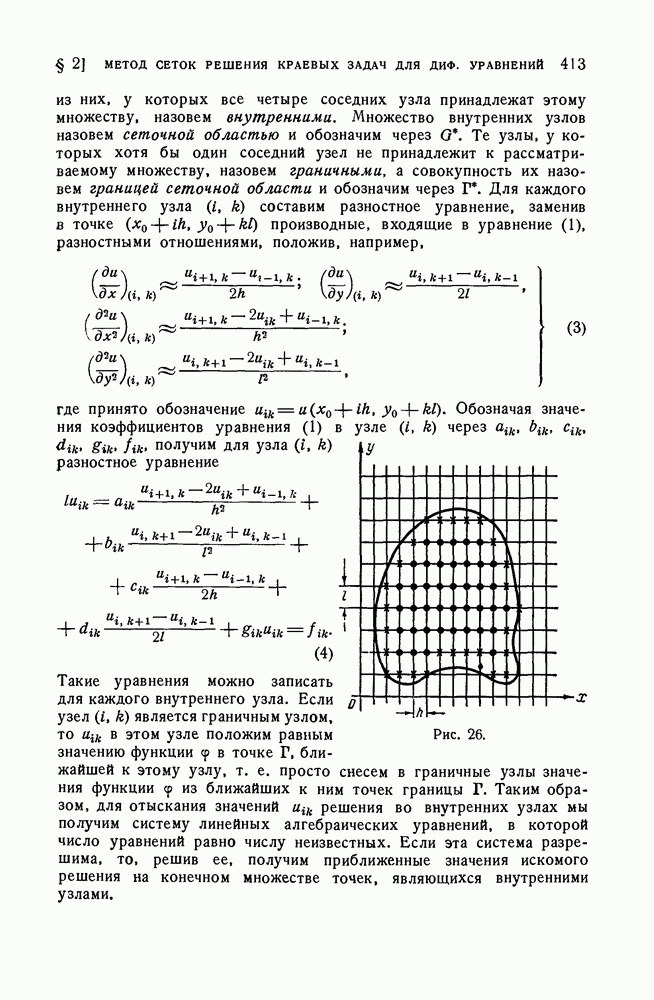
- § 2. Метод сеток решения краевых задач для дифференциальных уравнений эллиптического типа
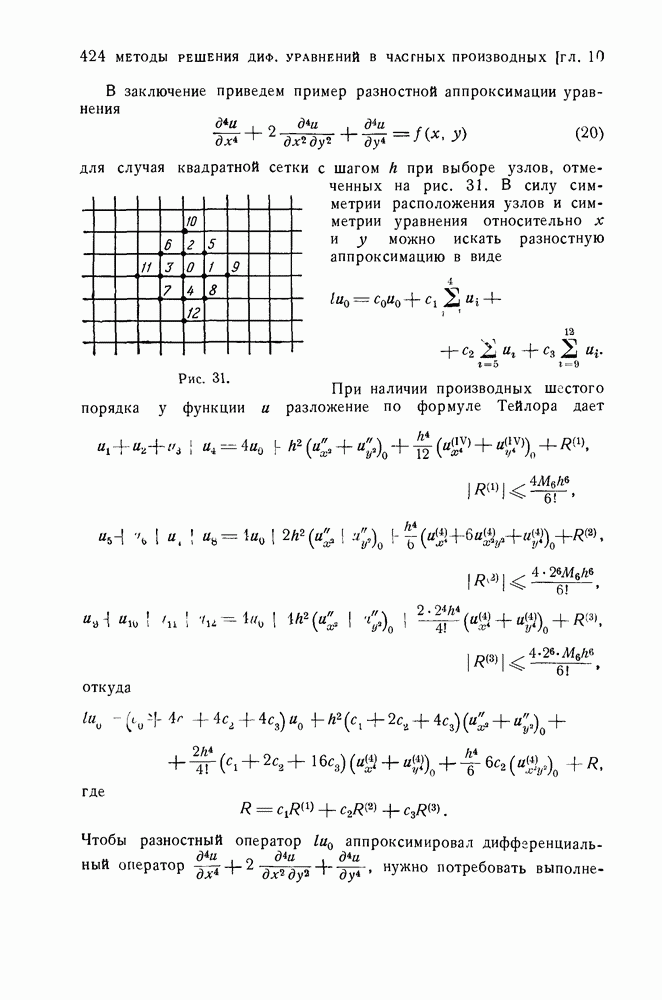
- 2. Аппроксимация дифференциальных уравнений разностными.
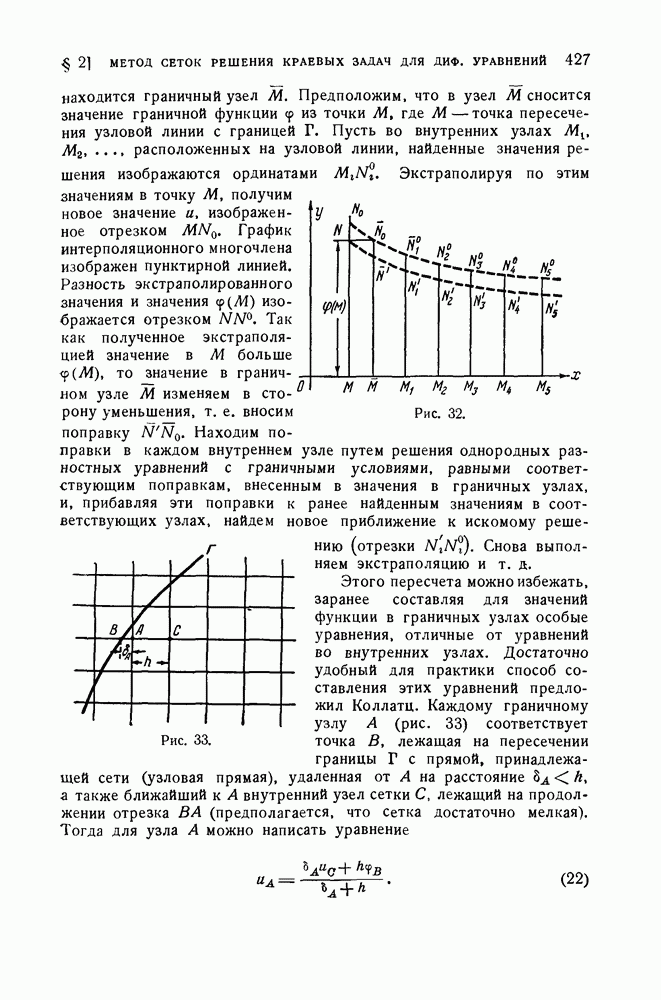
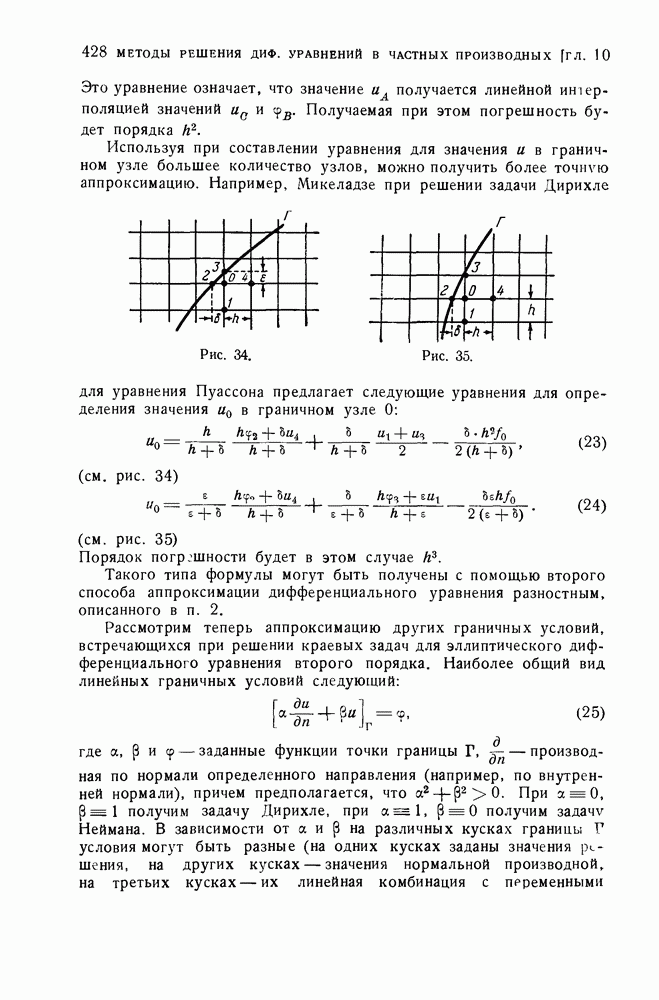
- 3. Аппроксимация граничных условий.
- 4. Разрешимость разностных уравнений и способы их решения.
- 5. Оценка погрешности и сходимость метода сеток.
- § 3. Метод сеток решения линейных дифференциальных уравнений гиперболического типа
- 1. Метод сеток для решения задачи Коши.
- 2. Оценка погрешности и сходимость метода сеток для неоднородного волнового уравнения.
- 3. Метод сеток решения смешанной задачи.
- 4. Другие разностные схемы.
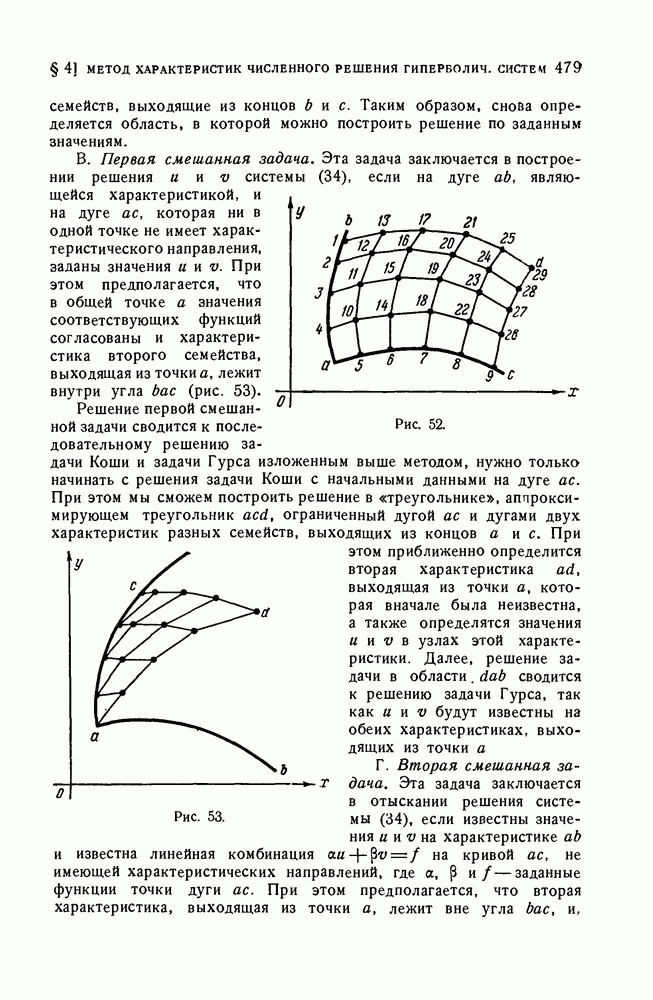
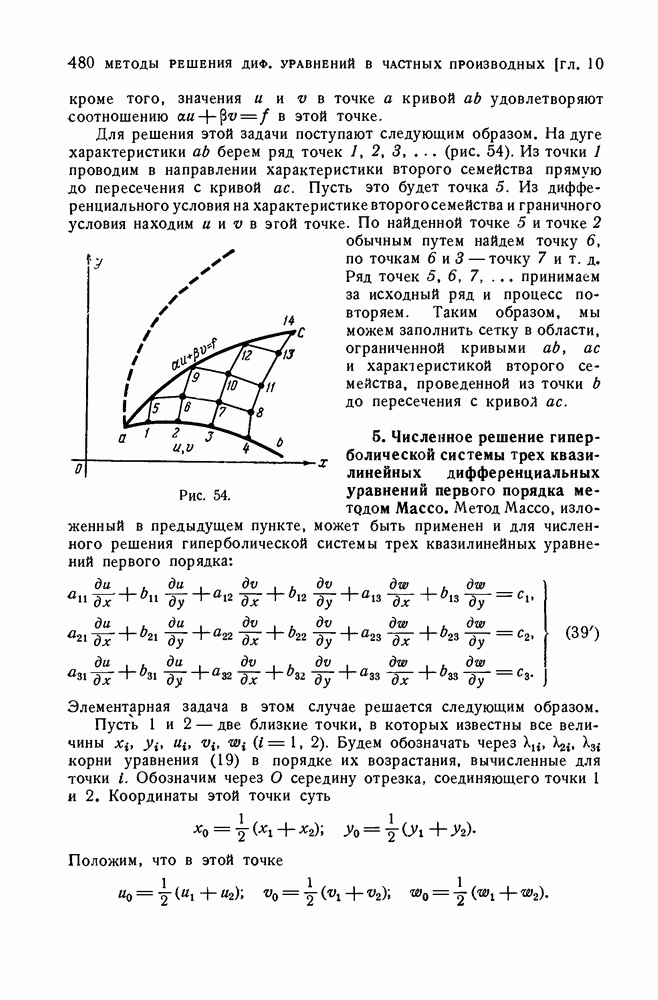
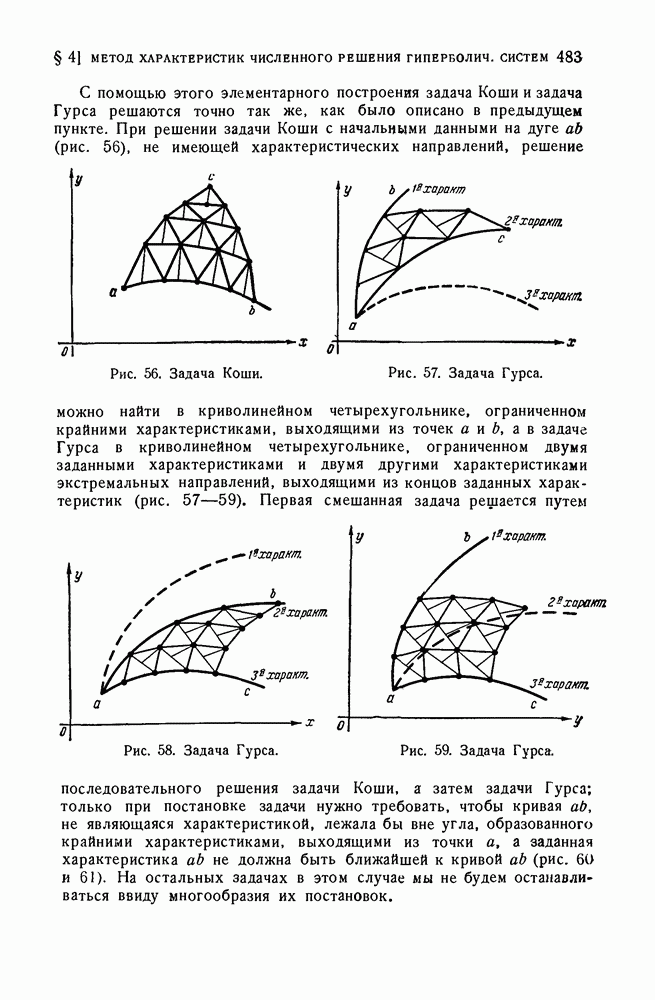
- § 4. Метод характеристик численного решения гиперболических систем квазилинейных дифференциальных уравнений в частных производных
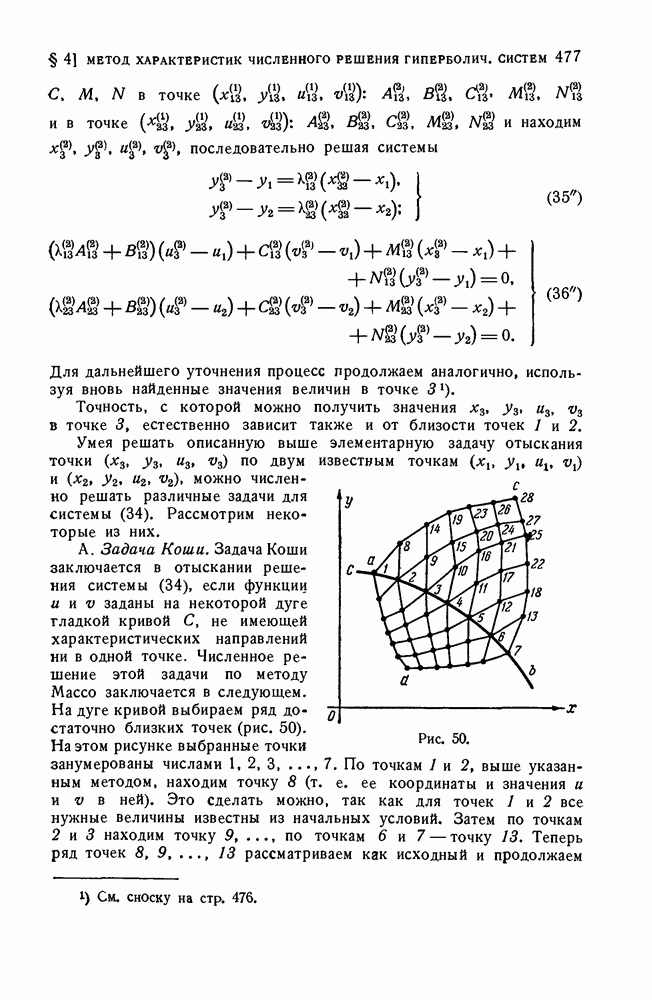
- 2. Примеры.
- 3. Уравнения характеристик квазилинейного гиперболического дифференциального уравнения второго порядка.
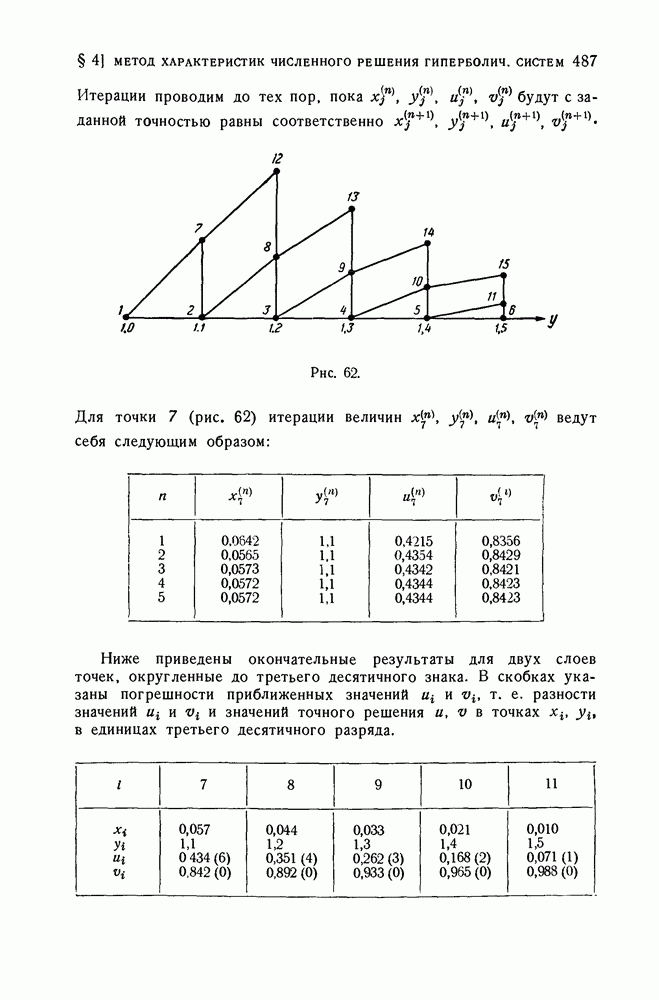
- 4. Численное решение квазилинейной гиперболической системы двух дифференциальных уравнений первого порядка методом Массо.
- 5. Численное решение гиперболической системы трех квазилинейных дифференциальных уравнений первого порядка методом Массо.
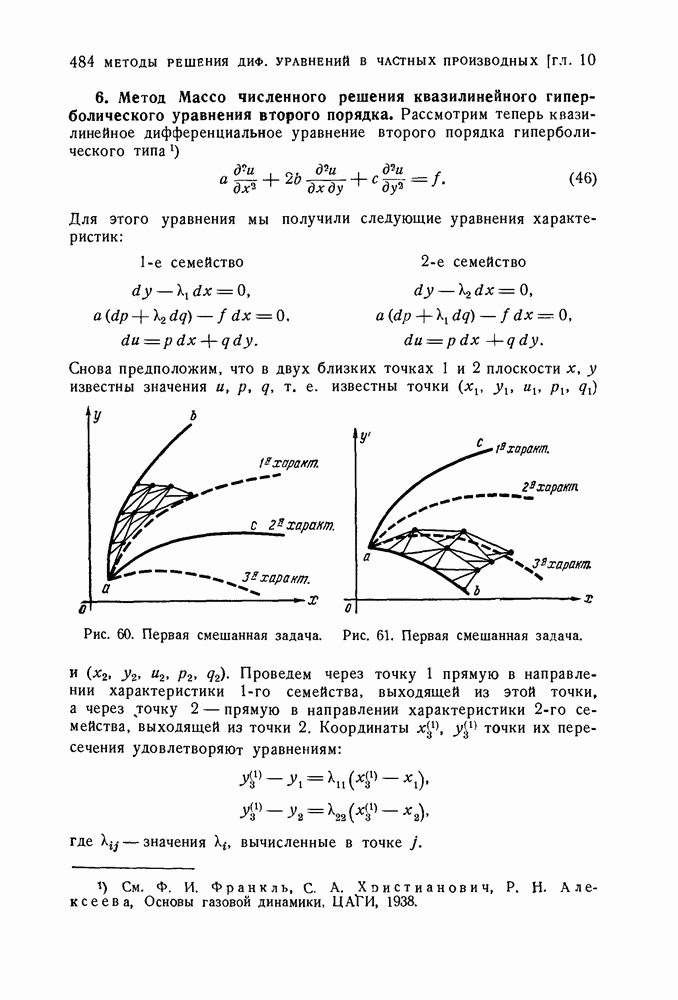
- 6. Метод Массо численного решения квазилинейного гиперболического уравнения второго порядка.
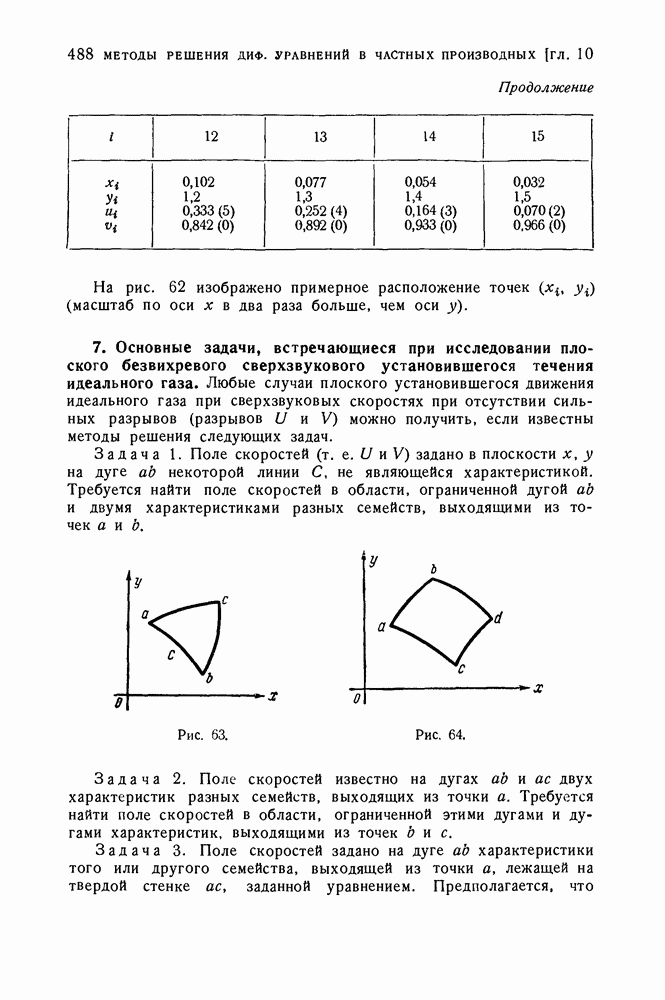
- 7. Основные задачи, встречающиеся при исследовании плоского безвихревого сверхзвукового установившегося течения идеального газа.
- § 5. Метод сеток решения линейных дифференциальных уравнений параболического типа
- 2. Метод сеток для решения смешанных задач. Понятие устойчивости разностных схем.
- § 6. Метод прогонки решения краевых задач для уравнений в частных производных
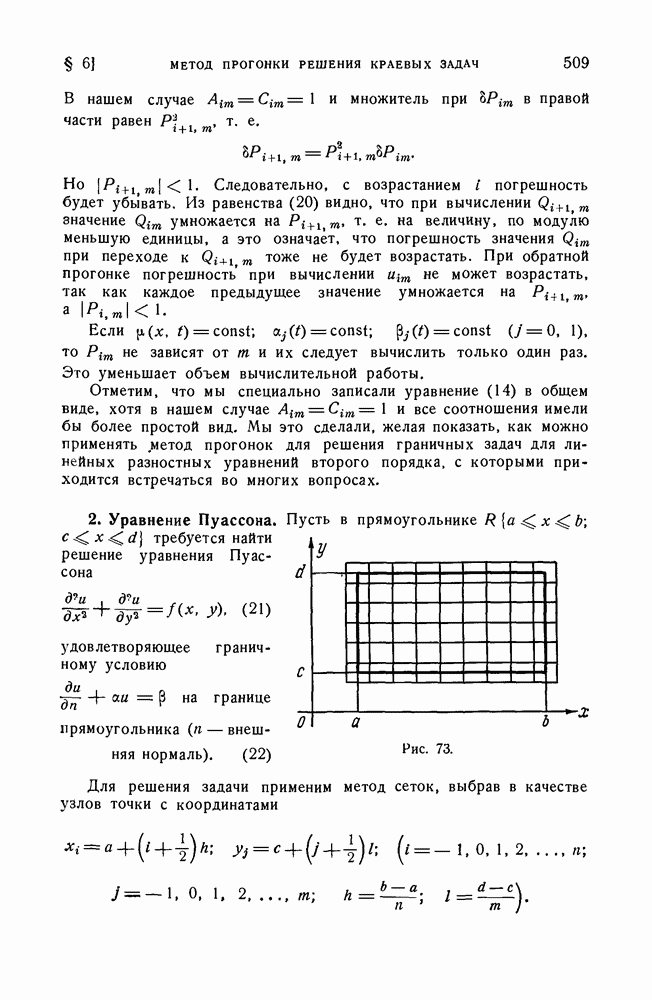
- 2. Уравнение Пуассона.
- § 7. Сходимость и устойчивость разностных схем
- 2. Понятие корректности и устойчивости разностной схемы.
- 3. Связь сходимости с корректностью разностной схемы.
- 4. Некоторые приемы исследования устойчивости разностных схем.
- 5. Некоторые общие замечания.
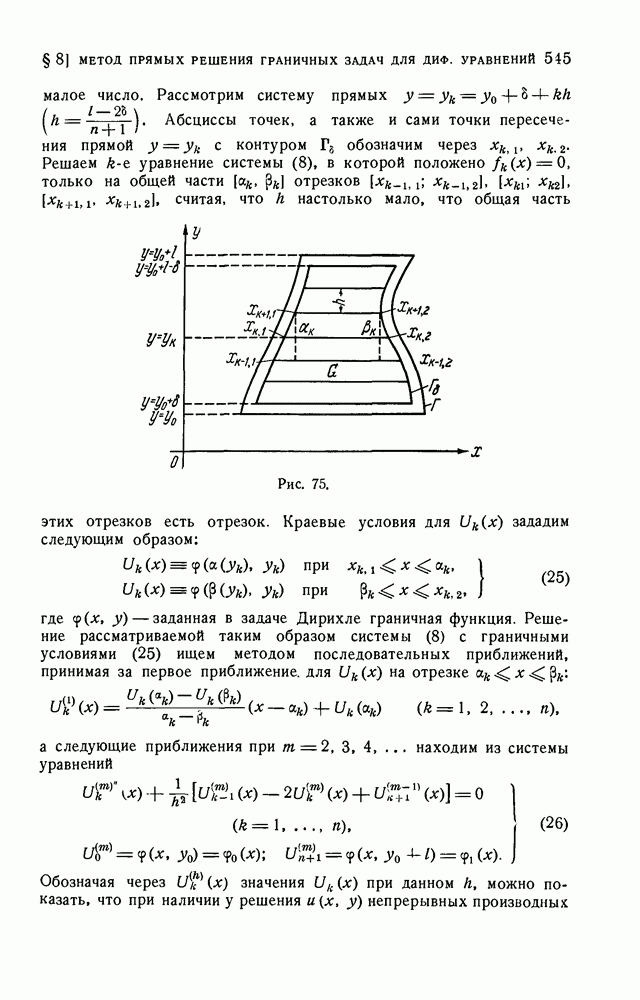
- § 8. Метод прямых решения граничных задач для дифференциальных уравнений в частных производных
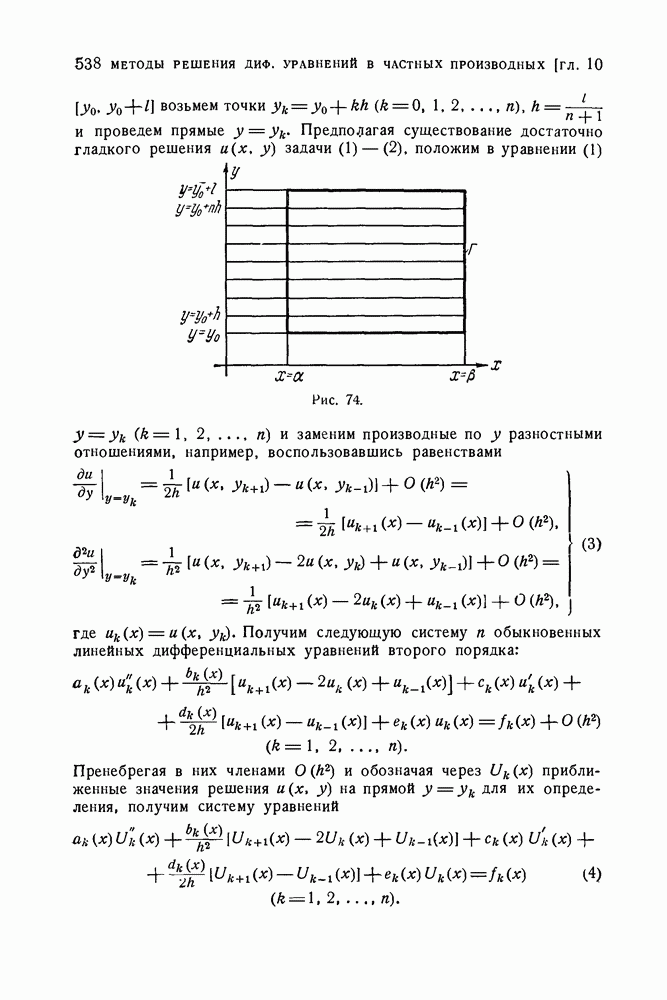
- 2. Метод прямых решения задачи Дирихле для уравнения Пуассона.
- 3. Метод прямых решения смешанной задачи для уравнения колебаний струны.
- 4. Метод прямых решения смешанной задачи для уравнения теплопроводности.
- § 9. Вариационные методы решения краевых задач для дифференциальных уравнений математической физики
- 2. Метод Ритца приближенного решения краевых задач для линейных дифференциальных уравнений в частных производных второго порядка эллиптического типа.
- 3. Некоторые другие вариационные методы.
- 4. Метод Ритца решения задачи о собственных значениях.
- 5. Метод Галеркина решения краевых задач.
- § 10. Приближенные методы решения интегральных уравнений
- 2. Решение интегральных уравнений Фредгольма второго рода методом замены ядра на вырожденное.
- 3. Метод моментов.
- 4. Метод наименьших квадратов.
- 5. Метод последовательных приближений.
- 6. Приближенное решение уравнений Вольтерра.