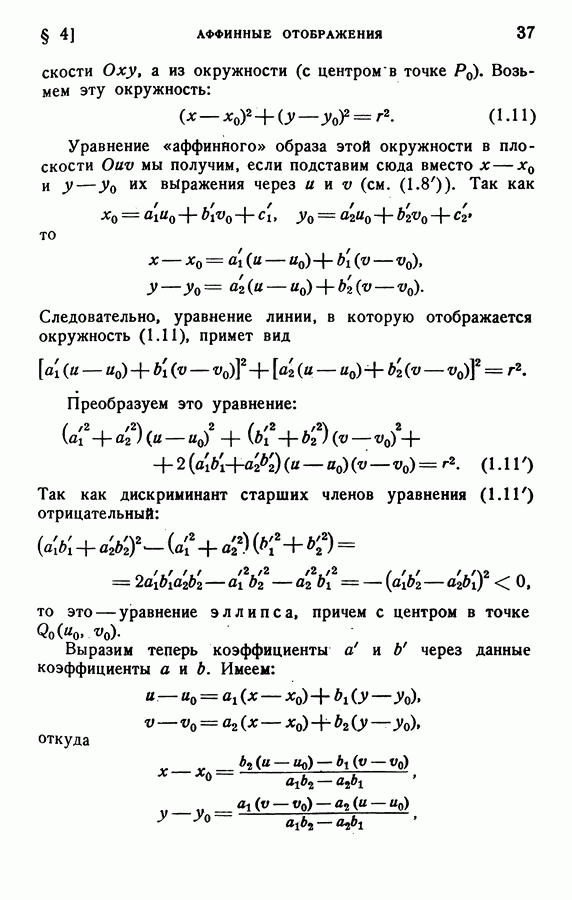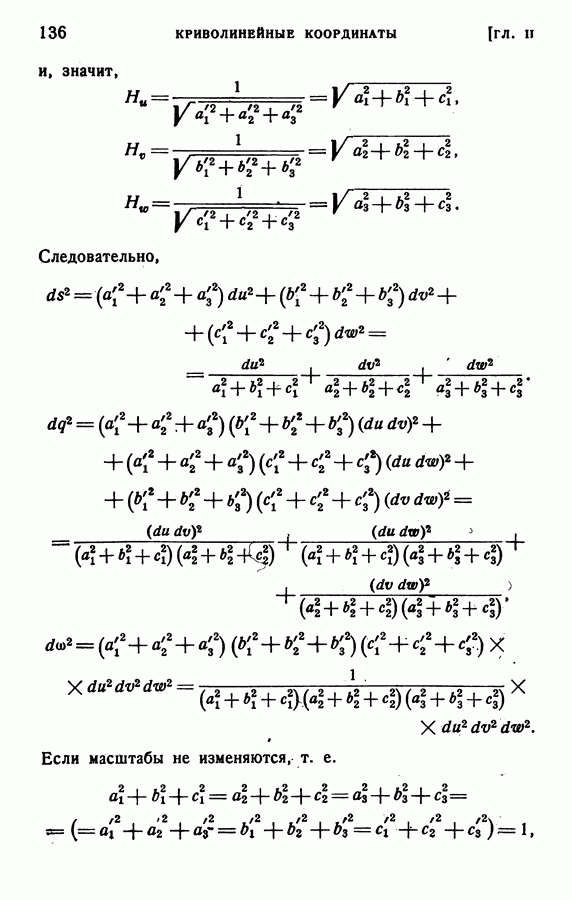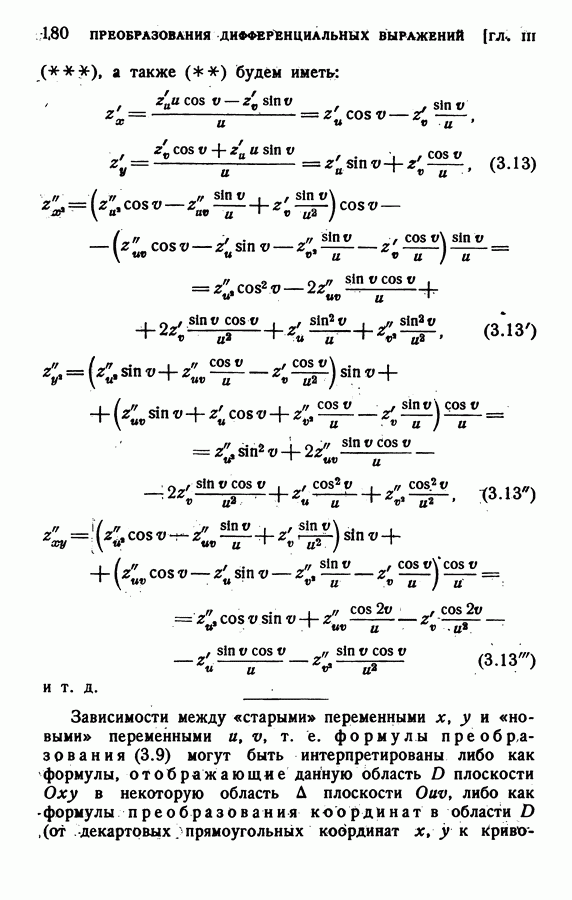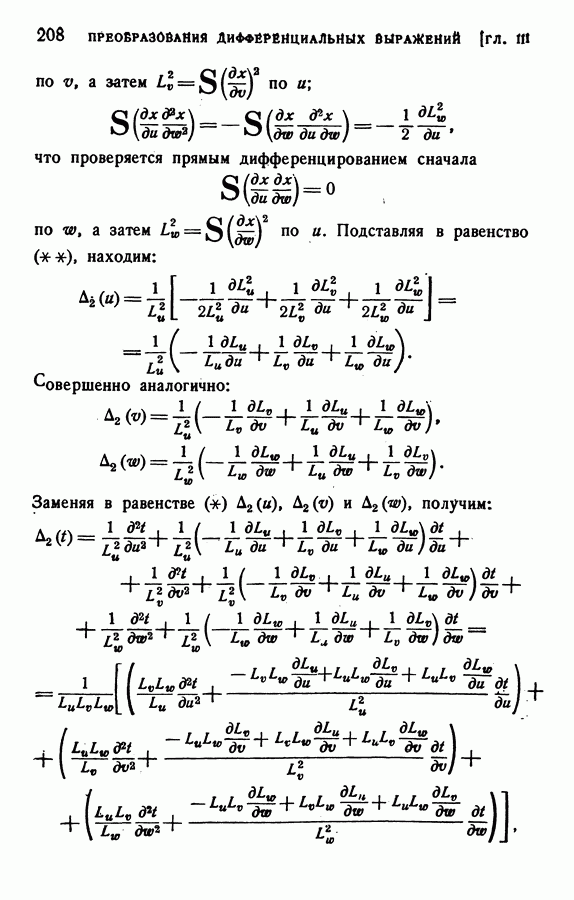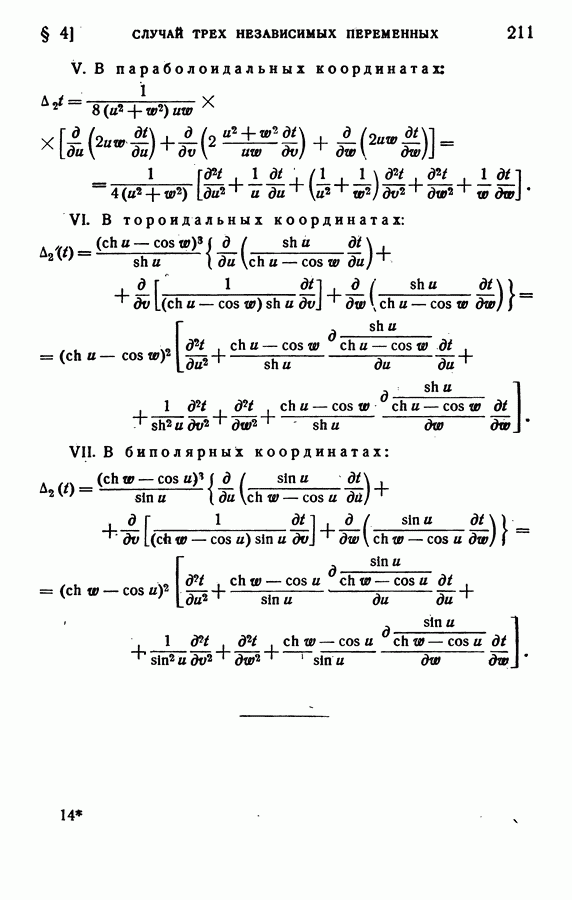| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
88. Двойной интеграл.
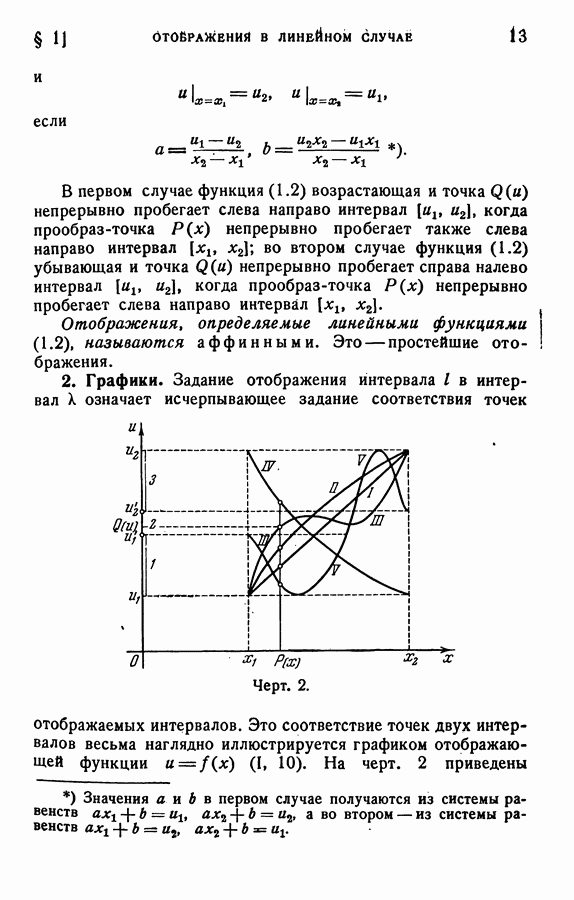
Рассмотрим приведение двойного интеграла к двукратному интегралу для важнейших систем криволинейных координат на плоскости и соответствующие примеры преобразований интегралов от декартовых прямоугольных координат к криволинейным.
I. Полярные координаты. Пусть дан интеграл

где  — полярные координаты точки плоской области
— полярные координаты точки плоской области  (для большей наглядности здесь мы взяли обычные обозначения полярных координат; см. п°39). При вычислении этого интеграла посредством двух однократных интегрирований по
(для большей наглядности здесь мы взяли обычные обозначения полярных координат; см. п°39). При вычислении этого интеграла посредством двух однократных интегрирований по  и по
и по  следует различать два случая: а) полюс системы лежит вне области
следует различать два случая: а) полюс системы лежит вне области  (или на ее границе); б) полюс системы лежит в области
(или на ее границе); б) полюс системы лежит в области 
а) Если область  обладает тем свойством, что любой луч, исходящий из полюса (координатная, линия
обладает тем свойством, что любой луч, исходящий из полюса (координатная, линия  ), имеет не больше одной точки «входа» в область
), имеет не больше одной точки «входа» в область  (и, значит, не больше одной точки «выхода» из нее), то
(и, значит, не больше одной точки «выхода» из нее), то

где  — полярные радиусы соответственно точек «входа» и «выхода» из области
— полярные радиусы соответственно точек «входа» и «выхода» из области  прямой линии
прямой линии  а интервал
а интервал  есть наибольший интервал изменения координаты
есть наибольший интервал изменения координаты  в области
в области  (Другой порядок интегрирования, когда сначала интегрирование производится по
(Другой порядок интегрирования, когда сначала интегрирование производится по  а затем по
а затем по  обычно не применяется.)
обычно не применяется.)
б) Если область  обладает тем свойством, что любой луч, исходящий из полюса (координатная линия
обладает тем свойством, что любой луч, исходящий из полюса (координатная линия  ), имеет одну точку «выхода» из области
), имеет одну точку «выхода» из области  (т. е. если
(т. е. если
область  как говорят, звездная относительно полюса), то
как говорят, звездная относительно полюса), то

где  — полярный радиус точки выхода из области
— полярный радиус точки выхода из области  линии
линии  — полярное уравнение линии — границы области
— полярное уравнение линии — границы области 
Пример 1. Пусть

где  — круг, ограниченный окружностью
— круг, ограниченный окружностью  (окружность с центром в точке
(окружность с центром в точке  радиуса а, проходящая через начало координат), а функция Ф (6) непрерывна при
радиуса а, проходящая через начало координат), а функция Ф (6) непрерывна при  Вычисление этого интеграла с помощью двукратного дает:
Вычисление этого интеграла с помощью двукратного дает:

или

Гораздо проще выглядят и двойной и соответствующий двукратный интегралы, если перейти к полярным координатам:

причем в системе полярных координат уравнение окружности, ограничивающей круг  будет
будет  Значит,
Значит,

Если рассматривать формулы замены переменных как формулы, отображающие круг  на декартову плоскость
на декартову плоскость  то
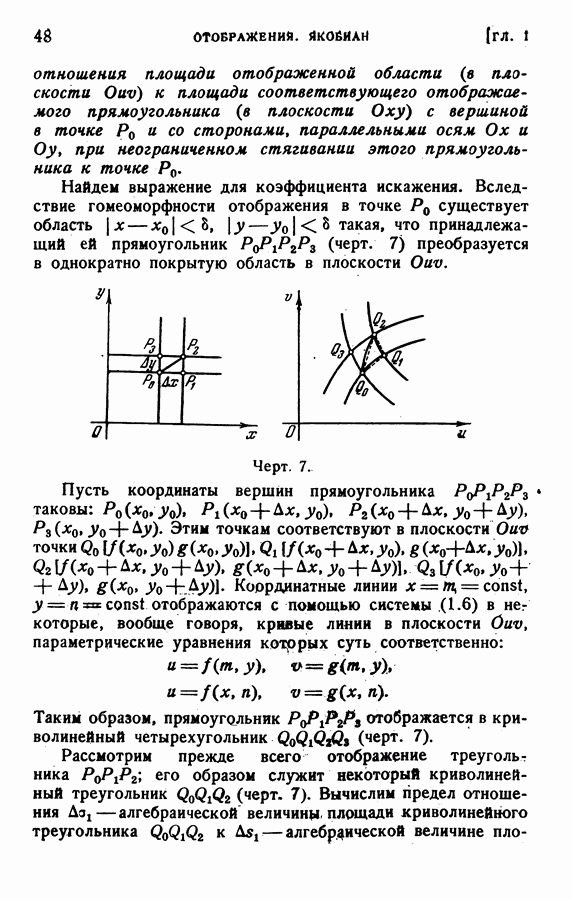
то

где  криволинейная трапеция, ограниченная интервалом
криволинейная трапеция, ограниченная интервалом

оси  и косинусоидой
и косинусоидой 
Пример 2. Пусть

где  — вся плоскость без какой-нибудь окрестности точки
— вся плоскость без какой-нибудь окрестности точки  . Перейдем к полярным координатам:
. Перейдем к полярным координатам:

где  — радиус окружности, ограничивающей исключаемую окрестность начала координат. Отсюда видно, что данный несобственный интеграл (в смысле главного значения) существует, если
— радиус окружности, ограничивающей исключаемую окрестность начала координат. Отсюда видно, что данный несобственный интеграл (в смысле главного значения) существует, если  и тогда он равен
и тогда он равен  он не существует, если
он не существует, если  (То же самое имеет место и для интеграла
(То же самое имеет место и для интеграла  распространенного на всю плоскость без какой-нибудь области, содержащей точку
распространенного на всю плоскость без какой-нибудь области, содержащей точку  Легко доказать, что полученные результаты относятся вообще к рассматриваемому несобственному интегралу, а не только, к главному его значению.
Легко доказать, что полученные результаты относятся вообще к рассматриваемому несобственному интегралу, а не только, к главному его значению.
Пример 3. Пусть

где  — какая-нибудь окрестность точки
— какая-нибудь окрестность точки  (эта окрестность ограничена окружностью радиуса
(эта окрестность ограничена окружностью радиуса  Переходя к полярным координатам, найдем:
Переходя к полярным координатам, найдем:

Отсюда видно, что данный несобственный интеграл (в смысле главного значения) существует, если  (и тогда он равен
(и тогда он равен  ); он не существует, если
); он не существует, если  (То
(То
же самое имеет место и для интеграла  взятого по какой-нибудь конечной области, содержащей точку
взятого по какой-нибудь конечной области, содержащей точку  Легко доказать, что полученные результаты относятся вообще к рассматриваемому несобственному интегралу, а не только к его главному значению.
Легко доказать, что полученные результаты относятся вообще к рассматриваемому несобственному интегралу, а не только к его главному значению.
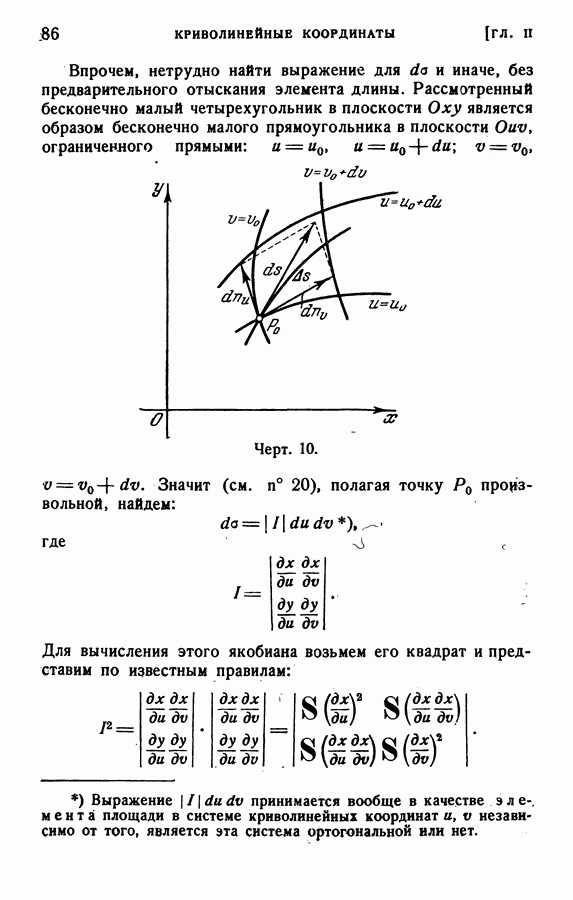
II. Другие координаты. Вполне аналогично приводится двойной интеграл к двукратным в случае других криволинейных координат.
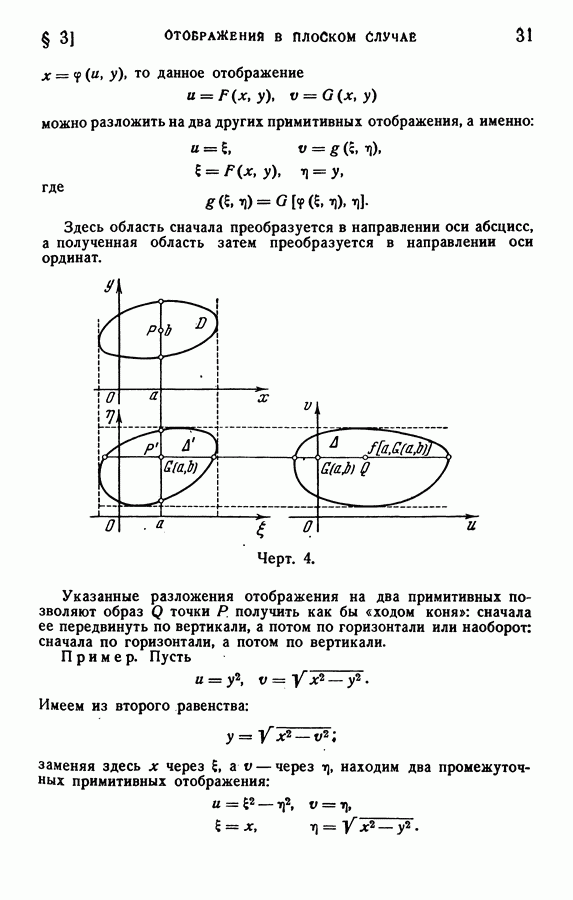
Если же система координат не имеет простого геометрического смысла, то при замене переменных в двойном интеграле удобнее пользоваться первой Интерпретацией формул преобразования, чем второй, т. е. удобнее представлять преобразованный интеграл в виде (4.6), чем в виде (4.7), и, значит, сохранять систему декартовых координат, но в другой, отображенной, области.
Пример 4. Пусть

где  — область, ограниченная эллипсом
— область, ограниченная эллипсом  а функция
а функция  непрерывна при
непрерывна при  . В декартовых координатах этот интеграл выражается довольно сложным двукратным интегралом (и совпадение левой части уравнения эллипса с аргументом подынтегральной функции нисколько не облегчает вычислений). Но если перейти к обобщенным полярным координатам, связанным с декартовыми координатами формулами (см. п°40)
. В декартовых координатах этот интеграл выражается довольно сложным двукратным интегралом (и совпадение левой части уравнения эллипса с аргументом подынтегральной функции нисколько не облегчает вычислений). Но если перейти к обобщенным полярным координатам, связанным с декартовыми координатами формулами (см. п°40)

где  — положительные константы, то всё значительно упрощаете Имеем:
— положительные константы, то всё значительно упрощаете Имеем:

причем в системе обобщенных полярных координат уравнением эллипса, ограничивающего область  будет
будет  Интегрируя сначала по
Интегрируя сначала по  при постоянном, но произвольном у, а затем по
при постоянном, но произвольном у, а затем по  в границах наибольшего изменения этой переменной в области
в границах наибольшего изменения этой переменной в области  т. е. в интервале
т. е. в интервале  получим:
получим:

Мы видим, насколько проще стало интегральное выражение для величины 
Пример 5. Пусть

где  — треугольник, ограниченный прямыми:
— треугольник, ограниченный прямыми:  непрерывные функции своих аргументов. Имеем в данных координатах:
непрерывные функции своих аргументов. Имеем в данных координатах:

Однако заменим переменные интегрирования новыми переменными  в соответствии с формулами:
в соответствии с формулами:

Обращая эти равенства, находим:

Отсюда видно, что формулы преобразования гомеоморфно отображают всю плоскость  лишенную прямой
лишенную прямой  на плоскость
на плоскость  причем треугольник
причем треугольник  отображается в квадрат А, ограниченный прямыми:
отображается в квадрат А, ограниченный прямыми:  (Заметим, что Точке (0,0) треугольника
(Заметим, что Точке (0,0) треугольника  соответствует отрезок:
соответствует отрезок: 
Так как

то

и, значит,

Хотя подынтегральное выражение заметно не упростилось, но зато область интегрирования в новых координатах оказалась просто квадратом, так что преобразованный двойной интеграл привелся к двукратному интегралу с постоянными пределами.
Если

Первый из интегралов в правой части есть так называемый эйлеров интеграл первого рода; он обозначается символом  («бета от
(«бета от  и
и  ). Нетрудно (с помощью замены переменной
). Нетрудно (с помощью замены переменной  показать, что
показать, что  ,
,
следовательно, мы приходим к формуле

которая называется формулой Лиувилля  . В частности,
. В частности,  находим значение так называемого интеграла Дирихле:
находим значение так называемого интеграла Дирихле:

Если  то имеем:
то имеем:

Вычисляя интеграл слева в декартовых координатах, получаем соотношение

выражающее одно из свойств эйлерова интеграла 
Пример 6. Пусть

где  первый квадрант плоскости
первый квадрант плоскости  причем
причем  Нетрудно убедиться, хотя бы при помощи усиления подынтегрального выражения заменой множителя единицей, что этот несобственный интеграл сходится. Очевидно, имеем:
Нетрудно убедиться, хотя бы при помощи усиления подынтегрального выражения заменой множителя единицей, что этот несобственный интеграл сходится. Очевидно, имеем:

Каждый из этих интегралов есть так называемый эйлеров интеграл второго рода. Он обозначается символом Г («гамма») от соответствующего параметра:  Итак:
Итак:

Однако произведем в данном двойном интеграле замену переменных по формулам (пример 5):

Первому квадранту в плоскости  соответствует бесконечная полоса А в плоскости
соответствует бесконечная полоса А в плоскости  ограниченная прямыми:
ограниченная прямыми:  Имеем:
Имеем:

Приводя последний двойной интеграл к двукратному, получим:

Первый из интегралов справа есть, как известно (см. пример 5), эйлеров интеграл  рода
рода  а второй — эйлеров интеграл
а второй — эйлеров интеграл  рода
рода  Значит,
Значит,

что дает важное соотношение между эйлеровыми интегралами 1-го и 2-го родов. Его записывают обычно так:

Благодаря соотношению (4.8) можно, между прочим, интегралу Дирихле (пример 5) придать очень удобный вид:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОТОБРАЖЕНИЯ. ЯКОБИАН
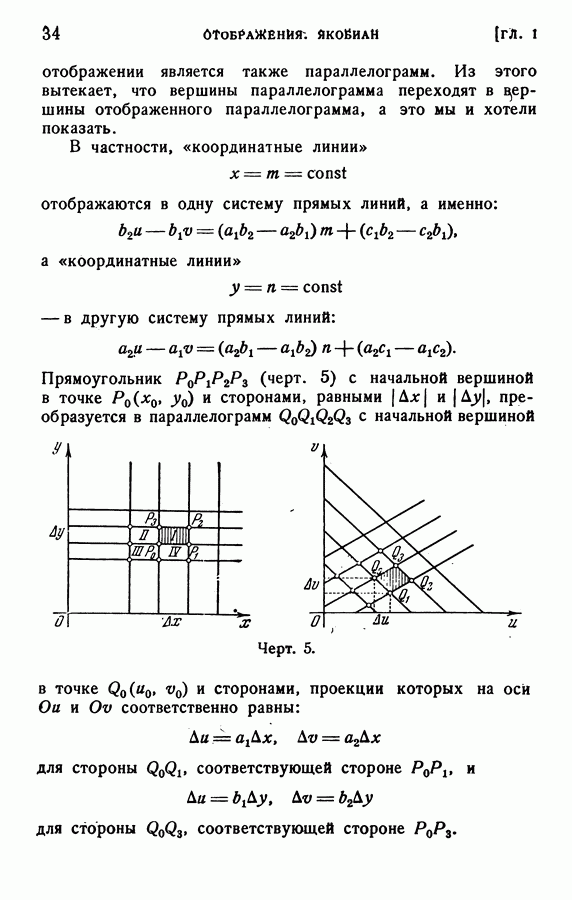
- 1. Определения. Аффинные отображения.
- 2. Графики.
- 3. Обращение. Гомеоморфизм.
- 4. Суперпозиция.
- § 2. КОЭФФИЦИЕНТ ИСКАЖЕНИЯ И ПРОИЗВОДНАЯ
- 6. Направление перемещения. Обратное отображение.
- 7. Суперпозиция.
- § 3. ОТОБРАЖЕНИЯ В ПЛОСКОМ СЛУЧАЕ
- 9. Обращение.
- 10. Гомеоморфизм.
- 11. Суперпозиция.
- § 4. АФФИННЫЕ ОТОБРАЖЕНИЯ
- 13. Равномерно распределенные точки.
- 14. Коэффициент искажения.
- 15. Направление перемещения.
- § 5. НЕКОТОРЫЕ ЧАСТНЫЕ АФФИННЫЕ ОТОБРАЖЕНИЯ. СВОЙСТВА ОПРЕДЕЛИТЕЛЯ
- 17. Сохранение площади. Движение.
- 18. Отображения гомотетии и подобия.
- 19. Свойства определителя.
- § 6. КОЭФФИЦИЕНТ ИСКАЖЕНИЯ (ОБЩИЙ СЛУЧАЙ) И ЯКОБИАН. РЕГУЛЯРНЫЕ ОТОБРАЖЕНИЯ
- 21. Обобщение.
- 22. Направление перемещения.
- 23. Регулярные отображения.
- § 7. СВОЙСТВА ЯКОБИАНА
- 25. Якобиан обратного отображения.
- 26. Суперпозиция.
- § 8. ВЫРОЖДЕНИЕ ОТОБРАЖЕНИЯ ЗАВИСИМОСТЬ ФУНКЦИИ
- 28. Зависимость функций.
- § 9. ОТОБРАЖЕНИЯ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- 30. Свойства якобиана. Зависимость функций.
- ГЛАВА II. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
- 32. Функциональная шкала
- § 2. ПЛОСКИЙ СЛУЧАЙ
- 33. Определения. Координатные линии.
- 34. Ортогональность системы.
- 35. Коэффициенты Ламе.
- 36. Элементы длины и площади.
- 37. Другой вывод.
- § 3. ВАЖНЕЙШИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ НА ПЛОСКОСТИ
- 38. Декартовы координаты.
- 39. Полярные координаты.
- 40. Обобщенные полярные координаты.
- § 4. ЭЛЛИПТИЧЕСКИЕ КООРДИНАТЫ И ИХ ВЫРОЖДЕНИЯ
- 41. Общие эллиптические координаты.
- 42. Вырожденные эллиптические координаты. Униформизация.
- § 5. ДРУГИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ ОРТОГОНАЛЬНЫХ КООРДИНАТ НА ПЛОСКОСТИ
- 43. Параболические координаты.
- 44. Биполярные координаты.
- § 6. ПРОСТРАНСТВЕННЫЙ СЛУЧАЙ
- 45. Определения. Координатные поверхности и линии.
- 46. Ортогональность системы.
- 47. Коэффициенты Ламе.
- § 7. ЭЛЕМЕНТЫ ДЛИНЫ, ОБЪЕМА И ПЛОЩАДИ ПОВЕРХНОСТИ
- 49. Элемент объема.
- 50. Другой вывод.
- 51. Элемент площади поверхности. Направляющие косинусы нормали.
- 52. Элемент площади поверхности в криволинейных координатах в пространстве.
- § 8. ВАЖНЕЙШИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ В ПРОСТРАНСТВЕ
- 54. Цилиндрические координаты.
- 55. Сферические координаты.
- 56. Телесный угол.
- 57. Обобщенные сферические координаты.
- § 9. ЭЛЛИПСОИДАЛЬНЫЕ КООРДИНАТЫ И ИХ ВЫРОЖДЕНИЯ
- 59. Вырожденные эллипсоидальные координаты. Униформизация.
- 60. Сферические координаты.
- 61. Вырожденные эллипсоидальные «вытянутые» координаты.
- 62. Вырожденные эллипсоидальные «сплюснутые» координаты.
- $ 10. ДРУГИЕ СИСТЕМЫ КРИВОЛИНЕЙНЫХ ОРТОГОНАЛЬНЫХ КООРДИНАТ В ПРОСТРАНСТВЕ
- 64. Параболоидальные координаты.
- 65. Тороидальные координаты.
- 66. Биполярные координаты.
- 67. Цилиндрические координаты.
- ГЛАВА III. ПРЕОБРАЗОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ ВЫРАЖЕНИЙ
- 69. Замена функции.
- 70. Замена независимой переменной и функции.
- § 2. СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- 71. Замена независимых переменных.
- 72. Замена функции.
- 73. Замена независимых переменных и функции.
- § 3. ПРЕОБРАЗОВАНИЯ «ДИФФЕРЕНЦИАЛЬНЫХ ПАРАМЕТРОВ» И «УСЛОВИЙ РЕГУЛЯРНОСТИ»
- 75. Параметр второго порядка (лапласиан).
- 76. Условия регулярности.
- § 4. СЛУЧАЙ ТРЕХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ. ПРЕОБРАЗОВАНИЯ «ДИФФЕРЕНЦИАЛЬНЫХ ПАРАМЕТРОВ»
- 78. Преобразования «дифференциальных параметров».
- 79. Выражения лапласиана в известных криволинейных координатах.
- ГЛАВА IV. ИНТЕГРАЛЬНЫЕ ВЫРАЖЕНИЯ И ИХ ПРЕОБРАЗОВАНИЯ
- § 1. ИНТЕГРАЛ ПО МЕРЕ ОБЛАСТИ
- 81. Основные свойства.
- 82. Вычисление интегралов.
- 83. Несобственные интегралы.
- § 2. ЗАМЕНА ПЕРЕМЕННЫХ В ИНТЕГРАЛЕ ПО МЕРЕ
- 85. Преобразования в декартовых координатах.
- 86. Преобразования в криволинейных координатах.
- § 3. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ. ПРИМЕРЫ
- 88. Двойной интеграл.
- 89. Тройной интеграл.
- § 4. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПО КООРДИНАТЕ
- 91. Определение и свойства интеграла.
- 92. Способы вычисления.
- 93, Интеграл как функционал. Дополнительные замечания.
- § 5. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ ПО КООРДИНАТАМ
- 95. Определение и свойства интеграла.
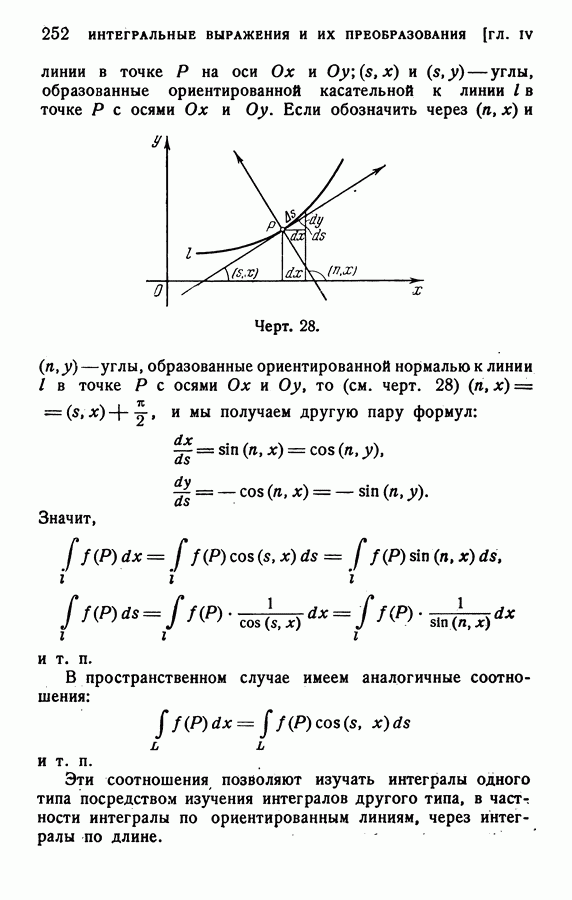
- 96. Способы вычисления.
- 97. Дополнительные замечания.
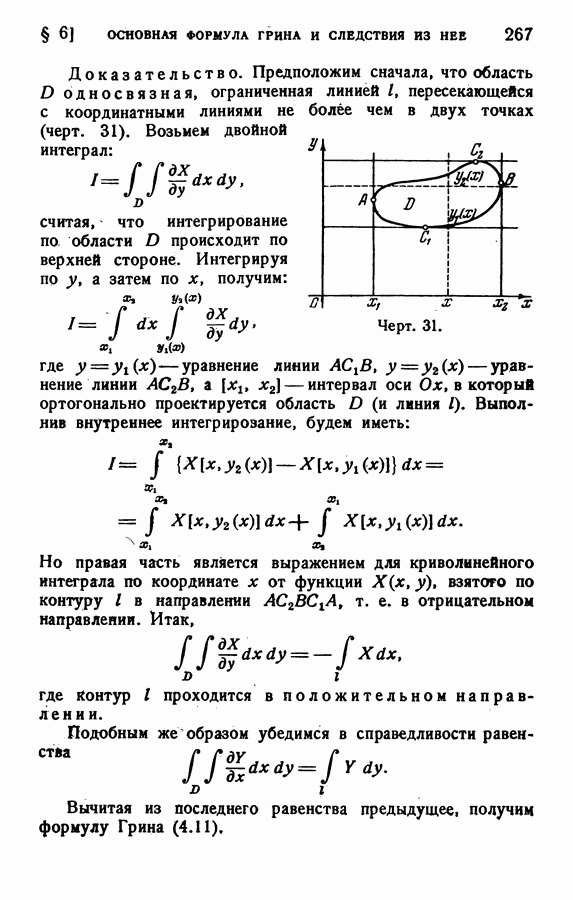
- § 6. ОСНОВНАЯ ФОРМУЛА ГРИНА И СЛЕДСТВИЯ ИЗ НЕЕ
- 99. Независимость интеграла от контура интегрирования.
- 100. Условие полного дифференциала. Формула Ньютона — Лейбница.
- 101. Применения. Задача термодинамики.
- § 7. ФОРМУЛЫ СТОКСА И ОСТРОГРАДСКОГО И СЛЕДСТВИЯ ИЗ НИХ
- 103. Независимость интеграла от контура интегрирования. Условие полного дифференциала. Формула Ньютона — Лейбница.
- 104. Формула Остроградского.
- 105. Независимость интеграла от поверхности интегрирования.
- § 8 ФОРМУЛЫ ГРИНА И ИХ ОБОБЩЕНИЯ
- 107. Плоский случай.
- 108. Пространственный случай.