| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.1.6.5. Оценка теплот образования алканов на основе инкрементов групп
Этот подход к установлению связи между структурой и энергией основан на индивидуальных вкладах групп атомов, а не групп связей. Разница в теплотах образования между структурно изомерными алканами обусловлена присутствием в каждом из них определенных групп атомов и их взаимного расположения. Идея о том, что отдельные группы, такие как  или
или  вносят вполне определенный вклад в теплоту образования молекулы, была высказана впервые Парксом и Хуфманом [64].
вносят вполне определенный вклад в теплоту образования молекулы, была высказана впервые Парксом и Хуфманом [64].
Общая энергия молекулы в состоянии идеального газа включает: 1) внутримолекулярную энергию, обусловленную связыванием атомов, на которую могут влиять пространственные затруднения, сверхсопряжение и другие эффекты, и 2) поступательную, вращательную и колебательную энергию. Для того чтобы групповой инкремент отражал действительность, вклад каждой группы в каждый из видов энергии должен быть практически постоянным от молекулы к молекуле. На самом деле, в большинстве схем содержатся поправочные члены на пространственные факторы; для алканов можно построить простую схему, которая отвечает экспериментальным данным в надежных пределах. Такая схема, содержащая параметры для  ,
,  и С, была предложена Бенсоном и Бассом [65], и при ее использовании было получено хорошее согласие с экспериментом для многих алканов, в которых не было больших пространственных затруднений. Только в случае очень сильно разветвленных алканов этот метод дал плохие результаты, и для них Бенсон и Басс ввели специальные поправки, учитывающие пространственные напряжения. Схемы такого типа были использованы также для оценки теплот образования воображаемых молекул, свободных от напряжения, что позволило оценивать энергию напряжения. Инкременты Бенсона и Басса составляют (в
и С, была предложена Бенсоном и Бассом [65], и при ее использовании было получено хорошее согласие с экспериментом для многих алканов, в которых не было больших пространственных затруднений. Только в случае очень сильно разветвленных алканов этот метод дал плохие результаты, и для них Бенсон и Басс ввели специальные поправки, учитывающие пространственные напряжения. Схемы такого типа были использованы также для оценки теплот образования воображаемых молекул, свободных от напряжения, что позволило оценивать энергию напряжения. Инкременты Бенсона и Басса составляют (в  ):
):

При их использовании  для ациклического алкана дается выражением:
для ациклического алкана дается выражением:

где N — число различных входящих в молекулу групп.
Обзор других схем этого типа дан Коксом и Пилчером [54] Существует много поправок, которые обычно вводят при наличии в молекуле структурных особенностей, связанных с увеличением пространственного напряжения, что требует введения в схему расчета теплот образования добавочных параметров. Введение таких поправок соблазнительно, однако к ним следует относиться с большой осторожностью. Даже в случае более обоснованного метода расчета молекулярных структур и энергий, основанного на молекулярной механике, чрезвычайно трудно отнести дестабилизацию к наличию в молекуле определенного типа напряжения; эти трудности возрастают при использовании для расчетов подхода на основе инкрементов простых групп. Тем не менее, можно построить схему, основанную на инкрементах простых групп, которая способна обеспечить точный расчет теплот образования ациклических алканов.

Рис. 2.1.5. Зависимость  от n
от n
Эта схема может быть ограничена той областью, в пределах которой можно использовать простое представление об аддитивности групп. Нашей целью в данном случае является предложение приемлемой схемы для всех ациклических алканов по возможности без введения поправок на пространственные факторы в значения энергии для отдельных взаимодействий. Вывод такой схемы полезен для понимания природы факторов, влияющих на устойчивость алканов.
Первым шагом в разработке такой схемы является определение вклада группы  . Это лучше всего достигается, если учесть, что неразветвленные алканы отличаются от соседних членов в гомологическом ряду на группу
. Это лучше всего достигается, если учесть, что неразветвленные алканы отличаются от соседних членов в гомологическом ряду на группу  , и вклад
, и вклад  -группы может быть найден на основе разницы в теплотах образования соседних членов гомологического ряда. Эти значения
-группы может быть найден на основе разницы в теплотах образования соседних членов гомологического ряда. Эти значения  из табл. 2.5 относят к числу атомов углерода и из графика на рис. 2.1.5 находят вклад теплоты образования метиленовой группы, равный
из табл. 2.5 относят к числу атомов углерода и из графика на рис. 2.1.5 находят вклад теплоты образования метиленовой группы, равный  . Следующим инкрементом, который необходимо определить, является инкремент метильной группы. Это можно осуществить, вычитая вклад метиленовой группы из теплоты образования неразветвленного алкана и деля остаток пополам (каждый неразветвленный алкан содержит две метальные группы). Найденное таким путем значение инкремента для метильной группы равно
. Следующим инкрементом, который необходимо определить, является инкремент метильной группы. Это можно осуществить, вычитая вклад метиленовой группы из теплоты образования неразветвленного алкана и деля остаток пополам (каждый неразветвленный алкан содержит две метальные группы). Найденное таким путем значение инкремента для метильной группы равно  . При использовании этой схемы для определения разницы в теплотах образования между структурными изомерами нельзя применять единый инкремент группы
. При использовании этой схемы для определения разницы в теплотах образования между структурными изомерами нельзя применять единый инкремент группы  . Эту задачу можно разрешить просто, если избрать инкременты групп —
. Эту задачу можно разрешить просто, если избрать инкременты групп — и
и  для пространственно незатрудненных алканов, которые зависят только от числа метильных групп, связанных с рассматриваемой группой. По методике, аналогичной определению инкремента
для пространственно незатрудненных алканов, которые зависят только от числа метильных групп, связанных с рассматриваемой группой. По методике, аналогичной определению инкремента  -группы, получают соответственно для групп
-группы, получают соответственно для групп  и
и  значения
значения
 и
и  . Несомненно, что лучшего согласия с экспериментальными данными можно достичь, если использовать раздельные инкременты для каждого типа групп
. Несомненно, что лучшего согласия с экспериментальными данными можно достичь, если использовать раздельные инкременты для каждого типа групп  .
.
Таблица 2.7. Сравнение экспериментальных теплот образования в газовой фазе и теплот образования, рассчитанных с использованием параметров, приведенных в табл. 2.6

Продолжение табл. 2.7.

Тем не менее, для многих ациклических алканов применение упомянутых выше четырех инкрементов приводит к великолепному согласию с экспериментальными данными. В случае сильно разветвленных алканов, в которых пространственные затруднения играют важную роль, величины термохимической устойчивости получаются завышенными. Однако в случае пространственных затруднений возможно использовать пять различных поправок двух типов.
Первый тип пространственных затруднений встречается в том случае, когда сильно замещенные углеродные атомы связаны друг с другом. Хотя  -взаимодействия имеют место вокруг каждой С—С-связи, они обычно отражены в основной системе инкрементов и их следует учитывать отдельно только для сильно пространственно затрудненных систем. Используют следующие поправки (в
-взаимодействия имеют место вокруг каждой С—С-связи, они обычно отражены в основной системе инкрементов и их следует учитывать отдельно только для сильно пространственно затрудненных систем. Используют следующие поправки (в  ): +3,00
): +3,00  для
для  , +9,55
, +9,55  для
для  и +20,80
и +20,80  для
для  . Эти поправки просто добавляют к инкрементам групп, когда в алкане встречается соответствующая структурная единица. Второй тип пространственных затруднений встречается, когда две сильно пространственно затрудненные группы Связаны с одним и тем же углеродным атомом.
. Эти поправки просто добавляют к инкрементам групп, когда в алкане встречается соответствующая структурная единица. Второй тип пространственных затруднений встречается, когда две сильно пространственно затрудненные группы Связаны с одним и тем же углеродным атомом.
Для таких случаев рекомендуются поправки: +9,55  для
для  и 22,5
и 22,5  для
для  . Ниже приведен весь набор девяти инкрементов, необходимых при применении приведенной выше схемы для определения теплоты образования любого ациклического алкана в газовой фазе (в
. Ниже приведен весь набор девяти инкрементов, необходимых при применении приведенной выше схемы для определения теплоты образования любого ациклического алкана в газовой фазе (в  ):
):

Таблица 2.8. Экспериментальные и рассчитанные теплоты образования изомерных гептанов в газовой фазе (в  )
)

В табл. 2.7 показаны результаты, полученные таким образом для 70 алканов, для которых известны экспериментальные данные. Коэффициент корреляции между рассчитанными и экспериментальными значениями составляет 0,9996, а наклон, найденный по линейной регрессии равен 1,01. Средняя квадратичная ошибка для всей области рассмотренных структур, составляет  . Если опустить «выпадающие» точки, характерные для очень больших алканов, для которых следует ожидать экспериментальных трудностей при определении теплот образования, то приведенные выше величины станут значительно более точными.
. Если опустить «выпадающие» точки, характерные для очень больших алканов, для которых следует ожидать экспериментальных трудностей при определении теплот образования, то приведенные выше величины станут значительно более точными.
Хотя оба подхода, как основанный на энергии связей, так и основанный на групповых инкрементах, могут быть усовершенствованы до такой степени, что может быть достигнуто отличное согласие с экспериментальными данными, последний метод проще, менее искусственен в своем окончательном варианте и может быть использован в рамках конформационного анализа. Теплоты образования алканов, определенные экспериментально и рассчитанные с помощью пяти схем, приведены в табл. 2.8.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ К ТОМУ 1 АНГЛИЙСКОГО ИЗДАНИЯ
- ЧАСТЬ I. НОМЕНКЛАТУРА И СТЕРЕОХИМИЯ
- 1.1. ВВЕДЕНИЕ И СТЕРЕОХИМИЯ
- 1.1.2. СИММЕТРИЯ И ХИРАЛЬНОСТЬ
- 1.1.3. ХИМИЧЕСКАЯ ТОПОЛОГИЯ
- 1.1.4. ИЗОМЕРИЯ
- 1.1.4.2. Строение
- 1.1.4.3. Абсолютная конфигурация
- 1.1.4.4. Относительная конфигурация
- 1.1.4.5. Конформация
- 1.1.4.6. Концепция изомерии
- 1.1.5. ТОПИЗМ
- 1.1.5.2. Прохиральность
- 1.1.5.3. Псевдоасимметрия (псевдохиральность)
- 1.1.6. ТОПОМЕРИЯ
- 1.1.7. ДИНАМИЧЕСКАЯ СТЕРЕОХИМИЯ. КРАТКИЕ СВЕДЕНИЯ
- ЧАСТЬ 2. УГЛЕВОДОРОДЫ
- 2.1. НАСЫЩЕННЫЕ УГЛЕВОДОРОДЫ
- 2.1.2. Строение и номенклатура
- 2.1.2.1. Номенклатура IUPAC
- 2.1.2.2. Алициклические алканы
- 2.1.2.3. Полициклоалканы
- 2.1.3. ИСТОЧНИКИ ПОЛУЧЕНИЯ НАСЫЩЕННЫХ УГЛЕВОДОРОДОВ
- 2.1.4. ФИЗИЧЕСКИЕ СВОЙСТВА
- 2.1.4.1. Ациклические алканы
- 2.1.4.2. Моно- и полициклоалканы
- 2.1.5. СТЕРЕОХИМИЯ И КОНФОРМАЦИОННЫЙ АНАЛИЗ
- 2.1.5.1. Углы и длины связей
- 2.1.5.2. Алкил- и полиалкилциклогексаны
- 2.1.5.3. Конформация карбоциклических колец, больших, чем циклогексан
- 2.1.6. ТЕРМОХИМИЧЕСКИЕ СВОЙСТВА
- 2.1.6.1. Горение. Алканы и циклоалканы как топливо
- 2.1.6.2. Определение теплот сгорания и термохимические свойства
- 2.1.6.3. Эмпирические методы оценки теплот образования алканов
- 2.1.6.4. Оценка теплот образования алканов на основе энергии связей
- 2.1.6.5. Оценка теплот образования алканов на основе инкрементов групп
- 2.1.6.6. Оценка теплот образования циклических, полициклических и мостиковых алканов на основе инкрементов «скошенных разобщенных» групп и «единственных» наиболее устойчивых конформаций
- 2.1.6.7. Молекулярно-механические расчеты теплот образования и энергии напряжения
- 2.1.6.8. Моно- и полициклоалкаиы
- 2.1.7. ПОЛУЧЕНИЕ АЦИКЛИЧЕСКИХ АЛКАНОВ
- 2.1.7.1. Получение алканов восстановлением олефинов
- 2.1.7.2. Получение алканов из альдегидов и кетонов
- 2.1.7.3. Получение алканов из спиртов и алкилгалогенидов
- 2.1.7.4. Получение алканов из карбоновых кислот
- 2.1.8. СИНТЕЗ МОНО- И ПОЛИЦИКЛОАЛКАНОВ
- 2.1.9. РЕАКЦИИ АЦИКЛИЧЕСКИХ АЛКАНОВ
- 2.1.9.1. Галогенирование
- 2.1.9.2. Нитрование
- 2.1.9.3. Окисление
- 2.1.9.4. Каталитическая изомеризация алканов
- 2.1.9.5. Каталитическое алкилирование алканов
- 2.1.9.6. Реакции крекинга алканов
- 2.1.9.7. Термический крекинг
- 2.1.9.8. Каталитический крекинг
- 2.1.9.9. Каталитический риформинг и дегидроциклизация алканов
- 2.1.10. РЕАКЦИИ ЦИКЛОАЛКАНОВ И ПОЛИЦИКЛОАЛКАНОВ
- 2.2. ОЛЕФИНОВЫЕ И АЦЕТИЛЕНОВЫЕ УГЛЕВОДОРОДЫ
- 2.2.2. ПОЛУЧЕНИЕ ОЛЕФИНОВ
- 2.2.2.1. Элиминирование в системах
- 2.2.2.2. Элиминирование из систем
- 2.2.2.3. Циклоэлиминирование
- 2.2.2.4. Частичное восстановление
- 2.2.2.5. Элиминирование сульфонилгидразонов
- 2.2.2.6. Реакция Виттига и родственные ей реакции
- 2.2.2.7. Различные реакции конденсации
- 2.2.2.8. Электроциклические реакции
- 2.2.2.9. Циклоолигомеризация
- 2.2.2.11. Реакции винильных производных
- 2.2.3. РЕАКЦИИ ОЛЕФИНОВ
- 2.2.3.1. Электрофильное присоединение
- 2.2.3.2. Нуклеофильное присоединение
- 2.2.3.3. Радикальное присоединение
- 2.2.3.4. Циклоприсоединение и родственные реакции
- 2.2.3.5. Окисление
- 2.2.3.6. Восстановление
- 2.2.3.7. Перегруппировки
- 2.2.3.8. Фотохимические реакции
- 2.2.3.9. Прочие реакции
- 2.3. ДИЕНЫ, ПОЛНЕНЫ И АЦЕТИЛЕНОВЫЕ УГЛЕВОДОРОДЫ
- 2.3.1. СОПРЯЖЕННЫЕ ДИЕНЫ И ПОЛНЕНЫ
- 2.3.1.2. Получение сопряженных диенов
- 2.3.2. РЕАКЦИИ СОПРЯЖЕННЫХ ДИЕНОВ
- 2.3.2.2. Восстановление
- 2.3.2.3. Гидроборирование
- 2.3.2.4. Реакция Дильса — Альдера
- 2.3.2.5. Комплексы с карбонилами железа
- 2.3.2.6. Фотохимические термические реакции
- 2.3.2.7. Прочие реакции
- 2.3.3. СОПРЯЖЕННЫЕ ПОЛИЕНЫ
- 2.3.4. ПРИРОДНЫЕ ДИЕНЫ И ПОЛНЕНЫ
- 2.3.5. АЛЛЕНЫ И КУМУЛЕНЫ
- 2.3.5.2. Получение алленов
- 2.3.6. РЕАКЦИИ АЛЛЕНОВ
- 2.3.6.2. Гидрирование
- 2.3.6.3. Реакции алленов в присутствии комплексов металлов
- 2.3.7. КУМУЛЕНЫ
- 2.3.8. ПРИРОДНЫЕ АЛЛЕНЫ И КУМУЛЕНЫ
- 2.3.9. АЦЕТИЛЕНЫ И ПОЛИАЦЕТИЛЕНЫ
- 2.3.9.2. Получение ацетиленов
- 2.3.10. РЕАКЦИИ АЦЕТИЛЕНОВ
- 2.3.10.2. Изомеризация
- 2.3.10.3. Пропаргильные перегруппировки
- 2.3.10.4. Реакции присоединения
- 2.3.10.5. Гидроборирование и гидроалюминирование
- 2.3.10.6. Реакции замещения
- 2.3.10.7. Восстановление
- 2.3.10.8. Окисление
- 2.3.10.9. Циклоприсоединение
- 2.3.10.10. Реакции катализуемые металлами
- 2.3.11. ПОЛИАЦЕТИЛЕНЫ
- 2.3.12. ПРИРОДНЫЕ АЦЕТИЛЕНЫ И ПОЛИАЦЕТИЛЕНЫ
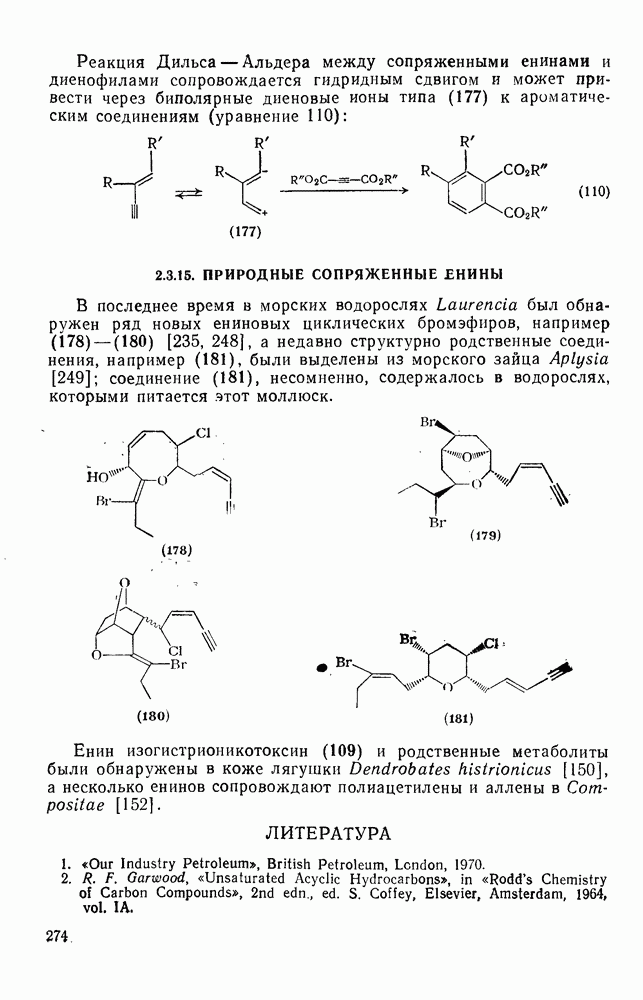
- 2.3.13. СОПРЯЖЕННЫЕ ЕНИНЫ
- 2.3.13.1. Получение сопряженных енинов
- 2.3.14. РЕАКЦИИ СОПРЯЖЕННЫХ ЕНИНОВ
- 2.3.15. ПРИРОДНЫЕ СОПРЯЖЕННЫЕ ЕНИНЫ
- 2.4. АРОМАТИЧНОСТЬ
- 2.4.2. ЭЛЕКТРОННЫЕ ТЕОРИИ СТРОЕНИЯ БЕНЗОЛА
- 2.4.3. КРИТЕРИИ АРОМАТИЧНОСТИ
- 2.4.3.1. Термодинамические свойства
- 2.4.3.2. Структурные особенности
- 2.4.3.3. Магнитные свойства
- 2.4.3.4. Прочие критерии
- 2.4.4. АНТИАРОМАТИЧНОСТЬ
- 2.4.4.1. Термодинамические свойства
- 2.4.4.2. Структурные особенности
- 2.4.4.3. Магнитные свойства
- 2.4.4.4. Прочие свойства
- 2.4.5. ТЕОРЕТИЧЕСКИЕ ОПРЕДЕЛЕНИЯ АРОМАТИЧНОСТИ
- 2.4.5.1. Полуэмпирические расчеты и дьюаровская резонансная энергия
- 2.4.5.2. Расчеты по методу валентных пар и применение резонансного метода
- 2.4.5.3. Локализация связей
- 2.4.5.4. Связь энергетических критериев с критериями локализации связей
- 2.4.6. АРОМАТИЧЕСКИЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
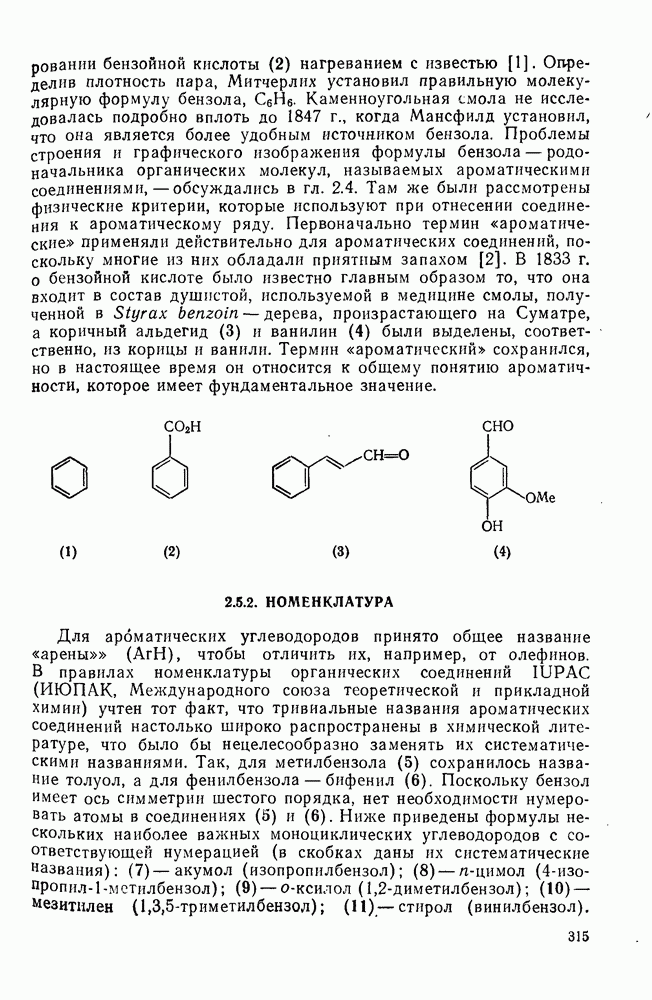
- 2.5. АРЕНЫ И ИХ РЕАКЦИИ
- 2.5.2. НОМЕНКЛАТУРА
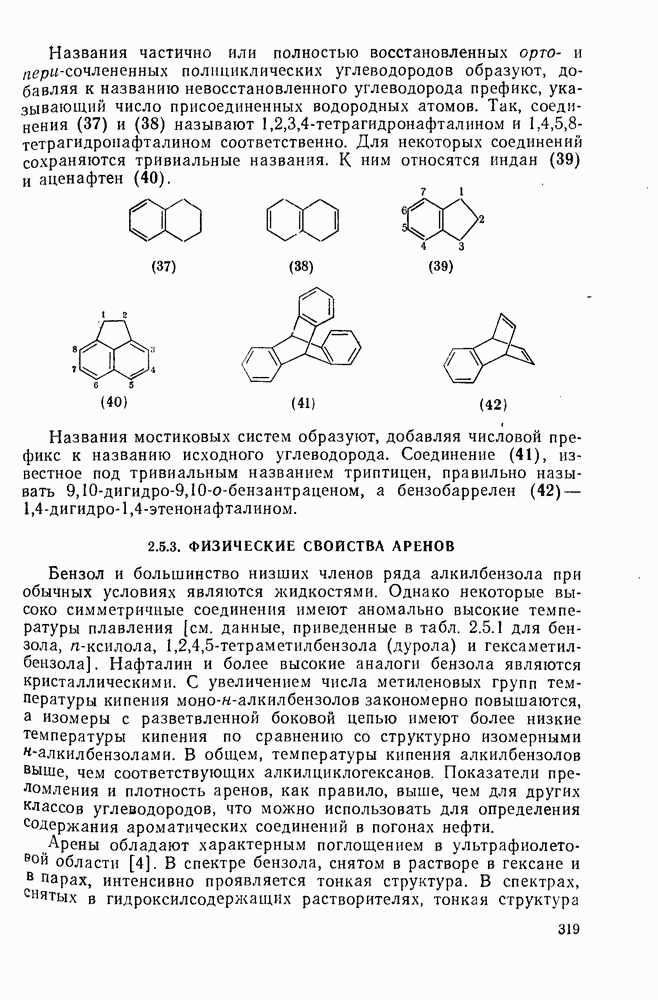
- 2.5.3. ФИЗИЧЕСКИЕ СВОЙСТВА АРЕНОВ
- 2.5.4. ПРОМЫШЛЕННОЕ ПРОИЗВОДСТВО АРЕНОВ
- 2.5.5. ЦИКЛОТРИМЕРИЗАЦИЯ АЦЕТИЛЕНОВ
- 2.5.6. РЕАКЦИИ ЭЛЕКТРОФИЛЬНОГО ПРИСОЕДИНЕНИЯ — ЭЛИМИНИРОВАНИЯ АРЕНОВ
- 2.5.6.1. Механизм ароматического нитрования [15]
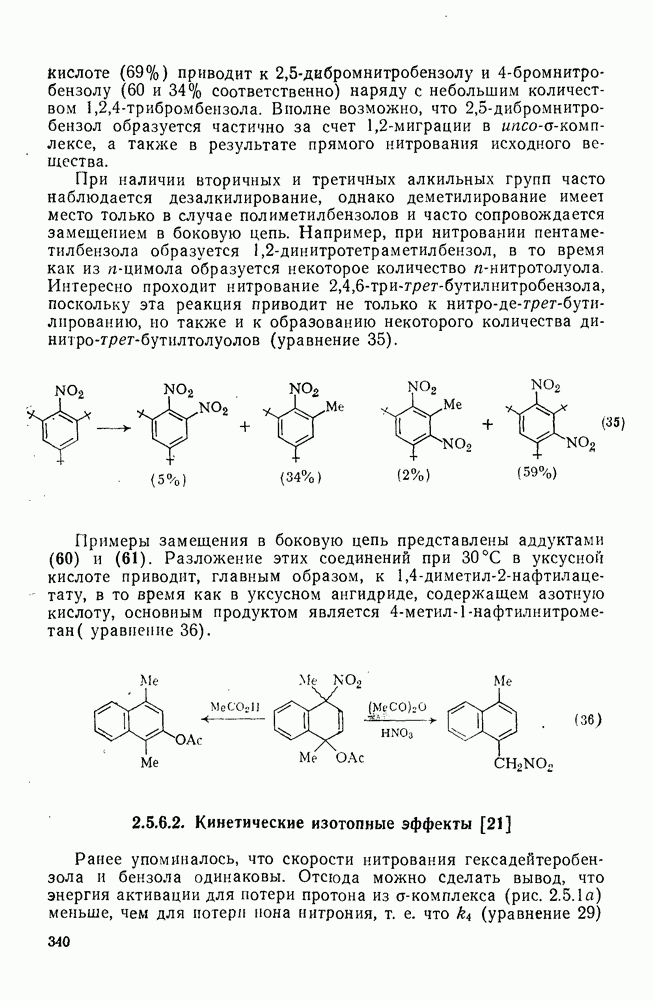
- 2.5.6.2. Кинетические изотопные эффекты [21]
- 2.5.6.3. Реакции, включающие ипсо-протонирование
- 2.5.6.4. Металлирование
- 2.5.6.5. Электрофилы IV группы
- 2.5.6.6. Электрофилы V группы
- 2.5.6.7. Электрофилы VI группы [18, 56]
- 2.5.6.8. Электрофилы VII группы [18, 25а, 56]
- 2.5.7. ОРИЕНТАЦИЯ В РЕАКЦИЯХ ЭЛЕКТРОФИЛЬНОГО ПРИСОЕДИНЕНИЯ — ЭЛИМИНИРОВАНИЯ
- 2.5.8. РАДИКАЛЬНОЕ ГАЛОГЕНИРОВАНИЕ АРЕНОВ В БОКОВУЮ ЦЕПЬ [96]
- 2.5.9. РЕАКЦИИ ПРИСОЕДИНЕНИЯ К АРЕНАМ
- 2.5.9.1. Восстановление аренов
- 2.5.9.2. Термическое циклоприсоединение к аренам
- 2.5.9.3. Фотоциклоприсоединение к моноциклическим аренам [126]
- 2.5.9.4. Фотохимические реакции полициклических аренов
- 2.6.10. ФОТОИЗОМЕРИЗАЦИЯ АРЕНОВ [126б]
- 2.5.11. ОКИСЛЕНИЕ АРЕНОВ [153]
- 2.5.12. РЕАКЦИИ АРЕНОВ С СИНГЛЕТНЫМ КИСЛОРОДОМ [162]
- 2.5.13. ПРИГОТОВЛЕНИЕ БИ- И ПОЛИАРИЛОВ
- 2.5.14. ВНУТРИМОЛЕКУЛЯРНАЯ ФОТОЦИКЛИЗАЦИЯ, ПРИВОДЯЩАЯ К ПОЛИЦИКЛИЧЕСКИМ АРЕНАМ
- 2.5.15. ВНУТРИМОЛЕКУЛЯРНАЯ ЦИКЛИЗАЦИЯ ДИЗАМЕЩЕННЫХ АРЕНОВ
- 2.5.16. ЦИКЛОФАНЫ
- 2.5.17. КОНФОРМАЦИЯ И ХИРАЛЬНОСТЬ АРЕНОВ
- 2.5.18. АЗУЛЕНЫ И НЕБЕНЗОИДНЫЕ АРЕНЫ
- 2.6. АННУЛЕНЫ И РОДСТВЕННЫЕ СИСТЕМЫ
- 2.6.2. МЕТОДЫ СИНТЕЗА
- 2.6.2.1. Окислительное сочетание терминальных ацетиленов (метод Зондхеймера)
- 2.6.2.2. Фотооблучение полициклических валентных таутомеров
- 2.6.2.3. Валентная таутомерия типа норкарадиен — циклогептатриен (метод Фогеля)
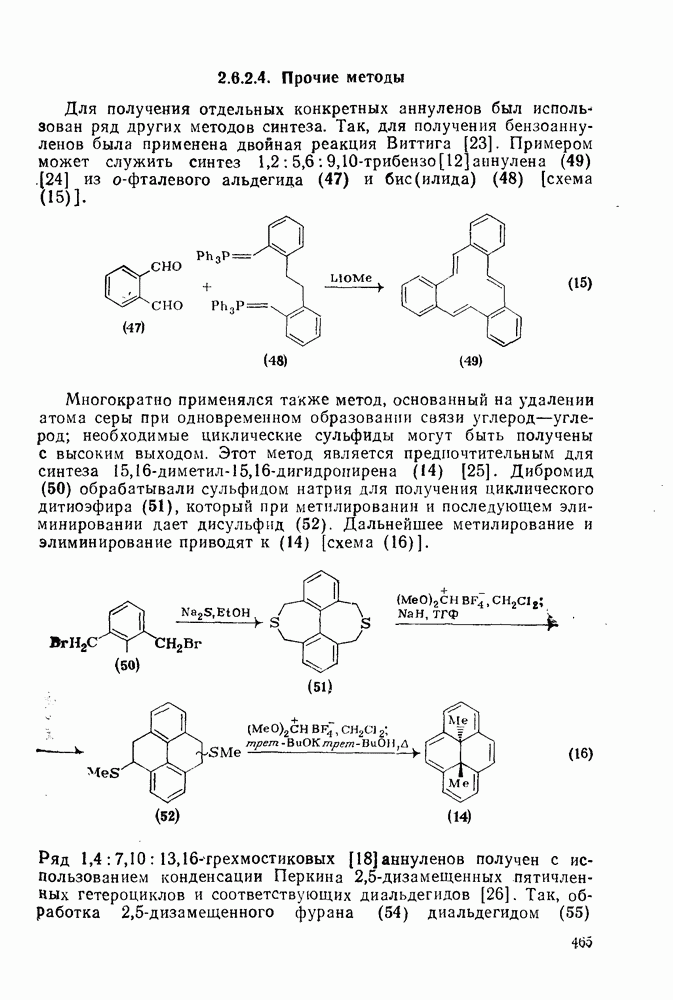
- 2.6.2.4. Прочие методы
- 2.6.3. СВОЙСТВА АННУЛЕНОВ
- 2.6.4. СВОЙСТВА 4n-АННУЛЕНОВ
- 2.6.5. ДЕГИДРОАННУЛЕНЫ
- 2.6.6. АННЕЛИРОВАННЫЕ АННУЛЕНЫ
- 2.6.7. АРОМАТИЧЕСКИЕ И АНТИАРОМАТИЧЕСКИЕ МОНОЦИКЛИЧЕСКИЕ ИОНЫ
- 2.6.8. АРОМАТИЧЕСКИЕ И АНТИАРОМАТИЧЕСКИЕ ПОЛИЦИКЛИЧЕСКИЕ ИОНЫ
- 2.6.9. ГОМОАРОМАТИЧЕСКИЕ СИСТЕМЫ
- 2.7. КАРБОКАТИОНЫ И КАРБАНИОНЫ
- 2.7.1.2. Краткий исторический очерк развития химии карбокатионов
- 2.7.1.3. Методы генерации карбокатионов
- 2.7.1.4. Типы карбокатионов
- 2.7.1.5. Изучение карбокатионов: методы и результаты
- 2.7.1.6. Реакции карбокатионов
- 2.7.2. КАРБАНИОНЫ
- 2.7.2.2. Методы генерации карбанионов
- 2.7.2.3. Типы карбанионов
- 2.7.2.4. Физические свойства карбанионов
- 2.7.5.2. Реакции карбанионов
- 2.8. РАДИКАЛЫ, КАРБЕНЫ, АРИНЫ
- 2.8.1. РАДИКАЛЫ
- 2.8.1.1. Структура, устойчивость и реакционная способность радикалов
- 2.8.1.2. Методы генерации и реакции радикалов
- 2.8.2. КАРБЕНЫ
- 2.8.2.1. Методы генерации карбенов и карбеноидов
- 2.8.2.2. Реакции карбенов
- 2.8.3. АРИНЫ
- 2.8.3.1. Структура и спектры аринов
- 2.8.3.2. Методы генерации аринов
- 2.8.3.3. Реакции аринов
- ЧАСТЬ 3. ГАЛОГЕНСОДЕРЖАЩИЕ СОЕДИНЕНИЯ
- 3.2. МЕТОДЫ ГАЛОГЕНИРОВАНИЯ
- 3.2.1. Гомолитическое замещение водорода
- 3.2.1.2. Использование галогенпроизводных в качестве реагентов
- 3.2.2. Гомолитическое замещение функциональных групп
- 3.2.3. Гомолитическое присоединение к ненасыщенным системам
- 3.2.3.1. Присоединение галогеноводородов
- 3.2.3.2. Присоединение галогенов
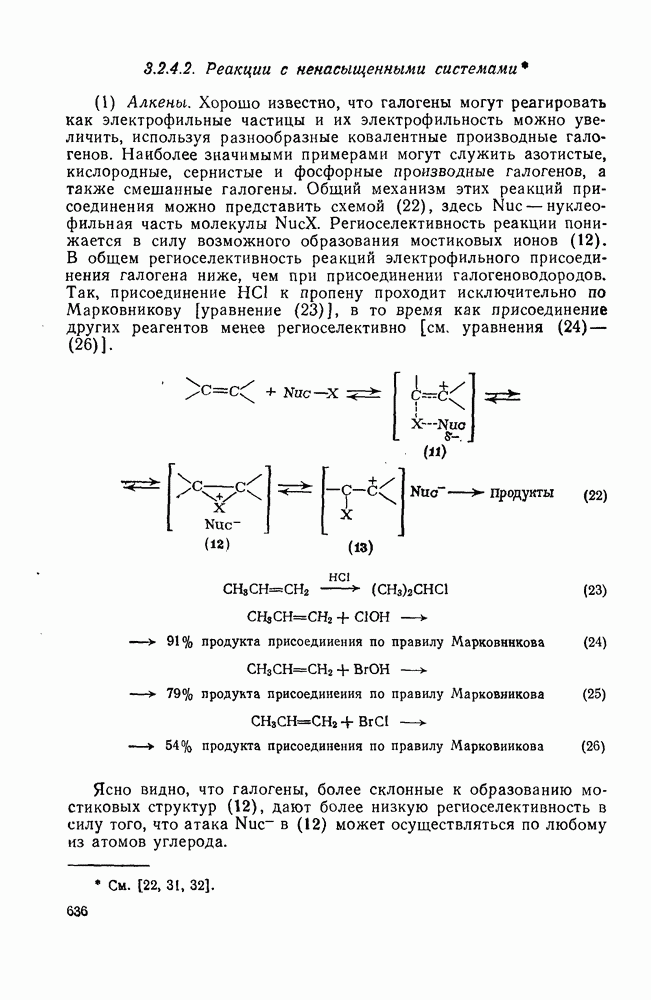
- 3.2.4. Электрофильное галогенирование
- 3.2.4.1. Замещение у насыщенной связи С-Н
- 3.2.4.2. Реакции с ненасыщенными системами
- 3.2.4.3. Реакции с карбанионами
- 3.2.5. Нуклеофильное галогенирование
- 3.2.5.1. Галогенирование с замещением функциональной группы
- 3.2.5.2. Галогенирование в ароматических системах
- 3.2.5.3. Галогенирование путем обмена галогенов
- 3.2.6. Синтез полигалогенированных соединений
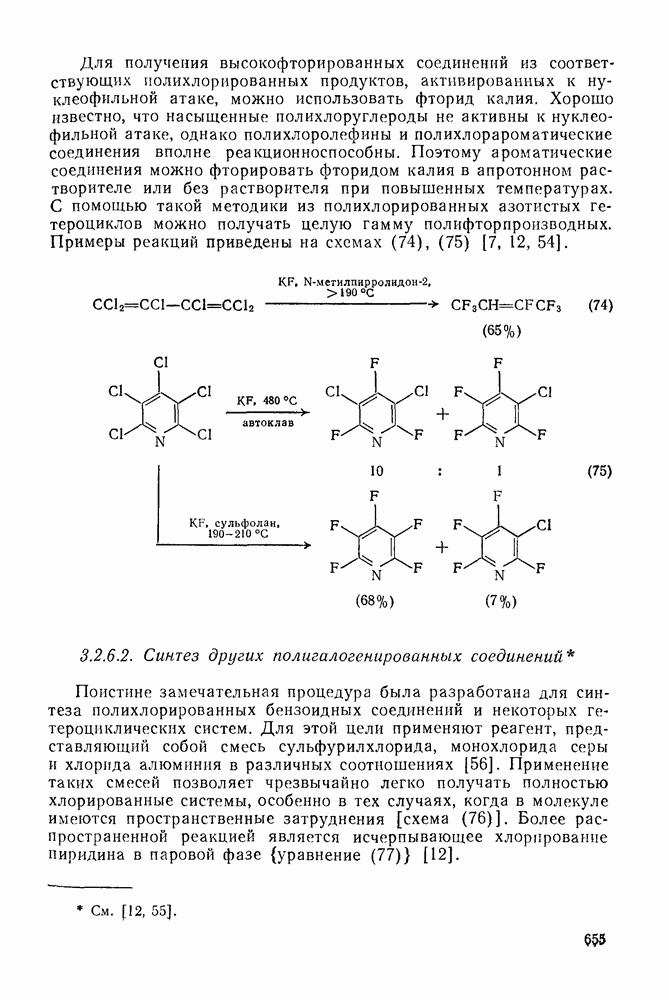
- 3.2.6.1. Синтез полифторированных соединений
- 3.2.6.2. Синтез других полигалогенированных соединений
- 3.3. ГАЛОГЕНАЛКАНЫ
- 3.3.1. Характеристика связей углерод-галоген
- 3.3.2. Промышленное применение
- 3.3.3. Нуклеофильное замещение галогена
- 3.3.3.1. Реакции SN2 и родственные процессы
- 3.3.3.2. Соучастие соседних групп
- 3.3.3.3. Реакции SN1 и относительно долгоживущие карбениевые ионы
- 3.3.3.4. Галогенониевые ионы
- 3.3.3.5. Галогенсодержащие карбениевые ионы
- 3.3.3.6. Механизм замещения с переносом электрона
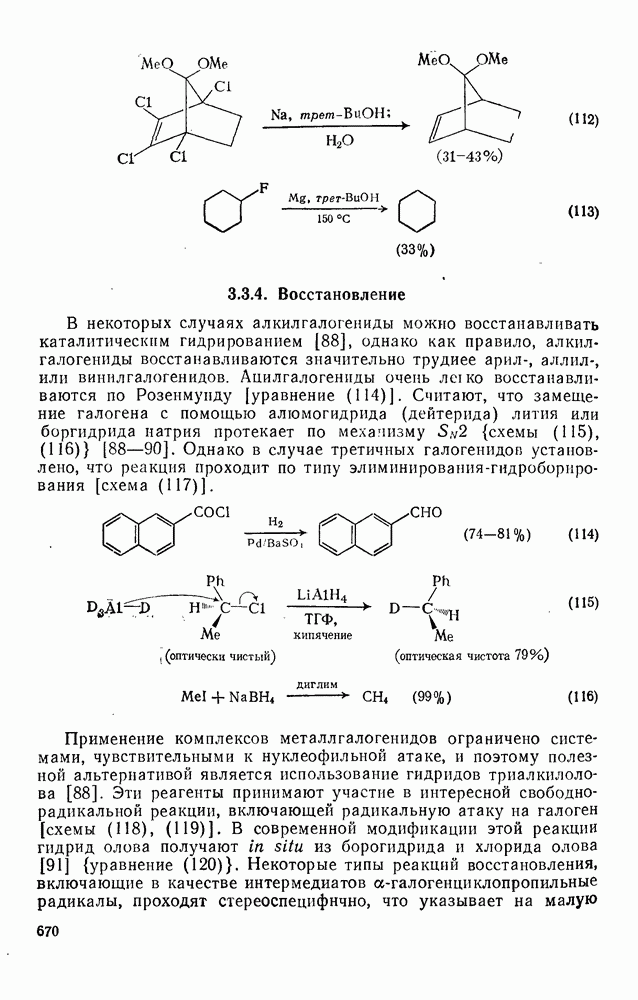
- 3.3.4. Восстановление
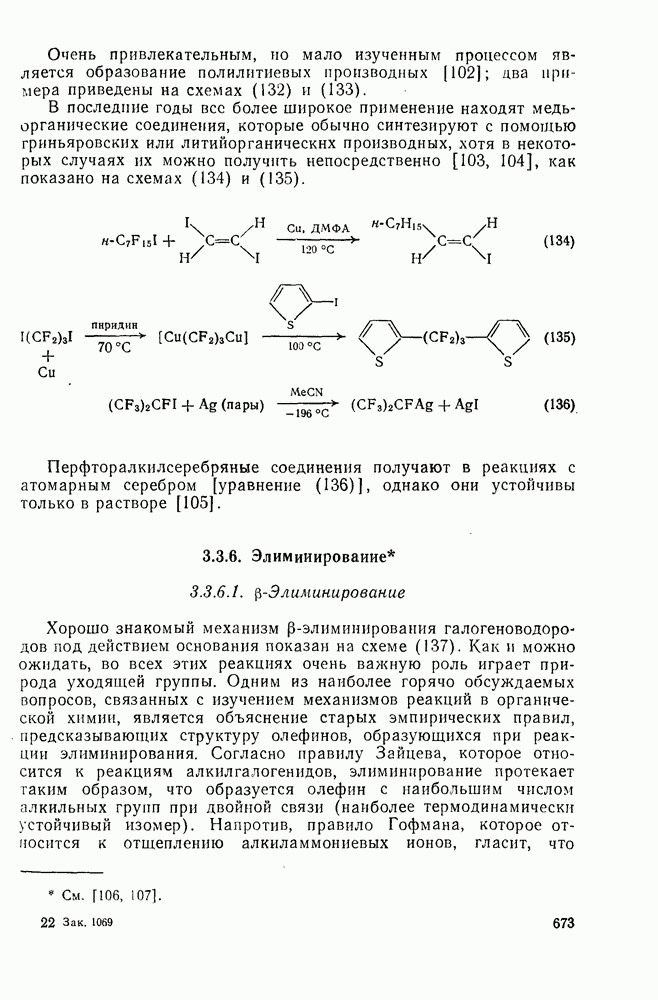
- 3.3.5. Замещение на металлы
- 3.3.6. Элиминирование
- 3.3.6.1. b-Элиминирование
- 3.3.6.2. Галогенкарбанионы
- 3.3.6.3. Элиминирование через карбанионы
- 3.3.6.4. b-Элиминирование из металлорганических соединений
- 3.3.6.5. a-Элиминирование (генерирование карбенов)
- 3.4. ГАЛОГЕНАЛКЕНЫ
- 3.4.1. Синтез галогеналкенов
- 3.4.2. Нуклеофильная атака
- 3.4.2.1. Реакции, индуцируемые фторид-ионом
- 3.4.2.2. Другие реакции замещения
- 3.4.3. Радикальное присоединение
- 3.4.4. Электрофильное присоединение
- 3.4.5. Циклоприсоединение
- 3.4.5.1. [2+2]-Циклоприсоединение
- 3.4.5.2. [4+2]-Циклоприсоединение
- 3.5. ГАЛОГЕНАЛКИНЫ
- 3.6. ГАЛОГЕНАРЕНЫ
- 3.6.1. Замещение галогена
- 3.6.1.2. Присоединение-элиминирование
- 3.6.1.3. Нуклеофильная атака на галоген
- 3.6.1.4. Перенос электрона
- 3.6.2. Перегруппировки
- 3.6.2.1. Перегруппировки под действием кислот Льюиса
- 3.6.2.2. Образование валентных изомеров