| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.1.3. ХИМИЧЕСКАЯ ТОПОЛОГИЯ
Вслед за проведенным выше критическим рассмотрением взаимоотношений между геометрическими фигурами и молекулами, рассмотрим теперь достаточно подробно и вопросы химической топологии.
Это поможет выявить и классифицировать различные причины хиральности молекул (см. разд. 1.1.4). Необходимо считаться с практическими задачами химических исследований. Хотя при рассмотрении абстрактных построений достаточно (или даже недостаточно!) связать хиральность с некоторыми свойствами молекулярной симметрии, перед химиками-экспериментаторами часто встает задача введения стереохимическнх модификации в тот или иной участок органической молекулы. Поэтому полезно, и даже необходимо, уметь найти и определить элементы хиральности в молекуле.
Прелог [26—28] обратил внимание на то, что хиральность может проявляться как в двухмерном, так и в трехмерном пространстве. В качестве простейших моделей, иллюстрирующих это положение, он использовал треугольники и тетраэдры. Некоторые примеры двухмерной хиральности приведены ниже:

Неправильный треугольник (27) в двухмерном пространстве является хиральным, так как его зеркальное отражение (27) относительно некоторой прямой не может быть совмещено с ним при поступательном или вращательном движении в плоскости (симметрия  ). Однако при переходе к трехмерному пространству эта двухмерная хиральность исчезает. Ниже прописные буквы латинского алфавита расположены как в ахиральном, так и в хиральном порядке относительно двухмерного пространства:
). Однако при переходе к трехмерному пространству эта двухмерная хиральность исчезает. Ниже прописные буквы латинского алфавита расположены как в ахиральном, так и в хиральном порядке относительно двухмерного пространства:

Различный порядок обозначения вершин равностороннего треугольника приводит к образованию энантиомерной (относительно двухмерного пространства) пары треугольников. Многие из простейших моделей могут быть использованы для описания плоских молекул. Например, треугольник (28) является прообразом ацетальдегида (29), модель (30) — прообразом малеиновой кислоты (31), а (32) — фумаровой кислоты (33).
Позднее мы убедимся, что хиральность ацетальдегида (29) или фумаровой кислоты (33) относительно плоскости может быть обнаружена и ферментами (см. разд. 1.1.5).
Такие понятия как стереогетеротопизм и прохиральность возникли из рассмотрения двухмерной хиральности. Для такой простой трехмерной модели как тетраэдр возможны восемь точечных групп симметрии:

Правильный тетраэдр с симметрией  (34) служит моделью для хорошо знакомого нам изображения центра хиральности, представленного формулой (42). Однако модели с симметрией
(34) служит моделью для хорошо знакомого нам изображения центра хиральности, представленного формулой (42). Однако модели с симметрией  (35) и
(35) и  (37), в принципе, тоже могут заключать в себе центр хиральности.
(37), в принципе, тоже могут заключать в себе центр хиральности.
Ниже показано, что правильный  тетраэдр (34) можно рассматривать также как модель-центров прохиральности, например (43), псевдоасимметрии (или псевдохиральности) [42, 43], например, в случаях (44) и (45), а также пропсевдоасимметрии (пропсевдохиральности), как в случае (46):
тетраэдр (34) можно рассматривать также как модель-центров прохиральности, например (43), псевдоасимметрии (или псевдохиральности) [42, 43], например, в случаях (44) и (45), а также пропсевдоасимметрии (пропсевдохиральности), как в случае (46):

Тетраэдр с симметрией  (38) служит моделью осевой хиральности, прохиральности и псевдоасимметрии (псевдохиральности), тогда как тетраэдр с симметрией
(38) служит моделью осевой хиральности, прохиральности и псевдоасимметрии (псевдохиральности), тогда как тетраэдр с симметрией  (39) моделирует плоскостную хиральность, прохиральность и псевдоасимметрию (псевдохиральность). Примеры осевой и плоскостной прохиральности и псевдоасимметрии (псевдохиральности) читатель может найти в оригинальной литературе [26—29, 32].
(39) моделирует плоскостную хиральность, прохиральность и псевдоасимметрию (псевдохиральность). Примеры осевой и плоскостной прохиральности и псевдоасимметрии (псевдохиральности) читатель может найти в оригинальной литературе [26—29, 32].
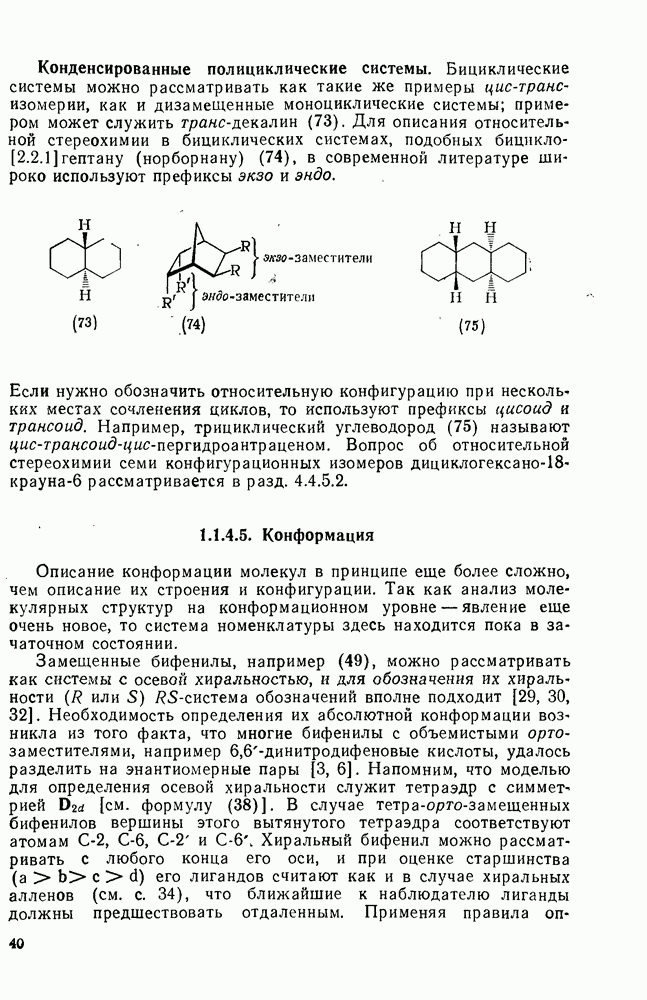
Хотя о центрах, осях и плоскостях хиральности подробнее сказано в разд. 1.1.4, по-видимому, целесообразно уже сейчас связать их с общими явлениями в архитектуре молекул. Соединения типа  (47) содержит знакомый нам хиральный центр, тогда как в
(47) содержит знакомый нам хиральный центр, тогда как в

соответствующим образом замещенных алленах (48) и бифенилах 49) элементом хиральности служит ось. В гранс-циклоалканах (50) и в полизамещенных парациклофанах (51) имеется плоскость хиральности.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ К ТОМУ 1 АНГЛИЙСКОГО ИЗДАНИЯ
- ЧАСТЬ I. НОМЕНКЛАТУРА И СТЕРЕОХИМИЯ
- 1.1. ВВЕДЕНИЕ И СТЕРЕОХИМИЯ
- 1.1.2. СИММЕТРИЯ И ХИРАЛЬНОСТЬ
- 1.1.3. ХИМИЧЕСКАЯ ТОПОЛОГИЯ
- 1.1.4. ИЗОМЕРИЯ
- 1.1.4.2. Строение
- 1.1.4.3. Абсолютная конфигурация
- 1.1.4.4. Относительная конфигурация
- 1.1.4.5. Конформация
- 1.1.4.6. Концепция изомерии
- 1.1.5. ТОПИЗМ
- 1.1.5.2. Прохиральность
- 1.1.5.3. Псевдоасимметрия (псевдохиральность)
- 1.1.6. ТОПОМЕРИЯ
- 1.1.7. ДИНАМИЧЕСКАЯ СТЕРЕОХИМИЯ. КРАТКИЕ СВЕДЕНИЯ
- ЧАСТЬ 2. УГЛЕВОДОРОДЫ
- 2.1. НАСЫЩЕННЫЕ УГЛЕВОДОРОДЫ
- 2.1.2. Строение и номенклатура
- 2.1.2.1. Номенклатура IUPAC
- 2.1.2.2. Алициклические алканы
- 2.1.2.3. Полициклоалканы
- 2.1.3. ИСТОЧНИКИ ПОЛУЧЕНИЯ НАСЫЩЕННЫХ УГЛЕВОДОРОДОВ
- 2.1.4. ФИЗИЧЕСКИЕ СВОЙСТВА
- 2.1.4.1. Ациклические алканы
- 2.1.4.2. Моно- и полициклоалканы
- 2.1.5. СТЕРЕОХИМИЯ И КОНФОРМАЦИОННЫЙ АНАЛИЗ
- 2.1.5.1. Углы и длины связей
- 2.1.5.2. Алкил- и полиалкилциклогексаны
- 2.1.5.3. Конформация карбоциклических колец, больших, чем циклогексан
- 2.1.6. ТЕРМОХИМИЧЕСКИЕ СВОЙСТВА
- 2.1.6.1. Горение. Алканы и циклоалканы как топливо
- 2.1.6.2. Определение теплот сгорания и термохимические свойства
- 2.1.6.3. Эмпирические методы оценки теплот образования алканов
- 2.1.6.4. Оценка теплот образования алканов на основе энергии связей
- 2.1.6.5. Оценка теплот образования алканов на основе инкрементов групп
- 2.1.6.6. Оценка теплот образования циклических, полициклических и мостиковых алканов на основе инкрементов «скошенных разобщенных» групп и «единственных» наиболее устойчивых конформаций
- 2.1.6.7. Молекулярно-механические расчеты теплот образования и энергии напряжения
- 2.1.6.8. Моно- и полициклоалкаиы
- 2.1.7. ПОЛУЧЕНИЕ АЦИКЛИЧЕСКИХ АЛКАНОВ
- 2.1.7.1. Получение алканов восстановлением олефинов
- 2.1.7.2. Получение алканов из альдегидов и кетонов
- 2.1.7.3. Получение алканов из спиртов и алкилгалогенидов
- 2.1.7.4. Получение алканов из карбоновых кислот
- 2.1.8. СИНТЕЗ МОНО- И ПОЛИЦИКЛОАЛКАНОВ
- 2.1.9. РЕАКЦИИ АЦИКЛИЧЕСКИХ АЛКАНОВ
- 2.1.9.1. Галогенирование
- 2.1.9.2. Нитрование
- 2.1.9.3. Окисление
- 2.1.9.4. Каталитическая изомеризация алканов
- 2.1.9.5. Каталитическое алкилирование алканов
- 2.1.9.6. Реакции крекинга алканов
- 2.1.9.7. Термический крекинг
- 2.1.9.8. Каталитический крекинг
- 2.1.9.9. Каталитический риформинг и дегидроциклизация алканов
- 2.1.10. РЕАКЦИИ ЦИКЛОАЛКАНОВ И ПОЛИЦИКЛОАЛКАНОВ
- 2.2. ОЛЕФИНОВЫЕ И АЦЕТИЛЕНОВЫЕ УГЛЕВОДОРОДЫ
- 2.2.2. ПОЛУЧЕНИЕ ОЛЕФИНОВ
- 2.2.2.1. Элиминирование в системах
- 2.2.2.2. Элиминирование из систем
- 2.2.2.3. Циклоэлиминирование
- 2.2.2.4. Частичное восстановление
- 2.2.2.5. Элиминирование сульфонилгидразонов
- 2.2.2.6. Реакция Виттига и родственные ей реакции
- 2.2.2.7. Различные реакции конденсации
- 2.2.2.8. Электроциклические реакции
- 2.2.2.9. Циклоолигомеризация
- 2.2.2.11. Реакции винильных производных
- 2.2.3. РЕАКЦИИ ОЛЕФИНОВ
- 2.2.3.1. Электрофильное присоединение
- 2.2.3.2. Нуклеофильное присоединение
- 2.2.3.3. Радикальное присоединение
- 2.2.3.4. Циклоприсоединение и родственные реакции
- 2.2.3.5. Окисление
- 2.2.3.6. Восстановление
- 2.2.3.7. Перегруппировки
- 2.2.3.8. Фотохимические реакции
- 2.2.3.9. Прочие реакции
- 2.3. ДИЕНЫ, ПОЛНЕНЫ И АЦЕТИЛЕНОВЫЕ УГЛЕВОДОРОДЫ
- 2.3.1. СОПРЯЖЕННЫЕ ДИЕНЫ И ПОЛНЕНЫ
- 2.3.1.2. Получение сопряженных диенов
- 2.3.2. РЕАКЦИИ СОПРЯЖЕННЫХ ДИЕНОВ
- 2.3.2.2. Восстановление
- 2.3.2.3. Гидроборирование
- 2.3.2.4. Реакция Дильса — Альдера
- 2.3.2.5. Комплексы с карбонилами железа
- 2.3.2.6. Фотохимические термические реакции
- 2.3.2.7. Прочие реакции
- 2.3.3. СОПРЯЖЕННЫЕ ПОЛИЕНЫ
- 2.3.4. ПРИРОДНЫЕ ДИЕНЫ И ПОЛНЕНЫ
- 2.3.5. АЛЛЕНЫ И КУМУЛЕНЫ
- 2.3.5.2. Получение алленов
- 2.3.6. РЕАКЦИИ АЛЛЕНОВ
- 2.3.6.2. Гидрирование
- 2.3.6.3. Реакции алленов в присутствии комплексов металлов
- 2.3.7. КУМУЛЕНЫ
- 2.3.8. ПРИРОДНЫЕ АЛЛЕНЫ И КУМУЛЕНЫ
- 2.3.9. АЦЕТИЛЕНЫ И ПОЛИАЦЕТИЛЕНЫ
- 2.3.9.2. Получение ацетиленов
- 2.3.10. РЕАКЦИИ АЦЕТИЛЕНОВ
- 2.3.10.2. Изомеризация
- 2.3.10.3. Пропаргильные перегруппировки
- 2.3.10.4. Реакции присоединения
- 2.3.10.5. Гидроборирование и гидроалюминирование
- 2.3.10.6. Реакции замещения
- 2.3.10.7. Восстановление
- 2.3.10.8. Окисление
- 2.3.10.9. Циклоприсоединение
- 2.3.10.10. Реакции катализуемые металлами
- 2.3.11. ПОЛИАЦЕТИЛЕНЫ
- 2.3.12. ПРИРОДНЫЕ АЦЕТИЛЕНЫ И ПОЛИАЦЕТИЛЕНЫ
- 2.3.13. СОПРЯЖЕННЫЕ ЕНИНЫ
- 2.3.13.1. Получение сопряженных енинов
- 2.3.14. РЕАКЦИИ СОПРЯЖЕННЫХ ЕНИНОВ
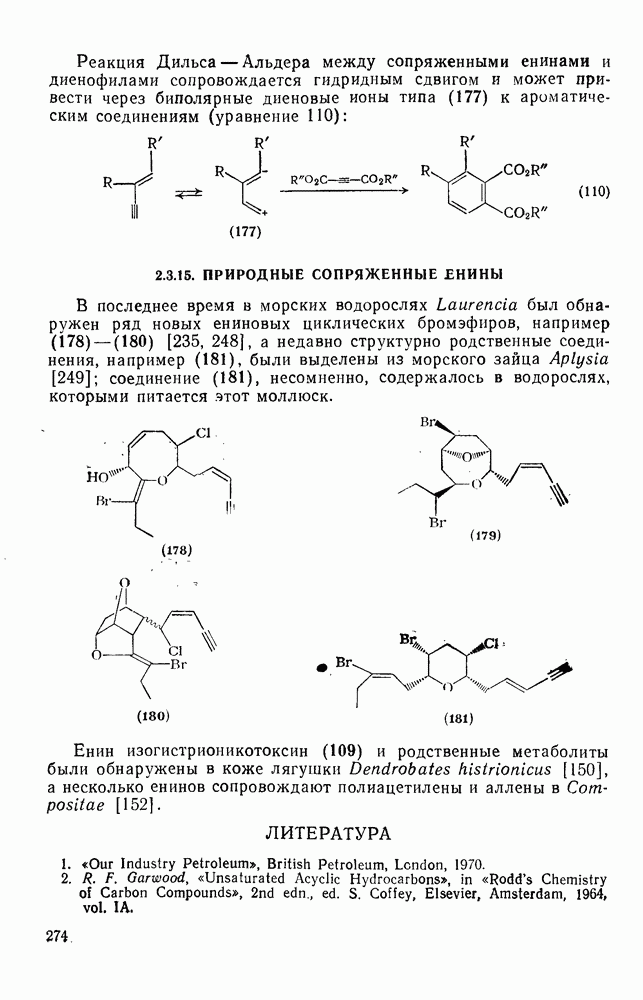
- 2.3.15. ПРИРОДНЫЕ СОПРЯЖЕННЫЕ ЕНИНЫ
- 2.4. АРОМАТИЧНОСТЬ
- 2.4.2. ЭЛЕКТРОННЫЕ ТЕОРИИ СТРОЕНИЯ БЕНЗОЛА
- 2.4.3. КРИТЕРИИ АРОМАТИЧНОСТИ
- 2.4.3.1. Термодинамические свойства
- 2.4.3.2. Структурные особенности
- 2.4.3.3. Магнитные свойства
- 2.4.3.4. Прочие критерии
- 2.4.4. АНТИАРОМАТИЧНОСТЬ
- 2.4.4.1. Термодинамические свойства
- 2.4.4.2. Структурные особенности
- 2.4.4.3. Магнитные свойства
- 2.4.4.4. Прочие свойства
- 2.4.5. ТЕОРЕТИЧЕСКИЕ ОПРЕДЕЛЕНИЯ АРОМАТИЧНОСТИ
- 2.4.5.1. Полуэмпирические расчеты и дьюаровская резонансная энергия
- 2.4.5.2. Расчеты по методу валентных пар и применение резонансного метода
- 2.4.5.3. Локализация связей
- 2.4.5.4. Связь энергетических критериев с критериями локализации связей
- 2.4.6. АРОМАТИЧЕСКИЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
- 2.5. АРЕНЫ И ИХ РЕАКЦИИ
- 2.5.2. НОМЕНКЛАТУРА
- 2.5.3. ФИЗИЧЕСКИЕ СВОЙСТВА АРЕНОВ
- 2.5.4. ПРОМЫШЛЕННОЕ ПРОИЗВОДСТВО АРЕНОВ
- 2.5.5. ЦИКЛОТРИМЕРИЗАЦИЯ АЦЕТИЛЕНОВ
- 2.5.6. РЕАКЦИИ ЭЛЕКТРОФИЛЬНОГО ПРИСОЕДИНЕНИЯ — ЭЛИМИНИРОВАНИЯ АРЕНОВ
- 2.5.6.1. Механизм ароматического нитрования [15]
- 2.5.6.2. Кинетические изотопные эффекты [21]
- 2.5.6.3. Реакции, включающие ипсо-протонирование
- 2.5.6.4. Металлирование
- 2.5.6.5. Электрофилы IV группы
- 2.5.6.6. Электрофилы V группы
- 2.5.6.7. Электрофилы VI группы [18, 56]
- 2.5.6.8. Электрофилы VII группы [18, 25а, 56]
- 2.5.7. ОРИЕНТАЦИЯ В РЕАКЦИЯХ ЭЛЕКТРОФИЛЬНОГО ПРИСОЕДИНЕНИЯ — ЭЛИМИНИРОВАНИЯ
- 2.5.8. РАДИКАЛЬНОЕ ГАЛОГЕНИРОВАНИЕ АРЕНОВ В БОКОВУЮ ЦЕПЬ [96]
- 2.5.9. РЕАКЦИИ ПРИСОЕДИНЕНИЯ К АРЕНАМ
- 2.5.9.1. Восстановление аренов
- 2.5.9.2. Термическое циклоприсоединение к аренам
- 2.5.9.3. Фотоциклоприсоединение к моноциклическим аренам [126]
- 2.5.9.4. Фотохимические реакции полициклических аренов
- 2.6.10. ФОТОИЗОМЕРИЗАЦИЯ АРЕНОВ [126б]
- 2.5.11. ОКИСЛЕНИЕ АРЕНОВ [153]
- 2.5.12. РЕАКЦИИ АРЕНОВ С СИНГЛЕТНЫМ КИСЛОРОДОМ [162]
- 2.5.13. ПРИГОТОВЛЕНИЕ БИ- И ПОЛИАРИЛОВ
- 2.5.14. ВНУТРИМОЛЕКУЛЯРНАЯ ФОТОЦИКЛИЗАЦИЯ, ПРИВОДЯЩАЯ К ПОЛИЦИКЛИЧЕСКИМ АРЕНАМ
- 2.5.15. ВНУТРИМОЛЕКУЛЯРНАЯ ЦИКЛИЗАЦИЯ ДИЗАМЕЩЕННЫХ АРЕНОВ
- 2.5.16. ЦИКЛОФАНЫ
- 2.5.17. КОНФОРМАЦИЯ И ХИРАЛЬНОСТЬ АРЕНОВ
- 2.5.18. АЗУЛЕНЫ И НЕБЕНЗОИДНЫЕ АРЕНЫ
- 2.6. АННУЛЕНЫ И РОДСТВЕННЫЕ СИСТЕМЫ
- 2.6.2. МЕТОДЫ СИНТЕЗА
- 2.6.2.1. Окислительное сочетание терминальных ацетиленов (метод Зондхеймера)
- 2.6.2.2. Фотооблучение полициклических валентных таутомеров
- 2.6.2.3. Валентная таутомерия типа норкарадиен — циклогептатриен (метод Фогеля)
- 2.6.2.4. Прочие методы
- 2.6.3. СВОЙСТВА АННУЛЕНОВ
- 2.6.4. СВОЙСТВА 4n-АННУЛЕНОВ
- 2.6.5. ДЕГИДРОАННУЛЕНЫ
- 2.6.6. АННЕЛИРОВАННЫЕ АННУЛЕНЫ
- 2.6.7. АРОМАТИЧЕСКИЕ И АНТИАРОМАТИЧЕСКИЕ МОНОЦИКЛИЧЕСКИЕ ИОНЫ
- 2.6.8. АРОМАТИЧЕСКИЕ И АНТИАРОМАТИЧЕСКИЕ ПОЛИЦИКЛИЧЕСКИЕ ИОНЫ
- 2.6.9. ГОМОАРОМАТИЧЕСКИЕ СИСТЕМЫ
- 2.7. КАРБОКАТИОНЫ И КАРБАНИОНЫ
- 2.7.1.2. Краткий исторический очерк развития химии карбокатионов
- 2.7.1.3. Методы генерации карбокатионов
- 2.7.1.4. Типы карбокатионов
- 2.7.1.5. Изучение карбокатионов: методы и результаты
- 2.7.1.6. Реакции карбокатионов
- 2.7.2. КАРБАНИОНЫ
- 2.7.2.2. Методы генерации карбанионов
- 2.7.2.3. Типы карбанионов
- 2.7.2.4. Физические свойства карбанионов
- 2.7.5.2. Реакции карбанионов
- 2.8. РАДИКАЛЫ, КАРБЕНЫ, АРИНЫ
- 2.8.1. РАДИКАЛЫ
- 2.8.1.1. Структура, устойчивость и реакционная способность радикалов
- 2.8.1.2. Методы генерации и реакции радикалов
- 2.8.2. КАРБЕНЫ
- 2.8.2.1. Методы генерации карбенов и карбеноидов
- 2.8.2.2. Реакции карбенов
- 2.8.3. АРИНЫ
- 2.8.3.1. Структура и спектры аринов
- 2.8.3.2. Методы генерации аринов
- 2.8.3.3. Реакции аринов
- ЧАСТЬ 3. ГАЛОГЕНСОДЕРЖАЩИЕ СОЕДИНЕНИЯ
- 3.2. МЕТОДЫ ГАЛОГЕНИРОВАНИЯ
- 3.2.1. Гомолитическое замещение водорода
- 3.2.1.2. Использование галогенпроизводных в качестве реагентов
- 3.2.2. Гомолитическое замещение функциональных групп
- 3.2.3. Гомолитическое присоединение к ненасыщенным системам
- 3.2.3.1. Присоединение галогеноводородов
- 3.2.3.2. Присоединение галогенов
- 3.2.4. Электрофильное галогенирование
- 3.2.4.1. Замещение у насыщенной связи С-Н
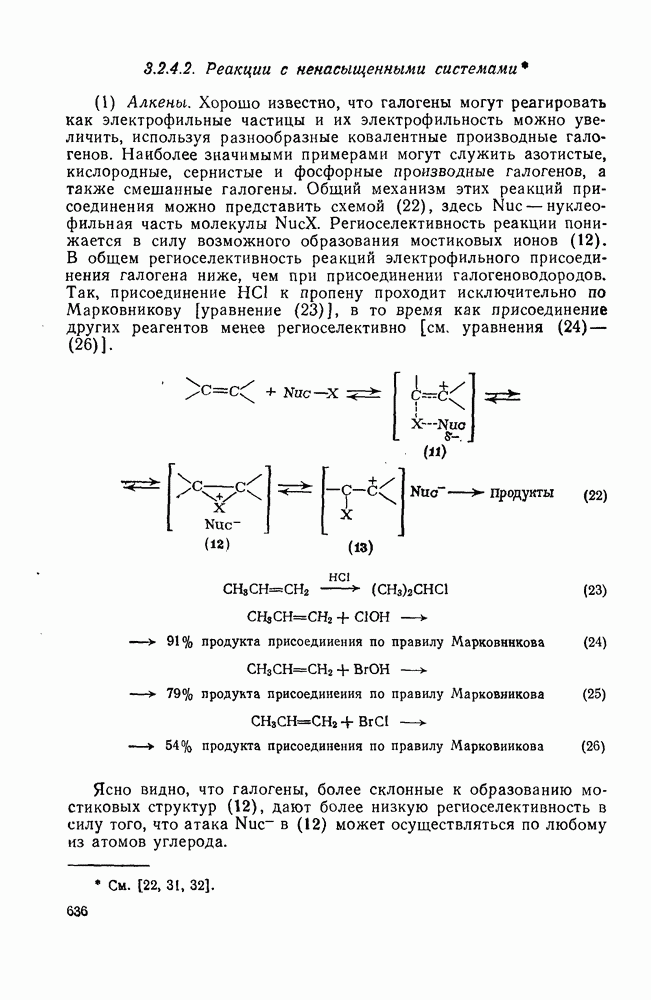
- 3.2.4.2. Реакции с ненасыщенными системами
- 3.2.4.3. Реакции с карбанионами
- 3.2.5. Нуклеофильное галогенирование
- 3.2.5.1. Галогенирование с замещением функциональной группы
- 3.2.5.2. Галогенирование в ароматических системах
- 3.2.5.3. Галогенирование путем обмена галогенов
- 3.2.6. Синтез полигалогенированных соединений
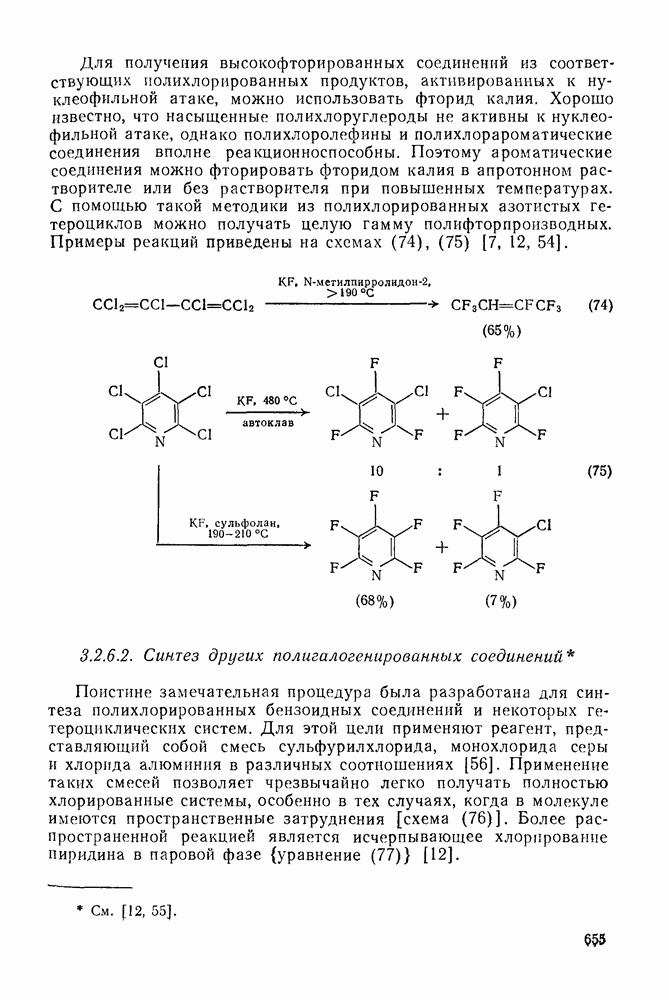
- 3.2.6.1. Синтез полифторированных соединений
- 3.2.6.2. Синтез других полигалогенированных соединений
- 3.3. ГАЛОГЕНАЛКАНЫ
- 3.3.1. Характеристика связей углерод-галоген
- 3.3.2. Промышленное применение
- 3.3.3. Нуклеофильное замещение галогена
- 3.3.3.1. Реакции SN2 и родственные процессы
- 3.3.3.2. Соучастие соседних групп
- 3.3.3.3. Реакции SN1 и относительно долгоживущие карбениевые ионы
- 3.3.3.4. Галогенониевые ионы
- 3.3.3.5. Галогенсодержащие карбениевые ионы
- 3.3.3.6. Механизм замещения с переносом электрона
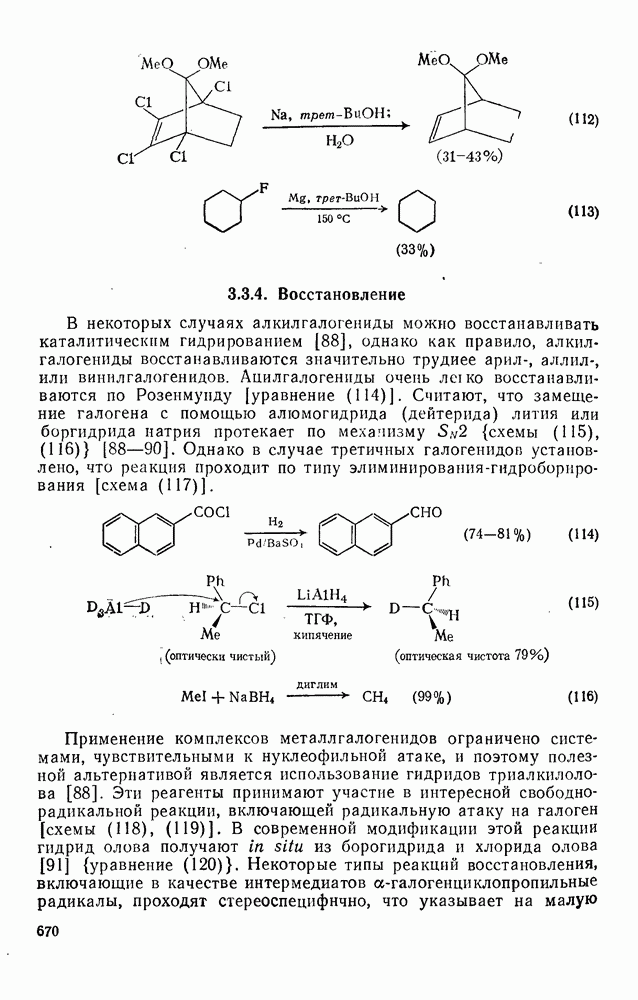
- 3.3.4. Восстановление
- 3.3.5. Замещение на металлы
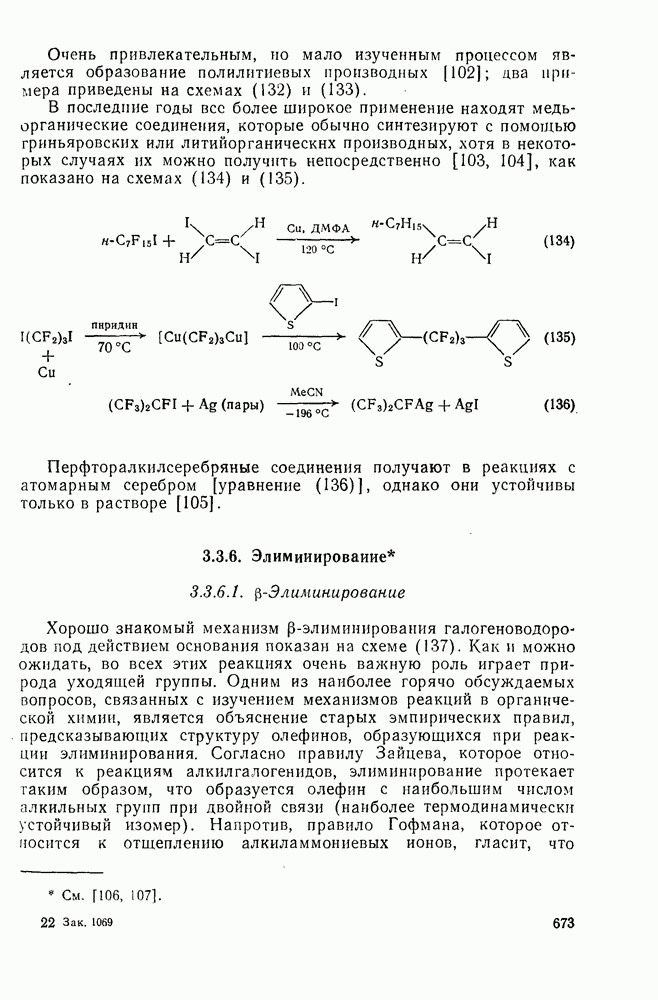
- 3.3.6. Элиминирование
- 3.3.6.1. b-Элиминирование
- 3.3.6.2. Галогенкарбанионы
- 3.3.6.3. Элиминирование через карбанионы
- 3.3.6.4. b-Элиминирование из металлорганических соединений
- 3.3.6.5. a-Элиминирование (генерирование карбенов)
- 3.4. ГАЛОГЕНАЛКЕНЫ
- 3.4.1. Синтез галогеналкенов
- 3.4.2. Нуклеофильная атака
- 3.4.2.1. Реакции, индуцируемые фторид-ионом
- 3.4.2.2. Другие реакции замещения
- 3.4.3. Радикальное присоединение
- 3.4.4. Электрофильное присоединение
- 3.4.5. Циклоприсоединение
- 3.4.5.1. [2+2]-Циклоприсоединение
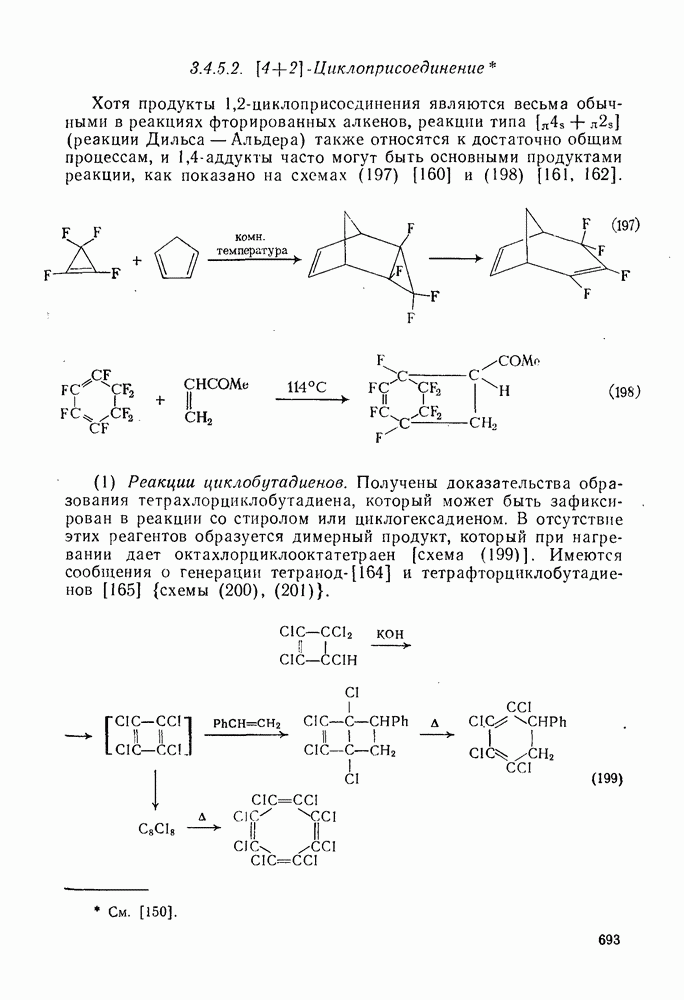
- 3.4.5.2. [4+2]-Циклоприсоединение
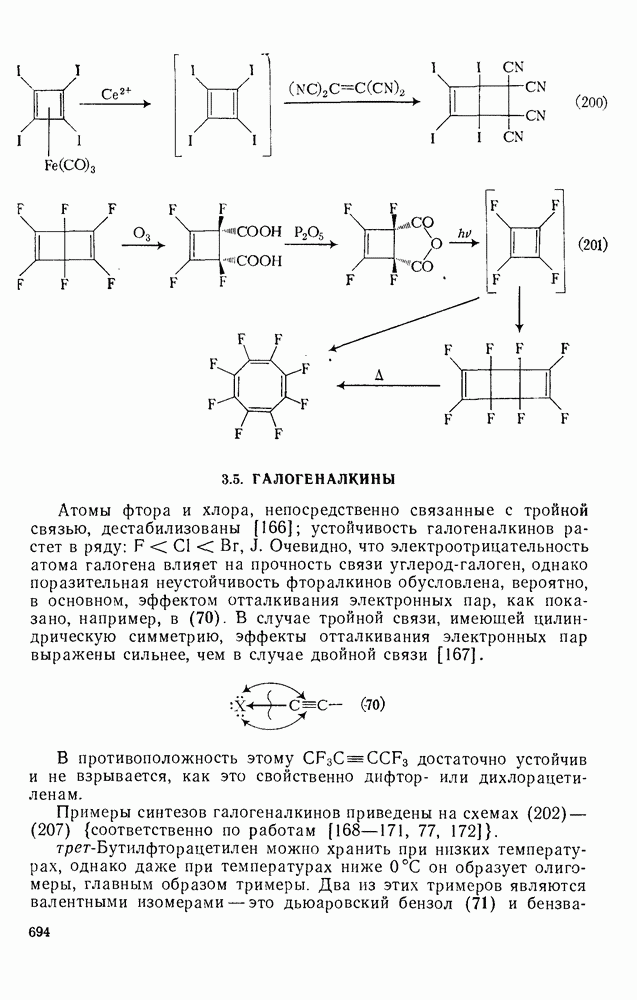
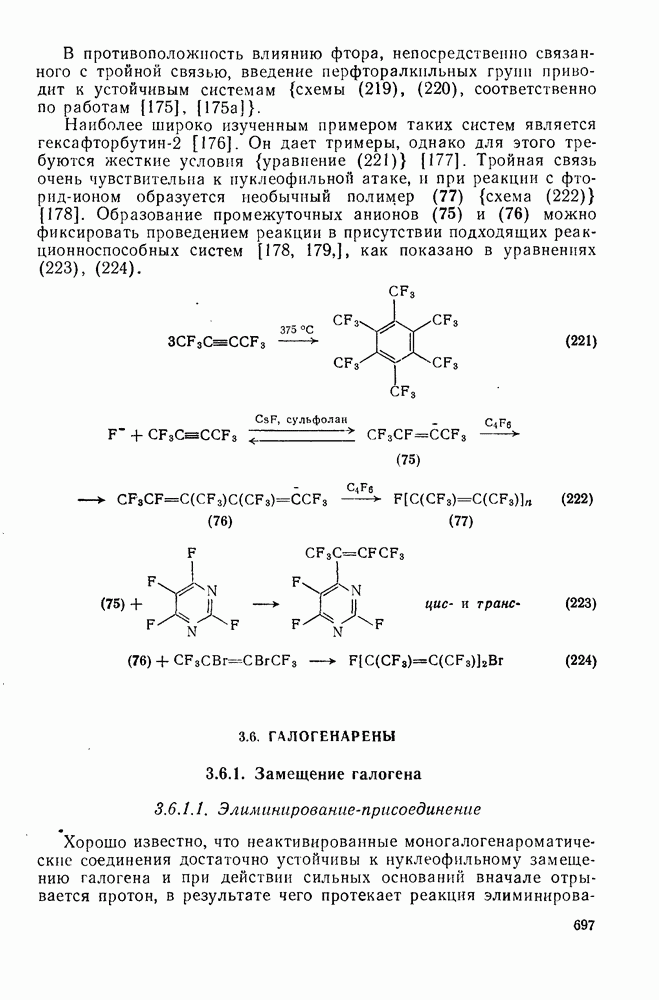
- 3.5. ГАЛОГЕНАЛКИНЫ
- 3.6. ГАЛОГЕНАРЕНЫ
- 3.6.1. Замещение галогена
- 3.6.1.2. Присоединение-элиминирование
- 3.6.1.3. Нуклеофильная атака на галоген
- 3.6.1.4. Перенос электрона
- 3.6.2. Перегруппировки
- 3.6.2.1. Перегруппировки под действием кислот Льюиса
- 3.6.2.2. Образование валентных изомеров