| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.1.2. СИММЕТРИЯ И ХИРАЛЬНОСТЬ
Свойства симметрии геометрических фигур характеризуются операциями симметрии, которыми в свою очередь определяются элементы симметрии (см. табл. 1.1), присутствующие в рассматриваемой модели [6, 20—24]. Если допустить [20—28], по крайней мере на сегодня, что молекулы образуют геометрические фигуры, то можно рассматривать их молекуляное строение с точки зрения их симметрии. Вначале полезно ограничить это рассмотрение молекулами, которые вследствие своей жесткости имеют строго определенную структуру, и такими гибкими молекулами, у которых структура однозначно определяется вследствие явной предпочтительности одной из конформаций. В основном, у молекул имеются два вида элементов симметрии: 1) оси вращения и 2) зеркально-поворотные оси, которые можно обнаружить при рассмотрении операций симметрии. Молекула, структура которой совмещается с ее исходным изображением в результате поворота вокруг некоторой оси на угол, равный  рад, обладает так называемой осью
рад, обладает так называемой осью  (символы элементов симметрии обычно даются курсивом). Например, молекула дихлорметана (1) содержит ось
(символы элементов симметрии обычно даются курсивом). Например, молекула дихлорметана (1) содержит ось  , а молекула хлороформа (2) — ось
, а молекула хлороформа (2) — ось  :
:

Разумеется, все молекулы содержат бесчисленное множество тривиальных осей  совокупность которых обычно рассматривается как элемент тождественного преобразования Е. Молекула, структура которой неотличима от исходной только после поворота на угол
совокупность которых обычно рассматривается как элемент тождественного преобразования Е. Молекула, структура которой неотличима от исходной только после поворота на угол  рад и последующего отражения в плоскости, перпендикулярной выбранной оси вращения, обладает так называемыми осями
рад и последующего отражения в плоскости, перпендикулярной выбранной оси вращения, обладает так называемыми осями  . При n=1 тривиальная ось
. При n=1 тривиальная ось  соответствует плоскости симметрии (а), перпендикулярной оси вращения. Плоскость о удобнее определить как зеркальную плоскость, которая делит молекулу пополам таким образом, что лиганды, находящиеся по одну сторону плоскости, точно «отражаются» по другую ее сторону. Например, дихлорметан (1) обладает двумя, а хлороформ (2) — тремя
соответствует плоскости симметрии (а), перпендикулярной оси вращения. Плоскость о удобнее определить как зеркальную плоскость, которая делит молекулу пополам таким образом, что лиганды, находящиеся по одну сторону плоскости, точно «отражаются» по другую ее сторону. Например, дихлорметан (1) обладает двумя, а хлороформ (2) — тремя  -плоскостями. При n=2 ось
-плоскостями. При n=2 ось  соответствует центру инверсии (i). Наличие последнего означает, что все лиганды в молекуле способны к обращению относительно центра, т. е. что любые два лиганда, находящиеся на прямой, проходящей через центр молекулы, отстоят от него на равное расстояние.
соответствует центру инверсии (i). Наличие последнего означает, что все лиганды в молекуле способны к обращению относительно центра, т. е. что любые два лиганда, находящиеся на прямой, проходящей через центр молекулы, отстоят от него на равное расстояние.
Таблица 1.1. Элементы симметрии и операции симметрии

У молекулы  одна из конформаций (3) имеет центр симметрии. Оси высшего порядка
одна из конформаций (3) имеет центр симметрии. Оси высшего порядка  (n — четное число) хотя и редко, но все же встречаются, например, в спиросоединениях типа (4).
(n — четное число) хотя и редко, но все же встречаются, например, в спиросоединениях типа (4).

Молекулы, которые содержат элементы симметрии вида  , например плоскость
, например плоскость  или центр
или центр  симметрии или же оси высшего порядка
симметрии или же оси высшего порядка  (n=4,6 и т. д.), обладают симметрией отражения и называются недиссимметричными или ахиральными [6, 7, 25—30]. Такие молекулы лишены хиральности и поэтому не могут образовать энантиомерных пар и, следовательно, не проявляют никаких хирооптических свойств, связанных с явлением энантиомерии. В отличие от них, молекулы, не обладающие симметрией отражения, называют диссиметричными или хиральными [6, 7, 25—30]. Эти молекулы не совпадают со своим зеркальным изображением и поэтому существуют в виде пары энантиомеров.
(n=4,6 и т. д.), обладают симметрией отражения и называются недиссимметричными или ахиральными [6, 7, 25—30]. Такие молекулы лишены хиральности и поэтому не могут образовать энантиомерных пар и, следовательно, не проявляют никаких хирооптических свойств, связанных с явлением энантиомерии. В отличие от них, молекулы, не обладающие симметрией отражения, называют диссиметричными или хиральными [6, 7, 25—30]. Эти молекулы не совпадают со своим зеркальным изображением и поэтому существуют в виде пары энантиомеров.
Они должны, по крайней мере в принципе, проявлять оптическую активность. Однако следует подчеркнуть, что у хиральных молекул хирооптические свойства иногда не обнаруживаются экспериментально [2, 25, 30], и понятие энантиомерии не основано на данных опыта. Оно относится к числу геометрических понятий и определяется в категориях молекулярной симметрии. Поэтому термин «энантиомерия» всегда предпочтительнее термина «оптическая изомерия», который применять не рекомендуется [30]. Следует отметить, что хиральные молекулы могут быть симметричны благодаря наличию осей  . Например, в определенных конформациях молекулы (
. Например, в определенных конформациях молекулы ( -винной кислоты (5) и (-)-маннита
-винной кислоты (5) и (-)-маннита

(6) обладают осью  . Если же молекулы не имеют иных элементов симметрии кроме тождественного преобразования, как, например, (+)-а-пинен (7) или (-)-холестерин (8), то их называют асимметричными. Таким образом, все асимметричные молекулы хиральны, но не все хиральные молекулы асимметричны. Поэтому термин «асимметрический центр» теперь заменяют [7, 29, 30, 32] термином «хиральный центр» или, точнее, «центр хиральности». Слово «хиральность» происходит от греческого слова cheir (рука) и было впервые употреблено в 1884 г. физиком Кельвином для описания геометрических фигур или любой группы точек, которые соотносятся между собой как правая и левая рука; это свойство он назвал хиральностью [33].
. Если же молекулы не имеют иных элементов симметрии кроме тождественного преобразования, как, например, (+)-а-пинен (7) или (-)-холестерин (8), то их называют асимметричными. Таким образом, все асимметричные молекулы хиральны, но не все хиральные молекулы асимметричны. Поэтому термин «асимметрический центр» теперь заменяют [7, 29, 30, 32] термином «хиральный центр» или, точнее, «центр хиральности». Слово «хиральность» происходит от греческого слова cheir (рука) и было впервые употреблено в 1884 г. физиком Кельвином для описания геометрических фигур или любой группы точек, которые соотносятся между собой как правая и левая рука; это свойство он назвал хиральностью [33].
Таблица 12. Важнейшие точечные группы симметрии

Хотя значение этого слова в химическом контексте обсуждалось еще в 50-е годы Уайтом [34], прошло немало времени пока термин «хиральность» был окончательно введен в химическую литературу Каном, Ингольдом и Прелогом [29] по предложению Мислоу (1966).
Геометрические фигуры, а следовательно и молекулы, могут быть отнесены к различным точечным группам симметрии в зависимости от сочетания имеющихся у них элементов симметрии [6, 20—24]. Поскольку такая классификация молекул оказалась полезной не только в разделе стереохимии, но и в других разделах органической химии, рассмотрим теперь так называемую систему Шенфлиса, приведенную в табл. 1.2, где указаны важнейшие точечные группы симметрии, характерные для органических молекул (кристаллографы обычно пользуются альтернативной системой обозначений Германа — Могена). Следует отметить, что выделенные более жирным шрифтом символы, употребляемые для обозначения точечных групп симметрии, обычно производятся от основного элемента симметрии, а цифровые и буквенные курсивные подстрочечные индексы помогают идентифицировать остальные элементы симметрии. Асимметричные молекулы, например а-пинен (7) и холестерин (8), не имеющие иных элементов симметрии кроме элемента тождественного преобразования Е, относятся к точечной группе  . Молекулы, не обладающие симметрией отражения и имеющие ось
. Молекулы, не обладающие симметрией отражения и имеющие ось  , относятся к точечным группам
, относятся к точечным группам  . Наиболее обычной точечной группой этого семейства является группа
. Наиболее обычной точечной группой этого семейства является группа  , к которой относятся винная кислота (5) и маннит (6). Молекулы, относящиеся к точечной группе
, к которой относятся винная кислота (5) и маннит (6). Молекулы, относящиеся к точечной группе  более высокого порядка
более высокого порядка  встречаются редко. Примерами таких молекул являются три-о-тимотид (9) с симметрией
встречаются редко. Примерами таких молекул являются три-о-тимотид (9) с симметрией  и циклогексаамилоза (10) с симметрией
и циклогексаамилоза (10) с симметрией  [36]:
[36]:

В отдельных случаях хиральные молекулы имеют не одну, а несколько осей  . В таких случаях говорят, что молекулы имеют диэдрическую симметрию и относятся к точечной группе
. В таких случаях говорят, что молекулы имеют диэдрическую симметрию и относятся к точечной группе  . Они имеют главную ось
. Они имеют главную ось  и n осей
и n осей  перпендикулярных к главной. К точечной группе
перпендикулярных к главной. К точечной группе  относится, например, твистан (11), а к редко встречаемой точечной группе
относится, например, твистан (11), а к редко встречаемой точечной группе  (12). Молекулы, имеющие точечную группу симметрии
(12). Молекулы, имеющие точечную группу симметрии 

(включая  ) или
) или  , хиральны. Действительно, подавляющее большинство хиральных молекул относится к этим точечным группам симметрии. Молекулы, обладающие симметрией отражения, могут быть отнесены к большому числу точечных групп симметрии. В простейших случаях они имеют либо плоскость
, хиральны. Действительно, подавляющее большинство хиральных молекул относится к этим точечным группам симметрии. Молекулы, обладающие симметрией отражения, могут быть отнесены к большому числу точечных групп симметрии. В простейших случаях они имеют либо плоскость  (иначе говоря, ось
(иначе говоря, ось  ) и тогда относятся к группе
) и тогда относятся к группе  , либо центр симметрии i (иначе говоря, ось
, либо центр симметрии i (иначе говоря, ось  ), и тогда принадлежат к группе
), и тогда принадлежат к группе  . Например, этанол (13) имеет симметрию
. Например, этанол (13) имеет симметрию  , а дифтордихлорцик-лобутан (14) — симметрию
, а дифтордихлорцик-лобутан (14) — симметрию  . В общем случае, молекулы, имеющие ось
. В общем случае, молекулы, имеющие ось  в дополнение к колинеарпым осям
в дополнение к колинеарпым осям  , относятся к точечным группам семейства
, относятся к точечным группам семейства  . Так, например, спиросоединение (4) имеет симметрию
. Так, например, спиросоединение (4) имеет симметрию  . Молекулы, у которых имеется n
. Молекулы, у которых имеется n  -плоскостей, делящих пополам ось
-плоскостей, делящих пополам ось  , относятся к точечным группам
, относятся к точечным группам  . Так, дихлорметан (1) имеет симметрию
. Так, дихлорметан (1) имеет симметрию  , а хлороформ (2) - симметрию
, а хлороформ (2) - симметрию  . Линейные молекулы с цилиндрической симметрией, подобные хлорацетилену (15), относятся к точечной группе
. Линейные молекулы с цилиндрической симметрией, подобные хлорацетилену (15), относятся к точечной группе  .
.
Молекулы, у которых  -плоскость перпендикулярна к оси
-плоскость перпендикулярна к оси  , принадлежат к точечным группам
, принадлежат к точечным группам  : например,
: например,

транс-бутен-2(16) имеет симметрию  . Молекулы, обладающие симметрией отражения, могут также иметь и диэдрическую симметрию. Если
. Молекулы, обладающие симметрией отражения, могут также иметь и диэдрическую симметрию. Если  -плоскость перпендикулярна к главной оси
-плоскость перпендикулярна к главной оси  , то молекула относится к точечной группе
, то молекула относится к точечной группе  ; так, этилен (17) имеет симметрию
; так, этилен (17) имеет симметрию  , циклопропан (18) — симметрию
, циклопропан (18) — симметрию  , а бензол (19) — симметрию
, а бензол (19) — симметрию  . Линейные молекулы с цилиндрической симметрией, например ацетилен (20), относятся к точечной группе
. Линейные молекулы с цилиндрической симметрией, например ацетилен (20), относятся к точечной группе  . В тех случаях, когда
. В тех случаях, когда  -плоскости пересекаются по главной оси
-плоскости пересекаются по главной оси  и делят пополам n осей
и делят пополам n осей  , молекула относится к семейству точечные групп
, молекула относится к семейству точечные групп  , например аллен (21) имеет симметрию
, например аллен (21) имеет симметрию  , циклогексан в конформации кресла (22) имеет симметрию
, циклогексан в конформации кресла (22) имеет симметрию  . Представителями высокосимметричных точечных групп
. Представителями высокосимметричных точечных групп  и
и  являются соответственно метан (23) и кубан (24):
являются соответственно метан (23) и кубан (24):

До сих пор в наших рассуждениях мы отождествляли молекулы с моделями, основанными на геометрических фигурах. Более подробный анализ показывает, однако, что описание реальных молекул с помощью абстрактных моделей не вполне корректно.
Исчерпывающее и весьма полезное рассмотрение возникающих здесь проблем читатель найдет в «Эпистемологических заметках о хиральности» Мнслоу и Бикарта [25]. Мы же ограничимся кратким обобщением их оценки этих проблем и повторением их выводов. Рассмотрим сначала поведение некоторого объема одноатомного газа при комнатной температуре. Хотя все доступные измерению макроскопические свойства образца показывают, что он является ахиральным, атомы в соединении в любой момент времени распределяются хирально, однако статистическое усреднение результатов измерения по шкале времени приводит к исключению эффекта хиральности. Поэтому говорят, что такая система обладает стохастической ахиральностью, т. е. что для случая распределения по объему молекул граница между хиральностью и ахиральностью нечетко выражена. Аналогичным образом определение точечных групп симметрии для молекул часто относится к идеализированной ситуации, которая, вероятно, никогда не может быть достигнута иначе как путем усреднения. Например выше было сказано, что пропеллерная форма три-о-тимотида (9) имеет симметрию  . На самом же деле в кристаллах этого вещества отклонение от симметрии
. На самом же деле в кристаллах этого вещества отклонение от симметрии  достаточно заметно [38]. Как и можно было ожидать на основании статистики, а следовательно, на основании оценки энтропийного фактора, неравносторонняя асимметрическая конформация
достаточно заметно [38]. Как и можно было ожидать на основании статистики, а следовательно, на основании оценки энтропийного фактора, неравносторонняя асимметрическая конформация  является термодинамически предпочтительной. Тот факт, что в низкотемпературном спектре протонного магнитного резонанса (
является термодинамически предпочтительной. Тот факт, что в низкотемпературном спектре протонного магнитного резонанса ( ) три-о-тимотида в растворе эта симметрия не проявляется [35], несомненно, является результатом процесса усреднения, присущего данному методу наблюдения. Можно сказать [39], что молекулы одного класса хиральности, например три-о-тимотид в конформации пропеллера (9), являются гомохиральными в том же смысле, в каком мы говорим, что у всех людей правые руки похожи, но не идентичны. По тому же принципу молекулы, родственные между собой в отношении энантиомерии и проявляющие ряд признаков хиральности, называют гетерохиральными. Другим примером стохастической ахиральности является процесс инверсии цикла, при котором устанавливается равновесие между двумя энантиомерными кресловидными конформациями (25а) и (25а)
) три-о-тимотида в растворе эта симметрия не проявляется [35], несомненно, является результатом процесса усреднения, присущего данному методу наблюдения. Можно сказать [39], что молекулы одного класса хиральности, например три-о-тимотид в конформации пропеллера (9), являются гомохиральными в том же смысле, в каком мы говорим, что у всех людей правые руки похожи, но не идентичны. По тому же принципу молекулы, родственные между собой в отношении энантиомерии и проявляющие ряд признаков хиральности, называют гетерохиральными. Другим примером стохастической ахиральности является процесс инверсии цикла, при котором устанавливается равновесие между двумя энантиомерными кресловидными конформациями (25а) и (25а)  -дизамещенных циклогексанов. Маловероятно, что смесь энантиомеров когда-либо бывает эквимольной. Тем не менее, процессы усреднения по шкале времени измерения приводят к тому, что система представляется ахираль-ной. Более того, динамическая спектроскопия ЯМР показывает, что хотя молекулы многих 1,2-дизамещенных циклогексанов при низких температурах проявляют симметрию
-дизамещенных циклогексанов. Маловероятно, что смесь энантиомеров когда-либо бывает эквимольной. Тем не менее, процессы усреднения по шкале времени измерения приводят к тому, что система представляется ахираль-ной. Более того, динамическая спектроскопия ЯМР показывает, что хотя молекулы многих 1,2-дизамещенных циклогексанов при низких температурах проявляют симметрию  , при комнатной температуре они ведут себя так,
, при комнатной температуре они ведут себя так,  если бы обладали симметрией
если бы обладали симметрией  (256), т. е. являются ахиральными.
(256), т. е. являются ахиральными.

Это положение можно экстраполировать и на случай циклогексана, который часто проявляет такие свойства, как если бы он имел симметрию  , а не присущую его кресловидной конформации (22) симметрию
, а не присущую его кресловидной конформации (22) симметрию  [40].
[40].
Отсутствие хиральности может иметь причиной не только стохастическую ахиральность. Если хиральность снижается ниже предела чувствительности всех доступных методов наблюдения, как, например, в случае дейтерированных алканов типа  по мере увеличения n, то имеет место ситуация, обозначаемая термином «криптохиральность». Этот случай встречается в химии триглицеридов (26), которые безусловно хиральны, но не проявляют хирооптических свойств.
по мере увеличения n, то имеет место ситуация, обозначаемая термином «криптохиральность». Этот случай встречается в химии триглицеридов (26), которые безусловно хиральны, но не проявляют хирооптических свойств.

Таким образом, говорить о степени хиральности не только допустимо, но и разумно. Как часто случается в химии, ситуация, для описания которой появилась на свет новая концепция — в данном случае хиральность, не отличается четкостью. В антиномии «хиральность ?— ахиральность» есть место для оттенков. Если макроскопические свойства вещества свидетельствуют о хиральности, то мы можем считать, что этот образец, т. е. ансамбль молекул, хирален. Однако отсутствие видимых признаков хиральности еще не позволяет считать вещество ахиральным.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ К ТОМУ 1 АНГЛИЙСКОГО ИЗДАНИЯ
- ЧАСТЬ I. НОМЕНКЛАТУРА И СТЕРЕОХИМИЯ
- 1.1. ВВЕДЕНИЕ И СТЕРЕОХИМИЯ
- 1.1.2. СИММЕТРИЯ И ХИРАЛЬНОСТЬ
- 1.1.3. ХИМИЧЕСКАЯ ТОПОЛОГИЯ
- 1.1.4. ИЗОМЕРИЯ
- 1.1.4.2. Строение
- 1.1.4.3. Абсолютная конфигурация
- 1.1.4.4. Относительная конфигурация
- 1.1.4.5. Конформация
- 1.1.4.6. Концепция изомерии
- 1.1.5. ТОПИЗМ
- 1.1.5.2. Прохиральность
- 1.1.5.3. Псевдоасимметрия (псевдохиральность)
- 1.1.6. ТОПОМЕРИЯ
- 1.1.7. ДИНАМИЧЕСКАЯ СТЕРЕОХИМИЯ. КРАТКИЕ СВЕДЕНИЯ
- ЧАСТЬ 2. УГЛЕВОДОРОДЫ
- 2.1. НАСЫЩЕННЫЕ УГЛЕВОДОРОДЫ
- 2.1.2. Строение и номенклатура
- 2.1.2.1. Номенклатура IUPAC
- 2.1.2.2. Алициклические алканы
- 2.1.2.3. Полициклоалканы
- 2.1.3. ИСТОЧНИКИ ПОЛУЧЕНИЯ НАСЫЩЕННЫХ УГЛЕВОДОРОДОВ
- 2.1.4. ФИЗИЧЕСКИЕ СВОЙСТВА
- 2.1.4.1. Ациклические алканы
- 2.1.4.2. Моно- и полициклоалканы
- 2.1.5. СТЕРЕОХИМИЯ И КОНФОРМАЦИОННЫЙ АНАЛИЗ
- 2.1.5.1. Углы и длины связей
- 2.1.5.2. Алкил- и полиалкилциклогексаны
- 2.1.5.3. Конформация карбоциклических колец, больших, чем циклогексан
- 2.1.6. ТЕРМОХИМИЧЕСКИЕ СВОЙСТВА
- 2.1.6.1. Горение. Алканы и циклоалканы как топливо
- 2.1.6.2. Определение теплот сгорания и термохимические свойства
- 2.1.6.3. Эмпирические методы оценки теплот образования алканов
- 2.1.6.4. Оценка теплот образования алканов на основе энергии связей
- 2.1.6.5. Оценка теплот образования алканов на основе инкрементов групп
- 2.1.6.6. Оценка теплот образования циклических, полициклических и мостиковых алканов на основе инкрементов «скошенных разобщенных» групп и «единственных» наиболее устойчивых конформаций
- 2.1.6.7. Молекулярно-механические расчеты теплот образования и энергии напряжения
- 2.1.6.8. Моно- и полициклоалкаиы
- 2.1.7. ПОЛУЧЕНИЕ АЦИКЛИЧЕСКИХ АЛКАНОВ
- 2.1.7.1. Получение алканов восстановлением олефинов
- 2.1.7.2. Получение алканов из альдегидов и кетонов
- 2.1.7.3. Получение алканов из спиртов и алкилгалогенидов
- 2.1.7.4. Получение алканов из карбоновых кислот
- 2.1.8. СИНТЕЗ МОНО- И ПОЛИЦИКЛОАЛКАНОВ
- 2.1.9. РЕАКЦИИ АЦИКЛИЧЕСКИХ АЛКАНОВ
- 2.1.9.1. Галогенирование
- 2.1.9.2. Нитрование
- 2.1.9.3. Окисление
- 2.1.9.4. Каталитическая изомеризация алканов
- 2.1.9.5. Каталитическое алкилирование алканов
- 2.1.9.6. Реакции крекинга алканов
- 2.1.9.7. Термический крекинг
- 2.1.9.8. Каталитический крекинг
- 2.1.9.9. Каталитический риформинг и дегидроциклизация алканов
- 2.1.10. РЕАКЦИИ ЦИКЛОАЛКАНОВ И ПОЛИЦИКЛОАЛКАНОВ
- 2.2. ОЛЕФИНОВЫЕ И АЦЕТИЛЕНОВЫЕ УГЛЕВОДОРОДЫ
- 2.2.2. ПОЛУЧЕНИЕ ОЛЕФИНОВ
- 2.2.2.1. Элиминирование в системах
- 2.2.2.2. Элиминирование из систем
- 2.2.2.3. Циклоэлиминирование
- 2.2.2.4. Частичное восстановление
- 2.2.2.5. Элиминирование сульфонилгидразонов
- 2.2.2.6. Реакция Виттига и родственные ей реакции
- 2.2.2.7. Различные реакции конденсации
- 2.2.2.8. Электроциклические реакции
- 2.2.2.9. Циклоолигомеризация
- 2.2.2.11. Реакции винильных производных
- 2.2.3. РЕАКЦИИ ОЛЕФИНОВ
- 2.2.3.1. Электрофильное присоединение
- 2.2.3.2. Нуклеофильное присоединение
- 2.2.3.3. Радикальное присоединение
- 2.2.3.4. Циклоприсоединение и родственные реакции
- 2.2.3.5. Окисление
- 2.2.3.6. Восстановление
- 2.2.3.7. Перегруппировки
- 2.2.3.8. Фотохимические реакции
- 2.2.3.9. Прочие реакции
- 2.3. ДИЕНЫ, ПОЛНЕНЫ И АЦЕТИЛЕНОВЫЕ УГЛЕВОДОРОДЫ
- 2.3.1. СОПРЯЖЕННЫЕ ДИЕНЫ И ПОЛНЕНЫ
- 2.3.1.2. Получение сопряженных диенов
- 2.3.2. РЕАКЦИИ СОПРЯЖЕННЫХ ДИЕНОВ
- 2.3.2.2. Восстановление
- 2.3.2.3. Гидроборирование
- 2.3.2.4. Реакция Дильса — Альдера
- 2.3.2.5. Комплексы с карбонилами железа
- 2.3.2.6. Фотохимические термические реакции
- 2.3.2.7. Прочие реакции
- 2.3.3. СОПРЯЖЕННЫЕ ПОЛИЕНЫ
- 2.3.4. ПРИРОДНЫЕ ДИЕНЫ И ПОЛНЕНЫ
- 2.3.5. АЛЛЕНЫ И КУМУЛЕНЫ
- 2.3.5.2. Получение алленов
- 2.3.6. РЕАКЦИИ АЛЛЕНОВ
- 2.3.6.2. Гидрирование
- 2.3.6.3. Реакции алленов в присутствии комплексов металлов
- 2.3.7. КУМУЛЕНЫ
- 2.3.8. ПРИРОДНЫЕ АЛЛЕНЫ И КУМУЛЕНЫ
- 2.3.9. АЦЕТИЛЕНЫ И ПОЛИАЦЕТИЛЕНЫ
- 2.3.9.2. Получение ацетиленов
- 2.3.10. РЕАКЦИИ АЦЕТИЛЕНОВ
- 2.3.10.2. Изомеризация
- 2.3.10.3. Пропаргильные перегруппировки
- 2.3.10.4. Реакции присоединения
- 2.3.10.5. Гидроборирование и гидроалюминирование
- 2.3.10.6. Реакции замещения
- 2.3.10.7. Восстановление
- 2.3.10.8. Окисление
- 2.3.10.9. Циклоприсоединение
- 2.3.10.10. Реакции катализуемые металлами
- 2.3.11. ПОЛИАЦЕТИЛЕНЫ
- 2.3.12. ПРИРОДНЫЕ АЦЕТИЛЕНЫ И ПОЛИАЦЕТИЛЕНЫ
- 2.3.13. СОПРЯЖЕННЫЕ ЕНИНЫ
- 2.3.13.1. Получение сопряженных енинов
- 2.3.14. РЕАКЦИИ СОПРЯЖЕННЫХ ЕНИНОВ
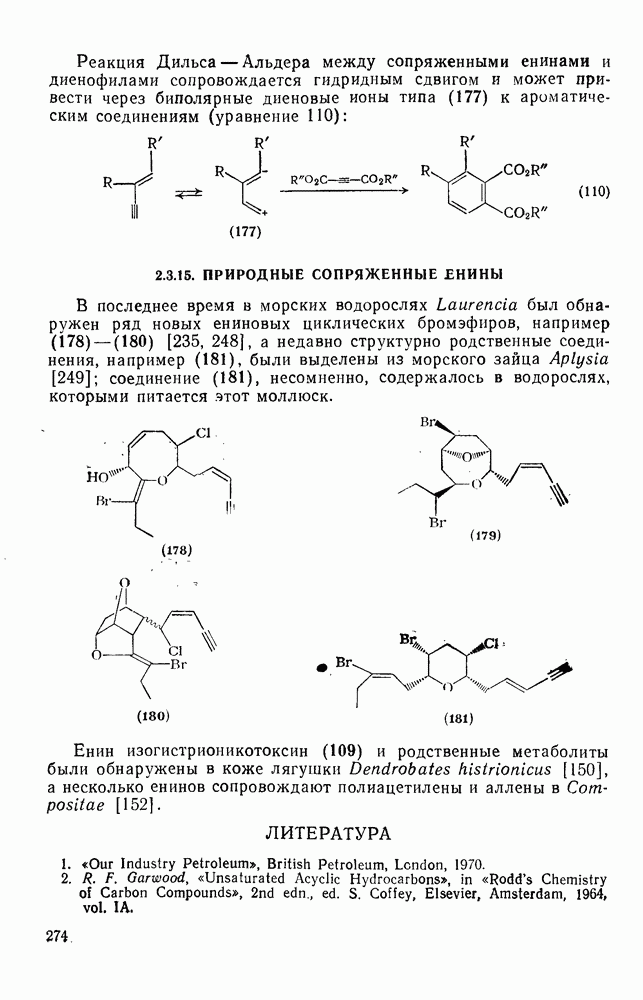
- 2.3.15. ПРИРОДНЫЕ СОПРЯЖЕННЫЕ ЕНИНЫ
- 2.4. АРОМАТИЧНОСТЬ
- 2.4.2. ЭЛЕКТРОННЫЕ ТЕОРИИ СТРОЕНИЯ БЕНЗОЛА
- 2.4.3. КРИТЕРИИ АРОМАТИЧНОСТИ
- 2.4.3.1. Термодинамические свойства
- 2.4.3.2. Структурные особенности
- 2.4.3.3. Магнитные свойства
- 2.4.3.4. Прочие критерии
- 2.4.4. АНТИАРОМАТИЧНОСТЬ
- 2.4.4.1. Термодинамические свойства
- 2.4.4.2. Структурные особенности
- 2.4.4.3. Магнитные свойства
- 2.4.4.4. Прочие свойства
- 2.4.5. ТЕОРЕТИЧЕСКИЕ ОПРЕДЕЛЕНИЯ АРОМАТИЧНОСТИ
- 2.4.5.1. Полуэмпирические расчеты и дьюаровская резонансная энергия
- 2.4.5.2. Расчеты по методу валентных пар и применение резонансного метода
- 2.4.5.3. Локализация связей
- 2.4.5.4. Связь энергетических критериев с критериями локализации связей
- 2.4.6. АРОМАТИЧЕСКИЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
- 2.5. АРЕНЫ И ИХ РЕАКЦИИ
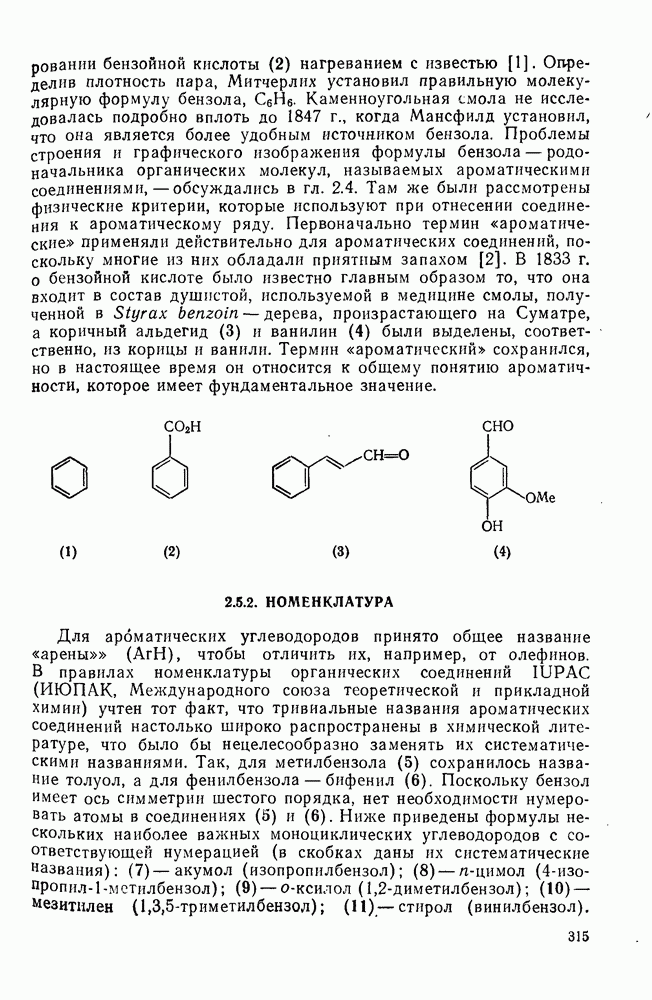
- 2.5.2. НОМЕНКЛАТУРА
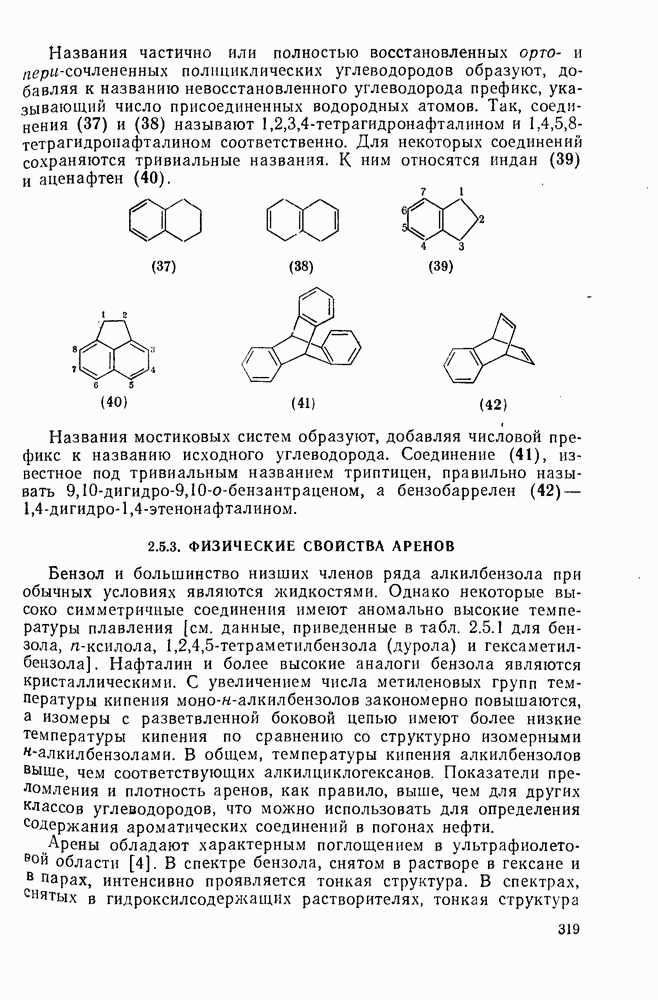
- 2.5.3. ФИЗИЧЕСКИЕ СВОЙСТВА АРЕНОВ
- 2.5.4. ПРОМЫШЛЕННОЕ ПРОИЗВОДСТВО АРЕНОВ
- 2.5.5. ЦИКЛОТРИМЕРИЗАЦИЯ АЦЕТИЛЕНОВ
- 2.5.6. РЕАКЦИИ ЭЛЕКТРОФИЛЬНОГО ПРИСОЕДИНЕНИЯ — ЭЛИМИНИРОВАНИЯ АРЕНОВ
- 2.5.6.1. Механизм ароматического нитрования [15]
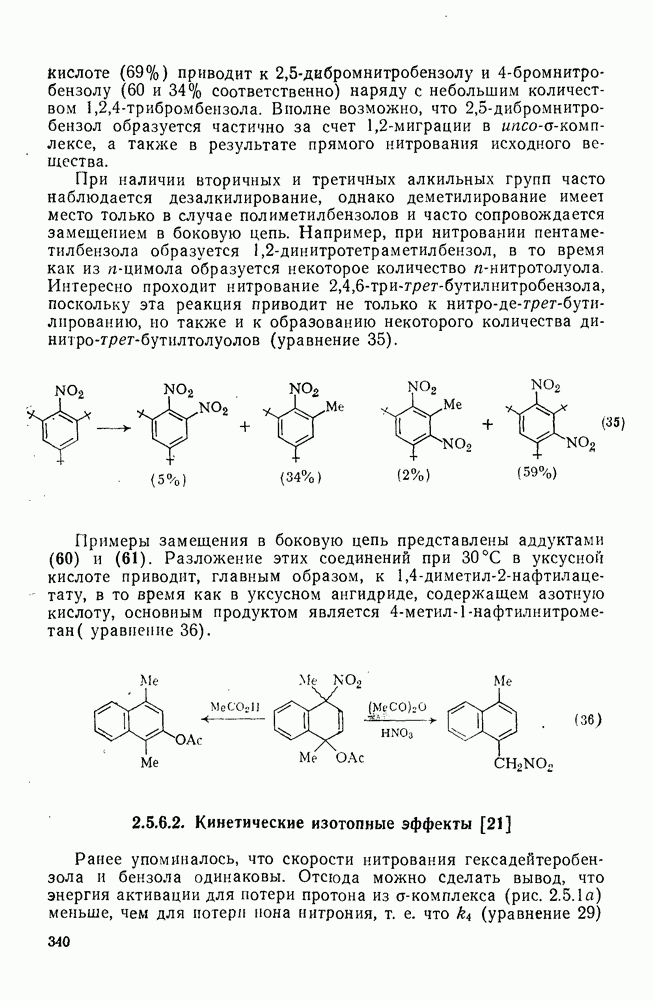
- 2.5.6.2. Кинетические изотопные эффекты [21]
- 2.5.6.3. Реакции, включающие ипсо-протонирование
- 2.5.6.4. Металлирование
- 2.5.6.5. Электрофилы IV группы
- 2.5.6.6. Электрофилы V группы
- 2.5.6.7. Электрофилы VI группы [18, 56]
- 2.5.6.8. Электрофилы VII группы [18, 25а, 56]
- 2.5.7. ОРИЕНТАЦИЯ В РЕАКЦИЯХ ЭЛЕКТРОФИЛЬНОГО ПРИСОЕДИНЕНИЯ — ЭЛИМИНИРОВАНИЯ
- 2.5.8. РАДИКАЛЬНОЕ ГАЛОГЕНИРОВАНИЕ АРЕНОВ В БОКОВУЮ ЦЕПЬ [96]
- 2.5.9. РЕАКЦИИ ПРИСОЕДИНЕНИЯ К АРЕНАМ
- 2.5.9.1. Восстановление аренов
- 2.5.9.2. Термическое циклоприсоединение к аренам
- 2.5.9.3. Фотоциклоприсоединение к моноциклическим аренам [126]
- 2.5.9.4. Фотохимические реакции полициклических аренов
- 2.6.10. ФОТОИЗОМЕРИЗАЦИЯ АРЕНОВ [126б]
- 2.5.11. ОКИСЛЕНИЕ АРЕНОВ [153]
- 2.5.12. РЕАКЦИИ АРЕНОВ С СИНГЛЕТНЫМ КИСЛОРОДОМ [162]
- 2.5.13. ПРИГОТОВЛЕНИЕ БИ- И ПОЛИАРИЛОВ
- 2.5.14. ВНУТРИМОЛЕКУЛЯРНАЯ ФОТОЦИКЛИЗАЦИЯ, ПРИВОДЯЩАЯ К ПОЛИЦИКЛИЧЕСКИМ АРЕНАМ
- 2.5.15. ВНУТРИМОЛЕКУЛЯРНАЯ ЦИКЛИЗАЦИЯ ДИЗАМЕЩЕННЫХ АРЕНОВ
- 2.5.16. ЦИКЛОФАНЫ
- 2.5.17. КОНФОРМАЦИЯ И ХИРАЛЬНОСТЬ АРЕНОВ
- 2.5.18. АЗУЛЕНЫ И НЕБЕНЗОИДНЫЕ АРЕНЫ
- 2.6. АННУЛЕНЫ И РОДСТВЕННЫЕ СИСТЕМЫ
- 2.6.2. МЕТОДЫ СИНТЕЗА
- 2.6.2.1. Окислительное сочетание терминальных ацетиленов (метод Зондхеймера)
- 2.6.2.2. Фотооблучение полициклических валентных таутомеров
- 2.6.2.3. Валентная таутомерия типа норкарадиен — циклогептатриен (метод Фогеля)
- 2.6.2.4. Прочие методы
- 2.6.3. СВОЙСТВА АННУЛЕНОВ
- 2.6.4. СВОЙСТВА 4n-АННУЛЕНОВ
- 2.6.5. ДЕГИДРОАННУЛЕНЫ
- 2.6.6. АННЕЛИРОВАННЫЕ АННУЛЕНЫ
- 2.6.7. АРОМАТИЧЕСКИЕ И АНТИАРОМАТИЧЕСКИЕ МОНОЦИКЛИЧЕСКИЕ ИОНЫ
- 2.6.8. АРОМАТИЧЕСКИЕ И АНТИАРОМАТИЧЕСКИЕ ПОЛИЦИКЛИЧЕСКИЕ ИОНЫ
- 2.6.9. ГОМОАРОМАТИЧЕСКИЕ СИСТЕМЫ
- 2.7. КАРБОКАТИОНЫ И КАРБАНИОНЫ
- 2.7.1.2. Краткий исторический очерк развития химии карбокатионов
- 2.7.1.3. Методы генерации карбокатионов
- 2.7.1.4. Типы карбокатионов
- 2.7.1.5. Изучение карбокатионов: методы и результаты
- 2.7.1.6. Реакции карбокатионов
- 2.7.2. КАРБАНИОНЫ
- 2.7.2.2. Методы генерации карбанионов
- 2.7.2.3. Типы карбанионов
- 2.7.2.4. Физические свойства карбанионов
- 2.7.5.2. Реакции карбанионов
- 2.8. РАДИКАЛЫ, КАРБЕНЫ, АРИНЫ
- 2.8.1. РАДИКАЛЫ
- 2.8.1.1. Структура, устойчивость и реакционная способность радикалов
- 2.8.1.2. Методы генерации и реакции радикалов
- 2.8.2. КАРБЕНЫ
- 2.8.2.1. Методы генерации карбенов и карбеноидов
- 2.8.2.2. Реакции карбенов
- 2.8.3. АРИНЫ
- 2.8.3.1. Структура и спектры аринов
- 2.8.3.2. Методы генерации аринов
- 2.8.3.3. Реакции аринов
- ЧАСТЬ 3. ГАЛОГЕНСОДЕРЖАЩИЕ СОЕДИНЕНИЯ
- 3.2. МЕТОДЫ ГАЛОГЕНИРОВАНИЯ
- 3.2.1. Гомолитическое замещение водорода
- 3.2.1.2. Использование галогенпроизводных в качестве реагентов
- 3.2.2. Гомолитическое замещение функциональных групп
- 3.2.3. Гомолитическое присоединение к ненасыщенным системам
- 3.2.3.1. Присоединение галогеноводородов
- 3.2.3.2. Присоединение галогенов
- 3.2.4. Электрофильное галогенирование
- 3.2.4.1. Замещение у насыщенной связи С-Н
- 3.2.4.2. Реакции с ненасыщенными системами
- 3.2.4.3. Реакции с карбанионами
- 3.2.5. Нуклеофильное галогенирование
- 3.2.5.1. Галогенирование с замещением функциональной группы
- 3.2.5.2. Галогенирование в ароматических системах
- 3.2.5.3. Галогенирование путем обмена галогенов
- 3.2.6. Синтез полигалогенированных соединений
- 3.2.6.1. Синтез полифторированных соединений
- 3.2.6.2. Синтез других полигалогенированных соединений
- 3.3. ГАЛОГЕНАЛКАНЫ
- 3.3.1. Характеристика связей углерод-галоген
- 3.3.2. Промышленное применение
- 3.3.3. Нуклеофильное замещение галогена
- 3.3.3.1. Реакции SN2 и родственные процессы
- 3.3.3.2. Соучастие соседних групп
- 3.3.3.3. Реакции SN1 и относительно долгоживущие карбениевые ионы
- 3.3.3.4. Галогенониевые ионы
- 3.3.3.5. Галогенсодержащие карбениевые ионы
- 3.3.3.6. Механизм замещения с переносом электрона
- 3.3.4. Восстановление
- 3.3.5. Замещение на металлы
- 3.3.6. Элиминирование
- 3.3.6.1. b-Элиминирование
- 3.3.6.2. Галогенкарбанионы
- 3.3.6.3. Элиминирование через карбанионы
- 3.3.6.4. b-Элиминирование из металлорганических соединений
- 3.3.6.5. a-Элиминирование (генерирование карбенов)
- 3.4. ГАЛОГЕНАЛКЕНЫ
- 3.4.1. Синтез галогеналкенов
- 3.4.2. Нуклеофильная атака
- 3.4.2.1. Реакции, индуцируемые фторид-ионом
- 3.4.2.2. Другие реакции замещения
- 3.4.3. Радикальное присоединение
- 3.4.4. Электрофильное присоединение
- 3.4.5. Циклоприсоединение
- 3.4.5.1. [2+2]-Циклоприсоединение
- 3.4.5.2. [4+2]-Циклоприсоединение
- 3.5. ГАЛОГЕНАЛКИНЫ
- 3.6. ГАЛОГЕНАРЕНЫ
- 3.6.1. Замещение галогена
- 3.6.1.2. Присоединение-элиминирование
- 3.6.1.3. Нуклеофильная атака на галоген
- 3.6.1.4. Перенос электрона
- 3.6.2. Перегруппировки
- 3.6.2.1. Перегруппировки под действием кислот Льюиса
- 3.6.2.2. Образование валентных изомеров